Index
Attributed-Based Encryption (ABE)

With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes. In this case, we can only generate the correct decryption key with the right attibutes.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
CP-Attributed Based Encryption
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
ASCON

ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
Light-weight cryptography (Benchark for NIST finalists)
- Finalixst benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON AEAD (Golang). ASCON AEAD (Golang). The outlines the usage of AEAD for ASCON using Golang.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
Light-weight crypto (Hash)
- ASCON. ASCON. ASCON is a light-weight hashing method.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
MAC and PRF
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
AWS

This page outlines some content related to the AWS Cloud Practioner certification. Some outline knowledge is [here].
Study guide
- Study Guide. Go. This provides a study guide for CLF-C01 - AWS Certified Cloud Practitioner.
Units
Units covered are:
- Unit 1: Cloud Concepts. Go. This provides an outline of cloud fundamentals.
- Unit 2: Cloud Economics and Billing. Go. This provides an outline to billing.
- Unit 3: Global Infrastructure. Go. This provides an outline of the AWS Infrastructure.
- Unit 4: Cloud Security. Go. This provides an outline of the AWS Cloud Security.
- Unit 5: AWS Networking. Go. This provides an outline of the AWS Networking.
- Unit 6: AWS Compute. Go. This provides an outline of the AWS Compute. Key areas include: EC2, Lambda, On-Demand Instances, Dedicated Hosts, Dedicated Instances, and Spot Instances.
- Unit 7: AWS Storage. Go. This provides an outline of the AWS Storage. It includes coverage of Key areas: EBS, EFS, S3, S3 Glacier, and Block/Object storage.
- Unit 8: Databases. Go. This provides an outline of the AWS Databases. Key areas of coverage include: RDS, DynamoDB, Aurora, Redshift and ElastiCache.
- Unit 9: Cloud Architecture. Go. This provides an outline of the AWS Cloud Architecture. This includes the Well-Engineering Framework and Trusted Advisor.
- Unit 10: Automatic Scaling and Monitoring. Go. This provides an outline of the AWS loading balancing and monitoring. This includes Load balancing, CloudWatch and Amazon SNS (Simple Notification Service).
- Final Test. Go. This provides a final test which covers all the previous units.
Additional Labs
- Additional Labs. Go. This provides additional labs.
Blake Hashing

For SHA-3, NIST published the new standard, based on Keccak, on 5 August 2015, and which beat off competition from BLAKE (Aumasson et al.), Grøstl (Knudsen et al), JH (Hongjun Wu), and Skein (Schneier et al.). After two rounds, the final round evaluated of security, performance and hardware space. For performance, BLAKE3 basically wipes the floor its previous version (BLAKE2b) [1], and which was already faster than SHA-3. It gives the equilavent of 128 bits of security. At its core is the Bao tree mode and the original BLAKE2 method, and it has been created by Jack O’Connor, Jean-Philippe Aumasson, Samuel Neves, and Zooko Wilcox-O’Hearn.
Blake 2 and 3 hashes
The following are the tips related to Blake 2 hashes:
- Hazmat Hashes. Hazmat Hashes. This includes the hashing methods in the Hazmat cryptography library. This includes Blake2p, Blake2s, MD5, SHA1, SHA224, SHA256, SGA384, SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHA512, SHA512-224, SHAKE128 and SHA256.
- Blake 3 in Python. Hashing. Blake 3 hashing.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
- Blake and Blake 2. Blake. Implements Blake and Blake 2 (SHA-3 contender).
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
- cSHAKE. cSHAKE. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS. With the SHA-3 hashing method, we have four different cryptographic hashing methods (SHA3-224, SHA3-256, SHA3-384, and SHA3-512) and two XOF functions (SHAKE128 and SHAKE256). With SHAKE128 and SHAKE256 we can integrate domain separation between different functions — and which are known as cSHAKE128 and cSHAKE256.
eXtendable-Output Function (XOF)
- eXtendable-Output Function (XOF) usign CIRCL. XOF. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS.
Message authentication codes (MACs)
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
Blockchain/Cryptocurrency

This page outlines some examples of blockchain and cryptocurrency.
Bitcoins
- Base58 (used in Bitcoins). Base58.
- Bitcoin keys. Bitcoin keys.
- Bitcoin signing. Bitcoin signing.
- Vanity Bitcoin Address Generation. Generating addresses.
- Split Vanity Bitcoin Address Generation Proof. Generating addresses proof.
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- BIP39 (Entropy to phase). BIP39. This generates for BIP39 for a entropy to phase.
- BIP39 (Phrase to entropy). BIP39. This generates for BIP39 for a phrase to entropy.
- Viewing Bitcoin blockchain with Python. Go.
- Schnorr multi-signatures. Go.
- BIP141 (SegWit). BIP141. This generates for BIP141 for SegWit.
- Bitcoin key generation using BX from libbitcoin. BX key generator. Bitcoin key generation using BX from libbitcoin.
- Bitcoin key generation . Bitcoin key generator. Bitcoin key generation using BX.
- Mnemonic BIP39 for different languages. Mnemonic BIP39. Mnemonic BIP39 for different languages.
Ethereum Test Network
- Math functions on Test Network. Go.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
Ethereum
- Creating Ethereum address with Python. Go.
- Creating Ethereum signing with Python. Go.
- ERC20 Tokens. Go.
- Ethereum address with Go. Addresses. This generates an Ethereum address.
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- PATRICIA trie. PATRICIA. Example of using PATRICIA (and which is used in Ethereum).
- Viewing Balance of account in Etheruem with Go. Balance. This views the balance of an account
- Viewing Block in Etheruem with Go. Block. This views a block.
- Viewing Cryptocurrency API with Python. Go.
- Viewing Ethereum blockchain with Python. Go.
- Viewing Transactions in Block in Etheruem with Go. Transactions. This views transactions.
Ethereum Blockchain
- IOTA Trytes. Trytes. `This outlines Trytes, as used in IOTA.
Ethereum Blockchain
- Blockchain: Adding Maths Functions. Go.
- Blockchain: Blocks, transactions and writing data. Go.
- Blockchain: Contracts and Addresses. Go.
- Blockchain: Getting transactions. Go.
- Blockchain: Hello World!. Go.
- Blockchain: Simple Purchasing System. Go.
- Blockchain: Viewing the blockchain. Go.
- Blockchain: Cracking Wallets. Go.
- Introduction to Blockchain. Go.
Barreto-Lynn-Scott (BLS) Curves

Barreto-Lynn-Scott (BLS) curves are pairing friendly. They can be used to implement Bilinear groups and which are a triplet of groups (\(G_1\), \(G_2\) and \(G_T\)), so that we can implement a function \(e()\) such that \(e({g_1}^x,{g_2}^y)={g_T}^{xy}\), and where \(g_x\) is the generator of the group. This is known as a pairing function. The main curves used are BLS12-381, BLS12-446, BLS12-455, BLS12-638 and BLS24-477. With BLS12-381 we have a Weierstrass curve with 381-bit field, and which takes the format of \(y^2=x^3+ax+b \mod p\).
Curves
- BLS12-381 points. BLS12-381. Find the \((x,y)\) point for a given \(x\) value..
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
Signatures
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. bls. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
Cracking
- MOV attack on elliptic curves with Kryptology (with BLS12-381). MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
ZKP and OT
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- ECC Accumulators. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
Hash to scalar and point
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
Background
The BLS12-381 curve is used in ZCash and has the form of \(y^2=x^3+ax+b \mod p\),. It has a prime number of:
p= 0x1a0111ea397fe69a4b1ba7b6434bacd764774b84f38512bf6730d2a0f6b0f6241eabfffeb153ffffb9feffffffffaaab
The \(a\) and \(b\) values are:
a 0x00
b 0x04
The base point is:
G= (0x17F1D3A73197D7942695638C4FA9AC0FC3688C4F9774B905A14E3A3F171BAC586C55E83FF97A1AEFFB3AF00ADB22C6BB, 0x08B3F481E3AAA0F1A09E30ED741D8AE4FCF5E095D5D00AF600DB18CB2C04B3EDD03CC744A2888AE40CAA232946C5E7E1)
BN (Barreto-Naehrig) Curve

Elliptic curves are used fairly extensively in public key encryption (such as in Bitcoin and Tor). A BN-curve (Barreto-Naehrig curve) [2] defines an elliptic curve which can be used for pairings that allow for a high security and efficiency level. This page uses pairings over a 256-bit BN curve and derives a signature for a message. The curve is defined by \(y^2 = x^3 + a.x + b \pmod p\).
They can be used to implement Bilinear groups and which are a triplet of groups (\(G_1\), \(G_2\) and \(G_T\)), so that we can implement a function \(e()\) such that \(e({g_1}^x,{g_2}^y)=g_T^{xy}\), and where \(g_x\) is the generator of the group. This is known as a pairing function.
BN Curve Applications (BN254)
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption (BN254)
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures (BN254)
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
BN256 Signatures
- BN256 Signatures. BNS. Implementation of BNS-256 for signatures using pairing-based cryptography.
- BN256 Signature Aggregation. BNS (Aggregation). In this page, we will aggregate signatures with BN256, along with aggregating the public keys. With this, we will have two key pairs of (\(sk_1,pk_1\)) and (\(sk_2,pk_2\)) and which will produce signatures of \(\sigma_1\) and \(\sigma_2\), respectively. We can then aggregate the signatures with \(\sigma_a = \sigma_1 + \sigma_2\), and the equivalent public key will be \(pk_a = pk_1 + pk_2\).
- BN256 Signature Aggregation ((The Rogue Public Key Attack)). BNS (Rogue Public Key). We can then aggregate the signatures with \(\sigma_a = \sigma_1 + \sigma_2\), and the equivalent public key will be \(pk_a = pk_1 + pk_2\). In this case, we will set \(pk_2=-pk_1\) and \(\sigma_2=-\sigma_1\), and which will set the aggregated public key at zero (or the point at infinity).
ZKP and OT (BN254 and BN128)
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
CipherCTF Needs You

This page includes cipher challenges for a capture the flag (CTF) activity (Quick link: cipherctf.com). Show leaderboard: [here]

Codes
If you want a printed version of the cipher challenge with answers (such as for teachers), click here [here].
If you want to jump to specific examples, you can do it here (and the system will generate a random ID for you):
- ADFGVX Code (Simple). ADFGVX. In this challenge the user has a number of ADFGVX codes to crack.
- AMCSO Code (Simple). AMCSO. In this challenge the user has a number of AMCSO codes to crack.
- Affine Code. Affine. In this challenge the user has a number of Affine codes to crack.
- Atbash Code. Atbash. In this challenge the user has a number of Atbash codes to crack.
- Bacon Code. Bacon. In this challenge the user has a number of Bacon codes to crack.
- Base64. Base64. In this challenge the user has a number of Base-64 codes to crack.
- Baud. Baud. In this challenge the user has a number of Baud codes to crack.
- Beaufort Cipher. Beaufort. In this challenge the user has two Beaufort ciphers to create.
- Beale Cipher. Beale. In this challenge the user has two Beale ciphers to decipher.
- Bible Code. Bible. In this challenge the user has two Bible codes to crack.
- Bifid Code. Bifid. In this challenge the user has a number of Bifid codes to crack.
- Braille Code. Braille. In this challenge the user has a number of Braille codes to crack.
- Caesar Code. Caesar. In this challenge the user has a number of Caesar codes to crack. With a Caesar code we move the alphabet by a certain number of shifts. The challenge only has one, two or three shifts.
- Columnar transposition cipher. Columnar. In this challenge the user has a number of Columnar codes to crack.
- Condi cipher. Condi. In this challenge the user has a number of Condi codes to crack.
- Covert Messages. Covert. In this challenge the user to find some covert messages.
- Delastelle Code. Delastelle. In this challenge the user has a number of Delastelle codes to crack.
- Diffie-Hellman. Diffie. In this challenge the user has a number of Diffie-Hellman keys to find.
- Dscript Code. Dscript. In this challenge the user has a number of Dscript codes to crack.
- Dvorak Code. Dvorak. In this challenge the user has a number of Dvorak codes to crack.
- Encode Code. Encode. In this challenge the user has a number of Encoded codes to crack.
- EX-OR Code. X-OR. In this challenge the user has a number of EX-oR codes to crack.
- Exponential Cipher. Exponential. In this challenge the user has a number of exponential ciphers to produce.
- Four Square Code. Four. In this challenge the user has a number of Four Square ciphers.
- Fractional Morse Cipher. Fractional. In this challenge the user has a number of Fractional Morse codes to crack.
- GCD. GCD. In this challenge the user has to find the GCD.
- Gold Bug. Gold. In this challenge the user to find the decoded Gold Bug ciphers.
- Hex Code. Hex. In this challenge the user has six codes to crack. These are defined as simple hexadecimal formats for the ASCII characters.
- Homophonic Substitution Code. Homophonic Substitution. In this challenge the user has a number of Homophonic Substitution codes to crack.
- Hill's Cipher. Hill's. In this challenge the user has a number of Hill's ciphers to crack.
- Huffman Coding. Huffman. In this challenge the user has a number of Huffman codes to crack.
- Jump. Jump. In this challenge the user to find messages that have been ciphered with the jump method.
- Keyword. Keyword. In this challenge the user has a number of Keyword codes to crack.
- Mary, Queen of Scots Code. Mary, Queen of Scots. In this challenge the user has a number of Mary, Queen of Scots codes to crack.
- Monk's Code. Monk. In this challenge the user has a number of Monk codes to crack.
- Morse Code. Morse. In this challenge the user has a number of Morse codes to crack. Morse code is made up with dots and dashes.
- Multiplier Code. Multiplier. In this challenge the user has a number of Multiplier codes to crack. With this cipher we multiple the values by a number and then use the (mod 26) operation.
- Mod 2 Multiply. Mod 2. In this challenge the user has a number of Mod 2 multiply values.
- Music cipher. Music. In this challenge the user has a number of Music ciphers to crack.
- Navajo Code. Navajo. In this challenge the user has a number of Navajo codes to crack.
- Nihlist Cipher. Nihlist. In this challenge the user has a number of Nihlist codes to crack.
- One Time Pad. OTP. In this challenge the user has a number of OTP codes to crack.
- Pigpen Code. Pigpen. In this challenge the user has two Pigpen codes to crack.
- Playfair. Playfair. In this challenge the user to find messages that have been ciphered with the jump method.
- Pollux. Pollux. In this challenge the user has a number of Pollux codes to crack.
- Polybius Code. Polybius. In this challenge the user has two Polybius codes to crack.
- Porta. Porta. In this challenge the user has a number of Porta codes to crack.
- QR Code. QR. In this challenge the user has a number of QR codes to crack.
- Rail Fence Code. Rail Fence. In this challenge the user has a number of Rail Fence codes to crack.
- Rot13 Code. Rot13. In this challenge the user has a number of Rot13 codes to crack.
- Rune Code. Rune. In this challenge the user has a number of Rune codes to crack.
- S-box Code. S-box. In this challenge we convert using an S-box.
- Scrambled Code. Scrambled. In this challenge the user has a number of scrambled alphabet codes to crack.
- Scrambled (Single mapping). Scrambled. In this challenge the user has a scrambled code to crack.
- Scrambled (Random mapping). Scrambled. In this challenge the user has a scrambled code to crack from any combination.
- Sequence. Sequence. This involves a sequence cipher.
- Semaphore. Semaphore. In this challenge involves semaphores.
- Straddling Code. Straddling. In this challenge the user has a number of Straddling codes to crack.
- Tap Code. Tap. In this challenge the user has a number of Tap codes to crack.
- Templar Cipher. Templar. In this challenge the user has a number of Templar codes to crack.
- Three square Code. Three square. In this challenge the user has a number of three square codes to crack. Morse code is made up with dots and dashes.
- Vigenère Code. Vigenère. In this challenge the user has a number of Vigenère codes to crack.
- Column Cipher . Column cipher. In this challenge the user uses a key for the columns.
Ciphers

Ciphers have been around for hundreds of years, and have often been used in love and war. In the following, we will analyse some traditional ciphers, and create a basic calculator to compute the cipher.
Fundamentals
- Frequency Analysis. Freq. This involves frequency analysis of text.
- Frequency Analysis (Example). Freq. This involves frequency analysis of text.
- ASCII to base codes using Python. Base. This converts an ASCII string into Base2, Base3, Base58 using Python.
- ASCII to codes. Coding. This converts an ASCII string into many other code, including Base2, Base45, and Base64.
- Detecting the cipher. Coding. This involves testing the cipher for the best match.
- Unbasing codes. Unbasing. This converts from a base format such as Base2, Base45, and Base64 into an ASCII string

Graphical Ciphers
- Bar Code. Barcode. This outlines the usage of Bar codes.
- Braille. Braille. This involves Braille coding.
- Dscript. Dscript. This involves Dscript coding.
- QR Code. QR. This outlines the usage of QR codes.
- Mary, Queen of Scots, polyalphabet cipher. Mary. This involves Mary's polyalphabet cipher.
- Pigpen Calculator. Pigpen. This involves a conversion of Pigpen.
- Semaphore flags. Semaphore flags. The creation of semaphore flags.
- Templar. Templar. The creation of a Templar cipher.
Key ciphers
- Autokey Cipher. Autokey. This involves the Autokey ciper.
- Keyword Code . Keyword. This involves the Keyword code.
Text-based Ciphers
These methods generally have some form of mapping that takes them from the plaintext to the ciphertext. Unfortunately knowing the conversion method leaves the code open to attack.
- a1z26. a1z26. This involves a1z26 cipher.
- ADFGVX. ADFGVX. ADFGVX example cipher.
- Affine. Affine. This involves affine cipher.
- Alder32. Alder32. This involves Alder32 cipher.
- Atbash. Atbash. This involves atbash cipher.
- Atbash (encode/decode). Atbash. This involves atbash cipher.
- Bacon Cipher. Bacon Cipher. This involves Bacon cipher.
- Barbie Cipher. Barbie Cipher. This involves Barbie cipher.
- Baudot. Baudot. This outlines the usage of Baudot codes.
- Beaufort Calculator. Beaufort . This involves a conversion of Beaufort cipher.
- Bifid Cipher. Bifid. This involves Bifid coding.
- Caeser. Caeser. This involves a conversion of Caeser.
- Citrix CTX1. Citrix CTX1. This cipher used the Citrix CTX1 password encoding method.
- Columnar Transposition Cipher. Columnar Transposition. In this cipher involves columnar transposition.
- Column Cipher . Column cipher. This cipher uses a key for the columns.
- Consonant index . Consonant index. This replaces constonant with their positions in a consonant index list.
- Delastelle. Delastelle. This involves the Delastelle cipher.
-
DNA-1 cipher. DNA-1. This represents a cipher with DNA codes for Adenine (A), Thymine (T), Cytosine (C) and Guanine (G).
- Dvorak. Dvorak. This involves Dvorak cipher.
- Enigma Machine. Enigma. This outlines the Enigma Machine.
- Ex-OR Coding. Ex-OR. This uses an EX-OR coding.
- Four Square. Four Square. Four square example cipher.
- Fractionated Morse cipher. Fractionated. Fractionated Morse cipher.
- Gold Bug cipher. Gold bug. Gold Bug cipher.
- Hill's Cipher. Hill's. This involves the Hill ciper.
- Homophonic Substition Code. Homophonic Substition. This involves Homophonic Substition coding.
- Huffman Coding. Huffman. This involves Huffman coding.
- Kenny (Southpark) Cipher. Kenny. In Southpark, the character of Kenny is famous for dying in almost every episode. Overall, Kenny comes from a poor family and wears an orange parka with a hood that muffles his speech. Thus, all we hear are mumbles with a M, F and P sound. For this, we can create a Kenny cipher by replacing each letter with a triplet using M, F and P.
- Leetspeak Cipher. Leetspeak Cipher. This involves Leetspeak Cipher coding.
- Lorem Ipsum Cipher. Lorem Ipsum Cipher. This involves Lorem Ipsum Cipher coding.
- Lorenz Cipher. Lorenz. This outlines the Lorenz cipher.
- Morse Code (encode/decode). Morse Code. This involves Morse coding for encoding and decoding.
- Morse Code. Morse Code. This involves Morse coding.
- Multiplication Code. Mult. This involves the Multiplication cipher.
- Navajo Code Talkers. Navajo. This involves the Navajo Code Talkers code.
- Nihlist Cipher. Nihlist. This outlines the Nihlist cipher.
- One-Time Pad Calculator. OTP. This involves a conversion of OTP.
- Playfair. Playfair. This involves Playfair coding, which uses a 5x5 matrix, with a secret key to change the coding.
- Pollux Code. Pollux. This involves the Pollux cipher.
- Polybius Calculator. Polybius. This involves a conversion of Polybius code.
- Porta cipher. Porta. Porta cipher.
- Radio Cipher. NATO/Military phonetic alphabet content encoding. This involves using NATO/Military phonetic alphabet content encoding.
- Rail Fence Cipher (3/5 rail) encode/decode. Rail Fence. This involves Rail Fence cipher for encoding and decoding, and with three or five rails.
- Rail. Rail. Rail code example cipher.
- Rail Fence Cipher (3 rail). Rail Fence. This involves Rail Fence cipher.
- Rail cipher with Rust. Rail. Rail cipher with Rust.
- Reverse cipher. Reverse. This involves a reverse of the words in a sentence.
- Reverse Words cipher. Reverse. This involves a reverse of the words, and reverse the words of the sentence.
- Rick Astley. Rick Astley. Rick Astley cipher.
- ROT13 Cipher. ROT13. This involves ROT13 coding.
- ROT47 Cipher. ROT47. This involves ROT47 coding.
- Scrambled. Scrambled. This involves a scrambled alphabet code.
- Scytale cipher with Rust. Scytale. Scytale cipher with Rust.
- SMS cipher. SMS. This involves the SMS cipher.
- Straddling Cipher. Straddling. This involves Straddling coding.
- Tom-tom Cipher. Tom-tom. This involves Tom-tom coding.
-
uuencoding Cipher. uuencoding .
(Unix-to-Unix encoding) encodes messages for their transmission over email systems. It allows for data to be transmitted for both text and binary data.
- Vigenère Calculator. Vigenère. This involves a conversion of Vigenère.
- Vigenère Key Generator . Vigenère. This involves the creation of the Vigenère key given the plain text and the cipher text.
- Vowel index . Vowel index. This replaces vowels with their positions in a vowel index list.
- Whitespace . Whitespace. In this cipher we use to whitespace characters: the tab space ('\t') and a space (' '). When we view the cipher, we possibly cannot see the characters. In ASCII a tab is 0x09 ('\t') and a space (0x20). We can now represent a tab space as a '0', and a space as a '1'. In ASCII, an 'e' is 0110 0101 and which gives 09 20 20 09 09 20 09 20. For a 'd' we have 0110 0100 and which gives 0920200909200909.
Key Cracking
These methods generally have some form of mapping that takes them from the plaintext to the ciphertext, which changes with the usage of a special key. The key normally means that it is more secure than standard key-less methods, but they can be broken using methods such as brute-force
- Index of Coincidence (IC). IC. This outlines the Index of Coincidence (IC).
- Kasiski examination. Kasiski. This outlines Kasiski examination.
- Skip cipher. Skip. This outlines a Skip Cipher.
Some tests
Cloudflare CIRCL

Cloudflare have continually push ever increasing security standards, and have proved their credentials by publishing a state-of-the-art cryptography library: Cloudflare Interoperable Reusable Cryptographic Library (CIRCL).
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
Hybrid Encryption
- ECIES (Kryptology). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Coinbase Kryptology library.
- ECIES (CIRCL). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Cloudflare CIRCL library.

Curve 25519
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
X448 and Ed448
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- Ed448 with Go. Ed448. Ed448 with Go.

FourQ
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with FourQ (Cloudflare). FourQ.
Pseudorandom Functions (PRFs)
- Verifiable Oblivious Pseudorandom Functions (VOPRF) with Cloudflare CIRCL. VOPRF. In our digital world, we give away too many of our secrets, especially where we just have to prove the knowledge of something, rather than actually revealing it. In many of the systems we use, we could just prove things in an oblivious way, and where we could pass a secret but in a blinded form. With this, a server does not discover our password and for us not to discover the identifier that a server holds on us. But, can we also provide a proof back that the right password has been used? Well, with Verifiable Oblivious Pseudorandom Functions (VOPRF), we can generate a random secret based on a key generated on the server (Alice), and which is based on Bob’s secret.
Hash to Curve
- Hash to Curve using Go (Cloudflare). Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). The method defined here is proposed an an Internet-Draft standard by the Internet Engineering Task Force (IETF) related to "Hashing to Elliptic Curves".
Blind signature
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
Schnorr ZKP
-
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Discrete Log Equivalence (DLEQ)
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Post Quantum Key Exchange with CIRCL
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.

Digital Signatures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signatures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signatures (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
eXtendable-Output Function (XOF)
- eXtendable-Output Function (XOF) usign CIRCL. XOF. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS.
Cloud Computing

Cloud Computing allows virtualised instances to run within a Cloud environment. This can include hardware-as-a-service, infrastructure-as-a-server (such as with AWS EC2), platform-as-a-service, and software-as-a-service.
Cloud Computing
-
Introduction to Cloud. Cloud introduction. The key objectives of this chapter are: provide an introduction to cluster, grid and cloud infrastructures; define an example of grid computing, and its advantages; and show an example of using a Cloud Infrastructure.
- AWS Lab. AWS Lab. The aim of this lab is setup AWS server instances and understand the setup of key security aspects.
Presentations
Codes

The following are a few challenges around codes. You can try some calculators [here].
Encoding
- ASCII table. ASCII. This shows an ASCII table.
- UTF-16 table. UTF-16. This shows a UTF-16 table.
- ASCII, Hex, Base-64 and Binary convertor. ASCII. This involves a conversion between different formats.
- Hex, Decimal and Binary convertor. Hex, Dec and Bin. This involves a conversion between hex, decimal, octal and binary.
- Binary conversion. Binary. This does a basic binary conversion.
- Floating point conversion. Floating. This does a basic floating point conversion for binary values.
- Malware obfuscation. Obfuscation. This converts from JavaScript encoding.
- Base-45. Base-45. This shows the conversion from ASCII into Base-45.
- ASCII to codes. Coding. This converts and ASCII string into many other code, including Base2, Base45, and Base64.
- Detecting the cipher. Coding. This involves testing the cipher for the best match.
- Unbasing codes. Unbasing. This coverts from a base format such as Base2, Base45, and Base64 into an ASCII string
- ASCII to base codes using Python. Base. This converts an ASCII string into Base2, Base3, Base58 using Python.
- UUID (GUID) and ULID. ULID. This creates a ULID (Universally Unique Lexicographically Sortable Identifier). UUIDs (Universally Unique IDentifiers) lack any real structure, and do not support the linking of objects and unique names. ULID aims to address this by created a cexicographically sortable system. It has a 26 character string and uses Base32 for its character (five bits per charater). With Base 32, we have a character set of "A-Z2–9=] - notice that '0' and '1' are not used, as they can be confused with 'O' and "I'.
Basic Security Principles
- Secret splitting. Secret splitting. This gives an example of secret splitting.
Others
- Inference. Infer. This involves the investigation of inference.
- Annual Loss Expectancy. ALE. This involves the investigation of Annual Loss Expectancy.
Some tests
- Hex and binary test. Test. Hex/Binary.
- Hex and binary test (Fun Test). Test. Hex/Binary.
- ASCII to Base64. Test. Convert from ASCII to Base64.
- ASCII to Base64. Test. Convert from ASCII to Base64.
- Caesar. Test. Caesar code.
- Caesar (Fun test). Test. Caesar code.
- MD5. Test. MD5 code.
Data Communications/Telecomms

This page outline related data communications and telecommunications material.
Fundamentals
- Data representation. Data. This outlines the conversion of values such as for hex, octal and decimal.
- Bit operations. Bitops. This outlines some basic bitwise operations.
- Bit operations (with eval()). Bitops. This outlines some basic bitwise operations.
- Bit shift. Shift. This outlines bit shift operators.
- Bit masking. Mask. This outlines bit masking.
- Bit mask. Mask. This outlines masking a single bit.
- Matrix multiplication. Calc. This outlines matrix multiplication.
Signals
- Signals and noise (Chart). Signals.
- Signals and harmonics. Signals.
- AM and FM (Chart). AM/FM.
- ASK, FSK and PSK (Chart). ASK/FSK/PSK.
- Data distributions. Dist.
- Laplace distribution. Laplace.
- Sampling. Quantisation.
- Pulse Analysis. Pulse.
Error Detecting/Correcting
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Hamming distance. Bin. This outlines the calculation of the Hamming distance.
- Hamming distance (between several bit strings). Bin. This outlines the calculation of the Hamming distance.
- Block parity (binary). Bin. This outlines block parity.
- Block parity (values). Bits. This outlines the calculation of block parity.
- CRC. CRC. This outlines the calculation of the CRC.
- Longitudinal/vertical redundancy checks (LRC/VRC). LRC. This outlines the calculation of the LRC.
- Bit errors. Bits. This outlines the calculation of bit error.
- Hamming (7,4) code. Hamming. This outlines the single bit error correcting code.
- Hamming (code. Hamming. This outlines Hamming coding.
- Reed Solomon. Reed. This outlines Reed Solomon coding.
Source Compression
- Huffman code. Huffman. This outlines Huffman coding.
- LZW code. LZW. This outlines Lempel-Ziv-Welch coding.
Image Compression
- GIF file format. GIF. This outlines the format of a GIF file
- GIF with Python. GFI. This page reads a GIF.
- JPEG - DCT Processing. DCT. This outlines DCT coding.
- JPEG - DCT Quantization. Quantization. This outlines DCT Quantization coding.
- JPEG - Face Detection. Faces. This outlines face detection.
- JPEG - Face Detection (Azure). Faces. This outlines face detection using Microsoft Cognitive Services.
- JPEG - Tags. Tags. This outlines the detection of JPEG tags in the file.
Video Compression
- MP4 file format. MP4. This outlines the format of an MP4 file
- MP4 File Forensics. File 1
- MP4 frame extraction. MP4. This outlines extracting images from MP4 stream
Others
- Barcodes. Barcode. This outlines the barcode format.
Commutative Encryption

Commutative Encryption involves Alice encrypting with her public key, and then Bob encrypting this with his public key. It is then possible to decrypt with either Alice using her private key first and then Bob private key, or the other way around.
Massey–Omura
The following are the tips related to Commutative encryption:
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
Commutative Encryption using stream ciphers
- Commutative Encryption using ChaCha20. ChaCha20. With commutative encryption we can encrypt and decrypt in any order. In this case we will use a stream chipher to X-OR a data stream with ChaCha20.
- Commutative Encryption with SHAKE-128/SHAKE-256 and Python. SHAKE-128/256. With commutative encryption we can encrypt and decrypt in any order. In this case we will use a stream chipher to X-OR a data stream with the SHAKE-128/256 byte output for a given password for Bob and Alice.
ElGamal Commutative Encryption
- Commutative Encyption (Modified ElGamal). Commutative Encyption. Commutative Encyption allow Bob and Alice to encrypt a message, and then for the data to be decrypted usign any order of the keys.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
CBOR and COSE

In computer security, we often have to represent binary data, in single values or groups of characters, bytes, words, long words, signed integers, floating-point values, double-precision floating-point values, and so on. This might be in the form of a data object, a signature or even encrypted content. For this, the ANS.1 DER format is often used, such as presenting digital certificates and signatures. An improvement on this for small messages with security is Concise Binary Object Representation (CBOR) — and which is defined in RFC8949 [1]. While JSON represents text-based data objects CBOR focuses on binary objects. It has been designed to create a lightweight encoder and decoder. This supports the use of CBOR within an IoT infrastructure. The data, also, does not require a data schema to be able to decode it, along with being extensible. CBOR defines the format of binary data with data objects and messages. We can then integrate security with CBOR Object Signing and Encryption (COSE), and which is defined in RFC8152 [2]. This includes signatures, message authentication codes (MACs), encryption and creating serialised objects.
Symmetric key
- 128-bit AES GCM. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) can then build on this to include signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use a symmetric key to encrypt a message, and then decrypt it. In this case we will use AES GCM with a static 128-bit key ("0x000102030405060708090a0b0c0d0e0f").
- 256-bit AES GCM. Go. In this case we will use AES GCM using a random 256-bit key (32 bytes).
Signatures
- EdDSA. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) [2] can then build on this to includes signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use EdDSA to create a signature for a message.
- ECDSA. Go. In this case we will use ECDSA to create a signature for a message.
- HMAC. Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
Tokens
- CWT. Go. In this case we create a CWT token, and sign with an HMAC signature.
ECDH and Content Encryption Key (CEK)
- ECDH. Go. In this case we create a symmetric key from ECDH. For this we will derive a shared key from the public key of Alice and Bob, and then define a single recipient which can derive the CEK (Content Encryption Key) using their private key. We will use the curves of P-256 (secp256r1), P-384 (secp384r1), P-521 (secp521r1) or SECP256K1 (as used with Bitcoin).
RSA
- RSA using COSE and CBOR. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\).
- RSA: dQ, dP and InvQ. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). The key pair also includes \(dQ\), \(dP\) and \(InvQ\), and these can be used with the Chinese remainder theory to optimize the decryption process.
References
[1] Bormann, C., & Hoffman, P. (2020). RFC 8949 Concise Binary Object Representation (CBOR). [here].
[2] Schaad, J. (2017), RFC 8152 – CBOR Object Signing and Encryption (COSE), 2017. [here]
[3] Jones, M., Wahlstroem, E., Erdtman, S., & Tschofenig, H. (2018). Cbor web token (cwt). RFC 8392, Standards Track, IETF. [here]
Cipher cracking

This page outlines a few cracks related to ciphers, AES, and public key. With hashing and symmetric key methods we might use cryptoanalysis, while RSA cracking can involve Chinese Remainder Theorem (CRT), copy-and-paste and weak random numbers.
Ciphers Cracking
The following are examples of cipher cracking:
- Index of Coincidence (IC). IC. This outlines the Index of Coincidence (IC).
- Kasiski examination. Kasiski. This outlines Kasiski examination.
- Vigenère Calculator Crack. Vig. This outlines Vigenère Crack.
- Frequency Analysis. Freq. This involves frequency analysis of text.
- Frequency Analysis (Example). Freq. This involves frequency analysis of text.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
Encryption cracking (RSA)
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA - Cracking the private key. Go.
- RSA Challenge Generator. RSA. This provides a value for e and N, and gives the cipher, and you must crack it by finding d.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
- RSA - Encrypted private key. Go. In this case we can generate a challenge where the student needs to find the password which encrypted an RSA rivate key.
RSA CTF Generators
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA. Low exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
Encryption cracking (Hashing)
- Differential Cryptanalysis (Hashing). Cryptanalysis. This provides an implementation of differential cryptanalysis for hashing methods.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA: Fault Attack. ECDSA: Fault Attack. In the fault attack in ECDSA we only require two signatures. One is produced without a fault \((r,s)\), and the other has a fault \((r_f,s_f)\). From these we can generate the private key.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
CTF Generators and Solvers

A Capture The Flag allows the creation of challenges which need to be solved, and which can be redeemed for points.
Cipher Examples
- Printed version of Cipher CTF challenges: [here].
- Electronic version of Cipher CTF challenges: [here].
Substitution ciphers
- CTF Generator: Kenny (Southpark) Cipher. Kenny. In Southpark, the character of Kenny is famous for dying in almost every episode. Overall, Kenny comes from a poor family and wears an orange parka with a hood that muffles his speech. Thus, all we hear are mumbles with a M, F and P sound. For this, we can create a Kenny cipher by replacing each letter with a triplet using M, F and P.
Bit rotate in messages
- CTF Generator: Rotate right. Rotate right. With the Rotate Right Cipher, we take the bits in each of the letters and rotate them by a number of positions to the right. It should be noted that this is done on a byte wise approach, and where we take each character at a time, and then rotate the bits by a given number of position. As we will possibly generate non-printing ASCII characters, we will represent the cipher as a hexademical value.
- CTF Generator: Rotate left. Rotate left. With the Rotate Left Cipher, we take the bits in each of the letters and rotate them by a number of positions to the left. It should be noted that this is done on a byte wise approach, and where we take each character at a time, and then rotate the bits by a given number of position. As we will possibly generate non-printing ASCII characters, we will represent the cipher as a hexademical value.
Vowel/consonant index cipher
- CTF Generator: consonant-index cipher. Consonant-index cipher. In this cipher we replace consonant with their index value.
- CTF Generator: vowel-index cipher. Rotate left. With the vowel-index cipher, we replace the vowels with their position. a - 1, e - 2, i - 3, o - 4, u - 5. Thus, this is the message, will be "This is a message" is "Th[i]s [i]s [a] m[e]ss[a]g[e]" becomes "TH3S3SS4M2T2XT".
Håstad’s Broadcast Attack
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
Finding the decryption exponent
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
Low exponent (e) in RSA
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
Wiener attack
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
Fermat’s attack
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
Different public exponent and the same modulus (N)
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
Low factor in the modulus
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
CTF: Cracking RSA with known partial bits
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
CTF Generator: RSA Fault in Signature Generation
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Curve 25519

Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page implements ECDH, and which is the method used in Tor to exchange the key. In this case we will use Python to implement X25519 (and which uses Curve 25519), but only uses the x-axis point for the sharing of values. The base point \(G\) on Curve 25519 is (9,1478161944 ... 7755586237401) [here].
Curve Points
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- Curve 25519 with Go for test vectors. ECC. This does a test on some private keys to test the public key generation.
Curve Adding/Multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Elliptic Curve (Point Adding with real curves). Elliptic Curve. Creating 2P from P with real curves (eg Curve 25519).
- Curve25519 with point adding Python. Curve25519. This outlines Curve25519 using basic point adding.
ECDH
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
-
Curve 25519 with Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Elliptic Curve (Signatures - EdDSA)
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Ed25519 for EdDSA signatures with Hazmat. EdDSA: Ed25519. This page uses the Hazmat primitives for the cryptography library.
- Ed25519 signature using NaCl. Ed25519. This page uses the NaCl port from libsodium.
- Ed25519 points using NaCl. Ed25519. This page uses the NaCl port from libsodium to determine Ed25519 points.
- Barebones Ed25519 with Go. ECC. This shows point addition and scalar multiply in Ed25519
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
- Ed25519 in Python. EdDSA in Python. This page implements EdDSA using the Pure25519 library and with the core functions of key generation, signature generation and signature verification.
- Ed25519 Vulnerability in Python. EdDSA Vulnerability in Python. This page implements EdDSA using the Pure25519 library and with the core functions of key generation, signature generation and signature verification.
- Ed25519 Vulnerability in Python (Proof of Concept). EdDSA Vulnerability in Python (PoC). This page implements EdDSA using the Pure25519 library and with the core functions of key generation, signature generation and signature verification.
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
.
Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
El Gamal
- ElGamal with ECC. ElGamal with ECC. ElGamal using ECC.
Signatures
Elliptic Curve (Keys)
The following are the tips related to ECC:
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Barebones Curve 25519
- Curve 25519 in Python. Barebones Curve 25519. This page implements Curve 25519 in pure Python.
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
- Curve 25519 in Python (Test Vectors from RFC 7748). Barebones Curve X25519. This page implements Curve 25519 in pure Python and tests against the IETF test vectors.
- Curve 25519 ECDH in Python (Test Vectors from RFC 7748). Barebones Curve X25519. This page implements Curve 25519 ECDH in pure Python and tests against the IETF test vectors.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 . EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
NaCl
Cyber&Data

This is the home page for the Cyber & Data course. There are four main units involved. Units 1 and 2 are self-study, but you can register for Units 3 and 4, and study towards an MSc module. Some unique features include: On-line Python integration, On-line Intrusion Detection Editor, Splunk Data Analysis, and Machine Learning Environment for Splunk. The Splunk elements of the course require a login (contact [email protected] for a login).
Unit 1: Fundamentals
- 1. Cyber and Intelligence. This topic provides an introduction to Cyber and Intelligence.
- 2. Defence Systems, Policies and Risk. This topic provides an overview of the some of the core defence mechanisms and risk approaches.
- 3. Open Source Intelligence. This topic outlines the usage of open source intelligence including using Shodan, Redit and Twitter mining.
- 4. So What is Data? This topics outlines the core data formats using in cybersecurity, and introduces the concept of magic numbers within files.
Unit 2: Data Capture and Analysis
- 5. Memory, Big Data and SIEM. This topic outlines some of the core principles used around Big Data methods and in the integration of SIEM (Security Information and Event Management).
- 6. Network Forensics. This topic provide fundamental knowledge in how networks works, and how we can analyse different network protocols, including ARP, IP, TCP, FTP and HTTP.
- 7. Intrusion Detection Systems. This topic outlines the usage of IDS and applies with using Snort.
Unit 3: Data Science and Cyber
- 8. Classification Metrics and ML.
- 9. Introduction to Data Science.
- 10. NumPy and Pandas. An outline of the integration of Numpy and Pandas for datasets.
- 11. Similarity and Matching. This unit outlines some of the key methods used within similarity and matching of text data. This includes the application of regular expressions, similarity metrics and similarity hashes.
Unit 4: Data Applications and Machine Learning
- 12. Splunk. An introduction to Splunk.
- 13. Splunk (Charting and Analysis). An introduction to Splunk with Charting and Analysis.
- 14. Machine Learning (Core Methods). An outline of the core methods.
- 15. Application of Machine Learning. A tutorial in applying ML with Splunk
Unit 5: Cyber Applications
- 16. Face Recognition. Implementation of face recognition.
DES, 3DES and Feistel ciphers

With DES and 3DES we have a 56-bit or 112-bit encryption key, respectively. Both are block ciphers and based on the Feistel ciphers, with a 64-bit block size.
Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- 3DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using 3DES encryption with Powershell.
- Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . With 3DES encryption, we use a 128-bit key and a 64-bit IV value. The two modes supported are ECB (without salt) and CBC (with salt). The DES algorithm has been around for a long time, and the 56-bit version is now easily crackable (in less than a day on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases, and splits the key into two. Overall the key size is typically 112 bits (with a combination of the three keys - of which two of the keys are the same). In this case we will use PKCS7 padding, and which fills the input data with a value that is equal to the number of padding bytes. Overall, DES has a 64-bit block size, and which equates to eight ASCII characters.
DES
The following are the tips related to DES, 3DES and Feistel ciphers:
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
Diffie-Hellman Key exchange (Discrete Logs)

Key exchange is a way for Bob and Alice to communicate and for them to agree on a shared secret. The original method defined uses discrete logarithms (Diffie-Hellman). With the Diffie-Hellman method, Alice generates \(a\) and shares \(A=g^a \pmod p\) with Bob. Bob generates \(b\) and shares \(B=g^b \pmod p\). Alice raises \(B\) to the power of \(a\), and Bob raises \(A\) to the power of \(b\). They should both end up with the same secret: \(K=g^{ab} \pmod p\).
Key interchange/generation (Diffie-Hellman)
The following relates to key interchange:
- Diffie-Hellman. Diffie-Hellman Calculation. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Real example). Diffie-Hellman Real. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Python). Diffie-Hellman. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (pre-compute). Diffie-Hellman (pre-compute). Many sites use the same prime numbers, which can then be cracked with a pre-computing attack.
- Selecting \(g\) in Diffie Hellman. G in Diffie Hellman. Picking a safe value of the generator \(g\) in discrete logarithms.
- Diffie-Hellman (Man-in-the-middle). DF. This outlines the man-in-the-middle method for Diffie-Hellman.
- An Alternative Diffie-Hellman method. Alterative DH. This outlines an alternative Diffie-Hellman method.
- Selecting g in discrete logs. g in discrete logs. This select a generator in discrete logs.
- Selecting g in discrete logs with random primes. g in discrete logs with random primes. This select a generator in discrete logs using random prime numbers which are define by a number of bits.
Authenticated Key Exchange
The following are the tips related to Key derivation hashing:
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- MTI/A0. MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{ax+by} \pmod p\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0. MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{x+y} \pmod p\)
- MTI/C0. MTI/C0. This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{xy} \pmod p\)
- MTI/C1. MTI/C1. This outlines MTI/C1, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{abxy} \pmod p\).
- HMQV (Menezes–Qu–Vanstone). HMQV. HMQV builds on MQV and adds the identity of Bob and Alice.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
Diffie-Hellman Parameter Generation
-
DH Parameters with OpenSSL [here]. With the Diffie-Hellman (DH) we use the form of \(g^x \pmod p\), and where \(g\) is the generator and \(p\) is a large prime number. In order to implement DH, we create either a generator value of 2 or 5, and then select a prime number which works with this generator value. In real-life we would generate a prime number of at least 2,048 bits. A command of "openssl dhparam -2 512" creates a random prime number with 512 bits and which works with a generator of \(g=2\).
Digital Certificates

Trust centres are responsible for storing private and/or public keys, and digital certificates are used to store and distribute private and/or public keys.
Trust Centres
- Simple Key Distribution Centre. KDC. This implements a simple KDC.
- Kerberos. Kerberos. This will implement a Kerberos method of generating a shared key.
Key Pair Generation and Code Signing Requests
The following are the tips related to digital certs:
- Generating key pair. View. This defines creating a 512-bit keypair.
- Code Signing Request (CSR). View. This defines the reading the CSR.
- Code Signing Request (CSR) with Python. View. This defines creating a CSR using Python.
Creating Digital Certificates
The following are the tips related to digital certs:
- Digital Certificate Digital Cert.
- Digital Certificate (PFX) Digital Cert.
- Certificate with Public/Private key. Cert. This includes the creation of the digital certificate.
- Generate X.509 certificate and key pair using Golang. X.509. This generates an X.509 certificate and shows the details.
- X.509 certificates in JavaScript. RSA and ECDSA Signed certificates. This page will generate either RSA and ECC key pairs, and then generate X.509 certificates, using either a signature of SHA1withRSA or SHA256withECDSA. For RSA signing we use an RSA private key to sign the certificate, and with ECDSA signing we use an ECC private key to sign the certificate.
Digital Certificate Format
The following are the tips related to digital certs:
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Certificate cracking
The following are the tips related to digital certs:
- Cracking certificates. Crack. This defines the cracking of digital certificates.
SSL
The following are the tips related to digital certs:
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Certificates (OpenSSL). View. This defines the viewing of digital certificates.
Theory
- Encryption Principles: [View]
- Proving identity and examining certificates: [View]
- Validating entities: [View]
DSA (Digital Signature Algorithm)

The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA with OpenSSL
- DSA Parameters. DSA parameters with OpenSSL. This page outlines the creation of a keypair for DSA signatures.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
DSA with PowerShell
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA and Node.js
- Key pair using Node.js. DSA and other keypairs. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
DSA and C#
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
DSA and OpenSSH
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
DSA Signatures with Hazmat
-
DSA Signatures. DSA Signatures. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. The ECDSA method is an extension of DSA, but implemented with elliptic curve (EC) methods. As with most public key signing methods, we take a hash of a message, and then apply a private key to create a signature (\(r,s\)). This is done by creating a random value (\(k\)) to produce the signature. The signature is then verified using the associated public key. This then verifies the creator of the signature and that the message has not been changed.
Outline
So, what does a digital signature look like? Well, it often has an r value and an s value: (r,s). So, let’s look at the DSA (Digital Signature Algorithm) signature. For this, Figure 1 shows an outline of the setup of the DSA signature, and where Bob uses his private key (sk) to sign a hash of a message, and Alice proves with his public key (pk,g,p,q). We also use a random nonce value (k) for the signature, and we must take care that we do not reuse the value.
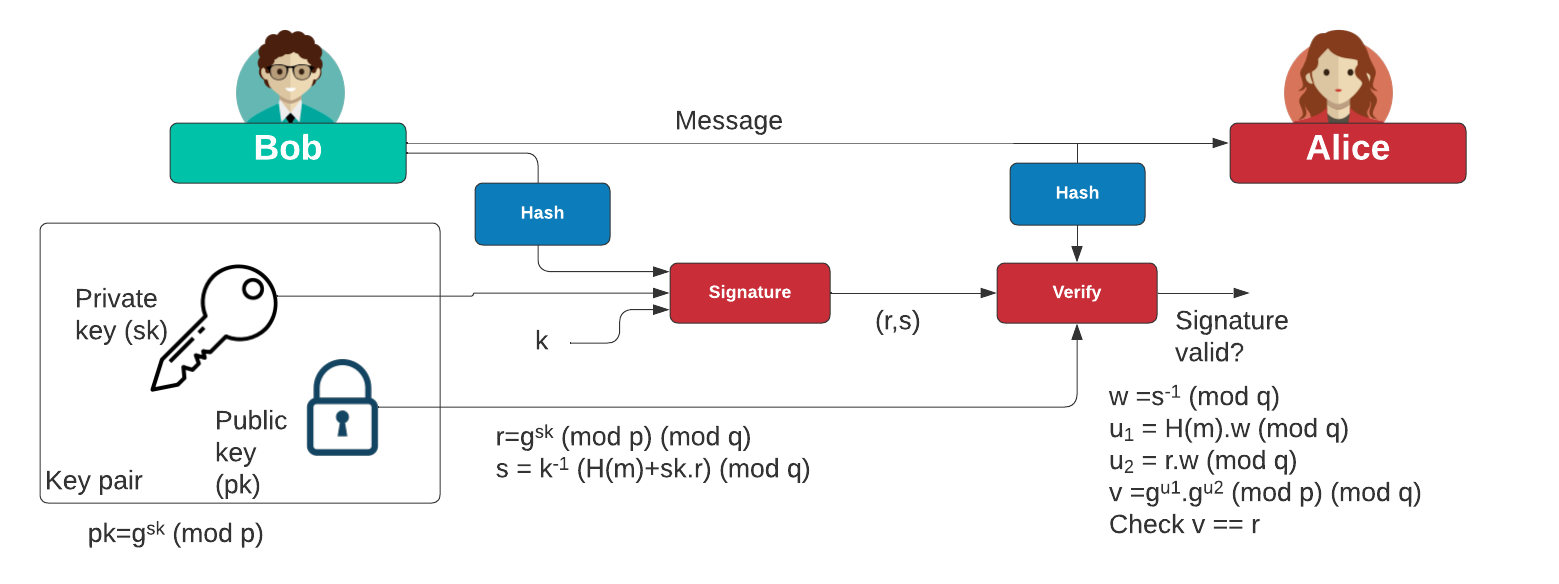
Figure 1: DSA signature
Initially, Bob creates two prime numbers (\(p\) and \(q\)) and generates a generator value of \(g\). Next, he generates his secret key (\(x\)) and then computes his public key:
\(Y=g^{x} \pmod p\)
To create a signature for a message (\(M\)), he creates a random value (\(k\)) and then computes two values for the signature:
\(r = g^{k} \pmod{p} \pmod{q}\)
\(s=(k^{-1}.(H(m)+x.r)) \pmod {q}\)
When Alice receives this signature, she takes Bob's public key \((p,q,g,Y)\) and the message can computes:
\(w = s^{-1} \pmod q\)
\(u_1 = H(M).w \pmod q\)
\(u_2 = r.w \pmod q\)
\(v = (g^{u_1} . y^{u_2}) \pmod {p} \pmod {q}\)
She then checks that \(v\) is equal to \(r\). If so, the signature checks out. This works because:
\(v = g^{h.w}.y^{r.w} = g^{h.w}.g^{x.r.w} = g^{h.w+x.r.w} = g^{h/s+x.r/s} = g^{(H+x.r)/(k^{-1}(H+x.r))} = g^k = r\)
Elliptic Curve Cryptography (ECC)

With elliptic curve methods, we take a base point (\(G\)) and then use a private key (\(n\)) to produce a public key point (\(nG\)).
Elliptic Curve (Points)
The following are the tips related to ECC:
- ECC types and nG. ECC types and nG. Outlining the parameters used for ECC types (eg Curve 25519, Curve 448 and secpt256k1).
- First 100 Elliptic Curve points in Finite Field. Elliptic Curve points. Locating the first 100 points in an elliptic curve in a finite field.
- Elliptic Curve - Point addition. Elliptic Curve Point Addition. This shows the addition of two points on an elliptic curve.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field.
- First 20 Elliptic Curve points in Finite Field (improved method). Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field.
- First 20 Elliptic Curve points in Finite Field (plot). Elliptic Curve points (plot). Locating the first 20 points in an elliptic curve in a finite field.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field for common curves with Libnum. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256 and using Libnum to compute the quadratic square.
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- ECC double-and-add for point multiplication. Elliptic Curve double-and-add. Calculation of \(aG\) using a double-and-add approach (and which is equivalent to square-and-multiply in exponential functions.
- ECC key generation with Hazmat. Elliptic Curve key gen. Creating ECC keys using Hazmat and Python.
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining \(n.G\) for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Operations Within a Solidity Contract. Go.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Embedding data in an ECC point
- Embedding data in a point. Go. With Elliptic Curve Cryptography (ECC), we use points on an elliptic curve to represent our data. These are defined with (x,y) points. With this, it is possible to embedded a certain amount of data into the point - as long as it still gives us a valid point on the curve. This example will Curve 25519 to embed data, and is achieved by storing the length of the data in a single byte in the point, and then store the data as byte values in the point (followed by random data). To decode, we can then just read the first byte for the length of the message, and then reveal the data encoded into the point..
Quadratic residues
- Quadratic residue (mod p). Go. Outline of quadratic residue \(\pmod p\).
Elliptic Curve (ECDH) - Python
The following are the tips related to ECC:
- Elliptic Curve. Elliptic Curve. Elliptic Curve is a public key method which can also be used to generate a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with simple parameters. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
Elliptic Curve (ECDH) - Golang and Node.js
The following are the tips related to ECC:
- ECDH with Go. ECDH. ECDH with Go.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with node.js. ECDH. ECDH with node.js.
- ECDH with JavaScript. ECDH. Elliptic Curve Diffie Hellman.
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret. We will use Golang and the Krytology library.
Elliptic Curve (Signatures - ECDSA)
The following are the tips related to ECC:
- ECDSA and EdDSA methods. ECDSA and EdDSA. This outlines ECDSA and EdDSA for NIST, secp, brainpool and Ed448/Ed25519.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with secp256k1. ECDSA (secp2561k1). Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with secp256k1.
- ECDSA using P256. Barebones ECDSA with P256. This page implements ECDSA with the NIST P256 curve.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces and using Lenstra–Lenstra–Lovász (LLL) method. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA with Hazmat. ECDSA wih Hazmat. This outlines ECDSA with Hazmat.
- Blinded ECDSA. Blinded ECDSA. With a blinded signature, Bob can sign for a message, without knowning what the message is. In this case Alice will create a blinded ECDSA signature, and where Bob can then sign it, and then Alice can unblind it. The method is based on one produced by Oleg Andreev for blinding signatures in Bitcoin.
- ECDSA: Fault Attack. ECDSA: Fault Attack. In the fault attack in ECDSA we only require two signatures. One is produced without a fault \((r,s)\), and the other has a fault \((r_f,s_f)\). From these we can generate the private key.
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
Elliptic Curve (DER)
The following are the tips related to ECC:
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Elliptic Curve (Signatures - EdDSA)
The following are the tips related to ECC:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. X448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Ed25519 for EdDSA signatures with Hazmat. EdDSA: Ed25519. This page uses the Hazmat primitives for the cryptography library.
- Ed25519 signature using NaCl. Ed25519. This page uses the NaCl port from libsodium.
- Ed25519 points using NaCl. Ed25519. This page uses the NaCl port from libsodium to determine Ed25519 points.
Elliptic Curve (Plots)
The following are the tips related to ECC:
- Elliptic Curve (Plot). Elliptic Curve (Plot). Elliptic Curve is a public key method which can also be used to generate a shared key. This page outlines a graphic of the curve.
- Elliptic Curve (Real plots). Elliptic Curve (Real plot). This provides a range of well-defined elliptic curve plots.
Elliptic Curve (Keys)
The following are the tips related to ECC:
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
Elliptic Curve (ECIES)
The following are the tips related to ECC:
- Elliptic Curve Integrated Encryption Scheme (ECIES with Rabbit Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with Rabbit (a light-weight stream cipher).
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
Elliptic Curve (Hash to curve)
The following are the tips related to ECC:
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve with libnum.
- Hash to password with Go. Hash to password. Hash to password with Go.
- Match random value to sepc256k1 with Python. Random value to curve. This involves generating a random value, and then finding the nearest valid point on the curve. It involves incrementing a value of \(x\) until we reach a valid point.
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
Elliptic Curve (Point adding)
The following are the tips related to ECC:
- Elliptic Curve (Point Adding). Elliptic Curve. Creating 2P from P.
- Elliptic Curve (Point Adding with real curves). Elliptic Curve. Creating 2P from P with real curves (eg Curve 25519).
- Elliptic Curve (Calculating nP - ECC Calculator). Elliptic Curve. Creating nP from P with real curves.
- Elliptic Curve (Point addition - ECC Calculator). Elliptic Curve. This calculator adds two points on an elliptic curve.
- Elliptic Curve (Point addition - ECC Calculator - range of points). Elliptic Curve. This calculator takes one point on the elliptic curve, and then adds the other the other points on the curve to see the result.
Elliptic Curve (Curve 25519)
The following are the tips related to ECC:
- Curve 25519 with Go for test vectors. ECC. This does a test on some private keys to test the public key generation.
- Curve 25519 with Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Curve25519 with Python. Curve25519. This outlines Curve25519, which is used in the Tor network.
- Curve25519 with point adding Python. Curve25519. This outlines Curve25519 using basic point adding.
ElGamal and ECC
- ElGamal with ECC. ElGamal with ECC. ElGamal using ECC.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
- Proving an Encrypted Shuffle With ElGamal and ECC. Shuffle. An encrypted shuffle with ElGamal.
Elliptic Curve (X448)
The following are the tips related to ECC:
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Python. X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH using Python and based on RFC 7748.
Elliptic Curve (ElGamal)
The following are the tips related to ECC:
- Proving an Encrypted Shuffle With ElGamal and ECC. Shuffle. An encrypted shuffle with ElGamal.
- ElGamal with ECC. ElGamal with ECC. ElGamal using ECC.
Elliptic Curve (Pedersen Commitment) and DLEQ
The following are the tips related to ECC:
- Elliptic Curve - Blinding factor (Pedersen Commitment). Elliptic Curve Blinding. This shows the addition of transactions with a blinding factor.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
Elliptic Curve (Box and Encryption)
The following are the tips related to ECC:
Go ECC
- Hash to password with Go. Hash to password. Hash to password with Go.
- ECDH with Go. ECDH. ECDH with Go.
- Box with Go. Box. Box with Go.
- ECC with Go. ECC. ECC with Go.
- Curve 25519 with Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ElGamal with ECC. ElGamal with ECC. ElGamal using ECC.
- Curve 25519 with Go for test vectors. ECC. This does a test on some private keys to test the public key generation.
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Barebones Ed25519 with Go. ECC. This shows point addition and scalar multiply in Ed25519
- Barebones NIST P256 with Go. ECC. This shows point addition and scalar multiply in P256
Key exchange
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). The resultant key is \(xyG \)
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
- Authenticated Key Exchange (ECC). YAK. Key exchange with public keys and uses elliptic curve methods.
IBE
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
Barebones ECC
- P192 in Python. Barebones P192. This page implements P192 in pure Python.
- P224 in Python. Barebones P224. This page implements P224 in pure Python.
- P256 in Python. Barebones P256. This page implements P256 in pure Python.
- P521 in Python. Barebones P521. This page implements P521 in pure Python.
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
- Curve 25519 in Python. Barebones Curve 25519. This page implements Curve 25519 in pure Python.
- Curve 25519 in Python (Test Vectors from RFC 7748). Barebones Curve X25519. This page implements Curve 25519 in pure Python and tests against the IETF test vectors.
- Curve 448 in Python (Test Vectors from RFC 7748). Barebones Curve X448. This page implements Curve 448 in pure Python and tests against the IETF test vectors.
- Curve 25519 ECDH in Python (Test Vectors from RFC 7748). Barebones Curve X25519. This page implements Curve 25519 ECDH in pure Python and tests against the IETF test vectors.
- Curve 448 ECDH in Python (Test Vectors from RFC 7748). Barebones Curve X448. This page implements Curve 448 ECDH in pure Python and tests against the IETF test vectors.
- ECDSA using P256. Barebones ECDSA with P256. This page implements ECDSA with the NIST P256 curve.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 . EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
Others
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.

Public Key (Elliptic Curve) in Rust
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Sage
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
Elliptic Curve Diffie-Hellman (ECDH)

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as secp256k1 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) - Python
The following are the tips related to ECC:
- Elliptic Curve Diffie-Hellman (ECDH) with simple parameters. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
- ECDH and COSE. Go. In this case we create a symmetric key from ECDH. For this we will derive a shared key from the public key of Alice and Bob, and then define a single recipient which can derive the CEK (Content Encryption Key) using their private key. We will use the curves of P-256 (secp256r1), P-384 (secp384r1), P-521 (secp521r1) or SECP256K1 (as used with Bitcoin).
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
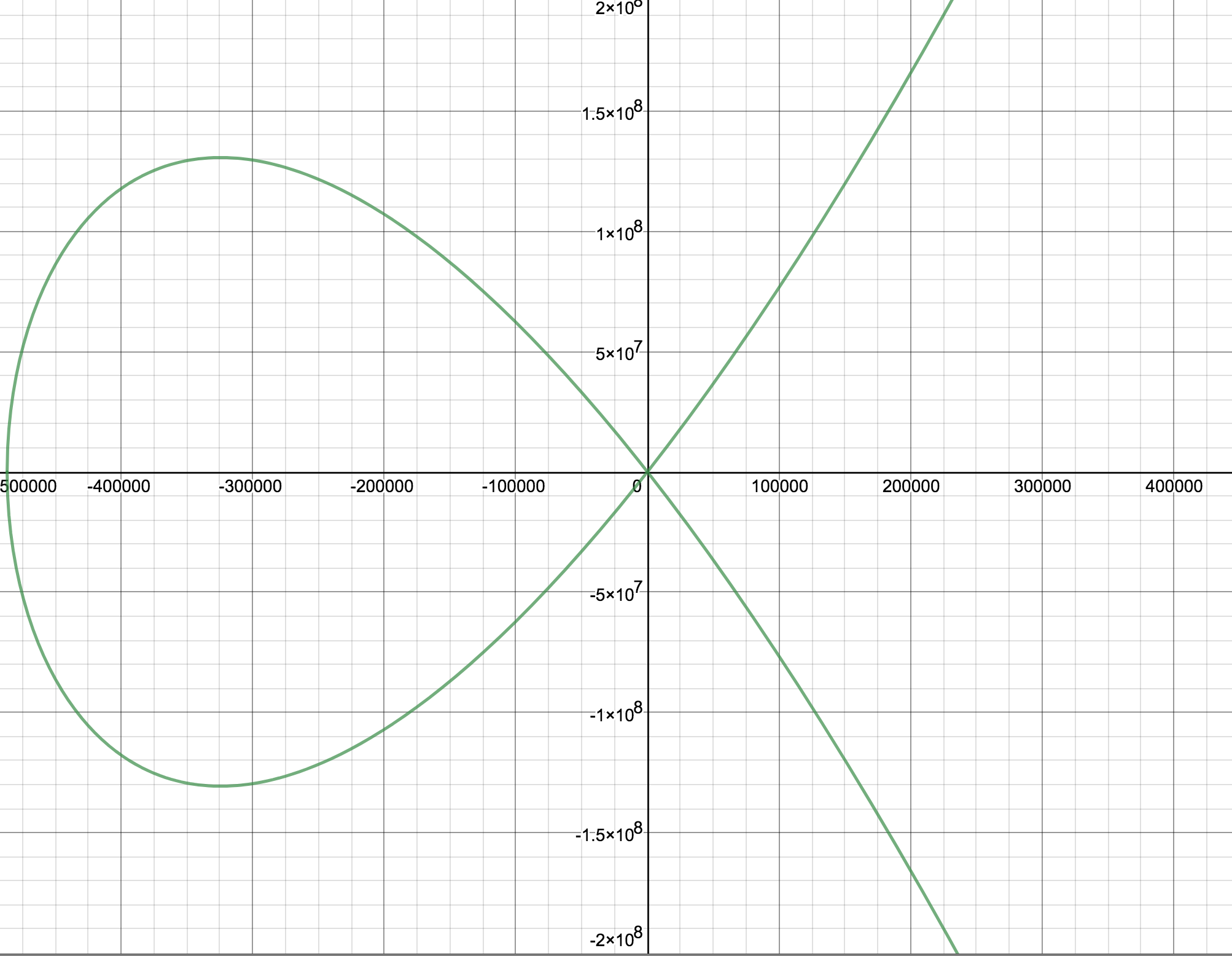
Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Go. ECDH. ECDH with Go.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret. We will use Golang and the Krytology library.
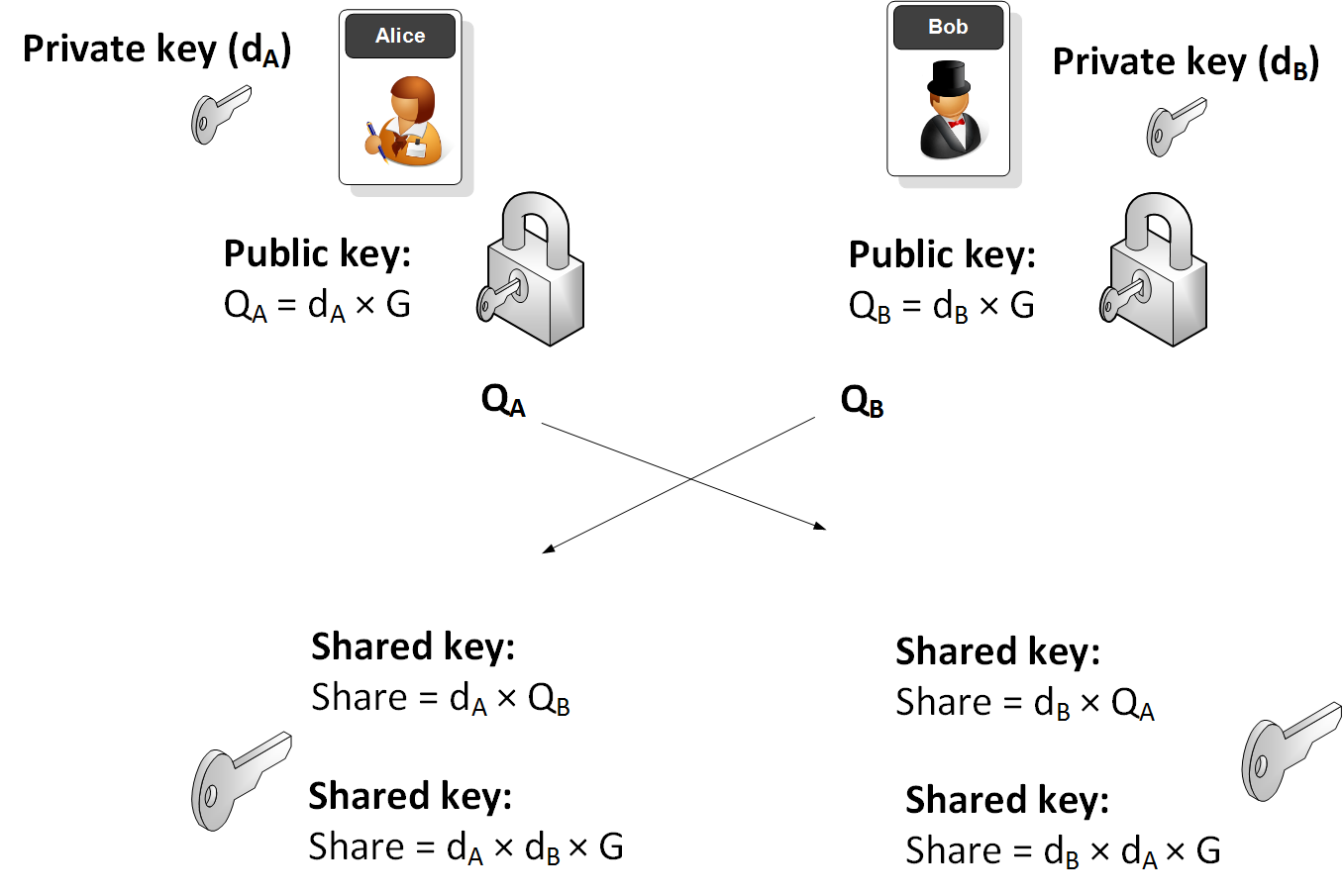
Elliptic Curve (ECDH) - Node.js
The following are the tips related to ECC:
- ECDH with node.js. ECDH. ECDH with node.js.
- ECDH with JavaScript. ECDH. Elliptic Curve Diffie Hellman.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Key exchange
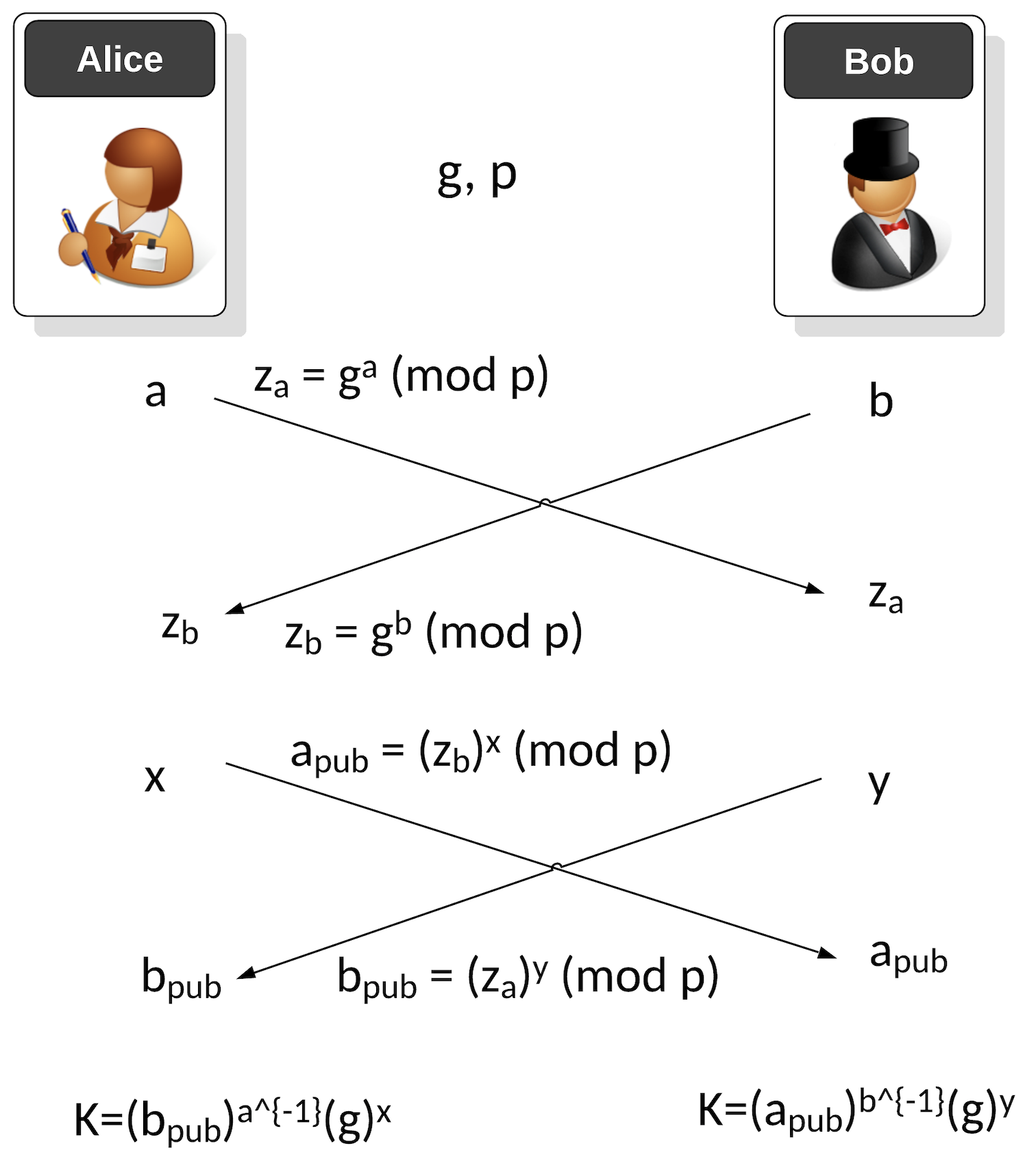
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). The resultant key is \(xyG \)
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
- Authenticated Key Exchange (ECC). YAK. Key exchange with public keys and uses elliptic curve methods.
ECDSA (Elliptic Curve Digital Signature Algorithm)

ECDSA has been around for over two decades and was first proposed in [1]. The ECDSA method significantly improved the performance of signing messages than the RSA-based DSA method. Its usage of elliptic curve methods speeded up the whole process and supported much smaller key sizes. Its crown and glory were being selected by Satoshi Nakamoto for his Bitcoin protocol, and then its adoption into Ethereum.
ECDSA Basics
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Recoving the public key from an ECDSA Signing in Python. Recoving public key from ECDSA Signing. This is an example of recovering the public key from the ECDSA signature with Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\)).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\)) and will check that the signature is valid.
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
-
ECDSA for Multiple Curves and Different Hashing Methods with Python
. ECDSA for Multiple Curves and Different Hashing Methods with Python. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
- ECDSA Signatures with Hazmat (SECP256R1, SECP384R1, SECP521R1, SECP224R1, SECP192R1, and SECP256K1). ECC Signatures. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and then creates an ECDSA signature for a given message.
- DSSE (Dead Single Signature Envelopes). DSSE. The Update Framework (TUF) provides a framework to secure the software within a system, while in-toto ("as-a-whole") can be used to protect the whole of software support chain. TUF thus delivers updates to a system while in-toto manages a complete software infrastructure. For this, it uses the Metablock format, and where we do not sign the byte values for the signature but sign the JSON data. This is known as canonicalisation - and which is the conversion of data in different forms to a standardised format.
Elliptic Curve (DER)
The following are the tips related to ECC:
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Google Tink with ECDSA
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
ECDSA Applications
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Blinded ECDSA. Blinded ECDSA. With a blinded signature, Bob can sign for a message, without knowning what the message is. In this case Alice will create a blinded ECDSA signature, and where Bob can then sign it, and then Alice can unblind it. The method is based on one produced by Oleg Andreev for blinding signatures in Bitcoin.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA: Fault Attack. ECDSA: Fault Attack. In the fault attack in ECDSA we only require two signatures. One is produced without a fault \((r,s)\), and the other has a fault \((r_f,s_f)\). From these we can generate the private key.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Elliptic Curve Integrated Encryption Scheme (ECIES)

With ECIES we integrate the power of elliptic curve (EC) public key encryption with symmetric key encryption. An outline of the method is:
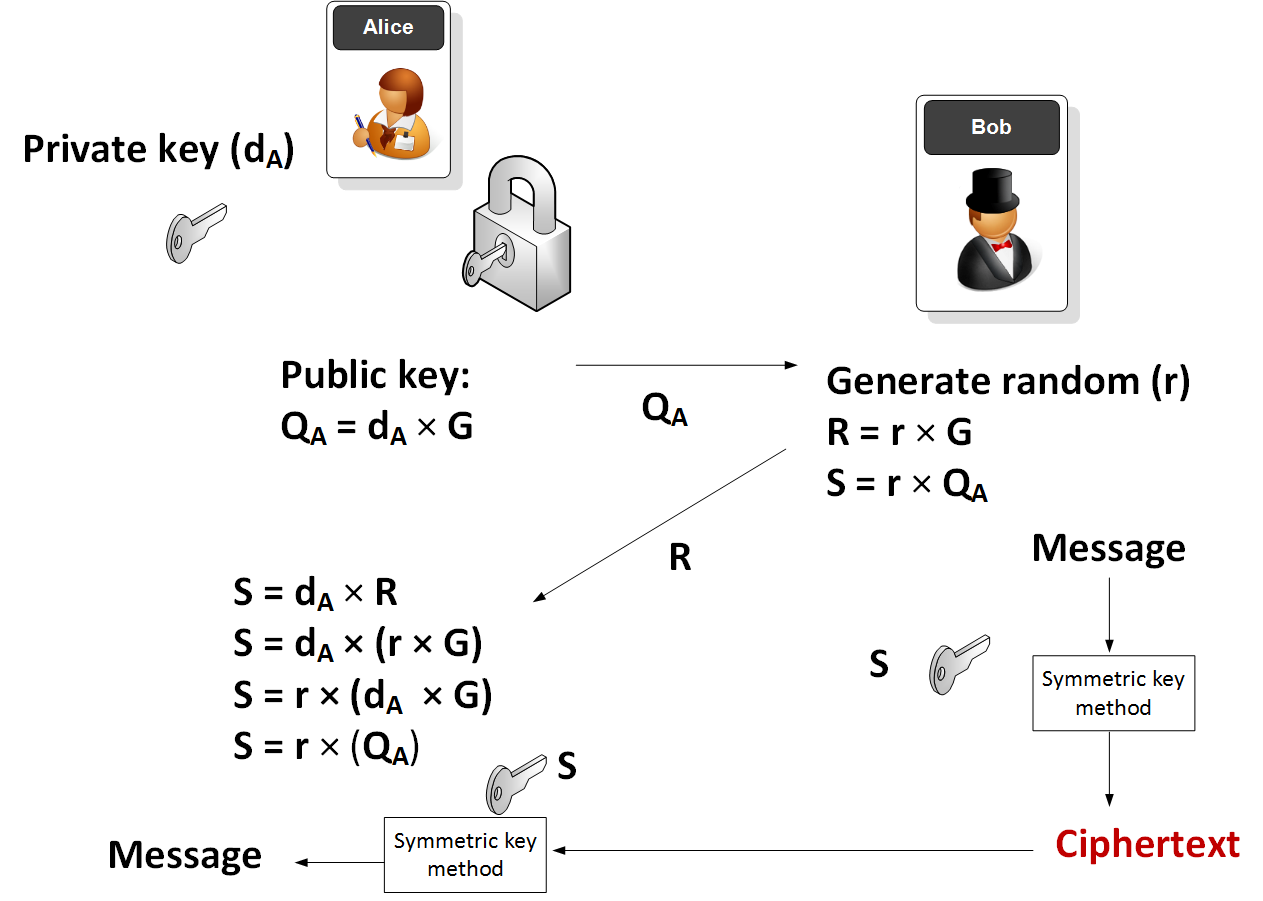
Elliptic Curve (ECIES)
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Elliptic Curve Integrated Encryption Scheme (ECIES with Rabbit Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with Rabbit (a light-weight stream cipher).
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
Applications
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- ECIES (Kryptology). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Coinbase Kryptology library.
- ECIES (CIRCL). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Cloudflare CIRCL library.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
Ethereum crypto
- ECIES with Go-Ethereum. Go.
EdDSA, Ed25519 and Ed448

Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). EdDSA (Edwards-curve Digital Signature Algorithm) is a fast and efficient digital signature method, and is based on the Schnorr signature scheme. Two important curves that are implemented with EdDSA are Curve 25519 (X25519) and Curve 448 (Ed448). EdDSA has been standardized in [RFC 8032]. With EdDSA, Alice generates a private key of \(sk\) and a public key of \(P=sk.G\) and where \(G\) is the base point of the curve.
Elliptic Curve (Signatures - EdDSA)
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Ed25519 in Python. EdDSA in Python. This page implements EdDSA using the Pure25519 library and with the core functions of key generation, signature generation and signature verification.
- Ed25519 Vulnerability in Python. EdDSA Vulnerability in Python. This page implements EdDSA using the Pure25519 library and with the core functions of key generation, signature generation and signature verification.
- Ed25519 Vulnerability in Python (Proof of Concept). EdDSA Vulnerability in Python (PoC). This page implements EdDSA using the Pure25519 library and with the core functions of key generation, signature generation and signature verification.
Hazmat (Ed448 and Ed25519)
- Ed25519 for EdDSA signatures with Hazmat. EdDSA: Ed25519. This page uses the Hazmat primitives for the cryptography library for X25519.
- Ed448 for EdDSA signatures with Hazmat. EdDSA: Ed25519. This page uses the Hazmat primitives for the cryptography library for X448
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
Golang
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
- Barebones Ed25519 with Go. ECC. This shows point addition and scalar multiply in Ed25519
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
COSE/COBR
- EdDSA. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) [2] can then build on this to includes signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case, we will use EdDSA to create a signature for a message.
Testing Ed25519
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
NaCl
- Ed25519 signature using NaCl. eddsa. This page uses the NaCl port from libsodium.
- Ed25519 points using NaCl. eddsa. This page uses the NaCl port from libsodium to determine Ed25519 points.
Theory
With EdDSA, Alice will sign a message with her private key, and then Bob will use her public key to verify that she signed the message (and that the message has now changed):
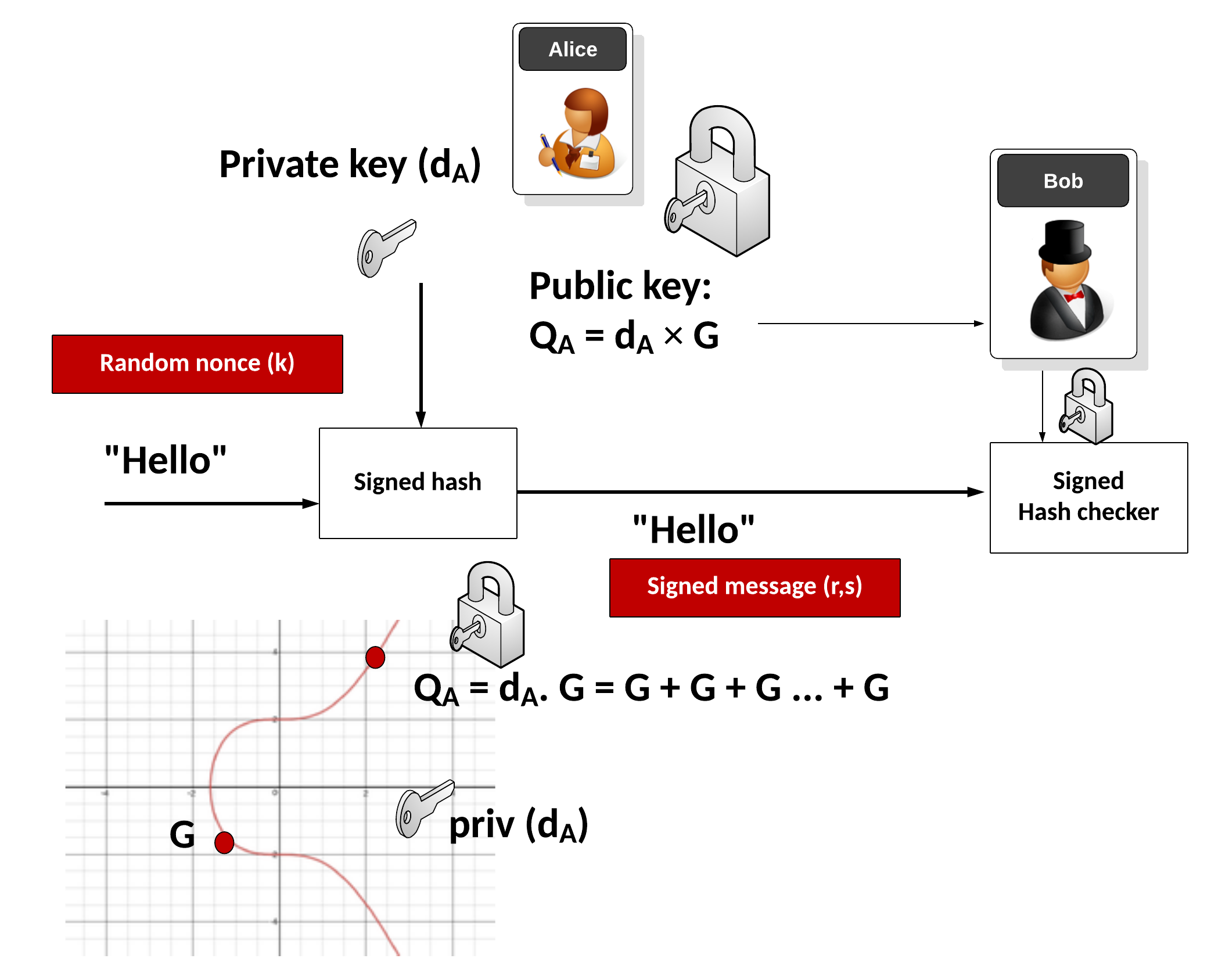
Key generation
Alice generates a random 32-byte secret key (\(sk\)) and then creates a public key of:
\(pk=sk \cdot G\)
and where \(G\) is the base point of the curve.
Signing
Alice creates a SHA-512 hash of her private key:
\(h=\textrm{HASH}(sk)\)
Create \(r\) from the upper 32 bytes of hash and the message:
\( r = \textrm{HASH}(h[32:] \: || \: m))\)
And where "||" represents a concatenation of the byte array values. Next she matches \(r\) onto curve with:
\(R=r \cdot G\)
Next Alice computes \(s\) with:
\(s=r + (\textrm{HASH}(R \: || \: pk \: || \: m)) \cdot sk\)
The signature is (\(R,s\)). The values of \(R\) and \(s\) are 32 bytes long, and thus the signature is 64 bytes long.
Verifying
Bob creates \(S\) using \(R\), \(pk\) and \(m\):
\(S =\textrm{HASH}(R \: || \: pk \: || \: m) \)
And next creates two verification values:
\(v_1=s \cdot G\)
\(v_2=R+ pk \cdot S\)
If \(v_1==v_2\) the signature checks. This is because:
\(
\begin{align}
v_1&=s.G\\
&= (r + (\textrm{HASH}(R \: || \: pk \: || \: m)) \cdot sk) \cdot G \\
&= rG + sk \cdot G \cdot (\textrm{HASH}(R \: || \: pk \: || \: m)) \\
&= R+ pk \cdot S \\
&= v_2
\end{align}
\)
ElGamal

Public key encryption is typically used to sign for things (and where we use the private key to encrypt something and prove this with the public key) and within key exchange methods. The core methods used are RSA and Elliptic Curve. But an alternative is to use discrete logarithms. One of the most interesting is ElGamal, and was created by Taher Elgamal in 1985.
ElGamal Method
- ElGamal. ElGamal. ElGamal is a public key method which uses discrete logarithms.
- ElGamal in Python. ElGamal in Python. ElGamal is a public key method which uses discrete logarithms.
- ElGamal in Python with variable prime sizes. ElGamal in Python for different prime sizes. ElGamal is a public key method which uses discrete logarithms.
- Selecting g in ElGamal. G in ElGamal. ElGamal is a public key method which uses discrete logarithms.
- Selecting g in discrete logs. g in discrete logs. This select a generator in discrete logs.
- Selecting g in discrete logs with random primes. g in discrete logs with random primes. This select a generator in discrete logs using random prime numbers which are define by a number of bits.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- Proving an Encrypted Shuffle With ElGamal and ECC. Shuffle. An encrypted shuffle with ElGamal.
- ElGamal encryption with Powershell. ElGamal encryption.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Commutative Encryption
- Commutative Encyption (Modified ElGamal). Commutative Encyption. Commutative Encyption allow Bob and Alice to encrypt a message, and then for the data to be decrypted usign any order of the keys.
ElGamal Signature
- ElGamal signatures. ElGamal. ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this.
- ElGamal signatures (alterative signing). ElGamal (Signing: s=ar + kh(m)). ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this. Normally we sign with \(s=k^{-1} (h(m)-ar) \pmod {p-1}\), but in this case we will use \(s=ar + kh(m))\).
- ElGamal signatures (alterative signing). ElGamal (Signing: s=ah(m) + kr). ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this. Normally we sign with \(s=k^{-1} (h(m)-ar) \pmod {p-1}\), but in this case we will use \(s=ah(m) + kr\).
- ElGamal signatures (alterative signing). ElGamal (Signing: r=as+kh(m)). ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this. Normally we sign with \(s=k^{-1} (h(m)-ar) \pmod {p-1}\), but in this case we will use \(r=as+kh(m)\).
- ElGamal signatures (alterative signing). ElGamal (Signing: r=ah(m) +ks). ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this. Normally we sign with \(s=k^{-1} (h(m)-ar) \pmod {p-1}\), but in this case we will use \(r=ah(m) +ks\).
- ElGamal encryption with Go. ElGamal. This implements ElGamal encryption.
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
ElGamal Homomorphic Encryption
- ElGamal Homomorphic Cipher for Multiplication (Python). ElGamal. This outlines ElGamal Homomorphic multiplication with Python.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (Python). ElGamal. This outlines ElGamal Homomorphic division with Python.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (Python). ElGamal. This outlines ElGamal Homomorphic addition with Python.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (Python). ElGamal. This outlines ElGamal Homomorphic subtraction with Python.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
- ElGamal Homomorphic Cipher (Go). ElGamal. This outlines ElGamal Homomorphic cipher with Go.
- ElGamal Homomorphic Cipher (Go) - Divide. ElGamal. This outlines ElGamal Homomorphic cipher with Go with divide.
- ElGamal Homomorphic Cipher (Go) - Additive. ElGamal. This outlines ElGamal Homomorphic cipher with Go with addition.
ElGamal and ECC
- ElGamal with ECC. ElGamal with ECC. ElGamal using ECC.
- Proving an Encrypted Shuffle With ElGamal and ECC. Shuffle. An encrypted shuffle with ElGamal.
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- ElGamal - Applying Multiple Public Key Operations (ECC). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use elliptic curve methods, and using the Edwards 25519 curve.
ElGamal (Authenticated and Verified Encryption)
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenticated ciphertext.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
ElGamal (Encrypting with multiple public keys)
- ElGamal - Applying Multiple Public Key Operations (Discrete Logs). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use discrete logs.
- ElGamal - Applying Multiple Public Key Operations (ECC). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use elliptic curve methods, and using the Edwards 25519 curve.
Ethereum

This page outlines some examples of blockchain and cryptocurrency.
Test Network
- Math functions on Local Network. Go.
- Math functions on Test Network. Go.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- Storing State in a Smart Contract. Go.
- Deleting Data From A Smart Contract. Go.
- A Caesar Cipher Quiz Generator from a Smart Contract. Go.
- Hashing in a Smart Contract. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
- Dealing With Decimals In Smart Contracts. Go.
- Creating A Scrambled Alphabet Challenge Generator In Ethereum and Solidity. Go.
- Deploying a Scrambled Alphabet Generator To Ethereum (With Ganache and Ropsten). Go.
- Deploying a Scrambled Alphabet Generator To Ethereum (With Hardhat). Go.
- Pigpen, IPFS and Ethereum. Go.
- Proof of \(x\) from \(H(x)\) using zkSnarks. Go.
- Elliptic Curve Operations Within a Solidity Contract. Go.

Ethereum
- Creating Ethereum address with Python. Go.
- Creating Ethereum signing with Python. Go.
- ERC20 Tokens. Go.
- Ethereum address with Go. Addresses. This generates an Ethereum address.
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- PATRICIA trie. PATRICIA. Example of using PATRICIA (and which is used in Ethereum).
- Viewing Balance of account in Etheruem with Go. Balance. This views the balance of an account
- Viewing Block in Etheruem with Go. Block. This views a block.
- Viewing Cryptocurrency API with Python. Go.
- Viewing Ethereum blockchain with Python. Go.
- Viewing Transactions in Block in Etheruem with Go. Transactions. This views transactions.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
- Symmetric Key Encryption For Smart Contracts. Symmetric key. Solidity does not natively support symmetric key encryption, such as with AES. Overall, AES would consume too much gas and thus be expensive to implement. But, we can use hashing and X-OR methods to do the encryption. In this case, we will create a 256-bit random value, and then encrypt it with an encryption key, and then decrypt it.
Calling from Python
- Calling smart contracts with Python. Python.
Ethereum crypto
- ECIES with Go-Ethereum. Go.
Ethereum Blockchain
- IOTA Trytes. Trytes. `This outlines Trytes, as used in IOTA.
Ethereum Blockchain
- Blockchain: Adding Maths Functions. Go.
- Blockchain: Blocks, transactions and writing data. Go.
- Blockchain: Contracts and Addresses. Go.
- Blockchain: Getting transactions. Go.
- Blockchain: Hello World!. Go.
- Blockchain: Simple Purchasing System. Go.
- Blockchain: Viewing the blockchain. Go.
- Blockchain: Cracking Wallets. Go.
- Introduction to Blockchain. Go.
Presentations
Factorization

Many public key problems involve the difficulity in factorizing a value two its prime number factors. For example, in RSA, we have a public modulus \(N\) and which is equal to the multiplication of two prime numbers \(p\) and \(q\). If we can factorize the public modulus, we will be able to break the RSA cipher related to it.
RSA Crack
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA Factorization. RSA. This outlines the factorisation of the N value in the RSA method.
Methods
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Dixon. Go. Dixon Method.
- Rho factorization. Rho. Rho alogorithm.
- Smooth numbers. Go. Outline of smooth numbers.
Methods (Elliptic curve
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Quadratic residues
- Quadratic residue (mod p). Go. Outline of quadratic residue \(\pmod p\).
- Quadratic residue (mod p) using Legendre symbol. Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
Factorizing
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
Lenstra–Lenstra–Lovász (LLL) with lattices
- Crack ECDSA with weak nonces. ECDSA with weak nonces and using Lenstra–Lenstra–Lovász (LLL) method. This outlines ECDSA how the private key can be recovered with weak nonce values.
Network Forensics

These pages outlines some network forensics. This includes the understanding of the network stack, and with protocols such as Etherenet, IP, TCP, HTTP, and others.
Network Forensics (Theory)
- Network Forensics (Wireshark). Network Forensics. This provides information on how to detect threats through network forensics with Wireshark.
- Advanced Network Forensics. Network Forensics. This provides information on how to detect threats through network forensics.
Network Forensics (Practice)
- Advanced Network Forensics (Wireshark). Adv Network Forensics. This provides information on how to detect threats through network forensics with Wireshark.
- Network Forensics (PCAP). Network Forensics. This provides information on network forensics (reading PCAP files)
- Network Forensics (Text). Network Forensics. This provides information on network forensics (reading text files)
Tshark
-
Filters with TShark. TShark. This page runs Tshark with a given Pcap file and a defined filter.
Other
- Advanced Digital Forensics . Adv Digital Forensics. This provides information on how analyse disk based systems using open source forensics.
- Partition Analyser. MBR. This page will analyse the details of the partition details within the MBR (put one space between fields).
Presentations
Format Preserving Encryption

Format Preserving Encryption (FPE) is a method which allows the basic formatting of a message to stay in a similar format, and where the value itself is encrypted. It can be used to hide credit card details.
Methods
- Format Preserving Encryption. FPE. This outlines Format Preserving Encryption.
- FPE with Python. FPE. An implementation of Format Preserving Encryption (FPE) using Python.
- FPE with node.js. FPR. FPE with node.js.
- FPE and PKBKDF2 in Python. FPE and PKBKDF2 in Python. FPE using PKBDF2 to password generation.
FFX (Format-preserving, Feistel-based encryption)
- FPE with Go. FPE. An implementation of Format Preserving Encryption (FPE) for FFX1 and FFX3.
- FFX schemes. FFX. Within tokenization we can apply format preserving encryption (FPE) methods, which will convert our data into a format which still looks valid, but which cannot be mapped to the original value. For example, we could hide Bob's credit card detail into another valid credit card number, and which would not reveal his real number. A tokenization server could then convert the real credit card number into a format which still looked valid. For this we have a key which takes the data, and then converts it into a form which the same length as the original.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher in Python.
FFX in Rust
- FFX. FFX. This is an implementation of FFX in Rust.
Honey Encryption
- Honey Encryption. Honey. This outlines Honey encryption.
Crypto Principles

This page outlines some crypto principles.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Galois fields (polynomial operations)

This page outlines a few basic principles around the usage of Galois fields and polynomial operations. In 1832, Évariste Galois died of duelling wounds at the age of 20 but left a great legacy. While he was a teenager he worked on polynomials and laid down the principles of Galois theory, along with defining the concept of a finite field. In cryptography, the finite field is one of the major concepts and involves limiting the number of possible values to a limiting factor (\(p\)). The values of the field then range from 0 to p-1. Within a field, we can operate on values in the field using arithmetic operations. We can thus have an infinite field, and where we could include all of the possible integers. A finite field or Galois field of GF(\(2^n\)) has \(2^n\) elements. If \(n\) is four, we have 16 output values. Let’s say we have a number \(a∈{0, ... ,2^{n−1}}\), and represent it as a vector in the form of a polynomial:
\( a=a0+a_1 x+a_2 x^2 ... a_{n−1} x^{n−1}\)
If we use \(a_n∈{0,1}\), this is exactly the same as representing a binary number modulo \(2^n\). In this \(x^n\) represents bit position \(n\) and \(a_n\) is the value of the bit at position \(x^n\). If a bit is a zero at a given position, it will be not included in the polynomial equation. So, 1011 can be represented by \(x^3+x+1\) and 1010 is represented as \(x^3+x\). We can then perform arithmetic operations on these polynomial values. So, to add two values of 1010+1100 we can represent this as \((x^3+x)+(x^3+x^2)\) and which is \(x^2+x\) as we are using modulo 2 addition, and where \(x^3+x^3=0\). With modulo 2 addition, 0+0=0, 0+1=1, 1+0=1, and 1+1=1.
An example of Galois Fields is within AES (Advanced Encryption Standard) and which uses a finite field GF(\(2^8\)). With AES we operate on bytes (8 bits) in the form of \(b_7 b_6 b_5 b_4 b_3 b_2 b_1 b_0\) and which are operated on a a polynomial of \(b_7x^7+b_6x^6+b_5x^5+b_4x^4+b_3x^3+b_2x^2+b_1x^1+b_0\).
Galois fields (polynomial operations) - GF(\(p^n\))
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Additive Group Table for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Additive Group Table for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of addition. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the additive group table for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values.
- Multiplicative Group Table for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Multiplicative Group Table for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the additive group table for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values.
- Additive, Division and Multiplicative Group Table for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Additive, Division and Multiplicative Group Table for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the Additive, Division and Multiplicative Group Table for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values.
- Additive and Multiplicative Group Table for GF(\(2^2\)) and GF(\(2^3\)). Galois Fields Table for GF(2^m) with polynomials. This page implements Galois Fields GF(\(2^n\)) with Python and provides a table of additional and multiplication. It outlines GF(\(2^2\)) and GF(\(2^3\)), but also gives a program that can be used for others. Overall, we have the form of GF(\(p^n\)) and which provides use both an additive and a multiplicative group operations that provide all the possible outputs within the finite field. The value of \(p\) is a prime number, and \(n\) is any positive integer.
- Additive and Multiplicative Group Table for GF(\(2^2\)) and GF(\(2^3\)). Galois Fields Table for GF(2^m) with coefficient values. This page implements Galois Fields GF(\(2^n\)) with Python and provides a table of additional and multiplication. It outlines GF(\(2^2\)) and GF(\(2^3\)), but also gives a program that can be used for others. Overall, we have the form of GF(\(p^n\)) and which provides use both an additive and a multiplicative group operations that provide all the possible outputs within the finite field. The value of \(p\) is a prime number, and \(n\) is any positive integer. This version will show the polynomial coefficent values within the Galois Field.
- Additive and Multiplicative Group Table for GF(\(2^2\)) and GF(\(2^3\)). Galois Fields Table for GF(2^m) with integer values. This page implements Galois Fields GF(\(2^n\)) with Python and provides a table of additional and multiplication. It outlines GF(\(2^2\)) and GF(\(2^3\)), but also gives a program that can be used for others. Overall, we have the form of GF(\(p^n\)) and which provides use both an additive and a multiplicative group operations that provide all the possible outputs within the finite field. The value of \(p\) is a prime number, and \(n\) is any positive integer. This version will show the integer values within the Galois Field.
Irreducible polynomial for GF(p^n)
- Irreducible polynomial for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Irreducible polynomial for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the parameters for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values. This includes finding the irreducible polynomial for the Galois Field.
- Irreducible polynomial for GF(\(p^n\)) for a given \(p\) and for \(n\) values. Irreducible polynomial for GF(p^n) for a given p and for n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the parameters for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values. This includes finding the irreducible polynomial for the Galois Field. Other important parameters include the degree (the highest polynomial power) and the order (the number of possible output values).
- Conway and primitive polynomial GF(\(p^n\)). Conway and primitive polynomial GF(p^n). This page outlines Conway and primitive polynomials for GF(\(p^n\)).
Galois fields (polynomial operations) - GF(\(p\))
- Additive and Multiplicative Group mod n (\(Z_n\)). Additive and Multiplicative Group mod n. In finite fields, we have a \(\pmod n\) operation for a list of integers (\(\mathbb{Z}\)), and where \(n\) is a prime number. This works for our add (+) and multiply (\(\times\)) operations, and where: \( a \pmod n + b \pmod n = (a+b) \pmod n\); and \(a \pmod n \times b \pmod n = (a \times b) \pmod n\).
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Polynomial GF(2) Factoring and Irreducible Polynomials. Factors. This outlines the search for polynomial factors for GF(2).
Polynomial operations
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
Post-quantum
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Rust
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Sage
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Golang and Cryptography

The new scripted languages such as Python and Node.js are convenient. But, unfortunately, they can be slow as they are scripted, and not compiled. Each time the scripted code is run, the scripting engine must then convert each line of code to the required machine level code. This makes the code much slower than compiled languages, and also less robust. Thus many applications in cryptography are written in C and C++, as they allow for fast execution and give low level access. Unfortunately it can be complex to compile programs, as we often need to install binary libraries and then link these in. The Go programming language, though, has a similar code syntax to C/C++, but is small and efficient and allows access to low-level functions, such as as pointers. Go thus aims to “Code less, compile quicker, execute faster”. So let’s use Go to implement some cryptography methods, including symmetric key, hashing, public keys and zero-knowledge proofs (ZKPs). The slides related to these methods are included [here]. An introduction to Golang and Cryptography is [here].

Go ECDH
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret.
Go Hex and Base64
- Base64 and Hex in Go. Base64/Hex. Two common formats for representing binary data are hexademical and Base64.
Go symmetric key
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Reuse IV attack and AES. Reuse IV and GCM. This provides an implementation of a reuse IV against AES GCM.
- ASCON AEAD (Golang). ASCON AEAD (Golang). The outlines the usage of AEAD for ASCON using Golang.
Go HMAC and HKDF
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HKDF in Go. HKDF. Implementation ofHKDF, and where we dervice a key based on a given secret.
Go secret shares
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.

Go ZKP
- Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL). DLEQ. Create a non-interactive ZKP for discrete logs.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Fiat Shamir and ECC (Interative ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP with Kryptology. This implements a range proof using a Schnorr proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?

Go ECIES (Hybrid Encryption)
With this, we can use the power of public key encryption (to generate the encryption key) with symmetric key encryption (to actually encrypt and decrpyt the data):
- ECIES (Kryptology). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Coinbase Kryptology library.
- ECIES (CIRCL). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Cloudflare CIRCL library.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt and which is used in Contract Tracing for COVID-19.
Go ECDSA
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Go RSA
- RSA Principles. RSA Principles. The basics of RSA.
- RSA with Go. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA. RSA encryption with Go using OAEP.
- RSA Encryption with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
Go ElGamal
ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Proving an Encrypted Shuffle With ElGamal and ECC. Shuffle. An encrypted shuffle with ElGamal.
- ElGamal encryption with Go. ElGamal. This implements ElGamal encryption.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
- ElGamal - Applying Multiple Public Key Operations (ECC). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use elliptic curve methods, and using the Edwards 25519 curve.
Go PGP
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
Go Public key
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.

Go Hashing
- Hashing with Go. Hashing. Hashes with Go.
- GP Hashing with Go. GP Hashing. GP Hashes with Go.
- SHAKE with Go. SHAKE. This implements SHAKE in Go.
- libDisco with Go. libDisco. This implements libDisco.
- cSHAKE in Golang. cSHAKE. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS. With the SHA-3 hashing method, we have four different cryptographic hashing methods (SHA3-224, SHA3-256, SHA3-384, and SHA3-512) and two XOF functions (SHAKE128 and SHAKE256). With SHAKE128 and SHAKE256 we can integrate domain separation between different functions — and which are known as cSHAKE128 and cSHAKE256.
- Homomorphic Hashing with Golang. Homomorphic hashing. Normally with hashing methods, we need to take all the previous data and new data in order to create a new hash value for our data. In a homomorphic hashing method, we can basically take the previous hash, and then add on any new data values. We can also remove previous data values from our hash, too. This is more efficient in computing, as we do not have to process all of our data into a new hash, and can use simple homomorphic operations for the computation. The method we will use (LtHash) was initially defined by Bellare and Micciancio and updated Lewi et al at Facebook.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
Go ECC
- Hash to password with Go. Hash to password. Hash to password with Go.
- ECDH with Go. ECDH. ECDH with Go.
- Box with Go. Box. Box with Go.
- ECC with Go. ECC. ECC with Go.
- Curve 25519 with Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ElGamal with ECC. ElGamal with ECC. ElGamal using ECC.
- Curve 25519 with Go for test vectors. ECC. This does a test on some private keys to test the public key generation.
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Barebones Ed25519 with Go. ECC. This shows point addition and scalar multiply in Ed25519
- Barebones NIST P256 with Go. ECC. This shows point addition and scalar multiply in P256
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining \(n.G\) for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Points (Base Point and Others). Elliptic Curve points. Two common curves used in ECC (Elliptic Curve Cryptography) are secp256k1 (as used in Bitcoin and Ethereum) and P256 (secp256r1). The "k1" refers to the Kolbitz curve 1 (named after the creator of ECC). With these we have a base point which are can operate on. This is typically defined as \(G\). We can then operate on this with add and multiply operation. For example, \(2G=G+G\) and \(P=n.G\). In this following we will show the base point for a number of common curves, such as secp256r1, P256, Pallas, Curve 25519, BLS12381G1, BLS12381G2, BLS12377G1 and BLS12377G2.
Go Blockchain
- Ethereum address with Go. Addresses. This generates an Ethereum address.
- Viewing Balance of account in Etheruem with Go. Balance. This views the balance of an account
- Viewing Block in Etheruem with Go. Block. This views a block.
- Viewing Transactions in Block in Etheruem with Go. Transactions. This views transactions.

Go Homomorphic
- SIDH Go. SIDH. Post-quantum key exchange.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- NTP. NTP. An overview of NTP.
- BiBa. BiBa. An overview of BiBa One Time Signature.
Go DNS
- DNSSEC. DNSSEC. An overview of DNSSEC.
Go Signatures
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Go Signcryption
- Ahmad-Afzal-Iqbal (AAI) signcryption with Golang. Ahmad-Afzal-Iqbal (AAI). Ahmad-Afzal-Iqbal (AAI) signcryption with Golang.

Go Crypto pairing
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
Go Homomorphic
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add. HEAAN Add. HEAAN Add.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- Anonymous crypto. Anon. Anonymous crypto.
- Rho factorization. Rho. Rho alogorithm.
- Post-quantum signing (BLISS). BLISS. BLISS method.
Go Post quantum
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.

Go CIRCL
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- Ed448 with Go. X448. Ed448 with Go.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with FourQ (Cloudflare). FourQ.
- Verifiable Oblivious Pseudorandom Functions (VOPRF) with Cloudflare CIRCL. VOPRF. In our digital world, we give away too many of our secrets, especially where we just have to prove the knowledge of something, rather than actually revealing it. In many of the systems we use, we could just prove things in an oblivious way, and where we could pass a secret but in a blinded form. With this, a server does not discover our password and for us not to discover the identifier that a server holds on us. But, can we also provide a proof back that the right password has been used? Well, with Verifiable Oblivious Pseudorandom Functions (VOPRF), we can generate a random secret based on a key generated on the server (Alice), and which is based on Bob’s secret.
- Hash to Curve using Go (Cloudflare). Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). The method defined here is proposed an an Internet-Draft standard by the Internet Engineering Task Force (IETF) related to "Hashing to Elliptic Curves".
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
here Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
- eXtendable-Output Function (XOF) usign CIRCL. XOF. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS.

Go Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Google Tink (Golang) ECIES. Google Tink (ECIE5). This outlines ECIES encryption with public key and AES using Golang with Google Tink
Go Credentials
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.

Go Kryptology
- Public key points for curves. Simple. Display public key points for scalars.
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.

Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.

Principles
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Paillier
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
Go Format Preserving Encryption (FPE)
- FPE with Go. FPE. An implementation of Format Preserving Encryption (FPE) for FFX1 and FFX3.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
AWS Encryption
- AWS Symmetric Key Encryption. AWS (Symmetric key). Using symmetric key in AWS.
Go Oblivious Transfer
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Dragon Fly
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
Embedding data in an ECC point
- Embedding data in a point. Go. With Elliptic Curve Cryptography (ECC), we use points on an elliptic curve to represent our data. These are defined with (x,y) points. With this, it is possible to embedded a certain amount of data into the point - as long as it still gives us a valid point on the curve. This example will Curve 25519 to embed data, and is achieved by storing the length of the data in a single byte in the point, and then store the data as byte values in the point (followed by random data). To decode, we can then just read the first byte for the length of the message, and then reveal the data encoded into the point..
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Hashing (Cryptographic)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
Benchmarks and Password strength
The following are the tips related to hashing:
- Password strength. Test. This outlines the strength of various passwords types.
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
Theory
The following are the tips related to hashing:
- Balls in bins. BiBa. This implemented balls in bins.
- Birthday attack (with Big Integers). Calc. This provides a simple example of the birthday attack.
- Birthday attack. Calc. This provides a simple example of the birthday attack.
- Differential Cryptanalysis (Hashing). Cryptanalysis. This provides an implementation of differential cryptanalysis for hashing methods.
MD5, SHA-1
The following are the tips related to hashing:
- MD2 and MD4 MD2/4. The MD2 and MD4 hashing functions were developed by Prof Ronald Rivest in 1989 and 1990, respectively. They both produce a 128-bit hash, but have been shown be vulnerable to attack (see the Collision section in the page).
- MD5 and SHA-1 (to Base-64) with salt Salt. It is possible to add salt to the MD5 algorithm, to mix it up a little.
- MD5 and SHA-1 (to Base-64) Hash. MD5 and SHA-1 produces a hash signature, and the output is typically shown in a hex format or a Base-64. In this example the output is converted into a Base-64 format.
- MD5 and SHA-1. Hash. MD5 and SHA-1 methods produce a hash signature, and are the two of the most widely used methods. The MD5 algorithm has been shown to have weaknesses, and a collision of message hashes has been shown to occur in less than one day. An MD5 signature has 128 bits, an SHA-1 signature has 160 bits, and an SHA-256 signature has 256 bits.
- MD5 Cracking. Hash Cracker. MD5 has a 128-bit signature and can be cracked using rainbow tables. This page tries to crack the MD5 signature.
- Hashing with Go. Hashing. Hashes with Go.
- Detecting hash types. Hash type. This detects has values.
- OpenSSL hashing. Range of methods. Outlines the methods used in OpenSSL
- Hash. Hash. Hashing using JavaScript
- Hashing with node.js. Hashing. Hashing with node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Hashing methods
-
Hazmat Hashes. Hazmat Hashes. This includes the hashing methods in the Hazmat cryptography library. This includes Blake2p, Blake2s, MD5, SHA1, SHA224, SHA256, SGA384, SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHA512, SHA512-224, SHAKE128 and SHA256.
-
Hazmat Hashes. Hazmat Hashes. In this case we will implement Python code to determine SHA1, SHA2, SHA3, Blake2, MD5 and SM3 hashes.
OpenSSL Passwords
-
Password example [here]
-
Hashed passwords with OpenSSL [here]
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Blake 3 hashes
The following are the tips related to similarity hashing:
- Blake 3 in Python. Hashing. Blake 3 hashing.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
Other Hash functions
The following are the tips related to hashing:
- Bloom Filter Bloom filter. A Bloom filter goes a probabilistic method of determining if an element is in a data structure, using indexed hashing methods.
- Cuckoo Table Cuckoo filter. A Cockoo table uses two hash funtions.
- Chaffing. Chaffing. This produces a keyless system.
- GP Hashing with Go. GP Hashing. GP Hashes with Go.
- LDAP. LDAP. This produces a LDAP hash signature for a password.
- LM Hash. LM Hash. This is an LM Hash Calculator. LM Hash is used in many versions of Windows to store user passwords that are fewer than 15 characters long.
- Murmur and FNV Murmur and FNV. While hashing methods such as MD5 and SHA-1 use crypto methods, the Murmur and FNV hashes uses a non-cryptographic hash function. This can be used for general hash-based lookup and was designed by Austin Appleby. It has good performance compared with other hashing methods.
- Pearson. Pearson. This uses a non-crypto hash.
- phpass. phpass. This produces a phpass hash signature for a password.
- Tiger. Tiger. Tiger is a 192-bit hash function and was designed by Ross Anderson and Eli Biham in 1995. It is often used by clients within Gnutella file-sharing networks and does not suffer from known attacks on MD5 and SHA-0/SHA-1. Tiger2 is an addition, in which the message is padded with a byte of 0x80 (in a similar way to MD4, MD5, and SHA), whereas in Tiger it is 0x01. Otherwise, the two methods are the same in their operation.
- Whirlpool. Whirlpool. Whirlpool is a 512-bit cryptographic hash function and was created by Vincent Rijmen (one of the AES creators) and Paulo Barreto, in 2000.
- WPA-2 hash . WPA-2 hash. Implements SHA-2 hash.
- Reusable hash collisions. Reusable hash collisions. Reusable hash collisions.
- The Length Extension Attack. Length Extension Attack. The MD construct has many weaknesses, and one of the most serious is the length extension attack. With this an adversary (Eve) can take a hash for an unknown message, and then add additional data to produce a new valid hash. The hash methods which are at risk against the length extension attack are MD5, SHA-1 and SHA-256. Please follow the code link below to run an example.
- Consistent hashing. Consistent hash. This outlines the usage of Consistent hashes.
- ROR13 (Module and Function). ROR13. With ROR13 we take each 8-bit character and then convert to a unicode value (with 16 bits). Then for each character we rotate the bits right by thirteen places. The resultant hash is then just the accumuluation of the rotated values.
- ROR13 (Function). ROR13 (Function). With ROR13 we take each 8-bit character and then convert to a unicode value (with 16 bits). Then for each character we rotate the bits right by thirteen places. The resultant hash is then just the accumuluation of the rotated values.
- GOST, Streebog256 and Streebog512. GOST, Streebog256 and Streebog512. GOST94 is a hashing method developed with Euro-Asian Council for Standardization, Metrology and Certification (EASC). This has since been developed in the Streebog256 and Streebog512 hashing method. In this case, we will use Libre OpenSSL to convert data into a hashed value.
RIPEMD
- RIPEMD (RACE Integrity Primitives Evaluation Message Digest) and GOST. RIPEM160. RIPEMD is a 128-bit, 160-bit, 256-bit or 320-bit cryptographic hash function, and was created by Hans Dobbertin, Antoon Bosselaers, and Bart Preneel. It is used on TrueCrypt and is open source. The 160-bit version is seen as an alternative to SHA-1, and is part of ISO/IEC 10118
- RIPEMD160. RIPEM160. RIPEMD160 is a 160-bit cryptographic hash function, and was created by Hans Dobbertin, Antoon Bosselaers and Bart Preneel. RIPEMD160 is used in Bitcoin applications.
Chameleon hashes
The following are the tips related to Chameleon hashing:
- Chameleon hash in Golang Chameleon. With a Chameleon hash, we have a normal hash value which is resistant to collisions, but with a known secret we can easily create a collision. The concept was first defined by Krawcyk and Rabin.
Similarity hashes
The following are the tips related to similarity hashing:
- Similarity hash: SimHash (Charikar similarity) in Python Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash (Nilsimsa similarity) Nilsimsa. The Nilsimsa similarity is used to find similarities between spam emails.
- Minhash (Jaccard similarity) Jaccard similarity. The Minhash method is used to find similarities between strings, files and metadata.
- String enthropy String enthropy. Measurement of the entropy of strings.
- Counting identical elements (HyperLogLog) HyperLogLog. Counting the number of identical elements.
SHA-3 and SHA-3 contenders
The following are the tips related to Key derivation hashing:
- Blake and Blake 2. Blake. Implements Blake and Blake 2 (SHA-3 contender).
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
- Grøstl. Grøstl. Implements Grøstl (SHA-3 contender).
- KangarooTwelve. KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- SHA-3, Keccak and SHAKE . SHA-3. Implements SHA-3, Keccak and SHAKE (SHA-3 winner).
- SHA-3. SHA-3. SHA-3 was known as Keccak and is a hash function designed by Guido Bertoni, Joan Daemen, Michaël Peeters, and Gilles Van Assche. MD5 and SHA-0 have been shown to be susceptible to attacks, along with theoretical attacks on SHA-1. NIST thus defined there was a need for a new hashing method which did not use the existing methods for hashing, and setup a competition for competing algorithms. In October 2012, Keccak won the NIST hash function competition and is proposed as the SHA-3 standard. It should be noted that it is not replacement SHA-2, which is currently a secure method. Overall Keccak uses the sponge construction where the message blocks are XORed into the initial bits of the state, and then inevitably permuted.
- cSHAKE. cSHAKE. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS. With the SHA-3 hashing method, we have four different cryptographic hashing methods (SHA3-224, SHA3-256, SHA3-384, and SHA3-512) and two XOF functions (SHAKE128 and SHAKE256). With SHAKE128 and SHAKE256 we can integrate domain separation between different functions — and which are known as cSHAKE128 and cSHAKE256.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- Skein. Skein. Implements Skein (SHA-3 contender).
Key derivation hashing
The following are the tips related to Key derivation hashing:
- Argon2. Go. Outline of Argon2.
- Argon2 with NaCl. Go. Outline of Argon2 using NaCl.
- Balloon. Go. Outline of Balloon.
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- Double ratchet. Go. Outline of double ratcheting.
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- Scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat HKDF. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
Non-crypto/fast hashing
The following are the tips related to non-crypto hashing:
- A perfect hash Perfect hash. This is a non-crypto hash which optimizes the hash value.
- The universal hash Universal hash. This related to the concept of a universal hash.
- FNV. FNV. FNV is one of the fastest hashing methods.
- Murmur. Murmur. Murmur is one of the fastest hashing methods.
- Siphash. Siphash. Siphash is a fast hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- xxHash. xxHash. xxHash is one of the fastest hashing methods.
- Meow. Meow. Meow is one of the fastest hashing methods.
- o1Hash. o1Hash. o1Hash is one of the fastest hashing methods.
- CRC-32. CRC-32. CRC-32 is one of the fastest hashing methods.
- wyhash. wyhash. wyhash is one of the fastest hashing methods.
- CityHash. CityHash. CityHash is one of the fastest hashing methods, and is generally free of security problems.
- FarmHash. FarmHash. FarmHash is one of the fastest hashing methods, and is generally free of security problems.
- Non-crypto. Non-crypto. This includes a range of fast non-cryptography hashing methods.
- Non-crypto hashes (C++): Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro. Non-crypto hashes: Farm, City, xxHash, MUM, Spooky 2, Murmur, Metro and t1ha0. This includes a range of fast non-cryptography hashing methods for Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro using C++ methods.
- Pearson. Pearson. Pearson is one of the fastest hashing methods, and has been designed for 8-bit processors.
- C++: t1ha. t1ha. t1ha is one of the fastest hashing methods, and has been designed for 64-bit processors.
- C++: Spooky. Spooky. Spooky is one of the fastest hashing methods, and V2 has a 32-bit, 64-bit and 128-bit version.
- C++: xxHash. xxHash. xxHash is one of the fastest hashing methods, and has good performance for short data inputs.
- C++: MUM. MUM. MUM is one of the fastest hashing methods.
- C++: FNV 1/1a. FNV 1/1a. FNV 1/1a is one of the fastest hashing methods, and is particularily useful when there are small changes in strings, such as with IP addresses and URLs.
- C++: MetroHash. MetroHash. MetroHash is one of the fastest hashing methods.
- C++: CityHash. CityHash. CityHash was created by Google and is one of the fastest hashing methods. It was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Farm. FarmHash. FarmHash was created by Google and is one of the fastest hashing methods. It is an improvement to CityHash.
- C++: Murmur. Murmur. Murmur is one of the fastest hashing methods, but was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Halftime. Halftime. Halftime is one of the fastest hashing methods and was created by Jim Apple at Apache.
- C++: Highway. Highway. Highway is an ultra-fast keyed-hash, and is more than five times faster than SipHash. It was created by Jyrki Alakuijala, Bill Cox, Jan Wassenberg at Google.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
- C++: CLHash. CLHash. CLHash is an ultra-fast hashing method and focused on improving performance of the hashing of long strings.
- C++: FalkHash. FalkHash. FalkHash is an ultra-fast hashing method and beats most of the other non-cryptography methods for performance. It is focused on the x64 architecture and integrates with AES-NI.
- C++: wyHash. wyHash. wyHash is an ultra-fast hashing method.
- C++: Fibonacci. Fibonacci. Fibonacci is an ultra-fast hashing method.
- C++: Lookup3. Lookup3. Lookup3 is an ultra-fast hashing method.
Key-based hashing
The following are the tips related to Key-based hashing:
- SiphashSiphash. Siphash is a fast key-based hashing method.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
One Time Passwords/Time Stamps
The following are the tips related to hashing:
- One Time Passwords. One Time. This allows a new unique password to be created each instance, based on an initial seed.
- Timed One Time Password (TOTP). Timed One Time Password. This allows a new unique passcode to be created each instance, based on an initial seed for a given time window. We will use a five second window in this case, where a new passcode is generated every five seconds, based on an initial seed of a pass phrase.
- Hashed One Time Password (HOTP). Hashed One Time Password. This allows a new unique passcode to be created each instance, based on a counter value and an initial seed.
- Time Stamp Protocol. TSP. This creates a time stamp for data.
- HOTP and TOTP (Python). OTP. This creates hashed passwords.
eXtendable-Output Function (XOF)
- eXtendable-Output Function (XOF) usign CIRCL. XOF. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS.
SHAKE
The following are the tips related to hashing:
- SHAKE. SHAKE. Implements SHAKE and which is an Extendable Output Function (XOF).
- SHAKE with Go. SHAKE. This implements SHAKE in Go.
- libDisco with Go. libDisco. This implements libDisco.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify
the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods
such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC methods using the Python cryptography primitives for HMAC-MD5.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
Quantum-robust Public Key (Hash-based signature)
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
Hash to ECC point
- Hash to password with Go. Hash to password. Hash to password with Go.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve with libnum.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.

Password-hashing functions using Rust
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing (Non-cryptographic)

You might know those slow old hashing methods, such as MD5, SHA-1, and SHA-256. Well, they were designed to be fast, but also highly secure. But, if we just need a hashing method, such as for a hashtable or Bloom filter, we often don’t need all the security that comes with the main cryptography hashing methods. And so we have the non-cryptography hashing methods, and which are often ultra-fast and highly efficient. To show the difference, in a test, SHA-1 — one of the fastest cryptography hashing methods — managed a processing rate of 364.95 MiB/s, while t1ha was nearly a 100 times faster, at 34,636 MiB/s.
Non-crypto/fast hashing
The following are the tips related to non-crypto hashing:
- A perfect hash Perfect hash. This is a non-crypto hash which optimizes the hash value.
- The universal hash Universal hash. This related to the concept of a universal hash.
- FNV. FNV. FNV is one of the fastest hashing methods.
- Murmur. Murmur. Murmur is one of the fastest hashing methods.
- Siphash. Siphash. Siphash is a fast hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- xxHash. xxHash. xxHash is one of the fastest hashing methods.
- Meow. Meow. Meow is one of the fastest hashing methods.
- o1Hash. o1Hash. o1Hash is one of the fastest hashing methods.
- CRC-32. CRC-32. CRC-32 is one of the fastest hashing methods.
- wyhash. wyhash. wyhash is one of the fastest hashing methods.
- CityHash. CityHash. CityHash is one of the fastest hashing methods, and is generally free of security problems.
- FarmHash. FarmHash. FarmHash is one of the fastest hashing methods, and is generally free of security problems.
- Non-crypto. Non-crypto. This includes a range of fast non-cryptography hashing methods.
- Non-crypto hashes (C++): Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro. Non-crypto hashes: Farm, City, xxHash, MUM, Spooky 2, Murmur, Metro and t1ha0. This includes a range of fast non-cryptography hashing methods for Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro using C++ methods.
- Pearson. Pearson. Pearson is one of the fastest hashing methods, and has been designed for 8-bit processors.
- C++: t1ha. t1ha. t1ha is one of the fastest hashing methods, and has been designed for 64-bit processors.
- C++: Spooky. Spooky. Spooky is one of the fastest hashing methods, and V2 has a 32-bit, 64-bit and 128-bit version.
- C++: xxHash. xxHash. xxHash is one of the fastest hashing methods, and has good performance for short data inputs.
- C++: MUM. MUM. MUM is one of the fastest hashing methods.
- C++: FNV 1/1a. FNV 1/1a. FNV 1/1a is one of the fastest hashing methods, and is particularily useful when there are small changes in strings, such as with IP addresses and URLs.
- C++: MetroHash. MetroHash. MetroHash is one of the fastest hashing methods.
- C++: CityHash. CityHash. CityHash was created by Google and is one of the fastest hashing methods. It was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Farm. FarmHash. FarmHash was created by Google and is one of the fastest hashing methods. It is an improvement to CityHash.
- C++: Murmur. Murmur. Murmur is one of the fastest hashing methods, but was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Halftime. Halftime. Halftime is one of the fastest hashing methods and was created by Jim Apple at Apache.
- C++: Highway. Highway. Highway is an ultra-fast keyed-hash, and is more than five times faster than SipHash. It was created by Jyrki Alakuijala, Bill Cox, Jan Wassenberg at Google.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
- C++: CLHash. CLHash. CLHash is an ultra-fast hashing method and focused on improving performance of the hashing of long strings.
- C++: FalkHash. FalkHash. FalkHash is an ultra-fast hashing method and beats most of the other non-cryptography methods for performance. It is focused on the x64 architecture and integrates with AES-NI.
- C++: wyHash. wyHash. wyHash is an ultra-fast hashing method.
- C++: Fibonacci. Fibonacci. Fibonacci is an ultra-fast hashing method.
- C++: Lookup3. Lookup3. Lookup3 is an ultra-fast hashing method.
A fuller test with SMHasher gives [here]:
Hash function MiB/sec cycl./hash cycl./map Quality problems
------------------------------------------------------------------
o1hash 12439661.09 16.77 166.13 insecure, no seed, zeros, fails all tests
crc32_hw1 23208.73 46.74 179.70 insecure, 100% bias, collisions, distrib, BIC, machine-specific (x86 SSE4.2)
t1ha0_aes_noavx 22785.26 38.71 180.61 LongNeighbors, machine-specific (x86 AES-NI)
t1ha0_aes_avx1 22714.85 48.12 226.52 LongNeighbors, machine-specific (x64 AVX.txt)
t1ha0_aes_avx2 22345.33 44.38 556.47 LongNeighbors, machine-specific (x64 AVX2)
falkhash 20202.42 173.63 321.52 Sparse, LongNeighbors, machine-specific (x64 AES-NI)
MeowHash64low 17378.06 85.48 237.60 Sparse, invertible, machine-specific (x64 AES-NI)
MeowHash32low 17374.64 85.48 258.53 Sparse, invertible, machine-specific (x64 AES-NI)
MeowHash 17371.91 85.48 247.96 Sparse, invertible, machine-specific (x64 AES-NI)
FarmHash32 17112.05 47.7 214.71 machine-specific (x64 SSE4/AVX)
xxh3 16538.52 32.81 184.86 DiffDist bit 7 w. 36 bits, BIC
xxh3low 16462.36 32.77 199.79
farmhash32_c 16299.81 47.79 219.19 machine-specific (x64 SSE4/AVX)
xxh128low 15174.85 33.79 187.05
xxh128 15174.14 40.46 195.65
farsh32 14053.09 74.29 245.33 insecure: AppendedZeroes, collisions+bias, MomentChi2, LongNeighbors
metrohash64crc_2 14034.84 48.94 162.54 UB, Cyclic 8/8 byte, DiffDist, BIC, machine-specific (SSE4.2/NEON)
metrohash64crc_1 14000.5 49.08 150.54 UB, Cyclic 8/8 byte, DiffDist, BIC, MomentChi2, machine-specific (SSE4.2/NEON)
metrohash128crc_1 13948.67 65.2 168.08 UB, machine-specific (SSE4.2/NEON)
metrohash128crc_2 13920.19 65.12 176.70 UB, machine-specific (SSE4.2/NEON)
halftime_hash128 13478.23 97.79 252.14
wyhash32low 12911.09 29.59 205.43 2 bad seeds
wyhash 12879 30.35 196.77 2^33 bad seeds
CityCrc128 12343.43 74.5 209.75
fletcher2 12011.15 25.29 298.60 bad seed 0, UB, fails all tests
fletcher4 11928.55 25.27 293.49 bad seed 0, UB, fails all tests
halftime_hash256 11620.28 98.44 252.60
fibonacci 11339.87 26.33 705.64 UB, zeros, fails all tests
ahash64 9862.62 27.32 181.68 rust
Spooky128 9751.14 63.84 192.47 UB
Spooky64 9747.47 62.2 191.71 UB
Spooky32 9747.13 62.24 196.96 UB
t1ha1_64le 9723.86 34.39 176.91 Avalanche
cmetrohash64_1 9683.33 45.2 161.01 UB, LongNeighbors, BIC, MomentChi2
cmetrohash64_2 9669.95 44.75 149.67 LongNeighbors
metrohash64_2 9668.51 44.45 164.30 UB, LongNeighbors
metrohash64 9664.61 44.59 150.74 UB, LongNeighbors, BIC
metrohash64_1 9664.57 45.37 152.31 UB, LongNeighbors, BIC, MomentChi2
cmetrohash64_1o 9658.31 42.84 163.45 UB, LongNeighbors, BIC, MomentChi2
FNV1a_YT 9643.42 32.06 175.19 bad seed, UB, fails all tests
City128 9640.19 88.45 225.38
metrohash128_2 9584.94 59.1 167.43 UB, LongNeighbors
metrohash128 9569.16 58.68 167.53 UB, LongNeighbors
metrohash128_1 9558.17 59.04 175.94 UB, LongNeighbors
FarmHash128 9409.63 74.52 210.25
VHASH_32 9404.99 77.01 250.57 sanity, Seed, MomentChi2
VHASH_64 9392.39 74.72 227.92 sanity, Seed, MomentChi2
farmhash128_c 9244.13 79.08 209.44
t1ha2_atonce 9237.12 38.94 194.32 Zeroes low3
City64noSeed 9090.42 32.23 171.53 Avalanche, Sparse, TwoBytes, MomentChi2, Seed
City64low 9089.45 47.75 201.73
t1ha2_stream 9068.55 74.56 219.85 Sparse, Permutation, LongNeighbors
City64 9066.9 47.81 197.78 Sparse, TwoBytes
t1ha2_stream128 9065.5 93.19 236.50 Sparse, Permutation, LongNeighbors
xxHash64 8936.63 51.31 174.34
pengyhash 8744.48 85.31 222.45
farmhash64_c 8713.16 47.96 201.00
FarmHash64 8684.76 48.13 200.51
crc64_hw 8440.13 34.94 141.15 insecure, 100% bias, collisions, distrib, BIC, machine-specific (SSE4.2/NEON)
t1ha2_atonce128 8350.99 55.65 203.53 LongNeighbors
PMPML_64 8161.19 53.2 179.16 unseeded: Seed, MomentChi2, BIC
halftime_hash512 7681.62 125.81 274.01
tabulation 7621.75 42.19 179.93
t1ha1_64be 7481.37 38.16 193.22 Avalanche
MUMlow 7225.18 37.85 197.92 UB, 5 bad seeds
farsh64 7216.29 130.3 302.44 insecure: AppendedZeroes, collisions+bias, MomentChi2, LongNeighbors
MUM 7134.56 37.85 172.34 UB, too many bad seeds, machine-specific (32/64 differs)
nmhash32 7003.3 68.93 216.59
PMPML_32 6704.53 53.5 197.43 Avalanche >512, unseeded: Seed, BIC, MomentChi2, PerlinNoise
nmhash32x 6342.95 56.41 217.75
crc32_hw 6330.42 35.55 170.16 insecure, 100% bias, collisions, distrib, BIC, machine-specific (SSE4.2/NEON)
FNV2 6258.84 33.25 142.89 fails all tests
FNV1A_Pippip_Yurii 6258.46 28.19 184.41 UB, sanity, fails all tests
FNV1A_Totenschiff 6258.23 27.99 198.20 UB, zeros, fails all tests
HighwayHash64 6242.58 99.55 248.41
mx3 6146.02 52.48 173.09 UB
xxHash32 6040.87 51.77 177.91 LongNeighbors, collisions with 4bit diff, MomentChi2 220
prvhash64s_64 5481.48 170.05 325.39
mirhash 5413.73 39.68 154.47 UB, 2^36 bad seeds, LongNeighbors, machine-specific (32/64 differs)
mirhash32low 5412.76 39.79 182.13 UB, 4 bad seeds, Cyclic, LongNeighbors, machine-specific (32/64 differs)
Murmur3F 5226.4 52.18 175.85 UB
prvhash64s_128 5161.33 260.96 442.70
t1ha0_32le 5132.18 54.83 193.53 Sparse, LongNeighbors
halftime_hash64 4990.72 120.55 281.64
Murmur2B 4882.95 39.72 149.43 UB, 1.8% bias, collisions, 3.4% distrib, BIC
seahash32low 4801.33 58.54 227.31 PerlinNoise 32, !msvc
seahash 4796.97 58.55 201.58 PerlinNoise, !msvc
fasthash32 4737.61 45.32 181.86 UB, insecure
fasthash64 4737.21 42.79 164.87 UB, insecure, Moment Chi2 5159 !
umash32_hi 4662.92 54.22 214.20
umash64 4662.09 53.42 188.09
umash32 4633.19 53.42 216.33
t1ha0_32be 4585.59 55.98 183.45 Sparse, LongNeighbors
clhash 4472.31 82.72 229.73 PerlinNoise, machine-specific (x64 SSE4.2)
tabulation32 4317.34 35.45 197.20 collisions
Murmur2C 4092.99 51.84 164.65 UB, 2^32 bad seeds, 91% bias, collisions, distr, BIC, LongNeighbors
farsh128 3776.92 232.48 398.67
City32 3675.04 57.73 212.04
TSip 3228.14 57.96 211.71 !msvc
Murmur3C 3197.63 67.9 198.00 UB, LongNeighbors, Text, DiffDist
Crap8 3149.63 36.23 195.11 UB, 2.42% bias, collisions, 2% distrib
Murmur2 3146.91 41.87 187.89 UB, 1 bad seed, 1.7% bias, 81x coll, 1.7% distrib, BIC
Murmur2A 3146.79 46.87 191.96 UB, 1 bad seed, 12.7% bias, LongNeighbors
aesnihash 2963.39 71.24 217.73 fails many tests, machine-specific (x64 AES-NI)
BEBB4185 2951.62 222.03 343.63 UB, too many bad seeds, msvc-specific
jodyhash6 2848.42 29.99 164.36 bias, collisions, distr, BIC, LongNeighbors
wyhash32 2532.89 48.4 484.57 2 bad seeds, 32-bit
umash128 2427.46 70.6 197.29
Murmur3A 2413.88 53.36 182.37 UB, 1 bad seed, Moment Chi2 69
prvhash64_64m 2386.19 51.18 186.87
prvhash64_128 2383.57 103.44 246.45
prvhash64_64 2375.72 51.61 190.97
hasshe2 2372.52 68.64 216.74 Permutation,TwoBytes,Zeroes,Seed
PMurHash32 2344.78 58.48 196.43 1 bad seed, Moment Chi2 69
mirhashstrict32low 2218.87 65.48 190.59 1 bad seed, MomentChi2 9
mirhashstrict 2217.32 65.53 182.07
sha1ni 2019.96 135.84 564.40 insecure,sanity, Permutation, Zeroes, machine-specific
sha1ni_32 2019.94 136.82 589.46 machine-specific
superfast 1956.25 53.61 180.10 UB, bad seed 0, 91% bias, 5273.01x collisions, 37% distr, BIC
sha2ni-256_64 1910.34 146.06 595.16 Zeroes, machine-specific
sha2ni-256 1906.77 145.47 603.08 insecure,sanity, Permutation, Zeroes, machine-specific
farsh256 1895.77 459.86 575.95
SipHash13 1889.1 89 199.95 0.9% bias
Murmur1 1804.67 51.51 188.41 UB, 1 bad seed, 511x collisions, Diff, BIC
lookup3 1658.31 48.84 194.15 UB, 28% bias, collisions, 30% distr, BIC
pearsonbhash64 1486.34 104.32 185.03
poly_1_mersenne 1431.65 54.49 189.52 fails most tests
jodyhash32 1428.37 44.36 185.85 bias, collisions, distr, BIC LongNeighbors
pearsonbhash128 1347.03 121.75 214.84
poly_2_mersenne 1323.69 66.93 190.88
poly_3_mersenne 1323.59 74.86 206.77
poly_4_mersenne 1323.57 82.67 200.36
blake3_c 1285.91 340.01 552.63 no 32bit portability
GoodOAAT 1052 71.62 192.19
pearsonbhash256 998.9 167.05 261.29
SipHash 980.88 127.77 246.19
MicroOAAT 977.6 59.61 185.06 100% bias, distrib, BIC
FNV1a 791.84 69.69 177.84 bad seed, zeros, fails all tests
sdbm 791.84 67.69 177.06 bad seed 0, fails all tests
FNV64 791.82 70.24 159.29 fails all tests
bernstein 791.82 68.63 180.71 bad seed 0, fails all tests
beamsplitter 789.22 682.45 1150.3 UB, too many bad seeds
HalfSipHash 755.78 114.47 243.72 zeroes
chaskey 753.23 153.42 288.26 PerlinNoise
x17 527.9 98.78 184.09 99.98% bias, fails all tests
JenkinsOOAT_perl 452.49 118.78 194.78 bad seed 0, test FAIL
MurmurOAAT 452.49 113.07 197.83 bad seed 0, 1.5-11.5% bias, 7.2x collisions, BIC, LongNeighbors
JenkinsOOAT 452.48 142.85 213.93 bad seed 0, 1.5-11.5% bias, 7.2x collisions, BIC, LongNeighbors
crc32 392.1 131.62 204.58 insecure, 8590x collisions, distrib, PerlinNoise
sha1-160 364.95 1470.55 1794.1 Comb/Cyclic low32
rmd256 362.49 617.02 815.44 Bad seeds
blake2b-256_64 356.97 1222.76 1435.0
blake2b-224 356.59 1228.5 1425.87
blake2b-160 356.08 1236.84 1458.15
blake2b-256 355.97 1232.22 1443.31 Sparse high 32-bit
md5-128 353.76 638.29 803.39
md5_32a 353.64 629.85 799.56 Sparse high 32-bit
sha1_32a 353.03 1385.8 1759.9 Cyclic low32, 36.6% distrib
rmd128 334.36 659.03 838.32 Bad seeds
blake2s-128 295.3 698.09 1059.2
pearsonhash64 287.95 174.11 196.50 Avalanche, Seed, SSSE3 only. broken MSVC
pearsonhash128 287.95 171.72 194.61 Avalanche, Seed, SSSE3 only. broken MSVC
pearsonhash256 264.51 184.87 218.79 Avalanche, Seed, SSSE3 only. broken MSVC
blake2s-256 215.28 1014.88 1230.38
blake2s-160 215.01 1026.74 1239.54
blake2s-256_64 211.52 1044.22 1228.43
blake2s-224 207.06 1063.86 1236.50
rmd160 202.16 1045.79 1287.74 Bad seeds, Cyclic hi32
sha2-256_64 148.01 1376.34 1624.71 Bad seeds, Moment Chi2 7
sha2-256 147.8 1374.9 1606.06 Bad seeds, Moment Chi2 4
sha2-224_64 147.6 1360.1 1620.93 Bad seeds, Cyclic low32
sha2-224 147.13 1354.81 1589.92 Bad seeds, Comb low32
asconhashv12 144.98 885.02 1324.23
sha3-256 100.58 3877.18 4159.79 PerlinNoise
sha3-256_64 100.57 3909 4174.63 PerlinNoise
asconhashv12_64 86.73 684.02 606.93
floppsyhash 35.72 1868.92 1411.07
tifuhash_64 35.6 1679.52 1212.75 Cyclic low32
Problems include:
- Bad Seeds. A random seed is often used to initialise the hash. This problem relates to having a bad seed..
- Undefined behaviour (UB). This includes Misaligned, oob (Out of bounds), Signed integer overflow and Shift exponent overflow.
o1hash is the fastest, and a quick and dirty hashing method. It is generally not secure. t1h (Fast Positive Hash) requires AES-NI (Intel Advanced Encryption Standard Instructions) and is one of the fastest hashes at 22.785 Gbps. It has fairly good security levels. Meow comes in around 17.378 Gbps. We can see that SHA-1-160 runs as 364 Mbps, while Meow runs at 17.378 Gbps. Blake 3 is one of the fast cryptography hash and has a rate of 1.285 Gbps, and Blake 2 gives a rate around 215 Mbps. SHA-3 gives hashing rates of 100.58 Mbps.
Google recommend the following for 64-bit hashes without quality problems:
- xxh3low
-
wyhash
-
ahash64
-
t1ha2_atonce
-
FarmHash
-
halftime_hash128
-
Spooky32
-
pengyhash
-
nmhash32
-
mx3
-
MUM/mir
- fasthash32
Hash-based Signatures

With hash-based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature, unless we create a stateless method, such as SPHINCS+ [1]. Currently NIST have the final round for the Post Quantum Cryptography competition, and for digital signatures, SPHINCS+ is one of the alterative finalists (alongside Picnic).
Hash-based signature (theory)
- BiBa (Go). BiBa. An overview of BiBa One Time Signature [9]. Basically the method involves us taking a hash of a value using a standard hashing method, such as with SHA-256. There will then be \(2^{256}\) different hashing values. We aim to create a signature for a message, so Bob (the signer) selects a number of random values for his private key value and then publishes the hash of each of these (\(P_1\), \(P_2\), etc). He then sends these public keys to Alice. Now when Bob wants to sign a message, he will take one of his private key values, and then hashes it, and then determines the bin that it should be placed. In this case, we could use the \(\pmod N\) function on the hash, and where \(N\) is the number of bins. If we select \(2^{10}\) there will be 1,024 bins.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature [9].
Hash-based signature (stateful)
- BLISS - Post-quantum signing. BLISS. One of the alteratives to the usage of our existing public key methods is the usage of lattice cryptography, and especially in the usage of Ring Learning With Errors (RLWE). An important application is within digital signatures, and where Bob will sign something with his private key, and then Alice can prove that he signed it with his public key. One post-quantum signature method is BLISS (short for Bimodal Lattice Signature Scheme) [8]. It was created by Léo Ducas, Alain Durmus, Tancrède Lepoint and Vadim Lyubashevsky in 2013.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Hash to Obtain Random Subset (HORS) [3] is a quantum robust hashed-based one-time signature. With this we create a series of integers for our private keys and organise into an indexable form. Then we hash them to a sequence of public key values. Next we segment the hash of the message into a series of n-bit integer values. The signature is then achieved through a look-up of the value in the public key list.
- Lamport Signatures. Lamport. Outlines Lamport signatures [7]. When we sign a message we take its hash and then encrypt with our private key. The public key is then used to prove it, and will prove that we signed it with our private key. The Lamport signature uses 512 random hashes for the private key, and which are split into Set A and Set B. The public key is the hash of each of these values. The size of the private key is 16KB (2×256×256 bits) and the public key size is also 16 KB (512 hashes with each of 256 bits).
- Winternitz Signatures (W-OTS). Winternitz. Outlines Winternitz signatures [4, 5]. W-OTS uses relatively small key and signatures sizes, and is thought to be quantum robust. It generates 32x256 bit random private keys. We then hash these a number of times, and is defined by a parameter (w). If we use w=8, we hash the private keys by (2w). This creates 32x256 bits public keys. The signature is the created by taking eight bits at a time, and then the 8-bit binary int (n) is subtracted from 256 and the private key is the hashed 256-n times. The signature is then 32 hashes which are derived from random private keys. To verify the signature, the recipient parses the hash of the signature (using 8 bits at a time, and extracting the 8 bit int, n).
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method [6], and which is used within speeds-up of Hashing-based signature methods. Using methods such as SHA-1 and SHA-2 (aka SHA-256) will be inefficient as they tend to compress the data inputs through a number of stages. Haraka v2 [6] is different as focuses on inputs of just 256 bits (32 bytes) or 512 bits (64 bytes). This makes the method useful when we are dealing with key and hash values, and is especially useful for hash-based signatures. The output is 256 bits long, but where the input can be either be 256 bits (Haraka256) or 512 bits (Haraka512). These lengths are typically for the outputs of modern hashing applications. The Haraka method, too, has been optimized with AES instructions (AES-NI - Intel Advanced Encryption Standard New Instructions) and which are supported within the hardware of the processor. As Haraka is focused on short messages, the number of rounds within the hashing process has been reduced.
Hash-based signature (stateless)
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ digital signature. SPHINCS digital signature. Outline of the a SPHINCS stateless digital signature method [1].
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
Hash-based signature (Merkle-based)
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
Introduction
Many of the problems we see on the Internet relate to the lack of trust within transactions. The emails you receive and the Web sites that you visit often have very little trust built into them. For trust the email address of the sender, but anyone can fake that address. So increasingly we create a digital signature, and where we sign our messages. In this way, we can check for authentication, integrity and non-repudiation.
With the Alice creates a key-pair: a public key and a private key. She then takes a hash of the message, and then encrypts this hash with her private key, and passes the message and the signature to Bob. Bob then reads the message and takes a hash of it. He then decrypts Alice's signature with her public and checks the hashes. If they match, he knows that she signed and that it has not been changed along the way:
Currently, we often use RSA, DSA and ECDSA to sign our messages. These are based on the difficulty of finding out the factors of a number and on the processing of discrete logarithms. At the current time these methods are computationally hard problems, but with quantum computers, they become much easier. This was shown by Peter Shor who illustrated that it was possible to crack them in polynomial time.
Of all the methods that are being proposed, the hash-based methods look as if they have a good chance of success of creating quantum robust signatures. methods and code-based methods are being researched, but the usage of hashing methods is already well and could provide the best alternative to the existing methods. Hashing methods, too, often bring other advantages, such as forward secure, which means that a key which is cracked will not reveal all the previous keys.
Merkle trees
The root of hash-based methods isin Merkle trees, and which are a way of hashing is used in many applications, including with Bitcoin, Ethereum, Git distribution systems, No SQL, and in many P2P applications. With a Merkle tree we take our data elements, and then hash them, and take pairs of these hashes to create a new hash, and so we build a table. At the top of the tree is the root element (in this case Hash1234):
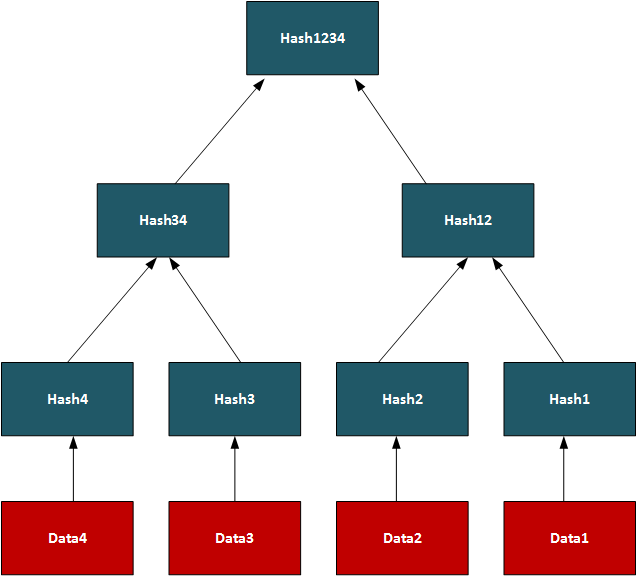
In this way, we can use the tree to see if we have matching data on systems.On a P2P network, we can transfer a file by splitting it into data segments and then distributing these segments across the network. A trusted source will have the complete Merkle tree for rebuilding the file, and a client can thus rebuild from the Merkle tree and determine the parts of the file which are still missing. Once transferred the root hash (and all the other hashes) will then match. In its core method, the Merkle Signature Scheme (MSS) has serious performance and memory issues, but enhanced methods such as XMSS create with much less of a performance hit.
One-time signatures (Lamport)
The core method used in hash-based signatures is that of the one-time signature, and where we create a new key pair for every method we need to create. If the keys were reused, an attacker could start to learn the private key, and thus spoof messages. One of the first methods was produced by Leslie Lamport and Whitfield Diffie, in 1979, and is defined as:
- We create two data sets with 256 random 256-bit numbers (Set A and Set B). These are the private key (512 values).
- we take the hash of each of the random numbers. This will give 512 hashes and will be the public key.
- We then hash the message using and then test each bit of the hash (0 ... 255). If it is a 0, we use the ith number in Set A, else we use the ith number from Set B.
- The signature is then 256 random numbers (taken from either Set A or Set B) and the public key is the 512 hashes (of Set A and Set B).
The public and private keys are then each 16KB in size. A demo of the method is here.
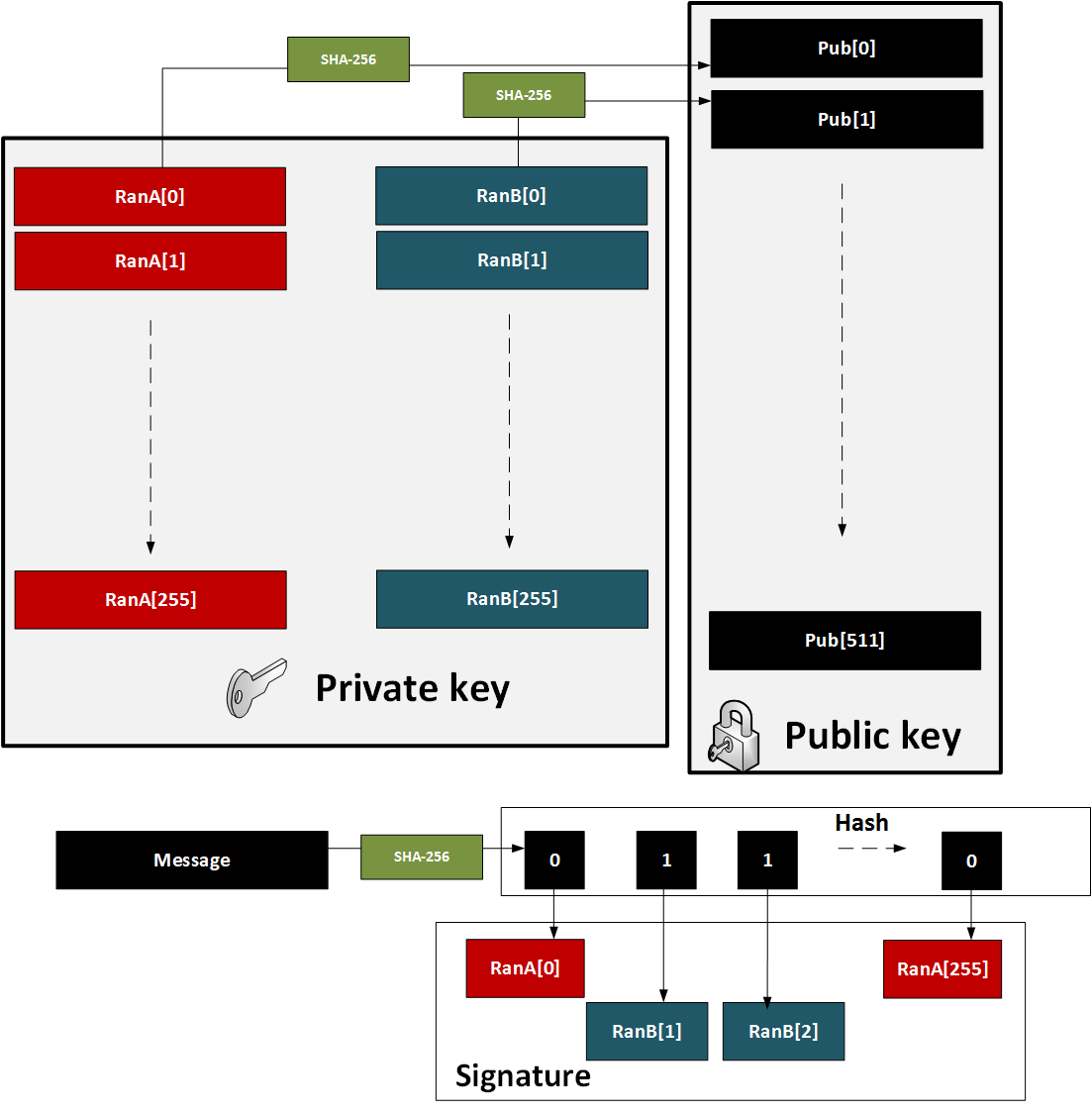
Figure 1: Lamport method
The major problem with the method is that a key pair for every message. also in 1979, found a solution with Merkle trees.
One-time signature (W-OTS)
To improve performance method (and which reduced key sizes), Merkle proposed Winternitz OTS (named after Robert Winternitz). With this method was possible to sign many bits at the same time. The method is:
- We create 32 256-bit random numbers. These 32 values will be our private key.
- We then hash each of these values 256 times. These 32 values will be our public key.
- We now take the message and hash it using SHA-256. This produces 32 8-bit values (N1, N2 ... N32).
- Next we take each 8-bit value in the hash of the message, and then hash 256-N times (where N is the value of the 8-bit value).
- To prove the signature, we take the message and hash it with SHA-256, and then take each 8-bit value. We then hash the 8-bit signature value by the number of times defined by the message hash value (N1, N2..). The result for each operation should equal the public key value.
This is illustrated below in Figure 2. A demo of the method is here.
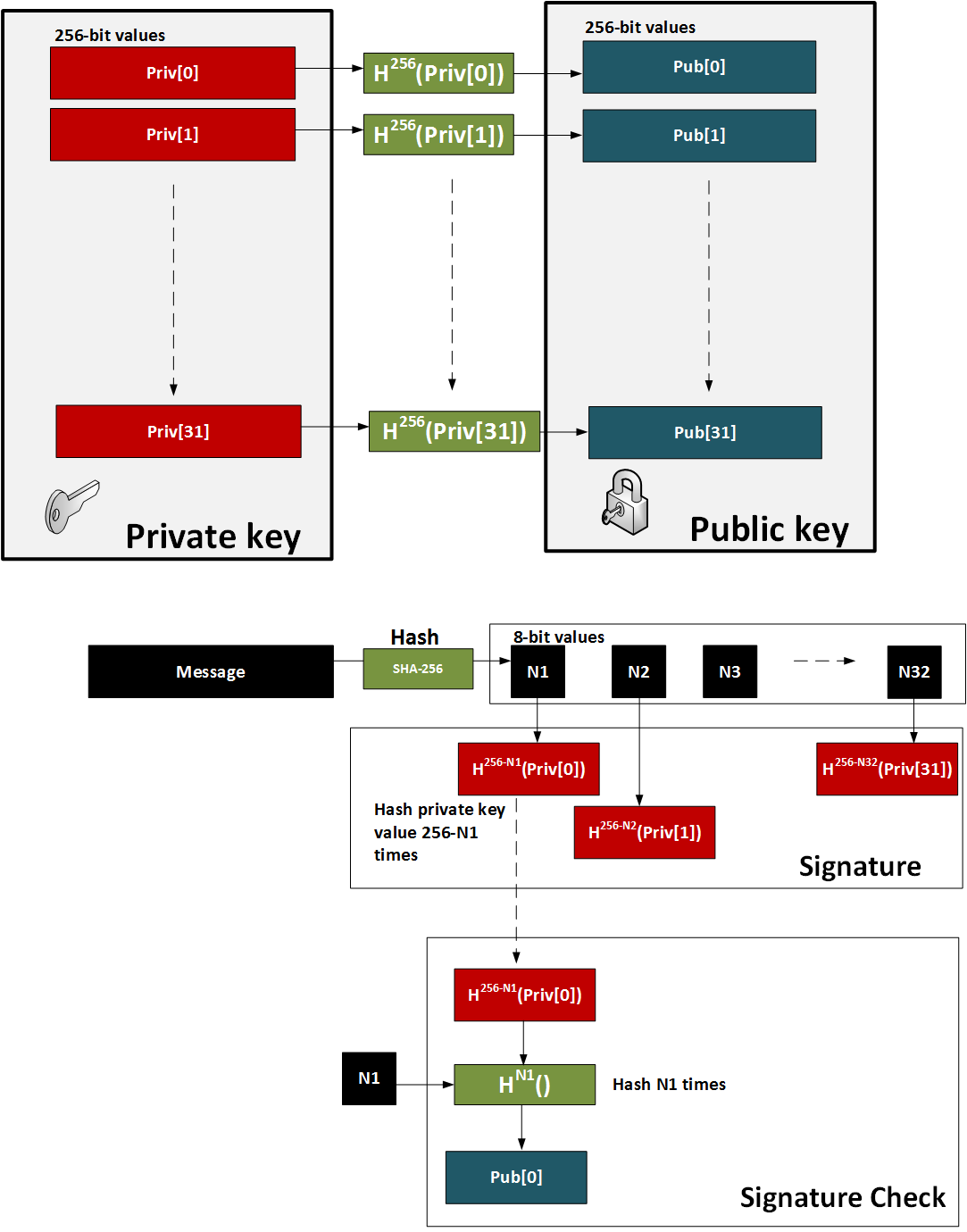
Figure 2: W-OTS
Hash-based Signatures
The methods such as W-OTS and Lamport only provide for a one-time signature. In order to sign many messages, we can use the Merkel signature scheme (MSS). With this we take a hash of the keys and build these as the leaves of the tree. The root of the tree is then the public key - the verification key. We then just use the private key of the W-OTS method to create the signature. The sender also sends the authentication path, which is the neighbouring nodes within the path and which leads to the root of the tree. The recipient can then rebuild the tree using the verification key (which can be received a digital certificate) and the authentication path. For the next message we move onto another key pair and where the index of the key part is revealed.
In the following example we have our root as the public key, and then want to sign with Key3. We then show the authentication path which takes us to the root (as defined in the bold arrows):
Conclusions
Hashed-based methods look to be a strong contender for weaning us off RSA, DSA and ECDSA, but we will have to look at the stateful generation of keys. For this we will have to generate a bank of key pairs (2, 4, 8, 16, etc) and then create the public key from the root of the Merkle tree. We must then remember the keys we have used previously, and only use an unused one. Once we use our new key pair, we then show our working-out as to how the private key is integrated into our tree. It is a bit like a teacher marking a question correctly, and asking for the working out that go you to the answer.
References
[1] Bernstein, D. J., Hopwood, D., Hülsing, A., Lange, T., Niederhagen, R., Papachristodoulou, L., ... & Wilcox-O’Hearn, Z. (2015, April). SPHINCS: practical stateless hash-based signatures. In Annual international conference on the theory and applications of cryptographic techniques (pp. 368-397). Springer, Berlin, Heidelberg [paper].
[2] Bernstein, D. J., Hülsing, A., Kölbl, S., Niederhagen, R., Rijneveld, J., & Schwabe, P. (2019, November). The SPHINCS+ signature framework. In Proceedings of the 2019 ACM SIGSAC conference on computer and communications security (pp. 2129-2146) [paper].
[3] Reyzin, L., & Reyzin, N. (2002, July). Better than BiBa: Short one-time signatures with fast signing and verifying. In Australasian Conference on Information Security and Privacy (pp. 144-153). Springer, Berlin, Heidelberg [paper].
[4] Merkle, R. C. (1989, August). A certified digital signature. In Conference on the Theory and Application of Cryptology (pp. 218-238). Springer, New York, NY.
[5] Hülsing, A. (2013, June). W-OTS+–shorter signatures for hash-based signature schemes. In International Conference on Cryptology in Africa (pp. 173-188). Springer, Berlin, Heidelberg.
[6] Kölbl, S., Lauridsen, M. M., Mendel, F., & Rechberger, C. (2016). Haraka v2–efficient short-input hashing for post-quantum applications. IACR Transactions on Symmetric Cryptology, 1-29. [here]
[7] Lamport, L. (1979). Constructing digital signatures from a one-way function (Vol. 238). Technical Report CSL-98, SRI International. [paper]
[8] Ducas, L., Durmus, A., Lepoint, T., & Lyubashevsky, V. (2013, August). Lattice signatures and bimodal Gaussians. In Annual Cryptology Conference (pp. 40-56). Springer, Berlin, Heidelberg [paper].
[9] Perrig, A. (2001, November). The BiBa one-time signature and broadcast authentication protocol. In Proceedings of the 8th ACM Conference on Computer and Communications Security (pp. 28-37) [paper] .
Hashing (Simularity)

Similarity hashes allow for two data objects to be compared for their similarity.
Similarity assessment methods
The following relate to the basic methods used for string similarity:
- String similarity String similarity. This measures edit distance (including Levenshtein distance), Jaro (including Jaro-Winkler), and QGrams.
- String enthropy String enthropy. Measurement of the entropy of strings.
- Soundex Soundex. Soundex uses a phonetic algorithm to classify a sound as it is pronounced. It focuses on matching phrases which have minor spelling errors.
Similarity hashes
The following are the tips related to similarity hashing:
- Similarity hash: SimHash (Charikar similarity) in Python Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash (Nilsimsa similarity) Nilsimsa. The Nilsimsa similarity is used to find similarities between spam emails.
- Context Triggered Piecewise Hashes (CTPH): ssdeep CTPH similarity. Kornblum [6] created ssdeep and which computes fuzzy hashes. This aims to match similar byte sequences, no matter if there are differences between these sequences. For this we break a file up into fragments with a rolling hash function. We then produce a small hash for each of those fragments. These are then aggregated to produce the complete hash of a file. In comparing file signatures, we treat the resultant hash value as a string, and then uses an edit distance method to compare.
- TLSH (A Locality Sensitive Hash) TLSH similarity. In malware analysis and in text similarity, we often have to identify areas of data within files which are similar. One method is TLSH (A Locality Sensitive Hash), and which was defined by Oliver et al [7]. It is used - along with ssdeep - by VirusTotal to identify a hash value for malware.
- Minhash (Jaccard similarity) Jaccard similarity. The Minhash method is used to find similarities between strings, files and metadata.
- Counting identical elements (HyperLogLog) HyperLogLog. Counting the number of identical elements.
Hazmat cryptography

The Cryptography library in Python contains interfaces to common cryptographic algorithms, including symmetric key methods, hashing, public key, and key derivation functions. Many of these are contained with the Hazmat (Harzardous Material) primative setup.
Hashing, HMAC, CMAC, Poly1305 and HKDF
-
Hazmat Hashes. Hazmat Hashes. This includes the hashing methods in the Hazmat cryptography library. This includes Blake2p, Blake2s, MD5, SHA1, SHA224, SHA256, SGA384, SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHA512, SHA512-224, SHAKE128 and SHA256.
-
Hazmat Hashes. Hazmat Hashes. In this case we will implement Python code to determine SHA1, SHA2, SHA3, Blake2, MD5 and SM3 hashes.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
- Hazmat HKDF. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
- Hazmat CMAC. Hazmat CMAC. CMAC methods using the Python cryptography primitives.
- Hazmat Poly1305. Hazmat Poly1305. Poly1305 methods using the Python cryptography primitives.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
Symmetric key
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat. Implementation of ChaCha20/Poly1305 with a random key using Hazmat.
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat. Implementation of AES GCM with a random key using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hazmat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Hazmat Symmetric Key Padding. Symmetric key. This includes the coverage of padding with Hazmat.
- Hazmat Symmetric Key Padding. Symmetric key. This includes the coverage of padding with Hazmat.
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
- Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . With 3DES encryption, we use a 128-bit key and a 64-bit IV value. The two modes supported are ECB (without salt) and CBC (with salt). The DES algorithm has been around for a long time, and the 56-bit version is now easily crackable (in less than a day on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases, and splits the key into two. Overall the key size is typically 112 bits (with a combination of the three keys - of which two of the keys are the same). In this case we will use PKCS7 padding, and which fills the input data with a value that is equal to the number of padding bytes. Overall, DES has a 64-bit block size, and which equates to eight ASCII characters.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key . And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.
Asymmetric key
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- ECC key generaton with Hazmat. Elliptic Curve key gen. Creating ECC keys using Hazmat and Python.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- Hazmat RSA signing (with key values). RSA signing with Hazmat. RSA signing using Python and with Hazmat (with key values).
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here]
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Signatures. DSA Signatures. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. The ECDSA method is an extension of DSA, but implemented with elliptic curve (EC) methods. As with most public key signing methods, we take a hash of a message, and then apply a private key to create a signature (\(r,s\)). This is done by creating a random value (\(k\)) to produce the signature. The signature is then verified using the associated public key. This then verifies the creator of the signature and that the message has not been changed.
Digital Signature: ECDSA/EdDSA
- ECDSA with Hazmat. ECDSA wih Hazmat. This outlines ECDSA with Hazmat.
- Ed25519 for EdDSA signatures with Hazmat. EdDSA: Ed25519. This page uses the Hazmat primitives for the cryptography library.
- Ed448 for EdDSA signatures with Hazmat. EdDSA: Ed448. This page uses the Hazmat primitives for the cryptography library.
- Ed25519 using NaCl. Ed25519. This page uses the NaCl port from libsodium.
- ECDSA Signatures with Hazmat (SECP256R1, SECP384R1, SECP521R1, SECP224R1, SECP192R1, and SECP256K1). ECC Signatures. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and then creates an ECDSA signature for a given message.
Digital Signature: RSA
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
Key exchange: ECDH/X25519
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives and showing the byte values for the key.
Tokens
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
Homomorphic Encryption

Homomorphic encryption supports mathematical operations on encrypted values. Partial Homomorphic Encryption (PHE) supports a few arithmatic operations, while Full Homomorphic Encryption (FHE) supports add, subtract, multiply, and divide. Homomorphic encryption normally involves a public key to encrypt the data, and a private key to decrypt it. There have been four main generations of homomorphic encryption, and the most recent being the HEAAN method.
Simple
- Simple Homomorphic Cipher. Hom. This outlines a Simple Homomorphic cipher.
- Simple Homomorphic Cipher (Python). Hom. This outlines a Simple Homomorphic cipher with Python.
- Full Homomorphic Cipher with a Public Key. Public key. This outlines a Simple Homomorphic cipher using a public key
ElGamal
- ElGamal Homomorphic Cipher (Go). ElGamal. This outlines ElGamal Homomorphic cipher with Go.
- ElGamal Homomorphic Cipher (Go) - Divide. ElGamal. This outlines ElGamal Homomorphic cipher with Go with divide.
- ElGamal Homomorphic Cipher (Go) - Additive. ElGamal. This outlines ElGamal Homomorphic cipher with Go with addition.
- ElGamal Homomorphic Cipher for Multiplication (Python). ElGamal. This outlines ElGamal Homomorphic multiplication with Python.
- ElGamal Homomorphic Cipher for Division (Python). ElGamal. This outlines ElGamal Homomorphic division with Python.
- ElGamal Homomorphic Cipher for Addition (Python). ElGamal. This outlines ElGamal Homomorphic addition with Python.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (Python). ElGamal. This outlines ElGamal Homomorphic subtraction with Python.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
RSA
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
ZKP
- Full Homomorphic Cipher to determine if Bob is older. Older. This outlines a Simple Homomorphic cipher to determine if Bob is older than Alice.
- Full Homomorphic Cipher to determine matching password. Password. This outlines a Simple Homomorphic cipher to determine if a password matches
- Interactive ZKP With Probablistic Methods. ZKP. Interactive ZKP With Probablistic Methods using Python.
- Full Homomorphic Cipher for Millionaire's Problem. Millionaire. This outlines a Simple Homomorphic cipher for the Millionaire's Problem
Voting
- Trusted voting. Trusted. A trusted voting method.
Secret share
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Lattice
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
Full Homomorphic Cipher
- Full Homomorphic Cipher for 2-bit Adder. Adder. This outlines a Simple Homomorphic cipher for a 2-bit adder with DGHV.
- Full Homomorphic Cipher for Full Adder. Full Adder. This outlines a Simple Homomorphic cipher for a full adder with DGHV.
- Full Homomorphic Cipher for 4-bit Adder. Adder. This outlines a Simple Homomorphic cipher for a 4-bit adder with DGHV.
- Full Homomorphic Cipher for 4-bit Adder/Subtractor. Subtract. This outlines a Simple Homomorphic cipher for a 4-bit adder/subtractor with DGHV.
- Full Homomorphic Cipher to XOR two integers. X-OR. This outlines a Simple Homomorphic cipher to X-OR two integers
Paillier
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier) .
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Damgård-Jurik Homomorphic Encryption With Secret Shares. Damgård-Jurik Method. Two of the major areas of developments within cybersecurity will be the usage of homomorphic encryption, and in the usage of Shamir secret sharing. With homomorphic encryption, we can encrypt values, and then operate on them with arithmetic functions (such as add, subtract and multiply), and with Shamir secret sharing, we can split secrets into shares, and then distributed them over networks. These approaches will take privacy to new levels. So let’s look at the Damgård-Jurik method.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Learning with Errors (LWE)
- Learning With Errors . LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret key value (s) and another value (e). Next we select a number of values (t[]) and calculate g[] = t[] x s + e. The values of g[] and t[] become our public key.
- Public Key Encryption with Learning With Errors (LWE). LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret value (s) and which is our private key. We then create a public key which is based on random numbers (A), and then generate another set of numbers (B) which is based on A,s and random errors e. An example of encryption with multiple bits is given.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE)
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Others
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
- SIDH Go. SIDH. Post-quantum key exchange.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Anonymous crypto. Anon. Anonymous crypto.
- Rho factorization. Rho. Rho alogorithm.
- Post-quantum signing (BLISS). BLISS. BLISS method.
Homomorphic Encryption with Krytology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Homomorphic hashing
- Homomorphic Hashing with Golang. Homomorphic hashing. Normally with hashing methods, we need to take all the previous data and new data in order to create a new hash value for our data. In a homomorphic hashing method, we can basically take the previous hash, and then add on any new data values. We can also remove previous data values from our hash, too. This is more efficient in computing, as we do not have to process all of our data into a new hash, and can use simple homomorphic operations for the computation. The method we will use (LtHash) was initially defined by Bellare and Micciancio and updated Lewi et al at Facebook.
Identity Based Encryption (IBE)

This page outlines a few basic principles around the usage of IBE.
Identity Based Encryption (Pairing based)
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pair-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Identity Based Encryption (Others)
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Güther's implicitly certified identity-based public keys (IBE). Günther. This method allows Bob to generate Alices public key from her identity and publicly available parameters.
- Girault's self-certified public keys (IBE). Girault. This method allows Bob to generate Alices public key from her identity and publicly available parameters, and where we use an RSA key pair to self-certify Alice's public key.
Intrusion Detection Systems (IDS)
- Intrusion Detection Systems. Snort. This outlines some of the basics of IDS, including the requirement for Intrusion Detection Systems (IDSs), and where they are used.
- Advanced Network Forensics (Snort). Adv Network Forensics. This provides information on how to detect threats through network forensics with Snort
Snort

- Snort IDS. Snort. This is a Snort Analyser.
- Snort IDS 2 with rules editor. Snort. This provides information on how to detect threats through network forensics with Snort, and with an editing function for rules.
Presentation
IoT

The key objectives of this page are: Understand how a Pen Tester can generate vulnerabilities and test using the Metasploit framework; Define the options and payloads required to generate and use vulnerabilities; and Gaining remote access.
Devices
- Access the Wi-fi kettle. Go. This page outines how to access a wi-fi enabled kettle.
- Philips Hue Wireless Lighting. Go. This page shows how to use RESTful Web services to access to the Hue Led Lamps.
- Kali and R-PI. Go. This page shows the setup of a security testing infrastructure using a Raspberry Pi (R-PI) and a wifi access point.
- Kali, R-PI and RF electrical socket. Go. This page shows the control of an RF electical socket from a RPI.
- Capture from a Polar H10 heat rate sensor. Go. This page shows the capture of the Polar H10 heart sensor with an Ubertooth One.
- Trusted IoT: Linking IoT Devices to NFTs. Go. This page outlines a research paper which links a device to an NFT (Non-fungible Token).
Shodan Scanning
-
IoT Scan (Shodan). Go. This page includes a search of the Internet for key terms, such as for "apache", "mysql" and "cisco".
- IoT Banner Scan (Shodan). Go. This page includes a search of the Internet for key terms with the banner as a result (for the Top 10)
- Internet Services (Shodan). Go. This page includes a search of the Internet for key terms and display the IP address and port.
IoT Libraries
- libDisco with Go. libDisco. libdisco is a Golang library which can be used to create secure connections. It is based on the STROBE protocol framework. Symmetric cryptographic primitives rely on SHA-3 permutation, and asymmetric cryptographic primitives on X25519 and ed25519. STROBE defines a range of cryptographic protocols to integrate with IoT devices. In order to reduce processing, energy and memory requirements, it only uses Keccak (SHA-3) to encrypt and authenticate messages.
COSE/COBR
In computer security, we often have to represent binary data, in single values or groups of characters, bytes, words, long words, signed integers, floating-point values, double-precision floating-point values, and so on. This might be in the form of a data object, a signature or even encrypted content. For this, the ANS.1 DER format is often used, such as presenting digital certificates and signatures. An improvement on this for small messages with security is Concise Binary Object Representation (CBOR) — and which is defined in RFC8949 [1]. While JSON represents text-based data objects CBOR focuses on binary objects. It has been designed to create a lightweight encoder and decoder. This supports the use of CBOR within an IoT infrastructure. The data, also, does not require a data schema to be able to decode it, along with being extensible. CBOR defines the format of binary data with data objects and messages. We can then integrate security with CBOR Object Signing and Encryption (COSE), and which is defined in RFC8152 [2]. This includes signatures, message authentication codes (MACs), encryption and creating serialised objects.
- 128-bit AES GCM. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) can then build on this to include signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use a symmetric key to encrypt a message, and then decrypt it. In this case we will use AES GCM with a static 128-bit key ("0x000102030405060708090a0b0c0d0e0f").
- 256-bit AES GCM. Go. In this case we will use AES GCM using a random 256-bit key (32 bytes).
- EdDSA. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) [2] can then build on this to includes signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use EdDSA to create a signature for a message.
- ECDSA. Go. In this case we will use ECDSA to create a signature for a message.
- HMAC. Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT. Go. In this case we create a CWT token, and sign with an HMAC signature.
- ECDH. Go. In this case we create a symmetric key from ECDH. For this we will derive a shared key from the public key of Alice and Bob, and then define a single recipient which can derive the CEK (Content Encryption Key) using their private key. We will use the curves of P-256 (secp256r1), P-384 (secp384r1), P-521 (secp521r1) or SECP256K1 (as used with Bitcoin).
- RSA using COSE and CBOR. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\).
- RSA: dQ, dP and InvQ. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). The key pair also includes \(dQ\), \(dP\) and \(InvQ\), and these can be used with the Chinese remainder theory to optimize the decryption process.
Metasploit
- Armitage and Metasploit. Go.
- Exploiting Android with Metasploit. Go.
- Exploiting Android with Metasploit - Part 2. Go.
- Exploiting Windows/Mac OS X with Metasploit. Go.
- Remote Desktop Windows/Mac OS X with Metasploit. Go.
- Metasploit. Go.
- Internet of Things Security. Go.
- Metasploit (Enumeration and Scanning). Go.
- Metasploit (Malware). Go.
IP

 The following are a few interesting techniques around IP addresses:
The following are a few interesting techniques around IP addresses:
- Your details. IP. This shows your browser details.
- IP address analyser. IP. This involves converting an IP address to the host and network part of the address.
- IP subnet analyser. IP subnets. This involves converting an IP address to the host and network part of the address.
- IP address analyser. IP. This involves analysing IP addresses.
- Max subnets. Max subnets. This involves converting an IP address to the host and network part of the address.
- Route summarization. Summarization. This involves converting an IP address to the host and network part of the address.
- Whois. Whois. This does a basic Whois on a domain.
- URL Obfuscation. Obfuscation. This outlines URL obfuscation.
- HTTP Responses. Test. HTTP.
- Capturing Network Packets (Python). WinPCap. HTTP.
Cisco related
- Routing table. Routing table. This involves viewing a routing table for a Cisco device.
- ACL Generator. ACL. This involves a simple calculator for ACLs on network ranges.
- EIGRP metrics. EIGRP. Learn the basics of EIGRP metrics.
- VoIP B/W. VoIP. Calculate bandwidth for VoIP.
- Wild Card. Wild Card. On a Cisco device a wildcard mask is used to identify the parts of an IP address that need to be matched. It thus uses a wildcard mask, where a 0 in the bit position identifies that the device should match that bit, else a 1 shows that it should ignore it.
Protocols
- HTTP. HTTP. Show the request and response for HTTP.
- Ping analyser. IP. This involves converting a ping of a site.
IP Challenges
-
IP Test 1. IP Test. IP Classification test. This is a simple test which generates a range of IP addresses, and you must determine the IP address classification.
IP Subnet Challenge 1 Demo
-
IP Test 2. IP Test. IP Classification test Part 2. This test provides an address classification, and the user must find the addresses which are of this classification.
IP Subnet Challenge 2 Demo
-
IP Test 3. IP Test. IP Classification test Part 3. This test provides an address classification, where the network part of the address is determined.
IP Subnet Challenge 3 Demo
Subnet Challenges
- Subnet Test 1. Subnet Test. Subnet Test.
-
Subnet Test 2. Subnet Test. Subnet bits.
- Subnet Test 3. Subnet Test. Find the nth usable subnet. This test involves finding the nth usable subnet.
- Subnet Test 4. Subnet Test. Maximum subnets. This is a test page to determine the maximum number of subnets and hosts/subnet for IP classed addressing.
- Subnet Test 5. Subnet Test. Maximum host/subnet. This is a test page to determine the maximum number of hosts per subnet.
- Subnet Test 6. Subnet Test. Determine the required subnet mask for a given number of subnets. This is a test page to determine the required subnet mask for a given number of subnets and a given IP address classification.
- Subnet Test 7. Subnet Test. Determine the required subnet mask for a given number of host/subnet. This is a test page to determine the required subnet mask for a given number of hosts per subnet and a given IP address classification.
- Subnet Test 8. Subnet Test. Route summarization. This involves a calculation on route summarization.
- Subnet Test 9. Subnet Test. Binary to IP.
- Subnet Test 10. Subnet Test. Hex to IP.
-
Subnet Test 13. Subnet Test. Wild card mask network bits. Find the number of bits in the network part of the wild card mask. IP Wildcard challenge
- Subnet Test 14. Subnet Test. Wild card mask host bits. Find the number of bits in the host part of the wild card mask. IP Wildcard challenge
- Subnet Test 15. Subnet Test. Wild card mask ... find the network address. Find the network for the wild card mask. IP Wildcard challenge 2
- Subnet Test 16. Subnet Test. Find a matching IP address for a network and wild card mask. Find the IP for a network and a wild card mask.
- Subnet Test 17. Subnet Test. Find an address which is on a given network. Find an IP address on a network, for a given network address and subnet mask.
- Subnet Test 18. Subnet Test. Find an IP address on the same network. Find an IP address on the same subnet.
- Subnet Test 19. Subnet Test. Find subnet. Convert subnet mask.
- Megatest. Subnet Test. Challenging test for subnets.
JavaScript

JavaScript code allows execution within the browser, rather than on the server. It is often faster than code that runs on a server. Along with this we can also use Node.js, and which runs JavaScript code on a server.
Symmetric key
- AES. AES. In this example, we will use either a pre-generated key or a random one, and use AES (Rijndael) encryption.
- ChaCha20 and Poly1305. ChaCha. This page outlines Poly1305 and ChaCha20. ChaCha20 is a symmetric key method and Poly1305 is a message authentication code (MAC). They were created by Daniel J. Bernstein, and are alternatives to AES and HMAC.
- CMS (Padding). CMS. This page uses PKIJS encrypting on CMS. With CMS we can This document describes the Cryptographic Message Syntax (CMS). With this we can encapsulate an message within an encrypted entity.

Hashing
- Hash. Hash. This page defines a JavaScript Hash calculator. This uses a client-side JavaScript code to determine the hash signatures of a text value.
Signatures
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
- Boneh–Lynn–Shacham (BLS) signature. BLS. Boneh–Lynn–Shacham (BLS) signature method produces short signatures. They use elliptic curve pairing (and which are also known as bilinear maps).
Key exchange
- ECDH. ECDH. Elliptic Curve Diffie Hellman (ECDH) is used to generate a shared key. This implementation uses Elliptic Curve Cryptography (ECC) with JavaScript.
CryptoJS
- CryptoJS. CryptoJS. This page uses client-side JavaScript code to hashing, encrypt and sign, including for symmetric key (AES), streaming ciphers, hashing methods, and HMAC.
Blockchain
- PATRICIA trie. PATRICIA. In the following, we have the Top 2,500 Web sites in the world, and implemented with a Radix Trie (aka PATRICIA trie) In the following we have the Top 2,000 web sites on the Internet, and which have been indexed using the PATRICIA trie.
Public key
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
- RSA. RSA. RSA is an asymmetric encryption algorithm, which uses two keys, one to encrypt and the other to decrypt. It was created in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman, and is still one of the most widely used encryption methods. A typical application is in authenticating a sender, where the senders private key is used to encrypt a message, and then is decrypted by the receiver with the senders public key (which is known to anyone who wants it). It is also typically used for encrypting disks/files, such as for EFS.
Digital Certificates
- X.509 certificates in JavaScript. RSA and ECDSA Signed certificates. This page will generate either RSA and ECC key pairs, and then generate X.509 certificates, using either a signature of SHA1withRSA or SHA256withECDSA. For RSA signing we use an RSA private key to sign the certificate, and with ECDSA signing we use an ECC private key to sign the certificate.
Tokens
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
Random
- Random number generator. Rand. In the past, encryption and decryption had to be done through native code libraries, such as with Bouncy Castle and OpenSSL. With the increasing processing power of Web browsers, it is now possible to use encryption using JavaScript, which thus provides client-side processing of data. This Web page uses Javascript encryption, and generates a random 256-bit text key or a hex version. The 256-bit key is generated by generating 60 random numbers (from 0-25), and converting these to an ASCII character.
Malware obfuscation
- Malware obfuscation. Obfuscation. A malware writer will often hide certain keywords from the browser/human by encoding them in another format. This is typically done for hex coding (\xZZ), 16-bit unicoding (\uZZZZ) and octal coding (\ZZZ). To test, enter a value, and then press the button and it will convert encoded string.
Message Authentication Codes
- Chaskey (MAC). Chaskey. Chaskey Cipher is light-weight cryptography method for signing messages (MAC) using a 128-bit key. The hardware implementation only requires 3,334.33 gate equivalent with an operating clock frequency of 1 MHz (whereas Keccak requires 4,658 GE). In the page we create the Mac signature and also encrypt for CBC.
Other
- Password generation/hashing. Hashing. Linux can use salted passwords where the username, hashing method and hashed password are stored in a password file [More details]. The main methods are
Hashing

At times we need to generate secrets, such as encryption keys, from passwords or nonce values. A Key Derivation Function (KDF) is a verifiable way of doing this.
Key Derivation Functions (KDFs)
The following are the tips related to hashing:
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Password strength. Test. This outlines the strength of various passwords types.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
HKDF
The following are the tips related to Key derivation hashing:
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Hazmat HKDF for different hashing methods. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
-
HKDF key derivation with OpenSSL [
here]
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
PBKDF2
The following are the tips related to Key derivation hashing:
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- AES GCM (Python) with PBKDF2. AES GCM (Python) with PBKDF2.
- Fernet with PBKDF2 . AES GCM (Python) with PBKDF2.
- PBKDF2 key derivation. AES GCM (Python) with PBKDF2.
- Key Rotation with Fernet. AES GCM (Python) with PBKDF2.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Bcrypt
The following are the tips related to Key derivation hashing:
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- BCrypt. BCrypt. BCrypt with Rust.
-
Hash to password with Go. Hashing to Argon2, Scrypt and BCrypt. Hash to password with Go, including Argon2, Scrypt and BCrypt.
scrypt
- scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Argon 2
The following are the tips related to Key derivation hashing:
- Argon 2. Go. Outline of Argon2.
- Argon 2 with NaCl. Go. Outline of Argon2 using NaCl.
- Argon 2. Argon 2. Argon 2 with Rust.
- Balloon. Go. Outline of Balloon.
Other
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
- Double ratchet. Go. Outline of double ratcheting.
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
Outline
HMAC Key Derivation function (HKDF) is used to derive an encryption key from a passphrase. Initially, HKDF creates a pseudorandom key (PRK) using a passphrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), and along with a salt value. Next, the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys [RFC 5869][article]. In this case, we will use SHA-256.
The following shows how an encryption key can be generated using HKDF, and where we need a secret and a salt value. Both Bob and Alice have the same secret and salt.
With PBKDF2 (Password Based Key Derivation Function 2), we hash for a given number of rounds:
Key exchange

Key exchange is a way for Bob and Alice to communicate and for them to agree on a shared secret. The original method defined uses discrete logarithms (Diffie-Hellman), but most modern methods use elliptic curve techniques (ECDH). As quantum computers can crack both discrete log and elliptic curve methods, there are post quantum cryptography methods proposed. This includes SIDH, CSIDH, SIKE, and NewHope.
Key interchange/generation (Diffie-Hellman)
The following relates to key interchange:
- Selecting \(g\) in Diffie Hellman. G in Diffie Hellman. Picking a safe value of the generator \(g\) in discrete logarithms.
- Diffie-Hellman. Diffie-Hellman Calculation. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Real example). Diffie-Hellman Real. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Python). Diffie-Hellman. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (pre-compute). Diffie-Hellman (pre-compute). Many sites use the same prime numbers, which can then be cracked with a pre-computing attack.
- Key generation. Key gen. This will generate keys for different methods based on a passphrase.
- Diffie-Hellman (Man-in-the-middle). DF. This outlines the man-in-the-middle method for Diffie-Hellman.
- An Alternative Diffie-Hellman method. Alterative DH. This outlines an alternative Diffie-Hellman method.
Authenticated Key Exchange
The following are the tips related to Key derivation hashing:
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- MTI/A0. MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{ax+by} \pmod p\). MTI (Matsumoto, Takashima, Imai).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0. MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{x+y} \pmod p\)
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). The resultant key is \(xyG \)
- MTI/C0. MTI/C0. This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{xy} \pmod p\)
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG\).
- MTI/C1. MTI/C1. This outlines MTI/C1, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{abxy} \pmod p\).
- MQV (Menezes–Qu–Vanstone). MQV. MQV was created Alfred Menezes, Minghua Qu and Scott Vanstone in 1995 and is an authenticated key exchange method. Alice holds a key pair \((A,a)\) and Bob has a key pair \((B,b)\). With this \(a\) is Alice's private key, and \(A=aG\) is her public key. For Bob, his public key will be \(B=aG\) and a private key of \(b\), and where \(G\) is the base point on the elliptic curve.
- HMQV (Menezes–Qu–Vanstone). HMQV. HMQV builds on MQV and adds the identity of Bob and Alice.
- ECDH with X25519 and Blake2b. ECDH with X25519 and Blake2b. This uses PyNaCl to create an authenticated key exchange and uses X25519 and Blake2b.
Elliptic Curve (ECDH) - Python
The following are the tips related to ECC:
- Elliptic Curve. Elliptic Curve. Elliptic Curve is a public key method which can also be used to generate a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with simple parameters. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
Elliptic Curve (ECDH) - Golang and Node.js
The following are the tips related to ECC:
- ECDH with Go. ECDH. ECDH with Go.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with node.js. ECDH. ECDH with node.js.
- ECDH with JavaScript. ECDH. Elliptic Curve Diffie Hellman.
Password Authenticated Key Exchange (PAKE)
The following are the tips related to Key derivation hashing:
- SPAKE2. Go. Outline of SPAKE2.
- OPAQUE. Go. Outline of OPAQUE.
- SPEKE. Go. Outline of SPEKE (Simple Password Exponential Key Exchange).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
- J-PAKE. J-PAKE. This example generates a shared key based on a shared password.
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses discrete logs.
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
PQC NIST Finalists (Key Exchange)
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Key interchange/generation (Other)

The following relates to key interchange:
- Curve25519. Curve25519. This outlines Curve25519, which is used in the Tor network.
- Authenticated Key Exchange (Discrete logs). YAK. Key exchange with public keys and uses discrete logs.
- Authenticated Key Exchange (ECC). YAK. Key exchange with public keys and uses elliptic curve methods.
- Shamir No-key protocol. Shamir No Key. In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated.
- Shamir No-key protocol (sepc256k1). Shamir No Key (EC). In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated using the sepc256k1 elliptic curve.
- Conference keying (Burmester-Desmedt method). Conference keying. In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it.
- Conference keying (Burmester-Desmedt method) - Elliptic Curve (sepc256k1). Conference keying Elliptic Curve (sepc256k1). In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it, and uses the sepc256k1 elliptic curve.
Key exchange (with pairing)
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Kryptology

We need to build a new Internet. One that is build on mathematics and certainty, rather than the patchy version we have now. For this we need a layer of cryptography at the lowest level, and build software interfaces on top of this. Along with this we now have cryptographic methods which can now provide a foundation of trust, and which preserve privacy. And so the old libraries of OpenSSL are being squeezed out in favour of the new ones which are built on a solid foundation. The latest of these new "privacy-aware" libraries is Kryptology, and created by Coinbase. This library provides the APIs that developers need, in order to apply to areas of blockchain development. This library include BLS (Boneh-Lynn-Shacham) signatures, Zero-knowledge Proofs (ZKPs) and Shamir Secret Shares (SSS). With BLS we can digitally sign for data, but also preserve its privacy. Applications of this include group signatures, where multiple entities can merge their signing keys together and provide a single signature for a transaction. With SSS, we can split encryption keys up into shares, and then distribute them across a network. When required, we can call these shares back to reconstruct the key.
The focus for Coinbase seems to be the application of privacy coins, and where no tracking can be applied to the usage of these digital coins. This should support full anonymity for transactions, as opposed to Bitcoin which only supports pseudo-anonymity.

ECC Basics
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining n.G for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Points (Base Point and Others). Elliptic Curve points. Two common curves used in ECC (Elliptic Curve Cryptography) are secp256k1 (as used in Bitcoin and Ethereum) and P256 (secp256r1). The "k1" refers to the Kolbitz curve 1 (named after the creator of ECC). With these we have a base point which are can operate on. This is typically defined as \(G\). We can then operate on this with add and multiply operation. For example, \(2G=G+G\) and \(P=n.G\). In this following we will show the base point for a number of common curves, such as secp256r1, P256, Pallas, Curve 25519, BLS12381G1, BLS12381G2, BLS12377G1 and BLS12377G2.
ECDH
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret. We will use Golang and the Krytology library.
Simple ECC on curves
- Public key points for curves. Simple. Display public key points for scalars.
BLS Curve
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
Accumulator and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
Pallas Curve
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
Pairing-based Crypto
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
ElGamal and ECC
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a numerical input.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
Shamir Secret Shares
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Homomorphic Encryption
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Zero knowledge proofs
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
Verifiable Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Hash to scalar and point
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
CP-ABE
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Lattice cryptography

Latice cryptography is proposed as a post-quantum robust method for public key encryption, especially focused on digital signatures and key exchange mechanisms (KEMs).
Principles
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
NTRU
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- Lattice Encryption: NTRU Key Generation Python). NTRU. Outlines how NTRU operates for key generation.
Homomorphic
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Digital Signatures
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
Public-Key Encryption/Key Exchange
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
Light-weight cryptography

While AES and SHA work well together within computer systems, they struggle in an IoT/embedded world as they take up: too much processing power; too much physical space; and consume too much battery power. So NIST outlines a number of methods which can be used for light-weight cryptography, and which could be useful in IoT and RFID devices [1]. They define the device spectrum as:
- Conventional cryptography. Servers and Desktops. Tablets and smart phones.
- Light-weight cryptography. Embedded Systems. RFID and Sensor Networks.
With embedded systems, we commonly see 8-bit, 16-bit and 32-bit microcontrollers, and which would struggle to cope with real-time demands for conventional cryptography methods. And in the 40+ years since the first 4-bit processor, there is even a strong market for 4-bit processors. RFID and sensor network devices, especially, have limited numbers of gates available for security, and are often highly constrained with the power drain on the device.
So AES is typically a non-starter for many embedded devices. In light-weight cryptography, we often see smaller block size (typically 64 bits or 80 bits), smaller keys (often less than 90 bits) and less complex rounds (and where the S-boxes often just have 4-bits).
For light-weight cryptography the main constraints that we have are typically related to ener requirements, gate equivalents (GEs), and timing. With passive RFID devices, we do not have an associated battery for the power supply, and where the chip must power itself from energy coupled from the radio wave. An RFID device is thus likely to be severely constrained in the power drain associated with any cryptography functions, along with being constrained for the timing requirements and for the number of gates used. Even if an RFID device has an associated battery (active RFID), it may be difficult to recharge the battery, so the drain on power must often be minimised.
There is thus often a compromise between the cryptography method used and the overall security of the method. Thus often light-weight cryptography methods balance performance (throughput) against power drain and GE, and do not perform as well as main-stream cryptography standards (such as AES and SHA-256). Along with this the method must also have a low requirement for RAM (where the method requires the usage of running memory to perform its operation) and ROM (where the method is stored on the device). In order to assess the strengths of various methods we often define the area that the cryptography function will use on the device – and which is defined in \(µm^2\). The NIST finalists are defined in this [article]
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- GIFT AEAD. GIFT. GIFT is a light-weight block cipher. It is a (NIST Finalist)
- Elephant. Elephant. Elephant is a light-weight stream cipher. It is a (NIST Finalist).
- TinyJambu. TinyJambu. TinyJambu is a light-weight block cipher. It is a (NIST Finalist)
- Isap AEAD. Isap. Isap is a light-weight block cipher. It is a (NIST Finalist)
- PHOTON-Beetle AEAD. PHOTON-Beetle. PHOTON-Beetle is a light-weight block cipher. It is a (NIST Finalist)
- Romulus AEAD. Romulus. Romulus is a light-weight block cipher. It is a (NIST Finalist)
- Sparkle AEAD. Sparkle. Sparkle is a light-weight block cipher. It is a (NIST Finalist)
- CLEFIA. CLEFIA. CLEFIA is a light-weight block cipher.
- LED. LED. LED is a light-weight block cipher.
- Piccolo. Piccolo. Piccolo is an ultra light-weight block cipher.
- PRESENT. PRESENT. Present is a light-weight block cipher.
- Pyjamask. Pyjamask. Pyjamask is a light-weight block cipher.
- SIMON. SIMON. SIMON is a light-weight block cipher.
- SKINNY. SKINNY. SKINNEY is a light-weight block cipher.
- SPECK. SPECK. SPECK is a light-weight block cipher.
- XTEA. XTEA. XTEA is a light-weight block cipher.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encryption/Decryption. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.
Light-weight crypto (Other)
- Chaskey (MAC). Chaskey. Chaskey is a light-weight MAC function.
- Chaskey (MAC). Chaskey (Python). Chaskey is a light-weight MAC function.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (ASCON)
ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRFF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
Discrete Logs (Solving)

A discrete log problem is in the form of \(g^x \pmod p\) and where we know \(g\) and \(p\) and must solve for \(x\).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Message Authentication Code (MAC)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
HMAC
The following are the tips related to Key-based hashing:
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authentication both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2), Blake2b, SM3 and SHA-3. This page outlines the HMAC-MD5 methods using the Hazmat cryptography layer.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- HMAC (COSE). Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT with HMMAC. Go. In this case we create a CWT token, and sign with an HMAC signature.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- HMAC with Rust. HMAC. HMAC with Rust.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HMAC with OpenSSL. MACs with OpenSSL. HMAC in OpenSSL for a given input value, password and hashing method.
Cipher MACs
The following are the tips related to Key-based hashing:
- MACs with OpenSSL. MACs with OpenSSL. MAC methods implemented in OpenSSL, including CMAC and GMAC.
Key-based hashing
The following are the tips related to Key-based hashing:
- SipHash. Siphash. Siphash is a fast key-based hashing method.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Meow. Meow. Meow is one of the fastest hashing methods.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
Magic Numbers

This pages contains information related to magic numbers in file formats.
Network and File Forensics
- Magic numbers. Magic. This provides information on magic number for file forensics.
Graphics formats
- JPEG Analysis. JPEGs. This provides an analysis of JPEG files.
- GIF Analysis. GIFs. This provides an analysis of GIF files.
- TIF Analysis. TIFs. This provides an analysis of TIF files.
- PNG Analysis. PNGs. This provides an analysis of PNG files.
- BMP Analysis. BMPs. This provides an analysis of BMP files.
- PSD Analysis. PSDs. This provides an analysis of PSD files.
- WMF Analysis. WMF. This provides an analysis of WMF files.
- Adobe Illustrator Analysis. AI. This provides an analysis of AI files.
- Adobe In Design Analysis. INDD. This provides an analysis of INDD files.
- MIDI file. MIDI. This provides an analysis of MID files.
- ICO file. ICO. This provides an analysis of ICO files.
- PS file. PS. This provides an analysis of PS files.
- EPS file. EPS. This provides an analysis of EPS files.
- VSD file. VSD. This provides an analysis of Microsft Visio (VSD) files.
Video and audio formats
- MP3 Analysis. MP3s. This provides an analysis of MP3 files.
- AVI Analysis. AVIs. This provides an analysis of AVI files.
- Flash SWF Analysis. SWFs. This provides an analysis of Flash files.
- Flash FLV Analysis. FLVs. This provides an analysis of FLV files.
- MP4 Analysis. MP4. This provides an analysis of MP4 files.
- MOV Analysis. MOV. This provides an analysis of MOV files.
- WMV Analysis. WMV. This provides an analysis of WMV files.
- WMA Analysis. WMA. This provides an analysis of WMA files.
- JPEG 2000 Analysis. JPEG 2. This provides an analysis of JPEG 2000 files.
- WAV Analysis. WAV. This provides an analysis of WAV files.
Zips, Archives and Library files
- ZIP/Archive Analysis. ZIPs. This provides an analysis of ZIP/Achive files.
- GZ Analysis. GZ. This provides an analysis of GZip files.
- Tar Analysis. Tar. This provides an analysis of TAR files.
- MSI Analysis. MSI. This provides an analysis of MSI files.
- OBJ Analysis. OBJ. This provides an analysis of OBJ files.
- DLL Analysis. DLL. This provides an analysis of DLL files.
- CAB Analysis. CAB. This provides an analysis of CAB files.
- EXE Analysis. EXE. This provides an analysis of EXE files.
- RAR Analysis. RAR. This provides an analysis of RAR files.
- SYS Analysis. SYS. This provides an analysis of SYS files.
- HLP Analysis. HLP. This provides an analysis of HLP files.
- VMDK Analysis. VMDK. This provides an analysis of VMDK files (VMWare Virtual Disks).
- PST Analysis. PST. This provides an analysis of PST files (Outlook Email File).
- JAR Analysis. JAR. This provides an analysis of JAR files.
- SLN Analysis. SLN. This provides an analysis of Microsoft SLN files.
- Class Analysis. Class. This provides an analysis of Java Class files.
- Zlib. Zlib. This provides an analysis of Zlib files.
Documents
- PDF Analysis. PDFs. This provides an analysis of PDF files.
- DOC Analysis. DOCs. This provides an analysis of DOC files.
- RTF Analysis. RTFs. This provides an analysis of RTF files.
- XLS Analysis. XLSs. This provides an analysis of XLS files.
- PPT Analysis. PPTs. This provides an analysis of PPT files.
- MMP File. MMP. This provides an analysis of MMP files.
- DOCX Analysis. DOCX. This provides an analysis of DOCX files.
- XLSX Analysis. XLSX. This provides an analysis of XLSX files.
- PPTX Analysis. PPTX. This provides an analysis of PPTX files.
- MDB Analysis. MDB. This provides an analysis of MDB files.
- Outlook Message Analysis. MSG. This provides an analysis of MSG files.
Disk Image
- Raw disk format. RAW. This provides an analysis of the RAW disk format.
Tests
- File Forensics Test. File Test File Forensics Test.
- File Forensics Test (Fun). File Test (Fun) File Forensics Test.
Presentations
MIRACL Core Library

MIRACL Core is an open source library, and includes a wide range of public key encryption methods. It is especially focused on elliptic curve and pairing-friendly methods, but also supports a wide range of encryption methods, including RSA, AES and hashing. Overall, it can be ported onto a wide range of systems and supports C, C++, Go, Rust, Python, Java, Javascript and Swift. Along with this it supports limited capability devices such as the Arduino infrastructure. The GitHub repository is [here].
BN254
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.

Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- CL Signatures. CL. CL Signatures in Go using MIRACL.
- CL Signatures (advanced pairing). CL. CL Signatures in Go using MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages using MIRACL.
- PS Signatures. PS. Signatures using PS for short signatures using MIRACL.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures using MIRACL.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.

Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
Rust examples
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
NaCl

PyNaCl is a Python port of LibSodium. It integrates the latest cryptography methods, such as AES, XChaCha20, Blake2b and X25519.
Symmetric Key
- Symmetric key. Symmetric key (XChaCha20 and Poly1305). With symmetric key, Bob and Alice have the same key. NaCl uses the XChaCha20 method, and which supports stream encryption (and which does not require padding as a block cipher does, and is also faster than block cipher modes). ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16 byte nonce. XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24 byte nonce. It has a lower propability of nonce misuse than ChaCha20.
- Encryption with a password. Symmetric Key with KDF. In symmetric key, we generate a secret key. This key is typically a random value or generated from a password and a salt value. If we use a password, we typically use a KDF (Key Derivation Function), and which uses a password and a salt value, in order to create a key of a given size. In this case we will use Argon2i, and which is memory resilent.
Hybrid Encryption
- Box. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Hashing
- Hashing and KDF (Argon2 and scrypt). Hashing and KDF. This case we will use PyNaCl (Networking and Cryptography) library, and which is a Python binding to libsodium. We will hash a password using SHA-256 and SHA-512, and also create a KDF (Key Derivation Function) using scrypt and Argon2.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
Ed25519
-
Ed25519. Ed25519. Using Ed25519 for digital signatures.
-
Finding Points on Ed25519. X25519 (Points).
In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 (Key Exchange)
- X25519 + BLAKE2b key-exchange. X25519. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
Curve 25519
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
Node.js

Node.js uses the JavaScript programming langauge as its base, and allows for code to be run on a server, rather than in the browser (such as with pure JavaScript). To run a node.js program, we run "node myfile.js", and use NPM to install libraries.
Symmetric key
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
RSA and public key
- RSA Opt imal Asymmetric Encryption Padding (OAEP) using Node.js. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
ECC Keys
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.

Hashing
- Hashing with node.js (All). Hashing. Hashing with node.js.
- Hashing with node.js (Selection). Hashing. Hashing with node.js.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- ECDSA with node.js. ECDSA. ECDSA with node.js.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
Key exchange
- Diffie-Hellman with node.js (random prime). DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method and uses a randomly generated prime number (press the button to generate a new prime).
- Diffie-Hellman with node.js. DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method. Each time the prime number will be fixed for the DH group selected.
- ECDH with node.js. ECDH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Elliptic Curve Diffie Hellman (ECDH) key exchange method.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
Key derivation
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
CryptoJS
- CryptoJS (in node.js). CryptoJS (Node.js). Various crypto methods in the browser.
Bulletproofs
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
Blockchain
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
Proxy encryption
- Proxy Encryption - Encrypting With Public Key, And Decrypt with Private Key. Proxy01. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This page just creates a key pair for Alice, and uses it to encrypt with the public key , and decrypt with the private key.
- Proxy Encryption. Proxy02. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This will go through the full use case of proxy re-encryption.
Tokens
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
Random
- Fortuna with node.js. Fortuna. Fortuna random numbers with node.js.
Other
- FPE with node.js. FPR. FPE with node.js.
- Puny with node.js. Puny. Puny character format with node.js.
Accumulators and Witnesses
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
PGP
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Password Entropy
- Password Entropy with Node.js. Password Entropy. Password entropy measures the strength of a password, and is measured as the number of bits which could represent all of the possibilities. An entropy score of less than 25 identifies a poor password, and between 25 and 50 is a weak password. For 50 to 75 we have a reasonable password, and between 75 and 100 is a very good password. Over 100 is an excellent password. The strength of the password relates to the number of characters used, and also the number of characters in the password.
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
- Homomorphic Encryption with Node.js and BGV. Homomorphic Encryption with Node.js and BFG. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BGV method.
Oblivious Transfer (OT)

Oblivious Transfer allows Bob to select data from Alice, but for Alice not to know which value has been selected.
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
OpenSSH

OpenSSH supports the usage of the SSH protocol. This allows for a remote login. One tool which is uses is ssh-keygen, and which allow for the generation of RSA, DSA and elliptic-curve keys that. These can be used for user and host authentication, such as for GitHub login and Cloud instance login.
OpenSSH
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here].
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
Outline

OpenSSL

OpenSSL is a standard library that implements cryptography.
Symmetric key (Command line)
-
Symmetric Key Encryption (OpenSSL 1.x) [here]. In this case we will create cipher text from OpenSSL 1.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 1.x) [here].In this case we will decrypt cipher text from OpenSSL 1.x using a key derived from a password
-
Symmetric Key Encryption (OpenSSL 3.x) [here]. In this case we will create cipher text from OpenSSL 3.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 3.x) [here].In this case we will decrypt cipher text from OpenSSL 3.x using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password.
Hashing
-
Hashing [here] OpenSSL supports a wide range of hashing methods including BLAKE2b, Gost, MD4, MD5, RMD-160, SHA-1, SHA-3, SHA-256 and SHA-512.
Libre OpenSSL
-
Symmetric Key Encryption using Libre OpenSSL [here]. In this case we will create cipher text from Libre OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption using Libre OpenSSL [here]. In this case we will decrypt ciphertext from Libre OpenSSL using a key derived from a password.
-
Hashing [here] Libre OpenSSL supports a wide range of hashing methods including Gost, MD4, MD5, RMD-160, SHA-1, SHA-256 and SHA-512.
Diffie-Hellman parameter generation
-
DH Parameters with OpenSSL [here]. The Diffie-Hellman (DH) method is perhaps one of the greatest inventions in Cybersecurity, and was created by Whitfield Diffie and Marty Hellman. With the DH method, Bob creates a random value (\(b\)) and Alice also creates a random value (\(a\)). Next Bob computes \(B=g^b \pmod p\) and sends it to Alice. Alice computes \(A=g^a \pmod p\) and sends this to Bob. Bob raises the value of \(A\) to the power of \(b\) and takes \(\pmod p\), and Alice raises \(B\) to the power of \(a\) and takes \(\pmod p\). In the end, they will have the same shared value: \(g^{ab} \pmod p\). This can then be used to derive an encryption key that they can use for a secure tunnel. Overall, \(p\) is the large prime number, and also known as the shared modulus between Bob and Alice.
Key derivation function
-
PBKDF2 key derivation with OpenSSL [here] PBKDF2 (Password Key Derivation Function 2) is a key derivation method. Overall it is relatively slow in its operation and where we take a password, a salt value, hashing method, and a number of iterations, in order to produce a given size of encryption key.
-
HKDF key derivation with OpenSSL [here] HKDF (HMAC Key Derivation function) is used to derive an encryption key from a pass phrase. Initially HKDF creates a pseudorandom key (PRK) using a pass phrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), andalong with a salt value. Next the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys.
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Passwords
-
Password example [here]. This page uses the OpenSSL library hash password generator, which is used in UNIX systems for the hashing of passwords which are contained in /etc/shadow and /etc/passwd. For newer passwords, the "-1" options is used to created the hashed value.
-
Hashed passwords with OpenSSL [here].
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
Public key
-
Generating an ECC key pair with OpenSSL [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)).
-
Generating an RSA key pair with OpenSSL [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2).
-
Generating an RSA key pair with OpenSSL with encryption [here]. This page implements RSA key pair generation with an encrypted key pair. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). In this case we will encrypt the key pair with either 3DES, 128-bit AES, 192-bit AES or 256-bit AES. The same password must be used to encrypt and decrypt.
-
Generate prime with OpenSSL [here]. Prime numbers are important in public key encrytion, and are used with RSA and ECC. For RSA, we generate two prime numbers (\(p\) and \(q\)) and which are multiplied together to create a modulus (\(N\)). If these prime numbers have 512 bit values, the modulus will be a 1,024 bit value. This defines the basic secure of RSA. With elliptic curve we use smaller prime numbers, such as 256-bit values for the secp256k1 curve.
ASN1 parsing
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). We will parse using asn1parse, and reveal the parameters.
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)) [RSA key pair]. We will parse using asn1parse, and reveal the parameters.
- DSA Parameters with asn1parse. DSA parameters with OpenSSL with asn1parse. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA (Digital Signature Algorithm)
- DSA Parameters. DSA parameters with OpenSSL. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
MAC (Message Authentication Code)
- HMAC with OpenSSL. MACs with OpenSSL. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authenticate both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2) and SHA-3. In this case we will use OpenSSL to generate the HMAC value.
- MACs with OpenSSL. MACs with OpenSSL. In the following we will generate MACs for HMAC, GMAC, CMAC, Blake2bmac, Blake2smac, KMAC128 and KMAC256. Overall, we will use an encryption key defined as a hex value for GMAC and CMAC, and a pass phrase for the others. The message is "hello".
Signing
- Digital signing a plaintext message with OpenSSL. Signing with OpenSSL. With digital signing, we can take a message, and create a signature. This normally involves signing with a private key and digital certificate. The signed message can be an a MIME format, and which can be integrated into an email message. In this can we have a 512-bit RSA key pair that will sign a plain text message.
Encrypting emails
- Encrypting an email message in OpenSSL. Encrypting messages with OpenSSL. With public key encryption, we can take a message, and encrypt it with the recipiant's public key. In this can we have a 512-bit RSA public key to encrypt a message.
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Random number generation with OpenSSL
-
Random number generator [here]. Random numbers are important in generating encryption keys and salt values. In this case OpenSSL generates a random number (in a Base64 format) for a given number of bytes.
Outline (C#/Python)
-
Symmetric Key Encryption (C#) [here]. This page uses the OpenSSL library through a C#/.NET wrapper. The DLLs it interfaces to are libeay32.dll and ssleay32.dll. OpenSSL supports a wide range of encryption methods, including 128-bit AES, 192-bit AES, 256-bit AES and Blowfish (bf). Different modes of ECB, CBC, and OFB are implemented. The examples use a default IV of "1234".
-
AES in Python with OpenSSL output [here]
-
Producing OpenSSL AES Encrypted String from C# [here]
Digital Certificates
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
Paillier - Partial Homomorphic Encryption

The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Fundamentals
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier).
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Using RSA
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
Applications
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
Background
The BLS12-381 curve is used in ZCash and has the form of \(y^2=x^3+ax+b \mod p\),. It has a prime number of:
p= 0x1a0111ea397fe69a4b1ba7b6434bacd764774b84f38512bf6730d2a0f6b0f6241eabfffeb153ffffb9feffffffffaaab
The \(a\) and \(b\) values are:
a 0x00
b 0x04
The base point is:
G= (0x17F1D3A73197D7942695638C4FA9AC0FC3688C4F9774B905A14E3A3F171BAC586C55E83FF97A1AEFFB3AF00ADB22C6BB, 0x08B3F481E3AAA0F1A09E30ED741D8AE4FCF5E095D5D00AF600DB18CB2C04B3EDD03CC744A2888AE40CAA232946C5E7E1)
BN (Barreto-Naehrig) Curve

BN Curve Applications (BN254)
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption (BN254)
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures (BN254)
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
BN256 Signatures
- BN256 Signatures. BNS. Implementation of BNS-256 for signatures using pairing-based cryptography.
- BN256 Signature Aggregation. BNS (Aggregation). In this page, we will aggregate signatures with BN256, along with aggregating the public keys. With this, we will have two key pairs of (\(sk_1,pk_1\)) and (\(sk_2,pk_2\)) and which will produce signatures of \(\sigma_1\) and \(\sigma_2\), respectively. We can then aggregate the signatures with \(\sigma_a = \sigma_1 + \sigma_2\), and the equivalent public key will be \(pk_a = pk_1 + pk_2\).
- BN256 Signature Aggregation ((The Rogue Public Key Attack)). BNS (Rogue Public Key). We can then aggregate the signatures with \(\sigma_a = \sigma_1 + \sigma_2\), and the equivalent public key will be \(pk_a = pk_1 + pk_2\). In this case, we will set \(pk_2=-pk_1\) and \(\sigma_2=-\sigma_1\), and which will set the aggregated public key at zero (or the point at infinity).
ZKP and OT (BN254 and BN128)
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
CipherCTF Needs You

This page includes cipher challenges for a capture the flag (CTF) activity (Quick link: cipherctf.com). Show leaderboard: [here]

Codes
If you want a printed version of the cipher challenge with answers (such as for teachers), click here [here].
If you want to jump to specific examples, you can do it here (and the system will generate a random ID for you):
- ADFGVX Code (Simple). ADFGVX. In this challenge the user has a number of ADFGVX codes to crack.
- AMCSO Code (Simple). AMCSO. In this challenge the user has a number of AMCSO codes to crack.
- Affine Code. Affine. In this challenge the user has a number of Affine codes to crack.
- Atbash Code. Atbash. In this challenge the user has a number of Atbash codes to crack.
- Bacon Code. Bacon. In this challenge the user has a number of Bacon codes to crack.
- Base64. Base64. In this challenge the user has a number of Base-64 codes to crack.
- Baud. Baud. In this challenge the user has a number of Baud codes to crack.
- Beaufort Cipher. Beaufort. In this challenge the user has two Beaufort ciphers to create.
- Beale Cipher. Beale. In this challenge the user has two Beale ciphers to decipher.
- Bible Code. Bible. In this challenge the user has two Bible codes to crack.
- Bifid Code. Bifid. In this challenge the user has a number of Bifid codes to crack.
- Braille Code. Braille. In this challenge the user has a number of Braille codes to crack.
- Caesar Code. Caesar. In this challenge the user has a number of Caesar codes to crack. With a Caesar code we move the alphabet by a certain number of shifts. The challenge only has one, two or three shifts.
- Columnar transposition cipher. Columnar. In this challenge the user has a number of Columnar codes to crack.
- Condi cipher. Condi. In this challenge the user has a number of Condi codes to crack.
- Covert Messages. Covert. In this challenge the user to find some covert messages.
- Delastelle Code. Delastelle. In this challenge the user has a number of Delastelle codes to crack.
- Diffie-Hellman. Diffie. In this challenge the user has a number of Diffie-Hellman keys to find.
- Dscript Code. Dscript. In this challenge the user has a number of Dscript codes to crack.
- Dvorak Code. Dvorak. In this challenge the user has a number of Dvorak codes to crack.
- Encode Code. Encode. In this challenge the user has a number of Encoded codes to crack.
- EX-OR Code. X-OR. In this challenge the user has a number of EX-oR codes to crack.
- Exponential Cipher. Exponential. In this challenge the user has a number of exponential ciphers to produce.
- Four Square Code. Four. In this challenge the user has a number of Four Square ciphers.
- Fractional Morse Cipher. Fractional. In this challenge the user has a number of Fractional Morse codes to crack.
- GCD. GCD. In this challenge the user has to find the GCD.
- Gold Bug. Gold. In this challenge the user to find the decoded Gold Bug ciphers.
- Hex Code. Hex. In this challenge the user has six codes to crack. These are defined as simple hexadecimal formats for the ASCII characters.
- Homophonic Substitution Code. Homophonic Substitution. In this challenge the user has a number of Homophonic Substitution codes to crack.
- Hill's Cipher. Hill's. In this challenge the user has a number of Hill's ciphers to crack.
- Huffman Coding. Huffman. In this challenge the user has a number of Huffman codes to crack.
- Jump. Jump. In this challenge the user to find messages that have been ciphered with the jump method.
- Keyword. Keyword. In this challenge the user has a number of Keyword codes to crack.
- Mary, Queen of Scots Code. Mary, Queen of Scots. In this challenge the user has a number of Mary, Queen of Scots codes to crack.
- Monk's Code. Monk. In this challenge the user has a number of Monk codes to crack.
- Morse Code. Morse. In this challenge the user has a number of Morse codes to crack. Morse code is made up with dots and dashes.
- Multiplier Code. Multiplier. In this challenge the user has a number of Multiplier codes to crack. With this cipher we multiple the values by a number and then use the (mod 26) operation.
- Mod 2 Multiply. Mod 2. In this challenge the user has a number of Mod 2 multiply values.
- Music cipher. Music. In this challenge the user has a number of Music ciphers to crack.
- Navajo Code. Navajo. In this challenge the user has a number of Navajo codes to crack.
- Nihlist Cipher. Nihlist. In this challenge the user has a number of Nihlist codes to crack.
- One Time Pad. OTP. In this challenge the user has a number of OTP codes to crack.
- Pigpen Code. Pigpen. In this challenge the user has two Pigpen codes to crack.
- Playfair. Playfair. In this challenge the user to find messages that have been ciphered with the jump method.
- Pollux. Pollux. In this challenge the user has a number of Pollux codes to crack.
- Polybius Code. Polybius. In this challenge the user has two Polybius codes to crack.
- Porta. Porta. In this challenge the user has a number of Porta codes to crack.
- QR Code. QR. In this challenge the user has a number of QR codes to crack.
- Rail Fence Code. Rail Fence. In this challenge the user has a number of Rail Fence codes to crack.
- Rot13 Code. Rot13. In this challenge the user has a number of Rot13 codes to crack.
- Rune Code. Rune. In this challenge the user has a number of Rune codes to crack.
- S-box Code. S-box. In this challenge we convert using an S-box.
- Scrambled Code. Scrambled. In this challenge the user has a number of scrambled alphabet codes to crack.
- Scrambled (Single mapping). Scrambled. In this challenge the user has a scrambled code to crack.
- Scrambled (Random mapping). Scrambled. In this challenge the user has a scrambled code to crack from any combination.
- Sequence. Sequence. This involves a sequence cipher.
- Semaphore. Semaphore. In this challenge involves semaphores.
- Straddling Code. Straddling. In this challenge the user has a number of Straddling codes to crack.
- Tap Code. Tap. In this challenge the user has a number of Tap codes to crack.
- Templar Cipher. Templar. In this challenge the user has a number of Templar codes to crack.
- Three square Code. Three square. In this challenge the user has a number of three square codes to crack. Morse code is made up with dots and dashes.
- Vigenère Code. Vigenère. In this challenge the user has a number of Vigenère codes to crack.
- Column Cipher . Column cipher. In this challenge the user uses a key for the columns.
Ciphers

Ciphers have been around for hundreds of years, and have often been used in love and war. In the following, we will analyse some traditional ciphers, and create a basic calculator to compute the cipher.
Fundamentals
- Frequency Analysis. Freq. This involves frequency analysis of text.
- Frequency Analysis (Example). Freq. This involves frequency analysis of text.
- ASCII to base codes using Python. Base. This converts an ASCII string into Base2, Base3, Base58 using Python.
- ASCII to codes. Coding. This converts an ASCII string into many other code, including Base2, Base45, and Base64.
- Detecting the cipher. Coding. This involves testing the cipher for the best match.
- Unbasing codes. Unbasing. This converts from a base format such as Base2, Base45, and Base64 into an ASCII string

Graphical Ciphers
- Bar Code. Barcode. This outlines the usage of Bar codes.
- Braille. Braille. This involves Braille coding.
- Dscript. Dscript. This involves Dscript coding.
- QR Code. QR. This outlines the usage of QR codes.
- Mary, Queen of Scots, polyalphabet cipher. Mary. This involves Mary's polyalphabet cipher.
- Pigpen Calculator. Pigpen. This involves a conversion of Pigpen.
- Semaphore flags. Semaphore flags. The creation of semaphore flags.
- Templar. Templar. The creation of a Templar cipher.
Key ciphers
- Autokey Cipher. Autokey. This involves the Autokey ciper.
- Keyword Code . Keyword. This involves the Keyword code.
Text-based Ciphers
These methods generally have some form of mapping that takes them from the plaintext to the ciphertext. Unfortunately knowing the conversion method leaves the code open to attack.
- a1z26. a1z26. This involves a1z26 cipher.
- ADFGVX. ADFGVX. ADFGVX example cipher.
- Affine. Affine. This involves affine cipher.
- Alder32. Alder32. This involves Alder32 cipher.
- Atbash. Atbash. This involves atbash cipher.
- Atbash (encode/decode). Atbash. This involves atbash cipher.
- Bacon Cipher. Bacon Cipher. This involves Bacon cipher.
- Barbie Cipher. Barbie Cipher. This involves Barbie cipher.
- Baudot. Baudot. This outlines the usage of Baudot codes.
- Beaufort Calculator. Beaufort . This involves a conversion of Beaufort cipher.
- Bifid Cipher. Bifid. This involves Bifid coding.
- Caeser. Caeser. This involves a conversion of Caeser.
- Citrix CTX1. Citrix CTX1. This cipher used the Citrix CTX1 password encoding method.
- Columnar Transposition Cipher. Columnar Transposition. In this cipher involves columnar transposition.
- Column Cipher . Column cipher. This cipher uses a key for the columns.
- Consonant index . Consonant index. This replaces constonant with their positions in a consonant index list.
- Delastelle. Delastelle. This involves the Delastelle cipher.
- DNA-1 cipher. DNA-1. This represents a cipher with DNA codes for Adenine (A), Thymine (T), Cytosine (C) and Guanine (G).
- Dvorak. Dvorak. This involves Dvorak cipher.
- Enigma Machine. Enigma. This outlines the Enigma Machine.
- Ex-OR Coding. Ex-OR. This uses an EX-OR coding.
- Four Square. Four Square. Four square example cipher.
- Fractionated Morse cipher. Fractionated. Fractionated Morse cipher.
- Gold Bug cipher. Gold bug. Gold Bug cipher.
- Hill's Cipher. Hill's. This involves the Hill ciper.
- Homophonic Substition Code. Homophonic Substition. This involves Homophonic Substition coding.
- Huffman Coding. Huffman. This involves Huffman coding.
- Kenny (Southpark) Cipher. Kenny. In Southpark, the character of Kenny is famous for dying in almost every episode. Overall, Kenny comes from a poor family and wears an orange parka with a hood that muffles his speech. Thus, all we hear are mumbles with a M, F and P sound. For this, we can create a Kenny cipher by replacing each letter with a triplet using M, F and P.
- Leetspeak Cipher. Leetspeak Cipher. This involves Leetspeak Cipher coding.
- Lorem Ipsum Cipher. Lorem Ipsum Cipher. This involves Lorem Ipsum Cipher coding.
- Lorenz Cipher. Lorenz. This outlines the Lorenz cipher.
- Morse Code (encode/decode). Morse Code. This involves Morse coding for encoding and decoding.
- Morse Code. Morse Code. This involves Morse coding.
- Multiplication Code. Mult. This involves the Multiplication cipher.
- Navajo Code Talkers. Navajo. This involves the Navajo Code Talkers code.
- Nihlist Cipher. Nihlist. This outlines the Nihlist cipher.
- One-Time Pad Calculator. OTP. This involves a conversion of OTP.
- Playfair. Playfair. This involves Playfair coding, which uses a 5x5 matrix, with a secret key to change the coding.
- Pollux Code. Pollux. This involves the Pollux cipher.
- Polybius Calculator. Polybius. This involves a conversion of Polybius code.
- Porta cipher. Porta. Porta cipher.
- Radio Cipher. NATO/Military phonetic alphabet content encoding. This involves using NATO/Military phonetic alphabet content encoding.
- Rail Fence Cipher (3/5 rail) encode/decode. Rail Fence. This involves Rail Fence cipher for encoding and decoding, and with three or five rails.
- Rail. Rail. Rail code example cipher.
- Rail Fence Cipher (3 rail). Rail Fence. This involves Rail Fence cipher.
- Rail cipher with Rust. Rail. Rail cipher with Rust.
- Reverse cipher. Reverse. This involves a reverse of the words in a sentence.
- Reverse Words cipher. Reverse. This involves a reverse of the words, and reverse the words of the sentence.
- Rick Astley. Rick Astley. Rick Astley cipher.
- ROT13 Cipher. ROT13. This involves ROT13 coding.
- ROT47 Cipher. ROT47. This involves ROT47 coding.
- Scrambled. Scrambled. This involves a scrambled alphabet code.
- Scytale cipher with Rust. Scytale. Scytale cipher with Rust.
- SMS cipher. SMS. This involves the SMS cipher.
- Straddling Cipher. Straddling. This involves Straddling coding.
- Tom-tom Cipher. Tom-tom. This involves Tom-tom coding.
- uuencoding Cipher. uuencoding . (Unix-to-Unix encoding) encodes messages for their transmission over email systems. It allows for data to be transmitted for both text and binary data.
- Vigenère Calculator. Vigenère. This involves a conversion of Vigenère.
- Vigenère Key Generator . Vigenère. This involves the creation of the Vigenère key given the plain text and the cipher text.
- Vowel index . Vowel index. This replaces vowels with their positions in a vowel index list.
- Whitespace . Whitespace. In this cipher we use to whitespace characters: the tab space ('\t') and a space (' '). When we view the cipher, we possibly cannot see the characters. In ASCII a tab is 0x09 ('\t') and a space (0x20). We can now represent a tab space as a '0', and a space as a '1'. In ASCII, an 'e' is 0110 0101 and which gives 09 20 20 09 09 20 09 20. For a 'd' we have 0110 0100 and which gives 0920200909200909.
Key Cracking
These methods generally have some form of mapping that takes them from the plaintext to the ciphertext, which changes with the usage of a special key. The key normally means that it is more secure than standard key-less methods, but they can be broken using methods such as brute-force
- Index of Coincidence (IC). IC. This outlines the Index of Coincidence (IC).
- Kasiski examination. Kasiski. This outlines Kasiski examination.
- Skip cipher. Skip. This outlines a Skip Cipher.
Some tests
Cloudflare CIRCL

Cloudflare have continually push ever increasing security standards, and have proved their credentials by publishing a state-of-the-art cryptography library: Cloudflare Interoperable Reusable Cryptographic Library (CIRCL).
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
Hybrid Encryption
- ECIES (Kryptology). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Coinbase Kryptology library.
- ECIES (CIRCL). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Cloudflare CIRCL library.

Curve 25519
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
X448 and Ed448
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- Ed448 with Go. Ed448. Ed448 with Go.

FourQ
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with FourQ (Cloudflare). FourQ.
Pseudorandom Functions (PRFs)
- Verifiable Oblivious Pseudorandom Functions (VOPRF) with Cloudflare CIRCL. VOPRF. In our digital world, we give away too many of our secrets, especially where we just have to prove the knowledge of something, rather than actually revealing it. In many of the systems we use, we could just prove things in an oblivious way, and where we could pass a secret but in a blinded form. With this, a server does not discover our password and for us not to discover the identifier that a server holds on us. But, can we also provide a proof back that the right password has been used? Well, with Verifiable Oblivious Pseudorandom Functions (VOPRF), we can generate a random secret based on a key generated on the server (Alice), and which is based on Bob’s secret.
Hash to Curve
- Hash to Curve using Go (Cloudflare). Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). The method defined here is proposed an an Internet-Draft standard by the Internet Engineering Task Force (IETF) related to "Hashing to Elliptic Curves".
Blind signature
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
Schnorr ZKP
- Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr NIZK proof into an elliptic curve method.
Discrete Log Equivalence (DLEQ)
- Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Post Quantum Key Exchange with CIRCL
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.

Digital Signatures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signatures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signatures (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
eXtendable-Output Function (XOF)
- eXtendable-Output Function (XOF) usign CIRCL. XOF. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS.
Cloud Computing

Cloud Computing allows virtualised instances to run within a Cloud environment. This can include hardware-as-a-service, infrastructure-as-a-server (such as with AWS EC2), platform-as-a-service, and software-as-a-service.
Cloud Computing
- Introduction to Cloud. Cloud introduction. The key objectives of this chapter are: provide an introduction to cluster, grid and cloud infrastructures; define an example of grid computing, and its advantages; and show an example of using a Cloud Infrastructure.
- AWS Lab. AWS Lab. The aim of this lab is setup AWS server instances and understand the setup of key security aspects.
Presentations
Codes

The following are a few challenges around codes. You can try some calculators [here].
Encoding
- ASCII table. ASCII. This shows an ASCII table.
- UTF-16 table. UTF-16. This shows a UTF-16 table.
- ASCII, Hex, Base-64 and Binary convertor. ASCII. This involves a conversion between different formats.
- Hex, Decimal and Binary convertor. Hex, Dec and Bin. This involves a conversion between hex, decimal, octal and binary.
- Binary conversion. Binary. This does a basic binary conversion.
- Floating point conversion. Floating. This does a basic floating point conversion for binary values.
- Malware obfuscation. Obfuscation. This converts from JavaScript encoding.
- Base-45. Base-45. This shows the conversion from ASCII into Base-45.
- ASCII to codes. Coding. This converts and ASCII string into many other code, including Base2, Base45, and Base64.
- Detecting the cipher. Coding. This involves testing the cipher for the best match.
- Unbasing codes. Unbasing. This coverts from a base format such as Base2, Base45, and Base64 into an ASCII string
- ASCII to base codes using Python. Base. This converts an ASCII string into Base2, Base3, Base58 using Python.
- UUID (GUID) and ULID. ULID. This creates a ULID (Universally Unique Lexicographically Sortable Identifier). UUIDs (Universally Unique IDentifiers) lack any real structure, and do not support the linking of objects and unique names. ULID aims to address this by created a cexicographically sortable system. It has a 26 character string and uses Base32 for its character (five bits per charater). With Base 32, we have a character set of "A-Z2–9=] - notice that '0' and '1' are not used, as they can be confused with 'O' and "I'.
Basic Security Principles
- Secret splitting. Secret splitting. This gives an example of secret splitting.
Others
- Inference. Infer. This involves the investigation of inference.
- Annual Loss Expectancy. ALE. This involves the investigation of Annual Loss Expectancy.
Some tests
- Hex and binary test. Test. Hex/Binary.
- Hex and binary test (Fun Test). Test. Hex/Binary.
- ASCII to Base64. Test. Convert from ASCII to Base64.
- ASCII to Base64. Test. Convert from ASCII to Base64.
- Caesar. Test. Caesar code.
- Caesar (Fun test). Test. Caesar code.
- MD5. Test. MD5 code.
Data Communications/Telecomms

This page outline related data communications and telecommunications material.
Fundamentals
- Data representation. Data. This outlines the conversion of values such as for hex, octal and decimal.
- Bit operations. Bitops. This outlines some basic bitwise operations.
- Bit operations (with eval()). Bitops. This outlines some basic bitwise operations.
- Bit shift. Shift. This outlines bit shift operators.
- Bit masking. Mask. This outlines bit masking.
- Bit mask. Mask. This outlines masking a single bit.
- Matrix multiplication. Calc. This outlines matrix multiplication.
Signals
- Signals and noise (Chart). Signals.
- Signals and harmonics. Signals.
- AM and FM (Chart). AM/FM.
- ASK, FSK and PSK (Chart). ASK/FSK/PSK.
- Data distributions. Dist.
- Laplace distribution. Laplace.
- Sampling. Quantisation.
- Pulse Analysis. Pulse.
Error Detecting/Correcting
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Hamming distance. Bin. This outlines the calculation of the Hamming distance.
- Hamming distance (between several bit strings). Bin. This outlines the calculation of the Hamming distance.
- Block parity (binary). Bin. This outlines block parity.
- Block parity (values). Bits. This outlines the calculation of block parity.
- CRC. CRC. This outlines the calculation of the CRC.
- Longitudinal/vertical redundancy checks (LRC/VRC). LRC. This outlines the calculation of the LRC.
- Bit errors. Bits. This outlines the calculation of bit error.
- Hamming (7,4) code. Hamming. This outlines the single bit error correcting code.
- Hamming (code. Hamming. This outlines Hamming coding.
- Reed Solomon. Reed. This outlines Reed Solomon coding.
Source Compression
- Huffman code. Huffman. This outlines Huffman coding.
- LZW code. LZW. This outlines Lempel-Ziv-Welch coding.
Image Compression
- GIF file format. GIF. This outlines the format of a GIF file
- GIF with Python. GFI. This page reads a GIF.
- JPEG - DCT Processing. DCT. This outlines DCT coding.
- JPEG - DCT Quantization. Quantization. This outlines DCT Quantization coding.
- JPEG - Face Detection. Faces. This outlines face detection.
- JPEG - Face Detection (Azure). Faces. This outlines face detection using Microsoft Cognitive Services.
- JPEG - Tags. Tags. This outlines the detection of JPEG tags in the file.
Video Compression
- MP4 file format. MP4. This outlines the format of an MP4 file
- MP4 File Forensics. File 1
- MP4 frame extraction. MP4. This outlines extracting images from MP4 stream
Others
- Barcodes. Barcode. This outlines the barcode format.
Commutative Encryption

Commutative Encryption involves Alice encrypting with her public key, and then Bob encrypting this with his public key. It is then possible to decrypt with either Alice using her private key first and then Bob private key, or the other way around.
Massey–Omura
The following are the tips related to Commutative encryption:
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
Commutative Encryption using stream ciphers
- Commutative Encryption using ChaCha20. ChaCha20. With commutative encryption we can encrypt and decrypt in any order. In this case we will use a stream chipher to X-OR a data stream with ChaCha20.
- Commutative Encryption with SHAKE-128/SHAKE-256 and Python. SHAKE-128/256. With commutative encryption we can encrypt and decrypt in any order. In this case we will use a stream chipher to X-OR a data stream with the SHAKE-128/256 byte output for a given password for Bob and Alice.
ElGamal Commutative Encryption
- Commutative Encyption (Modified ElGamal). Commutative Encyption. Commutative Encyption allow Bob and Alice to encrypt a message, and then for the data to be decrypted usign any order of the keys.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
CBOR and COSE

In computer security, we often have to represent binary data, in single values or groups of characters, bytes, words, long words, signed integers, floating-point values, double-precision floating-point values, and so on. This might be in the form of a data object, a signature or even encrypted content. For this, the ANS.1 DER format is often used, such as presenting digital certificates and signatures. An improvement on this for small messages with security is Concise Binary Object Representation (CBOR) — and which is defined in RFC8949 [1]. While JSON represents text-based data objects CBOR focuses on binary objects. It has been designed to create a lightweight encoder and decoder. This supports the use of CBOR within an IoT infrastructure. The data, also, does not require a data schema to be able to decode it, along with being extensible. CBOR defines the format of binary data with data objects and messages. We can then integrate security with CBOR Object Signing and Encryption (COSE), and which is defined in RFC8152 [2]. This includes signatures, message authentication codes (MACs), encryption and creating serialised objects.
Symmetric key
- 128-bit AES GCM. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) can then build on this to include signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use a symmetric key to encrypt a message, and then decrypt it. In this case we will use AES GCM with a static 128-bit key ("0x000102030405060708090a0b0c0d0e0f").
- 256-bit AES GCM. Go. In this case we will use AES GCM using a random 256-bit key (32 bytes).
Signatures
- EdDSA. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) [2] can then build on this to includes signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use EdDSA to create a signature for a message.
- ECDSA. Go. In this case we will use ECDSA to create a signature for a message.
- HMAC. Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
Tokens
- CWT. Go. In this case we create a CWT token, and sign with an HMAC signature.
ECDH and Content Encryption Key (CEK)
- ECDH. Go. In this case we create a symmetric key from ECDH. For this we will derive a shared key from the public key of Alice and Bob, and then define a single recipient which can derive the CEK (Content Encryption Key) using their private key. We will use the curves of P-256 (secp256r1), P-384 (secp384r1), P-521 (secp521r1) or SECP256K1 (as used with Bitcoin).
RSA
- RSA using COSE and CBOR. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\).
- RSA: dQ, dP and InvQ. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). The key pair also includes \(dQ\), \(dP\) and \(InvQ\), and these can be used with the Chinese remainder theory to optimize the decryption process.
References
[1] Bormann, C., & Hoffman, P. (2020). RFC 8949 Concise Binary Object Representation (CBOR). [here].
[2] Schaad, J. (2017), RFC 8152 – CBOR Object Signing and Encryption (COSE), 2017. [here]
[3] Jones, M., Wahlstroem, E., Erdtman, S., & Tschofenig, H. (2018). Cbor web token (cwt). RFC 8392, Standards Track, IETF. [here]
Cipher cracking

This page outlines a few cracks related to ciphers, AES, and public key. With hashing and symmetric key methods we might use cryptoanalysis, while RSA cracking can involve Chinese Remainder Theorem (CRT), copy-and-paste and weak random numbers.
Ciphers Cracking
The following are examples of cipher cracking:
- Index of Coincidence (IC). IC. This outlines the Index of Coincidence (IC).
- Kasiski examination. Kasiski. This outlines Kasiski examination.
- Vigenère Calculator Crack. Vig. This outlines Vigenère Crack.
- Frequency Analysis. Freq. This involves frequency analysis of text.
- Frequency Analysis (Example). Freq. This involves frequency analysis of text.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
Encryption cracking (RSA)
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA - Cracking the private key. Go.
- RSA Challenge Generator. RSA. This provides a value for e and N, and gives the cipher, and you must crack it by finding d.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
- RSA - Encrypted private key. Go. In this case we can generate a challenge where the student needs to find the password which encrypted an RSA rivate key.
RSA CTF Generators
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA. Low exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
Encryption cracking (Hashing)
- Differential Cryptanalysis (Hashing). Cryptanalysis. This provides an implementation of differential cryptanalysis for hashing methods.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA: Fault Attack. ECDSA: Fault Attack. In the fault attack in ECDSA we only require two signatures. One is produced without a fault \((r,s)\), and the other has a fault \((r_f,s_f)\). From these we can generate the private key.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
CTF Generators and Solvers

A Capture The Flag allows the creation of challenges which need to be solved, and which can be redeemed for points.
Cipher Examples
- Printed version of Cipher CTF challenges: [here].
- Electronic version of Cipher CTF challenges: [here].
Substitution ciphers
- CTF Generator: Kenny (Southpark) Cipher. Kenny. In Southpark, the character of Kenny is famous for dying in almost every episode. Overall, Kenny comes from a poor family and wears an orange parka with a hood that muffles his speech. Thus, all we hear are mumbles with a M, F and P sound. For this, we can create a Kenny cipher by replacing each letter with a triplet using M, F and P.
Bit rotate in messages
- CTF Generator: Rotate right. Rotate right. With the Rotate Right Cipher, we take the bits in each of the letters and rotate them by a number of positions to the right. It should be noted that this is done on a byte wise approach, and where we take each character at a time, and then rotate the bits by a given number of position. As we will possibly generate non-printing ASCII characters, we will represent the cipher as a hexademical value.
- CTF Generator: Rotate left. Rotate left. With the Rotate Left Cipher, we take the bits in each of the letters and rotate them by a number of positions to the left. It should be noted that this is done on a byte wise approach, and where we take each character at a time, and then rotate the bits by a given number of position. As we will possibly generate non-printing ASCII characters, we will represent the cipher as a hexademical value.
Vowel/consonant index cipher
- CTF Generator: consonant-index cipher. Consonant-index cipher. In this cipher we replace consonant with their index value.
- CTF Generator: vowel-index cipher. Rotate left. With the vowel-index cipher, we replace the vowels with their position. a - 1, e - 2, i - 3, o - 4, u - 5. Thus, this is the message, will be "This is a message" is "Th[i]s [i]s [a] m[e]ss[a]g[e]" becomes "TH3S3SS4M2T2XT".
Håstad’s Broadcast Attack
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
Finding the decryption exponent
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
Low exponent (e) in RSA
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
Wiener attack
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
Fermat’s attack
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
Different public exponent and the same modulus (N)
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
Low factor in the modulus
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
CTF: Cracking RSA with known partial bits
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
CTF Generator: RSA Fault in Signature Generation
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Curve 25519

Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page implements ECDH, and which is the method used in Tor to exchange the key. In this case we will use Python to implement X25519 (and which uses Curve 25519), but only uses the x-axis point for the sharing of values. The base point \(G\) on Curve 25519 is (9,1478161944 ... 7755586237401) [here].
Curve Points
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- Curve 25519 with Go for test vectors. ECC. This does a test on some private keys to test the public key generation.
Curve Adding/Multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Elliptic Curve (Point Adding with real curves). Elliptic Curve. Creating 2P from P with real curves (eg Curve 25519).
- Curve25519 with point adding Python. Curve25519. This outlines Curve25519 using basic point adding.
ECDH
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Curve 25519 with Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Elliptic Curve (Signatures - EdDSA)
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Ed25519 for EdDSA signatures with Hazmat. EdDSA: Ed25519. This page uses the Hazmat primitives for the cryptography library.
- Ed25519 signature using NaCl. Ed25519. This page uses the NaCl port from libsodium.
- Ed25519 points using NaCl. Ed25519. This page uses the NaCl port from libsodium to determine Ed25519 points.
- Barebones Ed25519 with Go. ECC. This shows point addition and scalar multiply in Ed25519
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
- Ed25519 in Python. EdDSA in Python. This page implements EdDSA using the Pure25519 library and with the core functions of key generation, signature generation and signature verification.
- Ed25519 Vulnerability in Python. EdDSA Vulnerability in Python. This page implements EdDSA using the Pure25519 library and with the core functions of key generation, signature generation and signature verification.
- Ed25519 Vulnerability in Python (Proof of Concept). EdDSA Vulnerability in Python (PoC). This page implements EdDSA using the Pure25519 library and with the core functions of key generation, signature generation and signature verification.
- Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw. .
Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
El Gamal
- ElGamal with ECC. ElGamal with ECC. ElGamal using ECC.
Signatures
Elliptic Curve (Keys)
The following are the tips related to ECC:
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Barebones Curve 25519
- Curve 25519 in Python. Barebones Curve 25519. This page implements Curve 25519 in pure Python.
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
- Curve 25519 in Python (Test Vectors from RFC 7748). Barebones Curve X25519. This page implements Curve 25519 in pure Python and tests against the IETF test vectors.
- Curve 25519 ECDH in Python (Test Vectors from RFC 7748). Barebones Curve X25519. This page implements Curve 25519 ECDH in pure Python and tests against the IETF test vectors.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 . EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
NaCl
Cyber&Data

This is the home page for the Cyber & Data course. There are four main units involved. Units 1 and 2 are self-study, but you can register for Units 3 and 4, and study towards an MSc module. Some unique features include: On-line Python integration, On-line Intrusion Detection Editor, Splunk Data Analysis, and Machine Learning Environment for Splunk. The Splunk elements of the course require a login (contact [email protected] for a login).
Unit 1: Fundamentals
- 1. Cyber and Intelligence. This topic provides an introduction to Cyber and Intelligence.
- 2. Defence Systems, Policies and Risk. This topic provides an overview of the some of the core defence mechanisms and risk approaches.
- 3. Open Source Intelligence. This topic outlines the usage of open source intelligence including using Shodan, Redit and Twitter mining.
- 4. So What is Data? This topics outlines the core data formats using in cybersecurity, and introduces the concept of magic numbers within files.
Unit 2: Data Capture and Analysis
- 5. Memory, Big Data and SIEM. This topic outlines some of the core principles used around Big Data methods and in the integration of SIEM (Security Information and Event Management).
- 6. Network Forensics. This topic provide fundamental knowledge in how networks works, and how we can analyse different network protocols, including ARP, IP, TCP, FTP and HTTP.
- 7. Intrusion Detection Systems. This topic outlines the usage of IDS and applies with using Snort.
Unit 3: Data Science and Cyber
- 8. Classification Metrics and ML.
- 9. Introduction to Data Science.
- 10. NumPy and Pandas. An outline of the integration of Numpy and Pandas for datasets.
- 11. Similarity and Matching. This unit outlines some of the key methods used within similarity and matching of text data. This includes the application of regular expressions, similarity metrics and similarity hashes.
Unit 4: Data Applications and Machine Learning
- 12. Splunk. An introduction to Splunk.
- 13. Splunk (Charting and Analysis). An introduction to Splunk with Charting and Analysis.
- 14. Machine Learning (Core Methods). An outline of the core methods.
- 15. Application of Machine Learning. A tutorial in applying ML with Splunk
Unit 5: Cyber Applications
- 16. Face Recognition. Implementation of face recognition.
DES, 3DES and Feistel ciphers

With DES and 3DES we have a 56-bit or 112-bit encryption key, respectively. Both are block ciphers and based on the Feistel ciphers, with a 64-bit block size.
Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- 3DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using 3DES encryption with Powershell.
- Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . With 3DES encryption, we use a 128-bit key and a 64-bit IV value. The two modes supported are ECB (without salt) and CBC (with salt). The DES algorithm has been around for a long time, and the 56-bit version is now easily crackable (in less than a day on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases, and splits the key into two. Overall the key size is typically 112 bits (with a combination of the three keys - of which two of the keys are the same). In this case we will use PKCS7 padding, and which fills the input data with a value that is equal to the number of padding bytes. Overall, DES has a 64-bit block size, and which equates to eight ASCII characters.
DES
The following are the tips related to DES, 3DES and Feistel ciphers:
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
Diffie-Hellman Key exchange (Discrete Logs)

Key exchange is a way for Bob and Alice to communicate and for them to agree on a shared secret. The original method defined uses discrete logarithms (Diffie-Hellman). With the Diffie-Hellman method, Alice generates \(a\) and shares \(A=g^a \pmod p\) with Bob. Bob generates \(b\) and shares \(B=g^b \pmod p\). Alice raises \(B\) to the power of \(a\), and Bob raises \(A\) to the power of \(b\). They should both end up with the same secret: \(K=g^{ab} \pmod p\).
Key interchange/generation (Diffie-Hellman)
The following relates to key interchange:
- Diffie-Hellman. Diffie-Hellman Calculation. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Real example). Diffie-Hellman Real. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Python). Diffie-Hellman. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (pre-compute). Diffie-Hellman (pre-compute). Many sites use the same prime numbers, which can then be cracked with a pre-computing attack.
- Selecting \(g\) in Diffie Hellman. G in Diffie Hellman. Picking a safe value of the generator \(g\) in discrete logarithms.
- Diffie-Hellman (Man-in-the-middle). DF. This outlines the man-in-the-middle method for Diffie-Hellman.
- An Alternative Diffie-Hellman method. Alterative DH. This outlines an alternative Diffie-Hellman method.
- Selecting g in discrete logs. g in discrete logs. This select a generator in discrete logs.
- Selecting g in discrete logs with random primes. g in discrete logs with random primes. This select a generator in discrete logs using random prime numbers which are define by a number of bits.
Authenticated Key Exchange
The following are the tips related to Key derivation hashing:
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- MTI/A0. MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{ax+by} \pmod p\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0. MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{x+y} \pmod p\)
- MTI/C0. MTI/C0. This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{xy} \pmod p\)
- MTI/C1. MTI/C1. This outlines MTI/C1, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{abxy} \pmod p\).
- HMQV (Menezes–Qu–Vanstone). HMQV. HMQV builds on MQV and adds the identity of Bob and Alice.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
Diffie-Hellman Parameter Generation
-
DH Parameters with OpenSSL [here]. With the Diffie-Hellman (DH) we use the form of \(g^x \pmod p\), and where \(g\) is the generator and \(p\) is a large prime number. In order to implement DH, we create either a generator value of 2 or 5, and then select a prime number which works with this generator value. In real-life we would generate a prime number of at least 2,048 bits. A command of "openssl dhparam -2 512" creates a random prime number with 512 bits and which works with a generator of \(g=2\).
Digital Certificates

Trust centres are responsible for storing private and/or public keys, and digital certificates are used to store and distribute private and/or public keys.
Trust Centres
- Simple Key Distribution Centre. KDC. This implements a simple KDC.
- Kerberos. Kerberos. This will implement a Kerberos method of generating a shared key.
Key Pair Generation and Code Signing Requests
The following are the tips related to digital certs:
- Generating key pair. View. This defines creating a 512-bit keypair.
- Code Signing Request (CSR). View. This defines the reading the CSR.
- Code Signing Request (CSR) with Python. View. This defines creating a CSR using Python.
Creating Digital Certificates
The following are the tips related to digital certs:
- Digital Certificate Digital Cert.
- Digital Certificate (PFX) Digital Cert.
- Certificate with Public/Private key. Cert. This includes the creation of the digital certificate.
- Generate X.509 certificate and key pair using Golang. X.509. This generates an X.509 certificate and shows the details.
- X.509 certificates in JavaScript. RSA and ECDSA Signed certificates. This page will generate either RSA and ECC key pairs, and then generate X.509 certificates, using either a signature of SHA1withRSA or SHA256withECDSA. For RSA signing we use an RSA private key to sign the certificate, and with ECDSA signing we use an ECC private key to sign the certificate.
Digital Certificate Format
The following are the tips related to digital certs:
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Certificate cracking
The following are the tips related to digital certs:
- Cracking certificates. Crack. This defines the cracking of digital certificates.
SSL
The following are the tips related to digital certs:
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Certificates (OpenSSL). View. This defines the viewing of digital certificates.
Theory
- Encryption Principles: [View]
- Proving identity and examining certificates: [View]
- Validating entities: [View]
DSA (Digital Signature Algorithm)

The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA with OpenSSL
- DSA Parameters. DSA parameters with OpenSSL. This page outlines the creation of a keypair for DSA signatures.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
DSA with PowerShell
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA and Node.js
- Key pair using Node.js. DSA and other keypairs. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
DSA and C#
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
DSA and OpenSSH
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
DSA Signatures with Hazmat
-
DSA Signatures. DSA Signatures. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. The ECDSA method is an extension of DSA, but implemented with elliptic curve (EC) methods. As with most public key signing methods, we take a hash of a message, and then apply a private key to create a signature (\(r,s\)). This is done by creating a random value (\(k\)) to produce the signature. The signature is then verified using the associated public key. This then verifies the creator of the signature and that the message has not been changed.
Outline
So, what does a digital signature look like? Well, it often has an r value and an s value: (r,s). So, let’s look at the DSA (Digital Signature Algorithm) signature. For this, Figure 1 shows an outline of the setup of the DSA signature, and where Bob uses his private key (sk) to sign a hash of a message, and Alice proves with his public key (pk,g,p,q). We also use a random nonce value (k) for the signature, and we must take care that we do not reuse the value.

Figure 1: DSA signature
Initially, Bob creates two prime numbers (\(p\) and \(q\)) and generates a generator value of \(g\). Next, he generates his secret key (\(x\)) and then computes his public key:
\(Y=g^{x} \pmod p\)
To create a signature for a message (\(M\)), he creates a random value (\(k\)) and then computes two values for the signature:
\(r = g^{k} \pmod{p} \pmod{q}\)
\(s=(k^{-1}.(H(m)+x.r)) \pmod {q}\)
When Alice receives this signature, she takes Bob's public key \((p,q,g,Y)\) and the message can computes:
\(w = s^{-1} \pmod q\)
\(u_1 = H(M).w \pmod q\)
\(u_2 = r.w \pmod q\)
\(v = (g^{u_1} . y^{u_2}) \pmod {p} \pmod {q}\)
She then checks that \(v\) is equal to \(r\). If so, the signature checks out. This works because:
\(v = g^{h.w}.y^{r.w} = g^{h.w}.g^{x.r.w} = g^{h.w+x.r.w} = g^{h/s+x.r/s} = g^{(H+x.r)/(k^{-1}(H+x.r))} = g^k = r\)
Elliptic Curve Cryptography (ECC)

With elliptic curve methods, we take a base point (\(G\)) and then use a private key (\(n\)) to produce a public key point (\(nG\)).
Elliptic Curve (Points)
The following are the tips related to ECC:
- ECC types and nG. ECC types and nG. Outlining the parameters used for ECC types (eg Curve 25519, Curve 448 and secpt256k1).
- First 100 Elliptic Curve points in Finite Field. Elliptic Curve points. Locating the first 100 points in an elliptic curve in a finite field.
- Elliptic Curve - Point addition. Elliptic Curve Point Addition. This shows the addition of two points on an elliptic curve.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field.
- First 20 Elliptic Curve points in Finite Field (improved method). Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field.
- First 20 Elliptic Curve points in Finite Field (plot). Elliptic Curve points (plot). Locating the first 20 points in an elliptic curve in a finite field.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field for common curves with Libnum. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256 and using Libnum to compute the quadratic square.
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- ECC double-and-add for point multiplication. Elliptic Curve double-and-add. Calculation of \(aG\) using a double-and-add approach (and which is equivalent to square-and-multiply in exponential functions.
- ECC key generation with Hazmat. Elliptic Curve key gen. Creating ECC keys using Hazmat and Python.
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining \(n.G\) for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Operations Within a Solidity Contract. Go.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Embedding data in an ECC point
- Embedding data in a point. Go. With Elliptic Curve Cryptography (ECC), we use points on an elliptic curve to represent our data. These are defined with (x,y) points. With this, it is possible to embedded a certain amount of data into the point - as long as it still gives us a valid point on the curve. This example will Curve 25519 to embed data, and is achieved by storing the length of the data in a single byte in the point, and then store the data as byte values in the point (followed by random data). To decode, we can then just read the first byte for the length of the message, and then reveal the data encoded into the point..
Quadratic residues
- Quadratic residue (mod p). Go. Outline of quadratic residue \(\pmod p\).
Elliptic Curve (ECDH) - Python
The following are the tips related to ECC:
- Elliptic Curve. Elliptic Curve. Elliptic Curve is a public key method which can also be used to generate a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with simple parameters. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
Elliptic Curve (ECDH) - Golang and Node.js
The following are the tips related to ECC:
- ECDH with Go. ECDH. ECDH with Go.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with node.js. ECDH. ECDH with node.js.
- ECDH with JavaScript. ECDH. Elliptic Curve Diffie Hellman.
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret. We will use Golang and the Krytology library.
Elliptic Curve (Signatures - ECDSA)
The following are the tips related to ECC:
- ECDSA and EdDSA methods. ECDSA and EdDSA. This outlines ECDSA and EdDSA for NIST, secp, brainpool and Ed448/Ed25519.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with secp256k1. ECDSA (secp2561k1). Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with secp256k1.
- ECDSA using P256. Barebones ECDSA with P256. This page implements ECDSA with the NIST P256 curve.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces and using Lenstra–Lenstra–Lovász (LLL) method. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA with Hazmat. ECDSA wih Hazmat. This outlines ECDSA with Hazmat.
- Blinded ECDSA. Blinded ECDSA. With a blinded signature, Bob can sign for a message, without knowning what the message is. In this case Alice will create a blinded ECDSA signature, and where Bob can then sign it, and then Alice can unblind it. The method is based on one produced by Oleg Andreev for blinding signatures in Bitcoin.
- ECDSA: Fault Attack. ECDSA: Fault Attack. In the fault attack in ECDSA we only require two signatures. One is produced without a fault \((r,s)\), and the other has a fault \((r_f,s_f)\). From these we can generate the private key.
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
Elliptic Curve (DER)
The following are the tips related to ECC:
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Elliptic Curve (Signatures - EdDSA)
The following are the tips related to ECC:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. X448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Ed25519 for EdDSA signatures with Hazmat. EdDSA: Ed25519. This page uses the Hazmat primitives for the cryptography library.
- Ed25519 signature using NaCl. Ed25519. This page uses the NaCl port from libsodium.
- Ed25519 points using NaCl. Ed25519. This page uses the NaCl port from libsodium to determine Ed25519 points.
Elliptic Curve (Plots)
The following are the tips related to ECC:
- Elliptic Curve (Plot). Elliptic Curve (Plot). Elliptic Curve is a public key method which can also be used to generate a shared key. This page outlines a graphic of the curve.
- Elliptic Curve (Real plots). Elliptic Curve (Real plot). This provides a range of well-defined elliptic curve plots.
Elliptic Curve (Keys)
The following are the tips related to ECC:
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
Elliptic Curve (ECIES)
The following are the tips related to ECC:
- Elliptic Curve Integrated Encryption Scheme (ECIES with Rabbit Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with Rabbit (a light-weight stream cipher).
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
Elliptic Curve (Hash to curve)
The following are the tips related to ECC:
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve with libnum.
- Hash to password with Go. Hash to password. Hash to password with Go.
- Match random value to sepc256k1 with Python. Random value to curve. This involves generating a random value, and then finding the nearest valid point on the curve. It involves incrementing a value of \(x\) until we reach a valid point.
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
Elliptic Curve (Point adding)
The following are the tips related to ECC:
- Elliptic Curve (Point Adding). Elliptic Curve. Creating 2P from P.
- Elliptic Curve (Point Adding with real curves). Elliptic Curve. Creating 2P from P with real curves (eg Curve 25519).
- Elliptic Curve (Calculating nP - ECC Calculator). Elliptic Curve. Creating nP from P with real curves.
- Elliptic Curve (Point addition - ECC Calculator). Elliptic Curve. This calculator adds two points on an elliptic curve.
- Elliptic Curve (Point addition - ECC Calculator - range of points). Elliptic Curve. This calculator takes one point on the elliptic curve, and then adds the other the other points on the curve to see the result.
Elliptic Curve (Curve 25519)
The following are the tips related to ECC:
- Curve 25519 with Go for test vectors. ECC. This does a test on some private keys to test the public key generation.
- Curve 25519 with Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Curve25519 with Python. Curve25519. This outlines Curve25519, which is used in the Tor network.
- Curve25519 with point adding Python. Curve25519. This outlines Curve25519 using basic point adding.
ElGamal and ECC
- ElGamal with ECC. ElGamal with ECC. ElGamal using ECC.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
- Proving an Encrypted Shuffle With ElGamal and ECC. Shuffle. An encrypted shuffle with ElGamal.
Elliptic Curve (X448)
The following are the tips related to ECC:
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Python. X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH using Python and based on RFC 7748.
Elliptic Curve (ElGamal)
The following are the tips related to ECC:
- Proving an Encrypted Shuffle With ElGamal and ECC. Shuffle. An encrypted shuffle with ElGamal.
- ElGamal with ECC. ElGamal with ECC. ElGamal using ECC.
Elliptic Curve (Pedersen Commitment) and DLEQ
The following are the tips related to ECC:
- Elliptic Curve - Blinding factor (Pedersen Commitment). Elliptic Curve Blinding. This shows the addition of transactions with a blinding factor.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
Elliptic Curve (Box and Encryption)
The following are the tips related to ECC:
Go ECC
- Hash to password with Go. Hash to password. Hash to password with Go.
- ECDH with Go. ECDH. ECDH with Go.
- Box with Go. Box. Box with Go.
- ECC with Go. ECC. ECC with Go.
- Curve 25519 with Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ElGamal with ECC. ElGamal with ECC. ElGamal using ECC.
- Curve 25519 with Go for test vectors. ECC. This does a test on some private keys to test the public key generation.
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Barebones Ed25519 with Go. ECC. This shows point addition and scalar multiply in Ed25519
- Barebones NIST P256 with Go. ECC. This shows point addition and scalar multiply in P256
Key exchange
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). The resultant key is \(xyG \)
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
- Authenticated Key Exchange (ECC). YAK. Key exchange with public keys and uses elliptic curve methods.
IBE
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
Barebones ECC
- P192 in Python. Barebones P192. This page implements P192 in pure Python.
- P224 in Python. Barebones P224. This page implements P224 in pure Python.
- P256 in Python. Barebones P256. This page implements P256 in pure Python.
- P521 in Python. Barebones P521. This page implements P521 in pure Python.
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
- Curve 25519 in Python. Barebones Curve 25519. This page implements Curve 25519 in pure Python.
- Curve 25519 in Python (Test Vectors from RFC 7748). Barebones Curve X25519. This page implements Curve 25519 in pure Python and tests against the IETF test vectors.
- Curve 448 in Python (Test Vectors from RFC 7748). Barebones Curve X448. This page implements Curve 448 in pure Python and tests against the IETF test vectors.
- Curve 25519 ECDH in Python (Test Vectors from RFC 7748). Barebones Curve X25519. This page implements Curve 25519 ECDH in pure Python and tests against the IETF test vectors.
- Curve 448 ECDH in Python (Test Vectors from RFC 7748). Barebones Curve X448. This page implements Curve 448 ECDH in pure Python and tests against the IETF test vectors.
- ECDSA using P256. Barebones ECDSA with P256. This page implements ECDSA with the NIST P256 curve.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 . EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
Others
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.

Public Key (Elliptic Curve) in Rust
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Sage
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
Elliptic Curve Diffie-Hellman (ECDH)

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as secp256k1 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) - Python
The following are the tips related to ECC:
- Elliptic Curve Diffie-Hellman (ECDH) with simple parameters. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
- ECDH and COSE. Go. In this case we create a symmetric key from ECDH. For this we will derive a shared key from the public key of Alice and Bob, and then define a single recipient which can derive the CEK (Content Encryption Key) using their private key. We will use the curves of P-256 (secp256r1), P-384 (secp384r1), P-521 (secp521r1) or SECP256K1 (as used with Bitcoin).
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Go. ECDH. ECDH with Go.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret. We will use Golang and the Krytology library.

Elliptic Curve (ECDH) - Node.js
The following are the tips related to ECC:
- ECDH with node.js. ECDH. ECDH with node.js.
- ECDH with JavaScript. ECDH. Elliptic Curve Diffie Hellman.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Key exchange

- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). The resultant key is \(xyG \)
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
- Authenticated Key Exchange (ECC). YAK. Key exchange with public keys and uses elliptic curve methods.
ECDSA (Elliptic Curve Digital Signature Algorithm)

ECDSA has been around for over two decades and was first proposed in [1]. The ECDSA method significantly improved the performance of signing messages than the RSA-based DSA method. Its usage of elliptic curve methods speeded up the whole process and supported much smaller key sizes. Its crown and glory were being selected by Satoshi Nakamoto for his Bitcoin protocol, and then its adoption into Ethereum.
ECDSA Basics
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Recoving the public key from an ECDSA Signing in Python. Recoving public key from ECDSA Signing. This is an example of recovering the public key from the ECDSA signature with Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\)).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\)) and will check that the signature is valid.
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
-
ECDSA for Multiple Curves and Different Hashing Methods with Python
. ECDSA for Multiple Curves and Different Hashing Methods with Python. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
- ECDSA Signatures with Hazmat (SECP256R1, SECP384R1, SECP521R1, SECP224R1, SECP192R1, and SECP256K1). ECC Signatures. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and then creates an ECDSA signature for a given message.
- DSSE (Dead Single Signature Envelopes). DSSE. The Update Framework (TUF) provides a framework to secure the software within a system, while in-toto ("as-a-whole") can be used to protect the whole of software support chain. TUF thus delivers updates to a system while in-toto manages a complete software infrastructure. For this, it uses the Metablock format, and where we do not sign the byte values for the signature but sign the JSON data. This is known as canonicalisation - and which is the conversion of data in different forms to a standardised format.
Elliptic Curve (DER)
The following are the tips related to ECC:
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Google Tink with ECDSA
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
ECDSA Applications
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Blinded ECDSA. Blinded ECDSA. With a blinded signature, Bob can sign for a message, without knowning what the message is. In this case Alice will create a blinded ECDSA signature, and where Bob can then sign it, and then Alice can unblind it. The method is based on one produced by Oleg Andreev for blinding signatures in Bitcoin.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA: Fault Attack. ECDSA: Fault Attack. In the fault attack in ECDSA we only require two signatures. One is produced without a fault \((r,s)\), and the other has a fault \((r_f,s_f)\). From these we can generate the private key.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Elliptic Curve Integrated Encryption Scheme (ECIES)

With ECIES we integrate the power of elliptic curve (EC) public key encryption with symmetric key encryption. An outline of the method is:

Elliptic Curve (ECIES)
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Elliptic Curve Integrated Encryption Scheme (ECIES with Rabbit Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with Rabbit (a light-weight stream cipher).
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
Applications
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- ECIES (Kryptology). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Coinbase Kryptology library.
- ECIES (CIRCL). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Cloudflare CIRCL library.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
Ethereum crypto
- ECIES with Go-Ethereum. Go.
EdDSA, Ed25519 and Ed448

Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). EdDSA (Edwards-curve Digital Signature Algorithm) is a fast and efficient digital signature method, and is based on the Schnorr signature scheme. Two important curves that are implemented with EdDSA are Curve 25519 (X25519) and Curve 448 (Ed448). EdDSA has been standardized in [RFC 8032]. With EdDSA, Alice generates a private key of \(sk\) and a public key of \(P=sk.G\) and where \(G\) is the base point of the curve.
Elliptic Curve (Signatures - EdDSA)
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Ed25519 in Python. EdDSA in Python. This page implements EdDSA using the Pure25519 library and with the core functions of key generation, signature generation and signature verification.
- Ed25519 Vulnerability in Python. EdDSA Vulnerability in Python. This page implements EdDSA using the Pure25519 library and with the core functions of key generation, signature generation and signature verification.
- Ed25519 Vulnerability in Python (Proof of Concept). EdDSA Vulnerability in Python (PoC). This page implements EdDSA using the Pure25519 library and with the core functions of key generation, signature generation and signature verification.
Hazmat (Ed448 and Ed25519)
- Ed25519 for EdDSA signatures with Hazmat. EdDSA: Ed25519. This page uses the Hazmat primitives for the cryptography library for X25519.
- Ed448 for EdDSA signatures with Hazmat. EdDSA: Ed25519. This page uses the Hazmat primitives for the cryptography library for X448
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
Golang
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
- Barebones Ed25519 with Go. ECC. This shows point addition and scalar multiply in Ed25519
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
COSE/COBR
- EdDSA. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) [2] can then build on this to includes signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case, we will use EdDSA to create a signature for a message.
Testing Ed25519
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
NaCl
- Ed25519 signature using NaCl. eddsa. This page uses the NaCl port from libsodium.
- Ed25519 points using NaCl. eddsa. This page uses the NaCl port from libsodium to determine Ed25519 points.
Theory
With EdDSA, Alice will sign a message with her private key, and then Bob will use her public key to verify that she signed the message (and that the message has now changed):

Key generation
Alice generates a random 32-byte secret key (\(sk\)) and then creates a public key of:
\(pk=sk \cdot G\)
and where \(G\) is the base point of the curve.
Signing
Alice creates a SHA-512 hash of her private key:
\(h=\textrm{HASH}(sk)\)
Create \(r\) from the upper 32 bytes of hash and the message:
\( r = \textrm{HASH}(h[32:] \: || \: m))\)
And where "||" represents a concatenation of the byte array values. Next she matches \(r\) onto curve with:
\(R=r \cdot G\)
Next Alice computes \(s\) with:
\(s=r + (\textrm{HASH}(R \: || \: pk \: || \: m)) \cdot sk\)
The signature is (\(R,s\)). The values of \(R\) and \(s\) are 32 bytes long, and thus the signature is 64 bytes long.
Verifying
Bob creates \(S\) using \(R\), \(pk\) and \(m\):
\(S =\textrm{HASH}(R \: || \: pk \: || \: m) \)
And next creates two verification values:
\(v_1=s \cdot G\)
\(v_2=R+ pk \cdot S\)
If \(v_1==v_2\) the signature checks. This is because:
\(
\begin{align}
v_1&=s.G\\
&= (r + (\textrm{HASH}(R \: || \: pk \: || \: m)) \cdot sk) \cdot G \\
&= rG + sk \cdot G \cdot (\textrm{HASH}(R \: || \: pk \: || \: m)) \\
&= R+ pk \cdot S \\
&= v_2
\end{align}
\)
ElGamal

Public key encryption is typically used to sign for things (and where we use the private key to encrypt something and prove this with the public key) and within key exchange methods. The core methods used are RSA and Elliptic Curve. But an alternative is to use discrete logarithms. One of the most interesting is ElGamal, and was created by Taher Elgamal in 1985.
ElGamal Method
- ElGamal. ElGamal. ElGamal is a public key method which uses discrete logarithms.
- ElGamal in Python. ElGamal in Python. ElGamal is a public key method which uses discrete logarithms.
- ElGamal in Python with variable prime sizes. ElGamal in Python for different prime sizes. ElGamal is a public key method which uses discrete logarithms.
- Selecting g in ElGamal. G in ElGamal. ElGamal is a public key method which uses discrete logarithms.
- Selecting g in discrete logs. g in discrete logs. This select a generator in discrete logs.
- Selecting g in discrete logs with random primes. g in discrete logs with random primes. This select a generator in discrete logs using random prime numbers which are define by a number of bits.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- Proving an Encrypted Shuffle With ElGamal and ECC. Shuffle. An encrypted shuffle with ElGamal.
- ElGamal encryption with Powershell. ElGamal encryption.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Commutative Encryption
- Commutative Encyption (Modified ElGamal). Commutative Encyption. Commutative Encyption allow Bob and Alice to encrypt a message, and then for the data to be decrypted usign any order of the keys.
ElGamal Signature
- ElGamal signatures. ElGamal. ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this.
- ElGamal signatures (alterative signing). ElGamal (Signing: s=ar + kh(m)). ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this. Normally we sign with \(s=k^{-1} (h(m)-ar) \pmod {p-1}\), but in this case we will use \(s=ar + kh(m))\).
- ElGamal signatures (alterative signing). ElGamal (Signing: s=ah(m) + kr). ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this. Normally we sign with \(s=k^{-1} (h(m)-ar) \pmod {p-1}\), but in this case we will use \(s=ah(m) + kr\).
- ElGamal signatures (alterative signing). ElGamal (Signing: r=as+kh(m)). ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this. Normally we sign with \(s=k^{-1} (h(m)-ar) \pmod {p-1}\), but in this case we will use \(r=as+kh(m)\).
- ElGamal signatures (alterative signing). ElGamal (Signing: r=ah(m) +ks). ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this. Normally we sign with \(s=k^{-1} (h(m)-ar) \pmod {p-1}\), but in this case we will use \(r=ah(m) +ks\).
- ElGamal encryption with Go. ElGamal. This implements ElGamal encryption.
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
ElGamal Homomorphic Encryption
- ElGamal Homomorphic Cipher for Multiplication (Python). ElGamal. This outlines ElGamal Homomorphic multiplication with Python.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (Python). ElGamal. This outlines ElGamal Homomorphic division with Python.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (Python). ElGamal. This outlines ElGamal Homomorphic addition with Python.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (Python). ElGamal. This outlines ElGamal Homomorphic subtraction with Python.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
- ElGamal Homomorphic Cipher (Go). ElGamal. This outlines ElGamal Homomorphic cipher with Go.
- ElGamal Homomorphic Cipher (Go) - Divide. ElGamal. This outlines ElGamal Homomorphic cipher with Go with divide.
- ElGamal Homomorphic Cipher (Go) - Additive. ElGamal. This outlines ElGamal Homomorphic cipher with Go with addition.
ElGamal and ECC
- ElGamal with ECC. ElGamal with ECC. ElGamal using ECC.
- Proving an Encrypted Shuffle With ElGamal and ECC. Shuffle. An encrypted shuffle with ElGamal.
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- ElGamal - Applying Multiple Public Key Operations (ECC). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use elliptic curve methods, and using the Edwards 25519 curve.
ElGamal (Authenticated and Verified Encryption)
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenticated ciphertext.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
ElGamal (Encrypting with multiple public keys)
- ElGamal - Applying Multiple Public Key Operations (Discrete Logs). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use discrete logs.
- ElGamal - Applying Multiple Public Key Operations (ECC). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use elliptic curve methods, and using the Edwards 25519 curve.
Ethereum

This page outlines some examples of blockchain and cryptocurrency.
Test Network
- Math functions on Local Network. Go.
- Math functions on Test Network. Go.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- Storing State in a Smart Contract. Go.
- Deleting Data From A Smart Contract. Go.
- A Caesar Cipher Quiz Generator from a Smart Contract. Go.
- Hashing in a Smart Contract. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
- Dealing With Decimals In Smart Contracts. Go.
- Creating A Scrambled Alphabet Challenge Generator In Ethereum and Solidity. Go.
- Deploying a Scrambled Alphabet Generator To Ethereum (With Ganache and Ropsten). Go.
- Deploying a Scrambled Alphabet Generator To Ethereum (With Hardhat). Go.
- Pigpen, IPFS and Ethereum. Go.
- Proof of \(x\) from \(H(x)\) using zkSnarks. Go.
- Elliptic Curve Operations Within a Solidity Contract. Go.

Ethereum
- Creating Ethereum address with Python. Go.
- Creating Ethereum signing with Python. Go.
- ERC20 Tokens. Go.
- Ethereum address with Go. Addresses. This generates an Ethereum address.
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- PATRICIA trie. PATRICIA. Example of using PATRICIA (and which is used in Ethereum).
- Viewing Balance of account in Etheruem with Go. Balance. This views the balance of an account
- Viewing Block in Etheruem with Go. Block. This views a block.
- Viewing Cryptocurrency API with Python. Go.
- Viewing Ethereum blockchain with Python. Go.
- Viewing Transactions in Block in Etheruem with Go. Transactions. This views transactions.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
- Symmetric Key Encryption For Smart Contracts. Symmetric key. Solidity does not natively support symmetric key encryption, such as with AES. Overall, AES would consume too much gas and thus be expensive to implement. But, we can use hashing and X-OR methods to do the encryption. In this case, we will create a 256-bit random value, and then encrypt it with an encryption key, and then decrypt it.
Calling from Python
- Calling smart contracts with Python. Python.
Ethereum crypto
- ECIES with Go-Ethereum. Go.
Ethereum Blockchain
- IOTA Trytes. Trytes. `This outlines Trytes, as used in IOTA.
Ethereum Blockchain
- Blockchain: Adding Maths Functions. Go.
- Blockchain: Blocks, transactions and writing data. Go.
- Blockchain: Contracts and Addresses. Go.
- Blockchain: Getting transactions. Go.
- Blockchain: Hello World!. Go.
- Blockchain: Simple Purchasing System. Go.
- Blockchain: Viewing the blockchain. Go.
- Blockchain: Cracking Wallets. Go.
- Introduction to Blockchain. Go.
Presentations
Factorization

Many public key problems involve the difficulity in factorizing a value two its prime number factors. For example, in RSA, we have a public modulus \(N\) and which is equal to the multiplication of two prime numbers \(p\) and \(q\). If we can factorize the public modulus, we will be able to break the RSA cipher related to it.
RSA Crack
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA Factorization. RSA. This outlines the factorisation of the N value in the RSA method.
Methods
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Dixon. Go. Dixon Method.
- Rho factorization. Rho. Rho alogorithm.
- Smooth numbers. Go. Outline of smooth numbers.
Methods (Elliptic curve
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Quadratic residues
- Quadratic residue (mod p). Go. Outline of quadratic residue \(\pmod p\).
- Quadratic residue (mod p) using Legendre symbol. Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
Factorizing
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
Lenstra–Lenstra–Lovász (LLL) with lattices
- Crack ECDSA with weak nonces. ECDSA with weak nonces and using Lenstra–Lenstra–Lovász (LLL) method. This outlines ECDSA how the private key can be recovered with weak nonce values.
Network Forensics

These pages outlines some network forensics. This includes the understanding of the network stack, and with protocols such as Etherenet, IP, TCP, HTTP, and others.
Network Forensics (Theory)
- Network Forensics (Wireshark). Network Forensics. This provides information on how to detect threats through network forensics with Wireshark.
- Advanced Network Forensics. Network Forensics. This provides information on how to detect threats through network forensics.
Network Forensics (Practice)
- Advanced Network Forensics (Wireshark). Adv Network Forensics. This provides information on how to detect threats through network forensics with Wireshark.
- Network Forensics (PCAP). Network Forensics. This provides information on network forensics (reading PCAP files)
- Network Forensics (Text). Network Forensics. This provides information on network forensics (reading text files)
Tshark
-
Filters with TShark. TShark. This page runs Tshark with a given Pcap file and a defined filter.
Other
- Advanced Digital Forensics . Adv Digital Forensics. This provides information on how analyse disk based systems using open source forensics.
- Partition Analyser. MBR. This page will analyse the details of the partition details within the MBR (put one space between fields).
Presentations
Format Preserving Encryption

Format Preserving Encryption (FPE) is a method which allows the basic formatting of a message to stay in a similar format, and where the value itself is encrypted. It can be used to hide credit card details.
Methods
- Format Preserving Encryption. FPE. This outlines Format Preserving Encryption.
- FPE with Python. FPE. An implementation of Format Preserving Encryption (FPE) using Python.
- FPE with node.js. FPR. FPE with node.js.
- FPE and PKBKDF2 in Python. FPE and PKBKDF2 in Python. FPE using PKBDF2 to password generation.
FFX (Format-preserving, Feistel-based encryption)
- FPE with Go. FPE. An implementation of Format Preserving Encryption (FPE) for FFX1 and FFX3.
- FFX schemes. FFX. Within tokenization we can apply format preserving encryption (FPE) methods, which will convert our data into a format which still looks valid, but which cannot be mapped to the original value. For example, we could hide Bob's credit card detail into another valid credit card number, and which would not reveal his real number. A tokenization server could then convert the real credit card number into a format which still looked valid. For this we have a key which takes the data, and then converts it into a form which the same length as the original.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher in Python.
FFX in Rust
- FFX. FFX. This is an implementation of FFX in Rust.
Honey Encryption
- Honey Encryption. Honey. This outlines Honey encryption.
Crypto Principles

This page outlines some crypto principles.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Galois fields (polynomial operations)

This page outlines a few basic principles around the usage of Galois fields and polynomial operations. In 1832, Évariste Galois died of duelling wounds at the age of 20 but left a great legacy. While he was a teenager he worked on polynomials and laid down the principles of Galois theory, along with defining the concept of a finite field. In cryptography, the finite field is one of the major concepts and involves limiting the number of possible values to a limiting factor (\(p\)). The values of the field then range from 0 to p-1. Within a field, we can operate on values in the field using arithmetic operations. We can thus have an infinite field, and where we could include all of the possible integers. A finite field or Galois field of GF(\(2^n\)) has \(2^n\) elements. If \(n\) is four, we have 16 output values. Let’s say we have a number \(a∈{0, ... ,2^{n−1}}\), and represent it as a vector in the form of a polynomial:
\( a=a0+a_1 x+a_2 x^2 ... a_{n−1} x^{n−1}\)
If we use \(a_n∈{0,1}\), this is exactly the same as representing a binary number modulo \(2^n\). In this \(x^n\) represents bit position \(n\) and \(a_n\) is the value of the bit at position \(x^n\). If a bit is a zero at a given position, it will be not included in the polynomial equation. So, 1011 can be represented by \(x^3+x+1\) and 1010 is represented as \(x^3+x\). We can then perform arithmetic operations on these polynomial values. So, to add two values of 1010+1100 we can represent this as \((x^3+x)+(x^3+x^2)\) and which is \(x^2+x\) as we are using modulo 2 addition, and where \(x^3+x^3=0\). With modulo 2 addition, 0+0=0, 0+1=1, 1+0=1, and 1+1=1.
An example of Galois Fields is within AES (Advanced Encryption Standard) and which uses a finite field GF(\(2^8\)). With AES we operate on bytes (8 bits) in the form of \(b_7 b_6 b_5 b_4 b_3 b_2 b_1 b_0\) and which are operated on a a polynomial of \(b_7x^7+b_6x^6+b_5x^5+b_4x^4+b_3x^3+b_2x^2+b_1x^1+b_0\).
Galois fields (polynomial operations) - GF(\(p^n\))
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Additive Group Table for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Additive Group Table for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of addition. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the additive group table for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values.
- Multiplicative Group Table for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Multiplicative Group Table for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the additive group table for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values.
- Additive, Division and Multiplicative Group Table for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Additive, Division and Multiplicative Group Table for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the Additive, Division and Multiplicative Group Table for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values.
- Additive and Multiplicative Group Table for GF(\(2^2\)) and GF(\(2^3\)). Galois Fields Table for GF(2^m) with polynomials. This page implements Galois Fields GF(\(2^n\)) with Python and provides a table of additional and multiplication. It outlines GF(\(2^2\)) and GF(\(2^3\)), but also gives a program that can be used for others. Overall, we have the form of GF(\(p^n\)) and which provides use both an additive and a multiplicative group operations that provide all the possible outputs within the finite field. The value of \(p\) is a prime number, and \(n\) is any positive integer.
- Additive and Multiplicative Group Table for GF(\(2^2\)) and GF(\(2^3\)). Galois Fields Table for GF(2^m) with coefficient values. This page implements Galois Fields GF(\(2^n\)) with Python and provides a table of additional and multiplication. It outlines GF(\(2^2\)) and GF(\(2^3\)), but also gives a program that can be used for others. Overall, we have the form of GF(\(p^n\)) and which provides use both an additive and a multiplicative group operations that provide all the possible outputs within the finite field. The value of \(p\) is a prime number, and \(n\) is any positive integer. This version will show the polynomial coefficent values within the Galois Field.
- Additive and Multiplicative Group Table for GF(\(2^2\)) and GF(\(2^3\)). Galois Fields Table for GF(2^m) with integer values. This page implements Galois Fields GF(\(2^n\)) with Python and provides a table of additional and multiplication. It outlines GF(\(2^2\)) and GF(\(2^3\)), but also gives a program that can be used for others. Overall, we have the form of GF(\(p^n\)) and which provides use both an additive and a multiplicative group operations that provide all the possible outputs within the finite field. The value of \(p\) is a prime number, and \(n\) is any positive integer. This version will show the integer values within the Galois Field.
Irreducible polynomial for GF(p^n)
- Irreducible polynomial for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Irreducible polynomial for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the parameters for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values. This includes finding the irreducible polynomial for the Galois Field.
- Irreducible polynomial for GF(\(p^n\)) for a given \(p\) and for \(n\) values. Irreducible polynomial for GF(p^n) for a given p and for n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the parameters for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values. This includes finding the irreducible polynomial for the Galois Field. Other important parameters include the degree (the highest polynomial power) and the order (the number of possible output values).
- Conway and primitive polynomial GF(\(p^n\)). Conway and primitive polynomial GF(p^n). This page outlines Conway and primitive polynomials for GF(\(p^n\)).
Galois fields (polynomial operations) - GF(\(p\))
- Additive and Multiplicative Group mod n (\(Z_n\)). Additive and Multiplicative Group mod n. In finite fields, we have a \(\pmod n\) operation for a list of integers (\(\mathbb{Z}\)), and where \(n\) is a prime number. This works for our add (+) and multiply (\(\times\)) operations, and where: \( a \pmod n + b \pmod n = (a+b) \pmod n\); and \(a \pmod n \times b \pmod n = (a \times b) \pmod n\).
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Polynomial GF(2) Factoring and Irreducible Polynomials. Factors. This outlines the search for polynomial factors for GF(2).
Polynomial operations
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
Post-quantum
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Rust
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Sage
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Golang and Cryptography

The new scripted languages such as Python and Node.js are convenient. But, unfortunately, they can be slow as they are scripted, and not compiled. Each time the scripted code is run, the scripting engine must then convert each line of code to the required machine level code. This makes the code much slower than compiled languages, and also less robust. Thus many applications in cryptography are written in C and C++, as they allow for fast execution and give low level access. Unfortunately it can be complex to compile programs, as we often need to install binary libraries and then link these in. The Go programming language, though, has a similar code syntax to C/C++, but is small and efficient and allows access to low-level functions, such as as pointers. Go thus aims to “Code less, compile quicker, execute faster”. So let’s use Go to implement some cryptography methods, including symmetric key, hashing, public keys and zero-knowledge proofs (ZKPs). The slides related to these methods are included [here]. An introduction to Golang and Cryptography is [here].

Go ECDH
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret.
Go Hex and Base64
- Base64 and Hex in Go. Base64/Hex. Two common formats for representing binary data are hexademical and Base64.
Go symmetric key
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Reuse IV attack and AES. Reuse IV and GCM. This provides an implementation of a reuse IV against AES GCM.
- ASCON AEAD (Golang). ASCON AEAD (Golang). The outlines the usage of AEAD for ASCON using Golang.
Go HMAC and HKDF
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HKDF in Go. HKDF. Implementation ofHKDF, and where we dervice a key based on a given secret.
Go secret shares
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.

Go ZKP
- Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL). DLEQ. Create a non-interactive ZKP for discrete logs.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Fiat Shamir and ECC (Interative ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP with Kryptology. This implements a range proof using a Schnorr proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?

Go ECIES (Hybrid Encryption)
With this, we can use the power of public key encryption (to generate the encryption key) with symmetric key encryption (to actually encrypt and decrpyt the data):
- ECIES (Kryptology). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Coinbase Kryptology library.
- ECIES (CIRCL). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Cloudflare CIRCL library.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt and which is used in Contract Tracing for COVID-19.
Go ECDSA
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Go RSA
- RSA Principles. RSA Principles. The basics of RSA.
- RSA with Go. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA. RSA encryption with Go using OAEP.
- RSA Encryption with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
Go ElGamal
ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Proving an Encrypted Shuffle With ElGamal and ECC. Shuffle. An encrypted shuffle with ElGamal.
- ElGamal encryption with Go. ElGamal. This implements ElGamal encryption.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
- ElGamal - Applying Multiple Public Key Operations (ECC). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use elliptic curve methods, and using the Edwards 25519 curve.
Go PGP
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
Go Public key
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.

Go Hashing
- Hashing with Go. Hashing. Hashes with Go.
- GP Hashing with Go. GP Hashing. GP Hashes with Go.
- SHAKE with Go. SHAKE. This implements SHAKE in Go.
- libDisco with Go. libDisco. This implements libDisco.
- cSHAKE in Golang. cSHAKE. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS. With the SHA-3 hashing method, we have four different cryptographic hashing methods (SHA3-224, SHA3-256, SHA3-384, and SHA3-512) and two XOF functions (SHAKE128 and SHAKE256). With SHAKE128 and SHAKE256 we can integrate domain separation between different functions — and which are known as cSHAKE128 and cSHAKE256.
- Homomorphic Hashing with Golang. Homomorphic hashing. Normally with hashing methods, we need to take all the previous data and new data in order to create a new hash value for our data. In a homomorphic hashing method, we can basically take the previous hash, and then add on any new data values. We can also remove previous data values from our hash, too. This is more efficient in computing, as we do not have to process all of our data into a new hash, and can use simple homomorphic operations for the computation. The method we will use (LtHash) was initially defined by Bellare and Micciancio and updated Lewi et al at Facebook.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
Go ECC
- Hash to password with Go. Hash to password. Hash to password with Go.
- ECDH with Go. ECDH. ECDH with Go.
- Box with Go. Box. Box with Go.
- ECC with Go. ECC. ECC with Go.
- Curve 25519 with Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ElGamal with ECC. ElGamal with ECC. ElGamal using ECC.
- Curve 25519 with Go for test vectors. ECC. This does a test on some private keys to test the public key generation.
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Barebones Ed25519 with Go. ECC. This shows point addition and scalar multiply in Ed25519
- Barebones NIST P256 with Go. ECC. This shows point addition and scalar multiply in P256
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining \(n.G\) for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Points (Base Point and Others). Elliptic Curve points. Two common curves used in ECC (Elliptic Curve Cryptography) are secp256k1 (as used in Bitcoin and Ethereum) and P256 (secp256r1). The "k1" refers to the Kolbitz curve 1 (named after the creator of ECC). With these we have a base point which are can operate on. This is typically defined as \(G\). We can then operate on this with add and multiply operation. For example, \(2G=G+G\) and \(P=n.G\). In this following we will show the base point for a number of common curves, such as secp256r1, P256, Pallas, Curve 25519, BLS12381G1, BLS12381G2, BLS12377G1 and BLS12377G2.
Go Blockchain
- Ethereum address with Go. Addresses. This generates an Ethereum address.
- Viewing Balance of account in Etheruem with Go. Balance. This views the balance of an account
- Viewing Block in Etheruem with Go. Block. This views a block.
- Viewing Transactions in Block in Etheruem with Go. Transactions. This views transactions.

Go Homomorphic
- SIDH Go. SIDH. Post-quantum key exchange.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- NTP. NTP. An overview of NTP.
- BiBa. BiBa. An overview of BiBa One Time Signature.
Go DNS
- DNSSEC. DNSSEC. An overview of DNSSEC.
Go Signatures
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Go Signcryption
- Ahmad-Afzal-Iqbal (AAI) signcryption with Golang. Ahmad-Afzal-Iqbal (AAI). Ahmad-Afzal-Iqbal (AAI) signcryption with Golang.

Go Crypto pairing
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
Go Homomorphic
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add. HEAAN Add. HEAAN Add.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- Anonymous crypto. Anon. Anonymous crypto.
- Rho factorization. Rho. Rho alogorithm.
- Post-quantum signing (BLISS). BLISS. BLISS method.
Go Post quantum
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.

Go CIRCL
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- Ed448 with Go. X448. Ed448 with Go.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with FourQ (Cloudflare). FourQ.
- Verifiable Oblivious Pseudorandom Functions (VOPRF) with Cloudflare CIRCL. VOPRF. In our digital world, we give away too many of our secrets, especially where we just have to prove the knowledge of something, rather than actually revealing it. In many of the systems we use, we could just prove things in an oblivious way, and where we could pass a secret but in a blinded form. With this, a server does not discover our password and for us not to discover the identifier that a server holds on us. But, can we also provide a proof back that the right password has been used? Well, with Verifiable Oblivious Pseudorandom Functions (VOPRF), we can generate a random secret based on a key generated on the server (Alice), and which is based on Bob’s secret.
- Hash to Curve using Go (Cloudflare). Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). The method defined here is proposed an an Internet-Draft standard by the Internet Engineering Task Force (IETF) related to "Hashing to Elliptic Curves".
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
here Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
- eXtendable-Output Function (XOF) usign CIRCL. XOF. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS.

Go Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Google Tink (Golang) ECIES. Google Tink (ECIE5). This outlines ECIES encryption with public key and AES using Golang with Google Tink
Go Credentials
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.

Go Kryptology
- Public key points for curves. Simple. Display public key points for scalars.
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.

Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.

Principles
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Paillier
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
Go Format Preserving Encryption (FPE)
- FPE with Go. FPE. An implementation of Format Preserving Encryption (FPE) for FFX1 and FFX3.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
AWS Encryption
- AWS Symmetric Key Encryption. AWS (Symmetric key). Using symmetric key in AWS.
Go Oblivious Transfer
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Dragon Fly
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
Embedding data in an ECC point
- Embedding data in a point. Go. With Elliptic Curve Cryptography (ECC), we use points on an elliptic curve to represent our data. These are defined with (x,y) points. With this, it is possible to embedded a certain amount of data into the point - as long as it still gives us a valid point on the curve. This example will Curve 25519 to embed data, and is achieved by storing the length of the data in a single byte in the point, and then store the data as byte values in the point (followed by random data). To decode, we can then just read the first byte for the length of the message, and then reveal the data encoded into the point..
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Hashing (Cryptographic)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
Benchmarks and Password strength
The following are the tips related to hashing:
- Password strength. Test. This outlines the strength of various passwords types.
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
Theory
The following are the tips related to hashing:
- Balls in bins. BiBa. This implemented balls in bins.
- Birthday attack (with Big Integers). Calc. This provides a simple example of the birthday attack.
- Birthday attack. Calc. This provides a simple example of the birthday attack.
- Differential Cryptanalysis (Hashing). Cryptanalysis. This provides an implementation of differential cryptanalysis for hashing methods.
MD5, SHA-1
The following are the tips related to hashing:
- MD2 and MD4 MD2/4. The MD2 and MD4 hashing functions were developed by Prof Ronald Rivest in 1989 and 1990, respectively. They both produce a 128-bit hash, but have been shown be vulnerable to attack (see the Collision section in the page).
- MD5 and SHA-1 (to Base-64) with salt Salt. It is possible to add salt to the MD5 algorithm, to mix it up a little.
- MD5 and SHA-1 (to Base-64) Hash. MD5 and SHA-1 produces a hash signature, and the output is typically shown in a hex format or a Base-64. In this example the output is converted into a Base-64 format.
- MD5 and SHA-1. Hash. MD5 and SHA-1 methods produce a hash signature, and are the two of the most widely used methods. The MD5 algorithm has been shown to have weaknesses, and a collision of message hashes has been shown to occur in less than one day. An MD5 signature has 128 bits, an SHA-1 signature has 160 bits, and an SHA-256 signature has 256 bits.
- MD5 Cracking. Hash Cracker. MD5 has a 128-bit signature and can be cracked using rainbow tables. This page tries to crack the MD5 signature.
- Hashing with Go. Hashing. Hashes with Go.
- Detecting hash types. Hash type. This detects has values.
- OpenSSL hashing. Range of methods. Outlines the methods used in OpenSSL
- Hash. Hash. Hashing using JavaScript
- Hashing with node.js. Hashing. Hashing with node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Hashing methods
-
Hazmat Hashes. Hazmat Hashes. This includes the hashing methods in the Hazmat cryptography library. This includes Blake2p, Blake2s, MD5, SHA1, SHA224, SHA256, SGA384, SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHA512, SHA512-224, SHAKE128 and SHA256.
-
Hazmat Hashes. Hazmat Hashes. In this case we will implement Python code to determine SHA1, SHA2, SHA3, Blake2, MD5 and SM3 hashes.
OpenSSL Passwords
-
Password example [here]
-
Hashed passwords with OpenSSL [here]
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Blake 3 hashes
The following are the tips related to similarity hashing:
- Blake 3 in Python. Hashing. Blake 3 hashing.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
Other Hash functions
The following are the tips related to hashing:
- Bloom Filter Bloom filter. A Bloom filter goes a probabilistic method of determining if an element is in a data structure, using indexed hashing methods.
- Cuckoo Table Cuckoo filter. A Cockoo table uses two hash funtions.
- Chaffing. Chaffing. This produces a keyless system.
- GP Hashing with Go. GP Hashing. GP Hashes with Go.
- LDAP. LDAP. This produces a LDAP hash signature for a password.
- LM Hash. LM Hash. This is an LM Hash Calculator. LM Hash is used in many versions of Windows to store user passwords that are fewer than 15 characters long.
- Murmur and FNV Murmur and FNV. While hashing methods such as MD5 and SHA-1 use crypto methods, the Murmur and FNV hashes uses a non-cryptographic hash function. This can be used for general hash-based lookup and was designed by Austin Appleby. It has good performance compared with other hashing methods.
- Pearson. Pearson. This uses a non-crypto hash.
- phpass. phpass. This produces a phpass hash signature for a password.
- Tiger. Tiger. Tiger is a 192-bit hash function and was designed by Ross Anderson and Eli Biham in 1995. It is often used by clients within Gnutella file-sharing networks and does not suffer from known attacks on MD5 and SHA-0/SHA-1. Tiger2 is an addition, in which the message is padded with a byte of 0x80 (in a similar way to MD4, MD5, and SHA), whereas in Tiger it is 0x01. Otherwise, the two methods are the same in their operation.
- Whirlpool. Whirlpool. Whirlpool is a 512-bit cryptographic hash function and was created by Vincent Rijmen (one of the AES creators) and Paulo Barreto, in 2000.
- WPA-2 hash . WPA-2 hash. Implements SHA-2 hash.
- Reusable hash collisions. Reusable hash collisions. Reusable hash collisions.
- The Length Extension Attack. Length Extension Attack. The MD construct has many weaknesses, and one of the most serious is the length extension attack. With this an adversary (Eve) can take a hash for an unknown message, and then add additional data to produce a new valid hash. The hash methods which are at risk against the length extension attack are MD5, SHA-1 and SHA-256. Please follow the code link below to run an example.
- Consistent hashing. Consistent hash. This outlines the usage of Consistent hashes.
- ROR13 (Module and Function). ROR13. With ROR13 we take each 8-bit character and then convert to a unicode value (with 16 bits). Then for each character we rotate the bits right by thirteen places. The resultant hash is then just the accumuluation of the rotated values.
- ROR13 (Function). ROR13 (Function). With ROR13 we take each 8-bit character and then convert to a unicode value (with 16 bits). Then for each character we rotate the bits right by thirteen places. The resultant hash is then just the accumuluation of the rotated values.
- GOST, Streebog256 and Streebog512. GOST, Streebog256 and Streebog512. GOST94 is a hashing method developed with Euro-Asian Council for Standardization, Metrology and Certification (EASC). This has since been developed in the Streebog256 and Streebog512 hashing method. In this case, we will use Libre OpenSSL to convert data into a hashed value.
RIPEMD
- RIPEMD (RACE Integrity Primitives Evaluation Message Digest) and GOST. RIPEM160. RIPEMD is a 128-bit, 160-bit, 256-bit or 320-bit cryptographic hash function, and was created by Hans Dobbertin, Antoon Bosselaers, and Bart Preneel. It is used on TrueCrypt and is open source. The 160-bit version is seen as an alternative to SHA-1, and is part of ISO/IEC 10118
- RIPEMD160. RIPEM160. RIPEMD160 is a 160-bit cryptographic hash function, and was created by Hans Dobbertin, Antoon Bosselaers and Bart Preneel. RIPEMD160 is used in Bitcoin applications.
Chameleon hashes
The following are the tips related to Chameleon hashing:
- Chameleon hash in Golang Chameleon. With a Chameleon hash, we have a normal hash value which is resistant to collisions, but with a known secret we can easily create a collision. The concept was first defined by Krawcyk and Rabin.
Similarity hashes
The following are the tips related to similarity hashing:
- Similarity hash: SimHash (Charikar similarity) in Python Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash (Nilsimsa similarity) Nilsimsa. The Nilsimsa similarity is used to find similarities between spam emails.
- Minhash (Jaccard similarity) Jaccard similarity. The Minhash method is used to find similarities between strings, files and metadata.
- String enthropy String enthropy. Measurement of the entropy of strings.
- Counting identical elements (HyperLogLog) HyperLogLog. Counting the number of identical elements.
SHA-3 and SHA-3 contenders
The following are the tips related to Key derivation hashing:
- Blake and Blake 2. Blake. Implements Blake and Blake 2 (SHA-3 contender).
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
- Grøstl. Grøstl. Implements Grøstl (SHA-3 contender).
- KangarooTwelve. KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- SHA-3, Keccak and SHAKE . SHA-3. Implements SHA-3, Keccak and SHAKE (SHA-3 winner).
- SHA-3. SHA-3. SHA-3 was known as Keccak and is a hash function designed by Guido Bertoni, Joan Daemen, Michaël Peeters, and Gilles Van Assche. MD5 and SHA-0 have been shown to be susceptible to attacks, along with theoretical attacks on SHA-1. NIST thus defined there was a need for a new hashing method which did not use the existing methods for hashing, and setup a competition for competing algorithms. In October 2012, Keccak won the NIST hash function competition and is proposed as the SHA-3 standard. It should be noted that it is not replacement SHA-2, which is currently a secure method. Overall Keccak uses the sponge construction where the message blocks are XORed into the initial bits of the state, and then inevitably permuted.
- cSHAKE. cSHAKE. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS. With the SHA-3 hashing method, we have four different cryptographic hashing methods (SHA3-224, SHA3-256, SHA3-384, and SHA3-512) and two XOF functions (SHAKE128 and SHAKE256). With SHAKE128 and SHAKE256 we can integrate domain separation between different functions — and which are known as cSHAKE128 and cSHAKE256.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- Skein. Skein. Implements Skein (SHA-3 contender).
Key derivation hashing
The following are the tips related to Key derivation hashing:
- Argon2. Go. Outline of Argon2.
- Argon2 with NaCl. Go. Outline of Argon2 using NaCl.
- Balloon. Go. Outline of Balloon.
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- Double ratchet. Go. Outline of double ratcheting.
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- Scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat HKDF. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
Non-crypto/fast hashing
The following are the tips related to non-crypto hashing:
- A perfect hash Perfect hash. This is a non-crypto hash which optimizes the hash value.
- The universal hash Universal hash. This related to the concept of a universal hash.
- FNV. FNV. FNV is one of the fastest hashing methods.
- Murmur. Murmur. Murmur is one of the fastest hashing methods.
- Siphash. Siphash. Siphash is a fast hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- xxHash. xxHash. xxHash is one of the fastest hashing methods.
- Meow. Meow. Meow is one of the fastest hashing methods.
- o1Hash. o1Hash. o1Hash is one of the fastest hashing methods.
- CRC-32. CRC-32. CRC-32 is one of the fastest hashing methods.
- wyhash. wyhash. wyhash is one of the fastest hashing methods.
- CityHash. CityHash. CityHash is one of the fastest hashing methods, and is generally free of security problems.
- FarmHash. FarmHash. FarmHash is one of the fastest hashing methods, and is generally free of security problems.
- Non-crypto. Non-crypto. This includes a range of fast non-cryptography hashing methods.
- Non-crypto hashes (C++): Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro. Non-crypto hashes: Farm, City, xxHash, MUM, Spooky 2, Murmur, Metro and t1ha0. This includes a range of fast non-cryptography hashing methods for Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro using C++ methods.
- Pearson. Pearson. Pearson is one of the fastest hashing methods, and has been designed for 8-bit processors.
- C++: t1ha. t1ha. t1ha is one of the fastest hashing methods, and has been designed for 64-bit processors.
- C++: Spooky. Spooky. Spooky is one of the fastest hashing methods, and V2 has a 32-bit, 64-bit and 128-bit version.
- C++: xxHash. xxHash. xxHash is one of the fastest hashing methods, and has good performance for short data inputs.
- C++: MUM. MUM. MUM is one of the fastest hashing methods.
- C++: FNV 1/1a. FNV 1/1a. FNV 1/1a is one of the fastest hashing methods, and is particularily useful when there are small changes in strings, such as with IP addresses and URLs.
- C++: MetroHash. MetroHash. MetroHash is one of the fastest hashing methods.
- C++: CityHash. CityHash. CityHash was created by Google and is one of the fastest hashing methods. It was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Farm. FarmHash. FarmHash was created by Google and is one of the fastest hashing methods. It is an improvement to CityHash.
- C++: Murmur. Murmur. Murmur is one of the fastest hashing methods, but was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Halftime. Halftime. Halftime is one of the fastest hashing methods and was created by Jim Apple at Apache.
- C++: Highway. Highway. Highway is an ultra-fast keyed-hash, and is more than five times faster than SipHash. It was created by Jyrki Alakuijala, Bill Cox, Jan Wassenberg at Google.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
- C++: CLHash. CLHash. CLHash is an ultra-fast hashing method and focused on improving performance of the hashing of long strings.
- C++: FalkHash. FalkHash. FalkHash is an ultra-fast hashing method and beats most of the other non-cryptography methods for performance. It is focused on the x64 architecture and integrates with AES-NI.
- C++: wyHash. wyHash. wyHash is an ultra-fast hashing method.
- C++: Fibonacci. Fibonacci. Fibonacci is an ultra-fast hashing method.
- C++: Lookup3. Lookup3. Lookup3 is an ultra-fast hashing method.
Key-based hashing
The following are the tips related to Key-based hashing:
- SiphashSiphash. Siphash is a fast key-based hashing method.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
One Time Passwords/Time Stamps
The following are the tips related to hashing:
- One Time Passwords. One Time. This allows a new unique password to be created each instance, based on an initial seed.
- Timed One Time Password (TOTP). Timed One Time Password. This allows a new unique passcode to be created each instance, based on an initial seed for a given time window. We will use a five second window in this case, where a new passcode is generated every five seconds, based on an initial seed of a pass phrase.
- Hashed One Time Password (HOTP). Hashed One Time Password. This allows a new unique passcode to be created each instance, based on a counter value and an initial seed.
- Time Stamp Protocol. TSP. This creates a time stamp for data.
- HOTP and TOTP (Python). OTP. This creates hashed passwords.
eXtendable-Output Function (XOF)
- eXtendable-Output Function (XOF) usign CIRCL. XOF. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS.
SHAKE
The following are the tips related to hashing:
- SHAKE. SHAKE. Implements SHAKE and which is an Extendable Output Function (XOF).
- SHAKE with Go. SHAKE. This implements SHAKE in Go.
- libDisco with Go. libDisco. This implements libDisco.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify
the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods
such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC methods using the Python cryptography primitives for HMAC-MD5.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
Quantum-robust Public Key (Hash-based signature)
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
Hash to ECC point
- Hash to password with Go. Hash to password. Hash to password with Go.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve with libnum.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.

Password-hashing functions using Rust
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing (Non-cryptographic)

You might know those slow old hashing methods, such as MD5, SHA-1, and SHA-256. Well, they were designed to be fast, but also highly secure. But, if we just need a hashing method, such as for a hashtable or Bloom filter, we often don’t need all the security that comes with the main cryptography hashing methods. And so we have the non-cryptography hashing methods, and which are often ultra-fast and highly efficient. To show the difference, in a test, SHA-1 — one of the fastest cryptography hashing methods — managed a processing rate of 364.95 MiB/s, while t1ha was nearly a 100 times faster, at 34,636 MiB/s.
Non-crypto/fast hashing
The following are the tips related to non-crypto hashing:
- A perfect hash Perfect hash. This is a non-crypto hash which optimizes the hash value.
- The universal hash Universal hash. This related to the concept of a universal hash.
- FNV. FNV. FNV is one of the fastest hashing methods.
- Murmur. Murmur. Murmur is one of the fastest hashing methods.
- Siphash. Siphash. Siphash is a fast hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- xxHash. xxHash. xxHash is one of the fastest hashing methods.
- Meow. Meow. Meow is one of the fastest hashing methods.
- o1Hash. o1Hash. o1Hash is one of the fastest hashing methods.
- CRC-32. CRC-32. CRC-32 is one of the fastest hashing methods.
- wyhash. wyhash. wyhash is one of the fastest hashing methods.
- CityHash. CityHash. CityHash is one of the fastest hashing methods, and is generally free of security problems.
- FarmHash. FarmHash. FarmHash is one of the fastest hashing methods, and is generally free of security problems.
- Non-crypto. Non-crypto. This includes a range of fast non-cryptography hashing methods.
- Non-crypto hashes (C++): Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro. Non-crypto hashes: Farm, City, xxHash, MUM, Spooky 2, Murmur, Metro and t1ha0. This includes a range of fast non-cryptography hashing methods for Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro using C++ methods.
- Pearson. Pearson. Pearson is one of the fastest hashing methods, and has been designed for 8-bit processors.
- C++: t1ha. t1ha. t1ha is one of the fastest hashing methods, and has been designed for 64-bit processors.
- C++: Spooky. Spooky. Spooky is one of the fastest hashing methods, and V2 has a 32-bit, 64-bit and 128-bit version.
- C++: xxHash. xxHash. xxHash is one of the fastest hashing methods, and has good performance for short data inputs.
- C++: MUM. MUM. MUM is one of the fastest hashing methods.
- C++: FNV 1/1a. FNV 1/1a. FNV 1/1a is one of the fastest hashing methods, and is particularily useful when there are small changes in strings, such as with IP addresses and URLs.
- C++: MetroHash. MetroHash. MetroHash is one of the fastest hashing methods.
- C++: CityHash. CityHash. CityHash was created by Google and is one of the fastest hashing methods. It was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Farm. FarmHash. FarmHash was created by Google and is one of the fastest hashing methods. It is an improvement to CityHash.
- C++: Murmur. Murmur. Murmur is one of the fastest hashing methods, but was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Halftime. Halftime. Halftime is one of the fastest hashing methods and was created by Jim Apple at Apache.
- C++: Highway. Highway. Highway is an ultra-fast keyed-hash, and is more than five times faster than SipHash. It was created by Jyrki Alakuijala, Bill Cox, Jan Wassenberg at Google.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
- C++: CLHash. CLHash. CLHash is an ultra-fast hashing method and focused on improving performance of the hashing of long strings.
- C++: FalkHash. FalkHash. FalkHash is an ultra-fast hashing method and beats most of the other non-cryptography methods for performance. It is focused on the x64 architecture and integrates with AES-NI.
- C++: wyHash. wyHash. wyHash is an ultra-fast hashing method.
- C++: Fibonacci. Fibonacci. Fibonacci is an ultra-fast hashing method.
- C++: Lookup3. Lookup3. Lookup3 is an ultra-fast hashing method.
A fuller test with SMHasher gives [here]:
Hash function MiB/sec cycl./hash cycl./map Quality problems
------------------------------------------------------------------
o1hash 12439661.09 16.77 166.13 insecure, no seed, zeros, fails all tests
crc32_hw1 23208.73 46.74 179.70 insecure, 100% bias, collisions, distrib, BIC, machine-specific (x86 SSE4.2)
t1ha0_aes_noavx 22785.26 38.71 180.61 LongNeighbors, machine-specific (x86 AES-NI)
t1ha0_aes_avx1 22714.85 48.12 226.52 LongNeighbors, machine-specific (x64 AVX.txt)
t1ha0_aes_avx2 22345.33 44.38 556.47 LongNeighbors, machine-specific (x64 AVX2)
falkhash 20202.42 173.63 321.52 Sparse, LongNeighbors, machine-specific (x64 AES-NI)
MeowHash64low 17378.06 85.48 237.60 Sparse, invertible, machine-specific (x64 AES-NI)
MeowHash32low 17374.64 85.48 258.53 Sparse, invertible, machine-specific (x64 AES-NI)
MeowHash 17371.91 85.48 247.96 Sparse, invertible, machine-specific (x64 AES-NI)
FarmHash32 17112.05 47.7 214.71 machine-specific (x64 SSE4/AVX)
xxh3 16538.52 32.81 184.86 DiffDist bit 7 w. 36 bits, BIC
xxh3low 16462.36 32.77 199.79
farmhash32_c 16299.81 47.79 219.19 machine-specific (x64 SSE4/AVX)
xxh128low 15174.85 33.79 187.05
xxh128 15174.14 40.46 195.65
farsh32 14053.09 74.29 245.33 insecure: AppendedZeroes, collisions+bias, MomentChi2, LongNeighbors
metrohash64crc_2 14034.84 48.94 162.54 UB, Cyclic 8/8 byte, DiffDist, BIC, machine-specific (SSE4.2/NEON)
metrohash64crc_1 14000.5 49.08 150.54 UB, Cyclic 8/8 byte, DiffDist, BIC, MomentChi2, machine-specific (SSE4.2/NEON)
metrohash128crc_1 13948.67 65.2 168.08 UB, machine-specific (SSE4.2/NEON)
metrohash128crc_2 13920.19 65.12 176.70 UB, machine-specific (SSE4.2/NEON)
halftime_hash128 13478.23 97.79 252.14
wyhash32low 12911.09 29.59 205.43 2 bad seeds
wyhash 12879 30.35 196.77 2^33 bad seeds
CityCrc128 12343.43 74.5 209.75
fletcher2 12011.15 25.29 298.60 bad seed 0, UB, fails all tests
fletcher4 11928.55 25.27 293.49 bad seed 0, UB, fails all tests
halftime_hash256 11620.28 98.44 252.60
fibonacci 11339.87 26.33 705.64 UB, zeros, fails all tests
ahash64 9862.62 27.32 181.68 rust
Spooky128 9751.14 63.84 192.47 UB
Spooky64 9747.47 62.2 191.71 UB
Spooky32 9747.13 62.24 196.96 UB
t1ha1_64le 9723.86 34.39 176.91 Avalanche
cmetrohash64_1 9683.33 45.2 161.01 UB, LongNeighbors, BIC, MomentChi2
cmetrohash64_2 9669.95 44.75 149.67 LongNeighbors
metrohash64_2 9668.51 44.45 164.30 UB, LongNeighbors
metrohash64 9664.61 44.59 150.74 UB, LongNeighbors, BIC
metrohash64_1 9664.57 45.37 152.31 UB, LongNeighbors, BIC, MomentChi2
cmetrohash64_1o 9658.31 42.84 163.45 UB, LongNeighbors, BIC, MomentChi2
FNV1a_YT 9643.42 32.06 175.19 bad seed, UB, fails all tests
City128 9640.19 88.45 225.38
metrohash128_2 9584.94 59.1 167.43 UB, LongNeighbors
metrohash128 9569.16 58.68 167.53 UB, LongNeighbors
metrohash128_1 9558.17 59.04 175.94 UB, LongNeighbors
FarmHash128 9409.63 74.52 210.25
VHASH_32 9404.99 77.01 250.57 sanity, Seed, MomentChi2
VHASH_64 9392.39 74.72 227.92 sanity, Seed, MomentChi2
farmhash128_c 9244.13 79.08 209.44
t1ha2_atonce 9237.12 38.94 194.32 Zeroes low3
City64noSeed 9090.42 32.23 171.53 Avalanche, Sparse, TwoBytes, MomentChi2, Seed
City64low 9089.45 47.75 201.73
t1ha2_stream 9068.55 74.56 219.85 Sparse, Permutation, LongNeighbors
City64 9066.9 47.81 197.78 Sparse, TwoBytes
t1ha2_stream128 9065.5 93.19 236.50 Sparse, Permutation, LongNeighbors
xxHash64 8936.63 51.31 174.34
pengyhash 8744.48 85.31 222.45
farmhash64_c 8713.16 47.96 201.00
FarmHash64 8684.76 48.13 200.51
crc64_hw 8440.13 34.94 141.15 insecure, 100% bias, collisions, distrib, BIC, machine-specific (SSE4.2/NEON)
t1ha2_atonce128 8350.99 55.65 203.53 LongNeighbors
PMPML_64 8161.19 53.2 179.16 unseeded: Seed, MomentChi2, BIC
halftime_hash512 7681.62 125.81 274.01
tabulation 7621.75 42.19 179.93
t1ha1_64be 7481.37 38.16 193.22 Avalanche
MUMlow 7225.18 37.85 197.92 UB, 5 bad seeds
farsh64 7216.29 130.3 302.44 insecure: AppendedZeroes, collisions+bias, MomentChi2, LongNeighbors
MUM 7134.56 37.85 172.34 UB, too many bad seeds, machine-specific (32/64 differs)
nmhash32 7003.3 68.93 216.59
PMPML_32 6704.53 53.5 197.43 Avalanche >512, unseeded: Seed, BIC, MomentChi2, PerlinNoise
nmhash32x 6342.95 56.41 217.75
crc32_hw 6330.42 35.55 170.16 insecure, 100% bias, collisions, distrib, BIC, machine-specific (SSE4.2/NEON)
FNV2 6258.84 33.25 142.89 fails all tests
FNV1A_Pippip_Yurii 6258.46 28.19 184.41 UB, sanity, fails all tests
FNV1A_Totenschiff 6258.23 27.99 198.20 UB, zeros, fails all tests
HighwayHash64 6242.58 99.55 248.41
mx3 6146.02 52.48 173.09 UB
xxHash32 6040.87 51.77 177.91 LongNeighbors, collisions with 4bit diff, MomentChi2 220
prvhash64s_64 5481.48 170.05 325.39
mirhash 5413.73 39.68 154.47 UB, 2^36 bad seeds, LongNeighbors, machine-specific (32/64 differs)
mirhash32low 5412.76 39.79 182.13 UB, 4 bad seeds, Cyclic, LongNeighbors, machine-specific (32/64 differs)
Murmur3F 5226.4 52.18 175.85 UB
prvhash64s_128 5161.33 260.96 442.70
t1ha0_32le 5132.18 54.83 193.53 Sparse, LongNeighbors
halftime_hash64 4990.72 120.55 281.64
Murmur2B 4882.95 39.72 149.43 UB, 1.8% bias, collisions, 3.4% distrib, BIC
seahash32low 4801.33 58.54 227.31 PerlinNoise 32, !msvc
seahash 4796.97 58.55 201.58 PerlinNoise, !msvc
fasthash32 4737.61 45.32 181.86 UB, insecure
fasthash64 4737.21 42.79 164.87 UB, insecure, Moment Chi2 5159 !
umash32_hi 4662.92 54.22 214.20
umash64 4662.09 53.42 188.09
umash32 4633.19 53.42 216.33
t1ha0_32be 4585.59 55.98 183.45 Sparse, LongNeighbors
clhash 4472.31 82.72 229.73 PerlinNoise, machine-specific (x64 SSE4.2)
tabulation32 4317.34 35.45 197.20 collisions
Murmur2C 4092.99 51.84 164.65 UB, 2^32 bad seeds, 91% bias, collisions, distr, BIC, LongNeighbors
farsh128 3776.92 232.48 398.67
City32 3675.04 57.73 212.04
TSip 3228.14 57.96 211.71 !msvc
Murmur3C 3197.63 67.9 198.00 UB, LongNeighbors, Text, DiffDist
Crap8 3149.63 36.23 195.11 UB, 2.42% bias, collisions, 2% distrib
Murmur2 3146.91 41.87 187.89 UB, 1 bad seed, 1.7% bias, 81x coll, 1.7% distrib, BIC
Murmur2A 3146.79 46.87 191.96 UB, 1 bad seed, 12.7% bias, LongNeighbors
aesnihash 2963.39 71.24 217.73 fails many tests, machine-specific (x64 AES-NI)
BEBB4185 2951.62 222.03 343.63 UB, too many bad seeds, msvc-specific
jodyhash6 2848.42 29.99 164.36 bias, collisions, distr, BIC, LongNeighbors
wyhash32 2532.89 48.4 484.57 2 bad seeds, 32-bit
umash128 2427.46 70.6 197.29
Murmur3A 2413.88 53.36 182.37 UB, 1 bad seed, Moment Chi2 69
prvhash64_64m 2386.19 51.18 186.87
prvhash64_128 2383.57 103.44 246.45
prvhash64_64 2375.72 51.61 190.97
hasshe2 2372.52 68.64 216.74 Permutation,TwoBytes,Zeroes,Seed
PMurHash32 2344.78 58.48 196.43 1 bad seed, Moment Chi2 69
mirhashstrict32low 2218.87 65.48 190.59 1 bad seed, MomentChi2 9
mirhashstrict 2217.32 65.53 182.07
sha1ni 2019.96 135.84 564.40 insecure,sanity, Permutation, Zeroes, machine-specific
sha1ni_32 2019.94 136.82 589.46 machine-specific
superfast 1956.25 53.61 180.10 UB, bad seed 0, 91% bias, 5273.01x collisions, 37% distr, BIC
sha2ni-256_64 1910.34 146.06 595.16 Zeroes, machine-specific
sha2ni-256 1906.77 145.47 603.08 insecure,sanity, Permutation, Zeroes, machine-specific
farsh256 1895.77 459.86 575.95
SipHash13 1889.1 89 199.95 0.9% bias
Murmur1 1804.67 51.51 188.41 UB, 1 bad seed, 511x collisions, Diff, BIC
lookup3 1658.31 48.84 194.15 UB, 28% bias, collisions, 30% distr, BIC
pearsonbhash64 1486.34 104.32 185.03
poly_1_mersenne 1431.65 54.49 189.52 fails most tests
jodyhash32 1428.37 44.36 185.85 bias, collisions, distr, BIC LongNeighbors
pearsonbhash128 1347.03 121.75 214.84
poly_2_mersenne 1323.69 66.93 190.88
poly_3_mersenne 1323.59 74.86 206.77
poly_4_mersenne 1323.57 82.67 200.36
blake3_c 1285.91 340.01 552.63 no 32bit portability
GoodOAAT 1052 71.62 192.19
pearsonbhash256 998.9 167.05 261.29
SipHash 980.88 127.77 246.19
MicroOAAT 977.6 59.61 185.06 100% bias, distrib, BIC
FNV1a 791.84 69.69 177.84 bad seed, zeros, fails all tests
sdbm 791.84 67.69 177.06 bad seed 0, fails all tests
FNV64 791.82 70.24 159.29 fails all tests
bernstein 791.82 68.63 180.71 bad seed 0, fails all tests
beamsplitter 789.22 682.45 1150.3 UB, too many bad seeds
HalfSipHash 755.78 114.47 243.72 zeroes
chaskey 753.23 153.42 288.26 PerlinNoise
x17 527.9 98.78 184.09 99.98% bias, fails all tests
JenkinsOOAT_perl 452.49 118.78 194.78 bad seed 0, test FAIL
MurmurOAAT 452.49 113.07 197.83 bad seed 0, 1.5-11.5% bias, 7.2x collisions, BIC, LongNeighbors
JenkinsOOAT 452.48 142.85 213.93 bad seed 0, 1.5-11.5% bias, 7.2x collisions, BIC, LongNeighbors
crc32 392.1 131.62 204.58 insecure, 8590x collisions, distrib, PerlinNoise
sha1-160 364.95 1470.55 1794.1 Comb/Cyclic low32
rmd256 362.49 617.02 815.44 Bad seeds
blake2b-256_64 356.97 1222.76 1435.0
blake2b-224 356.59 1228.5 1425.87
blake2b-160 356.08 1236.84 1458.15
blake2b-256 355.97 1232.22 1443.31 Sparse high 32-bit
md5-128 353.76 638.29 803.39
md5_32a 353.64 629.85 799.56 Sparse high 32-bit
sha1_32a 353.03 1385.8 1759.9 Cyclic low32, 36.6% distrib
rmd128 334.36 659.03 838.32 Bad seeds
blake2s-128 295.3 698.09 1059.2
pearsonhash64 287.95 174.11 196.50 Avalanche, Seed, SSSE3 only. broken MSVC
pearsonhash128 287.95 171.72 194.61 Avalanche, Seed, SSSE3 only. broken MSVC
pearsonhash256 264.51 184.87 218.79 Avalanche, Seed, SSSE3 only. broken MSVC
blake2s-256 215.28 1014.88 1230.38
blake2s-160 215.01 1026.74 1239.54
blake2s-256_64 211.52 1044.22 1228.43
blake2s-224 207.06 1063.86 1236.50
rmd160 202.16 1045.79 1287.74 Bad seeds, Cyclic hi32
sha2-256_64 148.01 1376.34 1624.71 Bad seeds, Moment Chi2 7
sha2-256 147.8 1374.9 1606.06 Bad seeds, Moment Chi2 4
sha2-224_64 147.6 1360.1 1620.93 Bad seeds, Cyclic low32
sha2-224 147.13 1354.81 1589.92 Bad seeds, Comb low32
asconhashv12 144.98 885.02 1324.23
sha3-256 100.58 3877.18 4159.79 PerlinNoise
sha3-256_64 100.57 3909 4174.63 PerlinNoise
asconhashv12_64 86.73 684.02 606.93
floppsyhash 35.72 1868.92 1411.07
tifuhash_64 35.6 1679.52 1212.75 Cyclic low32
Problems include:
- Bad Seeds. A random seed is often used to initialise the hash. This problem relates to having a bad seed..
- Undefined behaviour (UB). This includes Misaligned, oob (Out of bounds), Signed integer overflow and Shift exponent overflow.
o1hash is the fastest, and a quick and dirty hashing method. It is generally not secure. t1h (Fast Positive Hash) requires AES-NI (Intel Advanced Encryption Standard Instructions) and is one of the fastest hashes at 22.785 Gbps. It has fairly good security levels. Meow comes in around 17.378 Gbps. We can see that SHA-1-160 runs as 364 Mbps, while Meow runs at 17.378 Gbps. Blake 3 is one of the fast cryptography hash and has a rate of 1.285 Gbps, and Blake 2 gives a rate around 215 Mbps. SHA-3 gives hashing rates of 100.58 Mbps.
Google recommend the following for 64-bit hashes without quality problems:
- xxh3low
-
wyhash
-
ahash64
-
t1ha2_atonce
-
FarmHash
-
halftime_hash128
-
Spooky32
-
pengyhash
-
nmhash32
-
mx3
-
MUM/mir
- fasthash32
Hash-based Signatures

With hash-based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature, unless we create a stateless method, such as SPHINCS+ [1]. Currently NIST have the final round for the Post Quantum Cryptography competition, and for digital signatures, SPHINCS+ is one of the alterative finalists (alongside Picnic).
Hash-based signature (theory)
- BiBa (Go). BiBa. An overview of BiBa One Time Signature [9]. Basically the method involves us taking a hash of a value using a standard hashing method, such as with SHA-256. There will then be \(2^{256}\) different hashing values. We aim to create a signature for a message, so Bob (the signer) selects a number of random values for his private key value and then publishes the hash of each of these (\(P_1\), \(P_2\), etc). He then sends these public keys to Alice. Now when Bob wants to sign a message, he will take one of his private key values, and then hashes it, and then determines the bin that it should be placed. In this case, we could use the \(\pmod N\) function on the hash, and where \(N\) is the number of bins. If we select \(2^{10}\) there will be 1,024 bins.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature [9].
Hash-based signature (stateful)
- BLISS - Post-quantum signing. BLISS. One of the alteratives to the usage of our existing public key methods is the usage of lattice cryptography, and especially in the usage of Ring Learning With Errors (RLWE). An important application is within digital signatures, and where Bob will sign something with his private key, and then Alice can prove that he signed it with his public key. One post-quantum signature method is BLISS (short for Bimodal Lattice Signature Scheme) [8]. It was created by Léo Ducas, Alain Durmus, Tancrède Lepoint and Vadim Lyubashevsky in 2013.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Hash to Obtain Random Subset (HORS) [3] is a quantum robust hashed-based one-time signature. With this we create a series of integers for our private keys and organise into an indexable form. Then we hash them to a sequence of public key values. Next we segment the hash of the message into a series of n-bit integer values. The signature is then achieved through a look-up of the value in the public key list.
- Lamport Signatures. Lamport. Outlines Lamport signatures [7]. When we sign a message we take its hash and then encrypt with our private key. The public key is then used to prove it, and will prove that we signed it with our private key. The Lamport signature uses 512 random hashes for the private key, and which are split into Set A and Set B. The public key is the hash of each of these values. The size of the private key is 16KB (2×256×256 bits) and the public key size is also 16 KB (512 hashes with each of 256 bits).
- Winternitz Signatures (W-OTS). Winternitz. Outlines Winternitz signatures [4, 5]. W-OTS uses relatively small key and signatures sizes, and is thought to be quantum robust. It generates 32x256 bit random private keys. We then hash these a number of times, and is defined by a parameter (w). If we use w=8, we hash the private keys by (2w). This creates 32x256 bits public keys. The signature is the created by taking eight bits at a time, and then the 8-bit binary int (n) is subtracted from 256 and the private key is the hashed 256-n times. The signature is then 32 hashes which are derived from random private keys. To verify the signature, the recipient parses the hash of the signature (using 8 bits at a time, and extracting the 8 bit int, n).
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method [6], and which is used within speeds-up of Hashing-based signature methods. Using methods such as SHA-1 and SHA-2 (aka SHA-256) will be inefficient as they tend to compress the data inputs through a number of stages. Haraka v2 [6] is different as focuses on inputs of just 256 bits (32 bytes) or 512 bits (64 bytes). This makes the method useful when we are dealing with key and hash values, and is especially useful for hash-based signatures. The output is 256 bits long, but where the input can be either be 256 bits (Haraka256) or 512 bits (Haraka512). These lengths are typically for the outputs of modern hashing applications. The Haraka method, too, has been optimized with AES instructions (AES-NI - Intel Advanced Encryption Standard New Instructions) and which are supported within the hardware of the processor. As Haraka is focused on short messages, the number of rounds within the hashing process has been reduced.
Hash-based signature (stateless)
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ digital signature. SPHINCS digital signature. Outline of the a SPHINCS stateless digital signature method [1].
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
Hash-based signature (Merkle-based)
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
Introduction
Many of the problems we see on the Internet relate to the lack of trust within transactions. The emails you receive and the Web sites that you visit often have very little trust built into them. For trust the email address of the sender, but anyone can fake that address. So increasingly we create a digital signature, and where we sign our messages. In this way, we can check for authentication, integrity and non-repudiation.
With the Alice creates a key-pair: a public key and a private key. She then takes a hash of the message, and then encrypts this hash with her private key, and passes the message and the signature to Bob. Bob then reads the message and takes a hash of it. He then decrypts Alice's signature with her public and checks the hashes. If they match, he knows that she signed and that it has not been changed along the way:
Currently, we often use RSA, DSA and ECDSA to sign our messages. These are based on the difficulty of finding out the factors of a number and on the processing of discrete logarithms. At the current time these methods are computationally hard problems, but with quantum computers, they become much easier. This was shown by Peter Shor who illustrated that it was possible to crack them in polynomial time.
Of all the methods that are being proposed, the hash-based methods look as if they have a good chance of success of creating quantum robust signatures. methods and code-based methods are being researched, but the usage of hashing methods is already well and could provide the best alternative to the existing methods. Hashing methods, too, often bring other advantages, such as forward secure, which means that a key which is cracked will not reveal all the previous keys.
Merkle trees
The root of hash-based methods isin Merkle trees, and which are a way of hashing is used in many applications, including with Bitcoin, Ethereum, Git distribution systems, No SQL, and in many P2P applications. With a Merkle tree we take our data elements, and then hash them, and take pairs of these hashes to create a new hash, and so we build a table. At the top of the tree is the root element (in this case Hash1234):

In this way, we can use the tree to see if we have matching data on systems.On a P2P network, we can transfer a file by splitting it into data segments and then distributing these segments across the network. A trusted source will have the complete Merkle tree for rebuilding the file, and a client can thus rebuild from the Merkle tree and determine the parts of the file which are still missing. Once transferred the root hash (and all the other hashes) will then match. In its core method, the Merkle Signature Scheme (MSS) has serious performance and memory issues, but enhanced methods such as XMSS create with much less of a performance hit.
One-time signatures (Lamport)
The core method used in hash-based signatures is that of the one-time signature, and where we create a new key pair for every method we need to create. If the keys were reused, an attacker could start to learn the private key, and thus spoof messages. One of the first methods was produced by Leslie Lamport and Whitfield Diffie, in 1979, and is defined as:
- We create two data sets with 256 random 256-bit numbers (Set A and Set B). These are the private key (512 values).
- we take the hash of each of the random numbers. This will give 512 hashes and will be the public key.
- We then hash the message using and then test each bit of the hash (0 ... 255). If it is a 0, we use the ith number in Set A, else we use the ith number from Set B.
- The signature is then 256 random numbers (taken from either Set A or Set B) and the public key is the 512 hashes (of Set A and Set B).
The public and private keys are then each 16KB in size. A demo of the method is here.

Figure 1: Lamport method
The major problem with the method is that a key pair for every message. also in 1979, found a solution with Merkle trees.
One-time signature (W-OTS)
To improve performance method (and which reduced key sizes), Merkle proposed Winternitz OTS (named after Robert Winternitz). With this method was possible to sign many bits at the same time. The method is:
- We create 32 256-bit random numbers. These 32 values will be our private key.
- We then hash each of these values 256 times. These 32 values will be our public key.
- We now take the message and hash it using SHA-256. This produces 32 8-bit values (N1, N2 ... N32).
- Next we take each 8-bit value in the hash of the message, and then hash 256-N times (where N is the value of the 8-bit value).
- To prove the signature, we take the message and hash it with SHA-256, and then take each 8-bit value. We then hash the 8-bit signature value by the number of times defined by the message hash value (N1, N2..). The result for each operation should equal the public key value.
This is illustrated below in Figure 2. A demo of the method is here.

Figure 2: W-OTS
Hash-based Signatures
The methods such as W-OTS and Lamport only provide for a one-time signature. In order to sign many messages, we can use the Merkel signature scheme (MSS). With this we take a hash of the keys and build these as the leaves of the tree. The root of the tree is then the public key - the verification key. We then just use the private key of the W-OTS method to create the signature. The sender also sends the authentication path, which is the neighbouring nodes within the path and which leads to the root of the tree. The recipient can then rebuild the tree using the verification key (which can be received a digital certificate) and the authentication path. For the next message we move onto another key pair and where the index of the key part is revealed.
In the following example we have our root as the public key, and then want to sign with Key3. We then show the authentication path which takes us to the root (as defined in the bold arrows):

Conclusions
Hashed-based methods look to be a strong contender for weaning us off RSA, DSA and ECDSA, but we will have to look at the stateful generation of keys. For this we will have to generate a bank of key pairs (2, 4, 8, 16, etc) and then create the public key from the root of the Merkle tree. We must then remember the keys we have used previously, and only use an unused one. Once we use our new key pair, we then show our working-out as to how the private key is integrated into our tree. It is a bit like a teacher marking a question correctly, and asking for the working out that go you to the answer.
References
[1] Bernstein, D. J., Hopwood, D., Hülsing, A., Lange, T., Niederhagen, R., Papachristodoulou, L., ... & Wilcox-O’Hearn, Z. (2015, April). SPHINCS: practical stateless hash-based signatures. In Annual international conference on the theory and applications of cryptographic techniques (pp. 368-397). Springer, Berlin, Heidelberg [paper].
[2] Bernstein, D. J., Hülsing, A., Kölbl, S., Niederhagen, R., Rijneveld, J., & Schwabe, P. (2019, November). The SPHINCS+ signature framework. In Proceedings of the 2019 ACM SIGSAC conference on computer and communications security (pp. 2129-2146) [paper].
[3] Reyzin, L., & Reyzin, N. (2002, July). Better than BiBa: Short one-time signatures with fast signing and verifying. In Australasian Conference on Information Security and Privacy (pp. 144-153). Springer, Berlin, Heidelberg [paper].
[4] Merkle, R. C. (1989, August). A certified digital signature. In Conference on the Theory and Application of Cryptology (pp. 218-238). Springer, New York, NY.
[5] Hülsing, A. (2013, June). W-OTS+–shorter signatures for hash-based signature schemes. In International Conference on Cryptology in Africa (pp. 173-188). Springer, Berlin, Heidelberg.
[6] Kölbl, S., Lauridsen, M. M., Mendel, F., & Rechberger, C. (2016). Haraka v2–efficient short-input hashing for post-quantum applications. IACR Transactions on Symmetric Cryptology, 1-29. [here]
[7] Lamport, L. (1979). Constructing digital signatures from a one-way function (Vol. 238). Technical Report CSL-98, SRI International. [paper]
[8] Ducas, L., Durmus, A., Lepoint, T., & Lyubashevsky, V. (2013, August). Lattice signatures and bimodal Gaussians. In Annual Cryptology Conference (pp. 40-56). Springer, Berlin, Heidelberg [paper].
[9] Perrig, A. (2001, November). The BiBa one-time signature and broadcast authentication protocol. In Proceedings of the 8th ACM Conference on Computer and Communications Security (pp. 28-37) [paper] .
Hashing (Simularity)

Similarity hashes allow for two data objects to be compared for their similarity.
Similarity assessment methods
The following relate to the basic methods used for string similarity:
- String similarity String similarity. This measures edit distance (including Levenshtein distance), Jaro (including Jaro-Winkler), and QGrams.
- String enthropy String enthropy. Measurement of the entropy of strings.
- Soundex Soundex. Soundex uses a phonetic algorithm to classify a sound as it is pronounced. It focuses on matching phrases which have minor spelling errors.
Similarity hashes
The following are the tips related to similarity hashing:
- Similarity hash: SimHash (Charikar similarity) in Python Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash (Nilsimsa similarity) Nilsimsa. The Nilsimsa similarity is used to find similarities between spam emails.
- Context Triggered Piecewise Hashes (CTPH): ssdeep CTPH similarity. Kornblum [6] created ssdeep and which computes fuzzy hashes. This aims to match similar byte sequences, no matter if there are differences between these sequences. For this we break a file up into fragments with a rolling hash function. We then produce a small hash for each of those fragments. These are then aggregated to produce the complete hash of a file. In comparing file signatures, we treat the resultant hash value as a string, and then uses an edit distance method to compare.
- TLSH (A Locality Sensitive Hash) TLSH similarity. In malware analysis and in text similarity, we often have to identify areas of data within files which are similar. One method is TLSH (A Locality Sensitive Hash), and which was defined by Oliver et al [7]. It is used - along with ssdeep - by VirusTotal to identify a hash value for malware.
- Minhash (Jaccard similarity) Jaccard similarity. The Minhash method is used to find similarities between strings, files and metadata.
- Counting identical elements (HyperLogLog) HyperLogLog. Counting the number of identical elements.
Hazmat cryptography

The Cryptography library in Python contains interfaces to common cryptographic algorithms, including symmetric key methods, hashing, public key, and key derivation functions. Many of these are contained with the Hazmat (Harzardous Material) primative setup.
Hashing, HMAC, CMAC, Poly1305 and HKDF
-
Hazmat Hashes. Hazmat Hashes. This includes the hashing methods in the Hazmat cryptography library. This includes Blake2p, Blake2s, MD5, SHA1, SHA224, SHA256, SGA384, SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHA512, SHA512-224, SHAKE128 and SHA256.
-
Hazmat Hashes. Hazmat Hashes. In this case we will implement Python code to determine SHA1, SHA2, SHA3, Blake2, MD5 and SM3 hashes.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
- Hazmat HKDF. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
- Hazmat CMAC. Hazmat CMAC. CMAC methods using the Python cryptography primitives.
- Hazmat Poly1305. Hazmat Poly1305. Poly1305 methods using the Python cryptography primitives.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
Symmetric key
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat. Implementation of ChaCha20/Poly1305 with a random key using Hazmat.
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat. Implementation of AES GCM with a random key using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hazmat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Hazmat Symmetric Key Padding. Symmetric key. This includes the coverage of padding with Hazmat.
- Hazmat Symmetric Key Padding. Symmetric key. This includes the coverage of padding with Hazmat.
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
- Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . With 3DES encryption, we use a 128-bit key and a 64-bit IV value. The two modes supported are ECB (without salt) and CBC (with salt). The DES algorithm has been around for a long time, and the 56-bit version is now easily crackable (in less than a day on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases, and splits the key into two. Overall the key size is typically 112 bits (with a combination of the three keys - of which two of the keys are the same). In this case we will use PKCS7 padding, and which fills the input data with a value that is equal to the number of padding bytes. Overall, DES has a 64-bit block size, and which equates to eight ASCII characters.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key . And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.
Asymmetric key
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- ECC key generaton with Hazmat. Elliptic Curve key gen. Creating ECC keys using Hazmat and Python.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- Hazmat RSA signing (with key values). RSA signing with Hazmat. RSA signing using Python and with Hazmat (with key values).
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here]
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Signatures. DSA Signatures. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. The ECDSA method is an extension of DSA, but implemented with elliptic curve (EC) methods. As with most public key signing methods, we take a hash of a message, and then apply a private key to create a signature (\(r,s\)). This is done by creating a random value (\(k\)) to produce the signature. The signature is then verified using the associated public key. This then verifies the creator of the signature and that the message has not been changed.
Digital Signature: ECDSA/EdDSA
- ECDSA with Hazmat. ECDSA wih Hazmat. This outlines ECDSA with Hazmat.
- Ed25519 for EdDSA signatures with Hazmat. EdDSA: Ed25519. This page uses the Hazmat primitives for the cryptography library.
- Ed448 for EdDSA signatures with Hazmat. EdDSA: Ed448. This page uses the Hazmat primitives for the cryptography library.
- Ed25519 using NaCl. Ed25519. This page uses the NaCl port from libsodium.
- ECDSA Signatures with Hazmat (SECP256R1, SECP384R1, SECP521R1, SECP224R1, SECP192R1, and SECP256K1). ECC Signatures. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and then creates an ECDSA signature for a given message.
Digital Signature: RSA
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
Key exchange: ECDH/X25519
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives and showing the byte values for the key.
Tokens
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
Homomorphic Encryption

Homomorphic encryption supports mathematical operations on encrypted values. Partial Homomorphic Encryption (PHE) supports a few arithmatic operations, while Full Homomorphic Encryption (FHE) supports add, subtract, multiply, and divide. Homomorphic encryption normally involves a public key to encrypt the data, and a private key to decrypt it. There have been four main generations of homomorphic encryption, and the most recent being the HEAAN method.
Simple
- Simple Homomorphic Cipher. Hom. This outlines a Simple Homomorphic cipher.
- Simple Homomorphic Cipher (Python). Hom. This outlines a Simple Homomorphic cipher with Python.
- Full Homomorphic Cipher with a Public Key. Public key. This outlines a Simple Homomorphic cipher using a public key
ElGamal
- ElGamal Homomorphic Cipher (Go). ElGamal. This outlines ElGamal Homomorphic cipher with Go.
- ElGamal Homomorphic Cipher (Go) - Divide. ElGamal. This outlines ElGamal Homomorphic cipher with Go with divide.
- ElGamal Homomorphic Cipher (Go) - Additive. ElGamal. This outlines ElGamal Homomorphic cipher with Go with addition.
- ElGamal Homomorphic Cipher for Multiplication (Python). ElGamal. This outlines ElGamal Homomorphic multiplication with Python.
- ElGamal Homomorphic Cipher for Division (Python). ElGamal. This outlines ElGamal Homomorphic division with Python.
- ElGamal Homomorphic Cipher for Addition (Python). ElGamal. This outlines ElGamal Homomorphic addition with Python.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (Python). ElGamal. This outlines ElGamal Homomorphic subtraction with Python.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
RSA
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
ZKP
- Full Homomorphic Cipher to determine if Bob is older. Older. This outlines a Simple Homomorphic cipher to determine if Bob is older than Alice.
- Full Homomorphic Cipher to determine matching password. Password. This outlines a Simple Homomorphic cipher to determine if a password matches
- Interactive ZKP With Probablistic Methods. ZKP. Interactive ZKP With Probablistic Methods using Python.
- Full Homomorphic Cipher for Millionaire's Problem. Millionaire. This outlines a Simple Homomorphic cipher for the Millionaire's Problem
Voting
- Trusted voting. Trusted. A trusted voting method.
Secret share
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Lattice
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
Full Homomorphic Cipher
- Full Homomorphic Cipher for 2-bit Adder. Adder. This outlines a Simple Homomorphic cipher for a 2-bit adder with DGHV.
- Full Homomorphic Cipher for Full Adder. Full Adder. This outlines a Simple Homomorphic cipher for a full adder with DGHV.
- Full Homomorphic Cipher for 4-bit Adder. Adder. This outlines a Simple Homomorphic cipher for a 4-bit adder with DGHV.
- Full Homomorphic Cipher for 4-bit Adder/Subtractor. Subtract. This outlines a Simple Homomorphic cipher for a 4-bit adder/subtractor with DGHV.
- Full Homomorphic Cipher to XOR two integers. X-OR. This outlines a Simple Homomorphic cipher to X-OR two integers
Paillier
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier) .
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Damgård-Jurik Homomorphic Encryption With Secret Shares. Damgård-Jurik Method. Two of the major areas of developments within cybersecurity will be the usage of homomorphic encryption, and in the usage of Shamir secret sharing. With homomorphic encryption, we can encrypt values, and then operate on them with arithmetic functions (such as add, subtract and multiply), and with Shamir secret sharing, we can split secrets into shares, and then distributed them over networks. These approaches will take privacy to new levels. So let’s look at the Damgård-Jurik method.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Learning with Errors (LWE)
- Learning With Errors . LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret key value (s) and another value (e). Next we select a number of values (t[]) and calculate g[] = t[] x s + e. The values of g[] and t[] become our public key.
- Public Key Encryption with Learning With Errors (LWE). LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret value (s) and which is our private key. We then create a public key which is based on random numbers (A), and then generate another set of numbers (B) which is based on A,s and random errors e. An example of encryption with multiple bits is given.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE)
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Others
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
- SIDH Go. SIDH. Post-quantum key exchange.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Anonymous crypto. Anon. Anonymous crypto.
- Rho factorization. Rho. Rho alogorithm.
- Post-quantum signing (BLISS). BLISS. BLISS method.
Homomorphic Encryption with Krytology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Homomorphic hashing
- Homomorphic Hashing with Golang. Homomorphic hashing. Normally with hashing methods, we need to take all the previous data and new data in order to create a new hash value for our data. In a homomorphic hashing method, we can basically take the previous hash, and then add on any new data values. We can also remove previous data values from our hash, too. This is more efficient in computing, as we do not have to process all of our data into a new hash, and can use simple homomorphic operations for the computation. The method we will use (LtHash) was initially defined by Bellare and Micciancio and updated Lewi et al at Facebook.
Identity Based Encryption (IBE)

This page outlines a few basic principles around the usage of IBE.
Identity Based Encryption (Pairing based)
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pair-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Identity Based Encryption (Others)
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Güther's implicitly certified identity-based public keys (IBE). Günther. This method allows Bob to generate Alices public key from her identity and publicly available parameters.
- Girault's self-certified public keys (IBE). Girault. This method allows Bob to generate Alices public key from her identity and publicly available parameters, and where we use an RSA key pair to self-certify Alice's public key.
Intrusion Detection Systems (IDS)
- Intrusion Detection Systems. Snort. This outlines some of the basics of IDS, including the requirement for Intrusion Detection Systems (IDSs), and where they are used.
- Advanced Network Forensics (Snort). Adv Network Forensics. This provides information on how to detect threats through network forensics with Snort
Snort

- Snort IDS. Snort. This is a Snort Analyser.
- Snort IDS 2 with rules editor. Snort. This provides information on how to detect threats through network forensics with Snort, and with an editing function for rules.
Presentation
IoT

The key objectives of this page are: Understand how a Pen Tester can generate vulnerabilities and test using the Metasploit framework; Define the options and payloads required to generate and use vulnerabilities; and Gaining remote access.
Devices
- Access the Wi-fi kettle. Go. This page outines how to access a wi-fi enabled kettle.
- Philips Hue Wireless Lighting. Go. This page shows how to use RESTful Web services to access to the Hue Led Lamps.
- Kali and R-PI. Go. This page shows the setup of a security testing infrastructure using a Raspberry Pi (R-PI) and a wifi access point.
- Kali, R-PI and RF electrical socket. Go. This page shows the control of an RF electical socket from a RPI.
- Capture from a Polar H10 heat rate sensor. Go. This page shows the capture of the Polar H10 heart sensor with an Ubertooth One.
- Trusted IoT: Linking IoT Devices to NFTs. Go. This page outlines a research paper which links a device to an NFT (Non-fungible Token).
Shodan Scanning
-
IoT Scan (Shodan). Go. This page includes a search of the Internet for key terms, such as for "apache", "mysql" and "cisco".
- IoT Banner Scan (Shodan). Go. This page includes a search of the Internet for key terms with the banner as a result (for the Top 10)
- Internet Services (Shodan). Go. This page includes a search of the Internet for key terms and display the IP address and port.
IoT Libraries
- libDisco with Go. libDisco. libdisco is a Golang library which can be used to create secure connections. It is based on the STROBE protocol framework. Symmetric cryptographic primitives rely on SHA-3 permutation, and asymmetric cryptographic primitives on X25519 and ed25519. STROBE defines a range of cryptographic protocols to integrate with IoT devices. In order to reduce processing, energy and memory requirements, it only uses Keccak (SHA-3) to encrypt and authenticate messages.
COSE/COBR
In computer security, we often have to represent binary data, in single values or groups of characters, bytes, words, long words, signed integers, floating-point values, double-precision floating-point values, and so on. This might be in the form of a data object, a signature or even encrypted content. For this, the ANS.1 DER format is often used, such as presenting digital certificates and signatures. An improvement on this for small messages with security is Concise Binary Object Representation (CBOR) — and which is defined in RFC8949 [1]. While JSON represents text-based data objects CBOR focuses on binary objects. It has been designed to create a lightweight encoder and decoder. This supports the use of CBOR within an IoT infrastructure. The data, also, does not require a data schema to be able to decode it, along with being extensible. CBOR defines the format of binary data with data objects and messages. We can then integrate security with CBOR Object Signing and Encryption (COSE), and which is defined in RFC8152 [2]. This includes signatures, message authentication codes (MACs), encryption and creating serialised objects.
- 128-bit AES GCM. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) can then build on this to include signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use a symmetric key to encrypt a message, and then decrypt it. In this case we will use AES GCM with a static 128-bit key ("0x000102030405060708090a0b0c0d0e0f").
- 256-bit AES GCM. Go. In this case we will use AES GCM using a random 256-bit key (32 bytes).
- EdDSA. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) [2] can then build on this to includes signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use EdDSA to create a signature for a message.
- ECDSA. Go. In this case we will use ECDSA to create a signature for a message.
- HMAC. Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT. Go. In this case we create a CWT token, and sign with an HMAC signature.
- ECDH. Go. In this case we create a symmetric key from ECDH. For this we will derive a shared key from the public key of Alice and Bob, and then define a single recipient which can derive the CEK (Content Encryption Key) using their private key. We will use the curves of P-256 (secp256r1), P-384 (secp384r1), P-521 (secp521r1) or SECP256K1 (as used with Bitcoin).
- RSA using COSE and CBOR. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\).
- RSA: dQ, dP and InvQ. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). The key pair also includes \(dQ\), \(dP\) and \(InvQ\), and these can be used with the Chinese remainder theory to optimize the decryption process.
Metasploit
- Armitage and Metasploit. Go.
- Exploiting Android with Metasploit. Go.
- Exploiting Android with Metasploit - Part 2. Go.
- Exploiting Windows/Mac OS X with Metasploit. Go.
- Remote Desktop Windows/Mac OS X with Metasploit. Go.
- Metasploit. Go.
- Internet of Things Security. Go.
- Metasploit (Enumeration and Scanning). Go.
- Metasploit (Malware). Go.
IP

 The following are a few interesting techniques around IP addresses:
The following are a few interesting techniques around IP addresses:
- Your details. IP. This shows your browser details.
- IP address analyser. IP. This involves converting an IP address to the host and network part of the address.
- IP subnet analyser. IP subnets. This involves converting an IP address to the host and network part of the address.
- IP address analyser. IP. This involves analysing IP addresses.
- Max subnets. Max subnets. This involves converting an IP address to the host and network part of the address.
- Route summarization. Summarization. This involves converting an IP address to the host and network part of the address.
- Whois. Whois. This does a basic Whois on a domain.
- URL Obfuscation. Obfuscation. This outlines URL obfuscation.
- HTTP Responses. Test. HTTP.
- Capturing Network Packets (Python). WinPCap. HTTP.
Cisco related
- Routing table. Routing table. This involves viewing a routing table for a Cisco device.
- ACL Generator. ACL. This involves a simple calculator for ACLs on network ranges.
- EIGRP metrics. EIGRP. Learn the basics of EIGRP metrics.
- VoIP B/W. VoIP. Calculate bandwidth for VoIP.
- Wild Card. Wild Card. On a Cisco device a wildcard mask is used to identify the parts of an IP address that need to be matched. It thus uses a wildcard mask, where a 0 in the bit position identifies that the device should match that bit, else a 1 shows that it should ignore it.
Protocols
- HTTP. HTTP. Show the request and response for HTTP.
- Ping analyser. IP. This involves converting a ping of a site.
IP Challenges
-
IP Test 1. IP Test. IP Classification test. This is a simple test which generates a range of IP addresses, and you must determine the IP address classification.
IP Subnet Challenge 1 Demo
-
IP Test 2. IP Test. IP Classification test Part 2. This test provides an address classification, and the user must find the addresses which are of this classification.
IP Subnet Challenge 2 Demo
-
IP Test 3. IP Test. IP Classification test Part 3. This test provides an address classification, where the network part of the address is determined.
IP Subnet Challenge 3 Demo
Subnet Challenges
- Subnet Test 1. Subnet Test. Subnet Test.
-
Subnet Test 2. Subnet Test. Subnet bits.
- Subnet Test 3. Subnet Test. Find the nth usable subnet. This test involves finding the nth usable subnet.
- Subnet Test 4. Subnet Test. Maximum subnets. This is a test page to determine the maximum number of subnets and hosts/subnet for IP classed addressing.
- Subnet Test 5. Subnet Test. Maximum host/subnet. This is a test page to determine the maximum number of hosts per subnet.
- Subnet Test 6. Subnet Test. Determine the required subnet mask for a given number of subnets. This is a test page to determine the required subnet mask for a given number of subnets and a given IP address classification.
- Subnet Test 7. Subnet Test. Determine the required subnet mask for a given number of host/subnet. This is a test page to determine the required subnet mask for a given number of hosts per subnet and a given IP address classification.
- Subnet Test 8. Subnet Test. Route summarization. This involves a calculation on route summarization.
- Subnet Test 9. Subnet Test. Binary to IP.
- Subnet Test 10. Subnet Test. Hex to IP.
-
Subnet Test 13. Subnet Test. Wild card mask network bits. Find the number of bits in the network part of the wild card mask. IP Wildcard challenge
- Subnet Test 14. Subnet Test. Wild card mask host bits. Find the number of bits in the host part of the wild card mask. IP Wildcard challenge
- Subnet Test 15. Subnet Test. Wild card mask ... find the network address. Find the network for the wild card mask. IP Wildcard challenge 2
- Subnet Test 16. Subnet Test. Find a matching IP address for a network and wild card mask. Find the IP for a network and a wild card mask.
- Subnet Test 17. Subnet Test. Find an address which is on a given network. Find an IP address on a network, for a given network address and subnet mask.
- Subnet Test 18. Subnet Test. Find an IP address on the same network. Find an IP address on the same subnet.
- Subnet Test 19. Subnet Test. Find subnet. Convert subnet mask.
- Megatest. Subnet Test. Challenging test for subnets.
JavaScript

JavaScript code allows execution within the browser, rather than on the server. It is often faster than code that runs on a server. Along with this we can also use Node.js, and which runs JavaScript code on a server.
Symmetric key
- AES. AES. In this example, we will use either a pre-generated key or a random one, and use AES (Rijndael) encryption.
- ChaCha20 and Poly1305. ChaCha. This page outlines Poly1305 and ChaCha20. ChaCha20 is a symmetric key method and Poly1305 is a message authentication code (MAC). They were created by Daniel J. Bernstein, and are alternatives to AES and HMAC.
- CMS (Padding). CMS. This page uses PKIJS encrypting on CMS. With CMS we can This document describes the Cryptographic Message Syntax (CMS). With this we can encapsulate an message within an encrypted entity.

Hashing
- Hash. Hash. This page defines a JavaScript Hash calculator. This uses a client-side JavaScript code to determine the hash signatures of a text value.
Signatures
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
- Boneh–Lynn–Shacham (BLS) signature. BLS. Boneh–Lynn–Shacham (BLS) signature method produces short signatures. They use elliptic curve pairing (and which are also known as bilinear maps).
Key exchange
- ECDH. ECDH. Elliptic Curve Diffie Hellman (ECDH) is used to generate a shared key. This implementation uses Elliptic Curve Cryptography (ECC) with JavaScript.
CryptoJS
- CryptoJS. CryptoJS. This page uses client-side JavaScript code to hashing, encrypt and sign, including for symmetric key (AES), streaming ciphers, hashing methods, and HMAC.
Blockchain
- PATRICIA trie. PATRICIA. In the following, we have the Top 2,500 Web sites in the world, and implemented with a Radix Trie (aka PATRICIA trie) In the following we have the Top 2,000 web sites on the Internet, and which have been indexed using the PATRICIA trie.
Public key
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
- RSA. RSA. RSA is an asymmetric encryption algorithm, which uses two keys, one to encrypt and the other to decrypt. It was created in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman, and is still one of the most widely used encryption methods. A typical application is in authenticating a sender, where the senders private key is used to encrypt a message, and then is decrypted by the receiver with the senders public key (which is known to anyone who wants it). It is also typically used for encrypting disks/files, such as for EFS.
Digital Certificates
- X.509 certificates in JavaScript. RSA and ECDSA Signed certificates. This page will generate either RSA and ECC key pairs, and then generate X.509 certificates, using either a signature of SHA1withRSA or SHA256withECDSA. For RSA signing we use an RSA private key to sign the certificate, and with ECDSA signing we use an ECC private key to sign the certificate.
Tokens
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
Random
- Random number generator. Rand. In the past, encryption and decryption had to be done through native code libraries, such as with Bouncy Castle and OpenSSL. With the increasing processing power of Web browsers, it is now possible to use encryption using JavaScript, which thus provides client-side processing of data. This Web page uses Javascript encryption, and generates a random 256-bit text key or a hex version. The 256-bit key is generated by generating 60 random numbers (from 0-25), and converting these to an ASCII character.
Malware obfuscation
- Malware obfuscation. Obfuscation. A malware writer will often hide certain keywords from the browser/human by encoding them in another format. This is typically done for hex coding (\xZZ), 16-bit unicoding (\uZZZZ) and octal coding (\ZZZ). To test, enter a value, and then press the button and it will convert encoded string.
Message Authentication Codes
- Chaskey (MAC). Chaskey. Chaskey Cipher is light-weight cryptography method for signing messages (MAC) using a 128-bit key. The hardware implementation only requires 3,334.33 gate equivalent with an operating clock frequency of 1 MHz (whereas Keccak requires 4,658 GE). In the page we create the Mac signature and also encrypt for CBC.
Other
- Password generation/hashing. Hashing. Linux can use salted passwords where the username, hashing method and hashed password are stored in a password file [More details]. The main methods are
Hashing

At times we need to generate secrets, such as encryption keys, from passwords or nonce values. A Key Derivation Function (KDF) is a verifiable way of doing this.
Key Derivation Functions (KDFs)
The following are the tips related to hashing:
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Password strength. Test. This outlines the strength of various passwords types.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
HKDF
The following are the tips related to Key derivation hashing:
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Hazmat HKDF for different hashing methods. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
-
HKDF key derivation with OpenSSL [
here]
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
PBKDF2
The following are the tips related to Key derivation hashing:
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- AES GCM (Python) with PBKDF2. AES GCM (Python) with PBKDF2.
- Fernet with PBKDF2 . AES GCM (Python) with PBKDF2.
- PBKDF2 key derivation. AES GCM (Python) with PBKDF2.
- Key Rotation with Fernet. AES GCM (Python) with PBKDF2.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Bcrypt
The following are the tips related to Key derivation hashing:
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- BCrypt. BCrypt. BCrypt with Rust.
-
Hash to password with Go. Hashing to Argon2, Scrypt and BCrypt. Hash to password with Go, including Argon2, Scrypt and BCrypt.
scrypt
- scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Argon 2
The following are the tips related to Key derivation hashing:
- Argon 2. Go. Outline of Argon2.
- Argon 2 with NaCl. Go. Outline of Argon2 using NaCl.
- Argon 2. Argon 2. Argon 2 with Rust.
- Balloon. Go. Outline of Balloon.
Other
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
- Double ratchet. Go. Outline of double ratcheting.
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
Outline
HMAC Key Derivation function (HKDF) is used to derive an encryption key from a passphrase. Initially, HKDF creates a pseudorandom key (PRK) using a passphrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), and along with a salt value. Next, the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys [RFC 5869][article]. In this case, we will use SHA-256.
The following shows how an encryption key can be generated using HKDF, and where we need a secret and a salt value. Both Bob and Alice have the same secret and salt.

With PBKDF2 (Password Based Key Derivation Function 2), we hash for a given number of rounds:

Key exchange

Key exchange is a way for Bob and Alice to communicate and for them to agree on a shared secret. The original method defined uses discrete logarithms (Diffie-Hellman), but most modern methods use elliptic curve techniques (ECDH). As quantum computers can crack both discrete log and elliptic curve methods, there are post quantum cryptography methods proposed. This includes SIDH, CSIDH, SIKE, and NewHope.
Key interchange/generation (Diffie-Hellman)
The following relates to key interchange:
- Selecting \(g\) in Diffie Hellman. G in Diffie Hellman. Picking a safe value of the generator \(g\) in discrete logarithms.
- Diffie-Hellman. Diffie-Hellman Calculation. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Real example). Diffie-Hellman Real. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Python). Diffie-Hellman. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (pre-compute). Diffie-Hellman (pre-compute). Many sites use the same prime numbers, which can then be cracked with a pre-computing attack.
- Key generation. Key gen. This will generate keys for different methods based on a passphrase.
- Diffie-Hellman (Man-in-the-middle). DF. This outlines the man-in-the-middle method for Diffie-Hellman.
- An Alternative Diffie-Hellman method. Alterative DH. This outlines an alternative Diffie-Hellman method.
Authenticated Key Exchange
The following are the tips related to Key derivation hashing:
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- MTI/A0. MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{ax+by} \pmod p\). MTI (Matsumoto, Takashima, Imai).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0. MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{x+y} \pmod p\)
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). The resultant key is \(xyG \)
- MTI/C0. MTI/C0. This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{xy} \pmod p\)
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG\).
- MTI/C1. MTI/C1. This outlines MTI/C1, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{abxy} \pmod p\).
- MQV (Menezes–Qu–Vanstone). MQV. MQV was created Alfred Menezes, Minghua Qu and Scott Vanstone in 1995 and is an authenticated key exchange method. Alice holds a key pair \((A,a)\) and Bob has a key pair \((B,b)\). With this \(a\) is Alice's private key, and \(A=aG\) is her public key. For Bob, his public key will be \(B=aG\) and a private key of \(b\), and where \(G\) is the base point on the elliptic curve.
- HMQV (Menezes–Qu–Vanstone). HMQV. HMQV builds on MQV and adds the identity of Bob and Alice.
- ECDH with X25519 and Blake2b. ECDH with X25519 and Blake2b. This uses PyNaCl to create an authenticated key exchange and uses X25519 and Blake2b.
Elliptic Curve (ECDH) - Python
The following are the tips related to ECC:
- Elliptic Curve. Elliptic Curve. Elliptic Curve is a public key method which can also be used to generate a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with simple parameters. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
Elliptic Curve (ECDH) - Golang and Node.js
The following are the tips related to ECC:
- ECDH with Go. ECDH. ECDH with Go.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with node.js. ECDH. ECDH with node.js.
- ECDH with JavaScript. ECDH. Elliptic Curve Diffie Hellman.
Password Authenticated Key Exchange (PAKE)
The following are the tips related to Key derivation hashing:
- SPAKE2. Go. Outline of SPAKE2.
- OPAQUE. Go. Outline of OPAQUE.
- SPEKE. Go. Outline of SPEKE (Simple Password Exponential Key Exchange).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
- J-PAKE. J-PAKE. This example generates a shared key based on a shared password.
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses discrete logs.
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
PQC NIST Finalists (Key Exchange)
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Key interchange/generation (Other)

The following relates to key interchange:
- Curve25519. Curve25519. This outlines Curve25519, which is used in the Tor network.
- Authenticated Key Exchange (Discrete logs). YAK. Key exchange with public keys and uses discrete logs.
- Authenticated Key Exchange (ECC). YAK. Key exchange with public keys and uses elliptic curve methods.
- Shamir No-key protocol. Shamir No Key. In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated.
- Shamir No-key protocol (sepc256k1). Shamir No Key (EC). In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated using the sepc256k1 elliptic curve.
- Conference keying (Burmester-Desmedt method). Conference keying. In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it.
- Conference keying (Burmester-Desmedt method) - Elliptic Curve (sepc256k1). Conference keying Elliptic Curve (sepc256k1). In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it, and uses the sepc256k1 elliptic curve.
Key exchange (with pairing)
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Kryptology

We need to build a new Internet. One that is build on mathematics and certainty, rather than the patchy version we have now. For this we need a layer of cryptography at the lowest level, and build software interfaces on top of this. Along with this we now have cryptographic methods which can now provide a foundation of trust, and which preserve privacy. And so the old libraries of OpenSSL are being squeezed out in favour of the new ones which are built on a solid foundation. The latest of these new "privacy-aware" libraries is Kryptology, and created by Coinbase. This library provides the APIs that developers need, in order to apply to areas of blockchain development. This library include BLS (Boneh-Lynn-Shacham) signatures, Zero-knowledge Proofs (ZKPs) and Shamir Secret Shares (SSS). With BLS we can digitally sign for data, but also preserve its privacy. Applications of this include group signatures, where multiple entities can merge their signing keys together and provide a single signature for a transaction. With SSS, we can split encryption keys up into shares, and then distribute them across a network. When required, we can call these shares back to reconstruct the key.
The focus for Coinbase seems to be the application of privacy coins, and where no tracking can be applied to the usage of these digital coins. This should support full anonymity for transactions, as opposed to Bitcoin which only supports pseudo-anonymity.

ECC Basics
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining n.G for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Points (Base Point and Others). Elliptic Curve points. Two common curves used in ECC (Elliptic Curve Cryptography) are secp256k1 (as used in Bitcoin and Ethereum) and P256 (secp256r1). The "k1" refers to the Kolbitz curve 1 (named after the creator of ECC). With these we have a base point which are can operate on. This is typically defined as \(G\). We can then operate on this with add and multiply operation. For example, \(2G=G+G\) and \(P=n.G\). In this following we will show the base point for a number of common curves, such as secp256r1, P256, Pallas, Curve 25519, BLS12381G1, BLS12381G2, BLS12377G1 and BLS12377G2.
ECDH
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret. We will use Golang and the Krytology library.
Simple ECC on curves
- Public key points for curves. Simple. Display public key points for scalars.
BLS Curve
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
Accumulator and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
Pallas Curve
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
Pairing-based Crypto
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
ElGamal and ECC
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a numerical input.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
Shamir Secret Shares
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Homomorphic Encryption
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Zero knowledge proofs
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
Verifiable Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Hash to scalar and point
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
CP-ABE
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Lattice cryptography

Latice cryptography is proposed as a post-quantum robust method for public key encryption, especially focused on digital signatures and key exchange mechanisms (KEMs).
Principles
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
NTRU
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- Lattice Encryption: NTRU Key Generation Python). NTRU. Outlines how NTRU operates for key generation.
Homomorphic
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Digital Signatures
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
Public-Key Encryption/Key Exchange
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
Light-weight cryptography

While AES and SHA work well together within computer systems, they struggle in an IoT/embedded world as they take up: too much processing power; too much physical space; and consume too much battery power. So NIST outlines a number of methods which can be used for light-weight cryptography, and which could be useful in IoT and RFID devices [1]. They define the device spectrum as:
- Conventional cryptography. Servers and Desktops. Tablets and smart phones.
- Light-weight cryptography. Embedded Systems. RFID and Sensor Networks.
With embedded systems, we commonly see 8-bit, 16-bit and 32-bit microcontrollers, and which would struggle to cope with real-time demands for conventional cryptography methods. And in the 40+ years since the first 4-bit processor, there is even a strong market for 4-bit processors. RFID and sensor network devices, especially, have limited numbers of gates available for security, and are often highly constrained with the power drain on the device.
So AES is typically a non-starter for many embedded devices. In light-weight cryptography, we often see smaller block size (typically 64 bits or 80 bits), smaller keys (often less than 90 bits) and less complex rounds (and where the S-boxes often just have 4-bits).
For light-weight cryptography the main constraints that we have are typically related to ener requirements, gate equivalents (GEs), and timing. With passive RFID devices, we do not have an associated battery for the power supply, and where the chip must power itself from energy coupled from the radio wave. An RFID device is thus likely to be severely constrained in the power drain associated with any cryptography functions, along with being constrained for the timing requirements and for the number of gates used. Even if an RFID device has an associated battery (active RFID), it may be difficult to recharge the battery, so the drain on power must often be minimised.
There is thus often a compromise between the cryptography method used and the overall security of the method. Thus often light-weight cryptography methods balance performance (throughput) against power drain and GE, and do not perform as well as main-stream cryptography standards (such as AES and SHA-256). Along with this the method must also have a low requirement for RAM (where the method requires the usage of running memory to perform its operation) and ROM (where the method is stored on the device). In order to assess the strengths of various methods we often define the area that the cryptography function will use on the device – and which is defined in \(µm^2\). The NIST finalists are defined in this [article]
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- GIFT AEAD. GIFT. GIFT is a light-weight block cipher. It is a (NIST Finalist)
- Elephant. Elephant. Elephant is a light-weight stream cipher. It is a (NIST Finalist).
- TinyJambu. TinyJambu. TinyJambu is a light-weight block cipher. It is a (NIST Finalist)
- Isap AEAD. Isap. Isap is a light-weight block cipher. It is a (NIST Finalist)
- PHOTON-Beetle AEAD. PHOTON-Beetle. PHOTON-Beetle is a light-weight block cipher. It is a (NIST Finalist)
- Romulus AEAD. Romulus. Romulus is a light-weight block cipher. It is a (NIST Finalist)
- Sparkle AEAD. Sparkle. Sparkle is a light-weight block cipher. It is a (NIST Finalist)
- CLEFIA. CLEFIA. CLEFIA is a light-weight block cipher.
- LED. LED. LED is a light-weight block cipher.
- Piccolo. Piccolo. Piccolo is an ultra light-weight block cipher.
- PRESENT. PRESENT. Present is a light-weight block cipher.
- Pyjamask. Pyjamask. Pyjamask is a light-weight block cipher.
- SIMON. SIMON. SIMON is a light-weight block cipher.
- SKINNY. SKINNY. SKINNEY is a light-weight block cipher.
- SPECK. SPECK. SPECK is a light-weight block cipher.
- XTEA. XTEA. XTEA is a light-weight block cipher.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encryption/Decryption. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.
Light-weight crypto (Other)
- Chaskey (MAC). Chaskey. Chaskey is a light-weight MAC function.
- Chaskey (MAC). Chaskey (Python). Chaskey is a light-weight MAC function.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (ASCON)
ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRFF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
Discrete Logs (Solving)

A discrete log problem is in the form of \(g^x \pmod p\) and where we know \(g\) and \(p\) and must solve for \(x\).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Message Authentication Code (MAC)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
HMAC
The following are the tips related to Key-based hashing:
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authentication both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2), Blake2b, SM3 and SHA-3. This page outlines the HMAC-MD5 methods using the Hazmat cryptography layer.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- HMAC (COSE). Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT with HMMAC. Go. In this case we create a CWT token, and sign with an HMAC signature.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- HMAC with Rust. HMAC. HMAC with Rust.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HMAC with OpenSSL. MACs with OpenSSL. HMAC in OpenSSL for a given input value, password and hashing method.
Cipher MACs
The following are the tips related to Key-based hashing:
- MACs with OpenSSL. MACs with OpenSSL. MAC methods implemented in OpenSSL, including CMAC and GMAC.
Key-based hashing
The following are the tips related to Key-based hashing:
- SipHash. Siphash. Siphash is a fast key-based hashing method.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Meow. Meow. Meow is one of the fastest hashing methods.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
Magic Numbers

This pages contains information related to magic numbers in file formats.
Network and File Forensics
- Magic numbers. Magic. This provides information on magic number for file forensics.
Graphics formats
- JPEG Analysis. JPEGs. This provides an analysis of JPEG files.
- GIF Analysis. GIFs. This provides an analysis of GIF files.
- TIF Analysis. TIFs. This provides an analysis of TIF files.
- PNG Analysis. PNGs. This provides an analysis of PNG files.
- BMP Analysis. BMPs. This provides an analysis of BMP files.
- PSD Analysis. PSDs. This provides an analysis of PSD files.
- WMF Analysis. WMF. This provides an analysis of WMF files.
- Adobe Illustrator Analysis. AI. This provides an analysis of AI files.
- Adobe In Design Analysis. INDD. This provides an analysis of INDD files.
- MIDI file. MIDI. This provides an analysis of MID files.
- ICO file. ICO. This provides an analysis of ICO files.
- PS file. PS. This provides an analysis of PS files.
- EPS file. EPS. This provides an analysis of EPS files.
- VSD file. VSD. This provides an analysis of Microsft Visio (VSD) files.
Video and audio formats
- MP3 Analysis. MP3s. This provides an analysis of MP3 files.
- AVI Analysis. AVIs. This provides an analysis of AVI files.
- Flash SWF Analysis. SWFs. This provides an analysis of Flash files.
- Flash FLV Analysis. FLVs. This provides an analysis of FLV files.
- MP4 Analysis. MP4. This provides an analysis of MP4 files.
- MOV Analysis. MOV. This provides an analysis of MOV files.
- WMV Analysis. WMV. This provides an analysis of WMV files.
- WMA Analysis. WMA. This provides an analysis of WMA files.
- JPEG 2000 Analysis. JPEG 2. This provides an analysis of JPEG 2000 files.
- WAV Analysis. WAV. This provides an analysis of WAV files.
Zips, Archives and Library files
- ZIP/Archive Analysis. ZIPs. This provides an analysis of ZIP/Achive files.
- GZ Analysis. GZ. This provides an analysis of GZip files.
- Tar Analysis. Tar. This provides an analysis of TAR files.
- MSI Analysis. MSI. This provides an analysis of MSI files.
- OBJ Analysis. OBJ. This provides an analysis of OBJ files.
- DLL Analysis. DLL. This provides an analysis of DLL files.
- CAB Analysis. CAB. This provides an analysis of CAB files.
- EXE Analysis. EXE. This provides an analysis of EXE files.
- RAR Analysis. RAR. This provides an analysis of RAR files.
- SYS Analysis. SYS. This provides an analysis of SYS files.
- HLP Analysis. HLP. This provides an analysis of HLP files.
- VMDK Analysis. VMDK. This provides an analysis of VMDK files (VMWare Virtual Disks).
- PST Analysis. PST. This provides an analysis of PST files (Outlook Email File).
- JAR Analysis. JAR. This provides an analysis of JAR files.
- SLN Analysis. SLN. This provides an analysis of Microsoft SLN files.
- Class Analysis. Class. This provides an analysis of Java Class files.
- Zlib. Zlib. This provides an analysis of Zlib files.
Documents
- PDF Analysis. PDFs. This provides an analysis of PDF files.
- DOC Analysis. DOCs. This provides an analysis of DOC files.
- RTF Analysis. RTFs. This provides an analysis of RTF files.
- XLS Analysis. XLSs. This provides an analysis of XLS files.
- PPT Analysis. PPTs. This provides an analysis of PPT files.
- MMP File. MMP. This provides an analysis of MMP files.
- DOCX Analysis. DOCX. This provides an analysis of DOCX files.
- XLSX Analysis. XLSX. This provides an analysis of XLSX files.
- PPTX Analysis. PPTX. This provides an analysis of PPTX files.
- MDB Analysis. MDB. This provides an analysis of MDB files.
- Outlook Message Analysis. MSG. This provides an analysis of MSG files.
Disk Image
- Raw disk format. RAW. This provides an analysis of the RAW disk format.
Tests
- File Forensics Test. File Test File Forensics Test.
- File Forensics Test (Fun). File Test (Fun) File Forensics Test.
Presentations
MIRACL Core Library

MIRACL Core is an open source library, and includes a wide range of public key encryption methods. It is especially focused on elliptic curve and pairing-friendly methods, but also supports a wide range of encryption methods, including RSA, AES and hashing. Overall, it can be ported onto a wide range of systems and supports C, C++, Go, Rust, Python, Java, Javascript and Swift. Along with this it supports limited capability devices such as the Arduino infrastructure. The GitHub repository is [here].
BN254
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.

Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- CL Signatures. CL. CL Signatures in Go using MIRACL.
- CL Signatures (advanced pairing). CL. CL Signatures in Go using MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages using MIRACL.
- PS Signatures. PS. Signatures using PS for short signatures using MIRACL.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures using MIRACL.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.

Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
Rust examples
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
NaCl

PyNaCl is a Python port of LibSodium. It integrates the latest cryptography methods, such as AES, XChaCha20, Blake2b and X25519.
Symmetric Key
- Symmetric key. Symmetric key (XChaCha20 and Poly1305). With symmetric key, Bob and Alice have the same key. NaCl uses the XChaCha20 method, and which supports stream encryption (and which does not require padding as a block cipher does, and is also faster than block cipher modes). ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16 byte nonce. XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24 byte nonce. It has a lower propability of nonce misuse than ChaCha20.
- Encryption with a password. Symmetric Key with KDF. In symmetric key, we generate a secret key. This key is typically a random value or generated from a password and a salt value. If we use a password, we typically use a KDF (Key Derivation Function), and which uses a password and a salt value, in order to create a key of a given size. In this case we will use Argon2i, and which is memory resilent.
Hybrid Encryption
- Box. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Hashing
- Hashing and KDF (Argon2 and scrypt). Hashing and KDF. This case we will use PyNaCl (Networking and Cryptography) library, and which is a Python binding to libsodium. We will hash a password using SHA-256 and SHA-512, and also create a KDF (Key Derivation Function) using scrypt and Argon2.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
Ed25519
-
Ed25519. Ed25519. Using Ed25519 for digital signatures.
-
Finding Points on Ed25519. X25519 (Points).
In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 (Key Exchange)
- X25519 + BLAKE2b key-exchange. X25519. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
Curve 25519
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
Node.js

Node.js uses the JavaScript programming langauge as its base, and allows for code to be run on a server, rather than in the browser (such as with pure JavaScript). To run a node.js program, we run "node myfile.js", and use NPM to install libraries.
Symmetric key
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
RSA and public key
- RSA Opt imal Asymmetric Encryption Padding (OAEP) using Node.js. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
ECC Keys
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.

Hashing
- Hashing with node.js (All). Hashing. Hashing with node.js.
- Hashing with node.js (Selection). Hashing. Hashing with node.js.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- ECDSA with node.js. ECDSA. ECDSA with node.js.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
Key exchange
- Diffie-Hellman with node.js (random prime). DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method and uses a randomly generated prime number (press the button to generate a new prime).
- Diffie-Hellman with node.js. DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method. Each time the prime number will be fixed for the DH group selected.
- ECDH with node.js. ECDH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Elliptic Curve Diffie Hellman (ECDH) key exchange method.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
Key derivation
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
CryptoJS
- CryptoJS (in node.js). CryptoJS (Node.js). Various crypto methods in the browser.
Bulletproofs
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
Blockchain
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
Proxy encryption
- Proxy Encryption - Encrypting With Public Key, And Decrypt with Private Key. Proxy01. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This page just creates a key pair for Alice, and uses it to encrypt with the public key , and decrypt with the private key.
- Proxy Encryption. Proxy02. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This will go through the full use case of proxy re-encryption.
Tokens
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
Random
- Fortuna with node.js. Fortuna. Fortuna random numbers with node.js.
Other
- FPE with node.js. FPR. FPE with node.js.
- Puny with node.js. Puny. Puny character format with node.js.
Accumulators and Witnesses
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
PGP
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Password Entropy
- Password Entropy with Node.js. Password Entropy. Password entropy measures the strength of a password, and is measured as the number of bits which could represent all of the possibilities. An entropy score of less than 25 identifies a poor password, and between 25 and 50 is a weak password. For 50 to 75 we have a reasonable password, and between 75 and 100 is a very good password. Over 100 is an excellent password. The strength of the password relates to the number of characters used, and also the number of characters in the password.
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
- Homomorphic Encryption with Node.js and BGV. Homomorphic Encryption with Node.js and BFG. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BGV method.
Oblivious Transfer (OT)

Oblivious Transfer allows Bob to select data from Alice, but for Alice not to know which value has been selected.
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
OpenSSH

OpenSSH supports the usage of the SSH protocol. This allows for a remote login. One tool which is uses is ssh-keygen, and which allow for the generation of RSA, DSA and elliptic-curve keys that. These can be used for user and host authentication, such as for GitHub login and Cloud instance login.
OpenSSH
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here].
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
Outline

OpenSSL

OpenSSL is a standard library that implements cryptography.
Symmetric key (Command line)
-
Symmetric Key Encryption (OpenSSL 1.x) [here]. In this case we will create cipher text from OpenSSL 1.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 1.x) [here].In this case we will decrypt cipher text from OpenSSL 1.x using a key derived from a password
-
Symmetric Key Encryption (OpenSSL 3.x) [here]. In this case we will create cipher text from OpenSSL 3.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 3.x) [here].In this case we will decrypt cipher text from OpenSSL 3.x using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password.
Hashing
-
Hashing [here] OpenSSL supports a wide range of hashing methods including BLAKE2b, Gost, MD4, MD5, RMD-160, SHA-1, SHA-3, SHA-256 and SHA-512.
Libre OpenSSL
-
Symmetric Key Encryption using Libre OpenSSL [here]. In this case we will create cipher text from Libre OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption using Libre OpenSSL [here]. In this case we will decrypt ciphertext from Libre OpenSSL using a key derived from a password.
-
Hashing [here] Libre OpenSSL supports a wide range of hashing methods including Gost, MD4, MD5, RMD-160, SHA-1, SHA-256 and SHA-512.
Diffie-Hellman parameter generation
-
DH Parameters with OpenSSL [here]. The Diffie-Hellman (DH) method is perhaps one of the greatest inventions in Cybersecurity, and was created by Whitfield Diffie and Marty Hellman. With the DH method, Bob creates a random value (\(b\)) and Alice also creates a random value (\(a\)). Next Bob computes \(B=g^b \pmod p\) and sends it to Alice. Alice computes \(A=g^a \pmod p\) and sends this to Bob. Bob raises the value of \(A\) to the power of \(b\) and takes \(\pmod p\), and Alice raises \(B\) to the power of \(a\) and takes \(\pmod p\). In the end, they will have the same shared value: \(g^{ab} \pmod p\). This can then be used to derive an encryption key that they can use for a secure tunnel. Overall, \(p\) is the large prime number, and also known as the shared modulus between Bob and Alice.
Key derivation function
-
PBKDF2 key derivation with OpenSSL [here] PBKDF2 (Password Key Derivation Function 2) is a key derivation method. Overall it is relatively slow in its operation and where we take a password, a salt value, hashing method, and a number of iterations, in order to produce a given size of encryption key.
-
HKDF key derivation with OpenSSL [here] HKDF (HMAC Key Derivation function) is used to derive an encryption key from a pass phrase. Initially HKDF creates a pseudorandom key (PRK) using a pass phrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), andalong with a salt value. Next the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys.
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Passwords
-
Password example [here]. This page uses the OpenSSL library hash password generator, which is used in UNIX systems for the hashing of passwords which are contained in /etc/shadow and /etc/passwd. For newer passwords, the "-1" options is used to created the hashed value.
-
Hashed passwords with OpenSSL [here].
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
Public key
-
Generating an ECC key pair with OpenSSL [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)).
-
Generating an RSA key pair with OpenSSL [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2).
-
Generating an RSA key pair with OpenSSL with encryption [here]. This page implements RSA key pair generation with an encrypted key pair. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). In this case we will encrypt the key pair with either 3DES, 128-bit AES, 192-bit AES or 256-bit AES. The same password must be used to encrypt and decrypt.
-
Generate prime with OpenSSL [here]. Prime numbers are important in public key encrytion, and are used with RSA and ECC. For RSA, we generate two prime numbers (\(p\) and \(q\)) and which are multiplied together to create a modulus (\(N\)). If these prime numbers have 512 bit values, the modulus will be a 1,024 bit value. This defines the basic secure of RSA. With elliptic curve we use smaller prime numbers, such as 256-bit values for the secp256k1 curve.
ASN1 parsing
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). We will parse using asn1parse, and reveal the parameters.
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)) [RSA key pair]. We will parse using asn1parse, and reveal the parameters.
- DSA Parameters with asn1parse. DSA parameters with OpenSSL with asn1parse. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA (Digital Signature Algorithm)
- DSA Parameters. DSA parameters with OpenSSL. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
MAC (Message Authentication Code)
- HMAC with OpenSSL. MACs with OpenSSL. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authenticate both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2) and SHA-3. In this case we will use OpenSSL to generate the HMAC value.
- MACs with OpenSSL. MACs with OpenSSL. In the following we will generate MACs for HMAC, GMAC, CMAC, Blake2bmac, Blake2smac, KMAC128 and KMAC256. Overall, we will use an encryption key defined as a hex value for GMAC and CMAC, and a pass phrase for the others. The message is "hello".
Signing
- Digital signing a plaintext message with OpenSSL. Signing with OpenSSL. With digital signing, we can take a message, and create a signature. This normally involves signing with a private key and digital certificate. The signed message can be an a MIME format, and which can be integrated into an email message. In this can we have a 512-bit RSA key pair that will sign a plain text message.
Encrypting emails
- Encrypting an email message in OpenSSL. Encrypting messages with OpenSSL. With public key encryption, we can take a message, and encrypt it with the recipiant's public key. In this can we have a 512-bit RSA public key to encrypt a message.
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Random number generation with OpenSSL
-
Random number generator [here]. Random numbers are important in generating encryption keys and salt values. In this case OpenSSL generates a random number (in a Base64 format) for a given number of bytes.
Outline (C#/Python)
-
Symmetric Key Encryption (C#) [here]. This page uses the OpenSSL library through a C#/.NET wrapper. The DLLs it interfaces to are libeay32.dll and ssleay32.dll. OpenSSL supports a wide range of encryption methods, including 128-bit AES, 192-bit AES, 256-bit AES and Blowfish (bf). Different modes of ECB, CBC, and OFB are implemented. The examples use a default IV of "1234".
-
AES in Python with OpenSSL output [here]
-
Producing OpenSSL AES Encrypted String from C# [here]
Digital Certificates
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
Paillier - Partial Homomorphic Encryption

The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Fundamentals
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier).
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Using RSA
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
Applications
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Curve 25519 in Python. Barebones Curve 25519. This page implements Curve 25519 in pure Python.
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
- Curve 25519 in Python (Test Vectors from RFC 7748). Barebones Curve X25519. This page implements Curve 25519 in pure Python and tests against the IETF test vectors.
- Curve 25519 ECDH in Python (Test Vectors from RFC 7748). Barebones Curve X25519. This page implements Curve 25519 ECDH in pure Python and tests against the IETF test vectors.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 . EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
NaCl
Cyber&Data

This is the home page for the Cyber & Data course. There are four main units involved. Units 1 and 2 are self-study, but you can register for Units 3 and 4, and study towards an MSc module. Some unique features include: On-line Python integration, On-line Intrusion Detection Editor, Splunk Data Analysis, and Machine Learning Environment for Splunk. The Splunk elements of the course require a login (contact [email protected] for a login).
Unit 1: Fundamentals
- 1. Cyber and Intelligence. This topic provides an introduction to Cyber and Intelligence.
- 2. Defence Systems, Policies and Risk. This topic provides an overview of the some of the core defence mechanisms and risk approaches.
- 3. Open Source Intelligence. This topic outlines the usage of open source intelligence including using Shodan, Redit and Twitter mining.
- 4. So What is Data? This topics outlines the core data formats using in cybersecurity, and introduces the concept of magic numbers within files.
Unit 2: Data Capture and Analysis
- 5. Memory, Big Data and SIEM. This topic outlines some of the core principles used around Big Data methods and in the integration of SIEM (Security Information and Event Management).
- 6. Network Forensics. This topic provide fundamental knowledge in how networks works, and how we can analyse different network protocols, including ARP, IP, TCP, FTP and HTTP.
- 7. Intrusion Detection Systems. This topic outlines the usage of IDS and applies with using Snort.
Unit 3: Data Science and Cyber
- 8. Classification Metrics and ML.
- 9. Introduction to Data Science.
- 10. NumPy and Pandas. An outline of the integration of Numpy and Pandas for datasets.
- 11. Similarity and Matching. This unit outlines some of the key methods used within similarity and matching of text data. This includes the application of regular expressions, similarity metrics and similarity hashes.
Unit 4: Data Applications and Machine Learning
- 12. Splunk. An introduction to Splunk.
- 13. Splunk (Charting and Analysis). An introduction to Splunk with Charting and Analysis.
- 14. Machine Learning (Core Methods). An outline of the core methods.
- 15. Application of Machine Learning. A tutorial in applying ML with Splunk
Unit 5: Cyber Applications
- 16. Face Recognition. Implementation of face recognition.
DES, 3DES and Feistel ciphers

With DES and 3DES we have a 56-bit or 112-bit encryption key, respectively. Both are block ciphers and based on the Feistel ciphers, with a 64-bit block size.
Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- 3DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using 3DES encryption with Powershell.
- Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . With 3DES encryption, we use a 128-bit key and a 64-bit IV value. The two modes supported are ECB (without salt) and CBC (with salt). The DES algorithm has been around for a long time, and the 56-bit version is now easily crackable (in less than a day on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases, and splits the key into two. Overall the key size is typically 112 bits (with a combination of the three keys - of which two of the keys are the same). In this case we will use PKCS7 padding, and which fills the input data with a value that is equal to the number of padding bytes. Overall, DES has a 64-bit block size, and which equates to eight ASCII characters.
DES
The following are the tips related to DES, 3DES and Feistel ciphers:
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
Diffie-Hellman Key exchange (Discrete Logs)

Key exchange is a way for Bob and Alice to communicate and for them to agree on a shared secret. The original method defined uses discrete logarithms (Diffie-Hellman). With the Diffie-Hellman method, Alice generates \(a\) and shares \(A=g^a \pmod p\) with Bob. Bob generates \(b\) and shares \(B=g^b \pmod p\). Alice raises \(B\) to the power of \(a\), and Bob raises \(A\) to the power of \(b\). They should both end up with the same secret: \(K=g^{ab} \pmod p\).
Key interchange/generation (Diffie-Hellman)
The following relates to key interchange:
- Diffie-Hellman. Diffie-Hellman Calculation. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Real example). Diffie-Hellman Real. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Python). Diffie-Hellman. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (pre-compute). Diffie-Hellman (pre-compute). Many sites use the same prime numbers, which can then be cracked with a pre-computing attack.
- Selecting \(g\) in Diffie Hellman. G in Diffie Hellman. Picking a safe value of the generator \(g\) in discrete logarithms.
- Diffie-Hellman (Man-in-the-middle). DF. This outlines the man-in-the-middle method for Diffie-Hellman.
- An Alternative Diffie-Hellman method. Alterative DH. This outlines an alternative Diffie-Hellman method.
- Selecting g in discrete logs. g in discrete logs. This select a generator in discrete logs.
- Selecting g in discrete logs with random primes. g in discrete logs with random primes. This select a generator in discrete logs using random prime numbers which are define by a number of bits.
Authenticated Key Exchange
The following are the tips related to Key derivation hashing:
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- MTI/A0. MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{ax+by} \pmod p\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0. MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{x+y} \pmod p\)
- MTI/C0. MTI/C0. This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{xy} \pmod p\)
- MTI/C1. MTI/C1. This outlines MTI/C1, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{abxy} \pmod p\).
- HMQV (Menezes–Qu–Vanstone). HMQV. HMQV builds on MQV and adds the identity of Bob and Alice.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
Diffie-Hellman Parameter Generation
-
DH Parameters with OpenSSL [here]. With the Diffie-Hellman (DH) we use the form of \(g^x \pmod p\), and where \(g\) is the generator and \(p\) is a large prime number. In order to implement DH, we create either a generator value of 2 or 5, and then select a prime number which works with this generator value. In real-life we would generate a prime number of at least 2,048 bits. A command of "openssl dhparam -2 512" creates a random prime number with 512 bits and which works with a generator of \(g=2\).
Digital Certificates

Trust centres are responsible for storing private and/or public keys, and digital certificates are used to store and distribute private and/or public keys.
Trust Centres
- Simple Key Distribution Centre. KDC. This implements a simple KDC.
- Kerberos. Kerberos. This will implement a Kerberos method of generating a shared key.
Key Pair Generation and Code Signing Requests
The following are the tips related to digital certs:
- Generating key pair. View. This defines creating a 512-bit keypair.
- Code Signing Request (CSR). View. This defines the reading the CSR.
- Code Signing Request (CSR) with Python. View. This defines creating a CSR using Python.
Creating Digital Certificates
The following are the tips related to digital certs:
- Digital Certificate Digital Cert.
- Digital Certificate (PFX) Digital Cert.
- Certificate with Public/Private key. Cert. This includes the creation of the digital certificate.
- Generate X.509 certificate and key pair using Golang. X.509. This generates an X.509 certificate and shows the details.
- X.509 certificates in JavaScript. RSA and ECDSA Signed certificates. This page will generate either RSA and ECC key pairs, and then generate X.509 certificates, using either a signature of SHA1withRSA or SHA256withECDSA. For RSA signing we use an RSA private key to sign the certificate, and with ECDSA signing we use an ECC private key to sign the certificate.
Digital Certificate Format
The following are the tips related to digital certs:
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Certificate cracking
The following are the tips related to digital certs:
- Cracking certificates. Crack. This defines the cracking of digital certificates.
SSL
The following are the tips related to digital certs:
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Certificates (OpenSSL). View. This defines the viewing of digital certificates.
Theory
- Encryption Principles: [View]
- Proving identity and examining certificates: [View]
- Validating entities: [View]
DSA (Digital Signature Algorithm)

The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA with OpenSSL
- DSA Parameters. DSA parameters with OpenSSL. This page outlines the creation of a keypair for DSA signatures.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
DSA with PowerShell
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA and Node.js
- Key pair using Node.js. DSA and other keypairs. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
DSA and C#
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
DSA and OpenSSH
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
DSA Signatures with Hazmat
-
DSA Signatures. DSA Signatures. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. The ECDSA method is an extension of DSA, but implemented with elliptic curve (EC) methods. As with most public key signing methods, we take a hash of a message, and then apply a private key to create a signature (\(r,s\)). This is done by creating a random value (\(k\)) to produce the signature. The signature is then verified using the associated public key. This then verifies the creator of the signature and that the message has not been changed.
Outline
So, what does a digital signature look like? Well, it often has an r value and an s value: (r,s). So, let’s look at the DSA (Digital Signature Algorithm) signature. For this, Figure 1 shows an outline of the setup of the DSA signature, and where Bob uses his private key (sk) to sign a hash of a message, and Alice proves with his public key (pk,g,p,q). We also use a random nonce value (k) for the signature, and we must take care that we do not reuse the value.

Figure 1: DSA signature
Initially, Bob creates two prime numbers (\(p\) and \(q\)) and generates a generator value of \(g\). Next, he generates his secret key (\(x\)) and then computes his public key:
\(Y=g^{x} \pmod p\)
To create a signature for a message (\(M\)), he creates a random value (\(k\)) and then computes two values for the signature:
\(r = g^{k} \pmod{p} \pmod{q}\)
\(s=(k^{-1}.(H(m)+x.r)) \pmod {q}\)
When Alice receives this signature, she takes Bob's public key \((p,q,g,Y)\) and the message can computes:
\(w = s^{-1} \pmod q\)
\(u_1 = H(M).w \pmod q\)
\(u_2 = r.w \pmod q\)
\(v = (g^{u_1} . y^{u_2}) \pmod {p} \pmod {q}\)
She then checks that \(v\) is equal to \(r\). If so, the signature checks out. This works because:
\(v = g^{h.w}.y^{r.w} = g^{h.w}.g^{x.r.w} = g^{h.w+x.r.w} = g^{h/s+x.r/s} = g^{(H+x.r)/(k^{-1}(H+x.r))} = g^k = r\)
Elliptic Curve Cryptography (ECC)

With elliptic curve methods, we take a base point (\(G\)) and then use a private key (\(n\)) to produce a public key point (\(nG\)).
Elliptic Curve (Points)
The following are the tips related to ECC:
- ECC types and nG. ECC types and nG. Outlining the parameters used for ECC types (eg Curve 25519, Curve 448 and secpt256k1).
- First 100 Elliptic Curve points in Finite Field. Elliptic Curve points. Locating the first 100 points in an elliptic curve in a finite field.
- Elliptic Curve - Point addition. Elliptic Curve Point Addition. This shows the addition of two points on an elliptic curve.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field.
- First 20 Elliptic Curve points in Finite Field (improved method). Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field.
- First 20 Elliptic Curve points in Finite Field (plot). Elliptic Curve points (plot). Locating the first 20 points in an elliptic curve in a finite field.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field for common curves with Libnum. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256 and using Libnum to compute the quadratic square.
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- ECC double-and-add for point multiplication. Elliptic Curve double-and-add. Calculation of \(aG\) using a double-and-add approach (and which is equivalent to square-and-multiply in exponential functions.
- ECC key generation with Hazmat. Elliptic Curve key gen. Creating ECC keys using Hazmat and Python.
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining \(n.G\) for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Operations Within a Solidity Contract. Go.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Embedding data in an ECC point
- Embedding data in a point. Go. With Elliptic Curve Cryptography (ECC), we use points on an elliptic curve to represent our data. These are defined with (x,y) points. With this, it is possible to embedded a certain amount of data into the point - as long as it still gives us a valid point on the curve. This example will Curve 25519 to embed data, and is achieved by storing the length of the data in a single byte in the point, and then store the data as byte values in the point (followed by random data). To decode, we can then just read the first byte for the length of the message, and then reveal the data encoded into the point..
Quadratic residues
- Quadratic residue (mod p). Go. Outline of quadratic residue \(\pmod p\).
Elliptic Curve (ECDH) - Python
The following are the tips related to ECC:
- Elliptic Curve. Elliptic Curve. Elliptic Curve is a public key method which can also be used to generate a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with simple parameters. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
Elliptic Curve (ECDH) - Golang and Node.js
The following are the tips related to ECC:
- ECDH with Go. ECDH. ECDH with Go.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with node.js. ECDH. ECDH with node.js.
- ECDH with JavaScript. ECDH. Elliptic Curve Diffie Hellman.
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret. We will use Golang and the Krytology library.
Elliptic Curve (Signatures - ECDSA)
The following are the tips related to ECC:
- ECDSA and EdDSA methods. ECDSA and EdDSA. This outlines ECDSA and EdDSA for NIST, secp, brainpool and Ed448/Ed25519.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with secp256k1. ECDSA (secp2561k1). Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with secp256k1.
- ECDSA using P256. Barebones ECDSA with P256. This page implements ECDSA with the NIST P256 curve.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces and using Lenstra–Lenstra–Lovász (LLL) method. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA with Hazmat. ECDSA wih Hazmat. This outlines ECDSA with Hazmat.
- Blinded ECDSA. Blinded ECDSA. With a blinded signature, Bob can sign for a message, without knowning what the message is. In this case Alice will create a blinded ECDSA signature, and where Bob can then sign it, and then Alice can unblind it. The method is based on one produced by Oleg Andreev for blinding signatures in Bitcoin.
- ECDSA: Fault Attack. ECDSA: Fault Attack. In the fault attack in ECDSA we only require two signatures. One is produced without a fault \((r,s)\), and the other has a fault \((r_f,s_f)\). From these we can generate the private key.
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
Elliptic Curve (DER)
The following are the tips related to ECC:
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Elliptic Curve (Signatures - EdDSA)
The following are the tips related to ECC:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. X448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Ed25519 for EdDSA signatures with Hazmat. EdDSA: Ed25519. This page uses the Hazmat primitives for the cryptography library.
- Ed25519 signature using NaCl. Ed25519. This page uses the NaCl port from libsodium.
- Ed25519 points using NaCl. Ed25519. This page uses the NaCl port from libsodium to determine Ed25519 points.
Elliptic Curve (Plots)
The following are the tips related to ECC:
- Elliptic Curve (Plot). Elliptic Curve (Plot). Elliptic Curve is a public key method which can also be used to generate a shared key. This page outlines a graphic of the curve.
- Elliptic Curve (Real plots). Elliptic Curve (Real plot). This provides a range of well-defined elliptic curve plots.
Elliptic Curve (Keys)
The following are the tips related to ECC:
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
Elliptic Curve (ECIES)
The following are the tips related to ECC:
- Elliptic Curve Integrated Encryption Scheme (ECIES with Rabbit Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with Rabbit (a light-weight stream cipher).
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
Elliptic Curve (Hash to curve)
The following are the tips related to ECC:
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve with libnum.
- Hash to password with Go. Hash to password. Hash to password with Go.
- Match random value to sepc256k1 with Python. Random value to curve. This involves generating a random value, and then finding the nearest valid point on the curve. It involves incrementing a value of \(x\) until we reach a valid point.
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
Elliptic Curve (Point adding)
The following are the tips related to ECC:
- Elliptic Curve (Point Adding). Elliptic Curve. Creating 2P from P.
- Elliptic Curve (Point Adding with real curves). Elliptic Curve. Creating 2P from P with real curves (eg Curve 25519).
- Elliptic Curve (Calculating nP - ECC Calculator). Elliptic Curve. Creating nP from P with real curves.
- Elliptic Curve (Point addition - ECC Calculator). Elliptic Curve. This calculator adds two points on an elliptic curve.
- Elliptic Curve (Point addition - ECC Calculator - range of points). Elliptic Curve. This calculator takes one point on the elliptic curve, and then adds the other the other points on the curve to see the result.
Elliptic Curve (Curve 25519)
The following are the tips related to ECC:
- Curve 25519 with Go for test vectors. ECC. This does a test on some private keys to test the public key generation.
- Curve 25519 with Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Curve25519 with Python. Curve25519. This outlines Curve25519, which is used in the Tor network.
- Curve25519 with point adding Python. Curve25519. This outlines Curve25519 using basic point adding.
ElGamal and ECC
- ElGamal with ECC. ElGamal with ECC. ElGamal using ECC.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
- Proving an Encrypted Shuffle With ElGamal and ECC. Shuffle. An encrypted shuffle with ElGamal.
Elliptic Curve (X448)
The following are the tips related to ECC:
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Python. X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH using Python and based on RFC 7748.
Elliptic Curve (ElGamal)
The following are the tips related to ECC:
- Proving an Encrypted Shuffle With ElGamal and ECC. Shuffle. An encrypted shuffle with ElGamal.
- ElGamal with ECC. ElGamal with ECC. ElGamal using ECC.
Elliptic Curve (Pedersen Commitment) and DLEQ
The following are the tips related to ECC:
- Elliptic Curve - Blinding factor (Pedersen Commitment). Elliptic Curve Blinding. This shows the addition of transactions with a blinding factor.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
Elliptic Curve (Box and Encryption)
The following are the tips related to ECC:
Go ECC
- Hash to password with Go. Hash to password. Hash to password with Go.
- ECDH with Go. ECDH. ECDH with Go.
- Box with Go. Box. Box with Go.
- ECC with Go. ECC. ECC with Go.
- Curve 25519 with Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ElGamal with ECC. ElGamal with ECC. ElGamal using ECC.
- Curve 25519 with Go for test vectors. ECC. This does a test on some private keys to test the public key generation.
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Barebones Ed25519 with Go. ECC. This shows point addition and scalar multiply in Ed25519
- Barebones NIST P256 with Go. ECC. This shows point addition and scalar multiply in P256
Key exchange
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). The resultant key is \(xyG \)
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
- Authenticated Key Exchange (ECC). YAK. Key exchange with public keys and uses elliptic curve methods.
IBE
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
Barebones ECC
- P192 in Python. Barebones P192. This page implements P192 in pure Python.
- P224 in Python. Barebones P224. This page implements P224 in pure Python.
- P256 in Python. Barebones P256. This page implements P256 in pure Python.
- P521 in Python. Barebones P521. This page implements P521 in pure Python.
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
- Curve 25519 in Python. Barebones Curve 25519. This page implements Curve 25519 in pure Python.
- Curve 25519 in Python (Test Vectors from RFC 7748). Barebones Curve X25519. This page implements Curve 25519 in pure Python and tests against the IETF test vectors.
- Curve 448 in Python (Test Vectors from RFC 7748). Barebones Curve X448. This page implements Curve 448 in pure Python and tests against the IETF test vectors.
- Curve 25519 ECDH in Python (Test Vectors from RFC 7748). Barebones Curve X25519. This page implements Curve 25519 ECDH in pure Python and tests against the IETF test vectors.
- Curve 448 ECDH in Python (Test Vectors from RFC 7748). Barebones Curve X448. This page implements Curve 448 ECDH in pure Python and tests against the IETF test vectors.
- ECDSA using P256. Barebones ECDSA with P256. This page implements ECDSA with the NIST P256 curve.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 . EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
Others
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.

Public Key (Elliptic Curve) in Rust
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Sage
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
Elliptic Curve Diffie-Hellman (ECDH)

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as secp256k1 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) - Python
The following are the tips related to ECC:
- Elliptic Curve Diffie-Hellman (ECDH) with simple parameters. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
- ECDH and COSE. Go. In this case we create a symmetric key from ECDH. For this we will derive a shared key from the public key of Alice and Bob, and then define a single recipient which can derive the CEK (Content Encryption Key) using their private key. We will use the curves of P-256 (secp256r1), P-384 (secp384r1), P-521 (secp521r1) or SECP256K1 (as used with Bitcoin).
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Go. ECDH. ECDH with Go.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret. We will use Golang and the Krytology library.

Elliptic Curve (ECDH) - Node.js
The following are the tips related to ECC:
- ECDH with node.js. ECDH. ECDH with node.js.
- ECDH with JavaScript. ECDH. Elliptic Curve Diffie Hellman.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Key exchange

- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). The resultant key is \(xyG \)
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
- Authenticated Key Exchange (ECC). YAK. Key exchange with public keys and uses elliptic curve methods.
ECDSA (Elliptic Curve Digital Signature Algorithm)

ECDSA has been around for over two decades and was first proposed in [1]. The ECDSA method significantly improved the performance of signing messages than the RSA-based DSA method. Its usage of elliptic curve methods speeded up the whole process and supported much smaller key sizes. Its crown and glory were being selected by Satoshi Nakamoto for his Bitcoin protocol, and then its adoption into Ethereum.
ECDSA Basics
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Recoving the public key from an ECDSA Signing in Python. Recoving public key from ECDSA Signing. This is an example of recovering the public key from the ECDSA signature with Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\)).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\)) and will check that the signature is valid.
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
-
ECDSA for Multiple Curves and Different Hashing Methods with Python
. ECDSA for Multiple Curves and Different Hashing Methods with Python. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
- ECDSA Signatures with Hazmat (SECP256R1, SECP384R1, SECP521R1, SECP224R1, SECP192R1, and SECP256K1). ECC Signatures. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and then creates an ECDSA signature for a given message.
- DSSE (Dead Single Signature Envelopes). DSSE. The Update Framework (TUF) provides a framework to secure the software within a system, while in-toto ("as-a-whole") can be used to protect the whole of software support chain. TUF thus delivers updates to a system while in-toto manages a complete software infrastructure. For this, it uses the Metablock format, and where we do not sign the byte values for the signature but sign the JSON data. This is known as canonicalisation - and which is the conversion of data in different forms to a standardised format.
Elliptic Curve (DER)
The following are the tips related to ECC:
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Google Tink with ECDSA
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
ECDSA Applications
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Blinded ECDSA. Blinded ECDSA. With a blinded signature, Bob can sign for a message, without knowning what the message is. In this case Alice will create a blinded ECDSA signature, and where Bob can then sign it, and then Alice can unblind it. The method is based on one produced by Oleg Andreev for blinding signatures in Bitcoin.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA: Fault Attack. ECDSA: Fault Attack. In the fault attack in ECDSA we only require two signatures. One is produced without a fault \((r,s)\), and the other has a fault \((r_f,s_f)\). From these we can generate the private key.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Elliptic Curve Integrated Encryption Scheme (ECIES)

With ECIES we integrate the power of elliptic curve (EC) public key encryption with symmetric key encryption. An outline of the method is:

Elliptic Curve (ECIES)
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Elliptic Curve Integrated Encryption Scheme (ECIES with Rabbit Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with Rabbit (a light-weight stream cipher).
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
Applications
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- ECIES (Kryptology). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Coinbase Kryptology library.
- ECIES (CIRCL). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Cloudflare CIRCL library.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
Ethereum crypto
- ECIES with Go-Ethereum. Go.
EdDSA, Ed25519 and Ed448

Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). EdDSA (Edwards-curve Digital Signature Algorithm) is a fast and efficient digital signature method, and is based on the Schnorr signature scheme. Two important curves that are implemented with EdDSA are Curve 25519 (X25519) and Curve 448 (Ed448). EdDSA has been standardized in [RFC 8032]. With EdDSA, Alice generates a private key of \(sk\) and a public key of \(P=sk.G\) and where \(G\) is the base point of the curve.
Elliptic Curve (Signatures - EdDSA)
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Ed25519 in Python. EdDSA in Python. This page implements EdDSA using the Pure25519 library and with the core functions of key generation, signature generation and signature verification.
- Ed25519 Vulnerability in Python. EdDSA Vulnerability in Python. This page implements EdDSA using the Pure25519 library and with the core functions of key generation, signature generation and signature verification.
- Ed25519 Vulnerability in Python (Proof of Concept). EdDSA Vulnerability in Python (PoC). This page implements EdDSA using the Pure25519 library and with the core functions of key generation, signature generation and signature verification.
Hazmat (Ed448 and Ed25519)
- Ed25519 for EdDSA signatures with Hazmat. EdDSA: Ed25519. This page uses the Hazmat primitives for the cryptography library for X25519.
- Ed448 for EdDSA signatures with Hazmat. EdDSA: Ed25519. This page uses the Hazmat primitives for the cryptography library for X448
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
Golang
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
- Barebones Ed25519 with Go. ECC. This shows point addition and scalar multiply in Ed25519
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
COSE/COBR
- EdDSA. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) [2] can then build on this to includes signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case, we will use EdDSA to create a signature for a message.
Testing Ed25519
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
NaCl
- Ed25519 signature using NaCl. eddsa. This page uses the NaCl port from libsodium.
- Ed25519 points using NaCl. eddsa. This page uses the NaCl port from libsodium to determine Ed25519 points.
Theory
With EdDSA, Alice will sign a message with her private key, and then Bob will use her public key to verify that she signed the message (and that the message has now changed):

Key generation
Alice generates a random 32-byte secret key (\(sk\)) and then creates a public key of:
\(pk=sk \cdot G\)
and where \(G\) is the base point of the curve.
Signing
Alice creates a SHA-512 hash of her private key:
\(h=\textrm{HASH}(sk)\)
Create \(r\) from the upper 32 bytes of hash and the message:
\( r = \textrm{HASH}(h[32:] \: || \: m))\)
And where "||" represents a concatenation of the byte array values. Next she matches \(r\) onto curve with:
\(R=r \cdot G\)
Next Alice computes \(s\) with:
\(s=r + (\textrm{HASH}(R \: || \: pk \: || \: m)) \cdot sk\)
The signature is (\(R,s\)). The values of \(R\) and \(s\) are 32 bytes long, and thus the signature is 64 bytes long.
Verifying
Bob creates \(S\) using \(R\), \(pk\) and \(m\):
\(S =\textrm{HASH}(R \: || \: pk \: || \: m) \)
And next creates two verification values:
\(v_1=s \cdot G\)
\(v_2=R+ pk \cdot S\)
If \(v_1==v_2\) the signature checks. This is because:
\(
\begin{align}
v_1&=s.G\\
&= (r + (\textrm{HASH}(R \: || \: pk \: || \: m)) \cdot sk) \cdot G \\
&= rG + sk \cdot G \cdot (\textrm{HASH}(R \: || \: pk \: || \: m)) \\
&= R+ pk \cdot S \\
&= v_2
\end{align}
\)
ElGamal

Public key encryption is typically used to sign for things (and where we use the private key to encrypt something and prove this with the public key) and within key exchange methods. The core methods used are RSA and Elliptic Curve. But an alternative is to use discrete logarithms. One of the most interesting is ElGamal, and was created by Taher Elgamal in 1985.
ElGamal Method
- ElGamal. ElGamal. ElGamal is a public key method which uses discrete logarithms.
- ElGamal in Python. ElGamal in Python. ElGamal is a public key method which uses discrete logarithms.
- ElGamal in Python with variable prime sizes. ElGamal in Python for different prime sizes. ElGamal is a public key method which uses discrete logarithms.
- Selecting g in ElGamal. G in ElGamal. ElGamal is a public key method which uses discrete logarithms.
- Selecting g in discrete logs. g in discrete logs. This select a generator in discrete logs.
- Selecting g in discrete logs with random primes. g in discrete logs with random primes. This select a generator in discrete logs using random prime numbers which are define by a number of bits.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- Proving an Encrypted Shuffle With ElGamal and ECC. Shuffle. An encrypted shuffle with ElGamal.
- ElGamal encryption with Powershell. ElGamal encryption.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Commutative Encryption
- Commutative Encyption (Modified ElGamal). Commutative Encyption. Commutative Encyption allow Bob and Alice to encrypt a message, and then for the data to be decrypted usign any order of the keys.
ElGamal Signature
- ElGamal signatures. ElGamal. ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this.
- ElGamal signatures (alterative signing). ElGamal (Signing: s=ar + kh(m)). ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this. Normally we sign with \(s=k^{-1} (h(m)-ar) \pmod {p-1}\), but in this case we will use \(s=ar + kh(m))\).
- ElGamal signatures (alterative signing). ElGamal (Signing: s=ah(m) + kr). ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this. Normally we sign with \(s=k^{-1} (h(m)-ar) \pmod {p-1}\), but in this case we will use \(s=ah(m) + kr\).
- ElGamal signatures (alterative signing). ElGamal (Signing: r=as+kh(m)). ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this. Normally we sign with \(s=k^{-1} (h(m)-ar) \pmod {p-1}\), but in this case we will use \(r=as+kh(m)\).
- ElGamal signatures (alterative signing). ElGamal (Signing: r=ah(m) +ks). ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this. Normally we sign with \(s=k^{-1} (h(m)-ar) \pmod {p-1}\), but in this case we will use \(r=ah(m) +ks\).
- ElGamal encryption with Go. ElGamal. This implements ElGamal encryption.
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
ElGamal Homomorphic Encryption
- ElGamal Homomorphic Cipher for Multiplication (Python). ElGamal. This outlines ElGamal Homomorphic multiplication with Python.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (Python). ElGamal. This outlines ElGamal Homomorphic division with Python.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (Python). ElGamal. This outlines ElGamal Homomorphic addition with Python.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (Python). ElGamal. This outlines ElGamal Homomorphic subtraction with Python.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
- ElGamal Homomorphic Cipher (Go). ElGamal. This outlines ElGamal Homomorphic cipher with Go.
- ElGamal Homomorphic Cipher (Go) - Divide. ElGamal. This outlines ElGamal Homomorphic cipher with Go with divide.
- ElGamal Homomorphic Cipher (Go) - Additive. ElGamal. This outlines ElGamal Homomorphic cipher with Go with addition.
ElGamal and ECC
- ElGamal with ECC. ElGamal with ECC. ElGamal using ECC.
- Proving an Encrypted Shuffle With ElGamal and ECC. Shuffle. An encrypted shuffle with ElGamal.
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- ElGamal - Applying Multiple Public Key Operations (ECC). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use elliptic curve methods, and using the Edwards 25519 curve.
ElGamal (Authenticated and Verified Encryption)
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenticated ciphertext.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
ElGamal (Encrypting with multiple public keys)
- ElGamal - Applying Multiple Public Key Operations (Discrete Logs). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use discrete logs.
- ElGamal - Applying Multiple Public Key Operations (ECC). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use elliptic curve methods, and using the Edwards 25519 curve.
Ethereum

This page outlines some examples of blockchain and cryptocurrency.
Test Network
- Math functions on Local Network. Go.
- Math functions on Test Network. Go.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- Storing State in a Smart Contract. Go.
- Deleting Data From A Smart Contract. Go.
- A Caesar Cipher Quiz Generator from a Smart Contract. Go.
- Hashing in a Smart Contract. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
- Dealing With Decimals In Smart Contracts. Go.
- Creating A Scrambled Alphabet Challenge Generator In Ethereum and Solidity. Go.
- Deploying a Scrambled Alphabet Generator To Ethereum (With Ganache and Ropsten). Go.
- Deploying a Scrambled Alphabet Generator To Ethereum (With Hardhat). Go.
- Pigpen, IPFS and Ethereum. Go.
- Proof of \(x\) from \(H(x)\) using zkSnarks. Go.
- Elliptic Curve Operations Within a Solidity Contract. Go.

Ethereum
- Creating Ethereum address with Python. Go.
- Creating Ethereum signing with Python. Go.
- ERC20 Tokens. Go.
- Ethereum address with Go. Addresses. This generates an Ethereum address.
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- PATRICIA trie. PATRICIA. Example of using PATRICIA (and which is used in Ethereum).
- Viewing Balance of account in Etheruem with Go. Balance. This views the balance of an account
- Viewing Block in Etheruem with Go. Block. This views a block.
- Viewing Cryptocurrency API with Python. Go.
- Viewing Ethereum blockchain with Python. Go.
- Viewing Transactions in Block in Etheruem with Go. Transactions. This views transactions.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
- Symmetric Key Encryption For Smart Contracts. Symmetric key. Solidity does not natively support symmetric key encryption, such as with AES. Overall, AES would consume too much gas and thus be expensive to implement. But, we can use hashing and X-OR methods to do the encryption. In this case, we will create a 256-bit random value, and then encrypt it with an encryption key, and then decrypt it.
Calling from Python
- Calling smart contracts with Python. Python.
Ethereum crypto
- ECIES with Go-Ethereum. Go.
Ethereum Blockchain
- IOTA Trytes. Trytes. `This outlines Trytes, as used in IOTA.
Ethereum Blockchain
- Blockchain: Adding Maths Functions. Go.
- Blockchain: Blocks, transactions and writing data. Go.
- Blockchain: Contracts and Addresses. Go.
- Blockchain: Getting transactions. Go.
- Blockchain: Hello World!. Go.
- Blockchain: Simple Purchasing System. Go.
- Blockchain: Viewing the blockchain. Go.
- Blockchain: Cracking Wallets. Go.
- Introduction to Blockchain. Go.
Presentations
Factorization

Many public key problems involve the difficulity in factorizing a value two its prime number factors. For example, in RSA, we have a public modulus \(N\) and which is equal to the multiplication of two prime numbers \(p\) and \(q\). If we can factorize the public modulus, we will be able to break the RSA cipher related to it.
RSA Crack
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA Factorization. RSA. This outlines the factorisation of the N value in the RSA method.
Methods
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Dixon. Go. Dixon Method.
- Rho factorization. Rho. Rho alogorithm.
- Smooth numbers. Go. Outline of smooth numbers.
Methods (Elliptic curve
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Quadratic residues
- Quadratic residue (mod p). Go. Outline of quadratic residue \(\pmod p\).
- Quadratic residue (mod p) using Legendre symbol. Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
Factorizing
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
Lenstra–Lenstra–Lovász (LLL) with lattices
- Crack ECDSA with weak nonces. ECDSA with weak nonces and using Lenstra–Lenstra–Lovász (LLL) method. This outlines ECDSA how the private key can be recovered with weak nonce values.
Network Forensics

These pages outlines some network forensics. This includes the understanding of the network stack, and with protocols such as Etherenet, IP, TCP, HTTP, and others.
Network Forensics (Theory)
- Network Forensics (Wireshark). Network Forensics. This provides information on how to detect threats through network forensics with Wireshark.
- Advanced Network Forensics. Network Forensics. This provides information on how to detect threats through network forensics.
Network Forensics (Practice)
- Advanced Network Forensics (Wireshark). Adv Network Forensics. This provides information on how to detect threats through network forensics with Wireshark.
- Network Forensics (PCAP). Network Forensics. This provides information on network forensics (reading PCAP files)
- Network Forensics (Text). Network Forensics. This provides information on network forensics (reading text files)
Tshark
-
Filters with TShark. TShark. This page runs Tshark with a given Pcap file and a defined filter.
Other
- Advanced Digital Forensics . Adv Digital Forensics. This provides information on how analyse disk based systems using open source forensics.
- Partition Analyser. MBR. This page will analyse the details of the partition details within the MBR (put one space between fields).
Presentations
Format Preserving Encryption

Format Preserving Encryption (FPE) is a method which allows the basic formatting of a message to stay in a similar format, and where the value itself is encrypted. It can be used to hide credit card details.
Methods
- Format Preserving Encryption. FPE. This outlines Format Preserving Encryption.
- FPE with Python. FPE. An implementation of Format Preserving Encryption (FPE) using Python.
- FPE with node.js. FPR. FPE with node.js.
- FPE and PKBKDF2 in Python. FPE and PKBKDF2 in Python. FPE using PKBDF2 to password generation.
FFX (Format-preserving, Feistel-based encryption)
- FPE with Go. FPE. An implementation of Format Preserving Encryption (FPE) for FFX1 and FFX3.
- FFX schemes. FFX. Within tokenization we can apply format preserving encryption (FPE) methods, which will convert our data into a format which still looks valid, but which cannot be mapped to the original value. For example, we could hide Bob's credit card detail into another valid credit card number, and which would not reveal his real number. A tokenization server could then convert the real credit card number into a format which still looked valid. For this we have a key which takes the data, and then converts it into a form which the same length as the original.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher in Python.
FFX in Rust
- FFX. FFX. This is an implementation of FFX in Rust.
Honey Encryption
- Honey Encryption. Honey. This outlines Honey encryption.
Crypto Principles

This page outlines some crypto principles.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Galois fields (polynomial operations)

This page outlines a few basic principles around the usage of Galois fields and polynomial operations. In 1832, Évariste Galois died of duelling wounds at the age of 20 but left a great legacy. While he was a teenager he worked on polynomials and laid down the principles of Galois theory, along with defining the concept of a finite field. In cryptography, the finite field is one of the major concepts and involves limiting the number of possible values to a limiting factor (\(p\)). The values of the field then range from 0 to p-1. Within a field, we can operate on values in the field using arithmetic operations. We can thus have an infinite field, and where we could include all of the possible integers. A finite field or Galois field of GF(\(2^n\)) has \(2^n\) elements. If \(n\) is four, we have 16 output values. Let’s say we have a number \(a∈{0, ... ,2^{n−1}}\), and represent it as a vector in the form of a polynomial:
\( a=a0+a_1 x+a_2 x^2 ... a_{n−1} x^{n−1}\)
If we use \(a_n∈{0,1}\), this is exactly the same as representing a binary number modulo \(2^n\). In this \(x^n\) represents bit position \(n\) and \(a_n\) is the value of the bit at position \(x^n\). If a bit is a zero at a given position, it will be not included in the polynomial equation. So, 1011 can be represented by \(x^3+x+1\) and 1010 is represented as \(x^3+x\). We can then perform arithmetic operations on these polynomial values. So, to add two values of 1010+1100 we can represent this as \((x^3+x)+(x^3+x^2)\) and which is \(x^2+x\) as we are using modulo 2 addition, and where \(x^3+x^3=0\). With modulo 2 addition, 0+0=0, 0+1=1, 1+0=1, and 1+1=1.
An example of Galois Fields is within AES (Advanced Encryption Standard) and which uses a finite field GF(\(2^8\)). With AES we operate on bytes (8 bits) in the form of \(b_7 b_6 b_5 b_4 b_3 b_2 b_1 b_0\) and which are operated on a a polynomial of \(b_7x^7+b_6x^6+b_5x^5+b_4x^4+b_3x^3+b_2x^2+b_1x^1+b_0\).
Galois fields (polynomial operations) - GF(\(p^n\))
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Additive Group Table for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Additive Group Table for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of addition. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the additive group table for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values.
- Multiplicative Group Table for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Multiplicative Group Table for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the additive group table for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values.
- Additive, Division and Multiplicative Group Table for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Additive, Division and Multiplicative Group Table for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the Additive, Division and Multiplicative Group Table for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values.
- Additive and Multiplicative Group Table for GF(\(2^2\)) and GF(\(2^3\)). Galois Fields Table for GF(2^m) with polynomials. This page implements Galois Fields GF(\(2^n\)) with Python and provides a table of additional and multiplication. It outlines GF(\(2^2\)) and GF(\(2^3\)), but also gives a program that can be used for others. Overall, we have the form of GF(\(p^n\)) and which provides use both an additive and a multiplicative group operations that provide all the possible outputs within the finite field. The value of \(p\) is a prime number, and \(n\) is any positive integer.
- Additive and Multiplicative Group Table for GF(\(2^2\)) and GF(\(2^3\)). Galois Fields Table for GF(2^m) with coefficient values. This page implements Galois Fields GF(\(2^n\)) with Python and provides a table of additional and multiplication. It outlines GF(\(2^2\)) and GF(\(2^3\)), but also gives a program that can be used for others. Overall, we have the form of GF(\(p^n\)) and which provides use both an additive and a multiplicative group operations that provide all the possible outputs within the finite field. The value of \(p\) is a prime number, and \(n\) is any positive integer. This version will show the polynomial coefficent values within the Galois Field.
- Additive and Multiplicative Group Table for GF(\(2^2\)) and GF(\(2^3\)). Galois Fields Table for GF(2^m) with integer values. This page implements Galois Fields GF(\(2^n\)) with Python and provides a table of additional and multiplication. It outlines GF(\(2^2\)) and GF(\(2^3\)), but also gives a program that can be used for others. Overall, we have the form of GF(\(p^n\)) and which provides use both an additive and a multiplicative group operations that provide all the possible outputs within the finite field. The value of \(p\) is a prime number, and \(n\) is any positive integer. This version will show the integer values within the Galois Field.
Irreducible polynomial for GF(p^n)
- Irreducible polynomial for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Irreducible polynomial for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the parameters for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values. This includes finding the irreducible polynomial for the Galois Field.
- Irreducible polynomial for GF(\(p^n\)) for a given \(p\) and for \(n\) values. Irreducible polynomial for GF(p^n) for a given p and for n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the parameters for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values. This includes finding the irreducible polynomial for the Galois Field. Other important parameters include the degree (the highest polynomial power) and the order (the number of possible output values).
- Conway and primitive polynomial GF(\(p^n\)). Conway and primitive polynomial GF(p^n). This page outlines Conway and primitive polynomials for GF(\(p^n\)).
Galois fields (polynomial operations) - GF(\(p\))
- Additive and Multiplicative Group mod n (\(Z_n\)). Additive and Multiplicative Group mod n. In finite fields, we have a \(\pmod n\) operation for a list of integers (\(\mathbb{Z}\)), and where \(n\) is a prime number. This works for our add (+) and multiply (\(\times\)) operations, and where: \( a \pmod n + b \pmod n = (a+b) \pmod n\); and \(a \pmod n \times b \pmod n = (a \times b) \pmod n\).
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Polynomial GF(2) Factoring and Irreducible Polynomials. Factors. This outlines the search for polynomial factors for GF(2).
Polynomial operations
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
Post-quantum
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Rust
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Sage
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Golang and Cryptography

The new scripted languages such as Python and Node.js are convenient. But, unfortunately, they can be slow as they are scripted, and not compiled. Each time the scripted code is run, the scripting engine must then convert each line of code to the required machine level code. This makes the code much slower than compiled languages, and also less robust. Thus many applications in cryptography are written in C and C++, as they allow for fast execution and give low level access. Unfortunately it can be complex to compile programs, as we often need to install binary libraries and then link these in. The Go programming language, though, has a similar code syntax to C/C++, but is small and efficient and allows access to low-level functions, such as as pointers. Go thus aims to “Code less, compile quicker, execute faster”. So let’s use Go to implement some cryptography methods, including symmetric key, hashing, public keys and zero-knowledge proofs (ZKPs). The slides related to these methods are included [here]. An introduction to Golang and Cryptography is [here].

Go ECDH
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret.
Go Hex and Base64
- Base64 and Hex in Go. Base64/Hex. Two common formats for representing binary data are hexademical and Base64.
Go symmetric key
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Reuse IV attack and AES. Reuse IV and GCM. This provides an implementation of a reuse IV against AES GCM.
- ASCON AEAD (Golang). ASCON AEAD (Golang). The outlines the usage of AEAD for ASCON using Golang.
Go HMAC and HKDF
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HKDF in Go. HKDF. Implementation ofHKDF, and where we dervice a key based on a given secret.
Go secret shares
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.

Go ZKP
- Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL). DLEQ. Create a non-interactive ZKP for discrete logs.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Fiat Shamir and ECC (Interative ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP with Kryptology. This implements a range proof using a Schnorr proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?

Go ECIES (Hybrid Encryption)
With this, we can use the power of public key encryption (to generate the encryption key) with symmetric key encryption (to actually encrypt and decrpyt the data):
- ECIES (Kryptology). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Coinbase Kryptology library.
- ECIES (CIRCL). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Cloudflare CIRCL library.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt and which is used in Contract Tracing for COVID-19.
Go ECDSA
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Go RSA
- RSA Principles. RSA Principles. The basics of RSA.
- RSA with Go. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA. RSA encryption with Go using OAEP.
- RSA Encryption with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
Go ElGamal
ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Proving an Encrypted Shuffle With ElGamal and ECC. Shuffle. An encrypted shuffle with ElGamal.
- ElGamal encryption with Go. ElGamal. This implements ElGamal encryption.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
- ElGamal - Applying Multiple Public Key Operations (ECC). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use elliptic curve methods, and using the Edwards 25519 curve.
Go PGP
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
Go Public key
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.

Go Hashing
- Hashing with Go. Hashing. Hashes with Go.
- GP Hashing with Go. GP Hashing. GP Hashes with Go.
- SHAKE with Go. SHAKE. This implements SHAKE in Go.
- libDisco with Go. libDisco. This implements libDisco.
- cSHAKE in Golang. cSHAKE. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS. With the SHA-3 hashing method, we have four different cryptographic hashing methods (SHA3-224, SHA3-256, SHA3-384, and SHA3-512) and two XOF functions (SHAKE128 and SHAKE256). With SHAKE128 and SHAKE256 we can integrate domain separation between different functions — and which are known as cSHAKE128 and cSHAKE256.
- Homomorphic Hashing with Golang. Homomorphic hashing. Normally with hashing methods, we need to take all the previous data and new data in order to create a new hash value for our data. In a homomorphic hashing method, we can basically take the previous hash, and then add on any new data values. We can also remove previous data values from our hash, too. This is more efficient in computing, as we do not have to process all of our data into a new hash, and can use simple homomorphic operations for the computation. The method we will use (LtHash) was initially defined by Bellare and Micciancio and updated Lewi et al at Facebook.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
Go ECC
- Hash to password with Go. Hash to password. Hash to password with Go.
- ECDH with Go. ECDH. ECDH with Go.
- Box with Go. Box. Box with Go.
- ECC with Go. ECC. ECC with Go.
- Curve 25519 with Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ElGamal with ECC. ElGamal with ECC. ElGamal using ECC.
- Curve 25519 with Go for test vectors. ECC. This does a test on some private keys to test the public key generation.
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Barebones Ed25519 with Go. ECC. This shows point addition and scalar multiply in Ed25519
- Barebones NIST P256 with Go. ECC. This shows point addition and scalar multiply in P256
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining \(n.G\) for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Points (Base Point and Others). Elliptic Curve points. Two common curves used in ECC (Elliptic Curve Cryptography) are secp256k1 (as used in Bitcoin and Ethereum) and P256 (secp256r1). The "k1" refers to the Kolbitz curve 1 (named after the creator of ECC). With these we have a base point which are can operate on. This is typically defined as \(G\). We can then operate on this with add and multiply operation. For example, \(2G=G+G\) and \(P=n.G\). In this following we will show the base point for a number of common curves, such as secp256r1, P256, Pallas, Curve 25519, BLS12381G1, BLS12381G2, BLS12377G1 and BLS12377G2.
Go Blockchain
- Ethereum address with Go. Addresses. This generates an Ethereum address.
- Viewing Balance of account in Etheruem with Go. Balance. This views the balance of an account
- Viewing Block in Etheruem with Go. Block. This views a block.
- Viewing Transactions in Block in Etheruem with Go. Transactions. This views transactions.

Go Homomorphic
- SIDH Go. SIDH. Post-quantum key exchange.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- NTP. NTP. An overview of NTP.
- BiBa. BiBa. An overview of BiBa One Time Signature.
Go DNS
- DNSSEC. DNSSEC. An overview of DNSSEC.
Go Signatures
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Go Signcryption
- Ahmad-Afzal-Iqbal (AAI) signcryption with Golang. Ahmad-Afzal-Iqbal (AAI). Ahmad-Afzal-Iqbal (AAI) signcryption with Golang.

Go Crypto pairing
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
Go Homomorphic
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add. HEAAN Add. HEAAN Add.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- Anonymous crypto. Anon. Anonymous crypto.
- Rho factorization. Rho. Rho alogorithm.
- Post-quantum signing (BLISS). BLISS. BLISS method.
Go Post quantum
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.

Go CIRCL
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- Ed448 with Go. X448. Ed448 with Go.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with FourQ (Cloudflare). FourQ.
- Verifiable Oblivious Pseudorandom Functions (VOPRF) with Cloudflare CIRCL. VOPRF. In our digital world, we give away too many of our secrets, especially where we just have to prove the knowledge of something, rather than actually revealing it. In many of the systems we use, we could just prove things in an oblivious way, and where we could pass a secret but in a blinded form. With this, a server does not discover our password and for us not to discover the identifier that a server holds on us. But, can we also provide a proof back that the right password has been used? Well, with Verifiable Oblivious Pseudorandom Functions (VOPRF), we can generate a random secret based on a key generated on the server (Alice), and which is based on Bob’s secret.
- Hash to Curve using Go (Cloudflare). Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). The method defined here is proposed an an Internet-Draft standard by the Internet Engineering Task Force (IETF) related to "Hashing to Elliptic Curves".
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
here Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
- eXtendable-Output Function (XOF) usign CIRCL. XOF. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS.

Go Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Google Tink (Golang) ECIES. Google Tink (ECIE5). This outlines ECIES encryption with public key and AES using Golang with Google Tink
Go Credentials
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.

Go Kryptology
- Public key points for curves. Simple. Display public key points for scalars.
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.

Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.

Principles
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Paillier
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
Go Format Preserving Encryption (FPE)
- FPE with Go. FPE. An implementation of Format Preserving Encryption (FPE) for FFX1 and FFX3.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
AWS Encryption
- AWS Symmetric Key Encryption. AWS (Symmetric key). Using symmetric key in AWS.
Go Oblivious Transfer
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Dragon Fly
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
Embedding data in an ECC point
- Embedding data in a point. Go. With Elliptic Curve Cryptography (ECC), we use points on an elliptic curve to represent our data. These are defined with (x,y) points. With this, it is possible to embedded a certain amount of data into the point - as long as it still gives us a valid point on the curve. This example will Curve 25519 to embed data, and is achieved by storing the length of the data in a single byte in the point, and then store the data as byte values in the point (followed by random data). To decode, we can then just read the first byte for the length of the message, and then reveal the data encoded into the point..
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Hashing (Cryptographic)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
Benchmarks and Password strength
The following are the tips related to hashing:
- Password strength. Test. This outlines the strength of various passwords types.
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
Theory
The following are the tips related to hashing:
- Balls in bins. BiBa. This implemented balls in bins.
- Birthday attack (with Big Integers). Calc. This provides a simple example of the birthday attack.
- Birthday attack. Calc. This provides a simple example of the birthday attack.
- Differential Cryptanalysis (Hashing). Cryptanalysis. This provides an implementation of differential cryptanalysis for hashing methods.
MD5, SHA-1
The following are the tips related to hashing:
- MD2 and MD4 MD2/4. The MD2 and MD4 hashing functions were developed by Prof Ronald Rivest in 1989 and 1990, respectively. They both produce a 128-bit hash, but have been shown be vulnerable to attack (see the Collision section in the page).
- MD5 and SHA-1 (to Base-64) with salt Salt. It is possible to add salt to the MD5 algorithm, to mix it up a little.
- MD5 and SHA-1 (to Base-64) Hash. MD5 and SHA-1 produces a hash signature, and the output is typically shown in a hex format or a Base-64. In this example the output is converted into a Base-64 format.
- MD5 and SHA-1. Hash. MD5 and SHA-1 methods produce a hash signature, and are the two of the most widely used methods. The MD5 algorithm has been shown to have weaknesses, and a collision of message hashes has been shown to occur in less than one day. An MD5 signature has 128 bits, an SHA-1 signature has 160 bits, and an SHA-256 signature has 256 bits.
- MD5 Cracking. Hash Cracker. MD5 has a 128-bit signature and can be cracked using rainbow tables. This page tries to crack the MD5 signature.
- Hashing with Go. Hashing. Hashes with Go.
- Detecting hash types. Hash type. This detects has values.
- OpenSSL hashing. Range of methods. Outlines the methods used in OpenSSL
- Hash. Hash. Hashing using JavaScript
- Hashing with node.js. Hashing. Hashing with node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Hashing methods
-
Hazmat Hashes. Hazmat Hashes. This includes the hashing methods in the Hazmat cryptography library. This includes Blake2p, Blake2s, MD5, SHA1, SHA224, SHA256, SGA384, SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHA512, SHA512-224, SHAKE128 and SHA256.
-
Hazmat Hashes. Hazmat Hashes. In this case we will implement Python code to determine SHA1, SHA2, SHA3, Blake2, MD5 and SM3 hashes.
OpenSSL Passwords
-
Password example [here]
-
Hashed passwords with OpenSSL [here]
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Blake 3 hashes
The following are the tips related to similarity hashing:
- Blake 3 in Python. Hashing. Blake 3 hashing.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
Other Hash functions
The following are the tips related to hashing:
- Bloom Filter Bloom filter. A Bloom filter goes a probabilistic method of determining if an element is in a data structure, using indexed hashing methods.
- Cuckoo Table Cuckoo filter. A Cockoo table uses two hash funtions.
- Chaffing. Chaffing. This produces a keyless system.
- GP Hashing with Go. GP Hashing. GP Hashes with Go.
- LDAP. LDAP. This produces a LDAP hash signature for a password.
- LM Hash. LM Hash. This is an LM Hash Calculator. LM Hash is used in many versions of Windows to store user passwords that are fewer than 15 characters long.
- Murmur and FNV Murmur and FNV. While hashing methods such as MD5 and SHA-1 use crypto methods, the Murmur and FNV hashes uses a non-cryptographic hash function. This can be used for general hash-based lookup and was designed by Austin Appleby. It has good performance compared with other hashing methods.
- Pearson. Pearson. This uses a non-crypto hash.
- phpass. phpass. This produces a phpass hash signature for a password.
- Tiger. Tiger. Tiger is a 192-bit hash function and was designed by Ross Anderson and Eli Biham in 1995. It is often used by clients within Gnutella file-sharing networks and does not suffer from known attacks on MD5 and SHA-0/SHA-1. Tiger2 is an addition, in which the message is padded with a byte of 0x80 (in a similar way to MD4, MD5, and SHA), whereas in Tiger it is 0x01. Otherwise, the two methods are the same in their operation.
- Whirlpool. Whirlpool. Whirlpool is a 512-bit cryptographic hash function and was created by Vincent Rijmen (one of the AES creators) and Paulo Barreto, in 2000.
- WPA-2 hash . WPA-2 hash. Implements SHA-2 hash.
- Reusable hash collisions. Reusable hash collisions. Reusable hash collisions.
- The Length Extension Attack. Length Extension Attack. The MD construct has many weaknesses, and one of the most serious is the length extension attack. With this an adversary (Eve) can take a hash for an unknown message, and then add additional data to produce a new valid hash. The hash methods which are at risk against the length extension attack are MD5, SHA-1 and SHA-256. Please follow the code link below to run an example.
- Consistent hashing. Consistent hash. This outlines the usage of Consistent hashes.
- ROR13 (Module and Function). ROR13. With ROR13 we take each 8-bit character and then convert to a unicode value (with 16 bits). Then for each character we rotate the bits right by thirteen places. The resultant hash is then just the accumuluation of the rotated values.
- ROR13 (Function). ROR13 (Function). With ROR13 we take each 8-bit character and then convert to a unicode value (with 16 bits). Then for each character we rotate the bits right by thirteen places. The resultant hash is then just the accumuluation of the rotated values.
- GOST, Streebog256 and Streebog512. GOST, Streebog256 and Streebog512. GOST94 is a hashing method developed with Euro-Asian Council for Standardization, Metrology and Certification (EASC). This has since been developed in the Streebog256 and Streebog512 hashing method. In this case, we will use Libre OpenSSL to convert data into a hashed value.
RIPEMD
- RIPEMD (RACE Integrity Primitives Evaluation Message Digest) and GOST. RIPEM160. RIPEMD is a 128-bit, 160-bit, 256-bit or 320-bit cryptographic hash function, and was created by Hans Dobbertin, Antoon Bosselaers, and Bart Preneel. It is used on TrueCrypt and is open source. The 160-bit version is seen as an alternative to SHA-1, and is part of ISO/IEC 10118
- RIPEMD160. RIPEM160. RIPEMD160 is a 160-bit cryptographic hash function, and was created by Hans Dobbertin, Antoon Bosselaers and Bart Preneel. RIPEMD160 is used in Bitcoin applications.
Chameleon hashes
The following are the tips related to Chameleon hashing:
- Chameleon hash in Golang Chameleon. With a Chameleon hash, we have a normal hash value which is resistant to collisions, but with a known secret we can easily create a collision. The concept was first defined by Krawcyk and Rabin.
Similarity hashes
The following are the tips related to similarity hashing:
- Similarity hash: SimHash (Charikar similarity) in Python Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash (Nilsimsa similarity) Nilsimsa. The Nilsimsa similarity is used to find similarities between spam emails.
- Minhash (Jaccard similarity) Jaccard similarity. The Minhash method is used to find similarities between strings, files and metadata.
- String enthropy String enthropy. Measurement of the entropy of strings.
- Counting identical elements (HyperLogLog) HyperLogLog. Counting the number of identical elements.
SHA-3 and SHA-3 contenders
The following are the tips related to Key derivation hashing:
- Blake and Blake 2. Blake. Implements Blake and Blake 2 (SHA-3 contender).
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
- Grøstl. Grøstl. Implements Grøstl (SHA-3 contender).
- KangarooTwelve. KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- SHA-3, Keccak and SHAKE . SHA-3. Implements SHA-3, Keccak and SHAKE (SHA-3 winner).
- SHA-3. SHA-3. SHA-3 was known as Keccak and is a hash function designed by Guido Bertoni, Joan Daemen, Michaël Peeters, and Gilles Van Assche. MD5 and SHA-0 have been shown to be susceptible to attacks, along with theoretical attacks on SHA-1. NIST thus defined there was a need for a new hashing method which did not use the existing methods for hashing, and setup a competition for competing algorithms. In October 2012, Keccak won the NIST hash function competition and is proposed as the SHA-3 standard. It should be noted that it is not replacement SHA-2, which is currently a secure method. Overall Keccak uses the sponge construction where the message blocks are XORed into the initial bits of the state, and then inevitably permuted.
- cSHAKE. cSHAKE. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS. With the SHA-3 hashing method, we have four different cryptographic hashing methods (SHA3-224, SHA3-256, SHA3-384, and SHA3-512) and two XOF functions (SHAKE128 and SHAKE256). With SHAKE128 and SHAKE256 we can integrate domain separation between different functions — and which are known as cSHAKE128 and cSHAKE256.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- Skein. Skein. Implements Skein (SHA-3 contender).
Key derivation hashing
The following are the tips related to Key derivation hashing:
- Argon2. Go. Outline of Argon2.
- Argon2 with NaCl. Go. Outline of Argon2 using NaCl.
- Balloon. Go. Outline of Balloon.
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- Double ratchet. Go. Outline of double ratcheting.
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- Scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat HKDF. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
Non-crypto/fast hashing
The following are the tips related to non-crypto hashing:
- A perfect hash Perfect hash. This is a non-crypto hash which optimizes the hash value.
- The universal hash Universal hash. This related to the concept of a universal hash.
- FNV. FNV. FNV is one of the fastest hashing methods.
- Murmur. Murmur. Murmur is one of the fastest hashing methods.
- Siphash. Siphash. Siphash is a fast hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- xxHash. xxHash. xxHash is one of the fastest hashing methods.
- Meow. Meow. Meow is one of the fastest hashing methods.
- o1Hash. o1Hash. o1Hash is one of the fastest hashing methods.
- CRC-32. CRC-32. CRC-32 is one of the fastest hashing methods.
- wyhash. wyhash. wyhash is one of the fastest hashing methods.
- CityHash. CityHash. CityHash is one of the fastest hashing methods, and is generally free of security problems.
- FarmHash. FarmHash. FarmHash is one of the fastest hashing methods, and is generally free of security problems.
- Non-crypto. Non-crypto. This includes a range of fast non-cryptography hashing methods.
- Non-crypto hashes (C++): Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro. Non-crypto hashes: Farm, City, xxHash, MUM, Spooky 2, Murmur, Metro and t1ha0. This includes a range of fast non-cryptography hashing methods for Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro using C++ methods.
- Pearson. Pearson. Pearson is one of the fastest hashing methods, and has been designed for 8-bit processors.
- C++: t1ha. t1ha. t1ha is one of the fastest hashing methods, and has been designed for 64-bit processors.
- C++: Spooky. Spooky. Spooky is one of the fastest hashing methods, and V2 has a 32-bit, 64-bit and 128-bit version.
- C++: xxHash. xxHash. xxHash is one of the fastest hashing methods, and has good performance for short data inputs.
- C++: MUM. MUM. MUM is one of the fastest hashing methods.
- C++: FNV 1/1a. FNV 1/1a. FNV 1/1a is one of the fastest hashing methods, and is particularily useful when there are small changes in strings, such as with IP addresses and URLs.
- C++: MetroHash. MetroHash. MetroHash is one of the fastest hashing methods.
- C++: CityHash. CityHash. CityHash was created by Google and is one of the fastest hashing methods. It was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Farm. FarmHash. FarmHash was created by Google and is one of the fastest hashing methods. It is an improvement to CityHash.
- C++: Murmur. Murmur. Murmur is one of the fastest hashing methods, but was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Halftime. Halftime. Halftime is one of the fastest hashing methods and was created by Jim Apple at Apache.
- C++: Highway. Highway. Highway is an ultra-fast keyed-hash, and is more than five times faster than SipHash. It was created by Jyrki Alakuijala, Bill Cox, Jan Wassenberg at Google.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
- C++: CLHash. CLHash. CLHash is an ultra-fast hashing method and focused on improving performance of the hashing of long strings.
- C++: FalkHash. FalkHash. FalkHash is an ultra-fast hashing method and beats most of the other non-cryptography methods for performance. It is focused on the x64 architecture and integrates with AES-NI.
- C++: wyHash. wyHash. wyHash is an ultra-fast hashing method.
- C++: Fibonacci. Fibonacci. Fibonacci is an ultra-fast hashing method.
- C++: Lookup3. Lookup3. Lookup3 is an ultra-fast hashing method.
Key-based hashing
The following are the tips related to Key-based hashing:
- SiphashSiphash. Siphash is a fast key-based hashing method.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
One Time Passwords/Time Stamps
The following are the tips related to hashing:
- One Time Passwords. One Time. This allows a new unique password to be created each instance, based on an initial seed.
- Timed One Time Password (TOTP). Timed One Time Password. This allows a new unique passcode to be created each instance, based on an initial seed for a given time window. We will use a five second window in this case, where a new passcode is generated every five seconds, based on an initial seed of a pass phrase.
- Hashed One Time Password (HOTP). Hashed One Time Password. This allows a new unique passcode to be created each instance, based on a counter value and an initial seed.
- Time Stamp Protocol. TSP. This creates a time stamp for data.
- HOTP and TOTP (Python). OTP. This creates hashed passwords.
eXtendable-Output Function (XOF)
- eXtendable-Output Function (XOF) usign CIRCL. XOF. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS.
SHAKE
The following are the tips related to hashing:
- SHAKE. SHAKE. Implements SHAKE and which is an Extendable Output Function (XOF).
- SHAKE with Go. SHAKE. This implements SHAKE in Go.
- libDisco with Go. libDisco. This implements libDisco.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify
the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods
such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC methods using the Python cryptography primitives for HMAC-MD5.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
Quantum-robust Public Key (Hash-based signature)
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
Hash to ECC point
- Hash to password with Go. Hash to password. Hash to password with Go.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve with libnum.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.

Password-hashing functions using Rust
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing (Non-cryptographic)

You might know those slow old hashing methods, such as MD5, SHA-1, and SHA-256. Well, they were designed to be fast, but also highly secure. But, if we just need a hashing method, such as for a hashtable or Bloom filter, we often don’t need all the security that comes with the main cryptography hashing methods. And so we have the non-cryptography hashing methods, and which are often ultra-fast and highly efficient. To show the difference, in a test, SHA-1 — one of the fastest cryptography hashing methods — managed a processing rate of 364.95 MiB/s, while t1ha was nearly a 100 times faster, at 34,636 MiB/s.
Non-crypto/fast hashing
The following are the tips related to non-crypto hashing:
- A perfect hash Perfect hash. This is a non-crypto hash which optimizes the hash value.
- The universal hash Universal hash. This related to the concept of a universal hash.
- FNV. FNV. FNV is one of the fastest hashing methods.
- Murmur. Murmur. Murmur is one of the fastest hashing methods.
- Siphash. Siphash. Siphash is a fast hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- xxHash. xxHash. xxHash is one of the fastest hashing methods.
- Meow. Meow. Meow is one of the fastest hashing methods.
- o1Hash. o1Hash. o1Hash is one of the fastest hashing methods.
- CRC-32. CRC-32. CRC-32 is one of the fastest hashing methods.
- wyhash. wyhash. wyhash is one of the fastest hashing methods.
- CityHash. CityHash. CityHash is one of the fastest hashing methods, and is generally free of security problems.
- FarmHash. FarmHash. FarmHash is one of the fastest hashing methods, and is generally free of security problems.
- Non-crypto. Non-crypto. This includes a range of fast non-cryptography hashing methods.
- Non-crypto hashes (C++): Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro. Non-crypto hashes: Farm, City, xxHash, MUM, Spooky 2, Murmur, Metro and t1ha0. This includes a range of fast non-cryptography hashing methods for Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro using C++ methods.
- Pearson. Pearson. Pearson is one of the fastest hashing methods, and has been designed for 8-bit processors.
- C++: t1ha. t1ha. t1ha is one of the fastest hashing methods, and has been designed for 64-bit processors.
- C++: Spooky. Spooky. Spooky is one of the fastest hashing methods, and V2 has a 32-bit, 64-bit and 128-bit version.
- C++: xxHash. xxHash. xxHash is one of the fastest hashing methods, and has good performance for short data inputs.
- C++: MUM. MUM. MUM is one of the fastest hashing methods.
- C++: FNV 1/1a. FNV 1/1a. FNV 1/1a is one of the fastest hashing methods, and is particularily useful when there are small changes in strings, such as with IP addresses and URLs.
- C++: MetroHash. MetroHash. MetroHash is one of the fastest hashing methods.
- C++: CityHash. CityHash. CityHash was created by Google and is one of the fastest hashing methods. It was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Farm. FarmHash. FarmHash was created by Google and is one of the fastest hashing methods. It is an improvement to CityHash.
- C++: Murmur. Murmur. Murmur is one of the fastest hashing methods, but was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Halftime. Halftime. Halftime is one of the fastest hashing methods and was created by Jim Apple at Apache.
- C++: Highway. Highway. Highway is an ultra-fast keyed-hash, and is more than five times faster than SipHash. It was created by Jyrki Alakuijala, Bill Cox, Jan Wassenberg at Google.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
- C++: CLHash. CLHash. CLHash is an ultra-fast hashing method and focused on improving performance of the hashing of long strings.
- C++: FalkHash. FalkHash. FalkHash is an ultra-fast hashing method and beats most of the other non-cryptography methods for performance. It is focused on the x64 architecture and integrates with AES-NI.
- C++: wyHash. wyHash. wyHash is an ultra-fast hashing method.
- C++: Fibonacci. Fibonacci. Fibonacci is an ultra-fast hashing method.
- C++: Lookup3. Lookup3. Lookup3 is an ultra-fast hashing method.
A fuller test with SMHasher gives [here]:
Hash function MiB/sec cycl./hash cycl./map Quality problems
------------------------------------------------------------------
o1hash 12439661.09 16.77 166.13 insecure, no seed, zeros, fails all tests
crc32_hw1 23208.73 46.74 179.70 insecure, 100% bias, collisions, distrib, BIC, machine-specific (x86 SSE4.2)
t1ha0_aes_noavx 22785.26 38.71 180.61 LongNeighbors, machine-specific (x86 AES-NI)
t1ha0_aes_avx1 22714.85 48.12 226.52 LongNeighbors, machine-specific (x64 AVX.txt)
t1ha0_aes_avx2 22345.33 44.38 556.47 LongNeighbors, machine-specific (x64 AVX2)
falkhash 20202.42 173.63 321.52 Sparse, LongNeighbors, machine-specific (x64 AES-NI)
MeowHash64low 17378.06 85.48 237.60 Sparse, invertible, machine-specific (x64 AES-NI)
MeowHash32low 17374.64 85.48 258.53 Sparse, invertible, machine-specific (x64 AES-NI)
MeowHash 17371.91 85.48 247.96 Sparse, invertible, machine-specific (x64 AES-NI)
FarmHash32 17112.05 47.7 214.71 machine-specific (x64 SSE4/AVX)
xxh3 16538.52 32.81 184.86 DiffDist bit 7 w. 36 bits, BIC
xxh3low 16462.36 32.77 199.79
farmhash32_c 16299.81 47.79 219.19 machine-specific (x64 SSE4/AVX)
xxh128low 15174.85 33.79 187.05
xxh128 15174.14 40.46 195.65
farsh32 14053.09 74.29 245.33 insecure: AppendedZeroes, collisions+bias, MomentChi2, LongNeighbors
metrohash64crc_2 14034.84 48.94 162.54 UB, Cyclic 8/8 byte, DiffDist, BIC, machine-specific (SSE4.2/NEON)
metrohash64crc_1 14000.5 49.08 150.54 UB, Cyclic 8/8 byte, DiffDist, BIC, MomentChi2, machine-specific (SSE4.2/NEON)
metrohash128crc_1 13948.67 65.2 168.08 UB, machine-specific (SSE4.2/NEON)
metrohash128crc_2 13920.19 65.12 176.70 UB, machine-specific (SSE4.2/NEON)
halftime_hash128 13478.23 97.79 252.14
wyhash32low 12911.09 29.59 205.43 2 bad seeds
wyhash 12879 30.35 196.77 2^33 bad seeds
CityCrc128 12343.43 74.5 209.75
fletcher2 12011.15 25.29 298.60 bad seed 0, UB, fails all tests
fletcher4 11928.55 25.27 293.49 bad seed 0, UB, fails all tests
halftime_hash256 11620.28 98.44 252.60
fibonacci 11339.87 26.33 705.64 UB, zeros, fails all tests
ahash64 9862.62 27.32 181.68 rust
Spooky128 9751.14 63.84 192.47 UB
Spooky64 9747.47 62.2 191.71 UB
Spooky32 9747.13 62.24 196.96 UB
t1ha1_64le 9723.86 34.39 176.91 Avalanche
cmetrohash64_1 9683.33 45.2 161.01 UB, LongNeighbors, BIC, MomentChi2
cmetrohash64_2 9669.95 44.75 149.67 LongNeighbors
metrohash64_2 9668.51 44.45 164.30 UB, LongNeighbors
metrohash64 9664.61 44.59 150.74 UB, LongNeighbors, BIC
metrohash64_1 9664.57 45.37 152.31 UB, LongNeighbors, BIC, MomentChi2
cmetrohash64_1o 9658.31 42.84 163.45 UB, LongNeighbors, BIC, MomentChi2
FNV1a_YT 9643.42 32.06 175.19 bad seed, UB, fails all tests
City128 9640.19 88.45 225.38
metrohash128_2 9584.94 59.1 167.43 UB, LongNeighbors
metrohash128 9569.16 58.68 167.53 UB, LongNeighbors
metrohash128_1 9558.17 59.04 175.94 UB, LongNeighbors
FarmHash128 9409.63 74.52 210.25
VHASH_32 9404.99 77.01 250.57 sanity, Seed, MomentChi2
VHASH_64 9392.39 74.72 227.92 sanity, Seed, MomentChi2
farmhash128_c 9244.13 79.08 209.44
t1ha2_atonce 9237.12 38.94 194.32 Zeroes low3
City64noSeed 9090.42 32.23 171.53 Avalanche, Sparse, TwoBytes, MomentChi2, Seed
City64low 9089.45 47.75 201.73
t1ha2_stream 9068.55 74.56 219.85 Sparse, Permutation, LongNeighbors
City64 9066.9 47.81 197.78 Sparse, TwoBytes
t1ha2_stream128 9065.5 93.19 236.50 Sparse, Permutation, LongNeighbors
xxHash64 8936.63 51.31 174.34
pengyhash 8744.48 85.31 222.45
farmhash64_c 8713.16 47.96 201.00
FarmHash64 8684.76 48.13 200.51
crc64_hw 8440.13 34.94 141.15 insecure, 100% bias, collisions, distrib, BIC, machine-specific (SSE4.2/NEON)
t1ha2_atonce128 8350.99 55.65 203.53 LongNeighbors
PMPML_64 8161.19 53.2 179.16 unseeded: Seed, MomentChi2, BIC
halftime_hash512 7681.62 125.81 274.01
tabulation 7621.75 42.19 179.93
t1ha1_64be 7481.37 38.16 193.22 Avalanche
MUMlow 7225.18 37.85 197.92 UB, 5 bad seeds
farsh64 7216.29 130.3 302.44 insecure: AppendedZeroes, collisions+bias, MomentChi2, LongNeighbors
MUM 7134.56 37.85 172.34 UB, too many bad seeds, machine-specific (32/64 differs)
nmhash32 7003.3 68.93 216.59
PMPML_32 6704.53 53.5 197.43 Avalanche >512, unseeded: Seed, BIC, MomentChi2, PerlinNoise
nmhash32x 6342.95 56.41 217.75
crc32_hw 6330.42 35.55 170.16 insecure, 100% bias, collisions, distrib, BIC, machine-specific (SSE4.2/NEON)
FNV2 6258.84 33.25 142.89 fails all tests
FNV1A_Pippip_Yurii 6258.46 28.19 184.41 UB, sanity, fails all tests
FNV1A_Totenschiff 6258.23 27.99 198.20 UB, zeros, fails all tests
HighwayHash64 6242.58 99.55 248.41
mx3 6146.02 52.48 173.09 UB
xxHash32 6040.87 51.77 177.91 LongNeighbors, collisions with 4bit diff, MomentChi2 220
prvhash64s_64 5481.48 170.05 325.39
mirhash 5413.73 39.68 154.47 UB, 2^36 bad seeds, LongNeighbors, machine-specific (32/64 differs)
mirhash32low 5412.76 39.79 182.13 UB, 4 bad seeds, Cyclic, LongNeighbors, machine-specific (32/64 differs)
Murmur3F 5226.4 52.18 175.85 UB
prvhash64s_128 5161.33 260.96 442.70
t1ha0_32le 5132.18 54.83 193.53 Sparse, LongNeighbors
halftime_hash64 4990.72 120.55 281.64
Murmur2B 4882.95 39.72 149.43 UB, 1.8% bias, collisions, 3.4% distrib, BIC
seahash32low 4801.33 58.54 227.31 PerlinNoise 32, !msvc
seahash 4796.97 58.55 201.58 PerlinNoise, !msvc
fasthash32 4737.61 45.32 181.86 UB, insecure
fasthash64 4737.21 42.79 164.87 UB, insecure, Moment Chi2 5159 !
umash32_hi 4662.92 54.22 214.20
umash64 4662.09 53.42 188.09
umash32 4633.19 53.42 216.33
t1ha0_32be 4585.59 55.98 183.45 Sparse, LongNeighbors
clhash 4472.31 82.72 229.73 PerlinNoise, machine-specific (x64 SSE4.2)
tabulation32 4317.34 35.45 197.20 collisions
Murmur2C 4092.99 51.84 164.65 UB, 2^32 bad seeds, 91% bias, collisions, distr, BIC, LongNeighbors
farsh128 3776.92 232.48 398.67
City32 3675.04 57.73 212.04
TSip 3228.14 57.96 211.71 !msvc
Murmur3C 3197.63 67.9 198.00 UB, LongNeighbors, Text, DiffDist
Crap8 3149.63 36.23 195.11 UB, 2.42% bias, collisions, 2% distrib
Murmur2 3146.91 41.87 187.89 UB, 1 bad seed, 1.7% bias, 81x coll, 1.7% distrib, BIC
Murmur2A 3146.79 46.87 191.96 UB, 1 bad seed, 12.7% bias, LongNeighbors
aesnihash 2963.39 71.24 217.73 fails many tests, machine-specific (x64 AES-NI)
BEBB4185 2951.62 222.03 343.63 UB, too many bad seeds, msvc-specific
jodyhash6 2848.42 29.99 164.36 bias, collisions, distr, BIC, LongNeighbors
wyhash32 2532.89 48.4 484.57 2 bad seeds, 32-bit
umash128 2427.46 70.6 197.29
Murmur3A 2413.88 53.36 182.37 UB, 1 bad seed, Moment Chi2 69
prvhash64_64m 2386.19 51.18 186.87
prvhash64_128 2383.57 103.44 246.45
prvhash64_64 2375.72 51.61 190.97
hasshe2 2372.52 68.64 216.74 Permutation,TwoBytes,Zeroes,Seed
PMurHash32 2344.78 58.48 196.43 1 bad seed, Moment Chi2 69
mirhashstrict32low 2218.87 65.48 190.59 1 bad seed, MomentChi2 9
mirhashstrict 2217.32 65.53 182.07
sha1ni 2019.96 135.84 564.40 insecure,sanity, Permutation, Zeroes, machine-specific
sha1ni_32 2019.94 136.82 589.46 machine-specific
superfast 1956.25 53.61 180.10 UB, bad seed 0, 91% bias, 5273.01x collisions, 37% distr, BIC
sha2ni-256_64 1910.34 146.06 595.16 Zeroes, machine-specific
sha2ni-256 1906.77 145.47 603.08 insecure,sanity, Permutation, Zeroes, machine-specific
farsh256 1895.77 459.86 575.95
SipHash13 1889.1 89 199.95 0.9% bias
Murmur1 1804.67 51.51 188.41 UB, 1 bad seed, 511x collisions, Diff, BIC
lookup3 1658.31 48.84 194.15 UB, 28% bias, collisions, 30% distr, BIC
pearsonbhash64 1486.34 104.32 185.03
poly_1_mersenne 1431.65 54.49 189.52 fails most tests
jodyhash32 1428.37 44.36 185.85 bias, collisions, distr, BIC LongNeighbors
pearsonbhash128 1347.03 121.75 214.84
poly_2_mersenne 1323.69 66.93 190.88
poly_3_mersenne 1323.59 74.86 206.77
poly_4_mersenne 1323.57 82.67 200.36
blake3_c 1285.91 340.01 552.63 no 32bit portability
GoodOAAT 1052 71.62 192.19
pearsonbhash256 998.9 167.05 261.29
SipHash 980.88 127.77 246.19
MicroOAAT 977.6 59.61 185.06 100% bias, distrib, BIC
FNV1a 791.84 69.69 177.84 bad seed, zeros, fails all tests
sdbm 791.84 67.69 177.06 bad seed 0, fails all tests
FNV64 791.82 70.24 159.29 fails all tests
bernstein 791.82 68.63 180.71 bad seed 0, fails all tests
beamsplitter 789.22 682.45 1150.3 UB, too many bad seeds
HalfSipHash 755.78 114.47 243.72 zeroes
chaskey 753.23 153.42 288.26 PerlinNoise
x17 527.9 98.78 184.09 99.98% bias, fails all tests
JenkinsOOAT_perl 452.49 118.78 194.78 bad seed 0, test FAIL
MurmurOAAT 452.49 113.07 197.83 bad seed 0, 1.5-11.5% bias, 7.2x collisions, BIC, LongNeighbors
JenkinsOOAT 452.48 142.85 213.93 bad seed 0, 1.5-11.5% bias, 7.2x collisions, BIC, LongNeighbors
crc32 392.1 131.62 204.58 insecure, 8590x collisions, distrib, PerlinNoise
sha1-160 364.95 1470.55 1794.1 Comb/Cyclic low32
rmd256 362.49 617.02 815.44 Bad seeds
blake2b-256_64 356.97 1222.76 1435.0
blake2b-224 356.59 1228.5 1425.87
blake2b-160 356.08 1236.84 1458.15
blake2b-256 355.97 1232.22 1443.31 Sparse high 32-bit
md5-128 353.76 638.29 803.39
md5_32a 353.64 629.85 799.56 Sparse high 32-bit
sha1_32a 353.03 1385.8 1759.9 Cyclic low32, 36.6% distrib
rmd128 334.36 659.03 838.32 Bad seeds
blake2s-128 295.3 698.09 1059.2
pearsonhash64 287.95 174.11 196.50 Avalanche, Seed, SSSE3 only. broken MSVC
pearsonhash128 287.95 171.72 194.61 Avalanche, Seed, SSSE3 only. broken MSVC
pearsonhash256 264.51 184.87 218.79 Avalanche, Seed, SSSE3 only. broken MSVC
blake2s-256 215.28 1014.88 1230.38
blake2s-160 215.01 1026.74 1239.54
blake2s-256_64 211.52 1044.22 1228.43
blake2s-224 207.06 1063.86 1236.50
rmd160 202.16 1045.79 1287.74 Bad seeds, Cyclic hi32
sha2-256_64 148.01 1376.34 1624.71 Bad seeds, Moment Chi2 7
sha2-256 147.8 1374.9 1606.06 Bad seeds, Moment Chi2 4
sha2-224_64 147.6 1360.1 1620.93 Bad seeds, Cyclic low32
sha2-224 147.13 1354.81 1589.92 Bad seeds, Comb low32
asconhashv12 144.98 885.02 1324.23
sha3-256 100.58 3877.18 4159.79 PerlinNoise
sha3-256_64 100.57 3909 4174.63 PerlinNoise
asconhashv12_64 86.73 684.02 606.93
floppsyhash 35.72 1868.92 1411.07
tifuhash_64 35.6 1679.52 1212.75 Cyclic low32
Problems include:
- Bad Seeds. A random seed is often used to initialise the hash. This problem relates to having a bad seed..
- Undefined behaviour (UB). This includes Misaligned, oob (Out of bounds), Signed integer overflow and Shift exponent overflow.
o1hash is the fastest, and a quick and dirty hashing method. It is generally not secure. t1h (Fast Positive Hash) requires AES-NI (Intel Advanced Encryption Standard Instructions) and is one of the fastest hashes at 22.785 Gbps. It has fairly good security levels. Meow comes in around 17.378 Gbps. We can see that SHA-1-160 runs as 364 Mbps, while Meow runs at 17.378 Gbps. Blake 3 is one of the fast cryptography hash and has a rate of 1.285 Gbps, and Blake 2 gives a rate around 215 Mbps. SHA-3 gives hashing rates of 100.58 Mbps.
Google recommend the following for 64-bit hashes without quality problems:
- xxh3low
-
wyhash
-
ahash64
-
t1ha2_atonce
-
FarmHash
-
halftime_hash128
-
Spooky32
-
pengyhash
-
nmhash32
-
mx3
-
MUM/mir
- fasthash32
Hash-based Signatures

With hash-based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature, unless we create a stateless method, such as SPHINCS+ [1]. Currently NIST have the final round for the Post Quantum Cryptography competition, and for digital signatures, SPHINCS+ is one of the alterative finalists (alongside Picnic).
Hash-based signature (theory)
- BiBa (Go). BiBa. An overview of BiBa One Time Signature [9]. Basically the method involves us taking a hash of a value using a standard hashing method, such as with SHA-256. There will then be \(2^{256}\) different hashing values. We aim to create a signature for a message, so Bob (the signer) selects a number of random values for his private key value and then publishes the hash of each of these (\(P_1\), \(P_2\), etc). He then sends these public keys to Alice. Now when Bob wants to sign a message, he will take one of his private key values, and then hashes it, and then determines the bin that it should be placed. In this case, we could use the \(\pmod N\) function on the hash, and where \(N\) is the number of bins. If we select \(2^{10}\) there will be 1,024 bins.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature [9].
Hash-based signature (stateful)
- BLISS - Post-quantum signing. BLISS. One of the alteratives to the usage of our existing public key methods is the usage of lattice cryptography, and especially in the usage of Ring Learning With Errors (RLWE). An important application is within digital signatures, and where Bob will sign something with his private key, and then Alice can prove that he signed it with his public key. One post-quantum signature method is BLISS (short for Bimodal Lattice Signature Scheme) [8]. It was created by Léo Ducas, Alain Durmus, Tancrède Lepoint and Vadim Lyubashevsky in 2013.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Hash to Obtain Random Subset (HORS) [3] is a quantum robust hashed-based one-time signature. With this we create a series of integers for our private keys and organise into an indexable form. Then we hash them to a sequence of public key values. Next we segment the hash of the message into a series of n-bit integer values. The signature is then achieved through a look-up of the value in the public key list.
- Lamport Signatures. Lamport. Outlines Lamport signatures [7]. When we sign a message we take its hash and then encrypt with our private key. The public key is then used to prove it, and will prove that we signed it with our private key. The Lamport signature uses 512 random hashes for the private key, and which are split into Set A and Set B. The public key is the hash of each of these values. The size of the private key is 16KB (2×256×256 bits) and the public key size is also 16 KB (512 hashes with each of 256 bits).
- Winternitz Signatures (W-OTS). Winternitz. Outlines Winternitz signatures [4, 5]. W-OTS uses relatively small key and signatures sizes, and is thought to be quantum robust. It generates 32x256 bit random private keys. We then hash these a number of times, and is defined by a parameter (w). If we use w=8, we hash the private keys by (2w). This creates 32x256 bits public keys. The signature is the created by taking eight bits at a time, and then the 8-bit binary int (n) is subtracted from 256 and the private key is the hashed 256-n times. The signature is then 32 hashes which are derived from random private keys. To verify the signature, the recipient parses the hash of the signature (using 8 bits at a time, and extracting the 8 bit int, n).
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method [6], and which is used within speeds-up of Hashing-based signature methods. Using methods such as SHA-1 and SHA-2 (aka SHA-256) will be inefficient as they tend to compress the data inputs through a number of stages. Haraka v2 [6] is different as focuses on inputs of just 256 bits (32 bytes) or 512 bits (64 bytes). This makes the method useful when we are dealing with key and hash values, and is especially useful for hash-based signatures. The output is 256 bits long, but where the input can be either be 256 bits (Haraka256) or 512 bits (Haraka512). These lengths are typically for the outputs of modern hashing applications. The Haraka method, too, has been optimized with AES instructions (AES-NI - Intel Advanced Encryption Standard New Instructions) and which are supported within the hardware of the processor. As Haraka is focused on short messages, the number of rounds within the hashing process has been reduced.
Hash-based signature (stateless)
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ digital signature. SPHINCS digital signature. Outline of the a SPHINCS stateless digital signature method [1].
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
Hash-based signature (Merkle-based)
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
Introduction
Many of the problems we see on the Internet relate to the lack of trust within transactions. The emails you receive and the Web sites that you visit often have very little trust built into them. For trust the email address of the sender, but anyone can fake that address. So increasingly we create a digital signature, and where we sign our messages. In this way, we can check for authentication, integrity and non-repudiation.
With the Alice creates a key-pair: a public key and a private key. She then takes a hash of the message, and then encrypts this hash with her private key, and passes the message and the signature to Bob. Bob then reads the message and takes a hash of it. He then decrypts Alice's signature with her public and checks the hashes. If they match, he knows that she signed and that it has not been changed along the way:
Currently, we often use RSA, DSA and ECDSA to sign our messages. These are based on the difficulty of finding out the factors of a number and on the processing of discrete logarithms. At the current time these methods are computationally hard problems, but with quantum computers, they become much easier. This was shown by Peter Shor who illustrated that it was possible to crack them in polynomial time.
Of all the methods that are being proposed, the hash-based methods look as if they have a good chance of success of creating quantum robust signatures. methods and code-based methods are being researched, but the usage of hashing methods is already well and could provide the best alternative to the existing methods. Hashing methods, too, often bring other advantages, such as forward secure, which means that a key which is cracked will not reveal all the previous keys.
Merkle trees
The root of hash-based methods isin Merkle trees, and which are a way of hashing is used in many applications, including with Bitcoin, Ethereum, Git distribution systems, No SQL, and in many P2P applications. With a Merkle tree we take our data elements, and then hash them, and take pairs of these hashes to create a new hash, and so we build a table. At the top of the tree is the root element (in this case Hash1234):

In this way, we can use the tree to see if we have matching data on systems.On a P2P network, we can transfer a file by splitting it into data segments and then distributing these segments across the network. A trusted source will have the complete Merkle tree for rebuilding the file, and a client can thus rebuild from the Merkle tree and determine the parts of the file which are still missing. Once transferred the root hash (and all the other hashes) will then match. In its core method, the Merkle Signature Scheme (MSS) has serious performance and memory issues, but enhanced methods such as XMSS create with much less of a performance hit.
One-time signatures (Lamport)
The core method used in hash-based signatures is that of the one-time signature, and where we create a new key pair for every method we need to create. If the keys were reused, an attacker could start to learn the private key, and thus spoof messages. One of the first methods was produced by Leslie Lamport and Whitfield Diffie, in 1979, and is defined as:
- We create two data sets with 256 random 256-bit numbers (Set A and Set B). These are the private key (512 values).
- we take the hash of each of the random numbers. This will give 512 hashes and will be the public key.
- We then hash the message using and then test each bit of the hash (0 ... 255). If it is a 0, we use the ith number in Set A, else we use the ith number from Set B.
- The signature is then 256 random numbers (taken from either Set A or Set B) and the public key is the 512 hashes (of Set A and Set B).
The public and private keys are then each 16KB in size. A demo of the method is here.

Figure 1: Lamport method
The major problem with the method is that a key pair for every message. also in 1979, found a solution with Merkle trees.
One-time signature (W-OTS)
To improve performance method (and which reduced key sizes), Merkle proposed Winternitz OTS (named after Robert Winternitz). With this method was possible to sign many bits at the same time. The method is:
- We create 32 256-bit random numbers. These 32 values will be our private key.
- We then hash each of these values 256 times. These 32 values will be our public key.
- We now take the message and hash it using SHA-256. This produces 32 8-bit values (N1, N2 ... N32).
- Next we take each 8-bit value in the hash of the message, and then hash 256-N times (where N is the value of the 8-bit value).
- To prove the signature, we take the message and hash it with SHA-256, and then take each 8-bit value. We then hash the 8-bit signature value by the number of times defined by the message hash value (N1, N2..). The result for each operation should equal the public key value.
This is illustrated below in Figure 2. A demo of the method is here.

Figure 2: W-OTS
Hash-based Signatures
The methods such as W-OTS and Lamport only provide for a one-time signature. In order to sign many messages, we can use the Merkel signature scheme (MSS). With this we take a hash of the keys and build these as the leaves of the tree. The root of the tree is then the public key - the verification key. We then just use the private key of the W-OTS method to create the signature. The sender also sends the authentication path, which is the neighbouring nodes within the path and which leads to the root of the tree. The recipient can then rebuild the tree using the verification key (which can be received a digital certificate) and the authentication path. For the next message we move onto another key pair and where the index of the key part is revealed.
In the following example we have our root as the public key, and then want to sign with Key3. We then show the authentication path which takes us to the root (as defined in the bold arrows):

Conclusions
Hashed-based methods look to be a strong contender for weaning us off RSA, DSA and ECDSA, but we will have to look at the stateful generation of keys. For this we will have to generate a bank of key pairs (2, 4, 8, 16, etc) and then create the public key from the root of the Merkle tree. We must then remember the keys we have used previously, and only use an unused one. Once we use our new key pair, we then show our working-out as to how the private key is integrated into our tree. It is a bit like a teacher marking a question correctly, and asking for the working out that go you to the answer.
References
[1] Bernstein, D. J., Hopwood, D., Hülsing, A., Lange, T., Niederhagen, R., Papachristodoulou, L., ... & Wilcox-O’Hearn, Z. (2015, April). SPHINCS: practical stateless hash-based signatures. In Annual international conference on the theory and applications of cryptographic techniques (pp. 368-397). Springer, Berlin, Heidelberg [paper].
[2] Bernstein, D. J., Hülsing, A., Kölbl, S., Niederhagen, R., Rijneveld, J., & Schwabe, P. (2019, November). The SPHINCS+ signature framework. In Proceedings of the 2019 ACM SIGSAC conference on computer and communications security (pp. 2129-2146) [paper].
[3] Reyzin, L., & Reyzin, N. (2002, July). Better than BiBa: Short one-time signatures with fast signing and verifying. In Australasian Conference on Information Security and Privacy (pp. 144-153). Springer, Berlin, Heidelberg [paper].
[4] Merkle, R. C. (1989, August). A certified digital signature. In Conference on the Theory and Application of Cryptology (pp. 218-238). Springer, New York, NY.
[5] Hülsing, A. (2013, June). W-OTS+–shorter signatures for hash-based signature schemes. In International Conference on Cryptology in Africa (pp. 173-188). Springer, Berlin, Heidelberg.
[6] Kölbl, S., Lauridsen, M. M., Mendel, F., & Rechberger, C. (2016). Haraka v2–efficient short-input hashing for post-quantum applications. IACR Transactions on Symmetric Cryptology, 1-29. [here]
[7] Lamport, L. (1979). Constructing digital signatures from a one-way function (Vol. 238). Technical Report CSL-98, SRI International. [paper]
[8] Ducas, L., Durmus, A., Lepoint, T., & Lyubashevsky, V. (2013, August). Lattice signatures and bimodal Gaussians. In Annual Cryptology Conference (pp. 40-56). Springer, Berlin, Heidelberg [paper].
[9] Perrig, A. (2001, November). The BiBa one-time signature and broadcast authentication protocol. In Proceedings of the 8th ACM Conference on Computer and Communications Security (pp. 28-37) [paper] .
Hashing (Simularity)

Similarity hashes allow for two data objects to be compared for their similarity.
Similarity assessment methods
The following relate to the basic methods used for string similarity:
- String similarity String similarity. This measures edit distance (including Levenshtein distance), Jaro (including Jaro-Winkler), and QGrams.
- String enthropy String enthropy. Measurement of the entropy of strings.
- Soundex Soundex. Soundex uses a phonetic algorithm to classify a sound as it is pronounced. It focuses on matching phrases which have minor spelling errors.
Similarity hashes
The following are the tips related to similarity hashing:
- Similarity hash: SimHash (Charikar similarity) in Python Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash (Nilsimsa similarity) Nilsimsa. The Nilsimsa similarity is used to find similarities between spam emails.
- Context Triggered Piecewise Hashes (CTPH): ssdeep CTPH similarity. Kornblum [6] created ssdeep and which computes fuzzy hashes. This aims to match similar byte sequences, no matter if there are differences between these sequences. For this we break a file up into fragments with a rolling hash function. We then produce a small hash for each of those fragments. These are then aggregated to produce the complete hash of a file. In comparing file signatures, we treat the resultant hash value as a string, and then uses an edit distance method to compare.
- TLSH (A Locality Sensitive Hash) TLSH similarity. In malware analysis and in text similarity, we often have to identify areas of data within files which are similar. One method is TLSH (A Locality Sensitive Hash), and which was defined by Oliver et al [7]. It is used - along with ssdeep - by VirusTotal to identify a hash value for malware.
- Minhash (Jaccard similarity) Jaccard similarity. The Minhash method is used to find similarities between strings, files and metadata.
- Counting identical elements (HyperLogLog) HyperLogLog. Counting the number of identical elements.
Hazmat cryptography

The Cryptography library in Python contains interfaces to common cryptographic algorithms, including symmetric key methods, hashing, public key, and key derivation functions. Many of these are contained with the Hazmat (Harzardous Material) primative setup.
Hashing, HMAC, CMAC, Poly1305 and HKDF
-
Hazmat Hashes. Hazmat Hashes. This includes the hashing methods in the Hazmat cryptography library. This includes Blake2p, Blake2s, MD5, SHA1, SHA224, SHA256, SGA384, SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHA512, SHA512-224, SHAKE128 and SHA256.
-
Hazmat Hashes. Hazmat Hashes. In this case we will implement Python code to determine SHA1, SHA2, SHA3, Blake2, MD5 and SM3 hashes.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
- Hazmat HKDF. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
- Hazmat CMAC. Hazmat CMAC. CMAC methods using the Python cryptography primitives.
- Hazmat Poly1305. Hazmat Poly1305. Poly1305 methods using the Python cryptography primitives.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
Symmetric key
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat. Implementation of ChaCha20/Poly1305 with a random key using Hazmat.
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat. Implementation of AES GCM with a random key using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hazmat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Hazmat Symmetric Key Padding. Symmetric key. This includes the coverage of padding with Hazmat.
- Hazmat Symmetric Key Padding. Symmetric key. This includes the coverage of padding with Hazmat.
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
- Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . With 3DES encryption, we use a 128-bit key and a 64-bit IV value. The two modes supported are ECB (without salt) and CBC (with salt). The DES algorithm has been around for a long time, and the 56-bit version is now easily crackable (in less than a day on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases, and splits the key into two. Overall the key size is typically 112 bits (with a combination of the three keys - of which two of the keys are the same). In this case we will use PKCS7 padding, and which fills the input data with a value that is equal to the number of padding bytes. Overall, DES has a 64-bit block size, and which equates to eight ASCII characters.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key . And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.
Asymmetric key
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- ECC key generaton with Hazmat. Elliptic Curve key gen. Creating ECC keys using Hazmat and Python.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- Hazmat RSA signing (with key values). RSA signing with Hazmat. RSA signing using Python and with Hazmat (with key values).
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here]
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Signatures. DSA Signatures. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. The ECDSA method is an extension of DSA, but implemented with elliptic curve (EC) methods. As with most public key signing methods, we take a hash of a message, and then apply a private key to create a signature (\(r,s\)). This is done by creating a random value (\(k\)) to produce the signature. The signature is then verified using the associated public key. This then verifies the creator of the signature and that the message has not been changed.
Digital Signature: ECDSA/EdDSA
- ECDSA with Hazmat. ECDSA wih Hazmat. This outlines ECDSA with Hazmat.
- Ed25519 for EdDSA signatures with Hazmat. EdDSA: Ed25519. This page uses the Hazmat primitives for the cryptography library.
- Ed448 for EdDSA signatures with Hazmat. EdDSA: Ed448. This page uses the Hazmat primitives for the cryptography library.
- Ed25519 using NaCl. Ed25519. This page uses the NaCl port from libsodium.
- ECDSA Signatures with Hazmat (SECP256R1, SECP384R1, SECP521R1, SECP224R1, SECP192R1, and SECP256K1). ECC Signatures. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and then creates an ECDSA signature for a given message.
Digital Signature: RSA
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
Key exchange: ECDH/X25519
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives and showing the byte values for the key.
Tokens
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
Homomorphic Encryption

Homomorphic encryption supports mathematical operations on encrypted values. Partial Homomorphic Encryption (PHE) supports a few arithmatic operations, while Full Homomorphic Encryption (FHE) supports add, subtract, multiply, and divide. Homomorphic encryption normally involves a public key to encrypt the data, and a private key to decrypt it. There have been four main generations of homomorphic encryption, and the most recent being the HEAAN method.
Simple
- Simple Homomorphic Cipher. Hom. This outlines a Simple Homomorphic cipher.
- Simple Homomorphic Cipher (Python). Hom. This outlines a Simple Homomorphic cipher with Python.
- Full Homomorphic Cipher with a Public Key. Public key. This outlines a Simple Homomorphic cipher using a public key
ElGamal
- ElGamal Homomorphic Cipher (Go). ElGamal. This outlines ElGamal Homomorphic cipher with Go.
- ElGamal Homomorphic Cipher (Go) - Divide. ElGamal. This outlines ElGamal Homomorphic cipher with Go with divide.
- ElGamal Homomorphic Cipher (Go) - Additive. ElGamal. This outlines ElGamal Homomorphic cipher with Go with addition.
- ElGamal Homomorphic Cipher for Multiplication (Python). ElGamal. This outlines ElGamal Homomorphic multiplication with Python.
- ElGamal Homomorphic Cipher for Division (Python). ElGamal. This outlines ElGamal Homomorphic division with Python.
- ElGamal Homomorphic Cipher for Addition (Python). ElGamal. This outlines ElGamal Homomorphic addition with Python.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (Python). ElGamal. This outlines ElGamal Homomorphic subtraction with Python.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
RSA
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
ZKP
- Full Homomorphic Cipher to determine if Bob is older. Older. This outlines a Simple Homomorphic cipher to determine if Bob is older than Alice.
- Full Homomorphic Cipher to determine matching password. Password. This outlines a Simple Homomorphic cipher to determine if a password matches
- Interactive ZKP With Probablistic Methods. ZKP. Interactive ZKP With Probablistic Methods using Python.
- Full Homomorphic Cipher for Millionaire's Problem. Millionaire. This outlines a Simple Homomorphic cipher for the Millionaire's Problem
Voting
- Trusted voting. Trusted. A trusted voting method.
Secret share
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Lattice
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
Full Homomorphic Cipher
- Full Homomorphic Cipher for 2-bit Adder. Adder. This outlines a Simple Homomorphic cipher for a 2-bit adder with DGHV.
- Full Homomorphic Cipher for Full Adder. Full Adder. This outlines a Simple Homomorphic cipher for a full adder with DGHV.
- Full Homomorphic Cipher for 4-bit Adder. Adder. This outlines a Simple Homomorphic cipher for a 4-bit adder with DGHV.
- Full Homomorphic Cipher for 4-bit Adder/Subtractor. Subtract. This outlines a Simple Homomorphic cipher for a 4-bit adder/subtractor with DGHV.
- Full Homomorphic Cipher to XOR two integers. X-OR. This outlines a Simple Homomorphic cipher to X-OR two integers
Paillier
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier) .
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Damgård-Jurik Homomorphic Encryption With Secret Shares. Damgård-Jurik Method. Two of the major areas of developments within cybersecurity will be the usage of homomorphic encryption, and in the usage of Shamir secret sharing. With homomorphic encryption, we can encrypt values, and then operate on them with arithmetic functions (such as add, subtract and multiply), and with Shamir secret sharing, we can split secrets into shares, and then distributed them over networks. These approaches will take privacy to new levels. So let’s look at the Damgård-Jurik method.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Learning with Errors (LWE)
- Learning With Errors . LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret key value (s) and another value (e). Next we select a number of values (t[]) and calculate g[] = t[] x s + e. The values of g[] and t[] become our public key.
- Public Key Encryption with Learning With Errors (LWE). LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret value (s) and which is our private key. We then create a public key which is based on random numbers (A), and then generate another set of numbers (B) which is based on A,s and random errors e. An example of encryption with multiple bits is given.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE)
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Others
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
- SIDH Go. SIDH. Post-quantum key exchange.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Anonymous crypto. Anon. Anonymous crypto.
- Rho factorization. Rho. Rho alogorithm.
- Post-quantum signing (BLISS). BLISS. BLISS method.
Homomorphic Encryption with Krytology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Homomorphic hashing
- Homomorphic Hashing with Golang. Homomorphic hashing. Normally with hashing methods, we need to take all the previous data and new data in order to create a new hash value for our data. In a homomorphic hashing method, we can basically take the previous hash, and then add on any new data values. We can also remove previous data values from our hash, too. This is more efficient in computing, as we do not have to process all of our data into a new hash, and can use simple homomorphic operations for the computation. The method we will use (LtHash) was initially defined by Bellare and Micciancio and updated Lewi et al at Facebook.
Identity Based Encryption (IBE)

This page outlines a few basic principles around the usage of IBE.
Identity Based Encryption (Pairing based)
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pair-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Identity Based Encryption (Others)
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Güther's implicitly certified identity-based public keys (IBE). Günther. This method allows Bob to generate Alices public key from her identity and publicly available parameters.
- Girault's self-certified public keys (IBE). Girault. This method allows Bob to generate Alices public key from her identity and publicly available parameters, and where we use an RSA key pair to self-certify Alice's public key.
Intrusion Detection Systems (IDS)
- Intrusion Detection Systems. Snort. This outlines some of the basics of IDS, including the requirement for Intrusion Detection Systems (IDSs), and where they are used.
- Advanced Network Forensics (Snort). Adv Network Forensics. This provides information on how to detect threats through network forensics with Snort
Snort

- Snort IDS. Snort. This is a Snort Analyser.
- Snort IDS 2 with rules editor. Snort. This provides information on how to detect threats through network forensics with Snort, and with an editing function for rules.
Presentation
IoT

The key objectives of this page are: Understand how a Pen Tester can generate vulnerabilities and test using the Metasploit framework; Define the options and payloads required to generate and use vulnerabilities; and Gaining remote access.
Devices
- Access the Wi-fi kettle. Go. This page outines how to access a wi-fi enabled kettle.
- Philips Hue Wireless Lighting. Go. This page shows how to use RESTful Web services to access to the Hue Led Lamps.
- Kali and R-PI. Go. This page shows the setup of a security testing infrastructure using a Raspberry Pi (R-PI) and a wifi access point.
- Kali, R-PI and RF electrical socket. Go. This page shows the control of an RF electical socket from a RPI.
- Capture from a Polar H10 heat rate sensor. Go. This page shows the capture of the Polar H10 heart sensor with an Ubertooth One.
- Trusted IoT: Linking IoT Devices to NFTs. Go. This page outlines a research paper which links a device to an NFT (Non-fungible Token).
Shodan Scanning
-
IoT Scan (Shodan). Go. This page includes a search of the Internet for key terms, such as for "apache", "mysql" and "cisco".
- IoT Banner Scan (Shodan). Go. This page includes a search of the Internet for key terms with the banner as a result (for the Top 10)
- Internet Services (Shodan). Go. This page includes a search of the Internet for key terms and display the IP address and port.
IoT Libraries
- libDisco with Go. libDisco. libdisco is a Golang library which can be used to create secure connections. It is based on the STROBE protocol framework. Symmetric cryptographic primitives rely on SHA-3 permutation, and asymmetric cryptographic primitives on X25519 and ed25519. STROBE defines a range of cryptographic protocols to integrate with IoT devices. In order to reduce processing, energy and memory requirements, it only uses Keccak (SHA-3) to encrypt and authenticate messages.
COSE/COBR
In computer security, we often have to represent binary data, in single values or groups of characters, bytes, words, long words, signed integers, floating-point values, double-precision floating-point values, and so on. This might be in the form of a data object, a signature or even encrypted content. For this, the ANS.1 DER format is often used, such as presenting digital certificates and signatures. An improvement on this for small messages with security is Concise Binary Object Representation (CBOR) — and which is defined in RFC8949 [1]. While JSON represents text-based data objects CBOR focuses on binary objects. It has been designed to create a lightweight encoder and decoder. This supports the use of CBOR within an IoT infrastructure. The data, also, does not require a data schema to be able to decode it, along with being extensible. CBOR defines the format of binary data with data objects and messages. We can then integrate security with CBOR Object Signing and Encryption (COSE), and which is defined in RFC8152 [2]. This includes signatures, message authentication codes (MACs), encryption and creating serialised objects.
- 128-bit AES GCM. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) can then build on this to include signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use a symmetric key to encrypt a message, and then decrypt it. In this case we will use AES GCM with a static 128-bit key ("0x000102030405060708090a0b0c0d0e0f").
- 256-bit AES GCM. Go. In this case we will use AES GCM using a random 256-bit key (32 bytes).
- EdDSA. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) [2] can then build on this to includes signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use EdDSA to create a signature for a message.
- ECDSA. Go. In this case we will use ECDSA to create a signature for a message.
- HMAC. Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT. Go. In this case we create a CWT token, and sign with an HMAC signature.
- ECDH. Go. In this case we create a symmetric key from ECDH. For this we will derive a shared key from the public key of Alice and Bob, and then define a single recipient which can derive the CEK (Content Encryption Key) using their private key. We will use the curves of P-256 (secp256r1), P-384 (secp384r1), P-521 (secp521r1) or SECP256K1 (as used with Bitcoin).
- RSA using COSE and CBOR. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\).
- RSA: dQ, dP and InvQ. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). The key pair also includes \(dQ\), \(dP\) and \(InvQ\), and these can be used with the Chinese remainder theory to optimize the decryption process.
Metasploit
- Armitage and Metasploit. Go.
- Exploiting Android with Metasploit. Go.
- Exploiting Android with Metasploit - Part 2. Go.
- Exploiting Windows/Mac OS X with Metasploit. Go.
- Remote Desktop Windows/Mac OS X with Metasploit. Go.
- Metasploit. Go.
- Internet of Things Security. Go.
- Metasploit (Enumeration and Scanning). Go.
- Metasploit (Malware). Go.
IP

 The following are a few interesting techniques around IP addresses:
The following are a few interesting techniques around IP addresses:
- Your details. IP. This shows your browser details.
- IP address analyser. IP. This involves converting an IP address to the host and network part of the address.
- IP subnet analyser. IP subnets. This involves converting an IP address to the host and network part of the address.
- IP address analyser. IP. This involves analysing IP addresses.
- Max subnets. Max subnets. This involves converting an IP address to the host and network part of the address.
- Route summarization. Summarization. This involves converting an IP address to the host and network part of the address.
- Whois. Whois. This does a basic Whois on a domain.
- URL Obfuscation. Obfuscation. This outlines URL obfuscation.
- HTTP Responses. Test. HTTP.
- Capturing Network Packets (Python). WinPCap. HTTP.
Cisco related
- Routing table. Routing table. This involves viewing a routing table for a Cisco device.
- ACL Generator. ACL. This involves a simple calculator for ACLs on network ranges.
- EIGRP metrics. EIGRP. Learn the basics of EIGRP metrics.
- VoIP B/W. VoIP. Calculate bandwidth for VoIP.
- Wild Card. Wild Card. On a Cisco device a wildcard mask is used to identify the parts of an IP address that need to be matched. It thus uses a wildcard mask, where a 0 in the bit position identifies that the device should match that bit, else a 1 shows that it should ignore it.
Protocols
- HTTP. HTTP. Show the request and response for HTTP.
- Ping analyser. IP. This involves converting a ping of a site.
IP Challenges
-
IP Test 1. IP Test. IP Classification test. This is a simple test which generates a range of IP addresses, and you must determine the IP address classification.
IP Subnet Challenge 1 Demo
-
IP Test 2. IP Test. IP Classification test Part 2. This test provides an address classification, and the user must find the addresses which are of this classification.
IP Subnet Challenge 2 Demo
-
IP Test 3. IP Test. IP Classification test Part 3. This test provides an address classification, where the network part of the address is determined.
IP Subnet Challenge 3 Demo
Subnet Challenges
- Subnet Test 1. Subnet Test. Subnet Test.
-
Subnet Test 2. Subnet Test. Subnet bits.
- Subnet Test 3. Subnet Test. Find the nth usable subnet. This test involves finding the nth usable subnet.
- Subnet Test 4. Subnet Test. Maximum subnets. This is a test page to determine the maximum number of subnets and hosts/subnet for IP classed addressing.
- Subnet Test 5. Subnet Test. Maximum host/subnet. This is a test page to determine the maximum number of hosts per subnet.
- Subnet Test 6. Subnet Test. Determine the required subnet mask for a given number of subnets. This is a test page to determine the required subnet mask for a given number of subnets and a given IP address classification.
- Subnet Test 7. Subnet Test. Determine the required subnet mask for a given number of host/subnet. This is a test page to determine the required subnet mask for a given number of hosts per subnet and a given IP address classification.
- Subnet Test 8. Subnet Test. Route summarization. This involves a calculation on route summarization.
- Subnet Test 9. Subnet Test. Binary to IP.
- Subnet Test 10. Subnet Test. Hex to IP.
-
Subnet Test 13. Subnet Test. Wild card mask network bits. Find the number of bits in the network part of the wild card mask. IP Wildcard challenge
- Subnet Test 14. Subnet Test. Wild card mask host bits. Find the number of bits in the host part of the wild card mask. IP Wildcard challenge
- Subnet Test 15. Subnet Test. Wild card mask ... find the network address. Find the network for the wild card mask. IP Wildcard challenge 2
- Subnet Test 16. Subnet Test. Find a matching IP address for a network and wild card mask. Find the IP for a network and a wild card mask.
- Subnet Test 17. Subnet Test. Find an address which is on a given network. Find an IP address on a network, for a given network address and subnet mask.
- Subnet Test 18. Subnet Test. Find an IP address on the same network. Find an IP address on the same subnet.
- Subnet Test 19. Subnet Test. Find subnet. Convert subnet mask.
- Megatest. Subnet Test. Challenging test for subnets.
JavaScript

JavaScript code allows execution within the browser, rather than on the server. It is often faster than code that runs on a server. Along with this we can also use Node.js, and which runs JavaScript code on a server.
Symmetric key
- AES. AES. In this example, we will use either a pre-generated key or a random one, and use AES (Rijndael) encryption.
- ChaCha20 and Poly1305. ChaCha. This page outlines Poly1305 and ChaCha20. ChaCha20 is a symmetric key method and Poly1305 is a message authentication code (MAC). They were created by Daniel J. Bernstein, and are alternatives to AES and HMAC.
- CMS (Padding). CMS. This page uses PKIJS encrypting on CMS. With CMS we can This document describes the Cryptographic Message Syntax (CMS). With this we can encapsulate an message within an encrypted entity.

Hashing
- Hash. Hash. This page defines a JavaScript Hash calculator. This uses a client-side JavaScript code to determine the hash signatures of a text value.
Signatures
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
- Boneh–Lynn–Shacham (BLS) signature. BLS. Boneh–Lynn–Shacham (BLS) signature method produces short signatures. They use elliptic curve pairing (and which are also known as bilinear maps).
Key exchange
- ECDH. ECDH. Elliptic Curve Diffie Hellman (ECDH) is used to generate a shared key. This implementation uses Elliptic Curve Cryptography (ECC) with JavaScript.
CryptoJS
- CryptoJS. CryptoJS. This page uses client-side JavaScript code to hashing, encrypt and sign, including for symmetric key (AES), streaming ciphers, hashing methods, and HMAC.
Blockchain
- PATRICIA trie. PATRICIA. In the following, we have the Top 2,500 Web sites in the world, and implemented with a Radix Trie (aka PATRICIA trie) In the following we have the Top 2,000 web sites on the Internet, and which have been indexed using the PATRICIA trie.
Public key
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
- RSA. RSA. RSA is an asymmetric encryption algorithm, which uses two keys, one to encrypt and the other to decrypt. It was created in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman, and is still one of the most widely used encryption methods. A typical application is in authenticating a sender, where the senders private key is used to encrypt a message, and then is decrypted by the receiver with the senders public key (which is known to anyone who wants it). It is also typically used for encrypting disks/files, such as for EFS.
Digital Certificates
- X.509 certificates in JavaScript. RSA and ECDSA Signed certificates. This page will generate either RSA and ECC key pairs, and then generate X.509 certificates, using either a signature of SHA1withRSA or SHA256withECDSA. For RSA signing we use an RSA private key to sign the certificate, and with ECDSA signing we use an ECC private key to sign the certificate.
Tokens
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
Random
- Random number generator. Rand. In the past, encryption and decryption had to be done through native code libraries, such as with Bouncy Castle and OpenSSL. With the increasing processing power of Web browsers, it is now possible to use encryption using JavaScript, which thus provides client-side processing of data. This Web page uses Javascript encryption, and generates a random 256-bit text key or a hex version. The 256-bit key is generated by generating 60 random numbers (from 0-25), and converting these to an ASCII character.
Malware obfuscation
- Malware obfuscation. Obfuscation. A malware writer will often hide certain keywords from the browser/human by encoding them in another format. This is typically done for hex coding (\xZZ), 16-bit unicoding (\uZZZZ) and octal coding (\ZZZ). To test, enter a value, and then press the button and it will convert encoded string.
Message Authentication Codes
- Chaskey (MAC). Chaskey. Chaskey Cipher is light-weight cryptography method for signing messages (MAC) using a 128-bit key. The hardware implementation only requires 3,334.33 gate equivalent with an operating clock frequency of 1 MHz (whereas Keccak requires 4,658 GE). In the page we create the Mac signature and also encrypt for CBC.
Other
- Password generation/hashing. Hashing. Linux can use salted passwords where the username, hashing method and hashed password are stored in a password file [More details]. The main methods are
Hashing

At times we need to generate secrets, such as encryption keys, from passwords or nonce values. A Key Derivation Function (KDF) is a verifiable way of doing this.
Key Derivation Functions (KDFs)
The following are the tips related to hashing:
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Password strength. Test. This outlines the strength of various passwords types.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
HKDF
The following are the tips related to Key derivation hashing:
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Hazmat HKDF for different hashing methods. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
-
HKDF key derivation with OpenSSL [
here]
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
PBKDF2
The following are the tips related to Key derivation hashing:
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- AES GCM (Python) with PBKDF2. AES GCM (Python) with PBKDF2.
- Fernet with PBKDF2 . AES GCM (Python) with PBKDF2.
- PBKDF2 key derivation. AES GCM (Python) with PBKDF2.
- Key Rotation with Fernet. AES GCM (Python) with PBKDF2.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Bcrypt
The following are the tips related to Key derivation hashing:
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- BCrypt. BCrypt. BCrypt with Rust.
-
Hash to password with Go. Hashing to Argon2, Scrypt and BCrypt. Hash to password with Go, including Argon2, Scrypt and BCrypt.
scrypt
- scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Argon 2
The following are the tips related to Key derivation hashing:
- Argon 2. Go. Outline of Argon2.
- Argon 2 with NaCl. Go. Outline of Argon2 using NaCl.
- Argon 2. Argon 2. Argon 2 with Rust.
- Balloon. Go. Outline of Balloon.
Other
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
- Double ratchet. Go. Outline of double ratcheting.
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
Outline
HMAC Key Derivation function (HKDF) is used to derive an encryption key from a passphrase. Initially, HKDF creates a pseudorandom key (PRK) using a passphrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), and along with a salt value. Next, the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys [RFC 5869][article]. In this case, we will use SHA-256.
The following shows how an encryption key can be generated using HKDF, and where we need a secret and a salt value. Both Bob and Alice have the same secret and salt.

With PBKDF2 (Password Based Key Derivation Function 2), we hash for a given number of rounds:

Key exchange

Key exchange is a way for Bob and Alice to communicate and for them to agree on a shared secret. The original method defined uses discrete logarithms (Diffie-Hellman), but most modern methods use elliptic curve techniques (ECDH). As quantum computers can crack both discrete log and elliptic curve methods, there are post quantum cryptography methods proposed. This includes SIDH, CSIDH, SIKE, and NewHope.
Key interchange/generation (Diffie-Hellman)
The following relates to key interchange:
- Selecting \(g\) in Diffie Hellman. G in Diffie Hellman. Picking a safe value of the generator \(g\) in discrete logarithms.
- Diffie-Hellman. Diffie-Hellman Calculation. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Real example). Diffie-Hellman Real. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Python). Diffie-Hellman. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (pre-compute). Diffie-Hellman (pre-compute). Many sites use the same prime numbers, which can then be cracked with a pre-computing attack.
- Key generation. Key gen. This will generate keys for different methods based on a passphrase.
- Diffie-Hellman (Man-in-the-middle). DF. This outlines the man-in-the-middle method for Diffie-Hellman.
- An Alternative Diffie-Hellman method. Alterative DH. This outlines an alternative Diffie-Hellman method.
Authenticated Key Exchange
The following are the tips related to Key derivation hashing:
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- MTI/A0. MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{ax+by} \pmod p\). MTI (Matsumoto, Takashima, Imai).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0. MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{x+y} \pmod p\)
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). The resultant key is \(xyG \)
- MTI/C0. MTI/C0. This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{xy} \pmod p\)
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG\).
- MTI/C1. MTI/C1. This outlines MTI/C1, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{abxy} \pmod p\).
- MQV (Menezes–Qu–Vanstone). MQV. MQV was created Alfred Menezes, Minghua Qu and Scott Vanstone in 1995 and is an authenticated key exchange method. Alice holds a key pair \((A,a)\) and Bob has a key pair \((B,b)\). With this \(a\) is Alice's private key, and \(A=aG\) is her public key. For Bob, his public key will be \(B=aG\) and a private key of \(b\), and where \(G\) is the base point on the elliptic curve.
- HMQV (Menezes–Qu–Vanstone). HMQV. HMQV builds on MQV and adds the identity of Bob and Alice.
- ECDH with X25519 and Blake2b. ECDH with X25519 and Blake2b. This uses PyNaCl to create an authenticated key exchange and uses X25519 and Blake2b.
Elliptic Curve (ECDH) - Python
The following are the tips related to ECC:
- Elliptic Curve. Elliptic Curve. Elliptic Curve is a public key method which can also be used to generate a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with simple parameters. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
Elliptic Curve (ECDH) - Golang and Node.js
The following are the tips related to ECC:
- ECDH with Go. ECDH. ECDH with Go.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with node.js. ECDH. ECDH with node.js.
- ECDH with JavaScript. ECDH. Elliptic Curve Diffie Hellman.
Password Authenticated Key Exchange (PAKE)
The following are the tips related to Key derivation hashing:
- SPAKE2. Go. Outline of SPAKE2.
- OPAQUE. Go. Outline of OPAQUE.
- SPEKE. Go. Outline of SPEKE (Simple Password Exponential Key Exchange).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
- J-PAKE. J-PAKE. This example generates a shared key based on a shared password.
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses discrete logs.
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
PQC NIST Finalists (Key Exchange)
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Key interchange/generation (Other)

The following relates to key interchange:
- Curve25519. Curve25519. This outlines Curve25519, which is used in the Tor network.
- Authenticated Key Exchange (Discrete logs). YAK. Key exchange with public keys and uses discrete logs.
- Authenticated Key Exchange (ECC). YAK. Key exchange with public keys and uses elliptic curve methods.
- Shamir No-key protocol. Shamir No Key. In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated.
- Shamir No-key protocol (sepc256k1). Shamir No Key (EC). In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated using the sepc256k1 elliptic curve.
- Conference keying (Burmester-Desmedt method). Conference keying. In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it.
- Conference keying (Burmester-Desmedt method) - Elliptic Curve (sepc256k1). Conference keying Elliptic Curve (sepc256k1). In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it, and uses the sepc256k1 elliptic curve.
Key exchange (with pairing)
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Kryptology

We need to build a new Internet. One that is build on mathematics and certainty, rather than the patchy version we have now. For this we need a layer of cryptography at the lowest level, and build software interfaces on top of this. Along with this we now have cryptographic methods which can now provide a foundation of trust, and which preserve privacy. And so the old libraries of OpenSSL are being squeezed out in favour of the new ones which are built on a solid foundation. The latest of these new "privacy-aware" libraries is Kryptology, and created by Coinbase. This library provides the APIs that developers need, in order to apply to areas of blockchain development. This library include BLS (Boneh-Lynn-Shacham) signatures, Zero-knowledge Proofs (ZKPs) and Shamir Secret Shares (SSS). With BLS we can digitally sign for data, but also preserve its privacy. Applications of this include group signatures, where multiple entities can merge their signing keys together and provide a single signature for a transaction. With SSS, we can split encryption keys up into shares, and then distribute them across a network. When required, we can call these shares back to reconstruct the key.
The focus for Coinbase seems to be the application of privacy coins, and where no tracking can be applied to the usage of these digital coins. This should support full anonymity for transactions, as opposed to Bitcoin which only supports pseudo-anonymity.

ECC Basics
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining n.G for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Points (Base Point and Others). Elliptic Curve points. Two common curves used in ECC (Elliptic Curve Cryptography) are secp256k1 (as used in Bitcoin and Ethereum) and P256 (secp256r1). The "k1" refers to the Kolbitz curve 1 (named after the creator of ECC). With these we have a base point which are can operate on. This is typically defined as \(G\). We can then operate on this with add and multiply operation. For example, \(2G=G+G\) and \(P=n.G\). In this following we will show the base point for a number of common curves, such as secp256r1, P256, Pallas, Curve 25519, BLS12381G1, BLS12381G2, BLS12377G1 and BLS12377G2.
ECDH
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret. We will use Golang and the Krytology library.
Simple ECC on curves
- Public key points for curves. Simple. Display public key points for scalars.
BLS Curve
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
Accumulator and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
Pallas Curve
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
Pairing-based Crypto
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
ElGamal and ECC
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a numerical input.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
Shamir Secret Shares
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Homomorphic Encryption
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Zero knowledge proofs
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
Verifiable Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Hash to scalar and point
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
CP-ABE
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Lattice cryptography

Latice cryptography is proposed as a post-quantum robust method for public key encryption, especially focused on digital signatures and key exchange mechanisms (KEMs).
Principles
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
NTRU
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- Lattice Encryption: NTRU Key Generation Python). NTRU. Outlines how NTRU operates for key generation.
Homomorphic
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Digital Signatures
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
Public-Key Encryption/Key Exchange
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
Light-weight cryptography

While AES and SHA work well together within computer systems, they struggle in an IoT/embedded world as they take up: too much processing power; too much physical space; and consume too much battery power. So NIST outlines a number of methods which can be used for light-weight cryptography, and which could be useful in IoT and RFID devices [1]. They define the device spectrum as:
- Conventional cryptography. Servers and Desktops. Tablets and smart phones.
- Light-weight cryptography. Embedded Systems. RFID and Sensor Networks.
With embedded systems, we commonly see 8-bit, 16-bit and 32-bit microcontrollers, and which would struggle to cope with real-time demands for conventional cryptography methods. And in the 40+ years since the first 4-bit processor, there is even a strong market for 4-bit processors. RFID and sensor network devices, especially, have limited numbers of gates available for security, and are often highly constrained with the power drain on the device.
So AES is typically a non-starter for many embedded devices. In light-weight cryptography, we often see smaller block size (typically 64 bits or 80 bits), smaller keys (often less than 90 bits) and less complex rounds (and where the S-boxes often just have 4-bits).
For light-weight cryptography the main constraints that we have are typically related to ener requirements, gate equivalents (GEs), and timing. With passive RFID devices, we do not have an associated battery for the power supply, and where the chip must power itself from energy coupled from the radio wave. An RFID device is thus likely to be severely constrained in the power drain associated with any cryptography functions, along with being constrained for the timing requirements and for the number of gates used. Even if an RFID device has an associated battery (active RFID), it may be difficult to recharge the battery, so the drain on power must often be minimised.
There is thus often a compromise between the cryptography method used and the overall security of the method. Thus often light-weight cryptography methods balance performance (throughput) against power drain and GE, and do not perform as well as main-stream cryptography standards (such as AES and SHA-256). Along with this the method must also have a low requirement for RAM (where the method requires the usage of running memory to perform its operation) and ROM (where the method is stored on the device). In order to assess the strengths of various methods we often define the area that the cryptography function will use on the device – and which is defined in \(µm^2\). The NIST finalists are defined in this [article]
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- GIFT AEAD. GIFT. GIFT is a light-weight block cipher. It is a (NIST Finalist)
- Elephant. Elephant. Elephant is a light-weight stream cipher. It is a (NIST Finalist).
- TinyJambu. TinyJambu. TinyJambu is a light-weight block cipher. It is a (NIST Finalist)
- Isap AEAD. Isap. Isap is a light-weight block cipher. It is a (NIST Finalist)
- PHOTON-Beetle AEAD. PHOTON-Beetle. PHOTON-Beetle is a light-weight block cipher. It is a (NIST Finalist)
- Romulus AEAD. Romulus. Romulus is a light-weight block cipher. It is a (NIST Finalist)
- Sparkle AEAD. Sparkle. Sparkle is a light-weight block cipher. It is a (NIST Finalist)
- CLEFIA. CLEFIA. CLEFIA is a light-weight block cipher.
- LED. LED. LED is a light-weight block cipher.
- Piccolo. Piccolo. Piccolo is an ultra light-weight block cipher.
- PRESENT. PRESENT. Present is a light-weight block cipher.
- Pyjamask. Pyjamask. Pyjamask is a light-weight block cipher.
- SIMON. SIMON. SIMON is a light-weight block cipher.
- SKINNY. SKINNY. SKINNEY is a light-weight block cipher.
- SPECK. SPECK. SPECK is a light-weight block cipher.
- XTEA. XTEA. XTEA is a light-weight block cipher.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encryption/Decryption. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.
Light-weight crypto (Other)
- Chaskey (MAC). Chaskey. Chaskey is a light-weight MAC function.
- Chaskey (MAC). Chaskey (Python). Chaskey is a light-weight MAC function.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (ASCON)
ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRFF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
Discrete Logs (Solving)

A discrete log problem is in the form of \(g^x \pmod p\) and where we know \(g\) and \(p\) and must solve for \(x\).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Message Authentication Code (MAC)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
HMAC
The following are the tips related to Key-based hashing:
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authentication both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2), Blake2b, SM3 and SHA-3. This page outlines the HMAC-MD5 methods using the Hazmat cryptography layer.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- HMAC (COSE). Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT with HMMAC. Go. In this case we create a CWT token, and sign with an HMAC signature.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- HMAC with Rust. HMAC. HMAC with Rust.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HMAC with OpenSSL. MACs with OpenSSL. HMAC in OpenSSL for a given input value, password and hashing method.
Cipher MACs
The following are the tips related to Key-based hashing:
- MACs with OpenSSL. MACs with OpenSSL. MAC methods implemented in OpenSSL, including CMAC and GMAC.
Key-based hashing
The following are the tips related to Key-based hashing:
- SipHash. Siphash. Siphash is a fast key-based hashing method.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Meow. Meow. Meow is one of the fastest hashing methods.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
Magic Numbers

This pages contains information related to magic numbers in file formats.
Network and File Forensics
- Magic numbers. Magic. This provides information on magic number for file forensics.
Graphics formats
- JPEG Analysis. JPEGs. This provides an analysis of JPEG files.
- GIF Analysis. GIFs. This provides an analysis of GIF files.
- TIF Analysis. TIFs. This provides an analysis of TIF files.
- PNG Analysis. PNGs. This provides an analysis of PNG files.
- BMP Analysis. BMPs. This provides an analysis of BMP files.
- PSD Analysis. PSDs. This provides an analysis of PSD files.
- WMF Analysis. WMF. This provides an analysis of WMF files.
- Adobe Illustrator Analysis. AI. This provides an analysis of AI files.
- Adobe In Design Analysis. INDD. This provides an analysis of INDD files.
- MIDI file. MIDI. This provides an analysis of MID files.
- ICO file. ICO. This provides an analysis of ICO files.
- PS file. PS. This provides an analysis of PS files.
- EPS file. EPS. This provides an analysis of EPS files.
- VSD file. VSD. This provides an analysis of Microsft Visio (VSD) files.
Video and audio formats
- MP3 Analysis. MP3s. This provides an analysis of MP3 files.
- AVI Analysis. AVIs. This provides an analysis of AVI files.
- Flash SWF Analysis. SWFs. This provides an analysis of Flash files.
- Flash FLV Analysis. FLVs. This provides an analysis of FLV files.
- MP4 Analysis. MP4. This provides an analysis of MP4 files.
- MOV Analysis. MOV. This provides an analysis of MOV files.
- WMV Analysis. WMV. This provides an analysis of WMV files.
- WMA Analysis. WMA. This provides an analysis of WMA files.
- JPEG 2000 Analysis. JPEG 2. This provides an analysis of JPEG 2000 files.
- WAV Analysis. WAV. This provides an analysis of WAV files.
Zips, Archives and Library files
- ZIP/Archive Analysis. ZIPs. This provides an analysis of ZIP/Achive files.
- GZ Analysis. GZ. This provides an analysis of GZip files.
- Tar Analysis. Tar. This provides an analysis of TAR files.
- MSI Analysis. MSI. This provides an analysis of MSI files.
- OBJ Analysis. OBJ. This provides an analysis of OBJ files.
- DLL Analysis. DLL. This provides an analysis of DLL files.
- CAB Analysis. CAB. This provides an analysis of CAB files.
- EXE Analysis. EXE. This provides an analysis of EXE files.
- RAR Analysis. RAR. This provides an analysis of RAR files.
- SYS Analysis. SYS. This provides an analysis of SYS files.
- HLP Analysis. HLP. This provides an analysis of HLP files.
- VMDK Analysis. VMDK. This provides an analysis of VMDK files (VMWare Virtual Disks).
- PST Analysis. PST. This provides an analysis of PST files (Outlook Email File).
- JAR Analysis. JAR. This provides an analysis of JAR files.
- SLN Analysis. SLN. This provides an analysis of Microsoft SLN files.
- Class Analysis. Class. This provides an analysis of Java Class files.
- Zlib. Zlib. This provides an analysis of Zlib files.
Documents
- PDF Analysis. PDFs. This provides an analysis of PDF files.
- DOC Analysis. DOCs. This provides an analysis of DOC files.
- RTF Analysis. RTFs. This provides an analysis of RTF files.
- XLS Analysis. XLSs. This provides an analysis of XLS files.
- PPT Analysis. PPTs. This provides an analysis of PPT files.
- MMP File. MMP. This provides an analysis of MMP files.
- DOCX Analysis. DOCX. This provides an analysis of DOCX files.
- XLSX Analysis. XLSX. This provides an analysis of XLSX files.
- PPTX Analysis. PPTX. This provides an analysis of PPTX files.
- MDB Analysis. MDB. This provides an analysis of MDB files.
- Outlook Message Analysis. MSG. This provides an analysis of MSG files.
Disk Image
- Raw disk format. RAW. This provides an analysis of the RAW disk format.
Tests
- File Forensics Test. File Test File Forensics Test.
- File Forensics Test (Fun). File Test (Fun) File Forensics Test.
Presentations
MIRACL Core Library

MIRACL Core is an open source library, and includes a wide range of public key encryption methods. It is especially focused on elliptic curve and pairing-friendly methods, but also supports a wide range of encryption methods, including RSA, AES and hashing. Overall, it can be ported onto a wide range of systems and supports C, C++, Go, Rust, Python, Java, Javascript and Swift. Along with this it supports limited capability devices such as the Arduino infrastructure. The GitHub repository is [here].
BN254
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.

Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- CL Signatures. CL. CL Signatures in Go using MIRACL.
- CL Signatures (advanced pairing). CL. CL Signatures in Go using MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages using MIRACL.
- PS Signatures. PS. Signatures using PS for short signatures using MIRACL.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures using MIRACL.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.

Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
Rust examples
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
NaCl

PyNaCl is a Python port of LibSodium. It integrates the latest cryptography methods, such as AES, XChaCha20, Blake2b and X25519.
Symmetric Key
- Symmetric key. Symmetric key (XChaCha20 and Poly1305). With symmetric key, Bob and Alice have the same key. NaCl uses the XChaCha20 method, and which supports stream encryption (and which does not require padding as a block cipher does, and is also faster than block cipher modes). ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16 byte nonce. XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24 byte nonce. It has a lower propability of nonce misuse than ChaCha20.
- Encryption with a password. Symmetric Key with KDF. In symmetric key, we generate a secret key. This key is typically a random value or generated from a password and a salt value. If we use a password, we typically use a KDF (Key Derivation Function), and which uses a password and a salt value, in order to create a key of a given size. In this case we will use Argon2i, and which is memory resilent.
Hybrid Encryption
- Box. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Hashing
- Hashing and KDF (Argon2 and scrypt). Hashing and KDF. This case we will use PyNaCl (Networking and Cryptography) library, and which is a Python binding to libsodium. We will hash a password using SHA-256 and SHA-512, and also create a KDF (Key Derivation Function) using scrypt and Argon2.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
Ed25519
-
Ed25519. Ed25519. Using Ed25519 for digital signatures.
-
Finding Points on Ed25519. X25519 (Points).
In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 (Key Exchange)
- X25519 + BLAKE2b key-exchange. X25519. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
Curve 25519
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
Node.js

Node.js uses the JavaScript programming langauge as its base, and allows for code to be run on a server, rather than in the browser (such as with pure JavaScript). To run a node.js program, we run "node myfile.js", and use NPM to install libraries.
Symmetric key
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
RSA and public key
- RSA Opt imal Asymmetric Encryption Padding (OAEP) using Node.js. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
ECC Keys
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.

Hashing
- Hashing with node.js (All). Hashing. Hashing with node.js.
- Hashing with node.js (Selection). Hashing. Hashing with node.js.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- ECDSA with node.js. ECDSA. ECDSA with node.js.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
Key exchange
- Diffie-Hellman with node.js (random prime). DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method and uses a randomly generated prime number (press the button to generate a new prime).
- Diffie-Hellman with node.js. DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method. Each time the prime number will be fixed for the DH group selected.
- ECDH with node.js. ECDH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Elliptic Curve Diffie Hellman (ECDH) key exchange method.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
Key derivation
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
CryptoJS
- CryptoJS (in node.js). CryptoJS (Node.js). Various crypto methods in the browser.
Bulletproofs
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
Blockchain
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
Proxy encryption
- Proxy Encryption - Encrypting With Public Key, And Decrypt with Private Key. Proxy01. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This page just creates a key pair for Alice, and uses it to encrypt with the public key , and decrypt with the private key.
- Proxy Encryption. Proxy02. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This will go through the full use case of proxy re-encryption.
Tokens
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
Random
- Fortuna with node.js. Fortuna. Fortuna random numbers with node.js.
Other
- FPE with node.js. FPR. FPE with node.js.
- Puny with node.js. Puny. Puny character format with node.js.
Accumulators and Witnesses
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
PGP
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Password Entropy
- Password Entropy with Node.js. Password Entropy. Password entropy measures the strength of a password, and is measured as the number of bits which could represent all of the possibilities. An entropy score of less than 25 identifies a poor password, and between 25 and 50 is a weak password. For 50 to 75 we have a reasonable password, and between 75 and 100 is a very good password. Over 100 is an excellent password. The strength of the password relates to the number of characters used, and also the number of characters in the password.
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
- Homomorphic Encryption with Node.js and BGV. Homomorphic Encryption with Node.js and BFG. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BGV method.
Oblivious Transfer (OT)

Oblivious Transfer allows Bob to select data from Alice, but for Alice not to know which value has been selected.
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
OpenSSH

OpenSSH supports the usage of the SSH protocol. This allows for a remote login. One tool which is uses is ssh-keygen, and which allow for the generation of RSA, DSA and elliptic-curve keys that. These can be used for user and host authentication, such as for GitHub login and Cloud instance login.
OpenSSH
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here].
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
Outline

OpenSSL

OpenSSL is a standard library that implements cryptography.
Symmetric key (Command line)
-
Symmetric Key Encryption (OpenSSL 1.x) [here]. In this case we will create cipher text from OpenSSL 1.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 1.x) [here].In this case we will decrypt cipher text from OpenSSL 1.x using a key derived from a password
-
Symmetric Key Encryption (OpenSSL 3.x) [here]. In this case we will create cipher text from OpenSSL 3.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 3.x) [here].In this case we will decrypt cipher text from OpenSSL 3.x using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password.
Hashing
-
Hashing [here] OpenSSL supports a wide range of hashing methods including BLAKE2b, Gost, MD4, MD5, RMD-160, SHA-1, SHA-3, SHA-256 and SHA-512.
Libre OpenSSL
-
Symmetric Key Encryption using Libre OpenSSL [here]. In this case we will create cipher text from Libre OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption using Libre OpenSSL [here]. In this case we will decrypt ciphertext from Libre OpenSSL using a key derived from a password.
-
Hashing [here] Libre OpenSSL supports a wide range of hashing methods including Gost, MD4, MD5, RMD-160, SHA-1, SHA-256 and SHA-512.
Diffie-Hellman parameter generation
-
DH Parameters with OpenSSL [here]. The Diffie-Hellman (DH) method is perhaps one of the greatest inventions in Cybersecurity, and was created by Whitfield Diffie and Marty Hellman. With the DH method, Bob creates a random value (\(b\)) and Alice also creates a random value (\(a\)). Next Bob computes \(B=g^b \pmod p\) and sends it to Alice. Alice computes \(A=g^a \pmod p\) and sends this to Bob. Bob raises the value of \(A\) to the power of \(b\) and takes \(\pmod p\), and Alice raises \(B\) to the power of \(a\) and takes \(\pmod p\). In the end, they will have the same shared value: \(g^{ab} \pmod p\). This can then be used to derive an encryption key that they can use for a secure tunnel. Overall, \(p\) is the large prime number, and also known as the shared modulus between Bob and Alice.
Key derivation function
-
PBKDF2 key derivation with OpenSSL [here] PBKDF2 (Password Key Derivation Function 2) is a key derivation method. Overall it is relatively slow in its operation and where we take a password, a salt value, hashing method, and a number of iterations, in order to produce a given size of encryption key.
-
HKDF key derivation with OpenSSL [here] HKDF (HMAC Key Derivation function) is used to derive an encryption key from a pass phrase. Initially HKDF creates a pseudorandom key (PRK) using a pass phrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), andalong with a salt value. Next the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys.
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Passwords
-
Password example [here]. This page uses the OpenSSL library hash password generator, which is used in UNIX systems for the hashing of passwords which are contained in /etc/shadow and /etc/passwd. For newer passwords, the "-1" options is used to created the hashed value.
-
Hashed passwords with OpenSSL [here].
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
Public key
-
Generating an ECC key pair with OpenSSL [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)).
-
Generating an RSA key pair with OpenSSL [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2).
-
Generating an RSA key pair with OpenSSL with encryption [here]. This page implements RSA key pair generation with an encrypted key pair. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). In this case we will encrypt the key pair with either 3DES, 128-bit AES, 192-bit AES or 256-bit AES. The same password must be used to encrypt and decrypt.
-
Generate prime with OpenSSL [here]. Prime numbers are important in public key encrytion, and are used with RSA and ECC. For RSA, we generate two prime numbers (\(p\) and \(q\)) and which are multiplied together to create a modulus (\(N\)). If these prime numbers have 512 bit values, the modulus will be a 1,024 bit value. This defines the basic secure of RSA. With elliptic curve we use smaller prime numbers, such as 256-bit values for the secp256k1 curve.
ASN1 parsing
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). We will parse using asn1parse, and reveal the parameters.
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)) [RSA key pair]. We will parse using asn1parse, and reveal the parameters.
- DSA Parameters with asn1parse. DSA parameters with OpenSSL with asn1parse. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA (Digital Signature Algorithm)
- DSA Parameters. DSA parameters with OpenSSL. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
MAC (Message Authentication Code)
- HMAC with OpenSSL. MACs with OpenSSL. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authenticate both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2) and SHA-3. In this case we will use OpenSSL to generate the HMAC value.
- MACs with OpenSSL. MACs with OpenSSL. In the following we will generate MACs for HMAC, GMAC, CMAC, Blake2bmac, Blake2smac, KMAC128 and KMAC256. Overall, we will use an encryption key defined as a hex value for GMAC and CMAC, and a pass phrase for the others. The message is "hello".
Signing
- Digital signing a plaintext message with OpenSSL. Signing with OpenSSL. With digital signing, we can take a message, and create a signature. This normally involves signing with a private key and digital certificate. The signed message can be an a MIME format, and which can be integrated into an email message. In this can we have a 512-bit RSA key pair that will sign a plain text message.
Encrypting emails
- Encrypting an email message in OpenSSL. Encrypting messages with OpenSSL. With public key encryption, we can take a message, and encrypt it with the recipiant's public key. In this can we have a 512-bit RSA public key to encrypt a message.
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Random number generation with OpenSSL
-
Random number generator [here]. Random numbers are important in generating encryption keys and salt values. In this case OpenSSL generates a random number (in a Base64 format) for a given number of bytes.
Outline (C#/Python)
-
Symmetric Key Encryption (C#) [here]. This page uses the OpenSSL library through a C#/.NET wrapper. The DLLs it interfaces to are libeay32.dll and ssleay32.dll. OpenSSL supports a wide range of encryption methods, including 128-bit AES, 192-bit AES, 256-bit AES and Blowfish (bf). Different modes of ECB, CBC, and OFB are implemented. The examples use a default IV of "1234".
-
AES in Python with OpenSSL output [here]
-
Producing OpenSSL AES Encrypted String from C# [here]
Digital Certificates
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
Paillier - Partial Homomorphic Encryption

The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Fundamentals
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier).
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Using RSA
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
Applications
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
Cyber&Data

This is the home page for the Cyber & Data course. There are four main units involved. Units 1 and 2 are self-study, but you can register for Units 3 and 4, and study towards an MSc module. Some unique features include: On-line Python integration, On-line Intrusion Detection Editor, Splunk Data Analysis, and Machine Learning Environment for Splunk. The Splunk elements of the course require a login (contact [email protected] for a login).
Unit 1: Fundamentals
- 1. Cyber and Intelligence. This topic provides an introduction to Cyber and Intelligence.
- 2. Defence Systems, Policies and Risk. This topic provides an overview of the some of the core defence mechanisms and risk approaches.
- 3. Open Source Intelligence. This topic outlines the usage of open source intelligence including using Shodan, Redit and Twitter mining.
- 4. So What is Data? This topics outlines the core data formats using in cybersecurity, and introduces the concept of magic numbers within files.
Unit 2: Data Capture and Analysis
- 5. Memory, Big Data and SIEM. This topic outlines some of the core principles used around Big Data methods and in the integration of SIEM (Security Information and Event Management).
- 6. Network Forensics. This topic provide fundamental knowledge in how networks works, and how we can analyse different network protocols, including ARP, IP, TCP, FTP and HTTP.
- 7. Intrusion Detection Systems. This topic outlines the usage of IDS and applies with using Snort.
Unit 3: Data Science and Cyber
- 8. Classification Metrics and ML.
- 9. Introduction to Data Science.
- 10. NumPy and Pandas. An outline of the integration of Numpy and Pandas for datasets.
- 11. Similarity and Matching. This unit outlines some of the key methods used within similarity and matching of text data. This includes the application of regular expressions, similarity metrics and similarity hashes.
Unit 4: Data Applications and Machine Learning
- 12. Splunk. An introduction to Splunk.
- 13. Splunk (Charting and Analysis). An introduction to Splunk with Charting and Analysis.
- 14. Machine Learning (Core Methods). An outline of the core methods.
- 15. Application of Machine Learning. A tutorial in applying ML with Splunk
Unit 5: Cyber Applications
- 16. Face Recognition. Implementation of face recognition.
DES, 3DES and Feistel ciphers

With DES and 3DES we have a 56-bit or 112-bit encryption key, respectively. Both are block ciphers and based on the Feistel ciphers, with a 64-bit block size.
Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- 3DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using 3DES encryption with Powershell.
- Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . With 3DES encryption, we use a 128-bit key and a 64-bit IV value. The two modes supported are ECB (without salt) and CBC (with salt). The DES algorithm has been around for a long time, and the 56-bit version is now easily crackable (in less than a day on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases, and splits the key into two. Overall the key size is typically 112 bits (with a combination of the three keys - of which two of the keys are the same). In this case we will use PKCS7 padding, and which fills the input data with a value that is equal to the number of padding bytes. Overall, DES has a 64-bit block size, and which equates to eight ASCII characters.
DES
The following are the tips related to DES, 3DES and Feistel ciphers:
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
Diffie-Hellman Key exchange (Discrete Logs)

Key exchange is a way for Bob and Alice to communicate and for them to agree on a shared secret. The original method defined uses discrete logarithms (Diffie-Hellman). With the Diffie-Hellman method, Alice generates \(a\) and shares \(A=g^a \pmod p\) with Bob. Bob generates \(b\) and shares \(B=g^b \pmod p\). Alice raises \(B\) to the power of \(a\), and Bob raises \(A\) to the power of \(b\). They should both end up with the same secret: \(K=g^{ab} \pmod p\).
Key interchange/generation (Diffie-Hellman)
The following relates to key interchange:
- Diffie-Hellman. Diffie-Hellman Calculation. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Real example). Diffie-Hellman Real. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Python). Diffie-Hellman. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (pre-compute). Diffie-Hellman (pre-compute). Many sites use the same prime numbers, which can then be cracked with a pre-computing attack.
- Selecting \(g\) in Diffie Hellman. G in Diffie Hellman. Picking a safe value of the generator \(g\) in discrete logarithms.
- Diffie-Hellman (Man-in-the-middle). DF. This outlines the man-in-the-middle method for Diffie-Hellman.
- An Alternative Diffie-Hellman method. Alterative DH. This outlines an alternative Diffie-Hellman method.
- Selecting g in discrete logs. g in discrete logs. This select a generator in discrete logs.
- Selecting g in discrete logs with random primes. g in discrete logs with random primes. This select a generator in discrete logs using random prime numbers which are define by a number of bits.
Authenticated Key Exchange
The following are the tips related to Key derivation hashing:
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- MTI/A0. MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{ax+by} \pmod p\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0. MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{x+y} \pmod p\)
- MTI/C0. MTI/C0. This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{xy} \pmod p\)
- MTI/C1. MTI/C1. This outlines MTI/C1, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{abxy} \pmod p\).
- HMQV (Menezes–Qu–Vanstone). HMQV. HMQV builds on MQV and adds the identity of Bob and Alice.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
Diffie-Hellman Parameter Generation
- DH Parameters with OpenSSL [here]. With the Diffie-Hellman (DH) we use the form of \(g^x \pmod p\), and where \(g\) is the generator and \(p\) is a large prime number. In order to implement DH, we create either a generator value of 2 or 5, and then select a prime number which works with this generator value. In real-life we would generate a prime number of at least 2,048 bits. A command of "openssl dhparam -2 512" creates a random prime number with 512 bits and which works with a generator of \(g=2\).
Digital Certificates

Trust centres are responsible for storing private and/or public keys, and digital certificates are used to store and distribute private and/or public keys.
Trust Centres
- Simple Key Distribution Centre. KDC. This implements a simple KDC.
- Kerberos. Kerberos. This will implement a Kerberos method of generating a shared key.
Key Pair Generation and Code Signing Requests
The following are the tips related to digital certs:
- Generating key pair. View. This defines creating a 512-bit keypair.
- Code Signing Request (CSR). View. This defines the reading the CSR.
- Code Signing Request (CSR) with Python. View. This defines creating a CSR using Python.
Creating Digital Certificates
The following are the tips related to digital certs:
- Digital Certificate Digital Cert.
- Digital Certificate (PFX) Digital Cert.
- Certificate with Public/Private key. Cert. This includes the creation of the digital certificate.
- Generate X.509 certificate and key pair using Golang. X.509. This generates an X.509 certificate and shows the details.
- X.509 certificates in JavaScript. RSA and ECDSA Signed certificates. This page will generate either RSA and ECC key pairs, and then generate X.509 certificates, using either a signature of SHA1withRSA or SHA256withECDSA. For RSA signing we use an RSA private key to sign the certificate, and with ECDSA signing we use an ECC private key to sign the certificate.
Digital Certificate Format
The following are the tips related to digital certs:
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Certificate cracking
The following are the tips related to digital certs:
- Cracking certificates. Crack. This defines the cracking of digital certificates.
SSL
The following are the tips related to digital certs:
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Certificates (OpenSSL). View. This defines the viewing of digital certificates.
Theory
- Encryption Principles: [View]
- Proving identity and examining certificates: [View]
- Validating entities: [View]
DSA (Digital Signature Algorithm)

The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA with OpenSSL
- DSA Parameters. DSA parameters with OpenSSL. This page outlines the creation of a keypair for DSA signatures.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
DSA with PowerShell
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA and Node.js
- Key pair using Node.js. DSA and other keypairs. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
DSA and C#
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
DSA and OpenSSH
- DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
- DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
DSA Signatures with Hazmat
- DSA Signatures. DSA Signatures. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. The ECDSA method is an extension of DSA, but implemented with elliptic curve (EC) methods. As with most public key signing methods, we take a hash of a message, and then apply a private key to create a signature (\(r,s\)). This is done by creating a random value (\(k\)) to produce the signature. The signature is then verified using the associated public key. This then verifies the creator of the signature and that the message has not been changed.
Outline
So, what does a digital signature look like? Well, it often has an r value and an s value: (r,s). So, let’s look at the DSA (Digital Signature Algorithm) signature. For this, Figure 1 shows an outline of the setup of the DSA signature, and where Bob uses his private key (sk) to sign a hash of a message, and Alice proves with his public key (pk,g,p,q). We also use a random nonce value (k) for the signature, and we must take care that we do not reuse the value.

Figure 1: DSA signature
Initially, Bob creates two prime numbers (\(p\) and \(q\)) and generates a generator value of \(g\). Next, he generates his secret key (\(x\)) and then computes his public key:
\(Y=g^{x} \pmod p\)
To create a signature for a message (\(M\)), he creates a random value (\(k\)) and then computes two values for the signature:
\(r = g^{k} \pmod{p} \pmod{q}\)
\(s=(k^{-1}.(H(m)+x.r)) \pmod {q}\)
When Alice receives this signature, she takes Bob's public key \((p,q,g,Y)\) and the message can computes:
\(w = s^{-1} \pmod q\)
\(u_1 = H(M).w \pmod q\)
\(u_2 = r.w \pmod q\)
\(v = (g^{u_1} . y^{u_2}) \pmod {p} \pmod {q}\)
She then checks that \(v\) is equal to \(r\). If so, the signature checks out. This works because:
\(v = g^{h.w}.y^{r.w} = g^{h.w}.g^{x.r.w} = g^{h.w+x.r.w} = g^{h/s+x.r/s} = g^{(H+x.r)/(k^{-1}(H+x.r))} = g^k = r\)
Elliptic Curve Cryptography (ECC)

With elliptic curve methods, we take a base point (\(G\)) and then use a private key (\(n\)) to produce a public key point (\(nG\)).
Elliptic Curve (Points)
The following are the tips related to ECC:
- ECC types and nG. ECC types and nG. Outlining the parameters used for ECC types (eg Curve 25519, Curve 448 and secpt256k1).
- First 100 Elliptic Curve points in Finite Field. Elliptic Curve points. Locating the first 100 points in an elliptic curve in a finite field.
- Elliptic Curve - Point addition. Elliptic Curve Point Addition. This shows the addition of two points on an elliptic curve.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field.
- First 20 Elliptic Curve points in Finite Field (improved method). Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field.
- First 20 Elliptic Curve points in Finite Field (plot). Elliptic Curve points (plot). Locating the first 20 points in an elliptic curve in a finite field.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field for common curves with Libnum. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256 and using Libnum to compute the quadratic square.
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- ECC double-and-add for point multiplication. Elliptic Curve double-and-add. Calculation of \(aG\) using a double-and-add approach (and which is equivalent to square-and-multiply in exponential functions.
- ECC key generation with Hazmat. Elliptic Curve key gen. Creating ECC keys using Hazmat and Python.
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining \(n.G\) for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Operations Within a Solidity Contract. Go.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Embedding data in an ECC point
- Embedding data in a point. Go. With Elliptic Curve Cryptography (ECC), we use points on an elliptic curve to represent our data. These are defined with (x,y) points. With this, it is possible to embedded a certain amount of data into the point - as long as it still gives us a valid point on the curve. This example will Curve 25519 to embed data, and is achieved by storing the length of the data in a single byte in the point, and then store the data as byte values in the point (followed by random data). To decode, we can then just read the first byte for the length of the message, and then reveal the data encoded into the point..
Quadratic residues
- Quadratic residue (mod p). Go. Outline of quadratic residue \(\pmod p\).
Elliptic Curve (ECDH) - Python
The following are the tips related to ECC:
- Elliptic Curve. Elliptic Curve. Elliptic Curve is a public key method which can also be used to generate a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with simple parameters. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
Elliptic Curve (ECDH) - Golang and Node.js
The following are the tips related to ECC:
- ECDH with Go. ECDH. ECDH with Go.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with node.js. ECDH. ECDH with node.js.
- ECDH with JavaScript. ECDH. Elliptic Curve Diffie Hellman.
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret. We will use Golang and the Krytology library.
Elliptic Curve (Signatures - ECDSA)
The following are the tips related to ECC:
- ECDSA and EdDSA methods. ECDSA and EdDSA. This outlines ECDSA and EdDSA for NIST, secp, brainpool and Ed448/Ed25519.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with secp256k1. ECDSA (secp2561k1). Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with secp256k1.
- ECDSA using P256. Barebones ECDSA with P256. This page implements ECDSA with the NIST P256 curve.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces and using Lenstra–Lenstra–Lovász (LLL) method. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA with Hazmat. ECDSA wih Hazmat. This outlines ECDSA with Hazmat.
- Blinded ECDSA. Blinded ECDSA. With a blinded signature, Bob can sign for a message, without knowning what the message is. In this case Alice will create a blinded ECDSA signature, and where Bob can then sign it, and then Alice can unblind it. The method is based on one produced by Oleg Andreev for blinding signatures in Bitcoin.
- ECDSA: Fault Attack. ECDSA: Fault Attack. In the fault attack in ECDSA we only require two signatures. One is produced without a fault \((r,s)\), and the other has a fault \((r_f,s_f)\). From these we can generate the private key.
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
Elliptic Curve (DER)
The following are the tips related to ECC:
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Elliptic Curve (Signatures - EdDSA)
The following are the tips related to ECC:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. X448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Ed25519 for EdDSA signatures with Hazmat. EdDSA: Ed25519. This page uses the Hazmat primitives for the cryptography library.
- Ed25519 signature using NaCl. Ed25519. This page uses the NaCl port from libsodium.
- Ed25519 points using NaCl. Ed25519. This page uses the NaCl port from libsodium to determine Ed25519 points.
Elliptic Curve (Plots)
The following are the tips related to ECC:
- Elliptic Curve (Plot). Elliptic Curve (Plot). Elliptic Curve is a public key method which can also be used to generate a shared key. This page outlines a graphic of the curve.
- Elliptic Curve (Real plots). Elliptic Curve (Real plot). This provides a range of well-defined elliptic curve plots.
Elliptic Curve (Keys)
The following are the tips related to ECC:
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
- ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
Elliptic Curve (ECIES)
The following are the tips related to ECC:
- Elliptic Curve Integrated Encryption Scheme (ECIES with Rabbit Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with Rabbit (a light-weight stream cipher).
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
Elliptic Curve (Hash to curve)
The following are the tips related to ECC:
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve with libnum.
- Hash to password with Go. Hash to password. Hash to password with Go.
- Match random value to sepc256k1 with Python. Random value to curve. This involves generating a random value, and then finding the nearest valid point on the curve. It involves incrementing a value of \(x\) until we reach a valid point.
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
Elliptic Curve (Point adding)
The following are the tips related to ECC:
- Elliptic Curve (Point Adding). Elliptic Curve. Creating 2P from P.
- Elliptic Curve (Point Adding with real curves). Elliptic Curve. Creating 2P from P with real curves (eg Curve 25519).
- Elliptic Curve (Calculating nP - ECC Calculator). Elliptic Curve. Creating nP from P with real curves.
- Elliptic Curve (Point addition - ECC Calculator). Elliptic Curve. This calculator adds two points on an elliptic curve.
- Elliptic Curve (Point addition - ECC Calculator - range of points). Elliptic Curve. This calculator takes one point on the elliptic curve, and then adds the other the other points on the curve to see the result.
Elliptic Curve (Curve 25519)
The following are the tips related to ECC:
- Curve 25519 with Go for test vectors. ECC. This does a test on some private keys to test the public key generation.
- Curve 25519 with Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Curve25519 with Python. Curve25519. This outlines Curve25519, which is used in the Tor network.
- Curve25519 with point adding Python. Curve25519. This outlines Curve25519 using basic point adding.
ElGamal and ECC
- ElGamal with ECC. ElGamal with ECC. ElGamal using ECC.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
- Proving an Encrypted Shuffle With ElGamal and ECC. Shuffle. An encrypted shuffle with ElGamal.
Elliptic Curve (X448)
The following are the tips related to ECC:
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Python. X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH using Python and based on RFC 7748.
Elliptic Curve (ElGamal)
The following are the tips related to ECC:
- Proving an Encrypted Shuffle With ElGamal and ECC. Shuffle. An encrypted shuffle with ElGamal.
- ElGamal with ECC. ElGamal with ECC. ElGamal using ECC.
Elliptic Curve (Pedersen Commitment) and DLEQ
The following are the tips related to ECC:
- Elliptic Curve - Blinding factor (Pedersen Commitment). Elliptic Curve Blinding. This shows the addition of transactions with a blinding factor.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
Elliptic Curve (Box and Encryption)
The following are the tips related to ECC:
Go ECC
- Hash to password with Go. Hash to password. Hash to password with Go.
- ECDH with Go. ECDH. ECDH with Go.
- Box with Go. Box. Box with Go.
- ECC with Go. ECC. ECC with Go.
- Curve 25519 with Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ElGamal with ECC. ElGamal with ECC. ElGamal using ECC.
- Curve 25519 with Go for test vectors. ECC. This does a test on some private keys to test the public key generation.
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Barebones Ed25519 with Go. ECC. This shows point addition and scalar multiply in Ed25519
- Barebones NIST P256 with Go. ECC. This shows point addition and scalar multiply in P256
Key exchange
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). The resultant key is \(xyG \)
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
- Authenticated Key Exchange (ECC). YAK. Key exchange with public keys and uses elliptic curve methods.
IBE
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
Barebones ECC
- P192 in Python. Barebones P192. This page implements P192 in pure Python.
- P224 in Python. Barebones P224. This page implements P224 in pure Python.
- P256 in Python. Barebones P256. This page implements P256 in pure Python.
- P521 in Python. Barebones P521. This page implements P521 in pure Python.
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
- Curve 25519 in Python. Barebones Curve 25519. This page implements Curve 25519 in pure Python.
- Curve 25519 in Python (Test Vectors from RFC 7748). Barebones Curve X25519. This page implements Curve 25519 in pure Python and tests against the IETF test vectors.
- Curve 448 in Python (Test Vectors from RFC 7748). Barebones Curve X448. This page implements Curve 448 in pure Python and tests against the IETF test vectors.
- Curve 25519 ECDH in Python (Test Vectors from RFC 7748). Barebones Curve X25519. This page implements Curve 25519 ECDH in pure Python and tests against the IETF test vectors.
- Curve 448 ECDH in Python (Test Vectors from RFC 7748). Barebones Curve X448. This page implements Curve 448 ECDH in pure Python and tests against the IETF test vectors.
- ECDSA using P256. Barebones ECDSA with P256. This page implements ECDSA with the NIST P256 curve.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 . EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
Others
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.

Public Key (Elliptic Curve) in Rust
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Sage
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
Elliptic Curve Diffie-Hellman (ECDH)

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as secp256k1 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) - Python
The following are the tips related to ECC:
- Elliptic Curve Diffie-Hellman (ECDH) with simple parameters. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
- ECDH and COSE. Go. In this case we create a symmetric key from ECDH. For this we will derive a shared key from the public key of Alice and Bob, and then define a single recipient which can derive the CEK (Content Encryption Key) using their private key. We will use the curves of P-256 (secp256r1), P-384 (secp384r1), P-521 (secp521r1) or SECP256K1 (as used with Bitcoin).
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Go. ECDH. ECDH with Go.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret. We will use Golang and the Krytology library.

Elliptic Curve (ECDH) - Node.js
The following are the tips related to ECC:
- ECDH with node.js. ECDH. ECDH with node.js.
- ECDH with JavaScript. ECDH. Elliptic Curve Diffie Hellman.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Key exchange

- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). The resultant key is \(xyG \)
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
- Authenticated Key Exchange (ECC). YAK. Key exchange with public keys and uses elliptic curve methods.
ECDSA (Elliptic Curve Digital Signature Algorithm)

ECDSA has been around for over two decades and was first proposed in [1]. The ECDSA method significantly improved the performance of signing messages than the RSA-based DSA method. Its usage of elliptic curve methods speeded up the whole process and supported much smaller key sizes. Its crown and glory were being selected by Satoshi Nakamoto for his Bitcoin protocol, and then its adoption into Ethereum.
ECDSA Basics
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Recoving the public key from an ECDSA Signing in Python. Recoving public key from ECDSA Signing. This is an example of recovering the public key from the ECDSA signature with Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\)).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\)) and will check that the signature is valid.
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
-
ECDSA for Multiple Curves and Different Hashing Methods with Python
. ECDSA for Multiple Curves and Different Hashing Methods with Python. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
- ECDSA Signatures with Hazmat (SECP256R1, SECP384R1, SECP521R1, SECP224R1, SECP192R1, and SECP256K1). ECC Signatures. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and then creates an ECDSA signature for a given message.
- DSSE (Dead Single Signature Envelopes). DSSE. The Update Framework (TUF) provides a framework to secure the software within a system, while in-toto ("as-a-whole") can be used to protect the whole of software support chain. TUF thus delivers updates to a system while in-toto manages a complete software infrastructure. For this, it uses the Metablock format, and where we do not sign the byte values for the signature but sign the JSON data. This is known as canonicalisation - and which is the conversion of data in different forms to a standardised format.
Elliptic Curve (DER)
The following are the tips related to ECC:
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Google Tink with ECDSA
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
ECDSA Applications
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Blinded ECDSA. Blinded ECDSA. With a blinded signature, Bob can sign for a message, without knowning what the message is. In this case Alice will create a blinded ECDSA signature, and where Bob can then sign it, and then Alice can unblind it. The method is based on one produced by Oleg Andreev for blinding signatures in Bitcoin.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA: Fault Attack. ECDSA: Fault Attack. In the fault attack in ECDSA we only require two signatures. One is produced without a fault \((r,s)\), and the other has a fault \((r_f,s_f)\). From these we can generate the private key.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Elliptic Curve Integrated Encryption Scheme (ECIES)

With ECIES we integrate the power of elliptic curve (EC) public key encryption with symmetric key encryption. An outline of the method is:

Elliptic Curve (ECIES)
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Elliptic Curve Integrated Encryption Scheme (ECIES with Rabbit Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with Rabbit (a light-weight stream cipher).
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
Applications
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- ECIES (Kryptology). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Coinbase Kryptology library.
- ECIES (CIRCL). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Cloudflare CIRCL library.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
Ethereum crypto
- ECIES with Go-Ethereum. Go.
EdDSA, Ed25519 and Ed448

Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). EdDSA (Edwards-curve Digital Signature Algorithm) is a fast and efficient digital signature method, and is based on the Schnorr signature scheme. Two important curves that are implemented with EdDSA are Curve 25519 (X25519) and Curve 448 (Ed448). EdDSA has been standardized in [RFC 8032]. With EdDSA, Alice generates a private key of \(sk\) and a public key of \(P=sk.G\) and where \(G\) is the base point of the curve.
Elliptic Curve (Signatures - EdDSA)
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Ed25519 in Python. EdDSA in Python. This page implements EdDSA using the Pure25519 library and with the core functions of key generation, signature generation and signature verification.
- Ed25519 Vulnerability in Python. EdDSA Vulnerability in Python. This page implements EdDSA using the Pure25519 library and with the core functions of key generation, signature generation and signature verification.
- Ed25519 Vulnerability in Python (Proof of Concept). EdDSA Vulnerability in Python (PoC). This page implements EdDSA using the Pure25519 library and with the core functions of key generation, signature generation and signature verification.
Hazmat (Ed448 and Ed25519)
- Ed25519 for EdDSA signatures with Hazmat. EdDSA: Ed25519. This page uses the Hazmat primitives for the cryptography library for X25519.
- Ed448 for EdDSA signatures with Hazmat. EdDSA: Ed25519. This page uses the Hazmat primitives for the cryptography library for X448
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
Golang
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
- Barebones Ed25519 with Go. ECC. This shows point addition and scalar multiply in Ed25519
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
COSE/COBR
- EdDSA. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) [2] can then build on this to includes signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case, we will use EdDSA to create a signature for a message.
Testing Ed25519
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
NaCl
- Ed25519 signature using NaCl. eddsa. This page uses the NaCl port from libsodium.
- Ed25519 points using NaCl. eddsa. This page uses the NaCl port from libsodium to determine Ed25519 points.
Theory
With EdDSA, Alice will sign a message with her private key, and then Bob will use her public key to verify that she signed the message (and that the message has now changed):

Key generation
Alice generates a random 32-byte secret key (\(sk\)) and then creates a public key of:
\(pk=sk \cdot G\)
and where \(G\) is the base point of the curve.
Signing
Alice creates a SHA-512 hash of her private key:
\(h=\textrm{HASH}(sk)\)
Create \(r\) from the upper 32 bytes of hash and the message:
\( r = \textrm{HASH}(h[32:] \: || \: m))\)
And where "||" represents a concatenation of the byte array values. Next she matches \(r\) onto curve with:
\(R=r \cdot G\)
Next Alice computes \(s\) with:
\(s=r + (\textrm{HASH}(R \: || \: pk \: || \: m)) \cdot sk\)
The signature is (\(R,s\)). The values of \(R\) and \(s\) are 32 bytes long, and thus the signature is 64 bytes long.
Verifying
Bob creates \(S\) using \(R\), \(pk\) and \(m\):
\(S =\textrm{HASH}(R \: || \: pk \: || \: m) \)
And next creates two verification values:
\(v_1=s \cdot G\)
\(v_2=R+ pk \cdot S\)
If \(v_1==v_2\) the signature checks. This is because:
\(
\begin{align}
v_1&=s.G\\
&= (r + (\textrm{HASH}(R \: || \: pk \: || \: m)) \cdot sk) \cdot G \\
&= rG + sk \cdot G \cdot (\textrm{HASH}(R \: || \: pk \: || \: m)) \\
&= R+ pk \cdot S \\
&= v_2
\end{align}
\)
ElGamal

Public key encryption is typically used to sign for things (and where we use the private key to encrypt something and prove this with the public key) and within key exchange methods. The core methods used are RSA and Elliptic Curve. But an alternative is to use discrete logarithms. One of the most interesting is ElGamal, and was created by Taher Elgamal in 1985.
ElGamal Method
- ElGamal. ElGamal. ElGamal is a public key method which uses discrete logarithms.
- ElGamal in Python. ElGamal in Python. ElGamal is a public key method which uses discrete logarithms.
- ElGamal in Python with variable prime sizes. ElGamal in Python for different prime sizes. ElGamal is a public key method which uses discrete logarithms.
- Selecting g in ElGamal. G in ElGamal. ElGamal is a public key method which uses discrete logarithms.
- Selecting g in discrete logs. g in discrete logs. This select a generator in discrete logs.
- Selecting g in discrete logs with random primes. g in discrete logs with random primes. This select a generator in discrete logs using random prime numbers which are define by a number of bits.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- Proving an Encrypted Shuffle With ElGamal and ECC. Shuffle. An encrypted shuffle with ElGamal.
- ElGamal encryption with Powershell. ElGamal encryption.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Commutative Encryption
- Commutative Encyption (Modified ElGamal). Commutative Encyption. Commutative Encyption allow Bob and Alice to encrypt a message, and then for the data to be decrypted usign any order of the keys.
ElGamal Signature
- ElGamal signatures. ElGamal. ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this.
- ElGamal signatures (alterative signing). ElGamal (Signing: s=ar + kh(m)). ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this. Normally we sign with \(s=k^{-1} (h(m)-ar) \pmod {p-1}\), but in this case we will use \(s=ar + kh(m))\).
- ElGamal signatures (alterative signing). ElGamal (Signing: s=ah(m) + kr). ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this. Normally we sign with \(s=k^{-1} (h(m)-ar) \pmod {p-1}\), but in this case we will use \(s=ah(m) + kr\).
- ElGamal signatures (alterative signing). ElGamal (Signing: r=as+kh(m)). ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this. Normally we sign with \(s=k^{-1} (h(m)-ar) \pmod {p-1}\), but in this case we will use \(r=as+kh(m)\).
- ElGamal signatures (alterative signing). ElGamal (Signing: r=ah(m) +ks). ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this. Normally we sign with \(s=k^{-1} (h(m)-ar) \pmod {p-1}\), but in this case we will use \(r=ah(m) +ks\).
- ElGamal encryption with Go. ElGamal. This implements ElGamal encryption.
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
ElGamal Homomorphic Encryption
- ElGamal Homomorphic Cipher for Multiplication (Python). ElGamal. This outlines ElGamal Homomorphic multiplication with Python.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (Python). ElGamal. This outlines ElGamal Homomorphic division with Python.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (Python). ElGamal. This outlines ElGamal Homomorphic addition with Python.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (Python). ElGamal. This outlines ElGamal Homomorphic subtraction with Python.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
- ElGamal Homomorphic Cipher (Go). ElGamal. This outlines ElGamal Homomorphic cipher with Go.
- ElGamal Homomorphic Cipher (Go) - Divide. ElGamal. This outlines ElGamal Homomorphic cipher with Go with divide.
- ElGamal Homomorphic Cipher (Go) - Additive. ElGamal. This outlines ElGamal Homomorphic cipher with Go with addition.
ElGamal and ECC
- ElGamal with ECC. ElGamal with ECC. ElGamal using ECC.
- Proving an Encrypted Shuffle With ElGamal and ECC. Shuffle. An encrypted shuffle with ElGamal.
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- ElGamal - Applying Multiple Public Key Operations (ECC). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use elliptic curve methods, and using the Edwards 25519 curve.
ElGamal (Authenticated and Verified Encryption)
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenticated ciphertext.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
ElGamal (Encrypting with multiple public keys)
- ElGamal - Applying Multiple Public Key Operations (Discrete Logs). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use discrete logs.
- ElGamal - Applying Multiple Public Key Operations (ECC). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use elliptic curve methods, and using the Edwards 25519 curve.
Ethereum

This page outlines some examples of blockchain and cryptocurrency.
Test Network
- Math functions on Local Network. Go.
- Math functions on Test Network. Go.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- Storing State in a Smart Contract. Go.
- Deleting Data From A Smart Contract. Go.
- A Caesar Cipher Quiz Generator from a Smart Contract. Go.
- Hashing in a Smart Contract. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
- Dealing With Decimals In Smart Contracts. Go.
- Creating A Scrambled Alphabet Challenge Generator In Ethereum and Solidity. Go.
- Deploying a Scrambled Alphabet Generator To Ethereum (With Ganache and Ropsten). Go.
- Deploying a Scrambled Alphabet Generator To Ethereum (With Hardhat). Go.
- Pigpen, IPFS and Ethereum. Go.
- Proof of \(x\) from \(H(x)\) using zkSnarks. Go.
- Elliptic Curve Operations Within a Solidity Contract. Go.

Ethereum
- Creating Ethereum address with Python. Go.
- Creating Ethereum signing with Python. Go.
- ERC20 Tokens. Go.
- Ethereum address with Go. Addresses. This generates an Ethereum address.
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- PATRICIA trie. PATRICIA. Example of using PATRICIA (and which is used in Ethereum).
- Viewing Balance of account in Etheruem with Go. Balance. This views the balance of an account
- Viewing Block in Etheruem with Go. Block. This views a block.
- Viewing Cryptocurrency API with Python. Go.
- Viewing Ethereum blockchain with Python. Go.
- Viewing Transactions in Block in Etheruem with Go. Transactions. This views transactions.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
- Symmetric Key Encryption For Smart Contracts. Symmetric key. Solidity does not natively support symmetric key encryption, such as with AES. Overall, AES would consume too much gas and thus be expensive to implement. But, we can use hashing and X-OR methods to do the encryption. In this case, we will create a 256-bit random value, and then encrypt it with an encryption key, and then decrypt it.
Calling from Python
- Calling smart contracts with Python. Python.
Ethereum crypto
- ECIES with Go-Ethereum. Go.
Ethereum Blockchain
- IOTA Trytes. Trytes. `This outlines Trytes, as used in IOTA.
Ethereum Blockchain
- Blockchain: Adding Maths Functions. Go.
- Blockchain: Blocks, transactions and writing data. Go.
- Blockchain: Contracts and Addresses. Go.
- Blockchain: Getting transactions. Go.
- Blockchain: Hello World!. Go.
- Blockchain: Simple Purchasing System. Go.
- Blockchain: Viewing the blockchain. Go.
- Blockchain: Cracking Wallets. Go.
- Introduction to Blockchain. Go.
Presentations
Factorization

Many public key problems involve the difficulity in factorizing a value two its prime number factors. For example, in RSA, we have a public modulus \(N\) and which is equal to the multiplication of two prime numbers \(p\) and \(q\). If we can factorize the public modulus, we will be able to break the RSA cipher related to it.
RSA Crack
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA Factorization. RSA. This outlines the factorisation of the N value in the RSA method.
Methods
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Dixon. Go. Dixon Method.
- Rho factorization. Rho. Rho alogorithm.
- Smooth numbers. Go. Outline of smooth numbers.
Methods (Elliptic curve
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Quadratic residues
- Quadratic residue (mod p). Go. Outline of quadratic residue \(\pmod p\).
- Quadratic residue (mod p) using Legendre symbol. Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
Factorizing
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
Lenstra–Lenstra–Lovász (LLL) with lattices
- Crack ECDSA with weak nonces. ECDSA with weak nonces and using Lenstra–Lenstra–Lovász (LLL) method. This outlines ECDSA how the private key can be recovered with weak nonce values.
Network Forensics

These pages outlines some network forensics. This includes the understanding of the network stack, and with protocols such as Etherenet, IP, TCP, HTTP, and others.
Network Forensics (Theory)
- Network Forensics (Wireshark). Network Forensics. This provides information on how to detect threats through network forensics with Wireshark.
- Advanced Network Forensics. Network Forensics. This provides information on how to detect threats through network forensics.
Network Forensics (Practice)
- Advanced Network Forensics (Wireshark). Adv Network Forensics. This provides information on how to detect threats through network forensics with Wireshark.
- Network Forensics (PCAP). Network Forensics. This provides information on network forensics (reading PCAP files)
- Network Forensics (Text). Network Forensics. This provides information on network forensics (reading text files)
Tshark
-
Filters with TShark. TShark. This page runs Tshark with a given Pcap file and a defined filter.
Other
- Advanced Digital Forensics . Adv Digital Forensics. This provides information on how analyse disk based systems using open source forensics.
- Partition Analyser. MBR. This page will analyse the details of the partition details within the MBR (put one space between fields).
Presentations
Format Preserving Encryption

Format Preserving Encryption (FPE) is a method which allows the basic formatting of a message to stay in a similar format, and where the value itself is encrypted. It can be used to hide credit card details.
Methods
- Format Preserving Encryption. FPE. This outlines Format Preserving Encryption.
- FPE with Python. FPE. An implementation of Format Preserving Encryption (FPE) using Python.
- FPE with node.js. FPR. FPE with node.js.
- FPE and PKBKDF2 in Python. FPE and PKBKDF2 in Python. FPE using PKBDF2 to password generation.
FFX (Format-preserving, Feistel-based encryption)
- FPE with Go. FPE. An implementation of Format Preserving Encryption (FPE) for FFX1 and FFX3.
- FFX schemes. FFX. Within tokenization we can apply format preserving encryption (FPE) methods, which will convert our data into a format which still looks valid, but which cannot be mapped to the original value. For example, we could hide Bob's credit card detail into another valid credit card number, and which would not reveal his real number. A tokenization server could then convert the real credit card number into a format which still looked valid. For this we have a key which takes the data, and then converts it into a form which the same length as the original.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher in Python.
FFX in Rust
- FFX. FFX. This is an implementation of FFX in Rust.
Honey Encryption
- Honey Encryption. Honey. This outlines Honey encryption.
Crypto Principles

This page outlines some crypto principles.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Galois fields (polynomial operations)

This page outlines a few basic principles around the usage of Galois fields and polynomial operations. In 1832, Évariste Galois died of duelling wounds at the age of 20 but left a great legacy. While he was a teenager he worked on polynomials and laid down the principles of Galois theory, along with defining the concept of a finite field. In cryptography, the finite field is one of the major concepts and involves limiting the number of possible values to a limiting factor (\(p\)). The values of the field then range from 0 to p-1. Within a field, we can operate on values in the field using arithmetic operations. We can thus have an infinite field, and where we could include all of the possible integers. A finite field or Galois field of GF(\(2^n\)) has \(2^n\) elements. If \(n\) is four, we have 16 output values. Let’s say we have a number \(a∈{0, ... ,2^{n−1}}\), and represent it as a vector in the form of a polynomial:
\( a=a0+a_1 x+a_2 x^2 ... a_{n−1} x^{n−1}\)
If we use \(a_n∈{0,1}\), this is exactly the same as representing a binary number modulo \(2^n\). In this \(x^n\) represents bit position \(n\) and \(a_n\) is the value of the bit at position \(x^n\). If a bit is a zero at a given position, it will be not included in the polynomial equation. So, 1011 can be represented by \(x^3+x+1\) and 1010 is represented as \(x^3+x\). We can then perform arithmetic operations on these polynomial values. So, to add two values of 1010+1100 we can represent this as \((x^3+x)+(x^3+x^2)\) and which is \(x^2+x\) as we are using modulo 2 addition, and where \(x^3+x^3=0\). With modulo 2 addition, 0+0=0, 0+1=1, 1+0=1, and 1+1=1.
An example of Galois Fields is within AES (Advanced Encryption Standard) and which uses a finite field GF(\(2^8\)). With AES we operate on bytes (8 bits) in the form of \(b_7 b_6 b_5 b_4 b_3 b_2 b_1 b_0\) and which are operated on a a polynomial of \(b_7x^7+b_6x^6+b_5x^5+b_4x^4+b_3x^3+b_2x^2+b_1x^1+b_0\).
Galois fields (polynomial operations) - GF(\(p^n\))
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Additive Group Table for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Additive Group Table for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of addition. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the additive group table for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values.
- Multiplicative Group Table for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Multiplicative Group Table for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the additive group table for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values.
- Additive, Division and Multiplicative Group Table for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Additive, Division and Multiplicative Group Table for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the Additive, Division and Multiplicative Group Table for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values.
- Additive and Multiplicative Group Table for GF(\(2^2\)) and GF(\(2^3\)). Galois Fields Table for GF(2^m) with polynomials. This page implements Galois Fields GF(\(2^n\)) with Python and provides a table of additional and multiplication. It outlines GF(\(2^2\)) and GF(\(2^3\)), but also gives a program that can be used for others. Overall, we have the form of GF(\(p^n\)) and which provides use both an additive and a multiplicative group operations that provide all the possible outputs within the finite field. The value of \(p\) is a prime number, and \(n\) is any positive integer.
- Additive and Multiplicative Group Table for GF(\(2^2\)) and GF(\(2^3\)). Galois Fields Table for GF(2^m) with coefficient values. This page implements Galois Fields GF(\(2^n\)) with Python and provides a table of additional and multiplication. It outlines GF(\(2^2\)) and GF(\(2^3\)), but also gives a program that can be used for others. Overall, we have the form of GF(\(p^n\)) and which provides use both an additive and a multiplicative group operations that provide all the possible outputs within the finite field. The value of \(p\) is a prime number, and \(n\) is any positive integer. This version will show the polynomial coefficent values within the Galois Field.
- Additive and Multiplicative Group Table for GF(\(2^2\)) and GF(\(2^3\)). Galois Fields Table for GF(2^m) with integer values. This page implements Galois Fields GF(\(2^n\)) with Python and provides a table of additional and multiplication. It outlines GF(\(2^2\)) and GF(\(2^3\)), but also gives a program that can be used for others. Overall, we have the form of GF(\(p^n\)) and which provides use both an additive and a multiplicative group operations that provide all the possible outputs within the finite field. The value of \(p\) is a prime number, and \(n\) is any positive integer. This version will show the integer values within the Galois Field.
Irreducible polynomial for GF(p^n)
- Irreducible polynomial for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Irreducible polynomial for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the parameters for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values. This includes finding the irreducible polynomial for the Galois Field.
- Irreducible polynomial for GF(\(p^n\)) for a given \(p\) and for \(n\) values. Irreducible polynomial for GF(p^n) for a given p and for n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the parameters for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values. This includes finding the irreducible polynomial for the Galois Field. Other important parameters include the degree (the highest polynomial power) and the order (the number of possible output values).
- Conway and primitive polynomial GF(\(p^n\)). Conway and primitive polynomial GF(p^n). This page outlines Conway and primitive polynomials for GF(\(p^n\)).
Galois fields (polynomial operations) - GF(\(p\))
- Additive and Multiplicative Group mod n (\(Z_n\)). Additive and Multiplicative Group mod n. In finite fields, we have a \(\pmod n\) operation for a list of integers (\(\mathbb{Z}\)), and where \(n\) is a prime number. This works for our add (+) and multiply (\(\times\)) operations, and where: \( a \pmod n + b \pmod n = (a+b) \pmod n\); and \(a \pmod n \times b \pmod n = (a \times b) \pmod n\).
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Polynomial GF(2) Factoring and Irreducible Polynomials. Factors. This outlines the search for polynomial factors for GF(2).
Polynomial operations
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
Post-quantum
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Rust
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Sage
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Golang and Cryptography

The new scripted languages such as Python and Node.js are convenient. But, unfortunately, they can be slow as they are scripted, and not compiled. Each time the scripted code is run, the scripting engine must then convert each line of code to the required machine level code. This makes the code much slower than compiled languages, and also less robust. Thus many applications in cryptography are written in C and C++, as they allow for fast execution and give low level access. Unfortunately it can be complex to compile programs, as we often need to install binary libraries and then link these in. The Go programming language, though, has a similar code syntax to C/C++, but is small and efficient and allows access to low-level functions, such as as pointers. Go thus aims to “Code less, compile quicker, execute faster”. So let’s use Go to implement some cryptography methods, including symmetric key, hashing, public keys and zero-knowledge proofs (ZKPs). The slides related to these methods are included [here]. An introduction to Golang and Cryptography is [here].

Go ECDH
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret.
Go Hex and Base64
- Base64 and Hex in Go. Base64/Hex. Two common formats for representing binary data are hexademical and Base64.
Go symmetric key
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Reuse IV attack and AES. Reuse IV and GCM. This provides an implementation of a reuse IV against AES GCM.
- ASCON AEAD (Golang). ASCON AEAD (Golang). The outlines the usage of AEAD for ASCON using Golang.
Go HMAC and HKDF
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HKDF in Go. HKDF. Implementation ofHKDF, and where we dervice a key based on a given secret.
Go secret shares
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.

Go ZKP
- Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL). DLEQ. Create a non-interactive ZKP for discrete logs.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Fiat Shamir and ECC (Interative ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP with Kryptology. This implements a range proof using a Schnorr proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?

Go ECIES (Hybrid Encryption)
With this, we can use the power of public key encryption (to generate the encryption key) with symmetric key encryption (to actually encrypt and decrpyt the data):
- ECIES (Kryptology). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Coinbase Kryptology library.
- ECIES (CIRCL). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Cloudflare CIRCL library.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt and which is used in Contract Tracing for COVID-19.
Go ECDSA
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Go RSA
- RSA Principles. RSA Principles. The basics of RSA.
- RSA with Go. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA. RSA encryption with Go using OAEP.
- RSA Encryption with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
Go ElGamal
ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Proving an Encrypted Shuffle With ElGamal and ECC. Shuffle. An encrypted shuffle with ElGamal.
- ElGamal encryption with Go. ElGamal. This implements ElGamal encryption.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
- ElGamal - Applying Multiple Public Key Operations (ECC). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use elliptic curve methods, and using the Edwards 25519 curve.
Go PGP
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
Go Public key
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.

Go Hashing
- Hashing with Go. Hashing. Hashes with Go.
- GP Hashing with Go. GP Hashing. GP Hashes with Go.
- SHAKE with Go. SHAKE. This implements SHAKE in Go.
- libDisco with Go. libDisco. This implements libDisco.
- cSHAKE in Golang. cSHAKE. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS. With the SHA-3 hashing method, we have four different cryptographic hashing methods (SHA3-224, SHA3-256, SHA3-384, and SHA3-512) and two XOF functions (SHAKE128 and SHAKE256). With SHAKE128 and SHAKE256 we can integrate domain separation between different functions — and which are known as cSHAKE128 and cSHAKE256.
- Homomorphic Hashing with Golang. Homomorphic hashing. Normally with hashing methods, we need to take all the previous data and new data in order to create a new hash value for our data. In a homomorphic hashing method, we can basically take the previous hash, and then add on any new data values. We can also remove previous data values from our hash, too. This is more efficient in computing, as we do not have to process all of our data into a new hash, and can use simple homomorphic operations for the computation. The method we will use (LtHash) was initially defined by Bellare and Micciancio and updated Lewi et al at Facebook.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
Go ECC
- Hash to password with Go. Hash to password. Hash to password with Go.
- ECDH with Go. ECDH. ECDH with Go.
- Box with Go. Box. Box with Go.
- ECC with Go. ECC. ECC with Go.
- Curve 25519 with Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ElGamal with ECC. ElGamal with ECC. ElGamal using ECC.
- Curve 25519 with Go for test vectors. ECC. This does a test on some private keys to test the public key generation.
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Barebones Ed25519 with Go. ECC. This shows point addition and scalar multiply in Ed25519
- Barebones NIST P256 with Go. ECC. This shows point addition and scalar multiply in P256
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining \(n.G\) for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Points (Base Point and Others). Elliptic Curve points. Two common curves used in ECC (Elliptic Curve Cryptography) are secp256k1 (as used in Bitcoin and Ethereum) and P256 (secp256r1). The "k1" refers to the Kolbitz curve 1 (named after the creator of ECC). With these we have a base point which are can operate on. This is typically defined as \(G\). We can then operate on this with add and multiply operation. For example, \(2G=G+G\) and \(P=n.G\). In this following we will show the base point for a number of common curves, such as secp256r1, P256, Pallas, Curve 25519, BLS12381G1, BLS12381G2, BLS12377G1 and BLS12377G2.
Go Blockchain
- Ethereum address with Go. Addresses. This generates an Ethereum address.
- Viewing Balance of account in Etheruem with Go. Balance. This views the balance of an account
- Viewing Block in Etheruem with Go. Block. This views a block.
- Viewing Transactions in Block in Etheruem with Go. Transactions. This views transactions.

Go Homomorphic
- SIDH Go. SIDH. Post-quantum key exchange.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- NTP. NTP. An overview of NTP.
- BiBa. BiBa. An overview of BiBa One Time Signature.
Go DNS
- DNSSEC. DNSSEC. An overview of DNSSEC.
Go Signatures
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Go Signcryption
- Ahmad-Afzal-Iqbal (AAI) signcryption with Golang. Ahmad-Afzal-Iqbal (AAI). Ahmad-Afzal-Iqbal (AAI) signcryption with Golang.

Go Crypto pairing
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
Go Homomorphic
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add. HEAAN Add. HEAAN Add.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- Anonymous crypto. Anon. Anonymous crypto.
- Rho factorization. Rho. Rho alogorithm.
- Post-quantum signing (BLISS). BLISS. BLISS method.
Go Post quantum
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.

Go CIRCL
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- Ed448 with Go. X448. Ed448 with Go.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with FourQ (Cloudflare). FourQ.
- Verifiable Oblivious Pseudorandom Functions (VOPRF) with Cloudflare CIRCL. VOPRF. In our digital world, we give away too many of our secrets, especially where we just have to prove the knowledge of something, rather than actually revealing it. In many of the systems we use, we could just prove things in an oblivious way, and where we could pass a secret but in a blinded form. With this, a server does not discover our password and for us not to discover the identifier that a server holds on us. But, can we also provide a proof back that the right password has been used? Well, with Verifiable Oblivious Pseudorandom Functions (VOPRF), we can generate a random secret based on a key generated on the server (Alice), and which is based on Bob’s secret.
- Hash to Curve using Go (Cloudflare). Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). The method defined here is proposed an an Internet-Draft standard by the Internet Engineering Task Force (IETF) related to "Hashing to Elliptic Curves".
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
here Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
- eXtendable-Output Function (XOF) usign CIRCL. XOF. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS.

Go Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Google Tink (Golang) ECIES. Google Tink (ECIE5). This outlines ECIES encryption with public key and AES using Golang with Google Tink
Go Credentials
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.

Go Kryptology
- Public key points for curves. Simple. Display public key points for scalars.
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.

Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.

Principles
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Paillier
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
Go Format Preserving Encryption (FPE)
- FPE with Go. FPE. An implementation of Format Preserving Encryption (FPE) for FFX1 and FFX3.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
AWS Encryption
- AWS Symmetric Key Encryption. AWS (Symmetric key). Using symmetric key in AWS.
Go Oblivious Transfer
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Dragon Fly
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
Embedding data in an ECC point
- Embedding data in a point. Go. With Elliptic Curve Cryptography (ECC), we use points on an elliptic curve to represent our data. These are defined with (x,y) points. With this, it is possible to embedded a certain amount of data into the point - as long as it still gives us a valid point on the curve. This example will Curve 25519 to embed data, and is achieved by storing the length of the data in a single byte in the point, and then store the data as byte values in the point (followed by random data). To decode, we can then just read the first byte for the length of the message, and then reveal the data encoded into the point..
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Hashing (Cryptographic)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
Benchmarks and Password strength
The following are the tips related to hashing:
- Password strength. Test. This outlines the strength of various passwords types.
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
Theory
The following are the tips related to hashing:
- Balls in bins. BiBa. This implemented balls in bins.
- Birthday attack (with Big Integers). Calc. This provides a simple example of the birthday attack.
- Birthday attack. Calc. This provides a simple example of the birthday attack.
- Differential Cryptanalysis (Hashing). Cryptanalysis. This provides an implementation of differential cryptanalysis for hashing methods.
MD5, SHA-1
The following are the tips related to hashing:
- MD2 and MD4 MD2/4. The MD2 and MD4 hashing functions were developed by Prof Ronald Rivest in 1989 and 1990, respectively. They both produce a 128-bit hash, but have been shown be vulnerable to attack (see the Collision section in the page).
- MD5 and SHA-1 (to Base-64) with salt Salt. It is possible to add salt to the MD5 algorithm, to mix it up a little.
- MD5 and SHA-1 (to Base-64) Hash. MD5 and SHA-1 produces a hash signature, and the output is typically shown in a hex format or a Base-64. In this example the output is converted into a Base-64 format.
- MD5 and SHA-1. Hash. MD5 and SHA-1 methods produce a hash signature, and are the two of the most widely used methods. The MD5 algorithm has been shown to have weaknesses, and a collision of message hashes has been shown to occur in less than one day. An MD5 signature has 128 bits, an SHA-1 signature has 160 bits, and an SHA-256 signature has 256 bits.
- MD5 Cracking. Hash Cracker. MD5 has a 128-bit signature and can be cracked using rainbow tables. This page tries to crack the MD5 signature.
- Hashing with Go. Hashing. Hashes with Go.
- Detecting hash types. Hash type. This detects has values.
- OpenSSL hashing. Range of methods. Outlines the methods used in OpenSSL
- Hash. Hash. Hashing using JavaScript
- Hashing with node.js. Hashing. Hashing with node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Hashing methods
-
Hazmat Hashes. Hazmat Hashes. This includes the hashing methods in the Hazmat cryptography library. This includes Blake2p, Blake2s, MD5, SHA1, SHA224, SHA256, SGA384, SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHA512, SHA512-224, SHAKE128 and SHA256.
-
Hazmat Hashes. Hazmat Hashes. In this case we will implement Python code to determine SHA1, SHA2, SHA3, Blake2, MD5 and SM3 hashes.
OpenSSL Passwords
-
Password example [here]
-
Hashed passwords with OpenSSL [here]
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Blake 3 hashes
The following are the tips related to similarity hashing:
- Blake 3 in Python. Hashing. Blake 3 hashing.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
Other Hash functions
The following are the tips related to hashing:
- Bloom Filter Bloom filter. A Bloom filter goes a probabilistic method of determining if an element is in a data structure, using indexed hashing methods.
- Cuckoo Table Cuckoo filter. A Cockoo table uses two hash funtions.
- Chaffing. Chaffing. This produces a keyless system.
- GP Hashing with Go. GP Hashing. GP Hashes with Go.
- LDAP. LDAP. This produces a LDAP hash signature for a password.
- LM Hash. LM Hash. This is an LM Hash Calculator. LM Hash is used in many versions of Windows to store user passwords that are fewer than 15 characters long.
- Murmur and FNV Murmur and FNV. While hashing methods such as MD5 and SHA-1 use crypto methods, the Murmur and FNV hashes uses a non-cryptographic hash function. This can be used for general hash-based lookup and was designed by Austin Appleby. It has good performance compared with other hashing methods.
- Pearson. Pearson. This uses a non-crypto hash.
- phpass. phpass. This produces a phpass hash signature for a password.
- Tiger. Tiger. Tiger is a 192-bit hash function and was designed by Ross Anderson and Eli Biham in 1995. It is often used by clients within Gnutella file-sharing networks and does not suffer from known attacks on MD5 and SHA-0/SHA-1. Tiger2 is an addition, in which the message is padded with a byte of 0x80 (in a similar way to MD4, MD5, and SHA), whereas in Tiger it is 0x01. Otherwise, the two methods are the same in their operation.
- Whirlpool. Whirlpool. Whirlpool is a 512-bit cryptographic hash function and was created by Vincent Rijmen (one of the AES creators) and Paulo Barreto, in 2000.
- WPA-2 hash . WPA-2 hash. Implements SHA-2 hash.
- Reusable hash collisions. Reusable hash collisions. Reusable hash collisions.
- The Length Extension Attack. Length Extension Attack. The MD construct has many weaknesses, and one of the most serious is the length extension attack. With this an adversary (Eve) can take a hash for an unknown message, and then add additional data to produce a new valid hash. The hash methods which are at risk against the length extension attack are MD5, SHA-1 and SHA-256. Please follow the code link below to run an example.
- Consistent hashing. Consistent hash. This outlines the usage of Consistent hashes.
- ROR13 (Module and Function). ROR13. With ROR13 we take each 8-bit character and then convert to a unicode value (with 16 bits). Then for each character we rotate the bits right by thirteen places. The resultant hash is then just the accumuluation of the rotated values.
- ROR13 (Function). ROR13 (Function). With ROR13 we take each 8-bit character and then convert to a unicode value (with 16 bits). Then for each character we rotate the bits right by thirteen places. The resultant hash is then just the accumuluation of the rotated values.
- GOST, Streebog256 and Streebog512. GOST, Streebog256 and Streebog512. GOST94 is a hashing method developed with Euro-Asian Council for Standardization, Metrology and Certification (EASC). This has since been developed in the Streebog256 and Streebog512 hashing method. In this case, we will use Libre OpenSSL to convert data into a hashed value.
RIPEMD
- RIPEMD (RACE Integrity Primitives Evaluation Message Digest) and GOST. RIPEM160. RIPEMD is a 128-bit, 160-bit, 256-bit or 320-bit cryptographic hash function, and was created by Hans Dobbertin, Antoon Bosselaers, and Bart Preneel. It is used on TrueCrypt and is open source. The 160-bit version is seen as an alternative to SHA-1, and is part of ISO/IEC 10118
- RIPEMD160. RIPEM160. RIPEMD160 is a 160-bit cryptographic hash function, and was created by Hans Dobbertin, Antoon Bosselaers and Bart Preneel. RIPEMD160 is used in Bitcoin applications.
Chameleon hashes
The following are the tips related to Chameleon hashing:
- Chameleon hash in Golang Chameleon. With a Chameleon hash, we have a normal hash value which is resistant to collisions, but with a known secret we can easily create a collision. The concept was first defined by Krawcyk and Rabin.
Similarity hashes
The following are the tips related to similarity hashing:
- Similarity hash: SimHash (Charikar similarity) in Python Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash (Nilsimsa similarity) Nilsimsa. The Nilsimsa similarity is used to find similarities between spam emails.
- Minhash (Jaccard similarity) Jaccard similarity. The Minhash method is used to find similarities between strings, files and metadata.
- String enthropy String enthropy. Measurement of the entropy of strings.
- Counting identical elements (HyperLogLog) HyperLogLog. Counting the number of identical elements.
SHA-3 and SHA-3 contenders
The following are the tips related to Key derivation hashing:
- Blake and Blake 2. Blake. Implements Blake and Blake 2 (SHA-3 contender).
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
- Grøstl. Grøstl. Implements Grøstl (SHA-3 contender).
- KangarooTwelve. KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- SHA-3, Keccak and SHAKE . SHA-3. Implements SHA-3, Keccak and SHAKE (SHA-3 winner).
- SHA-3. SHA-3. SHA-3 was known as Keccak and is a hash function designed by Guido Bertoni, Joan Daemen, Michaël Peeters, and Gilles Van Assche. MD5 and SHA-0 have been shown to be susceptible to attacks, along with theoretical attacks on SHA-1. NIST thus defined there was a need for a new hashing method which did not use the existing methods for hashing, and setup a competition for competing algorithms. In October 2012, Keccak won the NIST hash function competition and is proposed as the SHA-3 standard. It should be noted that it is not replacement SHA-2, which is currently a secure method. Overall Keccak uses the sponge construction where the message blocks are XORed into the initial bits of the state, and then inevitably permuted.
- cSHAKE. cSHAKE. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS. With the SHA-3 hashing method, we have four different cryptographic hashing methods (SHA3-224, SHA3-256, SHA3-384, and SHA3-512) and two XOF functions (SHAKE128 and SHAKE256). With SHAKE128 and SHAKE256 we can integrate domain separation between different functions — and which are known as cSHAKE128 and cSHAKE256.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- Skein. Skein. Implements Skein (SHA-3 contender).
Key derivation hashing
The following are the tips related to Key derivation hashing:
- Argon2. Go. Outline of Argon2.
- Argon2 with NaCl. Go. Outline of Argon2 using NaCl.
- Balloon. Go. Outline of Balloon.
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- Double ratchet. Go. Outline of double ratcheting.
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- Scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat HKDF. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
Non-crypto/fast hashing
The following are the tips related to non-crypto hashing:
- A perfect hash Perfect hash. This is a non-crypto hash which optimizes the hash value.
- The universal hash Universal hash. This related to the concept of a universal hash.
- FNV. FNV. FNV is one of the fastest hashing methods.
- Murmur. Murmur. Murmur is one of the fastest hashing methods.
- Siphash. Siphash. Siphash is a fast hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- xxHash. xxHash. xxHash is one of the fastest hashing methods.
- Meow. Meow. Meow is one of the fastest hashing methods.
- o1Hash. o1Hash. o1Hash is one of the fastest hashing methods.
- CRC-32. CRC-32. CRC-32 is one of the fastest hashing methods.
- wyhash. wyhash. wyhash is one of the fastest hashing methods.
- CityHash. CityHash. CityHash is one of the fastest hashing methods, and is generally free of security problems.
- FarmHash. FarmHash. FarmHash is one of the fastest hashing methods, and is generally free of security problems.
- Non-crypto. Non-crypto. This includes a range of fast non-cryptography hashing methods.
- Non-crypto hashes (C++): Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro. Non-crypto hashes: Farm, City, xxHash, MUM, Spooky 2, Murmur, Metro and t1ha0. This includes a range of fast non-cryptography hashing methods for Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro using C++ methods.
- Pearson. Pearson. Pearson is one of the fastest hashing methods, and has been designed for 8-bit processors.
- C++: t1ha. t1ha. t1ha is one of the fastest hashing methods, and has been designed for 64-bit processors.
- C++: Spooky. Spooky. Spooky is one of the fastest hashing methods, and V2 has a 32-bit, 64-bit and 128-bit version.
- C++: xxHash. xxHash. xxHash is one of the fastest hashing methods, and has good performance for short data inputs.
- C++: MUM. MUM. MUM is one of the fastest hashing methods.
- C++: FNV 1/1a. FNV 1/1a. FNV 1/1a is one of the fastest hashing methods, and is particularily useful when there are small changes in strings, such as with IP addresses and URLs.
- C++: MetroHash. MetroHash. MetroHash is one of the fastest hashing methods.
- C++: CityHash. CityHash. CityHash was created by Google and is one of the fastest hashing methods. It was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Farm. FarmHash. FarmHash was created by Google and is one of the fastest hashing methods. It is an improvement to CityHash.
- C++: Murmur. Murmur. Murmur is one of the fastest hashing methods, but was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Halftime. Halftime. Halftime is one of the fastest hashing methods and was created by Jim Apple at Apache.
- C++: Highway. Highway. Highway is an ultra-fast keyed-hash, and is more than five times faster than SipHash. It was created by Jyrki Alakuijala, Bill Cox, Jan Wassenberg at Google.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
- C++: CLHash. CLHash. CLHash is an ultra-fast hashing method and focused on improving performance of the hashing of long strings.
- C++: FalkHash. FalkHash. FalkHash is an ultra-fast hashing method and beats most of the other non-cryptography methods for performance. It is focused on the x64 architecture and integrates with AES-NI.
- C++: wyHash. wyHash. wyHash is an ultra-fast hashing method.
- C++: Fibonacci. Fibonacci. Fibonacci is an ultra-fast hashing method.
- C++: Lookup3. Lookup3. Lookup3 is an ultra-fast hashing method.
Key-based hashing
The following are the tips related to Key-based hashing:
- SiphashSiphash. Siphash is a fast key-based hashing method.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
One Time Passwords/Time Stamps
The following are the tips related to hashing:
- One Time Passwords. One Time. This allows a new unique password to be created each instance, based on an initial seed.
- Timed One Time Password (TOTP). Timed One Time Password. This allows a new unique passcode to be created each instance, based on an initial seed for a given time window. We will use a five second window in this case, where a new passcode is generated every five seconds, based on an initial seed of a pass phrase.
- Hashed One Time Password (HOTP). Hashed One Time Password. This allows a new unique passcode to be created each instance, based on a counter value and an initial seed.
- Time Stamp Protocol. TSP. This creates a time stamp for data.
- HOTP and TOTP (Python). OTP. This creates hashed passwords.
eXtendable-Output Function (XOF)
- eXtendable-Output Function (XOF) usign CIRCL. XOF. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS.
SHAKE
The following are the tips related to hashing:
- SHAKE. SHAKE. Implements SHAKE and which is an Extendable Output Function (XOF).
- SHAKE with Go. SHAKE. This implements SHAKE in Go.
- libDisco with Go. libDisco. This implements libDisco.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify
the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods
such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC methods using the Python cryptography primitives for HMAC-MD5.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
Quantum-robust Public Key (Hash-based signature)
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
Hash to ECC point
- Hash to password with Go. Hash to password. Hash to password with Go.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve with libnum.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.

Password-hashing functions using Rust
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing (Non-cryptographic)

You might know those slow old hashing methods, such as MD5, SHA-1, and SHA-256. Well, they were designed to be fast, but also highly secure. But, if we just need a hashing method, such as for a hashtable or Bloom filter, we often don’t need all the security that comes with the main cryptography hashing methods. And so we have the non-cryptography hashing methods, and which are often ultra-fast and highly efficient. To show the difference, in a test, SHA-1 — one of the fastest cryptography hashing methods — managed a processing rate of 364.95 MiB/s, while t1ha was nearly a 100 times faster, at 34,636 MiB/s.
Non-crypto/fast hashing
The following are the tips related to non-crypto hashing:
- A perfect hash Perfect hash. This is a non-crypto hash which optimizes the hash value.
- The universal hash Universal hash. This related to the concept of a universal hash.
- FNV. FNV. FNV is one of the fastest hashing methods.
- Murmur. Murmur. Murmur is one of the fastest hashing methods.
- Siphash. Siphash. Siphash is a fast hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- xxHash. xxHash. xxHash is one of the fastest hashing methods.
- Meow. Meow. Meow is one of the fastest hashing methods.
- o1Hash. o1Hash. o1Hash is one of the fastest hashing methods.
- CRC-32. CRC-32. CRC-32 is one of the fastest hashing methods.
- wyhash. wyhash. wyhash is one of the fastest hashing methods.
- CityHash. CityHash. CityHash is one of the fastest hashing methods, and is generally free of security problems.
- FarmHash. FarmHash. FarmHash is one of the fastest hashing methods, and is generally free of security problems.
- Non-crypto. Non-crypto. This includes a range of fast non-cryptography hashing methods.
- Non-crypto hashes (C++): Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro. Non-crypto hashes: Farm, City, xxHash, MUM, Spooky 2, Murmur, Metro and t1ha0. This includes a range of fast non-cryptography hashing methods for Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro using C++ methods.
- Pearson. Pearson. Pearson is one of the fastest hashing methods, and has been designed for 8-bit processors.
- C++: t1ha. t1ha. t1ha is one of the fastest hashing methods, and has been designed for 64-bit processors.
- C++: Spooky. Spooky. Spooky is one of the fastest hashing methods, and V2 has a 32-bit, 64-bit and 128-bit version.
- C++: xxHash. xxHash. xxHash is one of the fastest hashing methods, and has good performance for short data inputs.
- C++: MUM. MUM. MUM is one of the fastest hashing methods.
- C++: FNV 1/1a. FNV 1/1a. FNV 1/1a is one of the fastest hashing methods, and is particularily useful when there are small changes in strings, such as with IP addresses and URLs.
- C++: MetroHash. MetroHash. MetroHash is one of the fastest hashing methods.
- C++: CityHash. CityHash. CityHash was created by Google and is one of the fastest hashing methods. It was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Farm. FarmHash. FarmHash was created by Google and is one of the fastest hashing methods. It is an improvement to CityHash.
- C++: Murmur. Murmur. Murmur is one of the fastest hashing methods, but was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Halftime. Halftime. Halftime is one of the fastest hashing methods and was created by Jim Apple at Apache.
- C++: Highway. Highway. Highway is an ultra-fast keyed-hash, and is more than five times faster than SipHash. It was created by Jyrki Alakuijala, Bill Cox, Jan Wassenberg at Google.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
- C++: CLHash. CLHash. CLHash is an ultra-fast hashing method and focused on improving performance of the hashing of long strings.
- C++: FalkHash. FalkHash. FalkHash is an ultra-fast hashing method and beats most of the other non-cryptography methods for performance. It is focused on the x64 architecture and integrates with AES-NI.
- C++: wyHash. wyHash. wyHash is an ultra-fast hashing method.
- C++: Fibonacci. Fibonacci. Fibonacci is an ultra-fast hashing method.
- C++: Lookup3. Lookup3. Lookup3 is an ultra-fast hashing method.
A fuller test with SMHasher gives [here]:
Hash function MiB/sec cycl./hash cycl./map Quality problems
------------------------------------------------------------------
o1hash 12439661.09 16.77 166.13 insecure, no seed, zeros, fails all tests
crc32_hw1 23208.73 46.74 179.70 insecure, 100% bias, collisions, distrib, BIC, machine-specific (x86 SSE4.2)
t1ha0_aes_noavx 22785.26 38.71 180.61 LongNeighbors, machine-specific (x86 AES-NI)
t1ha0_aes_avx1 22714.85 48.12 226.52 LongNeighbors, machine-specific (x64 AVX.txt)
t1ha0_aes_avx2 22345.33 44.38 556.47 LongNeighbors, machine-specific (x64 AVX2)
falkhash 20202.42 173.63 321.52 Sparse, LongNeighbors, machine-specific (x64 AES-NI)
MeowHash64low 17378.06 85.48 237.60 Sparse, invertible, machine-specific (x64 AES-NI)
MeowHash32low 17374.64 85.48 258.53 Sparse, invertible, machine-specific (x64 AES-NI)
MeowHash 17371.91 85.48 247.96 Sparse, invertible, machine-specific (x64 AES-NI)
FarmHash32 17112.05 47.7 214.71 machine-specific (x64 SSE4/AVX)
xxh3 16538.52 32.81 184.86 DiffDist bit 7 w. 36 bits, BIC
xxh3low 16462.36 32.77 199.79
farmhash32_c 16299.81 47.79 219.19 machine-specific (x64 SSE4/AVX)
xxh128low 15174.85 33.79 187.05
xxh128 15174.14 40.46 195.65
farsh32 14053.09 74.29 245.33 insecure: AppendedZeroes, collisions+bias, MomentChi2, LongNeighbors
metrohash64crc_2 14034.84 48.94 162.54 UB, Cyclic 8/8 byte, DiffDist, BIC, machine-specific (SSE4.2/NEON)
metrohash64crc_1 14000.5 49.08 150.54 UB, Cyclic 8/8 byte, DiffDist, BIC, MomentChi2, machine-specific (SSE4.2/NEON)
metrohash128crc_1 13948.67 65.2 168.08 UB, machine-specific (SSE4.2/NEON)
metrohash128crc_2 13920.19 65.12 176.70 UB, machine-specific (SSE4.2/NEON)
halftime_hash128 13478.23 97.79 252.14
wyhash32low 12911.09 29.59 205.43 2 bad seeds
wyhash 12879 30.35 196.77 2^33 bad seeds
CityCrc128 12343.43 74.5 209.75
fletcher2 12011.15 25.29 298.60 bad seed 0, UB, fails all tests
fletcher4 11928.55 25.27 293.49 bad seed 0, UB, fails all tests
halftime_hash256 11620.28 98.44 252.60
fibonacci 11339.87 26.33 705.64 UB, zeros, fails all tests
ahash64 9862.62 27.32 181.68 rust
Spooky128 9751.14 63.84 192.47 UB
Spooky64 9747.47 62.2 191.71 UB
Spooky32 9747.13 62.24 196.96 UB
t1ha1_64le 9723.86 34.39 176.91 Avalanche
cmetrohash64_1 9683.33 45.2 161.01 UB, LongNeighbors, BIC, MomentChi2
cmetrohash64_2 9669.95 44.75 149.67 LongNeighbors
metrohash64_2 9668.51 44.45 164.30 UB, LongNeighbors
metrohash64 9664.61 44.59 150.74 UB, LongNeighbors, BIC
metrohash64_1 9664.57 45.37 152.31 UB, LongNeighbors, BIC, MomentChi2
cmetrohash64_1o 9658.31 42.84 163.45 UB, LongNeighbors, BIC, MomentChi2
FNV1a_YT 9643.42 32.06 175.19 bad seed, UB, fails all tests
City128 9640.19 88.45 225.38
metrohash128_2 9584.94 59.1 167.43 UB, LongNeighbors
metrohash128 9569.16 58.68 167.53 UB, LongNeighbors
metrohash128_1 9558.17 59.04 175.94 UB, LongNeighbors
FarmHash128 9409.63 74.52 210.25
VHASH_32 9404.99 77.01 250.57 sanity, Seed, MomentChi2
VHASH_64 9392.39 74.72 227.92 sanity, Seed, MomentChi2
farmhash128_c 9244.13 79.08 209.44
t1ha2_atonce 9237.12 38.94 194.32 Zeroes low3
City64noSeed 9090.42 32.23 171.53 Avalanche, Sparse, TwoBytes, MomentChi2, Seed
City64low 9089.45 47.75 201.73
t1ha2_stream 9068.55 74.56 219.85 Sparse, Permutation, LongNeighbors
City64 9066.9 47.81 197.78 Sparse, TwoBytes
t1ha2_stream128 9065.5 93.19 236.50 Sparse, Permutation, LongNeighbors
xxHash64 8936.63 51.31 174.34
pengyhash 8744.48 85.31 222.45
farmhash64_c 8713.16 47.96 201.00
FarmHash64 8684.76 48.13 200.51
crc64_hw 8440.13 34.94 141.15 insecure, 100% bias, collisions, distrib, BIC, machine-specific (SSE4.2/NEON)
t1ha2_atonce128 8350.99 55.65 203.53 LongNeighbors
PMPML_64 8161.19 53.2 179.16 unseeded: Seed, MomentChi2, BIC
halftime_hash512 7681.62 125.81 274.01
tabulation 7621.75 42.19 179.93
t1ha1_64be 7481.37 38.16 193.22 Avalanche
MUMlow 7225.18 37.85 197.92 UB, 5 bad seeds
farsh64 7216.29 130.3 302.44 insecure: AppendedZeroes, collisions+bias, MomentChi2, LongNeighbors
MUM 7134.56 37.85 172.34 UB, too many bad seeds, machine-specific (32/64 differs)
nmhash32 7003.3 68.93 216.59
PMPML_32 6704.53 53.5 197.43 Avalanche >512, unseeded: Seed, BIC, MomentChi2, PerlinNoise
nmhash32x 6342.95 56.41 217.75
crc32_hw 6330.42 35.55 170.16 insecure, 100% bias, collisions, distrib, BIC, machine-specific (SSE4.2/NEON)
FNV2 6258.84 33.25 142.89 fails all tests
FNV1A_Pippip_Yurii 6258.46 28.19 184.41 UB, sanity, fails all tests
FNV1A_Totenschiff 6258.23 27.99 198.20 UB, zeros, fails all tests
HighwayHash64 6242.58 99.55 248.41
mx3 6146.02 52.48 173.09 UB
xxHash32 6040.87 51.77 177.91 LongNeighbors, collisions with 4bit diff, MomentChi2 220
prvhash64s_64 5481.48 170.05 325.39
mirhash 5413.73 39.68 154.47 UB, 2^36 bad seeds, LongNeighbors, machine-specific (32/64 differs)
mirhash32low 5412.76 39.79 182.13 UB, 4 bad seeds, Cyclic, LongNeighbors, machine-specific (32/64 differs)
Murmur3F 5226.4 52.18 175.85 UB
prvhash64s_128 5161.33 260.96 442.70
t1ha0_32le 5132.18 54.83 193.53 Sparse, LongNeighbors
halftime_hash64 4990.72 120.55 281.64
Murmur2B 4882.95 39.72 149.43 UB, 1.8% bias, collisions, 3.4% distrib, BIC
seahash32low 4801.33 58.54 227.31 PerlinNoise 32, !msvc
seahash 4796.97 58.55 201.58 PerlinNoise, !msvc
fasthash32 4737.61 45.32 181.86 UB, insecure
fasthash64 4737.21 42.79 164.87 UB, insecure, Moment Chi2 5159 !
umash32_hi 4662.92 54.22 214.20
umash64 4662.09 53.42 188.09
umash32 4633.19 53.42 216.33
t1ha0_32be 4585.59 55.98 183.45 Sparse, LongNeighbors
clhash 4472.31 82.72 229.73 PerlinNoise, machine-specific (x64 SSE4.2)
tabulation32 4317.34 35.45 197.20 collisions
Murmur2C 4092.99 51.84 164.65 UB, 2^32 bad seeds, 91% bias, collisions, distr, BIC, LongNeighbors
farsh128 3776.92 232.48 398.67
City32 3675.04 57.73 212.04
TSip 3228.14 57.96 211.71 !msvc
Murmur3C 3197.63 67.9 198.00 UB, LongNeighbors, Text, DiffDist
Crap8 3149.63 36.23 195.11 UB, 2.42% bias, collisions, 2% distrib
Murmur2 3146.91 41.87 187.89 UB, 1 bad seed, 1.7% bias, 81x coll, 1.7% distrib, BIC
Murmur2A 3146.79 46.87 191.96 UB, 1 bad seed, 12.7% bias, LongNeighbors
aesnihash 2963.39 71.24 217.73 fails many tests, machine-specific (x64 AES-NI)
BEBB4185 2951.62 222.03 343.63 UB, too many bad seeds, msvc-specific
jodyhash6 2848.42 29.99 164.36 bias, collisions, distr, BIC, LongNeighbors
wyhash32 2532.89 48.4 484.57 2 bad seeds, 32-bit
umash128 2427.46 70.6 197.29
Murmur3A 2413.88 53.36 182.37 UB, 1 bad seed, Moment Chi2 69
prvhash64_64m 2386.19 51.18 186.87
prvhash64_128 2383.57 103.44 246.45
prvhash64_64 2375.72 51.61 190.97
hasshe2 2372.52 68.64 216.74 Permutation,TwoBytes,Zeroes,Seed
PMurHash32 2344.78 58.48 196.43 1 bad seed, Moment Chi2 69
mirhashstrict32low 2218.87 65.48 190.59 1 bad seed, MomentChi2 9
mirhashstrict 2217.32 65.53 182.07
sha1ni 2019.96 135.84 564.40 insecure,sanity, Permutation, Zeroes, machine-specific
sha1ni_32 2019.94 136.82 589.46 machine-specific
superfast 1956.25 53.61 180.10 UB, bad seed 0, 91% bias, 5273.01x collisions, 37% distr, BIC
sha2ni-256_64 1910.34 146.06 595.16 Zeroes, machine-specific
sha2ni-256 1906.77 145.47 603.08 insecure,sanity, Permutation, Zeroes, machine-specific
farsh256 1895.77 459.86 575.95
SipHash13 1889.1 89 199.95 0.9% bias
Murmur1 1804.67 51.51 188.41 UB, 1 bad seed, 511x collisions, Diff, BIC
lookup3 1658.31 48.84 194.15 UB, 28% bias, collisions, 30% distr, BIC
pearsonbhash64 1486.34 104.32 185.03
poly_1_mersenne 1431.65 54.49 189.52 fails most tests
jodyhash32 1428.37 44.36 185.85 bias, collisions, distr, BIC LongNeighbors
pearsonbhash128 1347.03 121.75 214.84
poly_2_mersenne 1323.69 66.93 190.88
poly_3_mersenne 1323.59 74.86 206.77
poly_4_mersenne 1323.57 82.67 200.36
blake3_c 1285.91 340.01 552.63 no 32bit portability
GoodOAAT 1052 71.62 192.19
pearsonbhash256 998.9 167.05 261.29
SipHash 980.88 127.77 246.19
MicroOAAT 977.6 59.61 185.06 100% bias, distrib, BIC
FNV1a 791.84 69.69 177.84 bad seed, zeros, fails all tests
sdbm 791.84 67.69 177.06 bad seed 0, fails all tests
FNV64 791.82 70.24 159.29 fails all tests
bernstein 791.82 68.63 180.71 bad seed 0, fails all tests
beamsplitter 789.22 682.45 1150.3 UB, too many bad seeds
HalfSipHash 755.78 114.47 243.72 zeroes
chaskey 753.23 153.42 288.26 PerlinNoise
x17 527.9 98.78 184.09 99.98% bias, fails all tests
JenkinsOOAT_perl 452.49 118.78 194.78 bad seed 0, test FAIL
MurmurOAAT 452.49 113.07 197.83 bad seed 0, 1.5-11.5% bias, 7.2x collisions, BIC, LongNeighbors
JenkinsOOAT 452.48 142.85 213.93 bad seed 0, 1.5-11.5% bias, 7.2x collisions, BIC, LongNeighbors
crc32 392.1 131.62 204.58 insecure, 8590x collisions, distrib, PerlinNoise
sha1-160 364.95 1470.55 1794.1 Comb/Cyclic low32
rmd256 362.49 617.02 815.44 Bad seeds
blake2b-256_64 356.97 1222.76 1435.0
blake2b-224 356.59 1228.5 1425.87
blake2b-160 356.08 1236.84 1458.15
blake2b-256 355.97 1232.22 1443.31 Sparse high 32-bit
md5-128 353.76 638.29 803.39
md5_32a 353.64 629.85 799.56 Sparse high 32-bit
sha1_32a 353.03 1385.8 1759.9 Cyclic low32, 36.6% distrib
rmd128 334.36 659.03 838.32 Bad seeds
blake2s-128 295.3 698.09 1059.2
pearsonhash64 287.95 174.11 196.50 Avalanche, Seed, SSSE3 only. broken MSVC
pearsonhash128 287.95 171.72 194.61 Avalanche, Seed, SSSE3 only. broken MSVC
pearsonhash256 264.51 184.87 218.79 Avalanche, Seed, SSSE3 only. broken MSVC
blake2s-256 215.28 1014.88 1230.38
blake2s-160 215.01 1026.74 1239.54
blake2s-256_64 211.52 1044.22 1228.43
blake2s-224 207.06 1063.86 1236.50
rmd160 202.16 1045.79 1287.74 Bad seeds, Cyclic hi32
sha2-256_64 148.01 1376.34 1624.71 Bad seeds, Moment Chi2 7
sha2-256 147.8 1374.9 1606.06 Bad seeds, Moment Chi2 4
sha2-224_64 147.6 1360.1 1620.93 Bad seeds, Cyclic low32
sha2-224 147.13 1354.81 1589.92 Bad seeds, Comb low32
asconhashv12 144.98 885.02 1324.23
sha3-256 100.58 3877.18 4159.79 PerlinNoise
sha3-256_64 100.57 3909 4174.63 PerlinNoise
asconhashv12_64 86.73 684.02 606.93
floppsyhash 35.72 1868.92 1411.07
tifuhash_64 35.6 1679.52 1212.75 Cyclic low32
Problems include:
- Bad Seeds. A random seed is often used to initialise the hash. This problem relates to having a bad seed..
- Undefined behaviour (UB). This includes Misaligned, oob (Out of bounds), Signed integer overflow and Shift exponent overflow.
o1hash is the fastest, and a quick and dirty hashing method. It is generally not secure. t1h (Fast Positive Hash) requires AES-NI (Intel Advanced Encryption Standard Instructions) and is one of the fastest hashes at 22.785 Gbps. It has fairly good security levels. Meow comes in around 17.378 Gbps. We can see that SHA-1-160 runs as 364 Mbps, while Meow runs at 17.378 Gbps. Blake 3 is one of the fast cryptography hash and has a rate of 1.285 Gbps, and Blake 2 gives a rate around 215 Mbps. SHA-3 gives hashing rates of 100.58 Mbps.
Google recommend the following for 64-bit hashes without quality problems:
- xxh3low
-
wyhash
-
ahash64
-
t1ha2_atonce
-
FarmHash
-
halftime_hash128
-
Spooky32
-
pengyhash
-
nmhash32
-
mx3
-
MUM/mir
- fasthash32
Hash-based Signatures

With hash-based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature, unless we create a stateless method, such as SPHINCS+ [1]. Currently NIST have the final round for the Post Quantum Cryptography competition, and for digital signatures, SPHINCS+ is one of the alterative finalists (alongside Picnic).
Hash-based signature (theory)
- BiBa (Go). BiBa. An overview of BiBa One Time Signature [9]. Basically the method involves us taking a hash of a value using a standard hashing method, such as with SHA-256. There will then be \(2^{256}\) different hashing values. We aim to create a signature for a message, so Bob (the signer) selects a number of random values for his private key value and then publishes the hash of each of these (\(P_1\), \(P_2\), etc). He then sends these public keys to Alice. Now when Bob wants to sign a message, he will take one of his private key values, and then hashes it, and then determines the bin that it should be placed. In this case, we could use the \(\pmod N\) function on the hash, and where \(N\) is the number of bins. If we select \(2^{10}\) there will be 1,024 bins.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature [9].
Hash-based signature (stateful)
- BLISS - Post-quantum signing. BLISS. One of the alteratives to the usage of our existing public key methods is the usage of lattice cryptography, and especially in the usage of Ring Learning With Errors (RLWE). An important application is within digital signatures, and where Bob will sign something with his private key, and then Alice can prove that he signed it with his public key. One post-quantum signature method is BLISS (short for Bimodal Lattice Signature Scheme) [8]. It was created by Léo Ducas, Alain Durmus, Tancrède Lepoint and Vadim Lyubashevsky in 2013.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Hash to Obtain Random Subset (HORS) [3] is a quantum robust hashed-based one-time signature. With this we create a series of integers for our private keys and organise into an indexable form. Then we hash them to a sequence of public key values. Next we segment the hash of the message into a series of n-bit integer values. The signature is then achieved through a look-up of the value in the public key list.
- Lamport Signatures. Lamport. Outlines Lamport signatures [7]. When we sign a message we take its hash and then encrypt with our private key. The public key is then used to prove it, and will prove that we signed it with our private key. The Lamport signature uses 512 random hashes for the private key, and which are split into Set A and Set B. The public key is the hash of each of these values. The size of the private key is 16KB (2×256×256 bits) and the public key size is also 16 KB (512 hashes with each of 256 bits).
- Winternitz Signatures (W-OTS). Winternitz. Outlines Winternitz signatures [4, 5]. W-OTS uses relatively small key and signatures sizes, and is thought to be quantum robust. It generates 32x256 bit random private keys. We then hash these a number of times, and is defined by a parameter (w). If we use w=8, we hash the private keys by (2w). This creates 32x256 bits public keys. The signature is the created by taking eight bits at a time, and then the 8-bit binary int (n) is subtracted from 256 and the private key is the hashed 256-n times. The signature is then 32 hashes which are derived from random private keys. To verify the signature, the recipient parses the hash of the signature (using 8 bits at a time, and extracting the 8 bit int, n).
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method [6], and which is used within speeds-up of Hashing-based signature methods. Using methods such as SHA-1 and SHA-2 (aka SHA-256) will be inefficient as they tend to compress the data inputs through a number of stages. Haraka v2 [6] is different as focuses on inputs of just 256 bits (32 bytes) or 512 bits (64 bytes). This makes the method useful when we are dealing with key and hash values, and is especially useful for hash-based signatures. The output is 256 bits long, but where the input can be either be 256 bits (Haraka256) or 512 bits (Haraka512). These lengths are typically for the outputs of modern hashing applications. The Haraka method, too, has been optimized with AES instructions (AES-NI - Intel Advanced Encryption Standard New Instructions) and which are supported within the hardware of the processor. As Haraka is focused on short messages, the number of rounds within the hashing process has been reduced.
Hash-based signature (stateless)
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ digital signature. SPHINCS digital signature. Outline of the a SPHINCS stateless digital signature method [1].
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
Hash-based signature (Merkle-based)
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
Introduction
Many of the problems we see on the Internet relate to the lack of trust within transactions. The emails you receive and the Web sites that you visit often have very little trust built into them. For trust the email address of the sender, but anyone can fake that address. So increasingly we create a digital signature, and where we sign our messages. In this way, we can check for authentication, integrity and non-repudiation.
With the Alice creates a key-pair: a public key and a private key. She then takes a hash of the message, and then encrypts this hash with her private key, and passes the message and the signature to Bob. Bob then reads the message and takes a hash of it. He then decrypts Alice's signature with her public and checks the hashes. If they match, he knows that she signed and that it has not been changed along the way:
Currently, we often use RSA, DSA and ECDSA to sign our messages. These are based on the difficulty of finding out the factors of a number and on the processing of discrete logarithms. At the current time these methods are computationally hard problems, but with quantum computers, they become much easier. This was shown by Peter Shor who illustrated that it was possible to crack them in polynomial time.
Of all the methods that are being proposed, the hash-based methods look as if they have a good chance of success of creating quantum robust signatures. methods and code-based methods are being researched, but the usage of hashing methods is already well and could provide the best alternative to the existing methods. Hashing methods, too, often bring other advantages, such as forward secure, which means that a key which is cracked will not reveal all the previous keys.
Merkle trees
The root of hash-based methods isin Merkle trees, and which are a way of hashing is used in many applications, including with Bitcoin, Ethereum, Git distribution systems, No SQL, and in many P2P applications. With a Merkle tree we take our data elements, and then hash them, and take pairs of these hashes to create a new hash, and so we build a table. At the top of the tree is the root element (in this case Hash1234):

In this way, we can use the tree to see if we have matching data on systems.On a P2P network, we can transfer a file by splitting it into data segments and then distributing these segments across the network. A trusted source will have the complete Merkle tree for rebuilding the file, and a client can thus rebuild from the Merkle tree and determine the parts of the file which are still missing. Once transferred the root hash (and all the other hashes) will then match. In its core method, the Merkle Signature Scheme (MSS) has serious performance and memory issues, but enhanced methods such as XMSS create with much less of a performance hit.
One-time signatures (Lamport)
The core method used in hash-based signatures is that of the one-time signature, and where we create a new key pair for every method we need to create. If the keys were reused, an attacker could start to learn the private key, and thus spoof messages. One of the first methods was produced by Leslie Lamport and Whitfield Diffie, in 1979, and is defined as:
- We create two data sets with 256 random 256-bit numbers (Set A and Set B). These are the private key (512 values).
- we take the hash of each of the random numbers. This will give 512 hashes and will be the public key.
- We then hash the message using and then test each bit of the hash (0 ... 255). If it is a 0, we use the ith number in Set A, else we use the ith number from Set B.
- The signature is then 256 random numbers (taken from either Set A or Set B) and the public key is the 512 hashes (of Set A and Set B).
The public and private keys are then each 16KB in size. A demo of the method is here.

Figure 1: Lamport method
The major problem with the method is that a key pair for every message. also in 1979, found a solution with Merkle trees.
One-time signature (W-OTS)
To improve performance method (and which reduced key sizes), Merkle proposed Winternitz OTS (named after Robert Winternitz). With this method was possible to sign many bits at the same time. The method is:
- We create 32 256-bit random numbers. These 32 values will be our private key.
- We then hash each of these values 256 times. These 32 values will be our public key.
- We now take the message and hash it using SHA-256. This produces 32 8-bit values (N1, N2 ... N32).
- Next we take each 8-bit value in the hash of the message, and then hash 256-N times (where N is the value of the 8-bit value).
- To prove the signature, we take the message and hash it with SHA-256, and then take each 8-bit value. We then hash the 8-bit signature value by the number of times defined by the message hash value (N1, N2..). The result for each operation should equal the public key value.
This is illustrated below in Figure 2. A demo of the method is here.

Figure 2: W-OTS
Hash-based Signatures
The methods such as W-OTS and Lamport only provide for a one-time signature. In order to sign many messages, we can use the Merkel signature scheme (MSS). With this we take a hash of the keys and build these as the leaves of the tree. The root of the tree is then the public key - the verification key. We then just use the private key of the W-OTS method to create the signature. The sender also sends the authentication path, which is the neighbouring nodes within the path and which leads to the root of the tree. The recipient can then rebuild the tree using the verification key (which can be received a digital certificate) and the authentication path. For the next message we move onto another key pair and where the index of the key part is revealed.
In the following example we have our root as the public key, and then want to sign with Key3. We then show the authentication path which takes us to the root (as defined in the bold arrows):

Conclusions
Hashed-based methods look to be a strong contender for weaning us off RSA, DSA and ECDSA, but we will have to look at the stateful generation of keys. For this we will have to generate a bank of key pairs (2, 4, 8, 16, etc) and then create the public key from the root of the Merkle tree. We must then remember the keys we have used previously, and only use an unused one. Once we use our new key pair, we then show our working-out as to how the private key is integrated into our tree. It is a bit like a teacher marking a question correctly, and asking for the working out that go you to the answer.
References
[1] Bernstein, D. J., Hopwood, D., Hülsing, A., Lange, T., Niederhagen, R., Papachristodoulou, L., ... & Wilcox-O’Hearn, Z. (2015, April). SPHINCS: practical stateless hash-based signatures. In Annual international conference on the theory and applications of cryptographic techniques (pp. 368-397). Springer, Berlin, Heidelberg [paper].
[2] Bernstein, D. J., Hülsing, A., Kölbl, S., Niederhagen, R., Rijneveld, J., & Schwabe, P. (2019, November). The SPHINCS+ signature framework. In Proceedings of the 2019 ACM SIGSAC conference on computer and communications security (pp. 2129-2146) [paper].
[3] Reyzin, L., & Reyzin, N. (2002, July). Better than BiBa: Short one-time signatures with fast signing and verifying. In Australasian Conference on Information Security and Privacy (pp. 144-153). Springer, Berlin, Heidelberg [paper].
[4] Merkle, R. C. (1989, August). A certified digital signature. In Conference on the Theory and Application of Cryptology (pp. 218-238). Springer, New York, NY.
[5] Hülsing, A. (2013, June). W-OTS+–shorter signatures for hash-based signature schemes. In International Conference on Cryptology in Africa (pp. 173-188). Springer, Berlin, Heidelberg.
[6] Kölbl, S., Lauridsen, M. M., Mendel, F., & Rechberger, C. (2016). Haraka v2–efficient short-input hashing for post-quantum applications. IACR Transactions on Symmetric Cryptology, 1-29. [here]
[7] Lamport, L. (1979). Constructing digital signatures from a one-way function (Vol. 238). Technical Report CSL-98, SRI International. [paper]
[8] Ducas, L., Durmus, A., Lepoint, T., & Lyubashevsky, V. (2013, August). Lattice signatures and bimodal Gaussians. In Annual Cryptology Conference (pp. 40-56). Springer, Berlin, Heidelberg [paper].
[9] Perrig, A. (2001, November). The BiBa one-time signature and broadcast authentication protocol. In Proceedings of the 8th ACM Conference on Computer and Communications Security (pp. 28-37) [paper] .
Hashing (Simularity)

Similarity hashes allow for two data objects to be compared for their similarity.
Similarity assessment methods
The following relate to the basic methods used for string similarity:
- String similarity String similarity. This measures edit distance (including Levenshtein distance), Jaro (including Jaro-Winkler), and QGrams.
- String enthropy String enthropy. Measurement of the entropy of strings.
- Soundex Soundex. Soundex uses a phonetic algorithm to classify a sound as it is pronounced. It focuses on matching phrases which have minor spelling errors.
Similarity hashes
The following are the tips related to similarity hashing:
- Similarity hash: SimHash (Charikar similarity) in Python Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash (Nilsimsa similarity) Nilsimsa. The Nilsimsa similarity is used to find similarities between spam emails.
- Context Triggered Piecewise Hashes (CTPH): ssdeep CTPH similarity. Kornblum [6] created ssdeep and which computes fuzzy hashes. This aims to match similar byte sequences, no matter if there are differences between these sequences. For this we break a file up into fragments with a rolling hash function. We then produce a small hash for each of those fragments. These are then aggregated to produce the complete hash of a file. In comparing file signatures, we treat the resultant hash value as a string, and then uses an edit distance method to compare.
- TLSH (A Locality Sensitive Hash) TLSH similarity. In malware analysis and in text similarity, we often have to identify areas of data within files which are similar. One method is TLSH (A Locality Sensitive Hash), and which was defined by Oliver et al [7]. It is used - along with ssdeep - by VirusTotal to identify a hash value for malware.
- Minhash (Jaccard similarity) Jaccard similarity. The Minhash method is used to find similarities between strings, files and metadata.
- Counting identical elements (HyperLogLog) HyperLogLog. Counting the number of identical elements.
Hazmat cryptography

The Cryptography library in Python contains interfaces to common cryptographic algorithms, including symmetric key methods, hashing, public key, and key derivation functions. Many of these are contained with the Hazmat (Harzardous Material) primative setup.
Hashing, HMAC, CMAC, Poly1305 and HKDF
-
Hazmat Hashes. Hazmat Hashes. This includes the hashing methods in the Hazmat cryptography library. This includes Blake2p, Blake2s, MD5, SHA1, SHA224, SHA256, SGA384, SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHA512, SHA512-224, SHAKE128 and SHA256.
-
Hazmat Hashes. Hazmat Hashes. In this case we will implement Python code to determine SHA1, SHA2, SHA3, Blake2, MD5 and SM3 hashes.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
- Hazmat HKDF. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
- Hazmat CMAC. Hazmat CMAC. CMAC methods using the Python cryptography primitives.
- Hazmat Poly1305. Hazmat Poly1305. Poly1305 methods using the Python cryptography primitives.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
Symmetric key
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat. Implementation of ChaCha20/Poly1305 with a random key using Hazmat.
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat. Implementation of AES GCM with a random key using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hazmat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Hazmat Symmetric Key Padding. Symmetric key. This includes the coverage of padding with Hazmat.
- Hazmat Symmetric Key Padding. Symmetric key. This includes the coverage of padding with Hazmat.
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
- Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . With 3DES encryption, we use a 128-bit key and a 64-bit IV value. The two modes supported are ECB (without salt) and CBC (with salt). The DES algorithm has been around for a long time, and the 56-bit version is now easily crackable (in less than a day on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases, and splits the key into two. Overall the key size is typically 112 bits (with a combination of the three keys - of which two of the keys are the same). In this case we will use PKCS7 padding, and which fills the input data with a value that is equal to the number of padding bytes. Overall, DES has a 64-bit block size, and which equates to eight ASCII characters.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key . And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.
Asymmetric key
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- ECC key generaton with Hazmat. Elliptic Curve key gen. Creating ECC keys using Hazmat and Python.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- Hazmat RSA signing (with key values). RSA signing with Hazmat. RSA signing using Python and with Hazmat (with key values).
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here]
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Signatures. DSA Signatures. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. The ECDSA method is an extension of DSA, but implemented with elliptic curve (EC) methods. As with most public key signing methods, we take a hash of a message, and then apply a private key to create a signature (\(r,s\)). This is done by creating a random value (\(k\)) to produce the signature. The signature is then verified using the associated public key. This then verifies the creator of the signature and that the message has not been changed.
Digital Signature: ECDSA/EdDSA
- ECDSA with Hazmat. ECDSA wih Hazmat. This outlines ECDSA with Hazmat.
- Ed25519 for EdDSA signatures with Hazmat. EdDSA: Ed25519. This page uses the Hazmat primitives for the cryptography library.
- Ed448 for EdDSA signatures with Hazmat. EdDSA: Ed448. This page uses the Hazmat primitives for the cryptography library.
- Ed25519 using NaCl. Ed25519. This page uses the NaCl port from libsodium.
- ECDSA Signatures with Hazmat (SECP256R1, SECP384R1, SECP521R1, SECP224R1, SECP192R1, and SECP256K1). ECC Signatures. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and then creates an ECDSA signature for a given message.
Digital Signature: RSA
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
Key exchange: ECDH/X25519
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives and showing the byte values for the key.
Tokens
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
Homomorphic Encryption

Homomorphic encryption supports mathematical operations on encrypted values. Partial Homomorphic Encryption (PHE) supports a few arithmatic operations, while Full Homomorphic Encryption (FHE) supports add, subtract, multiply, and divide. Homomorphic encryption normally involves a public key to encrypt the data, and a private key to decrypt it. There have been four main generations of homomorphic encryption, and the most recent being the HEAAN method.
Simple
- Simple Homomorphic Cipher. Hom. This outlines a Simple Homomorphic cipher.
- Simple Homomorphic Cipher (Python). Hom. This outlines a Simple Homomorphic cipher with Python.
- Full Homomorphic Cipher with a Public Key. Public key. This outlines a Simple Homomorphic cipher using a public key
ElGamal
- ElGamal Homomorphic Cipher (Go). ElGamal. This outlines ElGamal Homomorphic cipher with Go.
- ElGamal Homomorphic Cipher (Go) - Divide. ElGamal. This outlines ElGamal Homomorphic cipher with Go with divide.
- ElGamal Homomorphic Cipher (Go) - Additive. ElGamal. This outlines ElGamal Homomorphic cipher with Go with addition.
- ElGamal Homomorphic Cipher for Multiplication (Python). ElGamal. This outlines ElGamal Homomorphic multiplication with Python.
- ElGamal Homomorphic Cipher for Division (Python). ElGamal. This outlines ElGamal Homomorphic division with Python.
- ElGamal Homomorphic Cipher for Addition (Python). ElGamal. This outlines ElGamal Homomorphic addition with Python.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (Python). ElGamal. This outlines ElGamal Homomorphic subtraction with Python.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
RSA
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
ZKP
- Full Homomorphic Cipher to determine if Bob is older. Older. This outlines a Simple Homomorphic cipher to determine if Bob is older than Alice.
- Full Homomorphic Cipher to determine matching password. Password. This outlines a Simple Homomorphic cipher to determine if a password matches
- Interactive ZKP With Probablistic Methods. ZKP. Interactive ZKP With Probablistic Methods using Python.
- Full Homomorphic Cipher for Millionaire's Problem. Millionaire. This outlines a Simple Homomorphic cipher for the Millionaire's Problem
Voting
- Trusted voting. Trusted. A trusted voting method.
Secret share
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Lattice
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
Full Homomorphic Cipher
- Full Homomorphic Cipher for 2-bit Adder. Adder. This outlines a Simple Homomorphic cipher for a 2-bit adder with DGHV.
- Full Homomorphic Cipher for Full Adder. Full Adder. This outlines a Simple Homomorphic cipher for a full adder with DGHV.
- Full Homomorphic Cipher for 4-bit Adder. Adder. This outlines a Simple Homomorphic cipher for a 4-bit adder with DGHV.
- Full Homomorphic Cipher for 4-bit Adder/Subtractor. Subtract. This outlines a Simple Homomorphic cipher for a 4-bit adder/subtractor with DGHV.
- Full Homomorphic Cipher to XOR two integers. X-OR. This outlines a Simple Homomorphic cipher to X-OR two integers
Paillier
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier) .
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Damgård-Jurik Homomorphic Encryption With Secret Shares. Damgård-Jurik Method. Two of the major areas of developments within cybersecurity will be the usage of homomorphic encryption, and in the usage of Shamir secret sharing. With homomorphic encryption, we can encrypt values, and then operate on them with arithmetic functions (such as add, subtract and multiply), and with Shamir secret sharing, we can split secrets into shares, and then distributed them over networks. These approaches will take privacy to new levels. So let’s look at the Damgård-Jurik method.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Learning with Errors (LWE)
- Learning With Errors . LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret key value (s) and another value (e). Next we select a number of values (t[]) and calculate g[] = t[] x s + e. The values of g[] and t[] become our public key.
- Public Key Encryption with Learning With Errors (LWE). LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret value (s) and which is our private key. We then create a public key which is based on random numbers (A), and then generate another set of numbers (B) which is based on A,s and random errors e. An example of encryption with multiple bits is given.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE)
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Others
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
- SIDH Go. SIDH. Post-quantum key exchange.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Anonymous crypto. Anon. Anonymous crypto.
- Rho factorization. Rho. Rho alogorithm.
- Post-quantum signing (BLISS). BLISS. BLISS method.
Homomorphic Encryption with Krytology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Homomorphic hashing
- Homomorphic Hashing with Golang. Homomorphic hashing. Normally with hashing methods, we need to take all the previous data and new data in order to create a new hash value for our data. In a homomorphic hashing method, we can basically take the previous hash, and then add on any new data values. We can also remove previous data values from our hash, too. This is more efficient in computing, as we do not have to process all of our data into a new hash, and can use simple homomorphic operations for the computation. The method we will use (LtHash) was initially defined by Bellare and Micciancio and updated Lewi et al at Facebook.
Identity Based Encryption (IBE)

This page outlines a few basic principles around the usage of IBE.
Identity Based Encryption (Pairing based)
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pair-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Identity Based Encryption (Others)
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Güther's implicitly certified identity-based public keys (IBE). Günther. This method allows Bob to generate Alices public key from her identity and publicly available parameters.
- Girault's self-certified public keys (IBE). Girault. This method allows Bob to generate Alices public key from her identity and publicly available parameters, and where we use an RSA key pair to self-certify Alice's public key.
Intrusion Detection Systems (IDS)
- Intrusion Detection Systems. Snort. This outlines some of the basics of IDS, including the requirement for Intrusion Detection Systems (IDSs), and where they are used.
- Advanced Network Forensics (Snort). Adv Network Forensics. This provides information on how to detect threats through network forensics with Snort
Snort

- Snort IDS. Snort. This is a Snort Analyser.
- Snort IDS 2 with rules editor. Snort. This provides information on how to detect threats through network forensics with Snort, and with an editing function for rules.
Presentation
IoT

The key objectives of this page are: Understand how a Pen Tester can generate vulnerabilities and test using the Metasploit framework; Define the options and payloads required to generate and use vulnerabilities; and Gaining remote access.
Devices
- Access the Wi-fi kettle. Go. This page outines how to access a wi-fi enabled kettle.
- Philips Hue Wireless Lighting. Go. This page shows how to use RESTful Web services to access to the Hue Led Lamps.
- Kali and R-PI. Go. This page shows the setup of a security testing infrastructure using a Raspberry Pi (R-PI) and a wifi access point.
- Kali, R-PI and RF electrical socket. Go. This page shows the control of an RF electical socket from a RPI.
- Capture from a Polar H10 heat rate sensor. Go. This page shows the capture of the Polar H10 heart sensor with an Ubertooth One.
- Trusted IoT: Linking IoT Devices to NFTs. Go. This page outlines a research paper which links a device to an NFT (Non-fungible Token).
Shodan Scanning
-
IoT Scan (Shodan). Go. This page includes a search of the Internet for key terms, such as for "apache", "mysql" and "cisco".
- IoT Banner Scan (Shodan). Go. This page includes a search of the Internet for key terms with the banner as a result (for the Top 10)
- Internet Services (Shodan). Go. This page includes a search of the Internet for key terms and display the IP address and port.
IoT Libraries
- libDisco with Go. libDisco. libdisco is a Golang library which can be used to create secure connections. It is based on the STROBE protocol framework. Symmetric cryptographic primitives rely on SHA-3 permutation, and asymmetric cryptographic primitives on X25519 and ed25519. STROBE defines a range of cryptographic protocols to integrate with IoT devices. In order to reduce processing, energy and memory requirements, it only uses Keccak (SHA-3) to encrypt and authenticate messages.
COSE/COBR
In computer security, we often have to represent binary data, in single values or groups of characters, bytes, words, long words, signed integers, floating-point values, double-precision floating-point values, and so on. This might be in the form of a data object, a signature or even encrypted content. For this, the ANS.1 DER format is often used, such as presenting digital certificates and signatures. An improvement on this for small messages with security is Concise Binary Object Representation (CBOR) — and which is defined in RFC8949 [1]. While JSON represents text-based data objects CBOR focuses on binary objects. It has been designed to create a lightweight encoder and decoder. This supports the use of CBOR within an IoT infrastructure. The data, also, does not require a data schema to be able to decode it, along with being extensible. CBOR defines the format of binary data with data objects and messages. We can then integrate security with CBOR Object Signing and Encryption (COSE), and which is defined in RFC8152 [2]. This includes signatures, message authentication codes (MACs), encryption and creating serialised objects.
- 128-bit AES GCM. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) can then build on this to include signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use a symmetric key to encrypt a message, and then decrypt it. In this case we will use AES GCM with a static 128-bit key ("0x000102030405060708090a0b0c0d0e0f").
- 256-bit AES GCM. Go. In this case we will use AES GCM using a random 256-bit key (32 bytes).
- EdDSA. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) [2] can then build on this to includes signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use EdDSA to create a signature for a message.
- ECDSA. Go. In this case we will use ECDSA to create a signature for a message.
- HMAC. Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT. Go. In this case we create a CWT token, and sign with an HMAC signature.
- ECDH. Go. In this case we create a symmetric key from ECDH. For this we will derive a shared key from the public key of Alice and Bob, and then define a single recipient which can derive the CEK (Content Encryption Key) using their private key. We will use the curves of P-256 (secp256r1), P-384 (secp384r1), P-521 (secp521r1) or SECP256K1 (as used with Bitcoin).
- RSA using COSE and CBOR. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\).
- RSA: dQ, dP and InvQ. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). The key pair also includes \(dQ\), \(dP\) and \(InvQ\), and these can be used with the Chinese remainder theory to optimize the decryption process.
Metasploit
- Armitage and Metasploit. Go.
- Exploiting Android with Metasploit. Go.
- Exploiting Android with Metasploit - Part 2. Go.
- Exploiting Windows/Mac OS X with Metasploit. Go.
- Remote Desktop Windows/Mac OS X with Metasploit. Go.
- Metasploit. Go.
- Internet of Things Security. Go.
- Metasploit (Enumeration and Scanning). Go.
- Metasploit (Malware). Go.
IP

 The following are a few interesting techniques around IP addresses:
The following are a few interesting techniques around IP addresses:
- Your details. IP. This shows your browser details.
- IP address analyser. IP. This involves converting an IP address to the host and network part of the address.
- IP subnet analyser. IP subnets. This involves converting an IP address to the host and network part of the address.
- IP address analyser. IP. This involves analysing IP addresses.
- Max subnets. Max subnets. This involves converting an IP address to the host and network part of the address.
- Route summarization. Summarization. This involves converting an IP address to the host and network part of the address.
- Whois. Whois. This does a basic Whois on a domain.
- URL Obfuscation. Obfuscation. This outlines URL obfuscation.
- HTTP Responses. Test. HTTP.
- Capturing Network Packets (Python). WinPCap. HTTP.
Cisco related
- Routing table. Routing table. This involves viewing a routing table for a Cisco device.
- ACL Generator. ACL. This involves a simple calculator for ACLs on network ranges.
- EIGRP metrics. EIGRP. Learn the basics of EIGRP metrics.
- VoIP B/W. VoIP. Calculate bandwidth for VoIP.
- Wild Card. Wild Card. On a Cisco device a wildcard mask is used to identify the parts of an IP address that need to be matched. It thus uses a wildcard mask, where a 0 in the bit position identifies that the device should match that bit, else a 1 shows that it should ignore it.
Protocols
- HTTP. HTTP. Show the request and response for HTTP.
- Ping analyser. IP. This involves converting a ping of a site.
IP Challenges
-
IP Test 1. IP Test. IP Classification test. This is a simple test which generates a range of IP addresses, and you must determine the IP address classification.
IP Subnet Challenge 1 Demo
-
IP Test 2. IP Test. IP Classification test Part 2. This test provides an address classification, and the user must find the addresses which are of this classification.
IP Subnet Challenge 2 Demo
-
IP Test 3. IP Test. IP Classification test Part 3. This test provides an address classification, where the network part of the address is determined.
IP Subnet Challenge 3 Demo
Subnet Challenges
- Subnet Test 1. Subnet Test. Subnet Test.
-
Subnet Test 2. Subnet Test. Subnet bits.
- Subnet Test 3. Subnet Test. Find the nth usable subnet. This test involves finding the nth usable subnet.
- Subnet Test 4. Subnet Test. Maximum subnets. This is a test page to determine the maximum number of subnets and hosts/subnet for IP classed addressing.
- Subnet Test 5. Subnet Test. Maximum host/subnet. This is a test page to determine the maximum number of hosts per subnet.
- Subnet Test 6. Subnet Test. Determine the required subnet mask for a given number of subnets. This is a test page to determine the required subnet mask for a given number of subnets and a given IP address classification.
- Subnet Test 7. Subnet Test. Determine the required subnet mask for a given number of host/subnet. This is a test page to determine the required subnet mask for a given number of hosts per subnet and a given IP address classification.
- Subnet Test 8. Subnet Test. Route summarization. This involves a calculation on route summarization.
- Subnet Test 9. Subnet Test. Binary to IP.
- Subnet Test 10. Subnet Test. Hex to IP.
-
Subnet Test 13. Subnet Test. Wild card mask network bits. Find the number of bits in the network part of the wild card mask. IP Wildcard challenge
- Subnet Test 14. Subnet Test. Wild card mask host bits. Find the number of bits in the host part of the wild card mask. IP Wildcard challenge
- Subnet Test 15. Subnet Test. Wild card mask ... find the network address. Find the network for the wild card mask. IP Wildcard challenge 2
- Subnet Test 16. Subnet Test. Find a matching IP address for a network and wild card mask. Find the IP for a network and a wild card mask.
- Subnet Test 17. Subnet Test. Find an address which is on a given network. Find an IP address on a network, for a given network address and subnet mask.
- Subnet Test 18. Subnet Test. Find an IP address on the same network. Find an IP address on the same subnet.
- Subnet Test 19. Subnet Test. Find subnet. Convert subnet mask.
- Megatest. Subnet Test. Challenging test for subnets.
JavaScript

JavaScript code allows execution within the browser, rather than on the server. It is often faster than code that runs on a server. Along with this we can also use Node.js, and which runs JavaScript code on a server.
Symmetric key
- AES. AES. In this example, we will use either a pre-generated key or a random one, and use AES (Rijndael) encryption.
- ChaCha20 and Poly1305. ChaCha. This page outlines Poly1305 and ChaCha20. ChaCha20 is a symmetric key method and Poly1305 is a message authentication code (MAC). They were created by Daniel J. Bernstein, and are alternatives to AES and HMAC.
- CMS (Padding). CMS. This page uses PKIJS encrypting on CMS. With CMS we can This document describes the Cryptographic Message Syntax (CMS). With this we can encapsulate an message within an encrypted entity.

Hashing
- Hash. Hash. This page defines a JavaScript Hash calculator. This uses a client-side JavaScript code to determine the hash signatures of a text value.
Signatures
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
- Boneh–Lynn–Shacham (BLS) signature. BLS. Boneh–Lynn–Shacham (BLS) signature method produces short signatures. They use elliptic curve pairing (and which are also known as bilinear maps).
Key exchange
- ECDH. ECDH. Elliptic Curve Diffie Hellman (ECDH) is used to generate a shared key. This implementation uses Elliptic Curve Cryptography (ECC) with JavaScript.
CryptoJS
- CryptoJS. CryptoJS. This page uses client-side JavaScript code to hashing, encrypt and sign, including for symmetric key (AES), streaming ciphers, hashing methods, and HMAC.
Blockchain
- PATRICIA trie. PATRICIA. In the following, we have the Top 2,500 Web sites in the world, and implemented with a Radix Trie (aka PATRICIA trie) In the following we have the Top 2,000 web sites on the Internet, and which have been indexed using the PATRICIA trie.
Public key
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
- RSA. RSA. RSA is an asymmetric encryption algorithm, which uses two keys, one to encrypt and the other to decrypt. It was created in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman, and is still one of the most widely used encryption methods. A typical application is in authenticating a sender, where the senders private key is used to encrypt a message, and then is decrypted by the receiver with the senders public key (which is known to anyone who wants it). It is also typically used for encrypting disks/files, such as for EFS.
Digital Certificates
- X.509 certificates in JavaScript. RSA and ECDSA Signed certificates. This page will generate either RSA and ECC key pairs, and then generate X.509 certificates, using either a signature of SHA1withRSA or SHA256withECDSA. For RSA signing we use an RSA private key to sign the certificate, and with ECDSA signing we use an ECC private key to sign the certificate.
Tokens
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
Random
- Random number generator. Rand. In the past, encryption and decryption had to be done through native code libraries, such as with Bouncy Castle and OpenSSL. With the increasing processing power of Web browsers, it is now possible to use encryption using JavaScript, which thus provides client-side processing of data. This Web page uses Javascript encryption, and generates a random 256-bit text key or a hex version. The 256-bit key is generated by generating 60 random numbers (from 0-25), and converting these to an ASCII character.
Malware obfuscation
- Malware obfuscation. Obfuscation. A malware writer will often hide certain keywords from the browser/human by encoding them in another format. This is typically done for hex coding (\xZZ), 16-bit unicoding (\uZZZZ) and octal coding (\ZZZ). To test, enter a value, and then press the button and it will convert encoded string.
Message Authentication Codes
- Chaskey (MAC). Chaskey. Chaskey Cipher is light-weight cryptography method for signing messages (MAC) using a 128-bit key. The hardware implementation only requires 3,334.33 gate equivalent with an operating clock frequency of 1 MHz (whereas Keccak requires 4,658 GE). In the page we create the Mac signature and also encrypt for CBC.
Other
- Password generation/hashing. Hashing. Linux can use salted passwords where the username, hashing method and hashed password are stored in a password file [More details]. The main methods are
Hashing

At times we need to generate secrets, such as encryption keys, from passwords or nonce values. A Key Derivation Function (KDF) is a verifiable way of doing this.
Key Derivation Functions (KDFs)
The following are the tips related to hashing:
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Password strength. Test. This outlines the strength of various passwords types.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
HKDF
The following are the tips related to Key derivation hashing:
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Hazmat HKDF for different hashing methods. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
-
HKDF key derivation with OpenSSL [
here]
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
PBKDF2
The following are the tips related to Key derivation hashing:
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- AES GCM (Python) with PBKDF2. AES GCM (Python) with PBKDF2.
- Fernet with PBKDF2 . AES GCM (Python) with PBKDF2.
- PBKDF2 key derivation. AES GCM (Python) with PBKDF2.
- Key Rotation with Fernet. AES GCM (Python) with PBKDF2.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Bcrypt
The following are the tips related to Key derivation hashing:
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- BCrypt. BCrypt. BCrypt with Rust.
-
Hash to password with Go. Hashing to Argon2, Scrypt and BCrypt. Hash to password with Go, including Argon2, Scrypt and BCrypt.
scrypt
- scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Argon 2
The following are the tips related to Key derivation hashing:
- Argon 2. Go. Outline of Argon2.
- Argon 2 with NaCl. Go. Outline of Argon2 using NaCl.
- Argon 2. Argon 2. Argon 2 with Rust.
- Balloon. Go. Outline of Balloon.
Other
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
- Double ratchet. Go. Outline of double ratcheting.
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
Outline
HMAC Key Derivation function (HKDF) is used to derive an encryption key from a passphrase. Initially, HKDF creates a pseudorandom key (PRK) using a passphrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), and along with a salt value. Next, the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys [RFC 5869][article]. In this case, we will use SHA-256.
The following shows how an encryption key can be generated using HKDF, and where we need a secret and a salt value. Both Bob and Alice have the same secret and salt.

With PBKDF2 (Password Based Key Derivation Function 2), we hash for a given number of rounds:

Key exchange

Key exchange is a way for Bob and Alice to communicate and for them to agree on a shared secret. The original method defined uses discrete logarithms (Diffie-Hellman), but most modern methods use elliptic curve techniques (ECDH). As quantum computers can crack both discrete log and elliptic curve methods, there are post quantum cryptography methods proposed. This includes SIDH, CSIDH, SIKE, and NewHope.
Key interchange/generation (Diffie-Hellman)
The following relates to key interchange:
- Selecting \(g\) in Diffie Hellman. G in Diffie Hellman. Picking a safe value of the generator \(g\) in discrete logarithms.
- Diffie-Hellman. Diffie-Hellman Calculation. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Real example). Diffie-Hellman Real. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Python). Diffie-Hellman. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (pre-compute). Diffie-Hellman (pre-compute). Many sites use the same prime numbers, which can then be cracked with a pre-computing attack.
- Key generation. Key gen. This will generate keys for different methods based on a passphrase.
- Diffie-Hellman (Man-in-the-middle). DF. This outlines the man-in-the-middle method for Diffie-Hellman.
- An Alternative Diffie-Hellman method. Alterative DH. This outlines an alternative Diffie-Hellman method.
Authenticated Key Exchange
The following are the tips related to Key derivation hashing:
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- MTI/A0. MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{ax+by} \pmod p\). MTI (Matsumoto, Takashima, Imai).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0. MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{x+y} \pmod p\)
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). The resultant key is \(xyG \)
- MTI/C0. MTI/C0. This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{xy} \pmod p\)
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG\).
- MTI/C1. MTI/C1. This outlines MTI/C1, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{abxy} \pmod p\).
- MQV (Menezes–Qu–Vanstone). MQV. MQV was created Alfred Menezes, Minghua Qu and Scott Vanstone in 1995 and is an authenticated key exchange method. Alice holds a key pair \((A,a)\) and Bob has a key pair \((B,b)\). With this \(a\) is Alice's private key, and \(A=aG\) is her public key. For Bob, his public key will be \(B=aG\) and a private key of \(b\), and where \(G\) is the base point on the elliptic curve.
- HMQV (Menezes–Qu–Vanstone). HMQV. HMQV builds on MQV and adds the identity of Bob and Alice.
- ECDH with X25519 and Blake2b. ECDH with X25519 and Blake2b. This uses PyNaCl to create an authenticated key exchange and uses X25519 and Blake2b.
Elliptic Curve (ECDH) - Python
The following are the tips related to ECC:
- Elliptic Curve. Elliptic Curve. Elliptic Curve is a public key method which can also be used to generate a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with simple parameters. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
Elliptic Curve (ECDH) - Golang and Node.js
The following are the tips related to ECC:
- ECDH with Go. ECDH. ECDH with Go.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with node.js. ECDH. ECDH with node.js.
- ECDH with JavaScript. ECDH. Elliptic Curve Diffie Hellman.
Password Authenticated Key Exchange (PAKE)
The following are the tips related to Key derivation hashing:
- SPAKE2. Go. Outline of SPAKE2.
- OPAQUE. Go. Outline of OPAQUE.
- SPEKE. Go. Outline of SPEKE (Simple Password Exponential Key Exchange).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
- J-PAKE. J-PAKE. This example generates a shared key based on a shared password.
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses discrete logs.
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
PQC NIST Finalists (Key Exchange)
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Key interchange/generation (Other)

The following relates to key interchange:
- Curve25519. Curve25519. This outlines Curve25519, which is used in the Tor network.
- Authenticated Key Exchange (Discrete logs). YAK. Key exchange with public keys and uses discrete logs.
- Authenticated Key Exchange (ECC). YAK. Key exchange with public keys and uses elliptic curve methods.
- Shamir No-key protocol. Shamir No Key. In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated.
- Shamir No-key protocol (sepc256k1). Shamir No Key (EC). In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated using the sepc256k1 elliptic curve.
- Conference keying (Burmester-Desmedt method). Conference keying. In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it.
- Conference keying (Burmester-Desmedt method) - Elliptic Curve (sepc256k1). Conference keying Elliptic Curve (sepc256k1). In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it, and uses the sepc256k1 elliptic curve.
Key exchange (with pairing)
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Kryptology

We need to build a new Internet. One that is build on mathematics and certainty, rather than the patchy version we have now. For this we need a layer of cryptography at the lowest level, and build software interfaces on top of this. Along with this we now have cryptographic methods which can now provide a foundation of trust, and which preserve privacy. And so the old libraries of OpenSSL are being squeezed out in favour of the new ones which are built on a solid foundation. The latest of these new "privacy-aware" libraries is Kryptology, and created by Coinbase. This library provides the APIs that developers need, in order to apply to areas of blockchain development. This library include BLS (Boneh-Lynn-Shacham) signatures, Zero-knowledge Proofs (ZKPs) and Shamir Secret Shares (SSS). With BLS we can digitally sign for data, but also preserve its privacy. Applications of this include group signatures, where multiple entities can merge their signing keys together and provide a single signature for a transaction. With SSS, we can split encryption keys up into shares, and then distribute them across a network. When required, we can call these shares back to reconstruct the key.
The focus for Coinbase seems to be the application of privacy coins, and where no tracking can be applied to the usage of these digital coins. This should support full anonymity for transactions, as opposed to Bitcoin which only supports pseudo-anonymity.

ECC Basics
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining n.G for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Points (Base Point and Others). Elliptic Curve points. Two common curves used in ECC (Elliptic Curve Cryptography) are secp256k1 (as used in Bitcoin and Ethereum) and P256 (secp256r1). The "k1" refers to the Kolbitz curve 1 (named after the creator of ECC). With these we have a base point which are can operate on. This is typically defined as \(G\). We can then operate on this with add and multiply operation. For example, \(2G=G+G\) and \(P=n.G\). In this following we will show the base point for a number of common curves, such as secp256r1, P256, Pallas, Curve 25519, BLS12381G1, BLS12381G2, BLS12377G1 and BLS12377G2.
ECDH
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret. We will use Golang and the Krytology library.
Simple ECC on curves
- Public key points for curves. Simple. Display public key points for scalars.
BLS Curve
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
Accumulator and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
Pallas Curve
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
Pairing-based Crypto
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
ElGamal and ECC
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a numerical input.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
Shamir Secret Shares
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Homomorphic Encryption
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Zero knowledge proofs
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
Verifiable Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Hash to scalar and point
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
CP-ABE
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Lattice cryptography

Latice cryptography is proposed as a post-quantum robust method for public key encryption, especially focused on digital signatures and key exchange mechanisms (KEMs).
Principles
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
NTRU
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- Lattice Encryption: NTRU Key Generation Python). NTRU. Outlines how NTRU operates for key generation.
Homomorphic
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Digital Signatures
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
Public-Key Encryption/Key Exchange
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
Light-weight cryptography

While AES and SHA work well together within computer systems, they struggle in an IoT/embedded world as they take up: too much processing power; too much physical space; and consume too much battery power. So NIST outlines a number of methods which can be used for light-weight cryptography, and which could be useful in IoT and RFID devices [1]. They define the device spectrum as:
- Conventional cryptography. Servers and Desktops. Tablets and smart phones.
- Light-weight cryptography. Embedded Systems. RFID and Sensor Networks.
With embedded systems, we commonly see 8-bit, 16-bit and 32-bit microcontrollers, and which would struggle to cope with real-time demands for conventional cryptography methods. And in the 40+ years since the first 4-bit processor, there is even a strong market for 4-bit processors. RFID and sensor network devices, especially, have limited numbers of gates available for security, and are often highly constrained with the power drain on the device.
So AES is typically a non-starter for many embedded devices. In light-weight cryptography, we often see smaller block size (typically 64 bits or 80 bits), smaller keys (often less than 90 bits) and less complex rounds (and where the S-boxes often just have 4-bits).
For light-weight cryptography the main constraints that we have are typically related to ener requirements, gate equivalents (GEs), and timing. With passive RFID devices, we do not have an associated battery for the power supply, and where the chip must power itself from energy coupled from the radio wave. An RFID device is thus likely to be severely constrained in the power drain associated with any cryptography functions, along with being constrained for the timing requirements and for the number of gates used. Even if an RFID device has an associated battery (active RFID), it may be difficult to recharge the battery, so the drain on power must often be minimised.
There is thus often a compromise between the cryptography method used and the overall security of the method. Thus often light-weight cryptography methods balance performance (throughput) against power drain and GE, and do not perform as well as main-stream cryptography standards (such as AES and SHA-256). Along with this the method must also have a low requirement for RAM (where the method requires the usage of running memory to perform its operation) and ROM (where the method is stored on the device). In order to assess the strengths of various methods we often define the area that the cryptography function will use on the device – and which is defined in \(µm^2\). The NIST finalists are defined in this [article]
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- GIFT AEAD. GIFT. GIFT is a light-weight block cipher. It is a (NIST Finalist)
- Elephant. Elephant. Elephant is a light-weight stream cipher. It is a (NIST Finalist).
- TinyJambu. TinyJambu. TinyJambu is a light-weight block cipher. It is a (NIST Finalist)
- Isap AEAD. Isap. Isap is a light-weight block cipher. It is a (NIST Finalist)
- PHOTON-Beetle AEAD. PHOTON-Beetle. PHOTON-Beetle is a light-weight block cipher. It is a (NIST Finalist)
- Romulus AEAD. Romulus. Romulus is a light-weight block cipher. It is a (NIST Finalist)
- Sparkle AEAD. Sparkle. Sparkle is a light-weight block cipher. It is a (NIST Finalist)
- CLEFIA. CLEFIA. CLEFIA is a light-weight block cipher.
- LED. LED. LED is a light-weight block cipher.
- Piccolo. Piccolo. Piccolo is an ultra light-weight block cipher.
- PRESENT. PRESENT. Present is a light-weight block cipher.
- Pyjamask. Pyjamask. Pyjamask is a light-weight block cipher.
- SIMON. SIMON. SIMON is a light-weight block cipher.
- SKINNY. SKINNY. SKINNEY is a light-weight block cipher.
- SPECK. SPECK. SPECK is a light-weight block cipher.
- XTEA. XTEA. XTEA is a light-weight block cipher.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encryption/Decryption. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.
Light-weight crypto (Other)
- Chaskey (MAC). Chaskey. Chaskey is a light-weight MAC function.
- Chaskey (MAC). Chaskey (Python). Chaskey is a light-weight MAC function.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (ASCON)
ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRFF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
Discrete Logs (Solving)

A discrete log problem is in the form of \(g^x \pmod p\) and where we know \(g\) and \(p\) and must solve for \(x\).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Message Authentication Code (MAC)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
HMAC
The following are the tips related to Key-based hashing:
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authentication both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2), Blake2b, SM3 and SHA-3. This page outlines the HMAC-MD5 methods using the Hazmat cryptography layer.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- HMAC (COSE). Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT with HMMAC. Go. In this case we create a CWT token, and sign with an HMAC signature.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- HMAC with Rust. HMAC. HMAC with Rust.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HMAC with OpenSSL. MACs with OpenSSL. HMAC in OpenSSL for a given input value, password and hashing method.
Cipher MACs
The following are the tips related to Key-based hashing:
- MACs with OpenSSL. MACs with OpenSSL. MAC methods implemented in OpenSSL, including CMAC and GMAC.
Key-based hashing
The following are the tips related to Key-based hashing:
- SipHash. Siphash. Siphash is a fast key-based hashing method.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Meow. Meow. Meow is one of the fastest hashing methods.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
Magic Numbers

This pages contains information related to magic numbers in file formats.
Network and File Forensics
- Magic numbers. Magic. This provides information on magic number for file forensics.
Graphics formats
- JPEG Analysis. JPEGs. This provides an analysis of JPEG files.
- GIF Analysis. GIFs. This provides an analysis of GIF files.
- TIF Analysis. TIFs. This provides an analysis of TIF files.
- PNG Analysis. PNGs. This provides an analysis of PNG files.
- BMP Analysis. BMPs. This provides an analysis of BMP files.
- PSD Analysis. PSDs. This provides an analysis of PSD files.
- WMF Analysis. WMF. This provides an analysis of WMF files.
- Adobe Illustrator Analysis. AI. This provides an analysis of AI files.
- Adobe In Design Analysis. INDD. This provides an analysis of INDD files.
- MIDI file. MIDI. This provides an analysis of MID files.
- ICO file. ICO. This provides an analysis of ICO files.
- PS file. PS. This provides an analysis of PS files.
- EPS file. EPS. This provides an analysis of EPS files.
- VSD file. VSD. This provides an analysis of Microsft Visio (VSD) files.
Video and audio formats
- MP3 Analysis. MP3s. This provides an analysis of MP3 files.
- AVI Analysis. AVIs. This provides an analysis of AVI files.
- Flash SWF Analysis. SWFs. This provides an analysis of Flash files.
- Flash FLV Analysis. FLVs. This provides an analysis of FLV files.
- MP4 Analysis. MP4. This provides an analysis of MP4 files.
- MOV Analysis. MOV. This provides an analysis of MOV files.
- WMV Analysis. WMV. This provides an analysis of WMV files.
- WMA Analysis. WMA. This provides an analysis of WMA files.
- JPEG 2000 Analysis. JPEG 2. This provides an analysis of JPEG 2000 files.
- WAV Analysis. WAV. This provides an analysis of WAV files.
Zips, Archives and Library files
- ZIP/Archive Analysis. ZIPs. This provides an analysis of ZIP/Achive files.
- GZ Analysis. GZ. This provides an analysis of GZip files.
- Tar Analysis. Tar. This provides an analysis of TAR files.
- MSI Analysis. MSI. This provides an analysis of MSI files.
- OBJ Analysis. OBJ. This provides an analysis of OBJ files.
- DLL Analysis. DLL. This provides an analysis of DLL files.
- CAB Analysis. CAB. This provides an analysis of CAB files.
- EXE Analysis. EXE. This provides an analysis of EXE files.
- RAR Analysis. RAR. This provides an analysis of RAR files.
- SYS Analysis. SYS. This provides an analysis of SYS files.
- HLP Analysis. HLP. This provides an analysis of HLP files.
- VMDK Analysis. VMDK. This provides an analysis of VMDK files (VMWare Virtual Disks).
- PST Analysis. PST. This provides an analysis of PST files (Outlook Email File).
- JAR Analysis. JAR. This provides an analysis of JAR files.
- SLN Analysis. SLN. This provides an analysis of Microsoft SLN files.
- Class Analysis. Class. This provides an analysis of Java Class files.
- Zlib. Zlib. This provides an analysis of Zlib files.
Documents
- PDF Analysis. PDFs. This provides an analysis of PDF files.
- DOC Analysis. DOCs. This provides an analysis of DOC files.
- RTF Analysis. RTFs. This provides an analysis of RTF files.
- XLS Analysis. XLSs. This provides an analysis of XLS files.
- PPT Analysis. PPTs. This provides an analysis of PPT files.
- MMP File. MMP. This provides an analysis of MMP files.
- DOCX Analysis. DOCX. This provides an analysis of DOCX files.
- XLSX Analysis. XLSX. This provides an analysis of XLSX files.
- PPTX Analysis. PPTX. This provides an analysis of PPTX files.
- MDB Analysis. MDB. This provides an analysis of MDB files.
- Outlook Message Analysis. MSG. This provides an analysis of MSG files.
Disk Image
- Raw disk format. RAW. This provides an analysis of the RAW disk format.
Tests
- File Forensics Test. File Test File Forensics Test.
- File Forensics Test (Fun). File Test (Fun) File Forensics Test.
Presentations
MIRACL Core Library

MIRACL Core is an open source library, and includes a wide range of public key encryption methods. It is especially focused on elliptic curve and pairing-friendly methods, but also supports a wide range of encryption methods, including RSA, AES and hashing. Overall, it can be ported onto a wide range of systems and supports C, C++, Go, Rust, Python, Java, Javascript and Swift. Along with this it supports limited capability devices such as the Arduino infrastructure. The GitHub repository is [here].
BN254
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.

Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- CL Signatures. CL. CL Signatures in Go using MIRACL.
- CL Signatures (advanced pairing). CL. CL Signatures in Go using MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages using MIRACL.
- PS Signatures. PS. Signatures using PS for short signatures using MIRACL.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures using MIRACL.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.

Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
Rust examples
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
NaCl

PyNaCl is a Python port of LibSodium. It integrates the latest cryptography methods, such as AES, XChaCha20, Blake2b and X25519.
Symmetric Key
- Symmetric key. Symmetric key (XChaCha20 and Poly1305). With symmetric key, Bob and Alice have the same key. NaCl uses the XChaCha20 method, and which supports stream encryption (and which does not require padding as a block cipher does, and is also faster than block cipher modes). ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16 byte nonce. XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24 byte nonce. It has a lower propability of nonce misuse than ChaCha20.
- Encryption with a password. Symmetric Key with KDF. In symmetric key, we generate a secret key. This key is typically a random value or generated from a password and a salt value. If we use a password, we typically use a KDF (Key Derivation Function), and which uses a password and a salt value, in order to create a key of a given size. In this case we will use Argon2i, and which is memory resilent.
Hybrid Encryption
- Box. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Hashing
- Hashing and KDF (Argon2 and scrypt). Hashing and KDF. This case we will use PyNaCl (Networking and Cryptography) library, and which is a Python binding to libsodium. We will hash a password using SHA-256 and SHA-512, and also create a KDF (Key Derivation Function) using scrypt and Argon2.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
Ed25519
-
Ed25519. Ed25519. Using Ed25519 for digital signatures.
-
Finding Points on Ed25519. X25519 (Points).
In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 (Key Exchange)
- X25519 + BLAKE2b key-exchange. X25519. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
Curve 25519
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
Node.js

Node.js uses the JavaScript programming langauge as its base, and allows for code to be run on a server, rather than in the browser (such as with pure JavaScript). To run a node.js program, we run "node myfile.js", and use NPM to install libraries.
Symmetric key
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
RSA and public key
- RSA Opt imal Asymmetric Encryption Padding (OAEP) using Node.js. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
ECC Keys
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.

Hashing
- Hashing with node.js (All). Hashing. Hashing with node.js.
- Hashing with node.js (Selection). Hashing. Hashing with node.js.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- ECDSA with node.js. ECDSA. ECDSA with node.js.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
Key exchange
- Diffie-Hellman with node.js (random prime). DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method and uses a randomly generated prime number (press the button to generate a new prime).
- Diffie-Hellman with node.js. DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method. Each time the prime number will be fixed for the DH group selected.
- ECDH with node.js. ECDH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Elliptic Curve Diffie Hellman (ECDH) key exchange method.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
Key derivation
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
CryptoJS
- CryptoJS (in node.js). CryptoJS (Node.js). Various crypto methods in the browser.
Bulletproofs
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
Blockchain
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
Proxy encryption
- Proxy Encryption - Encrypting With Public Key, And Decrypt with Private Key. Proxy01. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This page just creates a key pair for Alice, and uses it to encrypt with the public key , and decrypt with the private key.
- Proxy Encryption. Proxy02. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This will go through the full use case of proxy re-encryption.
Tokens
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
Random
- Fortuna with node.js. Fortuna. Fortuna random numbers with node.js.
Other
- FPE with node.js. FPR. FPE with node.js.
- Puny with node.js. Puny. Puny character format with node.js.
Accumulators and Witnesses
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
PGP
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Password Entropy
- Password Entropy with Node.js. Password Entropy. Password entropy measures the strength of a password, and is measured as the number of bits which could represent all of the possibilities. An entropy score of less than 25 identifies a poor password, and between 25 and 50 is a weak password. For 50 to 75 we have a reasonable password, and between 75 and 100 is a very good password. Over 100 is an excellent password. The strength of the password relates to the number of characters used, and also the number of characters in the password.
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
- Homomorphic Encryption with Node.js and BGV. Homomorphic Encryption with Node.js and BFG. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BGV method.
Oblivious Transfer (OT)

Oblivious Transfer allows Bob to select data from Alice, but for Alice not to know which value has been selected.
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
OpenSSH

OpenSSH supports the usage of the SSH protocol. This allows for a remote login. One tool which is uses is ssh-keygen, and which allow for the generation of RSA, DSA and elliptic-curve keys that. These can be used for user and host authentication, such as for GitHub login and Cloud instance login.
OpenSSH
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here].
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
Outline

OpenSSL

OpenSSL is a standard library that implements cryptography.
Symmetric key (Command line)
-
Symmetric Key Encryption (OpenSSL 1.x) [here]. In this case we will create cipher text from OpenSSL 1.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 1.x) [here].In this case we will decrypt cipher text from OpenSSL 1.x using a key derived from a password
-
Symmetric Key Encryption (OpenSSL 3.x) [here]. In this case we will create cipher text from OpenSSL 3.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 3.x) [here].In this case we will decrypt cipher text from OpenSSL 3.x using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password.
Hashing
-
Hashing [here] OpenSSL supports a wide range of hashing methods including BLAKE2b, Gost, MD4, MD5, RMD-160, SHA-1, SHA-3, SHA-256 and SHA-512.
Libre OpenSSL
-
Symmetric Key Encryption using Libre OpenSSL [here]. In this case we will create cipher text from Libre OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption using Libre OpenSSL [here]. In this case we will decrypt ciphertext from Libre OpenSSL using a key derived from a password.
-
Hashing [here] Libre OpenSSL supports a wide range of hashing methods including Gost, MD4, MD5, RMD-160, SHA-1, SHA-256 and SHA-512.
Diffie-Hellman parameter generation
-
DH Parameters with OpenSSL [here]. The Diffie-Hellman (DH) method is perhaps one of the greatest inventions in Cybersecurity, and was created by Whitfield Diffie and Marty Hellman. With the DH method, Bob creates a random value (\(b\)) and Alice also creates a random value (\(a\)). Next Bob computes \(B=g^b \pmod p\) and sends it to Alice. Alice computes \(A=g^a \pmod p\) and sends this to Bob. Bob raises the value of \(A\) to the power of \(b\) and takes \(\pmod p\), and Alice raises \(B\) to the power of \(a\) and takes \(\pmod p\). In the end, they will have the same shared value: \(g^{ab} \pmod p\). This can then be used to derive an encryption key that they can use for a secure tunnel. Overall, \(p\) is the large prime number, and also known as the shared modulus between Bob and Alice.
Key derivation function
-
PBKDF2 key derivation with OpenSSL [here] PBKDF2 (Password Key Derivation Function 2) is a key derivation method. Overall it is relatively slow in its operation and where we take a password, a salt value, hashing method, and a number of iterations, in order to produce a given size of encryption key.
-
HKDF key derivation with OpenSSL [here] HKDF (HMAC Key Derivation function) is used to derive an encryption key from a pass phrase. Initially HKDF creates a pseudorandom key (PRK) using a pass phrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), andalong with a salt value. Next the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys.
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Passwords
-
Password example [here]. This page uses the OpenSSL library hash password generator, which is used in UNIX systems for the hashing of passwords which are contained in /etc/shadow and /etc/passwd. For newer passwords, the "-1" options is used to created the hashed value.
-
Hashed passwords with OpenSSL [here].
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
Public key
-
Generating an ECC key pair with OpenSSL [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)).
-
Generating an RSA key pair with OpenSSL [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2).
-
Generating an RSA key pair with OpenSSL with encryption [here]. This page implements RSA key pair generation with an encrypted key pair. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). In this case we will encrypt the key pair with either 3DES, 128-bit AES, 192-bit AES or 256-bit AES. The same password must be used to encrypt and decrypt.
-
Generate prime with OpenSSL [here]. Prime numbers are important in public key encrytion, and are used with RSA and ECC. For RSA, we generate two prime numbers (\(p\) and \(q\)) and which are multiplied together to create a modulus (\(N\)). If these prime numbers have 512 bit values, the modulus will be a 1,024 bit value. This defines the basic secure of RSA. With elliptic curve we use smaller prime numbers, such as 256-bit values for the secp256k1 curve.
ASN1 parsing
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). We will parse using asn1parse, and reveal the parameters.
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)) [RSA key pair]. We will parse using asn1parse, and reveal the parameters.
- DSA Parameters with asn1parse. DSA parameters with OpenSSL with asn1parse. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA (Digital Signature Algorithm)
- DSA Parameters. DSA parameters with OpenSSL. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
MAC (Message Authentication Code)
- HMAC with OpenSSL. MACs with OpenSSL. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authenticate both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2) and SHA-3. In this case we will use OpenSSL to generate the HMAC value.
- MACs with OpenSSL. MACs with OpenSSL. In the following we will generate MACs for HMAC, GMAC, CMAC, Blake2bmac, Blake2smac, KMAC128 and KMAC256. Overall, we will use an encryption key defined as a hex value for GMAC and CMAC, and a pass phrase for the others. The message is "hello".
Signing
- Digital signing a plaintext message with OpenSSL. Signing with OpenSSL. With digital signing, we can take a message, and create a signature. This normally involves signing with a private key and digital certificate. The signed message can be an a MIME format, and which can be integrated into an email message. In this can we have a 512-bit RSA key pair that will sign a plain text message.
Encrypting emails
- Encrypting an email message in OpenSSL. Encrypting messages with OpenSSL. With public key encryption, we can take a message, and encrypt it with the recipiant's public key. In this can we have a 512-bit RSA public key to encrypt a message.
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Random number generation with OpenSSL
-
Random number generator [here]. Random numbers are important in generating encryption keys and salt values. In this case OpenSSL generates a random number (in a Base64 format) for a given number of bytes.
Outline (C#/Python)
-
Symmetric Key Encryption (C#) [here]. This page uses the OpenSSL library through a C#/.NET wrapper. The DLLs it interfaces to are libeay32.dll and ssleay32.dll. OpenSSL supports a wide range of encryption methods, including 128-bit AES, 192-bit AES, 256-bit AES and Blowfish (bf). Different modes of ECB, CBC, and OFB are implemented. The examples use a default IV of "1234".
-
AES in Python with OpenSSL output [here]
-
Producing OpenSSL AES Encrypted String from C# [here]
Digital Certificates
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
Paillier - Partial Homomorphic Encryption

The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Fundamentals
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier).
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Using RSA
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
Applications
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- P192 in Python. Barebones P192. This page implements P192 in pure Python.
- P224 in Python. Barebones P224. This page implements P224 in pure Python.
- P256 in Python. Barebones P256. This page implements P256 in pure Python.
- P521 in Python. Barebones P521. This page implements P521 in pure Python.
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
- Curve 25519 in Python. Barebones Curve 25519. This page implements Curve 25519 in pure Python.
- Curve 25519 in Python (Test Vectors from RFC 7748). Barebones Curve X25519. This page implements Curve 25519 in pure Python and tests against the IETF test vectors.
- Curve 448 in Python (Test Vectors from RFC 7748). Barebones Curve X448. This page implements Curve 448 in pure Python and tests against the IETF test vectors.
- Curve 25519 ECDH in Python (Test Vectors from RFC 7748). Barebones Curve X25519. This page implements Curve 25519 ECDH in pure Python and tests against the IETF test vectors.
- Curve 448 ECDH in Python (Test Vectors from RFC 7748). Barebones Curve X448. This page implements Curve 448 ECDH in pure Python and tests against the IETF test vectors.
- ECDSA using P256. Barebones ECDSA with P256. This page implements ECDSA with the NIST P256 curve.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 . EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
Others
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.

Public Key (Elliptic Curve) in Rust
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Sage
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
Elliptic Curve Diffie-Hellman (ECDH)

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as secp256k1 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) - Python
The following are the tips related to ECC:
- Elliptic Curve Diffie-Hellman (ECDH) with simple parameters. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
- ECDH and COSE. Go. In this case we create a symmetric key from ECDH. For this we will derive a shared key from the public key of Alice and Bob, and then define a single recipient which can derive the CEK (Content Encryption Key) using their private key. We will use the curves of P-256 (secp256r1), P-384 (secp384r1), P-521 (secp521r1) or SECP256K1 (as used with Bitcoin).
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Go. ECDH. ECDH with Go.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret. We will use Golang and the Krytology library.

Elliptic Curve (ECDH) - Node.js
The following are the tips related to ECC:
- ECDH with node.js. ECDH. ECDH with node.js.
- ECDH with JavaScript. ECDH. Elliptic Curve Diffie Hellman.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Key exchange

- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). The resultant key is \(xyG \)
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
- Authenticated Key Exchange (ECC). YAK. Key exchange with public keys and uses elliptic curve methods.
ECDSA (Elliptic Curve Digital Signature Algorithm)

ECDSA has been around for over two decades and was first proposed in [1]. The ECDSA method significantly improved the performance of signing messages than the RSA-based DSA method. Its usage of elliptic curve methods speeded up the whole process and supported much smaller key sizes. Its crown and glory were being selected by Satoshi Nakamoto for his Bitcoin protocol, and then its adoption into Ethereum.
ECDSA Basics
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Recoving the public key from an ECDSA Signing in Python. Recoving public key from ECDSA Signing. This is an example of recovering the public key from the ECDSA signature with Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\)).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\)) and will check that the signature is valid.
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
- ECDSA for Multiple Curves and Different Hashing Methods with PowerShell . ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
- ECDSA for Multiple Curves and Different Hashing Methods with Python . ECDSA for Multiple Curves and Different Hashing Methods with Python. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
- ECDSA Signatures with Hazmat (SECP256R1, SECP384R1, SECP521R1, SECP224R1, SECP192R1, and SECP256K1). ECC Signatures. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and then creates an ECDSA signature for a given message.
- DSSE (Dead Single Signature Envelopes). DSSE. The Update Framework (TUF) provides a framework to secure the software within a system, while in-toto ("as-a-whole") can be used to protect the whole of software support chain. TUF thus delivers updates to a system while in-toto manages a complete software infrastructure. For this, it uses the Metablock format, and where we do not sign the byte values for the signature but sign the JSON data. This is known as canonicalisation - and which is the conversion of data in different forms to a standardised format.
Elliptic Curve (DER)
The following are the tips related to ECC:
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Google Tink with ECDSA
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
ECDSA Applications
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Blinded ECDSA. Blinded ECDSA. With a blinded signature, Bob can sign for a message, without knowning what the message is. In this case Alice will create a blinded ECDSA signature, and where Bob can then sign it, and then Alice can unblind it. The method is based on one produced by Oleg Andreev for blinding signatures in Bitcoin.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA: Fault Attack. ECDSA: Fault Attack. In the fault attack in ECDSA we only require two signatures. One is produced without a fault \((r,s)\), and the other has a fault \((r_f,s_f)\). From these we can generate the private key.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Elliptic Curve Integrated Encryption Scheme (ECIES)

With ECIES we integrate the power of elliptic curve (EC) public key encryption with symmetric key encryption. An outline of the method is:

Elliptic Curve (ECIES)
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Elliptic Curve Integrated Encryption Scheme (ECIES with Rabbit Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with Rabbit (a light-weight stream cipher).
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
Applications
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- ECIES (Kryptology). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Coinbase Kryptology library.
- ECIES (CIRCL). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Cloudflare CIRCL library.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
Ethereum crypto
- ECIES with Go-Ethereum. Go.
EdDSA, Ed25519 and Ed448

Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). EdDSA (Edwards-curve Digital Signature Algorithm) is a fast and efficient digital signature method, and is based on the Schnorr signature scheme. Two important curves that are implemented with EdDSA are Curve 25519 (X25519) and Curve 448 (Ed448). EdDSA has been standardized in [RFC 8032]. With EdDSA, Alice generates a private key of \(sk\) and a public key of \(P=sk.G\) and where \(G\) is the base point of the curve.
Elliptic Curve (Signatures - EdDSA)
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Ed25519 in Python. EdDSA in Python. This page implements EdDSA using the Pure25519 library and with the core functions of key generation, signature generation and signature verification.
- Ed25519 Vulnerability in Python. EdDSA Vulnerability in Python. This page implements EdDSA using the Pure25519 library and with the core functions of key generation, signature generation and signature verification.
- Ed25519 Vulnerability in Python (Proof of Concept). EdDSA Vulnerability in Python (PoC). This page implements EdDSA using the Pure25519 library and with the core functions of key generation, signature generation and signature verification.
Hazmat (Ed448 and Ed25519)
- Ed25519 for EdDSA signatures with Hazmat. EdDSA: Ed25519. This page uses the Hazmat primitives for the cryptography library for X25519.
- Ed448 for EdDSA signatures with Hazmat. EdDSA: Ed25519. This page uses the Hazmat primitives for the cryptography library for X448
- Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
Golang
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
- Barebones Ed25519 with Go. ECC. This shows point addition and scalar multiply in Ed25519
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
COSE/COBR
- EdDSA. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) [2] can then build on this to includes signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case, we will use EdDSA to create a signature for a message.
Testing Ed25519
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
NaCl
- Ed25519 signature using NaCl. eddsa. This page uses the NaCl port from libsodium.
- Ed25519 points using NaCl. eddsa. This page uses the NaCl port from libsodium to determine Ed25519 points.
Theory
With EdDSA, Alice will sign a message with her private key, and then Bob will use her public key to verify that she signed the message (and that the message has now changed):

Key generation
Alice generates a random 32-byte secret key (\(sk\)) and then creates a public key of:
\(pk=sk \cdot G\)
and where \(G\) is the base point of the curve.
Signing
Alice creates a SHA-512 hash of her private key:
\(h=\textrm{HASH}(sk)\)
Create \(r\) from the upper 32 bytes of hash and the message:
\( r = \textrm{HASH}(h[32:] \: || \: m))\)
And where "||" represents a concatenation of the byte array values. Next she matches \(r\) onto curve with:
\(R=r \cdot G\)
Next Alice computes \(s\) with:
\(s=r + (\textrm{HASH}(R \: || \: pk \: || \: m)) \cdot sk\)
The signature is (\(R,s\)). The values of \(R\) and \(s\) are 32 bytes long, and thus the signature is 64 bytes long.
Verifying
Bob creates \(S\) using \(R\), \(pk\) and \(m\):
\(S =\textrm{HASH}(R \: || \: pk \: || \: m) \)
And next creates two verification values:
\(v_1=s \cdot G\)
\(v_2=R+ pk \cdot S\)
If \(v_1==v_2\) the signature checks. This is because:
\(
\begin{align}
v_1&=s.G\\
&= (r + (\textrm{HASH}(R \: || \: pk \: || \: m)) \cdot sk) \cdot G \\
&= rG + sk \cdot G \cdot (\textrm{HASH}(R \: || \: pk \: || \: m)) \\
&= R+ pk \cdot S \\
&= v_2
\end{align}
\)
ElGamal

Public key encryption is typically used to sign for things (and where we use the private key to encrypt something and prove this with the public key) and within key exchange methods. The core methods used are RSA and Elliptic Curve. But an alternative is to use discrete logarithms. One of the most interesting is ElGamal, and was created by Taher Elgamal in 1985.
ElGamal Method
- ElGamal. ElGamal. ElGamal is a public key method which uses discrete logarithms.
- ElGamal in Python. ElGamal in Python. ElGamal is a public key method which uses discrete logarithms.
- ElGamal in Python with variable prime sizes. ElGamal in Python for different prime sizes. ElGamal is a public key method which uses discrete logarithms.
- Selecting g in ElGamal. G in ElGamal. ElGamal is a public key method which uses discrete logarithms.
- Selecting g in discrete logs. g in discrete logs. This select a generator in discrete logs.
- Selecting g in discrete logs with random primes. g in discrete logs with random primes. This select a generator in discrete logs using random prime numbers which are define by a number of bits.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- Proving an Encrypted Shuffle With ElGamal and ECC. Shuffle. An encrypted shuffle with ElGamal.
- ElGamal encryption with Powershell. ElGamal encryption.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Commutative Encryption
- Commutative Encyption (Modified ElGamal). Commutative Encyption. Commutative Encyption allow Bob and Alice to encrypt a message, and then for the data to be decrypted usign any order of the keys.
ElGamal Signature
- ElGamal signatures. ElGamal. ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this.
- ElGamal signatures (alterative signing). ElGamal (Signing: s=ar + kh(m)). ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this. Normally we sign with \(s=k^{-1} (h(m)-ar) \pmod {p-1}\), but in this case we will use \(s=ar + kh(m))\).
- ElGamal signatures (alterative signing). ElGamal (Signing: s=ah(m) + kr). ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this. Normally we sign with \(s=k^{-1} (h(m)-ar) \pmod {p-1}\), but in this case we will use \(s=ah(m) + kr\).
- ElGamal signatures (alterative signing). ElGamal (Signing: r=as+kh(m)). ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this. Normally we sign with \(s=k^{-1} (h(m)-ar) \pmod {p-1}\), but in this case we will use \(r=as+kh(m)\).
- ElGamal signatures (alterative signing). ElGamal (Signing: r=ah(m) +ks). ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this. Normally we sign with \(s=k^{-1} (h(m)-ar) \pmod {p-1}\), but in this case we will use \(r=ah(m) +ks\).
- ElGamal encryption with Go. ElGamal. This implements ElGamal encryption.
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
ElGamal Homomorphic Encryption
- ElGamal Homomorphic Cipher for Multiplication (Python). ElGamal. This outlines ElGamal Homomorphic multiplication with Python.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (Python). ElGamal. This outlines ElGamal Homomorphic division with Python.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (Python). ElGamal. This outlines ElGamal Homomorphic addition with Python.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (Python). ElGamal. This outlines ElGamal Homomorphic subtraction with Python.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
- ElGamal Homomorphic Cipher (Go). ElGamal. This outlines ElGamal Homomorphic cipher with Go.
- ElGamal Homomorphic Cipher (Go) - Divide. ElGamal. This outlines ElGamal Homomorphic cipher with Go with divide.
- ElGamal Homomorphic Cipher (Go) - Additive. ElGamal. This outlines ElGamal Homomorphic cipher with Go with addition.
ElGamal and ECC
- ElGamal with ECC. ElGamal with ECC. ElGamal using ECC.
- Proving an Encrypted Shuffle With ElGamal and ECC. Shuffle. An encrypted shuffle with ElGamal.
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- ElGamal - Applying Multiple Public Key Operations (ECC). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use elliptic curve methods, and using the Edwards 25519 curve.
ElGamal (Authenticated and Verified Encryption)
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenticated ciphertext.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
ElGamal (Encrypting with multiple public keys)
- ElGamal - Applying Multiple Public Key Operations (Discrete Logs). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use discrete logs.
- ElGamal - Applying Multiple Public Key Operations (ECC). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use elliptic curve methods, and using the Edwards 25519 curve.
Ethereum

This page outlines some examples of blockchain and cryptocurrency.
Test Network
- Math functions on Local Network. Go.
- Math functions on Test Network. Go.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- Storing State in a Smart Contract. Go.
- Deleting Data From A Smart Contract. Go.
- A Caesar Cipher Quiz Generator from a Smart Contract. Go.
- Hashing in a Smart Contract. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
- Dealing With Decimals In Smart Contracts. Go.
- Creating A Scrambled Alphabet Challenge Generator In Ethereum and Solidity. Go.
- Deploying a Scrambled Alphabet Generator To Ethereum (With Ganache and Ropsten). Go.
- Deploying a Scrambled Alphabet Generator To Ethereum (With Hardhat). Go.
- Pigpen, IPFS and Ethereum. Go.
- Proof of \(x\) from \(H(x)\) using zkSnarks. Go.
- Elliptic Curve Operations Within a Solidity Contract. Go.

Ethereum
- Creating Ethereum address with Python. Go.
- Creating Ethereum signing with Python. Go.
- ERC20 Tokens. Go.
- Ethereum address with Go. Addresses. This generates an Ethereum address.
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- PATRICIA trie. PATRICIA. Example of using PATRICIA (and which is used in Ethereum).
- Viewing Balance of account in Etheruem with Go. Balance. This views the balance of an account
- Viewing Block in Etheruem with Go. Block. This views a block.
- Viewing Cryptocurrency API with Python. Go.
- Viewing Ethereum blockchain with Python. Go.
- Viewing Transactions in Block in Etheruem with Go. Transactions. This views transactions.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
- Symmetric Key Encryption For Smart Contracts. Symmetric key. Solidity does not natively support symmetric key encryption, such as with AES. Overall, AES would consume too much gas and thus be expensive to implement. But, we can use hashing and X-OR methods to do the encryption. In this case, we will create a 256-bit random value, and then encrypt it with an encryption key, and then decrypt it.
Calling from Python
- Calling smart contracts with Python. Python.
Ethereum crypto
- ECIES with Go-Ethereum. Go.
Ethereum Blockchain
- IOTA Trytes. Trytes. `This outlines Trytes, as used in IOTA.
Ethereum Blockchain
- Blockchain: Adding Maths Functions. Go.
- Blockchain: Blocks, transactions and writing data. Go.
- Blockchain: Contracts and Addresses. Go.
- Blockchain: Getting transactions. Go.
- Blockchain: Hello World!. Go.
- Blockchain: Simple Purchasing System. Go.
- Blockchain: Viewing the blockchain. Go.
- Blockchain: Cracking Wallets. Go.
- Introduction to Blockchain. Go.
Presentations
Factorization

Many public key problems involve the difficulity in factorizing a value two its prime number factors. For example, in RSA, we have a public modulus \(N\) and which is equal to the multiplication of two prime numbers \(p\) and \(q\). If we can factorize the public modulus, we will be able to break the RSA cipher related to it.
RSA Crack
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA Factorization. RSA. This outlines the factorisation of the N value in the RSA method.
Methods
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Dixon. Go. Dixon Method.
- Rho factorization. Rho. Rho alogorithm.
- Smooth numbers. Go. Outline of smooth numbers.
Methods (Elliptic curve
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Quadratic residues
- Quadratic residue (mod p). Go. Outline of quadratic residue \(\pmod p\).
- Quadratic residue (mod p) using Legendre symbol. Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
Factorizing
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
Lenstra–Lenstra–Lovász (LLL) with lattices
- Crack ECDSA with weak nonces. ECDSA with weak nonces and using Lenstra–Lenstra–Lovász (LLL) method. This outlines ECDSA how the private key can be recovered with weak nonce values.
Network Forensics

These pages outlines some network forensics. This includes the understanding of the network stack, and with protocols such as Etherenet, IP, TCP, HTTP, and others.
Network Forensics (Theory)
- Network Forensics (Wireshark). Network Forensics. This provides information on how to detect threats through network forensics with Wireshark.
- Advanced Network Forensics. Network Forensics. This provides information on how to detect threats through network forensics.
Network Forensics (Practice)
- Advanced Network Forensics (Wireshark). Adv Network Forensics. This provides information on how to detect threats through network forensics with Wireshark.
- Network Forensics (PCAP). Network Forensics. This provides information on network forensics (reading PCAP files)
- Network Forensics (Text). Network Forensics. This provides information on network forensics (reading text files)
Tshark
-
Filters with TShark. TShark. This page runs Tshark with a given Pcap file and a defined filter.
Other
- Advanced Digital Forensics . Adv Digital Forensics. This provides information on how analyse disk based systems using open source forensics.
- Partition Analyser. MBR. This page will analyse the details of the partition details within the MBR (put one space between fields).
Presentations
Format Preserving Encryption

Format Preserving Encryption (FPE) is a method which allows the basic formatting of a message to stay in a similar format, and where the value itself is encrypted. It can be used to hide credit card details.
Methods
- Format Preserving Encryption. FPE. This outlines Format Preserving Encryption.
- FPE with Python. FPE. An implementation of Format Preserving Encryption (FPE) using Python.
- FPE with node.js. FPR. FPE with node.js.
- FPE and PKBKDF2 in Python. FPE and PKBKDF2 in Python. FPE using PKBDF2 to password generation.
FFX (Format-preserving, Feistel-based encryption)
- FPE with Go. FPE. An implementation of Format Preserving Encryption (FPE) for FFX1 and FFX3.
- FFX schemes. FFX. Within tokenization we can apply format preserving encryption (FPE) methods, which will convert our data into a format which still looks valid, but which cannot be mapped to the original value. For example, we could hide Bob's credit card detail into another valid credit card number, and which would not reveal his real number. A tokenization server could then convert the real credit card number into a format which still looked valid. For this we have a key which takes the data, and then converts it into a form which the same length as the original.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher in Python.
FFX in Rust
- FFX. FFX. This is an implementation of FFX in Rust.
Honey Encryption
- Honey Encryption. Honey. This outlines Honey encryption.
Crypto Principles

This page outlines some crypto principles.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Galois fields (polynomial operations)

This page outlines a few basic principles around the usage of Galois fields and polynomial operations. In 1832, Évariste Galois died of duelling wounds at the age of 20 but left a great legacy. While he was a teenager he worked on polynomials and laid down the principles of Galois theory, along with defining the concept of a finite field. In cryptography, the finite field is one of the major concepts and involves limiting the number of possible values to a limiting factor (\(p\)). The values of the field then range from 0 to p-1. Within a field, we can operate on values in the field using arithmetic operations. We can thus have an infinite field, and where we could include all of the possible integers. A finite field or Galois field of GF(\(2^n\)) has \(2^n\) elements. If \(n\) is four, we have 16 output values. Let’s say we have a number \(a∈{0, ... ,2^{n−1}}\), and represent it as a vector in the form of a polynomial:
\( a=a0+a_1 x+a_2 x^2 ... a_{n−1} x^{n−1}\)
If we use \(a_n∈{0,1}\), this is exactly the same as representing a binary number modulo \(2^n\). In this \(x^n\) represents bit position \(n\) and \(a_n\) is the value of the bit at position \(x^n\). If a bit is a zero at a given position, it will be not included in the polynomial equation. So, 1011 can be represented by \(x^3+x+1\) and 1010 is represented as \(x^3+x\). We can then perform arithmetic operations on these polynomial values. So, to add two values of 1010+1100 we can represent this as \((x^3+x)+(x^3+x^2)\) and which is \(x^2+x\) as we are using modulo 2 addition, and where \(x^3+x^3=0\). With modulo 2 addition, 0+0=0, 0+1=1, 1+0=1, and 1+1=1.
An example of Galois Fields is within AES (Advanced Encryption Standard) and which uses a finite field GF(\(2^8\)). With AES we operate on bytes (8 bits) in the form of \(b_7 b_6 b_5 b_4 b_3 b_2 b_1 b_0\) and which are operated on a a polynomial of \(b_7x^7+b_6x^6+b_5x^5+b_4x^4+b_3x^3+b_2x^2+b_1x^1+b_0\).
Galois fields (polynomial operations) - GF(\(p^n\))
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Additive Group Table for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Additive Group Table for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of addition. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the additive group table for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values.
- Multiplicative Group Table for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Multiplicative Group Table for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the additive group table for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values.
- Additive, Division and Multiplicative Group Table for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Additive, Division and Multiplicative Group Table for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the Additive, Division and Multiplicative Group Table for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values.
- Additive and Multiplicative Group Table for GF(\(2^2\)) and GF(\(2^3\)). Galois Fields Table for GF(2^m) with polynomials. This page implements Galois Fields GF(\(2^n\)) with Python and provides a table of additional and multiplication. It outlines GF(\(2^2\)) and GF(\(2^3\)), but also gives a program that can be used for others. Overall, we have the form of GF(\(p^n\)) and which provides use both an additive and a multiplicative group operations that provide all the possible outputs within the finite field. The value of \(p\) is a prime number, and \(n\) is any positive integer.
- Additive and Multiplicative Group Table for GF(\(2^2\)) and GF(\(2^3\)). Galois Fields Table for GF(2^m) with coefficient values. This page implements Galois Fields GF(\(2^n\)) with Python and provides a table of additional and multiplication. It outlines GF(\(2^2\)) and GF(\(2^3\)), but also gives a program that can be used for others. Overall, we have the form of GF(\(p^n\)) and which provides use both an additive and a multiplicative group operations that provide all the possible outputs within the finite field. The value of \(p\) is a prime number, and \(n\) is any positive integer. This version will show the polynomial coefficent values within the Galois Field.
- Additive and Multiplicative Group Table for GF(\(2^2\)) and GF(\(2^3\)). Galois Fields Table for GF(2^m) with integer values. This page implements Galois Fields GF(\(2^n\)) with Python and provides a table of additional and multiplication. It outlines GF(\(2^2\)) and GF(\(2^3\)), but also gives a program that can be used for others. Overall, we have the form of GF(\(p^n\)) and which provides use both an additive and a multiplicative group operations that provide all the possible outputs within the finite field. The value of \(p\) is a prime number, and \(n\) is any positive integer. This version will show the integer values within the Galois Field.
Irreducible polynomial for GF(p^n)
- Irreducible polynomial for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Irreducible polynomial for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the parameters for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values. This includes finding the irreducible polynomial for the Galois Field.
- Irreducible polynomial for GF(\(p^n\)) for a given \(p\) and for \(n\) values. Irreducible polynomial for GF(p^n) for a given p and for n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the parameters for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values. This includes finding the irreducible polynomial for the Galois Field. Other important parameters include the degree (the highest polynomial power) and the order (the number of possible output values).
- Conway and primitive polynomial GF(\(p^n\)). Conway and primitive polynomial GF(p^n). This page outlines Conway and primitive polynomials for GF(\(p^n\)).
Galois fields (polynomial operations) - GF(\(p\))
- Additive and Multiplicative Group mod n (\(Z_n\)). Additive and Multiplicative Group mod n. In finite fields, we have a \(\pmod n\) operation for a list of integers (\(\mathbb{Z}\)), and where \(n\) is a prime number. This works for our add (+) and multiply (\(\times\)) operations, and where: \( a \pmod n + b \pmod n = (a+b) \pmod n\); and \(a \pmod n \times b \pmod n = (a \times b) \pmod n\).
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Polynomial GF(2) Factoring and Irreducible Polynomials. Factors. This outlines the search for polynomial factors for GF(2).
Polynomial operations
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
Post-quantum
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Rust
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Sage
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Golang and Cryptography

The new scripted languages such as Python and Node.js are convenient. But, unfortunately, they can be slow as they are scripted, and not compiled. Each time the scripted code is run, the scripting engine must then convert each line of code to the required machine level code. This makes the code much slower than compiled languages, and also less robust. Thus many applications in cryptography are written in C and C++, as they allow for fast execution and give low level access. Unfortunately it can be complex to compile programs, as we often need to install binary libraries and then link these in. The Go programming language, though, has a similar code syntax to C/C++, but is small and efficient and allows access to low-level functions, such as as pointers. Go thus aims to “Code less, compile quicker, execute faster”. So let’s use Go to implement some cryptography methods, including symmetric key, hashing, public keys and zero-knowledge proofs (ZKPs). The slides related to these methods are included [here]. An introduction to Golang and Cryptography is [here].

Go ECDH
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret.
Go Hex and Base64
- Base64 and Hex in Go. Base64/Hex. Two common formats for representing binary data are hexademical and Base64.
Go symmetric key
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Reuse IV attack and AES. Reuse IV and GCM. This provides an implementation of a reuse IV against AES GCM.
- ASCON AEAD (Golang). ASCON AEAD (Golang). The outlines the usage of AEAD for ASCON using Golang.
Go HMAC and HKDF
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HKDF in Go. HKDF. Implementation ofHKDF, and where we dervice a key based on a given secret.
Go secret shares
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.

Go ZKP
- Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL). DLEQ. Create a non-interactive ZKP for discrete logs.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Fiat Shamir and ECC (Interative ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP with Kryptology. This implements a range proof using a Schnorr proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?

Go ECIES (Hybrid Encryption)
With this, we can use the power of public key encryption (to generate the encryption key) with symmetric key encryption (to actually encrypt and decrpyt the data):
- ECIES (Kryptology). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Coinbase Kryptology library.
- ECIES (CIRCL). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Cloudflare CIRCL library.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt and which is used in Contract Tracing for COVID-19.
Go ECDSA
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Go RSA
- RSA Principles. RSA Principles. The basics of RSA.
- RSA with Go. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA. RSA encryption with Go using OAEP.
- RSA Encryption with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
Go ElGamal
ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Proving an Encrypted Shuffle With ElGamal and ECC. Shuffle. An encrypted shuffle with ElGamal.
- ElGamal encryption with Go. ElGamal. This implements ElGamal encryption.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
- ElGamal - Applying Multiple Public Key Operations (ECC). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use elliptic curve methods, and using the Edwards 25519 curve.
Go PGP
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
Go Public key
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.

Go Hashing
- Hashing with Go. Hashing. Hashes with Go.
- GP Hashing with Go. GP Hashing. GP Hashes with Go.
- SHAKE with Go. SHAKE. This implements SHAKE in Go.
- libDisco with Go. libDisco. This implements libDisco.
- cSHAKE in Golang. cSHAKE. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS. With the SHA-3 hashing method, we have four different cryptographic hashing methods (SHA3-224, SHA3-256, SHA3-384, and SHA3-512) and two XOF functions (SHAKE128 and SHAKE256). With SHAKE128 and SHAKE256 we can integrate domain separation between different functions — and which are known as cSHAKE128 and cSHAKE256.
- Homomorphic Hashing with Golang. Homomorphic hashing. Normally with hashing methods, we need to take all the previous data and new data in order to create a new hash value for our data. In a homomorphic hashing method, we can basically take the previous hash, and then add on any new data values. We can also remove previous data values from our hash, too. This is more efficient in computing, as we do not have to process all of our data into a new hash, and can use simple homomorphic operations for the computation. The method we will use (LtHash) was initially defined by Bellare and Micciancio and updated Lewi et al at Facebook.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
Go ECC
- Hash to password with Go. Hash to password. Hash to password with Go.
- ECDH with Go. ECDH. ECDH with Go.
- Box with Go. Box. Box with Go.
- ECC with Go. ECC. ECC with Go.
- Curve 25519 with Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ElGamal with ECC. ElGamal with ECC. ElGamal using ECC.
- Curve 25519 with Go for test vectors. ECC. This does a test on some private keys to test the public key generation.
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Barebones Ed25519 with Go. ECC. This shows point addition and scalar multiply in Ed25519
- Barebones NIST P256 with Go. ECC. This shows point addition and scalar multiply in P256
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining \(n.G\) for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Points (Base Point and Others). Elliptic Curve points. Two common curves used in ECC (Elliptic Curve Cryptography) are secp256k1 (as used in Bitcoin and Ethereum) and P256 (secp256r1). The "k1" refers to the Kolbitz curve 1 (named after the creator of ECC). With these we have a base point which are can operate on. This is typically defined as \(G\). We can then operate on this with add and multiply operation. For example, \(2G=G+G\) and \(P=n.G\). In this following we will show the base point for a number of common curves, such as secp256r1, P256, Pallas, Curve 25519, BLS12381G1, BLS12381G2, BLS12377G1 and BLS12377G2.
Go Blockchain
- Ethereum address with Go. Addresses. This generates an Ethereum address.
- Viewing Balance of account in Etheruem with Go. Balance. This views the balance of an account
- Viewing Block in Etheruem with Go. Block. This views a block.
- Viewing Transactions in Block in Etheruem with Go. Transactions. This views transactions.

Go Homomorphic
- SIDH Go. SIDH. Post-quantum key exchange.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- NTP. NTP. An overview of NTP.
- BiBa. BiBa. An overview of BiBa One Time Signature.
Go DNS
- DNSSEC. DNSSEC. An overview of DNSSEC.
Go Signatures
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Go Signcryption
- Ahmad-Afzal-Iqbal (AAI) signcryption with Golang. Ahmad-Afzal-Iqbal (AAI). Ahmad-Afzal-Iqbal (AAI) signcryption with Golang.

Go Crypto pairing
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
Go Homomorphic
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add. HEAAN Add. HEAAN Add.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- Anonymous crypto. Anon. Anonymous crypto.
- Rho factorization. Rho. Rho alogorithm.
- Post-quantum signing (BLISS). BLISS. BLISS method.
Go Post quantum
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.

Go CIRCL
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- Ed448 with Go. X448. Ed448 with Go.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with FourQ (Cloudflare). FourQ.
- Verifiable Oblivious Pseudorandom Functions (VOPRF) with Cloudflare CIRCL. VOPRF. In our digital world, we give away too many of our secrets, especially where we just have to prove the knowledge of something, rather than actually revealing it. In many of the systems we use, we could just prove things in an oblivious way, and where we could pass a secret but in a blinded form. With this, a server does not discover our password and for us not to discover the identifier that a server holds on us. But, can we also provide a proof back that the right password has been used? Well, with Verifiable Oblivious Pseudorandom Functions (VOPRF), we can generate a random secret based on a key generated on the server (Alice), and which is based on Bob’s secret.
- Hash to Curve using Go (Cloudflare). Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). The method defined here is proposed an an Internet-Draft standard by the Internet Engineering Task Force (IETF) related to "Hashing to Elliptic Curves".
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
here Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
- eXtendable-Output Function (XOF) usign CIRCL. XOF. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS.

Go Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Google Tink (Golang) ECIES. Google Tink (ECIE5). This outlines ECIES encryption with public key and AES using Golang with Google Tink
Go Credentials
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.

Go Kryptology
- Public key points for curves. Simple. Display public key points for scalars.
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.

Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.

Principles
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Paillier
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
Go Format Preserving Encryption (FPE)
- FPE with Go. FPE. An implementation of Format Preserving Encryption (FPE) for FFX1 and FFX3.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
AWS Encryption
- AWS Symmetric Key Encryption. AWS (Symmetric key). Using symmetric key in AWS.
Go Oblivious Transfer
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Dragon Fly
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
Embedding data in an ECC point
- Embedding data in a point. Go. With Elliptic Curve Cryptography (ECC), we use points on an elliptic curve to represent our data. These are defined with (x,y) points. With this, it is possible to embedded a certain amount of data into the point - as long as it still gives us a valid point on the curve. This example will Curve 25519 to embed data, and is achieved by storing the length of the data in a single byte in the point, and then store the data as byte values in the point (followed by random data). To decode, we can then just read the first byte for the length of the message, and then reveal the data encoded into the point..
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Hashing (Cryptographic)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
Benchmarks and Password strength
The following are the tips related to hashing:
- Password strength. Test. This outlines the strength of various passwords types.
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
Theory
The following are the tips related to hashing:
- Balls in bins. BiBa. This implemented balls in bins.
- Birthday attack (with Big Integers). Calc. This provides a simple example of the birthday attack.
- Birthday attack. Calc. This provides a simple example of the birthday attack.
- Differential Cryptanalysis (Hashing). Cryptanalysis. This provides an implementation of differential cryptanalysis for hashing methods.
MD5, SHA-1
The following are the tips related to hashing:
- MD2 and MD4 MD2/4. The MD2 and MD4 hashing functions were developed by Prof Ronald Rivest in 1989 and 1990, respectively. They both produce a 128-bit hash, but have been shown be vulnerable to attack (see the Collision section in the page).
- MD5 and SHA-1 (to Base-64) with salt Salt. It is possible to add salt to the MD5 algorithm, to mix it up a little.
- MD5 and SHA-1 (to Base-64) Hash. MD5 and SHA-1 produces a hash signature, and the output is typically shown in a hex format or a Base-64. In this example the output is converted into a Base-64 format.
- MD5 and SHA-1. Hash. MD5 and SHA-1 methods produce a hash signature, and are the two of the most widely used methods. The MD5 algorithm has been shown to have weaknesses, and a collision of message hashes has been shown to occur in less than one day. An MD5 signature has 128 bits, an SHA-1 signature has 160 bits, and an SHA-256 signature has 256 bits.
- MD5 Cracking. Hash Cracker. MD5 has a 128-bit signature and can be cracked using rainbow tables. This page tries to crack the MD5 signature.
- Hashing with Go. Hashing. Hashes with Go.
- Detecting hash types. Hash type. This detects has values.
- OpenSSL hashing. Range of methods. Outlines the methods used in OpenSSL
- Hash. Hash. Hashing using JavaScript
- Hashing with node.js. Hashing. Hashing with node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Hashing methods
-
Hazmat Hashes. Hazmat Hashes. This includes the hashing methods in the Hazmat cryptography library. This includes Blake2p, Blake2s, MD5, SHA1, SHA224, SHA256, SGA384, SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHA512, SHA512-224, SHAKE128 and SHA256.
-
Hazmat Hashes. Hazmat Hashes. In this case we will implement Python code to determine SHA1, SHA2, SHA3, Blake2, MD5 and SM3 hashes.
OpenSSL Passwords
-
Password example [here]
-
Hashed passwords with OpenSSL [here]
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Blake 3 hashes
The following are the tips related to similarity hashing:
- Blake 3 in Python. Hashing. Blake 3 hashing.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
Other Hash functions
The following are the tips related to hashing:
- Bloom Filter Bloom filter. A Bloom filter goes a probabilistic method of determining if an element is in a data structure, using indexed hashing methods.
- Cuckoo Table Cuckoo filter. A Cockoo table uses two hash funtions.
- Chaffing. Chaffing. This produces a keyless system.
- GP Hashing with Go. GP Hashing. GP Hashes with Go.
- LDAP. LDAP. This produces a LDAP hash signature for a password.
- LM Hash. LM Hash. This is an LM Hash Calculator. LM Hash is used in many versions of Windows to store user passwords that are fewer than 15 characters long.
- Murmur and FNV Murmur and FNV. While hashing methods such as MD5 and SHA-1 use crypto methods, the Murmur and FNV hashes uses a non-cryptographic hash function. This can be used for general hash-based lookup and was designed by Austin Appleby. It has good performance compared with other hashing methods.
- Pearson. Pearson. This uses a non-crypto hash.
- phpass. phpass. This produces a phpass hash signature for a password.
- Tiger. Tiger. Tiger is a 192-bit hash function and was designed by Ross Anderson and Eli Biham in 1995. It is often used by clients within Gnutella file-sharing networks and does not suffer from known attacks on MD5 and SHA-0/SHA-1. Tiger2 is an addition, in which the message is padded with a byte of 0x80 (in a similar way to MD4, MD5, and SHA), whereas in Tiger it is 0x01. Otherwise, the two methods are the same in their operation.
- Whirlpool. Whirlpool. Whirlpool is a 512-bit cryptographic hash function and was created by Vincent Rijmen (one of the AES creators) and Paulo Barreto, in 2000.
- WPA-2 hash . WPA-2 hash. Implements SHA-2 hash.
- Reusable hash collisions. Reusable hash collisions. Reusable hash collisions.
- The Length Extension Attack. Length Extension Attack. The MD construct has many weaknesses, and one of the most serious is the length extension attack. With this an adversary (Eve) can take a hash for an unknown message, and then add additional data to produce a new valid hash. The hash methods which are at risk against the length extension attack are MD5, SHA-1 and SHA-256. Please follow the code link below to run an example.
- Consistent hashing. Consistent hash. This outlines the usage of Consistent hashes.
- ROR13 (Module and Function). ROR13. With ROR13 we take each 8-bit character and then convert to a unicode value (with 16 bits). Then for each character we rotate the bits right by thirteen places. The resultant hash is then just the accumuluation of the rotated values.
- ROR13 (Function). ROR13 (Function). With ROR13 we take each 8-bit character and then convert to a unicode value (with 16 bits). Then for each character we rotate the bits right by thirteen places. The resultant hash is then just the accumuluation of the rotated values.
- GOST, Streebog256 and Streebog512. GOST, Streebog256 and Streebog512. GOST94 is a hashing method developed with Euro-Asian Council for Standardization, Metrology and Certification (EASC). This has since been developed in the Streebog256 and Streebog512 hashing method. In this case, we will use Libre OpenSSL to convert data into a hashed value.
RIPEMD
- RIPEMD (RACE Integrity Primitives Evaluation Message Digest) and GOST. RIPEM160. RIPEMD is a 128-bit, 160-bit, 256-bit or 320-bit cryptographic hash function, and was created by Hans Dobbertin, Antoon Bosselaers, and Bart Preneel. It is used on TrueCrypt and is open source. The 160-bit version is seen as an alternative to SHA-1, and is part of ISO/IEC 10118
- RIPEMD160. RIPEM160. RIPEMD160 is a 160-bit cryptographic hash function, and was created by Hans Dobbertin, Antoon Bosselaers and Bart Preneel. RIPEMD160 is used in Bitcoin applications.
Chameleon hashes
The following are the tips related to Chameleon hashing:
- Chameleon hash in Golang Chameleon. With a Chameleon hash, we have a normal hash value which is resistant to collisions, but with a known secret we can easily create a collision. The concept was first defined by Krawcyk and Rabin.
Similarity hashes
The following are the tips related to similarity hashing:
- Similarity hash: SimHash (Charikar similarity) in Python Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash (Nilsimsa similarity) Nilsimsa. The Nilsimsa similarity is used to find similarities between spam emails.
- Minhash (Jaccard similarity) Jaccard similarity. The Minhash method is used to find similarities between strings, files and metadata.
- String enthropy String enthropy. Measurement of the entropy of strings.
- Counting identical elements (HyperLogLog) HyperLogLog. Counting the number of identical elements.
SHA-3 and SHA-3 contenders
The following are the tips related to Key derivation hashing:
- Blake and Blake 2. Blake. Implements Blake and Blake 2 (SHA-3 contender).
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
- Grøstl. Grøstl. Implements Grøstl (SHA-3 contender).
- KangarooTwelve. KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- SHA-3, Keccak and SHAKE . SHA-3. Implements SHA-3, Keccak and SHAKE (SHA-3 winner).
- SHA-3. SHA-3. SHA-3 was known as Keccak and is a hash function designed by Guido Bertoni, Joan Daemen, Michaël Peeters, and Gilles Van Assche. MD5 and SHA-0 have been shown to be susceptible to attacks, along with theoretical attacks on SHA-1. NIST thus defined there was a need for a new hashing method which did not use the existing methods for hashing, and setup a competition for competing algorithms. In October 2012, Keccak won the NIST hash function competition and is proposed as the SHA-3 standard. It should be noted that it is not replacement SHA-2, which is currently a secure method. Overall Keccak uses the sponge construction where the message blocks are XORed into the initial bits of the state, and then inevitably permuted.
- cSHAKE. cSHAKE. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS. With the SHA-3 hashing method, we have four different cryptographic hashing methods (SHA3-224, SHA3-256, SHA3-384, and SHA3-512) and two XOF functions (SHAKE128 and SHAKE256). With SHAKE128 and SHAKE256 we can integrate domain separation between different functions — and which are known as cSHAKE128 and cSHAKE256.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- Skein. Skein. Implements Skein (SHA-3 contender).
Key derivation hashing
The following are the tips related to Key derivation hashing:
- Argon2. Go. Outline of Argon2.
- Argon2 with NaCl. Go. Outline of Argon2 using NaCl.
- Balloon. Go. Outline of Balloon.
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- Double ratchet. Go. Outline of double ratcheting.
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- Scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat HKDF. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
Non-crypto/fast hashing
The following are the tips related to non-crypto hashing:
- A perfect hash Perfect hash. This is a non-crypto hash which optimizes the hash value.
- The universal hash Universal hash. This related to the concept of a universal hash.
- FNV. FNV. FNV is one of the fastest hashing methods.
- Murmur. Murmur. Murmur is one of the fastest hashing methods.
- Siphash. Siphash. Siphash is a fast hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- xxHash. xxHash. xxHash is one of the fastest hashing methods.
- Meow. Meow. Meow is one of the fastest hashing methods.
- o1Hash. o1Hash. o1Hash is one of the fastest hashing methods.
- CRC-32. CRC-32. CRC-32 is one of the fastest hashing methods.
- wyhash. wyhash. wyhash is one of the fastest hashing methods.
- CityHash. CityHash. CityHash is one of the fastest hashing methods, and is generally free of security problems.
- FarmHash. FarmHash. FarmHash is one of the fastest hashing methods, and is generally free of security problems.
- Non-crypto. Non-crypto. This includes a range of fast non-cryptography hashing methods.
- Non-crypto hashes (C++): Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro. Non-crypto hashes: Farm, City, xxHash, MUM, Spooky 2, Murmur, Metro and t1ha0. This includes a range of fast non-cryptography hashing methods for Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro using C++ methods.
- Pearson. Pearson. Pearson is one of the fastest hashing methods, and has been designed for 8-bit processors.
- C++: t1ha. t1ha. t1ha is one of the fastest hashing methods, and has been designed for 64-bit processors.
- C++: Spooky. Spooky. Spooky is one of the fastest hashing methods, and V2 has a 32-bit, 64-bit and 128-bit version.
- C++: xxHash. xxHash. xxHash is one of the fastest hashing methods, and has good performance for short data inputs.
- C++: MUM. MUM. MUM is one of the fastest hashing methods.
- C++: FNV 1/1a. FNV 1/1a. FNV 1/1a is one of the fastest hashing methods, and is particularily useful when there are small changes in strings, such as with IP addresses and URLs.
- C++: MetroHash. MetroHash. MetroHash is one of the fastest hashing methods.
- C++: CityHash. CityHash. CityHash was created by Google and is one of the fastest hashing methods. It was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Farm. FarmHash. FarmHash was created by Google and is one of the fastest hashing methods. It is an improvement to CityHash.
- C++: Murmur. Murmur. Murmur is one of the fastest hashing methods, but was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Halftime. Halftime. Halftime is one of the fastest hashing methods and was created by Jim Apple at Apache.
- C++: Highway. Highway. Highway is an ultra-fast keyed-hash, and is more than five times faster than SipHash. It was created by Jyrki Alakuijala, Bill Cox, Jan Wassenberg at Google.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
- C++: CLHash. CLHash. CLHash is an ultra-fast hashing method and focused on improving performance of the hashing of long strings.
- C++: FalkHash. FalkHash. FalkHash is an ultra-fast hashing method and beats most of the other non-cryptography methods for performance. It is focused on the x64 architecture and integrates with AES-NI.
- C++: wyHash. wyHash. wyHash is an ultra-fast hashing method.
- C++: Fibonacci. Fibonacci. Fibonacci is an ultra-fast hashing method.
- C++: Lookup3. Lookup3. Lookup3 is an ultra-fast hashing method.
Key-based hashing
The following are the tips related to Key-based hashing:
- SiphashSiphash. Siphash is a fast key-based hashing method.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
One Time Passwords/Time Stamps
The following are the tips related to hashing:
- One Time Passwords. One Time. This allows a new unique password to be created each instance, based on an initial seed.
- Timed One Time Password (TOTP). Timed One Time Password. This allows a new unique passcode to be created each instance, based on an initial seed for a given time window. We will use a five second window in this case, where a new passcode is generated every five seconds, based on an initial seed of a pass phrase.
- Hashed One Time Password (HOTP). Hashed One Time Password. This allows a new unique passcode to be created each instance, based on a counter value and an initial seed.
- Time Stamp Protocol. TSP. This creates a time stamp for data.
- HOTP and TOTP (Python). OTP. This creates hashed passwords.
eXtendable-Output Function (XOF)
- eXtendable-Output Function (XOF) usign CIRCL. XOF. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS.
SHAKE
The following are the tips related to hashing:
- SHAKE. SHAKE. Implements SHAKE and which is an Extendable Output Function (XOF).
- SHAKE with Go. SHAKE. This implements SHAKE in Go.
- libDisco with Go. libDisco. This implements libDisco.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify
the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods
such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC methods using the Python cryptography primitives for HMAC-MD5.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
Quantum-robust Public Key (Hash-based signature)
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
Hash to ECC point
- Hash to password with Go. Hash to password. Hash to password with Go.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve with libnum.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.

Password-hashing functions using Rust
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing (Non-cryptographic)

You might know those slow old hashing methods, such as MD5, SHA-1, and SHA-256. Well, they were designed to be fast, but also highly secure. But, if we just need a hashing method, such as for a hashtable or Bloom filter, we often don’t need all the security that comes with the main cryptography hashing methods. And so we have the non-cryptography hashing methods, and which are often ultra-fast and highly efficient. To show the difference, in a test, SHA-1 — one of the fastest cryptography hashing methods — managed a processing rate of 364.95 MiB/s, while t1ha was nearly a 100 times faster, at 34,636 MiB/s.
Non-crypto/fast hashing
The following are the tips related to non-crypto hashing:
- A perfect hash Perfect hash. This is a non-crypto hash which optimizes the hash value.
- The universal hash Universal hash. This related to the concept of a universal hash.
- FNV. FNV. FNV is one of the fastest hashing methods.
- Murmur. Murmur. Murmur is one of the fastest hashing methods.
- Siphash. Siphash. Siphash is a fast hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- xxHash. xxHash. xxHash is one of the fastest hashing methods.
- Meow. Meow. Meow is one of the fastest hashing methods.
- o1Hash. o1Hash. o1Hash is one of the fastest hashing methods.
- CRC-32. CRC-32. CRC-32 is one of the fastest hashing methods.
- wyhash. wyhash. wyhash is one of the fastest hashing methods.
- CityHash. CityHash. CityHash is one of the fastest hashing methods, and is generally free of security problems.
- FarmHash. FarmHash. FarmHash is one of the fastest hashing methods, and is generally free of security problems.
- Non-crypto. Non-crypto. This includes a range of fast non-cryptography hashing methods.
- Non-crypto hashes (C++): Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro. Non-crypto hashes: Farm, City, xxHash, MUM, Spooky 2, Murmur, Metro and t1ha0. This includes a range of fast non-cryptography hashing methods for Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro using C++ methods.
- Pearson. Pearson. Pearson is one of the fastest hashing methods, and has been designed for 8-bit processors.
- C++: t1ha. t1ha. t1ha is one of the fastest hashing methods, and has been designed for 64-bit processors.
- C++: Spooky. Spooky. Spooky is one of the fastest hashing methods, and V2 has a 32-bit, 64-bit and 128-bit version.
- C++: xxHash. xxHash. xxHash is one of the fastest hashing methods, and has good performance for short data inputs.
- C++: MUM. MUM. MUM is one of the fastest hashing methods.
- C++: FNV 1/1a. FNV 1/1a. FNV 1/1a is one of the fastest hashing methods, and is particularily useful when there are small changes in strings, such as with IP addresses and URLs.
- C++: MetroHash. MetroHash. MetroHash is one of the fastest hashing methods.
- C++: CityHash. CityHash. CityHash was created by Google and is one of the fastest hashing methods. It was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Farm. FarmHash. FarmHash was created by Google and is one of the fastest hashing methods. It is an improvement to CityHash.
- C++: Murmur. Murmur. Murmur is one of the fastest hashing methods, but was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Halftime. Halftime. Halftime is one of the fastest hashing methods and was created by Jim Apple at Apache.
- C++: Highway. Highway. Highway is an ultra-fast keyed-hash, and is more than five times faster than SipHash. It was created by Jyrki Alakuijala, Bill Cox, Jan Wassenberg at Google.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
- C++: CLHash. CLHash. CLHash is an ultra-fast hashing method and focused on improving performance of the hashing of long strings.
- C++: FalkHash. FalkHash. FalkHash is an ultra-fast hashing method and beats most of the other non-cryptography methods for performance. It is focused on the x64 architecture and integrates with AES-NI.
- C++: wyHash. wyHash. wyHash is an ultra-fast hashing method.
- C++: Fibonacci. Fibonacci. Fibonacci is an ultra-fast hashing method.
- C++: Lookup3. Lookup3. Lookup3 is an ultra-fast hashing method.
A fuller test with SMHasher gives [here]:
Hash function MiB/sec cycl./hash cycl./map Quality problems
------------------------------------------------------------------
o1hash 12439661.09 16.77 166.13 insecure, no seed, zeros, fails all tests
crc32_hw1 23208.73 46.74 179.70 insecure, 100% bias, collisions, distrib, BIC, machine-specific (x86 SSE4.2)
t1ha0_aes_noavx 22785.26 38.71 180.61 LongNeighbors, machine-specific (x86 AES-NI)
t1ha0_aes_avx1 22714.85 48.12 226.52 LongNeighbors, machine-specific (x64 AVX.txt)
t1ha0_aes_avx2 22345.33 44.38 556.47 LongNeighbors, machine-specific (x64 AVX2)
falkhash 20202.42 173.63 321.52 Sparse, LongNeighbors, machine-specific (x64 AES-NI)
MeowHash64low 17378.06 85.48 237.60 Sparse, invertible, machine-specific (x64 AES-NI)
MeowHash32low 17374.64 85.48 258.53 Sparse, invertible, machine-specific (x64 AES-NI)
MeowHash 17371.91 85.48 247.96 Sparse, invertible, machine-specific (x64 AES-NI)
FarmHash32 17112.05 47.7 214.71 machine-specific (x64 SSE4/AVX)
xxh3 16538.52 32.81 184.86 DiffDist bit 7 w. 36 bits, BIC
xxh3low 16462.36 32.77 199.79
farmhash32_c 16299.81 47.79 219.19 machine-specific (x64 SSE4/AVX)
xxh128low 15174.85 33.79 187.05
xxh128 15174.14 40.46 195.65
farsh32 14053.09 74.29 245.33 insecure: AppendedZeroes, collisions+bias, MomentChi2, LongNeighbors
metrohash64crc_2 14034.84 48.94 162.54 UB, Cyclic 8/8 byte, DiffDist, BIC, machine-specific (SSE4.2/NEON)
metrohash64crc_1 14000.5 49.08 150.54 UB, Cyclic 8/8 byte, DiffDist, BIC, MomentChi2, machine-specific (SSE4.2/NEON)
metrohash128crc_1 13948.67 65.2 168.08 UB, machine-specific (SSE4.2/NEON)
metrohash128crc_2 13920.19 65.12 176.70 UB, machine-specific (SSE4.2/NEON)
halftime_hash128 13478.23 97.79 252.14
wyhash32low 12911.09 29.59 205.43 2 bad seeds
wyhash 12879 30.35 196.77 2^33 bad seeds
CityCrc128 12343.43 74.5 209.75
fletcher2 12011.15 25.29 298.60 bad seed 0, UB, fails all tests
fletcher4 11928.55 25.27 293.49 bad seed 0, UB, fails all tests
halftime_hash256 11620.28 98.44 252.60
fibonacci 11339.87 26.33 705.64 UB, zeros, fails all tests
ahash64 9862.62 27.32 181.68 rust
Spooky128 9751.14 63.84 192.47 UB
Spooky64 9747.47 62.2 191.71 UB
Spooky32 9747.13 62.24 196.96 UB
t1ha1_64le 9723.86 34.39 176.91 Avalanche
cmetrohash64_1 9683.33 45.2 161.01 UB, LongNeighbors, BIC, MomentChi2
cmetrohash64_2 9669.95 44.75 149.67 LongNeighbors
metrohash64_2 9668.51 44.45 164.30 UB, LongNeighbors
metrohash64 9664.61 44.59 150.74 UB, LongNeighbors, BIC
metrohash64_1 9664.57 45.37 152.31 UB, LongNeighbors, BIC, MomentChi2
cmetrohash64_1o 9658.31 42.84 163.45 UB, LongNeighbors, BIC, MomentChi2
FNV1a_YT 9643.42 32.06 175.19 bad seed, UB, fails all tests
City128 9640.19 88.45 225.38
metrohash128_2 9584.94 59.1 167.43 UB, LongNeighbors
metrohash128 9569.16 58.68 167.53 UB, LongNeighbors
metrohash128_1 9558.17 59.04 175.94 UB, LongNeighbors
FarmHash128 9409.63 74.52 210.25
VHASH_32 9404.99 77.01 250.57 sanity, Seed, MomentChi2
VHASH_64 9392.39 74.72 227.92 sanity, Seed, MomentChi2
farmhash128_c 9244.13 79.08 209.44
t1ha2_atonce 9237.12 38.94 194.32 Zeroes low3
City64noSeed 9090.42 32.23 171.53 Avalanche, Sparse, TwoBytes, MomentChi2, Seed
City64low 9089.45 47.75 201.73
t1ha2_stream 9068.55 74.56 219.85 Sparse, Permutation, LongNeighbors
City64 9066.9 47.81 197.78 Sparse, TwoBytes
t1ha2_stream128 9065.5 93.19 236.50 Sparse, Permutation, LongNeighbors
xxHash64 8936.63 51.31 174.34
pengyhash 8744.48 85.31 222.45
farmhash64_c 8713.16 47.96 201.00
FarmHash64 8684.76 48.13 200.51
crc64_hw 8440.13 34.94 141.15 insecure, 100% bias, collisions, distrib, BIC, machine-specific (SSE4.2/NEON)
t1ha2_atonce128 8350.99 55.65 203.53 LongNeighbors
PMPML_64 8161.19 53.2 179.16 unseeded: Seed, MomentChi2, BIC
halftime_hash512 7681.62 125.81 274.01
tabulation 7621.75 42.19 179.93
t1ha1_64be 7481.37 38.16 193.22 Avalanche
MUMlow 7225.18 37.85 197.92 UB, 5 bad seeds
farsh64 7216.29 130.3 302.44 insecure: AppendedZeroes, collisions+bias, MomentChi2, LongNeighbors
MUM 7134.56 37.85 172.34 UB, too many bad seeds, machine-specific (32/64 differs)
nmhash32 7003.3 68.93 216.59
PMPML_32 6704.53 53.5 197.43 Avalanche >512, unseeded: Seed, BIC, MomentChi2, PerlinNoise
nmhash32x 6342.95 56.41 217.75
crc32_hw 6330.42 35.55 170.16 insecure, 100% bias, collisions, distrib, BIC, machine-specific (SSE4.2/NEON)
FNV2 6258.84 33.25 142.89 fails all tests
FNV1A_Pippip_Yurii 6258.46 28.19 184.41 UB, sanity, fails all tests
FNV1A_Totenschiff 6258.23 27.99 198.20 UB, zeros, fails all tests
HighwayHash64 6242.58 99.55 248.41
mx3 6146.02 52.48 173.09 UB
xxHash32 6040.87 51.77 177.91 LongNeighbors, collisions with 4bit diff, MomentChi2 220
prvhash64s_64 5481.48 170.05 325.39
mirhash 5413.73 39.68 154.47 UB, 2^36 bad seeds, LongNeighbors, machine-specific (32/64 differs)
mirhash32low 5412.76 39.79 182.13 UB, 4 bad seeds, Cyclic, LongNeighbors, machine-specific (32/64 differs)
Murmur3F 5226.4 52.18 175.85 UB
prvhash64s_128 5161.33 260.96 442.70
t1ha0_32le 5132.18 54.83 193.53 Sparse, LongNeighbors
halftime_hash64 4990.72 120.55 281.64
Murmur2B 4882.95 39.72 149.43 UB, 1.8% bias, collisions, 3.4% distrib, BIC
seahash32low 4801.33 58.54 227.31 PerlinNoise 32, !msvc
seahash 4796.97 58.55 201.58 PerlinNoise, !msvc
fasthash32 4737.61 45.32 181.86 UB, insecure
fasthash64 4737.21 42.79 164.87 UB, insecure, Moment Chi2 5159 !
umash32_hi 4662.92 54.22 214.20
umash64 4662.09 53.42 188.09
umash32 4633.19 53.42 216.33
t1ha0_32be 4585.59 55.98 183.45 Sparse, LongNeighbors
clhash 4472.31 82.72 229.73 PerlinNoise, machine-specific (x64 SSE4.2)
tabulation32 4317.34 35.45 197.20 collisions
Murmur2C 4092.99 51.84 164.65 UB, 2^32 bad seeds, 91% bias, collisions, distr, BIC, LongNeighbors
farsh128 3776.92 232.48 398.67
City32 3675.04 57.73 212.04
TSip 3228.14 57.96 211.71 !msvc
Murmur3C 3197.63 67.9 198.00 UB, LongNeighbors, Text, DiffDist
Crap8 3149.63 36.23 195.11 UB, 2.42% bias, collisions, 2% distrib
Murmur2 3146.91 41.87 187.89 UB, 1 bad seed, 1.7% bias, 81x coll, 1.7% distrib, BIC
Murmur2A 3146.79 46.87 191.96 UB, 1 bad seed, 12.7% bias, LongNeighbors
aesnihash 2963.39 71.24 217.73 fails many tests, machine-specific (x64 AES-NI)
BEBB4185 2951.62 222.03 343.63 UB, too many bad seeds, msvc-specific
jodyhash6 2848.42 29.99 164.36 bias, collisions, distr, BIC, LongNeighbors
wyhash32 2532.89 48.4 484.57 2 bad seeds, 32-bit
umash128 2427.46 70.6 197.29
Murmur3A 2413.88 53.36 182.37 UB, 1 bad seed, Moment Chi2 69
prvhash64_64m 2386.19 51.18 186.87
prvhash64_128 2383.57 103.44 246.45
prvhash64_64 2375.72 51.61 190.97
hasshe2 2372.52 68.64 216.74 Permutation,TwoBytes,Zeroes,Seed
PMurHash32 2344.78 58.48 196.43 1 bad seed, Moment Chi2 69
mirhashstrict32low 2218.87 65.48 190.59 1 bad seed, MomentChi2 9
mirhashstrict 2217.32 65.53 182.07
sha1ni 2019.96 135.84 564.40 insecure,sanity, Permutation, Zeroes, machine-specific
sha1ni_32 2019.94 136.82 589.46 machine-specific
superfast 1956.25 53.61 180.10 UB, bad seed 0, 91% bias, 5273.01x collisions, 37% distr, BIC
sha2ni-256_64 1910.34 146.06 595.16 Zeroes, machine-specific
sha2ni-256 1906.77 145.47 603.08 insecure,sanity, Permutation, Zeroes, machine-specific
farsh256 1895.77 459.86 575.95
SipHash13 1889.1 89 199.95 0.9% bias
Murmur1 1804.67 51.51 188.41 UB, 1 bad seed, 511x collisions, Diff, BIC
lookup3 1658.31 48.84 194.15 UB, 28% bias, collisions, 30% distr, BIC
pearsonbhash64 1486.34 104.32 185.03
poly_1_mersenne 1431.65 54.49 189.52 fails most tests
jodyhash32 1428.37 44.36 185.85 bias, collisions, distr, BIC LongNeighbors
pearsonbhash128 1347.03 121.75 214.84
poly_2_mersenne 1323.69 66.93 190.88
poly_3_mersenne 1323.59 74.86 206.77
poly_4_mersenne 1323.57 82.67 200.36
blake3_c 1285.91 340.01 552.63 no 32bit portability
GoodOAAT 1052 71.62 192.19
pearsonbhash256 998.9 167.05 261.29
SipHash 980.88 127.77 246.19
MicroOAAT 977.6 59.61 185.06 100% bias, distrib, BIC
FNV1a 791.84 69.69 177.84 bad seed, zeros, fails all tests
sdbm 791.84 67.69 177.06 bad seed 0, fails all tests
FNV64 791.82 70.24 159.29 fails all tests
bernstein 791.82 68.63 180.71 bad seed 0, fails all tests
beamsplitter 789.22 682.45 1150.3 UB, too many bad seeds
HalfSipHash 755.78 114.47 243.72 zeroes
chaskey 753.23 153.42 288.26 PerlinNoise
x17 527.9 98.78 184.09 99.98% bias, fails all tests
JenkinsOOAT_perl 452.49 118.78 194.78 bad seed 0, test FAIL
MurmurOAAT 452.49 113.07 197.83 bad seed 0, 1.5-11.5% bias, 7.2x collisions, BIC, LongNeighbors
JenkinsOOAT 452.48 142.85 213.93 bad seed 0, 1.5-11.5% bias, 7.2x collisions, BIC, LongNeighbors
crc32 392.1 131.62 204.58 insecure, 8590x collisions, distrib, PerlinNoise
sha1-160 364.95 1470.55 1794.1 Comb/Cyclic low32
rmd256 362.49 617.02 815.44 Bad seeds
blake2b-256_64 356.97 1222.76 1435.0
blake2b-224 356.59 1228.5 1425.87
blake2b-160 356.08 1236.84 1458.15
blake2b-256 355.97 1232.22 1443.31 Sparse high 32-bit
md5-128 353.76 638.29 803.39
md5_32a 353.64 629.85 799.56 Sparse high 32-bit
sha1_32a 353.03 1385.8 1759.9 Cyclic low32, 36.6% distrib
rmd128 334.36 659.03 838.32 Bad seeds
blake2s-128 295.3 698.09 1059.2
pearsonhash64 287.95 174.11 196.50 Avalanche, Seed, SSSE3 only. broken MSVC
pearsonhash128 287.95 171.72 194.61 Avalanche, Seed, SSSE3 only. broken MSVC
pearsonhash256 264.51 184.87 218.79 Avalanche, Seed, SSSE3 only. broken MSVC
blake2s-256 215.28 1014.88 1230.38
blake2s-160 215.01 1026.74 1239.54
blake2s-256_64 211.52 1044.22 1228.43
blake2s-224 207.06 1063.86 1236.50
rmd160 202.16 1045.79 1287.74 Bad seeds, Cyclic hi32
sha2-256_64 148.01 1376.34 1624.71 Bad seeds, Moment Chi2 7
sha2-256 147.8 1374.9 1606.06 Bad seeds, Moment Chi2 4
sha2-224_64 147.6 1360.1 1620.93 Bad seeds, Cyclic low32
sha2-224 147.13 1354.81 1589.92 Bad seeds, Comb low32
asconhashv12 144.98 885.02 1324.23
sha3-256 100.58 3877.18 4159.79 PerlinNoise
sha3-256_64 100.57 3909 4174.63 PerlinNoise
asconhashv12_64 86.73 684.02 606.93
floppsyhash 35.72 1868.92 1411.07
tifuhash_64 35.6 1679.52 1212.75 Cyclic low32
Problems include:
- Bad Seeds. A random seed is often used to initialise the hash. This problem relates to having a bad seed..
- Undefined behaviour (UB). This includes Misaligned, oob (Out of bounds), Signed integer overflow and Shift exponent overflow.
o1hash is the fastest, and a quick and dirty hashing method. It is generally not secure. t1h (Fast Positive Hash) requires AES-NI (Intel Advanced Encryption Standard Instructions) and is one of the fastest hashes at 22.785 Gbps. It has fairly good security levels. Meow comes in around 17.378 Gbps. We can see that SHA-1-160 runs as 364 Mbps, while Meow runs at 17.378 Gbps. Blake 3 is one of the fast cryptography hash and has a rate of 1.285 Gbps, and Blake 2 gives a rate around 215 Mbps. SHA-3 gives hashing rates of 100.58 Mbps.
Google recommend the following for 64-bit hashes without quality problems:
- xxh3low
-
wyhash
-
ahash64
-
t1ha2_atonce
-
FarmHash
-
halftime_hash128
-
Spooky32
-
pengyhash
-
nmhash32
-
mx3
-
MUM/mir
- fasthash32
Hash-based Signatures

With hash-based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature, unless we create a stateless method, such as SPHINCS+ [1]. Currently NIST have the final round for the Post Quantum Cryptography competition, and for digital signatures, SPHINCS+ is one of the alterative finalists (alongside Picnic).
Hash-based signature (theory)
- BiBa (Go). BiBa. An overview of BiBa One Time Signature [9]. Basically the method involves us taking a hash of a value using a standard hashing method, such as with SHA-256. There will then be \(2^{256}\) different hashing values. We aim to create a signature for a message, so Bob (the signer) selects a number of random values for his private key value and then publishes the hash of each of these (\(P_1\), \(P_2\), etc). He then sends these public keys to Alice. Now when Bob wants to sign a message, he will take one of his private key values, and then hashes it, and then determines the bin that it should be placed. In this case, we could use the \(\pmod N\) function on the hash, and where \(N\) is the number of bins. If we select \(2^{10}\) there will be 1,024 bins.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature [9].
Hash-based signature (stateful)
- BLISS - Post-quantum signing. BLISS. One of the alteratives to the usage of our existing public key methods is the usage of lattice cryptography, and especially in the usage of Ring Learning With Errors (RLWE). An important application is within digital signatures, and where Bob will sign something with his private key, and then Alice can prove that he signed it with his public key. One post-quantum signature method is BLISS (short for Bimodal Lattice Signature Scheme) [8]. It was created by Léo Ducas, Alain Durmus, Tancrède Lepoint and Vadim Lyubashevsky in 2013.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Hash to Obtain Random Subset (HORS) [3] is a quantum robust hashed-based one-time signature. With this we create a series of integers for our private keys and organise into an indexable form. Then we hash them to a sequence of public key values. Next we segment the hash of the message into a series of n-bit integer values. The signature is then achieved through a look-up of the value in the public key list.
- Lamport Signatures. Lamport. Outlines Lamport signatures [7]. When we sign a message we take its hash and then encrypt with our private key. The public key is then used to prove it, and will prove that we signed it with our private key. The Lamport signature uses 512 random hashes for the private key, and which are split into Set A and Set B. The public key is the hash of each of these values. The size of the private key is 16KB (2×256×256 bits) and the public key size is also 16 KB (512 hashes with each of 256 bits).
- Winternitz Signatures (W-OTS). Winternitz. Outlines Winternitz signatures [4, 5]. W-OTS uses relatively small key and signatures sizes, and is thought to be quantum robust. It generates 32x256 bit random private keys. We then hash these a number of times, and is defined by a parameter (w). If we use w=8, we hash the private keys by (2w). This creates 32x256 bits public keys. The signature is the created by taking eight bits at a time, and then the 8-bit binary int (n) is subtracted from 256 and the private key is the hashed 256-n times. The signature is then 32 hashes which are derived from random private keys. To verify the signature, the recipient parses the hash of the signature (using 8 bits at a time, and extracting the 8 bit int, n).
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method [6], and which is used within speeds-up of Hashing-based signature methods. Using methods such as SHA-1 and SHA-2 (aka SHA-256) will be inefficient as they tend to compress the data inputs through a number of stages. Haraka v2 [6] is different as focuses on inputs of just 256 bits (32 bytes) or 512 bits (64 bytes). This makes the method useful when we are dealing with key and hash values, and is especially useful for hash-based signatures. The output is 256 bits long, but where the input can be either be 256 bits (Haraka256) or 512 bits (Haraka512). These lengths are typically for the outputs of modern hashing applications. The Haraka method, too, has been optimized with AES instructions (AES-NI - Intel Advanced Encryption Standard New Instructions) and which are supported within the hardware of the processor. As Haraka is focused on short messages, the number of rounds within the hashing process has been reduced.
Hash-based signature (stateless)
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ digital signature. SPHINCS digital signature. Outline of the a SPHINCS stateless digital signature method [1].
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
Hash-based signature (Merkle-based)
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
Introduction
Many of the problems we see on the Internet relate to the lack of trust within transactions. The emails you receive and the Web sites that you visit often have very little trust built into them. For trust the email address of the sender, but anyone can fake that address. So increasingly we create a digital signature, and where we sign our messages. In this way, we can check for authentication, integrity and non-repudiation.
With the Alice creates a key-pair: a public key and a private key. She then takes a hash of the message, and then encrypts this hash with her private key, and passes the message and the signature to Bob. Bob then reads the message and takes a hash of it. He then decrypts Alice's signature with her public and checks the hashes. If they match, he knows that she signed and that it has not been changed along the way:
Currently, we often use RSA, DSA and ECDSA to sign our messages. These are based on the difficulty of finding out the factors of a number and on the processing of discrete logarithms. At the current time these methods are computationally hard problems, but with quantum computers, they become much easier. This was shown by Peter Shor who illustrated that it was possible to crack them in polynomial time.
Of all the methods that are being proposed, the hash-based methods look as if they have a good chance of success of creating quantum robust signatures. methods and code-based methods are being researched, but the usage of hashing methods is already well and could provide the best alternative to the existing methods. Hashing methods, too, often bring other advantages, such as forward secure, which means that a key which is cracked will not reveal all the previous keys.
Merkle trees
The root of hash-based methods isin Merkle trees, and which are a way of hashing is used in many applications, including with Bitcoin, Ethereum, Git distribution systems, No SQL, and in many P2P applications. With a Merkle tree we take our data elements, and then hash them, and take pairs of these hashes to create a new hash, and so we build a table. At the top of the tree is the root element (in this case Hash1234):

In this way, we can use the tree to see if we have matching data on systems.On a P2P network, we can transfer a file by splitting it into data segments and then distributing these segments across the network. A trusted source will have the complete Merkle tree for rebuilding the file, and a client can thus rebuild from the Merkle tree and determine the parts of the file which are still missing. Once transferred the root hash (and all the other hashes) will then match. In its core method, the Merkle Signature Scheme (MSS) has serious performance and memory issues, but enhanced methods such as XMSS create with much less of a performance hit.
One-time signatures (Lamport)
The core method used in hash-based signatures is that of the one-time signature, and where we create a new key pair for every method we need to create. If the keys were reused, an attacker could start to learn the private key, and thus spoof messages. One of the first methods was produced by Leslie Lamport and Whitfield Diffie, in 1979, and is defined as:
- We create two data sets with 256 random 256-bit numbers (Set A and Set B). These are the private key (512 values).
- we take the hash of each of the random numbers. This will give 512 hashes and will be the public key.
- We then hash the message using and then test each bit of the hash (0 ... 255). If it is a 0, we use the ith number in Set A, else we use the ith number from Set B.
- The signature is then 256 random numbers (taken from either Set A or Set B) and the public key is the 512 hashes (of Set A and Set B).
The public and private keys are then each 16KB in size. A demo of the method is here.

Figure 1: Lamport method
The major problem with the method is that a key pair for every message. also in 1979, found a solution with Merkle trees.
One-time signature (W-OTS)
To improve performance method (and which reduced key sizes), Merkle proposed Winternitz OTS (named after Robert Winternitz). With this method was possible to sign many bits at the same time. The method is:
- We create 32 256-bit random numbers. These 32 values will be our private key.
- We then hash each of these values 256 times. These 32 values will be our public key.
- We now take the message and hash it using SHA-256. This produces 32 8-bit values (N1, N2 ... N32).
- Next we take each 8-bit value in the hash of the message, and then hash 256-N times (where N is the value of the 8-bit value).
- To prove the signature, we take the message and hash it with SHA-256, and then take each 8-bit value. We then hash the 8-bit signature value by the number of times defined by the message hash value (N1, N2..). The result for each operation should equal the public key value.
This is illustrated below in Figure 2. A demo of the method is here.

Figure 2: W-OTS
Hash-based Signatures
The methods such as W-OTS and Lamport only provide for a one-time signature. In order to sign many messages, we can use the Merkel signature scheme (MSS). With this we take a hash of the keys and build these as the leaves of the tree. The root of the tree is then the public key - the verification key. We then just use the private key of the W-OTS method to create the signature. The sender also sends the authentication path, which is the neighbouring nodes within the path and which leads to the root of the tree. The recipient can then rebuild the tree using the verification key (which can be received a digital certificate) and the authentication path. For the next message we move onto another key pair and where the index of the key part is revealed.
In the following example we have our root as the public key, and then want to sign with Key3. We then show the authentication path which takes us to the root (as defined in the bold arrows):

Conclusions
Hashed-based methods look to be a strong contender for weaning us off RSA, DSA and ECDSA, but we will have to look at the stateful generation of keys. For this we will have to generate a bank of key pairs (2, 4, 8, 16, etc) and then create the public key from the root of the Merkle tree. We must then remember the keys we have used previously, and only use an unused one. Once we use our new key pair, we then show our working-out as to how the private key is integrated into our tree. It is a bit like a teacher marking a question correctly, and asking for the working out that go you to the answer.
References
[1] Bernstein, D. J., Hopwood, D., Hülsing, A., Lange, T., Niederhagen, R., Papachristodoulou, L., ... & Wilcox-O’Hearn, Z. (2015, April). SPHINCS: practical stateless hash-based signatures. In Annual international conference on the theory and applications of cryptographic techniques (pp. 368-397). Springer, Berlin, Heidelberg [paper].
[2] Bernstein, D. J., Hülsing, A., Kölbl, S., Niederhagen, R., Rijneveld, J., & Schwabe, P. (2019, November). The SPHINCS+ signature framework. In Proceedings of the 2019 ACM SIGSAC conference on computer and communications security (pp. 2129-2146) [paper].
[3] Reyzin, L., & Reyzin, N. (2002, July). Better than BiBa: Short one-time signatures with fast signing and verifying. In Australasian Conference on Information Security and Privacy (pp. 144-153). Springer, Berlin, Heidelberg [paper].
[4] Merkle, R. C. (1989, August). A certified digital signature. In Conference on the Theory and Application of Cryptology (pp. 218-238). Springer, New York, NY.
[5] Hülsing, A. (2013, June). W-OTS+–shorter signatures for hash-based signature schemes. In International Conference on Cryptology in Africa (pp. 173-188). Springer, Berlin, Heidelberg.
[6] Kölbl, S., Lauridsen, M. M., Mendel, F., & Rechberger, C. (2016). Haraka v2–efficient short-input hashing for post-quantum applications. IACR Transactions on Symmetric Cryptology, 1-29. [here]
[7] Lamport, L. (1979). Constructing digital signatures from a one-way function (Vol. 238). Technical Report CSL-98, SRI International. [paper]
[8] Ducas, L., Durmus, A., Lepoint, T., & Lyubashevsky, V. (2013, August). Lattice signatures and bimodal Gaussians. In Annual Cryptology Conference (pp. 40-56). Springer, Berlin, Heidelberg [paper].
[9] Perrig, A. (2001, November). The BiBa one-time signature and broadcast authentication protocol. In Proceedings of the 8th ACM Conference on Computer and Communications Security (pp. 28-37) [paper] .
Hashing (Simularity)

Similarity hashes allow for two data objects to be compared for their similarity.
Similarity assessment methods
The following relate to the basic methods used for string similarity:
- String similarity String similarity. This measures edit distance (including Levenshtein distance), Jaro (including Jaro-Winkler), and QGrams.
- String enthropy String enthropy. Measurement of the entropy of strings.
- Soundex Soundex. Soundex uses a phonetic algorithm to classify a sound as it is pronounced. It focuses on matching phrases which have minor spelling errors.
Similarity hashes
The following are the tips related to similarity hashing:
- Similarity hash: SimHash (Charikar similarity) in Python Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash (Nilsimsa similarity) Nilsimsa. The Nilsimsa similarity is used to find similarities between spam emails.
- Context Triggered Piecewise Hashes (CTPH): ssdeep CTPH similarity. Kornblum [6] created ssdeep and which computes fuzzy hashes. This aims to match similar byte sequences, no matter if there are differences between these sequences. For this we break a file up into fragments with a rolling hash function. We then produce a small hash for each of those fragments. These are then aggregated to produce the complete hash of a file. In comparing file signatures, we treat the resultant hash value as a string, and then uses an edit distance method to compare.
- TLSH (A Locality Sensitive Hash) TLSH similarity. In malware analysis and in text similarity, we often have to identify areas of data within files which are similar. One method is TLSH (A Locality Sensitive Hash), and which was defined by Oliver et al [7]. It is used - along with ssdeep - by VirusTotal to identify a hash value for malware.
- Minhash (Jaccard similarity) Jaccard similarity. The Minhash method is used to find similarities between strings, files and metadata.
- Counting identical elements (HyperLogLog) HyperLogLog. Counting the number of identical elements.
Hazmat cryptography

The Cryptography library in Python contains interfaces to common cryptographic algorithms, including symmetric key methods, hashing, public key, and key derivation functions. Many of these are contained with the Hazmat (Harzardous Material) primative setup.
Hashing, HMAC, CMAC, Poly1305 and HKDF
-
Hazmat Hashes. Hazmat Hashes. This includes the hashing methods in the Hazmat cryptography library. This includes Blake2p, Blake2s, MD5, SHA1, SHA224, SHA256, SGA384, SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHA512, SHA512-224, SHAKE128 and SHA256.
-
Hazmat Hashes. Hazmat Hashes. In this case we will implement Python code to determine SHA1, SHA2, SHA3, Blake2, MD5 and SM3 hashes.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
- Hazmat HKDF. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
- Hazmat CMAC. Hazmat CMAC. CMAC methods using the Python cryptography primitives.
- Hazmat Poly1305. Hazmat Poly1305. Poly1305 methods using the Python cryptography primitives.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
Symmetric key
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat. Implementation of ChaCha20/Poly1305 with a random key using Hazmat.
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat. Implementation of AES GCM with a random key using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hazmat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Hazmat Symmetric Key Padding. Symmetric key. This includes the coverage of padding with Hazmat.
- Hazmat Symmetric Key Padding. Symmetric key. This includes the coverage of padding with Hazmat.
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
- Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . With 3DES encryption, we use a 128-bit key and a 64-bit IV value. The two modes supported are ECB (without salt) and CBC (with salt). The DES algorithm has been around for a long time, and the 56-bit version is now easily crackable (in less than a day on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases, and splits the key into two. Overall the key size is typically 112 bits (with a combination of the three keys - of which two of the keys are the same). In this case we will use PKCS7 padding, and which fills the input data with a value that is equal to the number of padding bytes. Overall, DES has a 64-bit block size, and which equates to eight ASCII characters.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key . And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.
Asymmetric key
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- ECC key generaton with Hazmat. Elliptic Curve key gen. Creating ECC keys using Hazmat and Python.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- Hazmat RSA signing (with key values). RSA signing with Hazmat. RSA signing using Python and with Hazmat (with key values).
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here]
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Signatures. DSA Signatures. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. The ECDSA method is an extension of DSA, but implemented with elliptic curve (EC) methods. As with most public key signing methods, we take a hash of a message, and then apply a private key to create a signature (\(r,s\)). This is done by creating a random value (\(k\)) to produce the signature. The signature is then verified using the associated public key. This then verifies the creator of the signature and that the message has not been changed.
Digital Signature: ECDSA/EdDSA
- ECDSA with Hazmat. ECDSA wih Hazmat. This outlines ECDSA with Hazmat.
- Ed25519 for EdDSA signatures with Hazmat. EdDSA: Ed25519. This page uses the Hazmat primitives for the cryptography library.
- Ed448 for EdDSA signatures with Hazmat. EdDSA: Ed448. This page uses the Hazmat primitives for the cryptography library.
- Ed25519 using NaCl. Ed25519. This page uses the NaCl port from libsodium.
- ECDSA Signatures with Hazmat (SECP256R1, SECP384R1, SECP521R1, SECP224R1, SECP192R1, and SECP256K1). ECC Signatures. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and then creates an ECDSA signature for a given message.
Digital Signature: RSA
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
Key exchange: ECDH/X25519
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives and showing the byte values for the key.
Tokens
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
Homomorphic Encryption

Homomorphic encryption supports mathematical operations on encrypted values. Partial Homomorphic Encryption (PHE) supports a few arithmatic operations, while Full Homomorphic Encryption (FHE) supports add, subtract, multiply, and divide. Homomorphic encryption normally involves a public key to encrypt the data, and a private key to decrypt it. There have been four main generations of homomorphic encryption, and the most recent being the HEAAN method.
Simple
- Simple Homomorphic Cipher. Hom. This outlines a Simple Homomorphic cipher.
- Simple Homomorphic Cipher (Python). Hom. This outlines a Simple Homomorphic cipher with Python.
- Full Homomorphic Cipher with a Public Key. Public key. This outlines a Simple Homomorphic cipher using a public key
ElGamal
- ElGamal Homomorphic Cipher (Go). ElGamal. This outlines ElGamal Homomorphic cipher with Go.
- ElGamal Homomorphic Cipher (Go) - Divide. ElGamal. This outlines ElGamal Homomorphic cipher with Go with divide.
- ElGamal Homomorphic Cipher (Go) - Additive. ElGamal. This outlines ElGamal Homomorphic cipher with Go with addition.
- ElGamal Homomorphic Cipher for Multiplication (Python). ElGamal. This outlines ElGamal Homomorphic multiplication with Python.
- ElGamal Homomorphic Cipher for Division (Python). ElGamal. This outlines ElGamal Homomorphic division with Python.
- ElGamal Homomorphic Cipher for Addition (Python). ElGamal. This outlines ElGamal Homomorphic addition with Python.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (Python). ElGamal. This outlines ElGamal Homomorphic subtraction with Python.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
RSA
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
ZKP
- Full Homomorphic Cipher to determine if Bob is older. Older. This outlines a Simple Homomorphic cipher to determine if Bob is older than Alice.
- Full Homomorphic Cipher to determine matching password. Password. This outlines a Simple Homomorphic cipher to determine if a password matches
- Interactive ZKP With Probablistic Methods. ZKP. Interactive ZKP With Probablistic Methods using Python.
- Full Homomorphic Cipher for Millionaire's Problem. Millionaire. This outlines a Simple Homomorphic cipher for the Millionaire's Problem
Voting
- Trusted voting. Trusted. A trusted voting method.
Secret share
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Lattice
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
Full Homomorphic Cipher
- Full Homomorphic Cipher for 2-bit Adder. Adder. This outlines a Simple Homomorphic cipher for a 2-bit adder with DGHV.
- Full Homomorphic Cipher for Full Adder. Full Adder. This outlines a Simple Homomorphic cipher for a full adder with DGHV.
- Full Homomorphic Cipher for 4-bit Adder. Adder. This outlines a Simple Homomorphic cipher for a 4-bit adder with DGHV.
- Full Homomorphic Cipher for 4-bit Adder/Subtractor. Subtract. This outlines a Simple Homomorphic cipher for a 4-bit adder/subtractor with DGHV.
- Full Homomorphic Cipher to XOR two integers. X-OR. This outlines a Simple Homomorphic cipher to X-OR two integers
Paillier
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier) .
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Damgård-Jurik Homomorphic Encryption With Secret Shares. Damgård-Jurik Method. Two of the major areas of developments within cybersecurity will be the usage of homomorphic encryption, and in the usage of Shamir secret sharing. With homomorphic encryption, we can encrypt values, and then operate on them with arithmetic functions (such as add, subtract and multiply), and with Shamir secret sharing, we can split secrets into shares, and then distributed them over networks. These approaches will take privacy to new levels. So let’s look at the Damgård-Jurik method.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Learning with Errors (LWE)
- Learning With Errors . LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret key value (s) and another value (e). Next we select a number of values (t[]) and calculate g[] = t[] x s + e. The values of g[] and t[] become our public key.
- Public Key Encryption with Learning With Errors (LWE). LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret value (s) and which is our private key. We then create a public key which is based on random numbers (A), and then generate another set of numbers (B) which is based on A,s and random errors e. An example of encryption with multiple bits is given.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE)
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Others
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
- SIDH Go. SIDH. Post-quantum key exchange.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Anonymous crypto. Anon. Anonymous crypto.
- Rho factorization. Rho. Rho alogorithm.
- Post-quantum signing (BLISS). BLISS. BLISS method.
Homomorphic Encryption with Krytology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Homomorphic hashing
- Homomorphic Hashing with Golang. Homomorphic hashing. Normally with hashing methods, we need to take all the previous data and new data in order to create a new hash value for our data. In a homomorphic hashing method, we can basically take the previous hash, and then add on any new data values. We can also remove previous data values from our hash, too. This is more efficient in computing, as we do not have to process all of our data into a new hash, and can use simple homomorphic operations for the computation. The method we will use (LtHash) was initially defined by Bellare and Micciancio and updated Lewi et al at Facebook.
Identity Based Encryption (IBE)

This page outlines a few basic principles around the usage of IBE.
Identity Based Encryption (Pairing based)
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pair-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Identity Based Encryption (Others)
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Güther's implicitly certified identity-based public keys (IBE). Günther. This method allows Bob to generate Alices public key from her identity and publicly available parameters.
- Girault's self-certified public keys (IBE). Girault. This method allows Bob to generate Alices public key from her identity and publicly available parameters, and where we use an RSA key pair to self-certify Alice's public key.
Intrusion Detection Systems (IDS)
- Intrusion Detection Systems. Snort. This outlines some of the basics of IDS, including the requirement for Intrusion Detection Systems (IDSs), and where they are used.
- Advanced Network Forensics (Snort). Adv Network Forensics. This provides information on how to detect threats through network forensics with Snort
Snort

- Snort IDS. Snort. This is a Snort Analyser.
- Snort IDS 2 with rules editor. Snort. This provides information on how to detect threats through network forensics with Snort, and with an editing function for rules.
Presentation
IoT

The key objectives of this page are: Understand how a Pen Tester can generate vulnerabilities and test using the Metasploit framework; Define the options and payloads required to generate and use vulnerabilities; and Gaining remote access.
Devices
- Access the Wi-fi kettle. Go. This page outines how to access a wi-fi enabled kettle.
- Philips Hue Wireless Lighting. Go. This page shows how to use RESTful Web services to access to the Hue Led Lamps.
- Kali and R-PI. Go. This page shows the setup of a security testing infrastructure using a Raspberry Pi (R-PI) and a wifi access point.
- Kali, R-PI and RF electrical socket. Go. This page shows the control of an RF electical socket from a RPI.
- Capture from a Polar H10 heat rate sensor. Go. This page shows the capture of the Polar H10 heart sensor with an Ubertooth One.
- Trusted IoT: Linking IoT Devices to NFTs. Go. This page outlines a research paper which links a device to an NFT (Non-fungible Token).
Shodan Scanning
-
IoT Scan (Shodan). Go. This page includes a search of the Internet for key terms, such as for "apache", "mysql" and "cisco".
- IoT Banner Scan (Shodan). Go. This page includes a search of the Internet for key terms with the banner as a result (for the Top 10)
- Internet Services (Shodan). Go. This page includes a search of the Internet for key terms and display the IP address and port.
IoT Libraries
- libDisco with Go. libDisco. libdisco is a Golang library which can be used to create secure connections. It is based on the STROBE protocol framework. Symmetric cryptographic primitives rely on SHA-3 permutation, and asymmetric cryptographic primitives on X25519 and ed25519. STROBE defines a range of cryptographic protocols to integrate with IoT devices. In order to reduce processing, energy and memory requirements, it only uses Keccak (SHA-3) to encrypt and authenticate messages.
COSE/COBR
In computer security, we often have to represent binary data, in single values or groups of characters, bytes, words, long words, signed integers, floating-point values, double-precision floating-point values, and so on. This might be in the form of a data object, a signature or even encrypted content. For this, the ANS.1 DER format is often used, such as presenting digital certificates and signatures. An improvement on this for small messages with security is Concise Binary Object Representation (CBOR) — and which is defined in RFC8949 [1]. While JSON represents text-based data objects CBOR focuses on binary objects. It has been designed to create a lightweight encoder and decoder. This supports the use of CBOR within an IoT infrastructure. The data, also, does not require a data schema to be able to decode it, along with being extensible. CBOR defines the format of binary data with data objects and messages. We can then integrate security with CBOR Object Signing and Encryption (COSE), and which is defined in RFC8152 [2]. This includes signatures, message authentication codes (MACs), encryption and creating serialised objects.
- 128-bit AES GCM. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) can then build on this to include signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use a symmetric key to encrypt a message, and then decrypt it. In this case we will use AES GCM with a static 128-bit key ("0x000102030405060708090a0b0c0d0e0f").
- 256-bit AES GCM. Go. In this case we will use AES GCM using a random 256-bit key (32 bytes).
- EdDSA. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) [2] can then build on this to includes signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use EdDSA to create a signature for a message.
- ECDSA. Go. In this case we will use ECDSA to create a signature for a message.
- HMAC. Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT. Go. In this case we create a CWT token, and sign with an HMAC signature.
- ECDH. Go. In this case we create a symmetric key from ECDH. For this we will derive a shared key from the public key of Alice and Bob, and then define a single recipient which can derive the CEK (Content Encryption Key) using their private key. We will use the curves of P-256 (secp256r1), P-384 (secp384r1), P-521 (secp521r1) or SECP256K1 (as used with Bitcoin).
- RSA using COSE and CBOR. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\).
- RSA: dQ, dP and InvQ. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). The key pair also includes \(dQ\), \(dP\) and \(InvQ\), and these can be used with the Chinese remainder theory to optimize the decryption process.
Metasploit
- Armitage and Metasploit. Go.
- Exploiting Android with Metasploit. Go.
- Exploiting Android with Metasploit - Part 2. Go.
- Exploiting Windows/Mac OS X with Metasploit. Go.
- Remote Desktop Windows/Mac OS X with Metasploit. Go.
- Metasploit. Go.
- Internet of Things Security. Go.
- Metasploit (Enumeration and Scanning). Go.
- Metasploit (Malware). Go.
IP

 The following are a few interesting techniques around IP addresses:
The following are a few interesting techniques around IP addresses:
- Your details. IP. This shows your browser details.
- IP address analyser. IP. This involves converting an IP address to the host and network part of the address.
- IP subnet analyser. IP subnets. This involves converting an IP address to the host and network part of the address.
- IP address analyser. IP. This involves analysing IP addresses.
- Max subnets. Max subnets. This involves converting an IP address to the host and network part of the address.
- Route summarization. Summarization. This involves converting an IP address to the host and network part of the address.
- Whois. Whois. This does a basic Whois on a domain.
- URL Obfuscation. Obfuscation. This outlines URL obfuscation.
- HTTP Responses. Test. HTTP.
- Capturing Network Packets (Python). WinPCap. HTTP.
Cisco related
- Routing table. Routing table. This involves viewing a routing table for a Cisco device.
- ACL Generator. ACL. This involves a simple calculator for ACLs on network ranges.
- EIGRP metrics. EIGRP. Learn the basics of EIGRP metrics.
- VoIP B/W. VoIP. Calculate bandwidth for VoIP.
- Wild Card. Wild Card. On a Cisco device a wildcard mask is used to identify the parts of an IP address that need to be matched. It thus uses a wildcard mask, where a 0 in the bit position identifies that the device should match that bit, else a 1 shows that it should ignore it.
Protocols
- HTTP. HTTP. Show the request and response for HTTP.
- Ping analyser. IP. This involves converting a ping of a site.
IP Challenges
-
IP Test 1. IP Test. IP Classification test. This is a simple test which generates a range of IP addresses, and you must determine the IP address classification.
IP Subnet Challenge 1 Demo
-
IP Test 2. IP Test. IP Classification test Part 2. This test provides an address classification, and the user must find the addresses which are of this classification.
IP Subnet Challenge 2 Demo
-
IP Test 3. IP Test. IP Classification test Part 3. This test provides an address classification, where the network part of the address is determined.
IP Subnet Challenge 3 Demo
Subnet Challenges
- Subnet Test 1. Subnet Test. Subnet Test.
-
Subnet Test 2. Subnet Test. Subnet bits.
- Subnet Test 3. Subnet Test. Find the nth usable subnet. This test involves finding the nth usable subnet.
- Subnet Test 4. Subnet Test. Maximum subnets. This is a test page to determine the maximum number of subnets and hosts/subnet for IP classed addressing.
- Subnet Test 5. Subnet Test. Maximum host/subnet. This is a test page to determine the maximum number of hosts per subnet.
- Subnet Test 6. Subnet Test. Determine the required subnet mask for a given number of subnets. This is a test page to determine the required subnet mask for a given number of subnets and a given IP address classification.
- Subnet Test 7. Subnet Test. Determine the required subnet mask for a given number of host/subnet. This is a test page to determine the required subnet mask for a given number of hosts per subnet and a given IP address classification.
- Subnet Test 8. Subnet Test. Route summarization. This involves a calculation on route summarization.
- Subnet Test 9. Subnet Test. Binary to IP.
- Subnet Test 10. Subnet Test. Hex to IP.
-
Subnet Test 13. Subnet Test. Wild card mask network bits. Find the number of bits in the network part of the wild card mask. IP Wildcard challenge
- Subnet Test 14. Subnet Test. Wild card mask host bits. Find the number of bits in the host part of the wild card mask. IP Wildcard challenge
- Subnet Test 15. Subnet Test. Wild card mask ... find the network address. Find the network for the wild card mask. IP Wildcard challenge 2
- Subnet Test 16. Subnet Test. Find a matching IP address for a network and wild card mask. Find the IP for a network and a wild card mask.
- Subnet Test 17. Subnet Test. Find an address which is on a given network. Find an IP address on a network, for a given network address and subnet mask.
- Subnet Test 18. Subnet Test. Find an IP address on the same network. Find an IP address on the same subnet.
- Subnet Test 19. Subnet Test. Find subnet. Convert subnet mask.
- Megatest. Subnet Test. Challenging test for subnets.
JavaScript

JavaScript code allows execution within the browser, rather than on the server. It is often faster than code that runs on a server. Along with this we can also use Node.js, and which runs JavaScript code on a server.
Symmetric key
- AES. AES. In this example, we will use either a pre-generated key or a random one, and use AES (Rijndael) encryption.
- ChaCha20 and Poly1305. ChaCha. This page outlines Poly1305 and ChaCha20. ChaCha20 is a symmetric key method and Poly1305 is a message authentication code (MAC). They were created by Daniel J. Bernstein, and are alternatives to AES and HMAC.
- CMS (Padding). CMS. This page uses PKIJS encrypting on CMS. With CMS we can This document describes the Cryptographic Message Syntax (CMS). With this we can encapsulate an message within an encrypted entity.

Hashing
- Hash. Hash. This page defines a JavaScript Hash calculator. This uses a client-side JavaScript code to determine the hash signatures of a text value.
Signatures
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
- Boneh–Lynn–Shacham (BLS) signature. BLS. Boneh–Lynn–Shacham (BLS) signature method produces short signatures. They use elliptic curve pairing (and which are also known as bilinear maps).
Key exchange
- ECDH. ECDH. Elliptic Curve Diffie Hellman (ECDH) is used to generate a shared key. This implementation uses Elliptic Curve Cryptography (ECC) with JavaScript.
CryptoJS
- CryptoJS. CryptoJS. This page uses client-side JavaScript code to hashing, encrypt and sign, including for symmetric key (AES), streaming ciphers, hashing methods, and HMAC.
Blockchain
- PATRICIA trie. PATRICIA. In the following, we have the Top 2,500 Web sites in the world, and implemented with a Radix Trie (aka PATRICIA trie) In the following we have the Top 2,000 web sites on the Internet, and which have been indexed using the PATRICIA trie.
Public key
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
- RSA. RSA. RSA is an asymmetric encryption algorithm, which uses two keys, one to encrypt and the other to decrypt. It was created in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman, and is still one of the most widely used encryption methods. A typical application is in authenticating a sender, where the senders private key is used to encrypt a message, and then is decrypted by the receiver with the senders public key (which is known to anyone who wants it). It is also typically used for encrypting disks/files, such as for EFS.
Digital Certificates
- X.509 certificates in JavaScript. RSA and ECDSA Signed certificates. This page will generate either RSA and ECC key pairs, and then generate X.509 certificates, using either a signature of SHA1withRSA or SHA256withECDSA. For RSA signing we use an RSA private key to sign the certificate, and with ECDSA signing we use an ECC private key to sign the certificate.
Tokens
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
Random
- Random number generator. Rand. In the past, encryption and decryption had to be done through native code libraries, such as with Bouncy Castle and OpenSSL. With the increasing processing power of Web browsers, it is now possible to use encryption using JavaScript, which thus provides client-side processing of data. This Web page uses Javascript encryption, and generates a random 256-bit text key or a hex version. The 256-bit key is generated by generating 60 random numbers (from 0-25), and converting these to an ASCII character.
Malware obfuscation
- Malware obfuscation. Obfuscation. A malware writer will often hide certain keywords from the browser/human by encoding them in another format. This is typically done for hex coding (\xZZ), 16-bit unicoding (\uZZZZ) and octal coding (\ZZZ). To test, enter a value, and then press the button and it will convert encoded string.
Message Authentication Codes
- Chaskey (MAC). Chaskey. Chaskey Cipher is light-weight cryptography method for signing messages (MAC) using a 128-bit key. The hardware implementation only requires 3,334.33 gate equivalent with an operating clock frequency of 1 MHz (whereas Keccak requires 4,658 GE). In the page we create the Mac signature and also encrypt for CBC.
Other
- Password generation/hashing. Hashing. Linux can use salted passwords where the username, hashing method and hashed password are stored in a password file [More details]. The main methods are
Hashing

At times we need to generate secrets, such as encryption keys, from passwords or nonce values. A Key Derivation Function (KDF) is a verifiable way of doing this.
Key Derivation Functions (KDFs)
The following are the tips related to hashing:
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Password strength. Test. This outlines the strength of various passwords types.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
HKDF
The following are the tips related to Key derivation hashing:
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Hazmat HKDF for different hashing methods. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
-
HKDF key derivation with OpenSSL [
here]
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
PBKDF2
The following are the tips related to Key derivation hashing:
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- AES GCM (Python) with PBKDF2. AES GCM (Python) with PBKDF2.
- Fernet with PBKDF2 . AES GCM (Python) with PBKDF2.
- PBKDF2 key derivation. AES GCM (Python) with PBKDF2.
- Key Rotation with Fernet. AES GCM (Python) with PBKDF2.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Bcrypt
The following are the tips related to Key derivation hashing:
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- BCrypt. BCrypt. BCrypt with Rust.
-
Hash to password with Go. Hashing to Argon2, Scrypt and BCrypt. Hash to password with Go, including Argon2, Scrypt and BCrypt.
scrypt
- scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Argon 2
The following are the tips related to Key derivation hashing:
- Argon 2. Go. Outline of Argon2.
- Argon 2 with NaCl. Go. Outline of Argon2 using NaCl.
- Argon 2. Argon 2. Argon 2 with Rust.
- Balloon. Go. Outline of Balloon.
Other
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
- Double ratchet. Go. Outline of double ratcheting.
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
Outline
HMAC Key Derivation function (HKDF) is used to derive an encryption key from a passphrase. Initially, HKDF creates a pseudorandom key (PRK) using a passphrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), and along with a salt value. Next, the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys [RFC 5869][article]. In this case, we will use SHA-256.
The following shows how an encryption key can be generated using HKDF, and where we need a secret and a salt value. Both Bob and Alice have the same secret and salt.

With PBKDF2 (Password Based Key Derivation Function 2), we hash for a given number of rounds:

Key exchange

Key exchange is a way for Bob and Alice to communicate and for them to agree on a shared secret. The original method defined uses discrete logarithms (Diffie-Hellman), but most modern methods use elliptic curve techniques (ECDH). As quantum computers can crack both discrete log and elliptic curve methods, there are post quantum cryptography methods proposed. This includes SIDH, CSIDH, SIKE, and NewHope.
Key interchange/generation (Diffie-Hellman)
The following relates to key interchange:
- Selecting \(g\) in Diffie Hellman. G in Diffie Hellman. Picking a safe value of the generator \(g\) in discrete logarithms.
- Diffie-Hellman. Diffie-Hellman Calculation. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Real example). Diffie-Hellman Real. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Python). Diffie-Hellman. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (pre-compute). Diffie-Hellman (pre-compute). Many sites use the same prime numbers, which can then be cracked with a pre-computing attack.
- Key generation. Key gen. This will generate keys for different methods based on a passphrase.
- Diffie-Hellman (Man-in-the-middle). DF. This outlines the man-in-the-middle method for Diffie-Hellman.
- An Alternative Diffie-Hellman method. Alterative DH. This outlines an alternative Diffie-Hellman method.
Authenticated Key Exchange
The following are the tips related to Key derivation hashing:
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- MTI/A0. MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{ax+by} \pmod p\). MTI (Matsumoto, Takashima, Imai).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0. MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{x+y} \pmod p\)
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). The resultant key is \(xyG \)
- MTI/C0. MTI/C0. This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{xy} \pmod p\)
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG\).
- MTI/C1. MTI/C1. This outlines MTI/C1, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{abxy} \pmod p\).
- MQV (Menezes–Qu–Vanstone). MQV. MQV was created Alfred Menezes, Minghua Qu and Scott Vanstone in 1995 and is an authenticated key exchange method. Alice holds a key pair \((A,a)\) and Bob has a key pair \((B,b)\). With this \(a\) is Alice's private key, and \(A=aG\) is her public key. For Bob, his public key will be \(B=aG\) and a private key of \(b\), and where \(G\) is the base point on the elliptic curve.
- HMQV (Menezes–Qu–Vanstone). HMQV. HMQV builds on MQV and adds the identity of Bob and Alice.
- ECDH with X25519 and Blake2b. ECDH with X25519 and Blake2b. This uses PyNaCl to create an authenticated key exchange and uses X25519 and Blake2b.
Elliptic Curve (ECDH) - Python
The following are the tips related to ECC:
- Elliptic Curve. Elliptic Curve. Elliptic Curve is a public key method which can also be used to generate a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with simple parameters. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
Elliptic Curve (ECDH) - Golang and Node.js
The following are the tips related to ECC:
- ECDH with Go. ECDH. ECDH with Go.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with node.js. ECDH. ECDH with node.js.
- ECDH with JavaScript. ECDH. Elliptic Curve Diffie Hellman.
Password Authenticated Key Exchange (PAKE)
The following are the tips related to Key derivation hashing:
- SPAKE2. Go. Outline of SPAKE2.
- OPAQUE. Go. Outline of OPAQUE.
- SPEKE. Go. Outline of SPEKE (Simple Password Exponential Key Exchange).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
- J-PAKE. J-PAKE. This example generates a shared key based on a shared password.
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses discrete logs.
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
PQC NIST Finalists (Key Exchange)
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Key interchange/generation (Other)

The following relates to key interchange:
- Curve25519. Curve25519. This outlines Curve25519, which is used in the Tor network.
- Authenticated Key Exchange (Discrete logs). YAK. Key exchange with public keys and uses discrete logs.
- Authenticated Key Exchange (ECC). YAK. Key exchange with public keys and uses elliptic curve methods.
- Shamir No-key protocol. Shamir No Key. In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated.
- Shamir No-key protocol (sepc256k1). Shamir No Key (EC). In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated using the sepc256k1 elliptic curve.
- Conference keying (Burmester-Desmedt method). Conference keying. In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it.
- Conference keying (Burmester-Desmedt method) - Elliptic Curve (sepc256k1). Conference keying Elliptic Curve (sepc256k1). In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it, and uses the sepc256k1 elliptic curve.
Key exchange (with pairing)
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Kryptology

We need to build a new Internet. One that is build on mathematics and certainty, rather than the patchy version we have now. For this we need a layer of cryptography at the lowest level, and build software interfaces on top of this. Along with this we now have cryptographic methods which can now provide a foundation of trust, and which preserve privacy. And so the old libraries of OpenSSL are being squeezed out in favour of the new ones which are built on a solid foundation. The latest of these new "privacy-aware" libraries is Kryptology, and created by Coinbase. This library provides the APIs that developers need, in order to apply to areas of blockchain development. This library include BLS (Boneh-Lynn-Shacham) signatures, Zero-knowledge Proofs (ZKPs) and Shamir Secret Shares (SSS). With BLS we can digitally sign for data, but also preserve its privacy. Applications of this include group signatures, where multiple entities can merge their signing keys together and provide a single signature for a transaction. With SSS, we can split encryption keys up into shares, and then distribute them across a network. When required, we can call these shares back to reconstruct the key.
The focus for Coinbase seems to be the application of privacy coins, and where no tracking can be applied to the usage of these digital coins. This should support full anonymity for transactions, as opposed to Bitcoin which only supports pseudo-anonymity.

ECC Basics
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining n.G for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Points (Base Point and Others). Elliptic Curve points. Two common curves used in ECC (Elliptic Curve Cryptography) are secp256k1 (as used in Bitcoin and Ethereum) and P256 (secp256r1). The "k1" refers to the Kolbitz curve 1 (named after the creator of ECC). With these we have a base point which are can operate on. This is typically defined as \(G\). We can then operate on this with add and multiply operation. For example, \(2G=G+G\) and \(P=n.G\). In this following we will show the base point for a number of common curves, such as secp256r1, P256, Pallas, Curve 25519, BLS12381G1, BLS12381G2, BLS12377G1 and BLS12377G2.
ECDH
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret. We will use Golang and the Krytology library.
Simple ECC on curves
- Public key points for curves. Simple. Display public key points for scalars.
BLS Curve
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
Accumulator and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
Pallas Curve
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
Pairing-based Crypto
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
ElGamal and ECC
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a numerical input.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
Shamir Secret Shares
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Homomorphic Encryption
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Zero knowledge proofs
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
Verifiable Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Hash to scalar and point
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
CP-ABE
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Lattice cryptography

Latice cryptography is proposed as a post-quantum robust method for public key encryption, especially focused on digital signatures and key exchange mechanisms (KEMs).
Principles
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
NTRU
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- Lattice Encryption: NTRU Key Generation Python). NTRU. Outlines how NTRU operates for key generation.
Homomorphic
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Digital Signatures
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
Public-Key Encryption/Key Exchange
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
Light-weight cryptography

While AES and SHA work well together within computer systems, they struggle in an IoT/embedded world as they take up: too much processing power; too much physical space; and consume too much battery power. So NIST outlines a number of methods which can be used for light-weight cryptography, and which could be useful in IoT and RFID devices [1]. They define the device spectrum as:
- Conventional cryptography. Servers and Desktops. Tablets and smart phones.
- Light-weight cryptography. Embedded Systems. RFID and Sensor Networks.
With embedded systems, we commonly see 8-bit, 16-bit and 32-bit microcontrollers, and which would struggle to cope with real-time demands for conventional cryptography methods. And in the 40+ years since the first 4-bit processor, there is even a strong market for 4-bit processors. RFID and sensor network devices, especially, have limited numbers of gates available for security, and are often highly constrained with the power drain on the device.
So AES is typically a non-starter for many embedded devices. In light-weight cryptography, we often see smaller block size (typically 64 bits or 80 bits), smaller keys (often less than 90 bits) and less complex rounds (and where the S-boxes often just have 4-bits).
For light-weight cryptography the main constraints that we have are typically related to ener requirements, gate equivalents (GEs), and timing. With passive RFID devices, we do not have an associated battery for the power supply, and where the chip must power itself from energy coupled from the radio wave. An RFID device is thus likely to be severely constrained in the power drain associated with any cryptography functions, along with being constrained for the timing requirements and for the number of gates used. Even if an RFID device has an associated battery (active RFID), it may be difficult to recharge the battery, so the drain on power must often be minimised.
There is thus often a compromise between the cryptography method used and the overall security of the method. Thus often light-weight cryptography methods balance performance (throughput) against power drain and GE, and do not perform as well as main-stream cryptography standards (such as AES and SHA-256). Along with this the method must also have a low requirement for RAM (where the method requires the usage of running memory to perform its operation) and ROM (where the method is stored on the device). In order to assess the strengths of various methods we often define the area that the cryptography function will use on the device – and which is defined in \(µm^2\). The NIST finalists are defined in this [article]
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- GIFT AEAD. GIFT. GIFT is a light-weight block cipher. It is a (NIST Finalist)
- Elephant. Elephant. Elephant is a light-weight stream cipher. It is a (NIST Finalist).
- TinyJambu. TinyJambu. TinyJambu is a light-weight block cipher. It is a (NIST Finalist)
- Isap AEAD. Isap. Isap is a light-weight block cipher. It is a (NIST Finalist)
- PHOTON-Beetle AEAD. PHOTON-Beetle. PHOTON-Beetle is a light-weight block cipher. It is a (NIST Finalist)
- Romulus AEAD. Romulus. Romulus is a light-weight block cipher. It is a (NIST Finalist)
- Sparkle AEAD. Sparkle. Sparkle is a light-weight block cipher. It is a (NIST Finalist)
- CLEFIA. CLEFIA. CLEFIA is a light-weight block cipher.
- LED. LED. LED is a light-weight block cipher.
- Piccolo. Piccolo. Piccolo is an ultra light-weight block cipher.
- PRESENT. PRESENT. Present is a light-weight block cipher.
- Pyjamask. Pyjamask. Pyjamask is a light-weight block cipher.
- SIMON. SIMON. SIMON is a light-weight block cipher.
- SKINNY. SKINNY. SKINNEY is a light-weight block cipher.
- SPECK. SPECK. SPECK is a light-weight block cipher.
- XTEA. XTEA. XTEA is a light-weight block cipher.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encryption/Decryption. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.
Light-weight crypto (Other)
- Chaskey (MAC). Chaskey. Chaskey is a light-weight MAC function.
- Chaskey (MAC). Chaskey (Python). Chaskey is a light-weight MAC function.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (ASCON)
ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRFF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
Discrete Logs (Solving)

A discrete log problem is in the form of \(g^x \pmod p\) and where we know \(g\) and \(p\) and must solve for \(x\).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Message Authentication Code (MAC)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
HMAC
The following are the tips related to Key-based hashing:
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authentication both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2), Blake2b, SM3 and SHA-3. This page outlines the HMAC-MD5 methods using the Hazmat cryptography layer.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- HMAC (COSE). Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT with HMMAC. Go. In this case we create a CWT token, and sign with an HMAC signature.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- HMAC with Rust. HMAC. HMAC with Rust.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HMAC with OpenSSL. MACs with OpenSSL. HMAC in OpenSSL for a given input value, password and hashing method.
Cipher MACs
The following are the tips related to Key-based hashing:
- MACs with OpenSSL. MACs with OpenSSL. MAC methods implemented in OpenSSL, including CMAC and GMAC.
Key-based hashing
The following are the tips related to Key-based hashing:
- SipHash. Siphash. Siphash is a fast key-based hashing method.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Meow. Meow. Meow is one of the fastest hashing methods.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
Magic Numbers

This pages contains information related to magic numbers in file formats.
Network and File Forensics
- Magic numbers. Magic. This provides information on magic number for file forensics.
Graphics formats
- JPEG Analysis. JPEGs. This provides an analysis of JPEG files.
- GIF Analysis. GIFs. This provides an analysis of GIF files.
- TIF Analysis. TIFs. This provides an analysis of TIF files.
- PNG Analysis. PNGs. This provides an analysis of PNG files.
- BMP Analysis. BMPs. This provides an analysis of BMP files.
- PSD Analysis. PSDs. This provides an analysis of PSD files.
- WMF Analysis. WMF. This provides an analysis of WMF files.
- Adobe Illustrator Analysis. AI. This provides an analysis of AI files.
- Adobe In Design Analysis. INDD. This provides an analysis of INDD files.
- MIDI file. MIDI. This provides an analysis of MID files.
- ICO file. ICO. This provides an analysis of ICO files.
- PS file. PS. This provides an analysis of PS files.
- EPS file. EPS. This provides an analysis of EPS files.
- VSD file. VSD. This provides an analysis of Microsft Visio (VSD) files.
Video and audio formats
- MP3 Analysis. MP3s. This provides an analysis of MP3 files.
- AVI Analysis. AVIs. This provides an analysis of AVI files.
- Flash SWF Analysis. SWFs. This provides an analysis of Flash files.
- Flash FLV Analysis. FLVs. This provides an analysis of FLV files.
- MP4 Analysis. MP4. This provides an analysis of MP4 files.
- MOV Analysis. MOV. This provides an analysis of MOV files.
- WMV Analysis. WMV. This provides an analysis of WMV files.
- WMA Analysis. WMA. This provides an analysis of WMA files.
- JPEG 2000 Analysis. JPEG 2. This provides an analysis of JPEG 2000 files.
- WAV Analysis. WAV. This provides an analysis of WAV files.
Zips, Archives and Library files
- ZIP/Archive Analysis. ZIPs. This provides an analysis of ZIP/Achive files.
- GZ Analysis. GZ. This provides an analysis of GZip files.
- Tar Analysis. Tar. This provides an analysis of TAR files.
- MSI Analysis. MSI. This provides an analysis of MSI files.
- OBJ Analysis. OBJ. This provides an analysis of OBJ files.
- DLL Analysis. DLL. This provides an analysis of DLL files.
- CAB Analysis. CAB. This provides an analysis of CAB files.
- EXE Analysis. EXE. This provides an analysis of EXE files.
- RAR Analysis. RAR. This provides an analysis of RAR files.
- SYS Analysis. SYS. This provides an analysis of SYS files.
- HLP Analysis. HLP. This provides an analysis of HLP files.
- VMDK Analysis. VMDK. This provides an analysis of VMDK files (VMWare Virtual Disks).
- PST Analysis. PST. This provides an analysis of PST files (Outlook Email File).
- JAR Analysis. JAR. This provides an analysis of JAR files.
- SLN Analysis. SLN. This provides an analysis of Microsoft SLN files.
- Class Analysis. Class. This provides an analysis of Java Class files.
- Zlib. Zlib. This provides an analysis of Zlib files.
Documents
- PDF Analysis. PDFs. This provides an analysis of PDF files.
- DOC Analysis. DOCs. This provides an analysis of DOC files.
- RTF Analysis. RTFs. This provides an analysis of RTF files.
- XLS Analysis. XLSs. This provides an analysis of XLS files.
- PPT Analysis. PPTs. This provides an analysis of PPT files.
- MMP File. MMP. This provides an analysis of MMP files.
- DOCX Analysis. DOCX. This provides an analysis of DOCX files.
- XLSX Analysis. XLSX. This provides an analysis of XLSX files.
- PPTX Analysis. PPTX. This provides an analysis of PPTX files.
- MDB Analysis. MDB. This provides an analysis of MDB files.
- Outlook Message Analysis. MSG. This provides an analysis of MSG files.
Disk Image
- Raw disk format. RAW. This provides an analysis of the RAW disk format.
Tests
- File Forensics Test. File Test File Forensics Test.
- File Forensics Test (Fun). File Test (Fun) File Forensics Test.
Presentations
MIRACL Core Library

MIRACL Core is an open source library, and includes a wide range of public key encryption methods. It is especially focused on elliptic curve and pairing-friendly methods, but also supports a wide range of encryption methods, including RSA, AES and hashing. Overall, it can be ported onto a wide range of systems and supports C, C++, Go, Rust, Python, Java, Javascript and Swift. Along with this it supports limited capability devices such as the Arduino infrastructure. The GitHub repository is [here].
BN254
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.

Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- CL Signatures. CL. CL Signatures in Go using MIRACL.
- CL Signatures (advanced pairing). CL. CL Signatures in Go using MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages using MIRACL.
- PS Signatures. PS. Signatures using PS for short signatures using MIRACL.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures using MIRACL.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.

Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
Rust examples
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
NaCl

PyNaCl is a Python port of LibSodium. It integrates the latest cryptography methods, such as AES, XChaCha20, Blake2b and X25519.
Symmetric Key
- Symmetric key. Symmetric key (XChaCha20 and Poly1305). With symmetric key, Bob and Alice have the same key. NaCl uses the XChaCha20 method, and which supports stream encryption (and which does not require padding as a block cipher does, and is also faster than block cipher modes). ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16 byte nonce. XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24 byte nonce. It has a lower propability of nonce misuse than ChaCha20.
- Encryption with a password. Symmetric Key with KDF. In symmetric key, we generate a secret key. This key is typically a random value or generated from a password and a salt value. If we use a password, we typically use a KDF (Key Derivation Function), and which uses a password and a salt value, in order to create a key of a given size. In this case we will use Argon2i, and which is memory resilent.
Hybrid Encryption
- Box. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Hashing
- Hashing and KDF (Argon2 and scrypt). Hashing and KDF. This case we will use PyNaCl (Networking and Cryptography) library, and which is a Python binding to libsodium. We will hash a password using SHA-256 and SHA-512, and also create a KDF (Key Derivation Function) using scrypt and Argon2.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
Ed25519
-
Ed25519. Ed25519. Using Ed25519 for digital signatures.
-
Finding Points on Ed25519. X25519 (Points).
In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 (Key Exchange)
- X25519 + BLAKE2b key-exchange. X25519. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
Curve 25519
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
Node.js

Node.js uses the JavaScript programming langauge as its base, and allows for code to be run on a server, rather than in the browser (such as with pure JavaScript). To run a node.js program, we run "node myfile.js", and use NPM to install libraries.
Symmetric key
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
RSA and public key
- RSA Opt imal Asymmetric Encryption Padding (OAEP) using Node.js. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
ECC Keys
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.

Hashing
- Hashing with node.js (All). Hashing. Hashing with node.js.
- Hashing with node.js (Selection). Hashing. Hashing with node.js.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- ECDSA with node.js. ECDSA. ECDSA with node.js.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
Key exchange
- Diffie-Hellman with node.js (random prime). DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method and uses a randomly generated prime number (press the button to generate a new prime).
- Diffie-Hellman with node.js. DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method. Each time the prime number will be fixed for the DH group selected.
- ECDH with node.js. ECDH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Elliptic Curve Diffie Hellman (ECDH) key exchange method.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
Key derivation
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
CryptoJS
- CryptoJS (in node.js). CryptoJS (Node.js). Various crypto methods in the browser.
Bulletproofs
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
Blockchain
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
Proxy encryption
- Proxy Encryption - Encrypting With Public Key, And Decrypt with Private Key. Proxy01. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This page just creates a key pair for Alice, and uses it to encrypt with the public key , and decrypt with the private key.
- Proxy Encryption. Proxy02. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This will go through the full use case of proxy re-encryption.
Tokens
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
Random
- Fortuna with node.js. Fortuna. Fortuna random numbers with node.js.
Other
- FPE with node.js. FPR. FPE with node.js.
- Puny with node.js. Puny. Puny character format with node.js.
Accumulators and Witnesses
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
PGP
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Password Entropy
- Password Entropy with Node.js. Password Entropy. Password entropy measures the strength of a password, and is measured as the number of bits which could represent all of the possibilities. An entropy score of less than 25 identifies a poor password, and between 25 and 50 is a weak password. For 50 to 75 we have a reasonable password, and between 75 and 100 is a very good password. Over 100 is an excellent password. The strength of the password relates to the number of characters used, and also the number of characters in the password.
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
- Homomorphic Encryption with Node.js and BGV. Homomorphic Encryption with Node.js and BFG. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BGV method.
Oblivious Transfer (OT)

Oblivious Transfer allows Bob to select data from Alice, but for Alice not to know which value has been selected.
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
OpenSSH

OpenSSH supports the usage of the SSH protocol. This allows for a remote login. One tool which is uses is ssh-keygen, and which allow for the generation of RSA, DSA and elliptic-curve keys that. These can be used for user and host authentication, such as for GitHub login and Cloud instance login.
OpenSSH
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here].
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
Outline

OpenSSL

OpenSSL is a standard library that implements cryptography.
Symmetric key (Command line)
-
Symmetric Key Encryption (OpenSSL 1.x) [here]. In this case we will create cipher text from OpenSSL 1.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 1.x) [here].In this case we will decrypt cipher text from OpenSSL 1.x using a key derived from a password
-
Symmetric Key Encryption (OpenSSL 3.x) [here]. In this case we will create cipher text from OpenSSL 3.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 3.x) [here].In this case we will decrypt cipher text from OpenSSL 3.x using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password.
Hashing
-
Hashing [here] OpenSSL supports a wide range of hashing methods including BLAKE2b, Gost, MD4, MD5, RMD-160, SHA-1, SHA-3, SHA-256 and SHA-512.
Libre OpenSSL
-
Symmetric Key Encryption using Libre OpenSSL [here]. In this case we will create cipher text from Libre OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption using Libre OpenSSL [here]. In this case we will decrypt ciphertext from Libre OpenSSL using a key derived from a password.
-
Hashing [here] Libre OpenSSL supports a wide range of hashing methods including Gost, MD4, MD5, RMD-160, SHA-1, SHA-256 and SHA-512.
Diffie-Hellman parameter generation
-
DH Parameters with OpenSSL [here]. The Diffie-Hellman (DH) method is perhaps one of the greatest inventions in Cybersecurity, and was created by Whitfield Diffie and Marty Hellman. With the DH method, Bob creates a random value (\(b\)) and Alice also creates a random value (\(a\)). Next Bob computes \(B=g^b \pmod p\) and sends it to Alice. Alice computes \(A=g^a \pmod p\) and sends this to Bob. Bob raises the value of \(A\) to the power of \(b\) and takes \(\pmod p\), and Alice raises \(B\) to the power of \(a\) and takes \(\pmod p\). In the end, they will have the same shared value: \(g^{ab} \pmod p\). This can then be used to derive an encryption key that they can use for a secure tunnel. Overall, \(p\) is the large prime number, and also known as the shared modulus between Bob and Alice.
Key derivation function
-
PBKDF2 key derivation with OpenSSL [here] PBKDF2 (Password Key Derivation Function 2) is a key derivation method. Overall it is relatively slow in its operation and where we take a password, a salt value, hashing method, and a number of iterations, in order to produce a given size of encryption key.
-
HKDF key derivation with OpenSSL [here] HKDF (HMAC Key Derivation function) is used to derive an encryption key from a pass phrase. Initially HKDF creates a pseudorandom key (PRK) using a pass phrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), andalong with a salt value. Next the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys.
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Passwords
-
Password example [here]. This page uses the OpenSSL library hash password generator, which is used in UNIX systems for the hashing of passwords which are contained in /etc/shadow and /etc/passwd. For newer passwords, the "-1" options is used to created the hashed value.
-
Hashed passwords with OpenSSL [here].
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
Public key
-
Generating an ECC key pair with OpenSSL [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)).
-
Generating an RSA key pair with OpenSSL [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2).
-
Generating an RSA key pair with OpenSSL with encryption [here]. This page implements RSA key pair generation with an encrypted key pair. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). In this case we will encrypt the key pair with either 3DES, 128-bit AES, 192-bit AES or 256-bit AES. The same password must be used to encrypt and decrypt.
-
Generate prime with OpenSSL [here]. Prime numbers are important in public key encrytion, and are used with RSA and ECC. For RSA, we generate two prime numbers (\(p\) and \(q\)) and which are multiplied together to create a modulus (\(N\)). If these prime numbers have 512 bit values, the modulus will be a 1,024 bit value. This defines the basic secure of RSA. With elliptic curve we use smaller prime numbers, such as 256-bit values for the secp256k1 curve.
ASN1 parsing
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). We will parse using asn1parse, and reveal the parameters.
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)) [RSA key pair]. We will parse using asn1parse, and reveal the parameters.
- DSA Parameters with asn1parse. DSA parameters with OpenSSL with asn1parse. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA (Digital Signature Algorithm)
- DSA Parameters. DSA parameters with OpenSSL. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
MAC (Message Authentication Code)
- HMAC with OpenSSL. MACs with OpenSSL. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authenticate both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2) and SHA-3. In this case we will use OpenSSL to generate the HMAC value.
- MACs with OpenSSL. MACs with OpenSSL. In the following we will generate MACs for HMAC, GMAC, CMAC, Blake2bmac, Blake2smac, KMAC128 and KMAC256. Overall, we will use an encryption key defined as a hex value for GMAC and CMAC, and a pass phrase for the others. The message is "hello".
Signing
- Digital signing a plaintext message with OpenSSL. Signing with OpenSSL. With digital signing, we can take a message, and create a signature. This normally involves signing with a private key and digital certificate. The signed message can be an a MIME format, and which can be integrated into an email message. In this can we have a 512-bit RSA key pair that will sign a plain text message.
Encrypting emails
- Encrypting an email message in OpenSSL. Encrypting messages with OpenSSL. With public key encryption, we can take a message, and encrypt it with the recipiant's public key. In this can we have a 512-bit RSA public key to encrypt a message.
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Random number generation with OpenSSL
-
Random number generator [here]. Random numbers are important in generating encryption keys and salt values. In this case OpenSSL generates a random number (in a Base64 format) for a given number of bytes.
Outline (C#/Python)
-
Symmetric Key Encryption (C#) [here]. This page uses the OpenSSL library through a C#/.NET wrapper. The DLLs it interfaces to are libeay32.dll and ssleay32.dll. OpenSSL supports a wide range of encryption methods, including 128-bit AES, 192-bit AES, 256-bit AES and Blowfish (bf). Different modes of ECB, CBC, and OFB are implemented. The examples use a default IV of "1234".
-
AES in Python with OpenSSL output [here]
-
Producing OpenSSL AES Encrypted String from C# [here]
Digital Certificates
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
Paillier - Partial Homomorphic Encryption

The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Fundamentals
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier).
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Using RSA
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
Applications
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
NaCl
- Ed25519 signature using NaCl. eddsa. This page uses the NaCl port from libsodium.
- Ed25519 points using NaCl. eddsa. This page uses the NaCl port from libsodium to determine Ed25519 points.
Theory
With EdDSA, Alice will sign a message with her private key, and then Bob will use her public key to verify that she signed the message (and that the message has now changed):

Key generation
Alice generates a random 32-byte secret key (\(sk\)) and then creates a public key of:
\(pk=sk \cdot G\)
and where \(G\) is the base point of the curve.
Signing
Alice creates a SHA-512 hash of her private key:
\(h=\textrm{HASH}(sk)\)
Create \(r\) from the upper 32 bytes of hash and the message:
\( r = \textrm{HASH}(h[32:] \: || \: m))\)
And where "||" represents a concatenation of the byte array values. Next she matches \(r\) onto curve with:
\(R=r \cdot G\)
Next Alice computes \(s\) with:
\(s=r + (\textrm{HASH}(R \: || \: pk \: || \: m)) \cdot sk\)
The signature is (\(R,s\)). The values of \(R\) and \(s\) are 32 bytes long, and thus the signature is 64 bytes long.
Verifying
Bob creates \(S\) using \(R\), \(pk\) and \(m\):
\(S =\textrm{HASH}(R \: || \: pk \: || \: m) \)
And next creates two verification values:
\(v_1=s \cdot G\)
\(v_2=R+ pk \cdot S\)
If \(v_1==v_2\) the signature checks. This is because:
\(
\begin{align}
v_1&=s.G\\
&= (r + (\textrm{HASH}(R \: || \: pk \: || \: m)) \cdot sk) \cdot G \\
&= rG + sk \cdot G \cdot (\textrm{HASH}(R \: || \: pk \: || \: m)) \\
&= R+ pk \cdot S \\
&= v_2
\end{align}
\)
ElGamal

Public key encryption is typically used to sign for things (and where we use the private key to encrypt something and prove this with the public key) and within key exchange methods. The core methods used are RSA and Elliptic Curve. But an alternative is to use discrete logarithms. One of the most interesting is ElGamal, and was created by Taher Elgamal in 1985.
ElGamal Method
- ElGamal. ElGamal. ElGamal is a public key method which uses discrete logarithms.
- ElGamal in Python. ElGamal in Python. ElGamal is a public key method which uses discrete logarithms.
- ElGamal in Python with variable prime sizes. ElGamal in Python for different prime sizes. ElGamal is a public key method which uses discrete logarithms.
- Selecting g in ElGamal. G in ElGamal. ElGamal is a public key method which uses discrete logarithms.
- Selecting g in discrete logs. g in discrete logs. This select a generator in discrete logs.
- Selecting g in discrete logs with random primes. g in discrete logs with random primes. This select a generator in discrete logs using random prime numbers which are define by a number of bits.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- Proving an Encrypted Shuffle With ElGamal and ECC. Shuffle. An encrypted shuffle with ElGamal.
- ElGamal encryption with Powershell. ElGamal encryption.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Commutative Encryption
- Commutative Encyption (Modified ElGamal). Commutative Encyption. Commutative Encyption allow Bob and Alice to encrypt a message, and then for the data to be decrypted usign any order of the keys.
ElGamal Signature
- ElGamal signatures. ElGamal. ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this.
- ElGamal signatures (alterative signing). ElGamal (Signing: s=ar + kh(m)). ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this. Normally we sign with \(s=k^{-1} (h(m)-ar) \pmod {p-1}\), but in this case we will use \(s=ar + kh(m))\).
- ElGamal signatures (alterative signing). ElGamal (Signing: s=ah(m) + kr). ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this. Normally we sign with \(s=k^{-1} (h(m)-ar) \pmod {p-1}\), but in this case we will use \(s=ah(m) + kr\).
- ElGamal signatures (alterative signing). ElGamal (Signing: r=as+kh(m)). ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this. Normally we sign with \(s=k^{-1} (h(m)-ar) \pmod {p-1}\), but in this case we will use \(r=as+kh(m)\).
- ElGamal signatures (alterative signing). ElGamal (Signing: r=ah(m) +ks). ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this. Normally we sign with \(s=k^{-1} (h(m)-ar) \pmod {p-1}\), but in this case we will use \(r=ah(m) +ks\).
- ElGamal encryption with Go. ElGamal. This implements ElGamal encryption.
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
ElGamal Homomorphic Encryption
- ElGamal Homomorphic Cipher for Multiplication (Python). ElGamal. This outlines ElGamal Homomorphic multiplication with Python.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (Python). ElGamal. This outlines ElGamal Homomorphic division with Python.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (Python). ElGamal. This outlines ElGamal Homomorphic addition with Python.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (Python). ElGamal. This outlines ElGamal Homomorphic subtraction with Python.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
- ElGamal Homomorphic Cipher (Go). ElGamal. This outlines ElGamal Homomorphic cipher with Go.
- ElGamal Homomorphic Cipher (Go) - Divide. ElGamal. This outlines ElGamal Homomorphic cipher with Go with divide.
- ElGamal Homomorphic Cipher (Go) - Additive. ElGamal. This outlines ElGamal Homomorphic cipher with Go with addition.
ElGamal and ECC
- ElGamal with ECC. ElGamal with ECC. ElGamal using ECC.
- Proving an Encrypted Shuffle With ElGamal and ECC. Shuffle. An encrypted shuffle with ElGamal.
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- ElGamal - Applying Multiple Public Key Operations (ECC). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use elliptic curve methods, and using the Edwards 25519 curve.
ElGamal (Authenticated and Verified Encryption)
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenticated ciphertext.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
ElGamal (Encrypting with multiple public keys)
- ElGamal - Applying Multiple Public Key Operations (Discrete Logs). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use discrete logs.
- ElGamal - Applying Multiple Public Key Operations (ECC). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use elliptic curve methods, and using the Edwards 25519 curve.
Ethereum

This page outlines some examples of blockchain and cryptocurrency.
Test Network
- Math functions on Local Network. Go.
- Math functions on Test Network. Go.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- Storing State in a Smart Contract. Go.
- Deleting Data From A Smart Contract. Go.
- A Caesar Cipher Quiz Generator from a Smart Contract. Go.
- Hashing in a Smart Contract. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
- Dealing With Decimals In Smart Contracts. Go.
- Creating A Scrambled Alphabet Challenge Generator In Ethereum and Solidity. Go.
- Deploying a Scrambled Alphabet Generator To Ethereum (With Ganache and Ropsten). Go.
- Deploying a Scrambled Alphabet Generator To Ethereum (With Hardhat). Go.
- Pigpen, IPFS and Ethereum. Go.
- Proof of \(x\) from \(H(x)\) using zkSnarks. Go.
- Elliptic Curve Operations Within a Solidity Contract. Go.

Ethereum
- Creating Ethereum address with Python. Go.
- Creating Ethereum signing with Python. Go.
- ERC20 Tokens. Go.
- Ethereum address with Go. Addresses. This generates an Ethereum address.
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- PATRICIA trie. PATRICIA. Example of using PATRICIA (and which is used in Ethereum).
- Viewing Balance of account in Etheruem with Go. Balance. This views the balance of an account
- Viewing Block in Etheruem with Go. Block. This views a block.
- Viewing Cryptocurrency API with Python. Go.
- Viewing Ethereum blockchain with Python. Go.
- Viewing Transactions in Block in Etheruem with Go. Transactions. This views transactions.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
- Symmetric Key Encryption For Smart Contracts. Symmetric key. Solidity does not natively support symmetric key encryption, such as with AES. Overall, AES would consume too much gas and thus be expensive to implement. But, we can use hashing and X-OR methods to do the encryption. In this case, we will create a 256-bit random value, and then encrypt it with an encryption key, and then decrypt it.
Calling from Python
- Calling smart contracts with Python. Python.
Ethereum crypto
- ECIES with Go-Ethereum. Go.
Ethereum Blockchain
- IOTA Trytes. Trytes. `This outlines Trytes, as used in IOTA.
Ethereum Blockchain
- Blockchain: Adding Maths Functions. Go.
- Blockchain: Blocks, transactions and writing data. Go.
- Blockchain: Contracts and Addresses. Go.
- Blockchain: Getting transactions. Go.
- Blockchain: Hello World!. Go.
- Blockchain: Simple Purchasing System. Go.
- Blockchain: Viewing the blockchain. Go.
- Blockchain: Cracking Wallets. Go.
- Introduction to Blockchain. Go.
Presentations
Factorization

Many public key problems involve the difficulity in factorizing a value two its prime number factors. For example, in RSA, we have a public modulus \(N\) and which is equal to the multiplication of two prime numbers \(p\) and \(q\). If we can factorize the public modulus, we will be able to break the RSA cipher related to it.
RSA Crack
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA Factorization. RSA. This outlines the factorisation of the N value in the RSA method.
Methods
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Dixon. Go. Dixon Method.
- Rho factorization. Rho. Rho alogorithm.
- Smooth numbers. Go. Outline of smooth numbers.
Methods (Elliptic curve
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Quadratic residues
- Quadratic residue (mod p). Go. Outline of quadratic residue \(\pmod p\).
- Quadratic residue (mod p) using Legendre symbol. Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
Factorizing
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
Lenstra–Lenstra–Lovász (LLL) with lattices
- Crack ECDSA with weak nonces. ECDSA with weak nonces and using Lenstra–Lenstra–Lovász (LLL) method. This outlines ECDSA how the private key can be recovered with weak nonce values.
Network Forensics

These pages outlines some network forensics. This includes the understanding of the network stack, and with protocols such as Etherenet, IP, TCP, HTTP, and others.
Network Forensics (Theory)
- Network Forensics (Wireshark). Network Forensics. This provides information on how to detect threats through network forensics with Wireshark.
- Advanced Network Forensics. Network Forensics. This provides information on how to detect threats through network forensics.
Network Forensics (Practice)
- Advanced Network Forensics (Wireshark). Adv Network Forensics. This provides information on how to detect threats through network forensics with Wireshark.
- Network Forensics (PCAP). Network Forensics. This provides information on network forensics (reading PCAP files)
- Network Forensics (Text). Network Forensics. This provides information on network forensics (reading text files)
Tshark
-
Filters with TShark. TShark. This page runs Tshark with a given Pcap file and a defined filter.
Other
- Advanced Digital Forensics . Adv Digital Forensics. This provides information on how analyse disk based systems using open source forensics.
- Partition Analyser. MBR. This page will analyse the details of the partition details within the MBR (put one space between fields).
Presentations
Format Preserving Encryption

Format Preserving Encryption (FPE) is a method which allows the basic formatting of a message to stay in a similar format, and where the value itself is encrypted. It can be used to hide credit card details.
Methods
- Format Preserving Encryption. FPE. This outlines Format Preserving Encryption.
- FPE with Python. FPE. An implementation of Format Preserving Encryption (FPE) using Python.
- FPE with node.js. FPR. FPE with node.js.
- FPE and PKBKDF2 in Python. FPE and PKBKDF2 in Python. FPE using PKBDF2 to password generation.
FFX (Format-preserving, Feistel-based encryption)
- FPE with Go. FPE. An implementation of Format Preserving Encryption (FPE) for FFX1 and FFX3.
- FFX schemes. FFX. Within tokenization we can apply format preserving encryption (FPE) methods, which will convert our data into a format which still looks valid, but which cannot be mapped to the original value. For example, we could hide Bob's credit card detail into another valid credit card number, and which would not reveal his real number. A tokenization server could then convert the real credit card number into a format which still looked valid. For this we have a key which takes the data, and then converts it into a form which the same length as the original.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher in Python.
FFX in Rust
- FFX. FFX. This is an implementation of FFX in Rust.
Honey Encryption
- Honey Encryption. Honey. This outlines Honey encryption.
Crypto Principles

This page outlines some crypto principles.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Galois fields (polynomial operations)

This page outlines a few basic principles around the usage of Galois fields and polynomial operations. In 1832, Évariste Galois died of duelling wounds at the age of 20 but left a great legacy. While he was a teenager he worked on polynomials and laid down the principles of Galois theory, along with defining the concept of a finite field. In cryptography, the finite field is one of the major concepts and involves limiting the number of possible values to a limiting factor (\(p\)). The values of the field then range from 0 to p-1. Within a field, we can operate on values in the field using arithmetic operations. We can thus have an infinite field, and where we could include all of the possible integers. A finite field or Galois field of GF(\(2^n\)) has \(2^n\) elements. If \(n\) is four, we have 16 output values. Let’s say we have a number \(a∈{0, ... ,2^{n−1}}\), and represent it as a vector in the form of a polynomial:
\( a=a0+a_1 x+a_2 x^2 ... a_{n−1} x^{n−1}\)
If we use \(a_n∈{0,1}\), this is exactly the same as representing a binary number modulo \(2^n\). In this \(x^n\) represents bit position \(n\) and \(a_n\) is the value of the bit at position \(x^n\). If a bit is a zero at a given position, it will be not included in the polynomial equation. So, 1011 can be represented by \(x^3+x+1\) and 1010 is represented as \(x^3+x\). We can then perform arithmetic operations on these polynomial values. So, to add two values of 1010+1100 we can represent this as \((x^3+x)+(x^3+x^2)\) and which is \(x^2+x\) as we are using modulo 2 addition, and where \(x^3+x^3=0\). With modulo 2 addition, 0+0=0, 0+1=1, 1+0=1, and 1+1=1.
An example of Galois Fields is within AES (Advanced Encryption Standard) and which uses a finite field GF(\(2^8\)). With AES we operate on bytes (8 bits) in the form of \(b_7 b_6 b_5 b_4 b_3 b_2 b_1 b_0\) and which are operated on a a polynomial of \(b_7x^7+b_6x^6+b_5x^5+b_4x^4+b_3x^3+b_2x^2+b_1x^1+b_0\).
Galois fields (polynomial operations) - GF(\(p^n\))
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Additive Group Table for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Additive Group Table for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of addition. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the additive group table for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values.
- Multiplicative Group Table for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Multiplicative Group Table for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the additive group table for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values.
- Additive, Division and Multiplicative Group Table for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Additive, Division and Multiplicative Group Table for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the Additive, Division and Multiplicative Group Table for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values.
- Additive and Multiplicative Group Table for GF(\(2^2\)) and GF(\(2^3\)). Galois Fields Table for GF(2^m) with polynomials. This page implements Galois Fields GF(\(2^n\)) with Python and provides a table of additional and multiplication. It outlines GF(\(2^2\)) and GF(\(2^3\)), but also gives a program that can be used for others. Overall, we have the form of GF(\(p^n\)) and which provides use both an additive and a multiplicative group operations that provide all the possible outputs within the finite field. The value of \(p\) is a prime number, and \(n\) is any positive integer.
- Additive and Multiplicative Group Table for GF(\(2^2\)) and GF(\(2^3\)). Galois Fields Table for GF(2^m) with coefficient values. This page implements Galois Fields GF(\(2^n\)) with Python and provides a table of additional and multiplication. It outlines GF(\(2^2\)) and GF(\(2^3\)), but also gives a program that can be used for others. Overall, we have the form of GF(\(p^n\)) and which provides use both an additive and a multiplicative group operations that provide all the possible outputs within the finite field. The value of \(p\) is a prime number, and \(n\) is any positive integer. This version will show the polynomial coefficent values within the Galois Field.
- Additive and Multiplicative Group Table for GF(\(2^2\)) and GF(\(2^3\)). Galois Fields Table for GF(2^m) with integer values. This page implements Galois Fields GF(\(2^n\)) with Python and provides a table of additional and multiplication. It outlines GF(\(2^2\)) and GF(\(2^3\)), but also gives a program that can be used for others. Overall, we have the form of GF(\(p^n\)) and which provides use both an additive and a multiplicative group operations that provide all the possible outputs within the finite field. The value of \(p\) is a prime number, and \(n\) is any positive integer. This version will show the integer values within the Galois Field.
Irreducible polynomial for GF(p^n)
- Irreducible polynomial for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Irreducible polynomial for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the parameters for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values. This includes finding the irreducible polynomial for the Galois Field.
- Irreducible polynomial for GF(\(p^n\)) for a given \(p\) and for \(n\) values. Irreducible polynomial for GF(p^n) for a given p and for n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the parameters for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values. This includes finding the irreducible polynomial for the Galois Field. Other important parameters include the degree (the highest polynomial power) and the order (the number of possible output values).
- Conway and primitive polynomial GF(\(p^n\)). Conway and primitive polynomial GF(p^n). This page outlines Conway and primitive polynomials for GF(\(p^n\)).
Galois fields (polynomial operations) - GF(\(p\))
- Additive and Multiplicative Group mod n (\(Z_n\)). Additive and Multiplicative Group mod n. In finite fields, we have a \(\pmod n\) operation for a list of integers (\(\mathbb{Z}\)), and where \(n\) is a prime number. This works for our add (+) and multiply (\(\times\)) operations, and where: \( a \pmod n + b \pmod n = (a+b) \pmod n\); and \(a \pmod n \times b \pmod n = (a \times b) \pmod n\).
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Polynomial GF(2) Factoring and Irreducible Polynomials. Factors. This outlines the search for polynomial factors for GF(2).
Polynomial operations
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
Post-quantum
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Rust
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Sage
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Golang and Cryptography

The new scripted languages such as Python and Node.js are convenient. But, unfortunately, they can be slow as they are scripted, and not compiled. Each time the scripted code is run, the scripting engine must then convert each line of code to the required machine level code. This makes the code much slower than compiled languages, and also less robust. Thus many applications in cryptography are written in C and C++, as they allow for fast execution and give low level access. Unfortunately it can be complex to compile programs, as we often need to install binary libraries and then link these in. The Go programming language, though, has a similar code syntax to C/C++, but is small and efficient and allows access to low-level functions, such as as pointers. Go thus aims to “Code less, compile quicker, execute faster”. So let’s use Go to implement some cryptography methods, including symmetric key, hashing, public keys and zero-knowledge proofs (ZKPs). The slides related to these methods are included [here]. An introduction to Golang and Cryptography is [here].

Go ECDH
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret.
Go Hex and Base64
- Base64 and Hex in Go. Base64/Hex. Two common formats for representing binary data are hexademical and Base64.
Go symmetric key
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Reuse IV attack and AES. Reuse IV and GCM. This provides an implementation of a reuse IV against AES GCM.
- ASCON AEAD (Golang). ASCON AEAD (Golang). The outlines the usage of AEAD for ASCON using Golang.
Go HMAC and HKDF
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HKDF in Go. HKDF. Implementation ofHKDF, and where we dervice a key based on a given secret.
Go secret shares
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.

Go ZKP
- Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL). DLEQ. Create a non-interactive ZKP for discrete logs.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Fiat Shamir and ECC (Interative ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP with Kryptology. This implements a range proof using a Schnorr proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?

Go ECIES (Hybrid Encryption)
With this, we can use the power of public key encryption (to generate the encryption key) with symmetric key encryption (to actually encrypt and decrpyt the data):
- ECIES (Kryptology). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Coinbase Kryptology library.
- ECIES (CIRCL). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Cloudflare CIRCL library.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt and which is used in Contract Tracing for COVID-19.
Go ECDSA
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Go RSA
- RSA Principles. RSA Principles. The basics of RSA.
- RSA with Go. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA. RSA encryption with Go using OAEP.
- RSA Encryption with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
Go ElGamal
ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Proving an Encrypted Shuffle With ElGamal and ECC. Shuffle. An encrypted shuffle with ElGamal.
- ElGamal encryption with Go. ElGamal. This implements ElGamal encryption.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
- ElGamal - Applying Multiple Public Key Operations (ECC). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use elliptic curve methods, and using the Edwards 25519 curve.
Go PGP
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
Go Public key
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.

Go Hashing
- Hashing with Go. Hashing. Hashes with Go.
- GP Hashing with Go. GP Hashing. GP Hashes with Go.
- SHAKE with Go. SHAKE. This implements SHAKE in Go.
- libDisco with Go. libDisco. This implements libDisco.
- cSHAKE in Golang. cSHAKE. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS. With the SHA-3 hashing method, we have four different cryptographic hashing methods (SHA3-224, SHA3-256, SHA3-384, and SHA3-512) and two XOF functions (SHAKE128 and SHAKE256). With SHAKE128 and SHAKE256 we can integrate domain separation between different functions — and which are known as cSHAKE128 and cSHAKE256.
- Homomorphic Hashing with Golang. Homomorphic hashing. Normally with hashing methods, we need to take all the previous data and new data in order to create a new hash value for our data. In a homomorphic hashing method, we can basically take the previous hash, and then add on any new data values. We can also remove previous data values from our hash, too. This is more efficient in computing, as we do not have to process all of our data into a new hash, and can use simple homomorphic operations for the computation. The method we will use (LtHash) was initially defined by Bellare and Micciancio and updated Lewi et al at Facebook.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
Go ECC
- Hash to password with Go. Hash to password. Hash to password with Go.
- ECDH with Go. ECDH. ECDH with Go.
- Box with Go. Box. Box with Go.
- ECC with Go. ECC. ECC with Go.
- Curve 25519 with Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ElGamal with ECC. ElGamal with ECC. ElGamal using ECC.
- Curve 25519 with Go for test vectors. ECC. This does a test on some private keys to test the public key generation.
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Barebones Ed25519 with Go. ECC. This shows point addition and scalar multiply in Ed25519
- Barebones NIST P256 with Go. ECC. This shows point addition and scalar multiply in P256
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining \(n.G\) for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Points (Base Point and Others). Elliptic Curve points. Two common curves used in ECC (Elliptic Curve Cryptography) are secp256k1 (as used in Bitcoin and Ethereum) and P256 (secp256r1). The "k1" refers to the Kolbitz curve 1 (named after the creator of ECC). With these we have a base point which are can operate on. This is typically defined as \(G\). We can then operate on this with add and multiply operation. For example, \(2G=G+G\) and \(P=n.G\). In this following we will show the base point for a number of common curves, such as secp256r1, P256, Pallas, Curve 25519, BLS12381G1, BLS12381G2, BLS12377G1 and BLS12377G2.
Go Blockchain
- Ethereum address with Go. Addresses. This generates an Ethereum address.
- Viewing Balance of account in Etheruem with Go. Balance. This views the balance of an account
- Viewing Block in Etheruem with Go. Block. This views a block.
- Viewing Transactions in Block in Etheruem with Go. Transactions. This views transactions.

Go Homomorphic
- SIDH Go. SIDH. Post-quantum key exchange.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- NTP. NTP. An overview of NTP.
- BiBa. BiBa. An overview of BiBa One Time Signature.
Go DNS
- DNSSEC. DNSSEC. An overview of DNSSEC.
Go Signatures
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Go Signcryption
- Ahmad-Afzal-Iqbal (AAI) signcryption with Golang. Ahmad-Afzal-Iqbal (AAI). Ahmad-Afzal-Iqbal (AAI) signcryption with Golang.

Go Crypto pairing
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
Go Homomorphic
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add. HEAAN Add. HEAAN Add.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- Anonymous crypto. Anon. Anonymous crypto.
- Rho factorization. Rho. Rho alogorithm.
- Post-quantum signing (BLISS). BLISS. BLISS method.
Go Post quantum
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.

Go CIRCL
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- Ed448 with Go. X448. Ed448 with Go.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with FourQ (Cloudflare). FourQ.
- Verifiable Oblivious Pseudorandom Functions (VOPRF) with Cloudflare CIRCL. VOPRF. In our digital world, we give away too many of our secrets, especially where we just have to prove the knowledge of something, rather than actually revealing it. In many of the systems we use, we could just prove things in an oblivious way, and where we could pass a secret but in a blinded form. With this, a server does not discover our password and for us not to discover the identifier that a server holds on us. But, can we also provide a proof back that the right password has been used? Well, with Verifiable Oblivious Pseudorandom Functions (VOPRF), we can generate a random secret based on a key generated on the server (Alice), and which is based on Bob’s secret.
- Hash to Curve using Go (Cloudflare). Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). The method defined here is proposed an an Internet-Draft standard by the Internet Engineering Task Force (IETF) related to "Hashing to Elliptic Curves".
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
here Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
- eXtendable-Output Function (XOF) usign CIRCL. XOF. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS.

Go Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Google Tink (Golang) ECIES. Google Tink (ECIE5). This outlines ECIES encryption with public key and AES using Golang with Google Tink
Go Credentials
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.

Go Kryptology
- Public key points for curves. Simple. Display public key points for scalars.
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.

Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.

Principles
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Paillier
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
Go Format Preserving Encryption (FPE)
- FPE with Go. FPE. An implementation of Format Preserving Encryption (FPE) for FFX1 and FFX3.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
AWS Encryption
- AWS Symmetric Key Encryption. AWS (Symmetric key). Using symmetric key in AWS.
Go Oblivious Transfer
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Dragon Fly
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
Embedding data in an ECC point
- Embedding data in a point. Go. With Elliptic Curve Cryptography (ECC), we use points on an elliptic curve to represent our data. These are defined with (x,y) points. With this, it is possible to embedded a certain amount of data into the point - as long as it still gives us a valid point on the curve. This example will Curve 25519 to embed data, and is achieved by storing the length of the data in a single byte in the point, and then store the data as byte values in the point (followed by random data). To decode, we can then just read the first byte for the length of the message, and then reveal the data encoded into the point..
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Hashing (Cryptographic)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
Benchmarks and Password strength
The following are the tips related to hashing:
- Password strength. Test. This outlines the strength of various passwords types.
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
Theory
The following are the tips related to hashing:
- Balls in bins. BiBa. This implemented balls in bins.
- Birthday attack (with Big Integers). Calc. This provides a simple example of the birthday attack.
- Birthday attack. Calc. This provides a simple example of the birthday attack.
- Differential Cryptanalysis (Hashing). Cryptanalysis. This provides an implementation of differential cryptanalysis for hashing methods.
MD5, SHA-1
The following are the tips related to hashing:
- MD2 and MD4 MD2/4. The MD2 and MD4 hashing functions were developed by Prof Ronald Rivest in 1989 and 1990, respectively. They both produce a 128-bit hash, but have been shown be vulnerable to attack (see the Collision section in the page).
- MD5 and SHA-1 (to Base-64) with salt Salt. It is possible to add salt to the MD5 algorithm, to mix it up a little.
- MD5 and SHA-1 (to Base-64) Hash. MD5 and SHA-1 produces a hash signature, and the output is typically shown in a hex format or a Base-64. In this example the output is converted into a Base-64 format.
- MD5 and SHA-1. Hash. MD5 and SHA-1 methods produce a hash signature, and are the two of the most widely used methods. The MD5 algorithm has been shown to have weaknesses, and a collision of message hashes has been shown to occur in less than one day. An MD5 signature has 128 bits, an SHA-1 signature has 160 bits, and an SHA-256 signature has 256 bits.
- MD5 Cracking. Hash Cracker. MD5 has a 128-bit signature and can be cracked using rainbow tables. This page tries to crack the MD5 signature.
- Hashing with Go. Hashing. Hashes with Go.
- Detecting hash types. Hash type. This detects has values.
- OpenSSL hashing. Range of methods. Outlines the methods used in OpenSSL
- Hash. Hash. Hashing using JavaScript
- Hashing with node.js. Hashing. Hashing with node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Hashing methods
-
Hazmat Hashes. Hazmat Hashes. This includes the hashing methods in the Hazmat cryptography library. This includes Blake2p, Blake2s, MD5, SHA1, SHA224, SHA256, SGA384, SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHA512, SHA512-224, SHAKE128 and SHA256.
-
Hazmat Hashes. Hazmat Hashes. In this case we will implement Python code to determine SHA1, SHA2, SHA3, Blake2, MD5 and SM3 hashes.
OpenSSL Passwords
-
Password example [here]
-
Hashed passwords with OpenSSL [here]
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Blake 3 hashes
The following are the tips related to similarity hashing:
- Blake 3 in Python. Hashing. Blake 3 hashing.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
Other Hash functions
The following are the tips related to hashing:
- Bloom Filter Bloom filter. A Bloom filter goes a probabilistic method of determining if an element is in a data structure, using indexed hashing methods.
- Cuckoo Table Cuckoo filter. A Cockoo table uses two hash funtions.
- Chaffing. Chaffing. This produces a keyless system.
- GP Hashing with Go. GP Hashing. GP Hashes with Go.
- LDAP. LDAP. This produces a LDAP hash signature for a password.
- LM Hash. LM Hash. This is an LM Hash Calculator. LM Hash is used in many versions of Windows to store user passwords that are fewer than 15 characters long.
- Murmur and FNV Murmur and FNV. While hashing methods such as MD5 and SHA-1 use crypto methods, the Murmur and FNV hashes uses a non-cryptographic hash function. This can be used for general hash-based lookup and was designed by Austin Appleby. It has good performance compared with other hashing methods.
- Pearson. Pearson. This uses a non-crypto hash.
- phpass. phpass. This produces a phpass hash signature for a password.
- Tiger. Tiger. Tiger is a 192-bit hash function and was designed by Ross Anderson and Eli Biham in 1995. It is often used by clients within Gnutella file-sharing networks and does not suffer from known attacks on MD5 and SHA-0/SHA-1. Tiger2 is an addition, in which the message is padded with a byte of 0x80 (in a similar way to MD4, MD5, and SHA), whereas in Tiger it is 0x01. Otherwise, the two methods are the same in their operation.
- Whirlpool. Whirlpool. Whirlpool is a 512-bit cryptographic hash function and was created by Vincent Rijmen (one of the AES creators) and Paulo Barreto, in 2000.
- WPA-2 hash . WPA-2 hash. Implements SHA-2 hash.
- Reusable hash collisions. Reusable hash collisions. Reusable hash collisions.
- The Length Extension Attack. Length Extension Attack. The MD construct has many weaknesses, and one of the most serious is the length extension attack. With this an adversary (Eve) can take a hash for an unknown message, and then add additional data to produce a new valid hash. The hash methods which are at risk against the length extension attack are MD5, SHA-1 and SHA-256. Please follow the code link below to run an example.
- Consistent hashing. Consistent hash. This outlines the usage of Consistent hashes.
- ROR13 (Module and Function). ROR13. With ROR13 we take each 8-bit character and then convert to a unicode value (with 16 bits). Then for each character we rotate the bits right by thirteen places. The resultant hash is then just the accumuluation of the rotated values.
- ROR13 (Function). ROR13 (Function). With ROR13 we take each 8-bit character and then convert to a unicode value (with 16 bits). Then for each character we rotate the bits right by thirteen places. The resultant hash is then just the accumuluation of the rotated values.
- GOST, Streebog256 and Streebog512. GOST, Streebog256 and Streebog512. GOST94 is a hashing method developed with Euro-Asian Council for Standardization, Metrology and Certification (EASC). This has since been developed in the Streebog256 and Streebog512 hashing method. In this case, we will use Libre OpenSSL to convert data into a hashed value.
RIPEMD
- RIPEMD (RACE Integrity Primitives Evaluation Message Digest) and GOST. RIPEM160. RIPEMD is a 128-bit, 160-bit, 256-bit or 320-bit cryptographic hash function, and was created by Hans Dobbertin, Antoon Bosselaers, and Bart Preneel. It is used on TrueCrypt and is open source. The 160-bit version is seen as an alternative to SHA-1, and is part of ISO/IEC 10118
- RIPEMD160. RIPEM160. RIPEMD160 is a 160-bit cryptographic hash function, and was created by Hans Dobbertin, Antoon Bosselaers and Bart Preneel. RIPEMD160 is used in Bitcoin applications.
Chameleon hashes
The following are the tips related to Chameleon hashing:
- Chameleon hash in Golang Chameleon. With a Chameleon hash, we have a normal hash value which is resistant to collisions, but with a known secret we can easily create a collision. The concept was first defined by Krawcyk and Rabin.
Similarity hashes
The following are the tips related to similarity hashing:
- Similarity hash: SimHash (Charikar similarity) in Python Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash (Nilsimsa similarity) Nilsimsa. The Nilsimsa similarity is used to find similarities between spam emails.
- Minhash (Jaccard similarity) Jaccard similarity. The Minhash method is used to find similarities between strings, files and metadata.
- String enthropy String enthropy. Measurement of the entropy of strings.
- Counting identical elements (HyperLogLog) HyperLogLog. Counting the number of identical elements.
SHA-3 and SHA-3 contenders
The following are the tips related to Key derivation hashing:
- Blake and Blake 2. Blake. Implements Blake and Blake 2 (SHA-3 contender).
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
- Grøstl. Grøstl. Implements Grøstl (SHA-3 contender).
- KangarooTwelve. KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- SHA-3, Keccak and SHAKE . SHA-3. Implements SHA-3, Keccak and SHAKE (SHA-3 winner).
- SHA-3. SHA-3. SHA-3 was known as Keccak and is a hash function designed by Guido Bertoni, Joan Daemen, Michaël Peeters, and Gilles Van Assche. MD5 and SHA-0 have been shown to be susceptible to attacks, along with theoretical attacks on SHA-1. NIST thus defined there was a need for a new hashing method which did not use the existing methods for hashing, and setup a competition for competing algorithms. In October 2012, Keccak won the NIST hash function competition and is proposed as the SHA-3 standard. It should be noted that it is not replacement SHA-2, which is currently a secure method. Overall Keccak uses the sponge construction where the message blocks are XORed into the initial bits of the state, and then inevitably permuted.
- cSHAKE. cSHAKE. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS. With the SHA-3 hashing method, we have four different cryptographic hashing methods (SHA3-224, SHA3-256, SHA3-384, and SHA3-512) and two XOF functions (SHAKE128 and SHAKE256). With SHAKE128 and SHAKE256 we can integrate domain separation between different functions — and which are known as cSHAKE128 and cSHAKE256.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- Skein. Skein. Implements Skein (SHA-3 contender).
Key derivation hashing
The following are the tips related to Key derivation hashing:
- Argon2. Go. Outline of Argon2.
- Argon2 with NaCl. Go. Outline of Argon2 using NaCl.
- Balloon. Go. Outline of Balloon.
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- Double ratchet. Go. Outline of double ratcheting.
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- Scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat HKDF. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
Non-crypto/fast hashing
The following are the tips related to non-crypto hashing:
- A perfect hash Perfect hash. This is a non-crypto hash which optimizes the hash value.
- The universal hash Universal hash. This related to the concept of a universal hash.
- FNV. FNV. FNV is one of the fastest hashing methods.
- Murmur. Murmur. Murmur is one of the fastest hashing methods.
- Siphash. Siphash. Siphash is a fast hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- xxHash. xxHash. xxHash is one of the fastest hashing methods.
- Meow. Meow. Meow is one of the fastest hashing methods.
- o1Hash. o1Hash. o1Hash is one of the fastest hashing methods.
- CRC-32. CRC-32. CRC-32 is one of the fastest hashing methods.
- wyhash. wyhash. wyhash is one of the fastest hashing methods.
- CityHash. CityHash. CityHash is one of the fastest hashing methods, and is generally free of security problems.
- FarmHash. FarmHash. FarmHash is one of the fastest hashing methods, and is generally free of security problems.
- Non-crypto. Non-crypto. This includes a range of fast non-cryptography hashing methods.
- Non-crypto hashes (C++): Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro. Non-crypto hashes: Farm, City, xxHash, MUM, Spooky 2, Murmur, Metro and t1ha0. This includes a range of fast non-cryptography hashing methods for Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro using C++ methods.
- Pearson. Pearson. Pearson is one of the fastest hashing methods, and has been designed for 8-bit processors.
- C++: t1ha. t1ha. t1ha is one of the fastest hashing methods, and has been designed for 64-bit processors.
- C++: Spooky. Spooky. Spooky is one of the fastest hashing methods, and V2 has a 32-bit, 64-bit and 128-bit version.
- C++: xxHash. xxHash. xxHash is one of the fastest hashing methods, and has good performance for short data inputs.
- C++: MUM. MUM. MUM is one of the fastest hashing methods.
- C++: FNV 1/1a. FNV 1/1a. FNV 1/1a is one of the fastest hashing methods, and is particularily useful when there are small changes in strings, such as with IP addresses and URLs.
- C++: MetroHash. MetroHash. MetroHash is one of the fastest hashing methods.
- C++: CityHash. CityHash. CityHash was created by Google and is one of the fastest hashing methods. It was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Farm. FarmHash. FarmHash was created by Google and is one of the fastest hashing methods. It is an improvement to CityHash.
- C++: Murmur. Murmur. Murmur is one of the fastest hashing methods, but was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Halftime. Halftime. Halftime is one of the fastest hashing methods and was created by Jim Apple at Apache.
- C++: Highway. Highway. Highway is an ultra-fast keyed-hash, and is more than five times faster than SipHash. It was created by Jyrki Alakuijala, Bill Cox, Jan Wassenberg at Google.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
- C++: CLHash. CLHash. CLHash is an ultra-fast hashing method and focused on improving performance of the hashing of long strings.
- C++: FalkHash. FalkHash. FalkHash is an ultra-fast hashing method and beats most of the other non-cryptography methods for performance. It is focused on the x64 architecture and integrates with AES-NI.
- C++: wyHash. wyHash. wyHash is an ultra-fast hashing method.
- C++: Fibonacci. Fibonacci. Fibonacci is an ultra-fast hashing method.
- C++: Lookup3. Lookup3. Lookup3 is an ultra-fast hashing method.
Key-based hashing
The following are the tips related to Key-based hashing:
- SiphashSiphash. Siphash is a fast key-based hashing method.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
One Time Passwords/Time Stamps
The following are the tips related to hashing:
- One Time Passwords. One Time. This allows a new unique password to be created each instance, based on an initial seed.
- Timed One Time Password (TOTP). Timed One Time Password. This allows a new unique passcode to be created each instance, based on an initial seed for a given time window. We will use a five second window in this case, where a new passcode is generated every five seconds, based on an initial seed of a pass phrase.
- Hashed One Time Password (HOTP). Hashed One Time Password. This allows a new unique passcode to be created each instance, based on a counter value and an initial seed.
- Time Stamp Protocol. TSP. This creates a time stamp for data.
- HOTP and TOTP (Python). OTP. This creates hashed passwords.
eXtendable-Output Function (XOF)
- eXtendable-Output Function (XOF) usign CIRCL. XOF. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS.
SHAKE
The following are the tips related to hashing:
- SHAKE. SHAKE. Implements SHAKE and which is an Extendable Output Function (XOF).
- SHAKE with Go. SHAKE. This implements SHAKE in Go.
- libDisco with Go. libDisco. This implements libDisco.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify
the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods
such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC methods using the Python cryptography primitives for HMAC-MD5.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
Quantum-robust Public Key (Hash-based signature)
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
Hash to ECC point
- Hash to password with Go. Hash to password. Hash to password with Go.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve with libnum.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.

Password-hashing functions using Rust
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing (Non-cryptographic)

You might know those slow old hashing methods, such as MD5, SHA-1, and SHA-256. Well, they were designed to be fast, but also highly secure. But, if we just need a hashing method, such as for a hashtable or Bloom filter, we often don’t need all the security that comes with the main cryptography hashing methods. And so we have the non-cryptography hashing methods, and which are often ultra-fast and highly efficient. To show the difference, in a test, SHA-1 — one of the fastest cryptography hashing methods — managed a processing rate of 364.95 MiB/s, while t1ha was nearly a 100 times faster, at 34,636 MiB/s.
Non-crypto/fast hashing
The following are the tips related to non-crypto hashing:
- A perfect hash Perfect hash. This is a non-crypto hash which optimizes the hash value.
- The universal hash Universal hash. This related to the concept of a universal hash.
- FNV. FNV. FNV is one of the fastest hashing methods.
- Murmur. Murmur. Murmur is one of the fastest hashing methods.
- Siphash. Siphash. Siphash is a fast hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- xxHash. xxHash. xxHash is one of the fastest hashing methods.
- Meow. Meow. Meow is one of the fastest hashing methods.
- o1Hash. o1Hash. o1Hash is one of the fastest hashing methods.
- CRC-32. CRC-32. CRC-32 is one of the fastest hashing methods.
- wyhash. wyhash. wyhash is one of the fastest hashing methods.
- CityHash. CityHash. CityHash is one of the fastest hashing methods, and is generally free of security problems.
- FarmHash. FarmHash. FarmHash is one of the fastest hashing methods, and is generally free of security problems.
- Non-crypto. Non-crypto. This includes a range of fast non-cryptography hashing methods.
- Non-crypto hashes (C++): Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro. Non-crypto hashes: Farm, City, xxHash, MUM, Spooky 2, Murmur, Metro and t1ha0. This includes a range of fast non-cryptography hashing methods for Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro using C++ methods.
- Pearson. Pearson. Pearson is one of the fastest hashing methods, and has been designed for 8-bit processors.
- C++: t1ha. t1ha. t1ha is one of the fastest hashing methods, and has been designed for 64-bit processors.
- C++: Spooky. Spooky. Spooky is one of the fastest hashing methods, and V2 has a 32-bit, 64-bit and 128-bit version.
- C++: xxHash. xxHash. xxHash is one of the fastest hashing methods, and has good performance for short data inputs.
- C++: MUM. MUM. MUM is one of the fastest hashing methods.
- C++: FNV 1/1a. FNV 1/1a. FNV 1/1a is one of the fastest hashing methods, and is particularily useful when there are small changes in strings, such as with IP addresses and URLs.
- C++: MetroHash. MetroHash. MetroHash is one of the fastest hashing methods.
- C++: CityHash. CityHash. CityHash was created by Google and is one of the fastest hashing methods. It was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Farm. FarmHash. FarmHash was created by Google and is one of the fastest hashing methods. It is an improvement to CityHash.
- C++: Murmur. Murmur. Murmur is one of the fastest hashing methods, but was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Halftime. Halftime. Halftime is one of the fastest hashing methods and was created by Jim Apple at Apache.
- C++: Highway. Highway. Highway is an ultra-fast keyed-hash, and is more than five times faster than SipHash. It was created by Jyrki Alakuijala, Bill Cox, Jan Wassenberg at Google.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
- C++: CLHash. CLHash. CLHash is an ultra-fast hashing method and focused on improving performance of the hashing of long strings.
- C++: FalkHash. FalkHash. FalkHash is an ultra-fast hashing method and beats most of the other non-cryptography methods for performance. It is focused on the x64 architecture and integrates with AES-NI.
- C++: wyHash. wyHash. wyHash is an ultra-fast hashing method.
- C++: Fibonacci. Fibonacci. Fibonacci is an ultra-fast hashing method.
- C++: Lookup3. Lookup3. Lookup3 is an ultra-fast hashing method.
A fuller test with SMHasher gives [here]:
Hash function MiB/sec cycl./hash cycl./map Quality problems
------------------------------------------------------------------
o1hash 12439661.09 16.77 166.13 insecure, no seed, zeros, fails all tests
crc32_hw1 23208.73 46.74 179.70 insecure, 100% bias, collisions, distrib, BIC, machine-specific (x86 SSE4.2)
t1ha0_aes_noavx 22785.26 38.71 180.61 LongNeighbors, machine-specific (x86 AES-NI)
t1ha0_aes_avx1 22714.85 48.12 226.52 LongNeighbors, machine-specific (x64 AVX.txt)
t1ha0_aes_avx2 22345.33 44.38 556.47 LongNeighbors, machine-specific (x64 AVX2)
falkhash 20202.42 173.63 321.52 Sparse, LongNeighbors, machine-specific (x64 AES-NI)
MeowHash64low 17378.06 85.48 237.60 Sparse, invertible, machine-specific (x64 AES-NI)
MeowHash32low 17374.64 85.48 258.53 Sparse, invertible, machine-specific (x64 AES-NI)
MeowHash 17371.91 85.48 247.96 Sparse, invertible, machine-specific (x64 AES-NI)
FarmHash32 17112.05 47.7 214.71 machine-specific (x64 SSE4/AVX)
xxh3 16538.52 32.81 184.86 DiffDist bit 7 w. 36 bits, BIC
xxh3low 16462.36 32.77 199.79
farmhash32_c 16299.81 47.79 219.19 machine-specific (x64 SSE4/AVX)
xxh128low 15174.85 33.79 187.05
xxh128 15174.14 40.46 195.65
farsh32 14053.09 74.29 245.33 insecure: AppendedZeroes, collisions+bias, MomentChi2, LongNeighbors
metrohash64crc_2 14034.84 48.94 162.54 UB, Cyclic 8/8 byte, DiffDist, BIC, machine-specific (SSE4.2/NEON)
metrohash64crc_1 14000.5 49.08 150.54 UB, Cyclic 8/8 byte, DiffDist, BIC, MomentChi2, machine-specific (SSE4.2/NEON)
metrohash128crc_1 13948.67 65.2 168.08 UB, machine-specific (SSE4.2/NEON)
metrohash128crc_2 13920.19 65.12 176.70 UB, machine-specific (SSE4.2/NEON)
halftime_hash128 13478.23 97.79 252.14
wyhash32low 12911.09 29.59 205.43 2 bad seeds
wyhash 12879 30.35 196.77 2^33 bad seeds
CityCrc128 12343.43 74.5 209.75
fletcher2 12011.15 25.29 298.60 bad seed 0, UB, fails all tests
fletcher4 11928.55 25.27 293.49 bad seed 0, UB, fails all tests
halftime_hash256 11620.28 98.44 252.60
fibonacci 11339.87 26.33 705.64 UB, zeros, fails all tests
ahash64 9862.62 27.32 181.68 rust
Spooky128 9751.14 63.84 192.47 UB
Spooky64 9747.47 62.2 191.71 UB
Spooky32 9747.13 62.24 196.96 UB
t1ha1_64le 9723.86 34.39 176.91 Avalanche
cmetrohash64_1 9683.33 45.2 161.01 UB, LongNeighbors, BIC, MomentChi2
cmetrohash64_2 9669.95 44.75 149.67 LongNeighbors
metrohash64_2 9668.51 44.45 164.30 UB, LongNeighbors
metrohash64 9664.61 44.59 150.74 UB, LongNeighbors, BIC
metrohash64_1 9664.57 45.37 152.31 UB, LongNeighbors, BIC, MomentChi2
cmetrohash64_1o 9658.31 42.84 163.45 UB, LongNeighbors, BIC, MomentChi2
FNV1a_YT 9643.42 32.06 175.19 bad seed, UB, fails all tests
City128 9640.19 88.45 225.38
metrohash128_2 9584.94 59.1 167.43 UB, LongNeighbors
metrohash128 9569.16 58.68 167.53 UB, LongNeighbors
metrohash128_1 9558.17 59.04 175.94 UB, LongNeighbors
FarmHash128 9409.63 74.52 210.25
VHASH_32 9404.99 77.01 250.57 sanity, Seed, MomentChi2
VHASH_64 9392.39 74.72 227.92 sanity, Seed, MomentChi2
farmhash128_c 9244.13 79.08 209.44
t1ha2_atonce 9237.12 38.94 194.32 Zeroes low3
City64noSeed 9090.42 32.23 171.53 Avalanche, Sparse, TwoBytes, MomentChi2, Seed
City64low 9089.45 47.75 201.73
t1ha2_stream 9068.55 74.56 219.85 Sparse, Permutation, LongNeighbors
City64 9066.9 47.81 197.78 Sparse, TwoBytes
t1ha2_stream128 9065.5 93.19 236.50 Sparse, Permutation, LongNeighbors
xxHash64 8936.63 51.31 174.34
pengyhash 8744.48 85.31 222.45
farmhash64_c 8713.16 47.96 201.00
FarmHash64 8684.76 48.13 200.51
crc64_hw 8440.13 34.94 141.15 insecure, 100% bias, collisions, distrib, BIC, machine-specific (SSE4.2/NEON)
t1ha2_atonce128 8350.99 55.65 203.53 LongNeighbors
PMPML_64 8161.19 53.2 179.16 unseeded: Seed, MomentChi2, BIC
halftime_hash512 7681.62 125.81 274.01
tabulation 7621.75 42.19 179.93
t1ha1_64be 7481.37 38.16 193.22 Avalanche
MUMlow 7225.18 37.85 197.92 UB, 5 bad seeds
farsh64 7216.29 130.3 302.44 insecure: AppendedZeroes, collisions+bias, MomentChi2, LongNeighbors
MUM 7134.56 37.85 172.34 UB, too many bad seeds, machine-specific (32/64 differs)
nmhash32 7003.3 68.93 216.59
PMPML_32 6704.53 53.5 197.43 Avalanche >512, unseeded: Seed, BIC, MomentChi2, PerlinNoise
nmhash32x 6342.95 56.41 217.75
crc32_hw 6330.42 35.55 170.16 insecure, 100% bias, collisions, distrib, BIC, machine-specific (SSE4.2/NEON)
FNV2 6258.84 33.25 142.89 fails all tests
FNV1A_Pippip_Yurii 6258.46 28.19 184.41 UB, sanity, fails all tests
FNV1A_Totenschiff 6258.23 27.99 198.20 UB, zeros, fails all tests
HighwayHash64 6242.58 99.55 248.41
mx3 6146.02 52.48 173.09 UB
xxHash32 6040.87 51.77 177.91 LongNeighbors, collisions with 4bit diff, MomentChi2 220
prvhash64s_64 5481.48 170.05 325.39
mirhash 5413.73 39.68 154.47 UB, 2^36 bad seeds, LongNeighbors, machine-specific (32/64 differs)
mirhash32low 5412.76 39.79 182.13 UB, 4 bad seeds, Cyclic, LongNeighbors, machine-specific (32/64 differs)
Murmur3F 5226.4 52.18 175.85 UB
prvhash64s_128 5161.33 260.96 442.70
t1ha0_32le 5132.18 54.83 193.53 Sparse, LongNeighbors
halftime_hash64 4990.72 120.55 281.64
Murmur2B 4882.95 39.72 149.43 UB, 1.8% bias, collisions, 3.4% distrib, BIC
seahash32low 4801.33 58.54 227.31 PerlinNoise 32, !msvc
seahash 4796.97 58.55 201.58 PerlinNoise, !msvc
fasthash32 4737.61 45.32 181.86 UB, insecure
fasthash64 4737.21 42.79 164.87 UB, insecure, Moment Chi2 5159 !
umash32_hi 4662.92 54.22 214.20
umash64 4662.09 53.42 188.09
umash32 4633.19 53.42 216.33
t1ha0_32be 4585.59 55.98 183.45 Sparse, LongNeighbors
clhash 4472.31 82.72 229.73 PerlinNoise, machine-specific (x64 SSE4.2)
tabulation32 4317.34 35.45 197.20 collisions
Murmur2C 4092.99 51.84 164.65 UB, 2^32 bad seeds, 91% bias, collisions, distr, BIC, LongNeighbors
farsh128 3776.92 232.48 398.67
City32 3675.04 57.73 212.04
TSip 3228.14 57.96 211.71 !msvc
Murmur3C 3197.63 67.9 198.00 UB, LongNeighbors, Text, DiffDist
Crap8 3149.63 36.23 195.11 UB, 2.42% bias, collisions, 2% distrib
Murmur2 3146.91 41.87 187.89 UB, 1 bad seed, 1.7% bias, 81x coll, 1.7% distrib, BIC
Murmur2A 3146.79 46.87 191.96 UB, 1 bad seed, 12.7% bias, LongNeighbors
aesnihash 2963.39 71.24 217.73 fails many tests, machine-specific (x64 AES-NI)
BEBB4185 2951.62 222.03 343.63 UB, too many bad seeds, msvc-specific
jodyhash6 2848.42 29.99 164.36 bias, collisions, distr, BIC, LongNeighbors
wyhash32 2532.89 48.4 484.57 2 bad seeds, 32-bit
umash128 2427.46 70.6 197.29
Murmur3A 2413.88 53.36 182.37 UB, 1 bad seed, Moment Chi2 69
prvhash64_64m 2386.19 51.18 186.87
prvhash64_128 2383.57 103.44 246.45
prvhash64_64 2375.72 51.61 190.97
hasshe2 2372.52 68.64 216.74 Permutation,TwoBytes,Zeroes,Seed
PMurHash32 2344.78 58.48 196.43 1 bad seed, Moment Chi2 69
mirhashstrict32low 2218.87 65.48 190.59 1 bad seed, MomentChi2 9
mirhashstrict 2217.32 65.53 182.07
sha1ni 2019.96 135.84 564.40 insecure,sanity, Permutation, Zeroes, machine-specific
sha1ni_32 2019.94 136.82 589.46 machine-specific
superfast 1956.25 53.61 180.10 UB, bad seed 0, 91% bias, 5273.01x collisions, 37% distr, BIC
sha2ni-256_64 1910.34 146.06 595.16 Zeroes, machine-specific
sha2ni-256 1906.77 145.47 603.08 insecure,sanity, Permutation, Zeroes, machine-specific
farsh256 1895.77 459.86 575.95
SipHash13 1889.1 89 199.95 0.9% bias
Murmur1 1804.67 51.51 188.41 UB, 1 bad seed, 511x collisions, Diff, BIC
lookup3 1658.31 48.84 194.15 UB, 28% bias, collisions, 30% distr, BIC
pearsonbhash64 1486.34 104.32 185.03
poly_1_mersenne 1431.65 54.49 189.52 fails most tests
jodyhash32 1428.37 44.36 185.85 bias, collisions, distr, BIC LongNeighbors
pearsonbhash128 1347.03 121.75 214.84
poly_2_mersenne 1323.69 66.93 190.88
poly_3_mersenne 1323.59 74.86 206.77
poly_4_mersenne 1323.57 82.67 200.36
blake3_c 1285.91 340.01 552.63 no 32bit portability
GoodOAAT 1052 71.62 192.19
pearsonbhash256 998.9 167.05 261.29
SipHash 980.88 127.77 246.19
MicroOAAT 977.6 59.61 185.06 100% bias, distrib, BIC
FNV1a 791.84 69.69 177.84 bad seed, zeros, fails all tests
sdbm 791.84 67.69 177.06 bad seed 0, fails all tests
FNV64 791.82 70.24 159.29 fails all tests
bernstein 791.82 68.63 180.71 bad seed 0, fails all tests
beamsplitter 789.22 682.45 1150.3 UB, too many bad seeds
HalfSipHash 755.78 114.47 243.72 zeroes
chaskey 753.23 153.42 288.26 PerlinNoise
x17 527.9 98.78 184.09 99.98% bias, fails all tests
JenkinsOOAT_perl 452.49 118.78 194.78 bad seed 0, test FAIL
MurmurOAAT 452.49 113.07 197.83 bad seed 0, 1.5-11.5% bias, 7.2x collisions, BIC, LongNeighbors
JenkinsOOAT 452.48 142.85 213.93 bad seed 0, 1.5-11.5% bias, 7.2x collisions, BIC, LongNeighbors
crc32 392.1 131.62 204.58 insecure, 8590x collisions, distrib, PerlinNoise
sha1-160 364.95 1470.55 1794.1 Comb/Cyclic low32
rmd256 362.49 617.02 815.44 Bad seeds
blake2b-256_64 356.97 1222.76 1435.0
blake2b-224 356.59 1228.5 1425.87
blake2b-160 356.08 1236.84 1458.15
blake2b-256 355.97 1232.22 1443.31 Sparse high 32-bit
md5-128 353.76 638.29 803.39
md5_32a 353.64 629.85 799.56 Sparse high 32-bit
sha1_32a 353.03 1385.8 1759.9 Cyclic low32, 36.6% distrib
rmd128 334.36 659.03 838.32 Bad seeds
blake2s-128 295.3 698.09 1059.2
pearsonhash64 287.95 174.11 196.50 Avalanche, Seed, SSSE3 only. broken MSVC
pearsonhash128 287.95 171.72 194.61 Avalanche, Seed, SSSE3 only. broken MSVC
pearsonhash256 264.51 184.87 218.79 Avalanche, Seed, SSSE3 only. broken MSVC
blake2s-256 215.28 1014.88 1230.38
blake2s-160 215.01 1026.74 1239.54
blake2s-256_64 211.52 1044.22 1228.43
blake2s-224 207.06 1063.86 1236.50
rmd160 202.16 1045.79 1287.74 Bad seeds, Cyclic hi32
sha2-256_64 148.01 1376.34 1624.71 Bad seeds, Moment Chi2 7
sha2-256 147.8 1374.9 1606.06 Bad seeds, Moment Chi2 4
sha2-224_64 147.6 1360.1 1620.93 Bad seeds, Cyclic low32
sha2-224 147.13 1354.81 1589.92 Bad seeds, Comb low32
asconhashv12 144.98 885.02 1324.23
sha3-256 100.58 3877.18 4159.79 PerlinNoise
sha3-256_64 100.57 3909 4174.63 PerlinNoise
asconhashv12_64 86.73 684.02 606.93
floppsyhash 35.72 1868.92 1411.07
tifuhash_64 35.6 1679.52 1212.75 Cyclic low32
Problems include:
- Bad Seeds. A random seed is often used to initialise the hash. This problem relates to having a bad seed..
- Undefined behaviour (UB). This includes Misaligned, oob (Out of bounds), Signed integer overflow and Shift exponent overflow.
o1hash is the fastest, and a quick and dirty hashing method. It is generally not secure. t1h (Fast Positive Hash) requires AES-NI (Intel Advanced Encryption Standard Instructions) and is one of the fastest hashes at 22.785 Gbps. It has fairly good security levels. Meow comes in around 17.378 Gbps. We can see that SHA-1-160 runs as 364 Mbps, while Meow runs at 17.378 Gbps. Blake 3 is one of the fast cryptography hash and has a rate of 1.285 Gbps, and Blake 2 gives a rate around 215 Mbps. SHA-3 gives hashing rates of 100.58 Mbps.
Google recommend the following for 64-bit hashes without quality problems:
- xxh3low
-
wyhash
-
ahash64
-
t1ha2_atonce
-
FarmHash
-
halftime_hash128
-
Spooky32
-
pengyhash
-
nmhash32
-
mx3
-
MUM/mir
- fasthash32
Hash-based Signatures

With hash-based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature, unless we create a stateless method, such as SPHINCS+ [1]. Currently NIST have the final round for the Post Quantum Cryptography competition, and for digital signatures, SPHINCS+ is one of the alterative finalists (alongside Picnic).
Hash-based signature (theory)
- BiBa (Go). BiBa. An overview of BiBa One Time Signature [9]. Basically the method involves us taking a hash of a value using a standard hashing method, such as with SHA-256. There will then be \(2^{256}\) different hashing values. We aim to create a signature for a message, so Bob (the signer) selects a number of random values for his private key value and then publishes the hash of each of these (\(P_1\), \(P_2\), etc). He then sends these public keys to Alice. Now when Bob wants to sign a message, he will take one of his private key values, and then hashes it, and then determines the bin that it should be placed. In this case, we could use the \(\pmod N\) function on the hash, and where \(N\) is the number of bins. If we select \(2^{10}\) there will be 1,024 bins.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature [9].
Hash-based signature (stateful)
- BLISS - Post-quantum signing. BLISS. One of the alteratives to the usage of our existing public key methods is the usage of lattice cryptography, and especially in the usage of Ring Learning With Errors (RLWE). An important application is within digital signatures, and where Bob will sign something with his private key, and then Alice can prove that he signed it with his public key. One post-quantum signature method is BLISS (short for Bimodal Lattice Signature Scheme) [8]. It was created by Léo Ducas, Alain Durmus, Tancrède Lepoint and Vadim Lyubashevsky in 2013.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Hash to Obtain Random Subset (HORS) [3] is a quantum robust hashed-based one-time signature. With this we create a series of integers for our private keys and organise into an indexable form. Then we hash them to a sequence of public key values. Next we segment the hash of the message into a series of n-bit integer values. The signature is then achieved through a look-up of the value in the public key list.
- Lamport Signatures. Lamport. Outlines Lamport signatures [7]. When we sign a message we take its hash and then encrypt with our private key. The public key is then used to prove it, and will prove that we signed it with our private key. The Lamport signature uses 512 random hashes for the private key, and which are split into Set A and Set B. The public key is the hash of each of these values. The size of the private key is 16KB (2×256×256 bits) and the public key size is also 16 KB (512 hashes with each of 256 bits).
- Winternitz Signatures (W-OTS). Winternitz. Outlines Winternitz signatures [4, 5]. W-OTS uses relatively small key and signatures sizes, and is thought to be quantum robust. It generates 32x256 bit random private keys. We then hash these a number of times, and is defined by a parameter (w). If we use w=8, we hash the private keys by (2w). This creates 32x256 bits public keys. The signature is the created by taking eight bits at a time, and then the 8-bit binary int (n) is subtracted from 256 and the private key is the hashed 256-n times. The signature is then 32 hashes which are derived from random private keys. To verify the signature, the recipient parses the hash of the signature (using 8 bits at a time, and extracting the 8 bit int, n).
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method [6], and which is used within speeds-up of Hashing-based signature methods. Using methods such as SHA-1 and SHA-2 (aka SHA-256) will be inefficient as they tend to compress the data inputs through a number of stages. Haraka v2 [6] is different as focuses on inputs of just 256 bits (32 bytes) or 512 bits (64 bytes). This makes the method useful when we are dealing with key and hash values, and is especially useful for hash-based signatures. The output is 256 bits long, but where the input can be either be 256 bits (Haraka256) or 512 bits (Haraka512). These lengths are typically for the outputs of modern hashing applications. The Haraka method, too, has been optimized with AES instructions (AES-NI - Intel Advanced Encryption Standard New Instructions) and which are supported within the hardware of the processor. As Haraka is focused on short messages, the number of rounds within the hashing process has been reduced.
Hash-based signature (stateless)
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ digital signature. SPHINCS digital signature. Outline of the a SPHINCS stateless digital signature method [1].
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
Hash-based signature (Merkle-based)
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
Introduction
Many of the problems we see on the Internet relate to the lack of trust within transactions. The emails you receive and the Web sites that you visit often have very little trust built into them. For trust the email address of the sender, but anyone can fake that address. So increasingly we create a digital signature, and where we sign our messages. In this way, we can check for authentication, integrity and non-repudiation.
With the Alice creates a key-pair: a public key and a private key. She then takes a hash of the message, and then encrypts this hash with her private key, and passes the message and the signature to Bob. Bob then reads the message and takes a hash of it. He then decrypts Alice's signature with her public and checks the hashes. If they match, he knows that she signed and that it has not been changed along the way:
Currently, we often use RSA, DSA and ECDSA to sign our messages. These are based on the difficulty of finding out the factors of a number and on the processing of discrete logarithms. At the current time these methods are computationally hard problems, but with quantum computers, they become much easier. This was shown by Peter Shor who illustrated that it was possible to crack them in polynomial time.
Of all the methods that are being proposed, the hash-based methods look as if they have a good chance of success of creating quantum robust signatures. methods and code-based methods are being researched, but the usage of hashing methods is already well and could provide the best alternative to the existing methods. Hashing methods, too, often bring other advantages, such as forward secure, which means that a key which is cracked will not reveal all the previous keys.
Merkle trees
The root of hash-based methods isin Merkle trees, and which are a way of hashing is used in many applications, including with Bitcoin, Ethereum, Git distribution systems, No SQL, and in many P2P applications. With a Merkle tree we take our data elements, and then hash them, and take pairs of these hashes to create a new hash, and so we build a table. At the top of the tree is the root element (in this case Hash1234):

In this way, we can use the tree to see if we have matching data on systems.On a P2P network, we can transfer a file by splitting it into data segments and then distributing these segments across the network. A trusted source will have the complete Merkle tree for rebuilding the file, and a client can thus rebuild from the Merkle tree and determine the parts of the file which are still missing. Once transferred the root hash (and all the other hashes) will then match. In its core method, the Merkle Signature Scheme (MSS) has serious performance and memory issues, but enhanced methods such as XMSS create with much less of a performance hit.
One-time signatures (Lamport)
The core method used in hash-based signatures is that of the one-time signature, and where we create a new key pair for every method we need to create. If the keys were reused, an attacker could start to learn the private key, and thus spoof messages. One of the first methods was produced by Leslie Lamport and Whitfield Diffie, in 1979, and is defined as:
- We create two data sets with 256 random 256-bit numbers (Set A and Set B). These are the private key (512 values).
- we take the hash of each of the random numbers. This will give 512 hashes and will be the public key.
- We then hash the message using and then test each bit of the hash (0 ... 255). If it is a 0, we use the ith number in Set A, else we use the ith number from Set B.
- The signature is then 256 random numbers (taken from either Set A or Set B) and the public key is the 512 hashes (of Set A and Set B).
The public and private keys are then each 16KB in size. A demo of the method is here.

Figure 1: Lamport method
The major problem with the method is that a key pair for every message. also in 1979, found a solution with Merkle trees.
One-time signature (W-OTS)
To improve performance method (and which reduced key sizes), Merkle proposed Winternitz OTS (named after Robert Winternitz). With this method was possible to sign many bits at the same time. The method is:
- We create 32 256-bit random numbers. These 32 values will be our private key.
- We then hash each of these values 256 times. These 32 values will be our public key.
- We now take the message and hash it using SHA-256. This produces 32 8-bit values (N1, N2 ... N32).
- Next we take each 8-bit value in the hash of the message, and then hash 256-N times (where N is the value of the 8-bit value).
- To prove the signature, we take the message and hash it with SHA-256, and then take each 8-bit value. We then hash the 8-bit signature value by the number of times defined by the message hash value (N1, N2..). The result for each operation should equal the public key value.
This is illustrated below in Figure 2. A demo of the method is here.

Figure 2: W-OTS
Hash-based Signatures
The methods such as W-OTS and Lamport only provide for a one-time signature. In order to sign many messages, we can use the Merkel signature scheme (MSS). With this we take a hash of the keys and build these as the leaves of the tree. The root of the tree is then the public key - the verification key. We then just use the private key of the W-OTS method to create the signature. The sender also sends the authentication path, which is the neighbouring nodes within the path and which leads to the root of the tree. The recipient can then rebuild the tree using the verification key (which can be received a digital certificate) and the authentication path. For the next message we move onto another key pair and where the index of the key part is revealed.
In the following example we have our root as the public key, and then want to sign with Key3. We then show the authentication path which takes us to the root (as defined in the bold arrows):

Conclusions
Hashed-based methods look to be a strong contender for weaning us off RSA, DSA and ECDSA, but we will have to look at the stateful generation of keys. For this we will have to generate a bank of key pairs (2, 4, 8, 16, etc) and then create the public key from the root of the Merkle tree. We must then remember the keys we have used previously, and only use an unused one. Once we use our new key pair, we then show our working-out as to how the private key is integrated into our tree. It is a bit like a teacher marking a question correctly, and asking for the working out that go you to the answer.
References
[1] Bernstein, D. J., Hopwood, D., Hülsing, A., Lange, T., Niederhagen, R., Papachristodoulou, L., ... & Wilcox-O’Hearn, Z. (2015, April). SPHINCS: practical stateless hash-based signatures. In Annual international conference on the theory and applications of cryptographic techniques (pp. 368-397). Springer, Berlin, Heidelberg [paper].
[2] Bernstein, D. J., Hülsing, A., Kölbl, S., Niederhagen, R., Rijneveld, J., & Schwabe, P. (2019, November). The SPHINCS+ signature framework. In Proceedings of the 2019 ACM SIGSAC conference on computer and communications security (pp. 2129-2146) [paper].
[3] Reyzin, L., & Reyzin, N. (2002, July). Better than BiBa: Short one-time signatures with fast signing and verifying. In Australasian Conference on Information Security and Privacy (pp. 144-153). Springer, Berlin, Heidelberg [paper].
[4] Merkle, R. C. (1989, August). A certified digital signature. In Conference on the Theory and Application of Cryptology (pp. 218-238). Springer, New York, NY.
[5] Hülsing, A. (2013, June). W-OTS+–shorter signatures for hash-based signature schemes. In International Conference on Cryptology in Africa (pp. 173-188). Springer, Berlin, Heidelberg.
[6] Kölbl, S., Lauridsen, M. M., Mendel, F., & Rechberger, C. (2016). Haraka v2–efficient short-input hashing for post-quantum applications. IACR Transactions on Symmetric Cryptology, 1-29. [here]
[7] Lamport, L. (1979). Constructing digital signatures from a one-way function (Vol. 238). Technical Report CSL-98, SRI International. [paper]
[8] Ducas, L., Durmus, A., Lepoint, T., & Lyubashevsky, V. (2013, August). Lattice signatures and bimodal Gaussians. In Annual Cryptology Conference (pp. 40-56). Springer, Berlin, Heidelberg [paper].
[9] Perrig, A. (2001, November). The BiBa one-time signature and broadcast authentication protocol. In Proceedings of the 8th ACM Conference on Computer and Communications Security (pp. 28-37) [paper] .
Hashing (Simularity)

Similarity hashes allow for two data objects to be compared for their similarity.
Similarity assessment methods
The following relate to the basic methods used for string similarity:
- String similarity String similarity. This measures edit distance (including Levenshtein distance), Jaro (including Jaro-Winkler), and QGrams.
- String enthropy String enthropy. Measurement of the entropy of strings.
- Soundex Soundex. Soundex uses a phonetic algorithm to classify a sound as it is pronounced. It focuses on matching phrases which have minor spelling errors.
Similarity hashes
The following are the tips related to similarity hashing:
- Similarity hash: SimHash (Charikar similarity) in Python Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash (Nilsimsa similarity) Nilsimsa. The Nilsimsa similarity is used to find similarities between spam emails.
- Context Triggered Piecewise Hashes (CTPH): ssdeep CTPH similarity. Kornblum [6] created ssdeep and which computes fuzzy hashes. This aims to match similar byte sequences, no matter if there are differences between these sequences. For this we break a file up into fragments with a rolling hash function. We then produce a small hash for each of those fragments. These are then aggregated to produce the complete hash of a file. In comparing file signatures, we treat the resultant hash value as a string, and then uses an edit distance method to compare.
- TLSH (A Locality Sensitive Hash) TLSH similarity. In malware analysis and in text similarity, we often have to identify areas of data within files which are similar. One method is TLSH (A Locality Sensitive Hash), and which was defined by Oliver et al [7]. It is used - along with ssdeep - by VirusTotal to identify a hash value for malware.
- Minhash (Jaccard similarity) Jaccard similarity. The Minhash method is used to find similarities between strings, files and metadata.
- Counting identical elements (HyperLogLog) HyperLogLog. Counting the number of identical elements.
Hazmat cryptography

The Cryptography library in Python contains interfaces to common cryptographic algorithms, including symmetric key methods, hashing, public key, and key derivation functions. Many of these are contained with the Hazmat (Harzardous Material) primative setup.
Hashing, HMAC, CMAC, Poly1305 and HKDF
-
Hazmat Hashes. Hazmat Hashes. This includes the hashing methods in the Hazmat cryptography library. This includes Blake2p, Blake2s, MD5, SHA1, SHA224, SHA256, SGA384, SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHA512, SHA512-224, SHAKE128 and SHA256.
-
Hazmat Hashes. Hazmat Hashes. In this case we will implement Python code to determine SHA1, SHA2, SHA3, Blake2, MD5 and SM3 hashes.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
- Hazmat HKDF. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
- Hazmat CMAC. Hazmat CMAC. CMAC methods using the Python cryptography primitives.
- Hazmat Poly1305. Hazmat Poly1305. Poly1305 methods using the Python cryptography primitives.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
Symmetric key
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat. Implementation of ChaCha20/Poly1305 with a random key using Hazmat.
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat. Implementation of AES GCM with a random key using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hazmat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Hazmat Symmetric Key Padding. Symmetric key. This includes the coverage of padding with Hazmat.
- Hazmat Symmetric Key Padding. Symmetric key. This includes the coverage of padding with Hazmat.
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
- Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . With 3DES encryption, we use a 128-bit key and a 64-bit IV value. The two modes supported are ECB (without salt) and CBC (with salt). The DES algorithm has been around for a long time, and the 56-bit version is now easily crackable (in less than a day on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases, and splits the key into two. Overall the key size is typically 112 bits (with a combination of the three keys - of which two of the keys are the same). In this case we will use PKCS7 padding, and which fills the input data with a value that is equal to the number of padding bytes. Overall, DES has a 64-bit block size, and which equates to eight ASCII characters.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key . And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.
Asymmetric key
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- ECC key generaton with Hazmat. Elliptic Curve key gen. Creating ECC keys using Hazmat and Python.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- Hazmat RSA signing (with key values). RSA signing with Hazmat. RSA signing using Python and with Hazmat (with key values).
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here]
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Signatures. DSA Signatures. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. The ECDSA method is an extension of DSA, but implemented with elliptic curve (EC) methods. As with most public key signing methods, we take a hash of a message, and then apply a private key to create a signature (\(r,s\)). This is done by creating a random value (\(k\)) to produce the signature. The signature is then verified using the associated public key. This then verifies the creator of the signature and that the message has not been changed.
Digital Signature: ECDSA/EdDSA
- ECDSA with Hazmat. ECDSA wih Hazmat. This outlines ECDSA with Hazmat.
- Ed25519 for EdDSA signatures with Hazmat. EdDSA: Ed25519. This page uses the Hazmat primitives for the cryptography library.
- Ed448 for EdDSA signatures with Hazmat. EdDSA: Ed448. This page uses the Hazmat primitives for the cryptography library.
- Ed25519 using NaCl. Ed25519. This page uses the NaCl port from libsodium.
- ECDSA Signatures with Hazmat (SECP256R1, SECP384R1, SECP521R1, SECP224R1, SECP192R1, and SECP256K1). ECC Signatures. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and then creates an ECDSA signature for a given message.
Digital Signature: RSA
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
Key exchange: ECDH/X25519
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives and showing the byte values for the key.
Tokens
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
Homomorphic Encryption

Homomorphic encryption supports mathematical operations on encrypted values. Partial Homomorphic Encryption (PHE) supports a few arithmatic operations, while Full Homomorphic Encryption (FHE) supports add, subtract, multiply, and divide. Homomorphic encryption normally involves a public key to encrypt the data, and a private key to decrypt it. There have been four main generations of homomorphic encryption, and the most recent being the HEAAN method.
Simple
- Simple Homomorphic Cipher. Hom. This outlines a Simple Homomorphic cipher.
- Simple Homomorphic Cipher (Python). Hom. This outlines a Simple Homomorphic cipher with Python.
- Full Homomorphic Cipher with a Public Key. Public key. This outlines a Simple Homomorphic cipher using a public key
ElGamal
- ElGamal Homomorphic Cipher (Go). ElGamal. This outlines ElGamal Homomorphic cipher with Go.
- ElGamal Homomorphic Cipher (Go) - Divide. ElGamal. This outlines ElGamal Homomorphic cipher with Go with divide.
- ElGamal Homomorphic Cipher (Go) - Additive. ElGamal. This outlines ElGamal Homomorphic cipher with Go with addition.
- ElGamal Homomorphic Cipher for Multiplication (Python). ElGamal. This outlines ElGamal Homomorphic multiplication with Python.
- ElGamal Homomorphic Cipher for Division (Python). ElGamal. This outlines ElGamal Homomorphic division with Python.
- ElGamal Homomorphic Cipher for Addition (Python). ElGamal. This outlines ElGamal Homomorphic addition with Python.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (Python). ElGamal. This outlines ElGamal Homomorphic subtraction with Python.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
RSA
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
ZKP
- Full Homomorphic Cipher to determine if Bob is older. Older. This outlines a Simple Homomorphic cipher to determine if Bob is older than Alice.
- Full Homomorphic Cipher to determine matching password. Password. This outlines a Simple Homomorphic cipher to determine if a password matches
- Interactive ZKP With Probablistic Methods. ZKP. Interactive ZKP With Probablistic Methods using Python.
- Full Homomorphic Cipher for Millionaire's Problem. Millionaire. This outlines a Simple Homomorphic cipher for the Millionaire's Problem
Voting
- Trusted voting. Trusted. A trusted voting method.
Secret share
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Lattice
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
Full Homomorphic Cipher
- Full Homomorphic Cipher for 2-bit Adder. Adder. This outlines a Simple Homomorphic cipher for a 2-bit adder with DGHV.
- Full Homomorphic Cipher for Full Adder. Full Adder. This outlines a Simple Homomorphic cipher for a full adder with DGHV.
- Full Homomorphic Cipher for 4-bit Adder. Adder. This outlines a Simple Homomorphic cipher for a 4-bit adder with DGHV.
- Full Homomorphic Cipher for 4-bit Adder/Subtractor. Subtract. This outlines a Simple Homomorphic cipher for a 4-bit adder/subtractor with DGHV.
- Full Homomorphic Cipher to XOR two integers. X-OR. This outlines a Simple Homomorphic cipher to X-OR two integers
Paillier
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier) .
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Damgård-Jurik Homomorphic Encryption With Secret Shares. Damgård-Jurik Method. Two of the major areas of developments within cybersecurity will be the usage of homomorphic encryption, and in the usage of Shamir secret sharing. With homomorphic encryption, we can encrypt values, and then operate on them with arithmetic functions (such as add, subtract and multiply), and with Shamir secret sharing, we can split secrets into shares, and then distributed them over networks. These approaches will take privacy to new levels. So let’s look at the Damgård-Jurik method.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Learning with Errors (LWE)
- Learning With Errors . LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret key value (s) and another value (e). Next we select a number of values (t[]) and calculate g[] = t[] x s + e. The values of g[] and t[] become our public key.
- Public Key Encryption with Learning With Errors (LWE). LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret value (s) and which is our private key. We then create a public key which is based on random numbers (A), and then generate another set of numbers (B) which is based on A,s and random errors e. An example of encryption with multiple bits is given.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE)
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Others
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
- SIDH Go. SIDH. Post-quantum key exchange.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Anonymous crypto. Anon. Anonymous crypto.
- Rho factorization. Rho. Rho alogorithm.
- Post-quantum signing (BLISS). BLISS. BLISS method.
Homomorphic Encryption with Krytology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Homomorphic hashing
- Homomorphic Hashing with Golang. Homomorphic hashing. Normally with hashing methods, we need to take all the previous data and new data in order to create a new hash value for our data. In a homomorphic hashing method, we can basically take the previous hash, and then add on any new data values. We can also remove previous data values from our hash, too. This is more efficient in computing, as we do not have to process all of our data into a new hash, and can use simple homomorphic operations for the computation. The method we will use (LtHash) was initially defined by Bellare and Micciancio and updated Lewi et al at Facebook.
Identity Based Encryption (IBE)

This page outlines a few basic principles around the usage of IBE.
Identity Based Encryption (Pairing based)
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pair-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Identity Based Encryption (Others)
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Güther's implicitly certified identity-based public keys (IBE). Günther. This method allows Bob to generate Alices public key from her identity and publicly available parameters.
- Girault's self-certified public keys (IBE). Girault. This method allows Bob to generate Alices public key from her identity and publicly available parameters, and where we use an RSA key pair to self-certify Alice's public key.
Intrusion Detection Systems (IDS)
- Intrusion Detection Systems. Snort. This outlines some of the basics of IDS, including the requirement for Intrusion Detection Systems (IDSs), and where they are used.
- Advanced Network Forensics (Snort). Adv Network Forensics. This provides information on how to detect threats through network forensics with Snort
Snort

- Snort IDS. Snort. This is a Snort Analyser.
- Snort IDS 2 with rules editor. Snort. This provides information on how to detect threats through network forensics with Snort, and with an editing function for rules.
Presentation
IoT

The key objectives of this page are: Understand how a Pen Tester can generate vulnerabilities and test using the Metasploit framework; Define the options and payloads required to generate and use vulnerabilities; and Gaining remote access.
Devices
- Access the Wi-fi kettle. Go. This page outines how to access a wi-fi enabled kettle.
- Philips Hue Wireless Lighting. Go. This page shows how to use RESTful Web services to access to the Hue Led Lamps.
- Kali and R-PI. Go. This page shows the setup of a security testing infrastructure using a Raspberry Pi (R-PI) and a wifi access point.
- Kali, R-PI and RF electrical socket. Go. This page shows the control of an RF electical socket from a RPI.
- Capture from a Polar H10 heat rate sensor. Go. This page shows the capture of the Polar H10 heart sensor with an Ubertooth One.
- Trusted IoT: Linking IoT Devices to NFTs. Go. This page outlines a research paper which links a device to an NFT (Non-fungible Token).
Shodan Scanning
-
IoT Scan (Shodan). Go. This page includes a search of the Internet for key terms, such as for "apache", "mysql" and "cisco".
- IoT Banner Scan (Shodan). Go. This page includes a search of the Internet for key terms with the banner as a result (for the Top 10)
- Internet Services (Shodan). Go. This page includes a search of the Internet for key terms and display the IP address and port.
IoT Libraries
- libDisco with Go. libDisco. libdisco is a Golang library which can be used to create secure connections. It is based on the STROBE protocol framework. Symmetric cryptographic primitives rely on SHA-3 permutation, and asymmetric cryptographic primitives on X25519 and ed25519. STROBE defines a range of cryptographic protocols to integrate with IoT devices. In order to reduce processing, energy and memory requirements, it only uses Keccak (SHA-3) to encrypt and authenticate messages.
COSE/COBR
In computer security, we often have to represent binary data, in single values or groups of characters, bytes, words, long words, signed integers, floating-point values, double-precision floating-point values, and so on. This might be in the form of a data object, a signature or even encrypted content. For this, the ANS.1 DER format is often used, such as presenting digital certificates and signatures. An improvement on this for small messages with security is Concise Binary Object Representation (CBOR) — and which is defined in RFC8949 [1]. While JSON represents text-based data objects CBOR focuses on binary objects. It has been designed to create a lightweight encoder and decoder. This supports the use of CBOR within an IoT infrastructure. The data, also, does not require a data schema to be able to decode it, along with being extensible. CBOR defines the format of binary data with data objects and messages. We can then integrate security with CBOR Object Signing and Encryption (COSE), and which is defined in RFC8152 [2]. This includes signatures, message authentication codes (MACs), encryption and creating serialised objects.
- 128-bit AES GCM. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) can then build on this to include signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use a symmetric key to encrypt a message, and then decrypt it. In this case we will use AES GCM with a static 128-bit key ("0x000102030405060708090a0b0c0d0e0f").
- 256-bit AES GCM. Go. In this case we will use AES GCM using a random 256-bit key (32 bytes).
- EdDSA. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) [2] can then build on this to includes signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use EdDSA to create a signature for a message.
- ECDSA. Go. In this case we will use ECDSA to create a signature for a message.
- HMAC. Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT. Go. In this case we create a CWT token, and sign with an HMAC signature.
- ECDH. Go. In this case we create a symmetric key from ECDH. For this we will derive a shared key from the public key of Alice and Bob, and then define a single recipient which can derive the CEK (Content Encryption Key) using their private key. We will use the curves of P-256 (secp256r1), P-384 (secp384r1), P-521 (secp521r1) or SECP256K1 (as used with Bitcoin).
- RSA using COSE and CBOR. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\).
- RSA: dQ, dP and InvQ. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). The key pair also includes \(dQ\), \(dP\) and \(InvQ\), and these can be used with the Chinese remainder theory to optimize the decryption process.
Metasploit
- Armitage and Metasploit. Go.
- Exploiting Android with Metasploit. Go.
- Exploiting Android with Metasploit - Part 2. Go.
- Exploiting Windows/Mac OS X with Metasploit. Go.
- Remote Desktop Windows/Mac OS X with Metasploit. Go.
- Metasploit. Go.
- Internet of Things Security. Go.
- Metasploit (Enumeration and Scanning). Go.
- Metasploit (Malware). Go.
IP

 The following are a few interesting techniques around IP addresses:
The following are a few interesting techniques around IP addresses:
- Your details. IP. This shows your browser details.
- IP address analyser. IP. This involves converting an IP address to the host and network part of the address.
- IP subnet analyser. IP subnets. This involves converting an IP address to the host and network part of the address.
- IP address analyser. IP. This involves analysing IP addresses.
- Max subnets. Max subnets. This involves converting an IP address to the host and network part of the address.
- Route summarization. Summarization. This involves converting an IP address to the host and network part of the address.
- Whois. Whois. This does a basic Whois on a domain.
- URL Obfuscation. Obfuscation. This outlines URL obfuscation.
- HTTP Responses. Test. HTTP.
- Capturing Network Packets (Python). WinPCap. HTTP.
Cisco related
- Routing table. Routing table. This involves viewing a routing table for a Cisco device.
- ACL Generator. ACL. This involves a simple calculator for ACLs on network ranges.
- EIGRP metrics. EIGRP. Learn the basics of EIGRP metrics.
- VoIP B/W. VoIP. Calculate bandwidth for VoIP.
- Wild Card. Wild Card. On a Cisco device a wildcard mask is used to identify the parts of an IP address that need to be matched. It thus uses a wildcard mask, where a 0 in the bit position identifies that the device should match that bit, else a 1 shows that it should ignore it.
Protocols
- HTTP. HTTP. Show the request and response for HTTP.
- Ping analyser. IP. This involves converting a ping of a site.
IP Challenges
-
IP Test 1. IP Test. IP Classification test. This is a simple test which generates a range of IP addresses, and you must determine the IP address classification.
IP Subnet Challenge 1 Demo
-
IP Test 2. IP Test. IP Classification test Part 2. This test provides an address classification, and the user must find the addresses which are of this classification.
IP Subnet Challenge 2 Demo
-
IP Test 3. IP Test. IP Classification test Part 3. This test provides an address classification, where the network part of the address is determined.
IP Subnet Challenge 3 Demo
Subnet Challenges
- Subnet Test 1. Subnet Test. Subnet Test.
-
Subnet Test 2. Subnet Test. Subnet bits.
- Subnet Test 3. Subnet Test. Find the nth usable subnet. This test involves finding the nth usable subnet.
- Subnet Test 4. Subnet Test. Maximum subnets. This is a test page to determine the maximum number of subnets and hosts/subnet for IP classed addressing.
- Subnet Test 5. Subnet Test. Maximum host/subnet. This is a test page to determine the maximum number of hosts per subnet.
- Subnet Test 6. Subnet Test. Determine the required subnet mask for a given number of subnets. This is a test page to determine the required subnet mask for a given number of subnets and a given IP address classification.
- Subnet Test 7. Subnet Test. Determine the required subnet mask for a given number of host/subnet. This is a test page to determine the required subnet mask for a given number of hosts per subnet and a given IP address classification.
- Subnet Test 8. Subnet Test. Route summarization. This involves a calculation on route summarization.
- Subnet Test 9. Subnet Test. Binary to IP.
- Subnet Test 10. Subnet Test. Hex to IP.
-
Subnet Test 13. Subnet Test. Wild card mask network bits. Find the number of bits in the network part of the wild card mask. IP Wildcard challenge
- Subnet Test 14. Subnet Test. Wild card mask host bits. Find the number of bits in the host part of the wild card mask. IP Wildcard challenge
- Subnet Test 15. Subnet Test. Wild card mask ... find the network address. Find the network for the wild card mask. IP Wildcard challenge 2
- Subnet Test 16. Subnet Test. Find a matching IP address for a network and wild card mask. Find the IP for a network and a wild card mask.
- Subnet Test 17. Subnet Test. Find an address which is on a given network. Find an IP address on a network, for a given network address and subnet mask.
- Subnet Test 18. Subnet Test. Find an IP address on the same network. Find an IP address on the same subnet.
- Subnet Test 19. Subnet Test. Find subnet. Convert subnet mask.
- Megatest. Subnet Test. Challenging test for subnets.
JavaScript

JavaScript code allows execution within the browser, rather than on the server. It is often faster than code that runs on a server. Along with this we can also use Node.js, and which runs JavaScript code on a server.
Symmetric key
- AES. AES. In this example, we will use either a pre-generated key or a random one, and use AES (Rijndael) encryption.
- ChaCha20 and Poly1305. ChaCha. This page outlines Poly1305 and ChaCha20. ChaCha20 is a symmetric key method and Poly1305 is a message authentication code (MAC). They were created by Daniel J. Bernstein, and are alternatives to AES and HMAC.
- CMS (Padding). CMS. This page uses PKIJS encrypting on CMS. With CMS we can This document describes the Cryptographic Message Syntax (CMS). With this we can encapsulate an message within an encrypted entity.

Hashing
- Hash. Hash. This page defines a JavaScript Hash calculator. This uses a client-side JavaScript code to determine the hash signatures of a text value.
Signatures
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
- Boneh–Lynn–Shacham (BLS) signature. BLS. Boneh–Lynn–Shacham (BLS) signature method produces short signatures. They use elliptic curve pairing (and which are also known as bilinear maps).
Key exchange
- ECDH. ECDH. Elliptic Curve Diffie Hellman (ECDH) is used to generate a shared key. This implementation uses Elliptic Curve Cryptography (ECC) with JavaScript.
CryptoJS
- CryptoJS. CryptoJS. This page uses client-side JavaScript code to hashing, encrypt and sign, including for symmetric key (AES), streaming ciphers, hashing methods, and HMAC.
Blockchain
- PATRICIA trie. PATRICIA. In the following, we have the Top 2,500 Web sites in the world, and implemented with a Radix Trie (aka PATRICIA trie) In the following we have the Top 2,000 web sites on the Internet, and which have been indexed using the PATRICIA trie.
Public key
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
- RSA. RSA. RSA is an asymmetric encryption algorithm, which uses two keys, one to encrypt and the other to decrypt. It was created in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman, and is still one of the most widely used encryption methods. A typical application is in authenticating a sender, where the senders private key is used to encrypt a message, and then is decrypted by the receiver with the senders public key (which is known to anyone who wants it). It is also typically used for encrypting disks/files, such as for EFS.
Digital Certificates
- X.509 certificates in JavaScript. RSA and ECDSA Signed certificates. This page will generate either RSA and ECC key pairs, and then generate X.509 certificates, using either a signature of SHA1withRSA or SHA256withECDSA. For RSA signing we use an RSA private key to sign the certificate, and with ECDSA signing we use an ECC private key to sign the certificate.
Tokens
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
Random
- Random number generator. Rand. In the past, encryption and decryption had to be done through native code libraries, such as with Bouncy Castle and OpenSSL. With the increasing processing power of Web browsers, it is now possible to use encryption using JavaScript, which thus provides client-side processing of data. This Web page uses Javascript encryption, and generates a random 256-bit text key or a hex version. The 256-bit key is generated by generating 60 random numbers (from 0-25), and converting these to an ASCII character.
Malware obfuscation
- Malware obfuscation. Obfuscation. A malware writer will often hide certain keywords from the browser/human by encoding them in another format. This is typically done for hex coding (\xZZ), 16-bit unicoding (\uZZZZ) and octal coding (\ZZZ). To test, enter a value, and then press the button and it will convert encoded string.
Message Authentication Codes
- Chaskey (MAC). Chaskey. Chaskey Cipher is light-weight cryptography method for signing messages (MAC) using a 128-bit key. The hardware implementation only requires 3,334.33 gate equivalent with an operating clock frequency of 1 MHz (whereas Keccak requires 4,658 GE). In the page we create the Mac signature and also encrypt for CBC.
Other
- Password generation/hashing. Hashing. Linux can use salted passwords where the username, hashing method and hashed password are stored in a password file [More details]. The main methods are
Hashing

At times we need to generate secrets, such as encryption keys, from passwords or nonce values. A Key Derivation Function (KDF) is a verifiable way of doing this.
Key Derivation Functions (KDFs)
The following are the tips related to hashing:
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Password strength. Test. This outlines the strength of various passwords types.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
HKDF
The following are the tips related to Key derivation hashing:
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Hazmat HKDF for different hashing methods. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
-
HKDF key derivation with OpenSSL [
here]
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
PBKDF2
The following are the tips related to Key derivation hashing:
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- AES GCM (Python) with PBKDF2. AES GCM (Python) with PBKDF2.
- Fernet with PBKDF2 . AES GCM (Python) with PBKDF2.
- PBKDF2 key derivation. AES GCM (Python) with PBKDF2.
- Key Rotation with Fernet. AES GCM (Python) with PBKDF2.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Bcrypt
The following are the tips related to Key derivation hashing:
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- BCrypt. BCrypt. BCrypt with Rust.
-
Hash to password with Go. Hashing to Argon2, Scrypt and BCrypt. Hash to password with Go, including Argon2, Scrypt and BCrypt.
scrypt
- scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Argon 2
The following are the tips related to Key derivation hashing:
- Argon 2. Go. Outline of Argon2.
- Argon 2 with NaCl. Go. Outline of Argon2 using NaCl.
- Argon 2. Argon 2. Argon 2 with Rust.
- Balloon. Go. Outline of Balloon.
Other
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
- Double ratchet. Go. Outline of double ratcheting.
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
Outline
HMAC Key Derivation function (HKDF) is used to derive an encryption key from a passphrase. Initially, HKDF creates a pseudorandom key (PRK) using a passphrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), and along with a salt value. Next, the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys [RFC 5869][article]. In this case, we will use SHA-256.
The following shows how an encryption key can be generated using HKDF, and where we need a secret and a salt value. Both Bob and Alice have the same secret and salt.

With PBKDF2 (Password Based Key Derivation Function 2), we hash for a given number of rounds:

Key exchange

Key exchange is a way for Bob and Alice to communicate and for them to agree on a shared secret. The original method defined uses discrete logarithms (Diffie-Hellman), but most modern methods use elliptic curve techniques (ECDH). As quantum computers can crack both discrete log and elliptic curve methods, there are post quantum cryptography methods proposed. This includes SIDH, CSIDH, SIKE, and NewHope.
Key interchange/generation (Diffie-Hellman)
The following relates to key interchange:
- Selecting \(g\) in Diffie Hellman. G in Diffie Hellman. Picking a safe value of the generator \(g\) in discrete logarithms.
- Diffie-Hellman. Diffie-Hellman Calculation. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Real example). Diffie-Hellman Real. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Python). Diffie-Hellman. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (pre-compute). Diffie-Hellman (pre-compute). Many sites use the same prime numbers, which can then be cracked with a pre-computing attack.
- Key generation. Key gen. This will generate keys for different methods based on a passphrase.
- Diffie-Hellman (Man-in-the-middle). DF. This outlines the man-in-the-middle method for Diffie-Hellman.
- An Alternative Diffie-Hellman method. Alterative DH. This outlines an alternative Diffie-Hellman method.
Authenticated Key Exchange
The following are the tips related to Key derivation hashing:
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- MTI/A0. MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{ax+by} \pmod p\). MTI (Matsumoto, Takashima, Imai).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0. MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{x+y} \pmod p\)
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). The resultant key is \(xyG \)
- MTI/C0. MTI/C0. This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{xy} \pmod p\)
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG\).
- MTI/C1. MTI/C1. This outlines MTI/C1, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{abxy} \pmod p\).
- MQV (Menezes–Qu–Vanstone). MQV. MQV was created Alfred Menezes, Minghua Qu and Scott Vanstone in 1995 and is an authenticated key exchange method. Alice holds a key pair \((A,a)\) and Bob has a key pair \((B,b)\). With this \(a\) is Alice's private key, and \(A=aG\) is her public key. For Bob, his public key will be \(B=aG\) and a private key of \(b\), and where \(G\) is the base point on the elliptic curve.
- HMQV (Menezes–Qu–Vanstone). HMQV. HMQV builds on MQV and adds the identity of Bob and Alice.
- ECDH with X25519 and Blake2b. ECDH with X25519 and Blake2b. This uses PyNaCl to create an authenticated key exchange and uses X25519 and Blake2b.
Elliptic Curve (ECDH) - Python
The following are the tips related to ECC:
- Elliptic Curve. Elliptic Curve. Elliptic Curve is a public key method which can also be used to generate a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with simple parameters. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
Elliptic Curve (ECDH) - Golang and Node.js
The following are the tips related to ECC:
- ECDH with Go. ECDH. ECDH with Go.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with node.js. ECDH. ECDH with node.js.
- ECDH with JavaScript. ECDH. Elliptic Curve Diffie Hellman.
Password Authenticated Key Exchange (PAKE)
The following are the tips related to Key derivation hashing:
- SPAKE2. Go. Outline of SPAKE2.
- OPAQUE. Go. Outline of OPAQUE.
- SPEKE. Go. Outline of SPEKE (Simple Password Exponential Key Exchange).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
- J-PAKE. J-PAKE. This example generates a shared key based on a shared password.
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses discrete logs.
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
PQC NIST Finalists (Key Exchange)
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Key interchange/generation (Other)

The following relates to key interchange:
- Curve25519. Curve25519. This outlines Curve25519, which is used in the Tor network.
- Authenticated Key Exchange (Discrete logs). YAK. Key exchange with public keys and uses discrete logs.
- Authenticated Key Exchange (ECC). YAK. Key exchange with public keys and uses elliptic curve methods.
- Shamir No-key protocol. Shamir No Key. In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated.
- Shamir No-key protocol (sepc256k1). Shamir No Key (EC). In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated using the sepc256k1 elliptic curve.
- Conference keying (Burmester-Desmedt method). Conference keying. In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it.
- Conference keying (Burmester-Desmedt method) - Elliptic Curve (sepc256k1). Conference keying Elliptic Curve (sepc256k1). In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it, and uses the sepc256k1 elliptic curve.
Key exchange (with pairing)
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Kryptology

We need to build a new Internet. One that is build on mathematics and certainty, rather than the patchy version we have now. For this we need a layer of cryptography at the lowest level, and build software interfaces on top of this. Along with this we now have cryptographic methods which can now provide a foundation of trust, and which preserve privacy. And so the old libraries of OpenSSL are being squeezed out in favour of the new ones which are built on a solid foundation. The latest of these new "privacy-aware" libraries is Kryptology, and created by Coinbase. This library provides the APIs that developers need, in order to apply to areas of blockchain development. This library include BLS (Boneh-Lynn-Shacham) signatures, Zero-knowledge Proofs (ZKPs) and Shamir Secret Shares (SSS). With BLS we can digitally sign for data, but also preserve its privacy. Applications of this include group signatures, where multiple entities can merge their signing keys together and provide a single signature for a transaction. With SSS, we can split encryption keys up into shares, and then distribute them across a network. When required, we can call these shares back to reconstruct the key.
The focus for Coinbase seems to be the application of privacy coins, and where no tracking can be applied to the usage of these digital coins. This should support full anonymity for transactions, as opposed to Bitcoin which only supports pseudo-anonymity.

ECC Basics
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining n.G for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Points (Base Point and Others). Elliptic Curve points. Two common curves used in ECC (Elliptic Curve Cryptography) are secp256k1 (as used in Bitcoin and Ethereum) and P256 (secp256r1). The "k1" refers to the Kolbitz curve 1 (named after the creator of ECC). With these we have a base point which are can operate on. This is typically defined as \(G\). We can then operate on this with add and multiply operation. For example, \(2G=G+G\) and \(P=n.G\). In this following we will show the base point for a number of common curves, such as secp256r1, P256, Pallas, Curve 25519, BLS12381G1, BLS12381G2, BLS12377G1 and BLS12377G2.
ECDH
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret. We will use Golang and the Krytology library.
Simple ECC on curves
- Public key points for curves. Simple. Display public key points for scalars.
BLS Curve
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
Accumulator and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
Pallas Curve
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
Pairing-based Crypto
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
ElGamal and ECC
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a numerical input.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
Shamir Secret Shares
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Homomorphic Encryption
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Zero knowledge proofs
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
Verifiable Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Hash to scalar and point
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
CP-ABE
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Lattice cryptography

Latice cryptography is proposed as a post-quantum robust method for public key encryption, especially focused on digital signatures and key exchange mechanisms (KEMs).
Principles
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
NTRU
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- Lattice Encryption: NTRU Key Generation Python). NTRU. Outlines how NTRU operates for key generation.
Homomorphic
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Digital Signatures
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
Public-Key Encryption/Key Exchange
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
Light-weight cryptography

While AES and SHA work well together within computer systems, they struggle in an IoT/embedded world as they take up: too much processing power; too much physical space; and consume too much battery power. So NIST outlines a number of methods which can be used for light-weight cryptography, and which could be useful in IoT and RFID devices [1]. They define the device spectrum as:
- Conventional cryptography. Servers and Desktops. Tablets and smart phones.
- Light-weight cryptography. Embedded Systems. RFID and Sensor Networks.
With embedded systems, we commonly see 8-bit, 16-bit and 32-bit microcontrollers, and which would struggle to cope with real-time demands for conventional cryptography methods. And in the 40+ years since the first 4-bit processor, there is even a strong market for 4-bit processors. RFID and sensor network devices, especially, have limited numbers of gates available for security, and are often highly constrained with the power drain on the device.
So AES is typically a non-starter for many embedded devices. In light-weight cryptography, we often see smaller block size (typically 64 bits or 80 bits), smaller keys (often less than 90 bits) and less complex rounds (and where the S-boxes often just have 4-bits).
For light-weight cryptography the main constraints that we have are typically related to ener requirements, gate equivalents (GEs), and timing. With passive RFID devices, we do not have an associated battery for the power supply, and where the chip must power itself from energy coupled from the radio wave. An RFID device is thus likely to be severely constrained in the power drain associated with any cryptography functions, along with being constrained for the timing requirements and for the number of gates used. Even if an RFID device has an associated battery (active RFID), it may be difficult to recharge the battery, so the drain on power must often be minimised.
There is thus often a compromise between the cryptography method used and the overall security of the method. Thus often light-weight cryptography methods balance performance (throughput) against power drain and GE, and do not perform as well as main-stream cryptography standards (such as AES and SHA-256). Along with this the method must also have a low requirement for RAM (where the method requires the usage of running memory to perform its operation) and ROM (where the method is stored on the device). In order to assess the strengths of various methods we often define the area that the cryptography function will use on the device – and which is defined in \(µm^2\). The NIST finalists are defined in this [article]
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- GIFT AEAD. GIFT. GIFT is a light-weight block cipher. It is a (NIST Finalist)
- Elephant. Elephant. Elephant is a light-weight stream cipher. It is a (NIST Finalist).
- TinyJambu. TinyJambu. TinyJambu is a light-weight block cipher. It is a (NIST Finalist)
- Isap AEAD. Isap. Isap is a light-weight block cipher. It is a (NIST Finalist)
- PHOTON-Beetle AEAD. PHOTON-Beetle. PHOTON-Beetle is a light-weight block cipher. It is a (NIST Finalist)
- Romulus AEAD. Romulus. Romulus is a light-weight block cipher. It is a (NIST Finalist)
- Sparkle AEAD. Sparkle. Sparkle is a light-weight block cipher. It is a (NIST Finalist)
- CLEFIA. CLEFIA. CLEFIA is a light-weight block cipher.
- LED. LED. LED is a light-weight block cipher.
- Piccolo. Piccolo. Piccolo is an ultra light-weight block cipher.
- PRESENT. PRESENT. Present is a light-weight block cipher.
- Pyjamask. Pyjamask. Pyjamask is a light-weight block cipher.
- SIMON. SIMON. SIMON is a light-weight block cipher.
- SKINNY. SKINNY. SKINNEY is a light-weight block cipher.
- SPECK. SPECK. SPECK is a light-weight block cipher.
- XTEA. XTEA. XTEA is a light-weight block cipher.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encryption/Decryption. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.
Light-weight crypto (Other)
- Chaskey (MAC). Chaskey. Chaskey is a light-weight MAC function.
- Chaskey (MAC). Chaskey (Python). Chaskey is a light-weight MAC function.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (ASCON)
ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRFF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
Discrete Logs (Solving)

A discrete log problem is in the form of \(g^x \pmod p\) and where we know \(g\) and \(p\) and must solve for \(x\).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Message Authentication Code (MAC)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
HMAC
The following are the tips related to Key-based hashing:
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authentication both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2), Blake2b, SM3 and SHA-3. This page outlines the HMAC-MD5 methods using the Hazmat cryptography layer.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- HMAC (COSE). Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT with HMMAC. Go. In this case we create a CWT token, and sign with an HMAC signature.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- HMAC with Rust. HMAC. HMAC with Rust.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HMAC with OpenSSL. MACs with OpenSSL. HMAC in OpenSSL for a given input value, password and hashing method.
Cipher MACs
The following are the tips related to Key-based hashing:
- MACs with OpenSSL. MACs with OpenSSL. MAC methods implemented in OpenSSL, including CMAC and GMAC.
Key-based hashing
The following are the tips related to Key-based hashing:
- SipHash. Siphash. Siphash is a fast key-based hashing method.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Meow. Meow. Meow is one of the fastest hashing methods.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
Magic Numbers

This pages contains information related to magic numbers in file formats.
Network and File Forensics
- Magic numbers. Magic. This provides information on magic number for file forensics.
Graphics formats
- JPEG Analysis. JPEGs. This provides an analysis of JPEG files.
- GIF Analysis. GIFs. This provides an analysis of GIF files.
- TIF Analysis. TIFs. This provides an analysis of TIF files.
- PNG Analysis. PNGs. This provides an analysis of PNG files.
- BMP Analysis. BMPs. This provides an analysis of BMP files.
- PSD Analysis. PSDs. This provides an analysis of PSD files.
- WMF Analysis. WMF. This provides an analysis of WMF files.
- Adobe Illustrator Analysis. AI. This provides an analysis of AI files.
- Adobe In Design Analysis. INDD. This provides an analysis of INDD files.
- MIDI file. MIDI. This provides an analysis of MID files.
- ICO file. ICO. This provides an analysis of ICO files.
- PS file. PS. This provides an analysis of PS files.
- EPS file. EPS. This provides an analysis of EPS files.
- VSD file. VSD. This provides an analysis of Microsft Visio (VSD) files.
Video and audio formats
- MP3 Analysis. MP3s. This provides an analysis of MP3 files.
- AVI Analysis. AVIs. This provides an analysis of AVI files.
- Flash SWF Analysis. SWFs. This provides an analysis of Flash files.
- Flash FLV Analysis. FLVs. This provides an analysis of FLV files.
- MP4 Analysis. MP4. This provides an analysis of MP4 files.
- MOV Analysis. MOV. This provides an analysis of MOV files.
- WMV Analysis. WMV. This provides an analysis of WMV files.
- WMA Analysis. WMA. This provides an analysis of WMA files.
- JPEG 2000 Analysis. JPEG 2. This provides an analysis of JPEG 2000 files.
- WAV Analysis. WAV. This provides an analysis of WAV files.
Zips, Archives and Library files
- ZIP/Archive Analysis. ZIPs. This provides an analysis of ZIP/Achive files.
- GZ Analysis. GZ. This provides an analysis of GZip files.
- Tar Analysis. Tar. This provides an analysis of TAR files.
- MSI Analysis. MSI. This provides an analysis of MSI files.
- OBJ Analysis. OBJ. This provides an analysis of OBJ files.
- DLL Analysis. DLL. This provides an analysis of DLL files.
- CAB Analysis. CAB. This provides an analysis of CAB files.
- EXE Analysis. EXE. This provides an analysis of EXE files.
- RAR Analysis. RAR. This provides an analysis of RAR files.
- SYS Analysis. SYS. This provides an analysis of SYS files.
- HLP Analysis. HLP. This provides an analysis of HLP files.
- VMDK Analysis. VMDK. This provides an analysis of VMDK files (VMWare Virtual Disks).
- PST Analysis. PST. This provides an analysis of PST files (Outlook Email File).
- JAR Analysis. JAR. This provides an analysis of JAR files.
- SLN Analysis. SLN. This provides an analysis of Microsoft SLN files.
- Class Analysis. Class. This provides an analysis of Java Class files.
- Zlib. Zlib. This provides an analysis of Zlib files.
Documents
- PDF Analysis. PDFs. This provides an analysis of PDF files.
- DOC Analysis. DOCs. This provides an analysis of DOC files.
- RTF Analysis. RTFs. This provides an analysis of RTF files.
- XLS Analysis. XLSs. This provides an analysis of XLS files.
- PPT Analysis. PPTs. This provides an analysis of PPT files.
- MMP File. MMP. This provides an analysis of MMP files.
- DOCX Analysis. DOCX. This provides an analysis of DOCX files.
- XLSX Analysis. XLSX. This provides an analysis of XLSX files.
- PPTX Analysis. PPTX. This provides an analysis of PPTX files.
- MDB Analysis. MDB. This provides an analysis of MDB files.
- Outlook Message Analysis. MSG. This provides an analysis of MSG files.
Disk Image
- Raw disk format. RAW. This provides an analysis of the RAW disk format.
Tests
- File Forensics Test. File Test File Forensics Test.
- File Forensics Test (Fun). File Test (Fun) File Forensics Test.
Presentations
MIRACL Core Library

MIRACL Core is an open source library, and includes a wide range of public key encryption methods. It is especially focused on elliptic curve and pairing-friendly methods, but also supports a wide range of encryption methods, including RSA, AES and hashing. Overall, it can be ported onto a wide range of systems and supports C, C++, Go, Rust, Python, Java, Javascript and Swift. Along with this it supports limited capability devices such as the Arduino infrastructure. The GitHub repository is [here].
BN254
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.

Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- CL Signatures. CL. CL Signatures in Go using MIRACL.
- CL Signatures (advanced pairing). CL. CL Signatures in Go using MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages using MIRACL.
- PS Signatures. PS. Signatures using PS for short signatures using MIRACL.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures using MIRACL.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.

Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
Rust examples
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
NaCl

PyNaCl is a Python port of LibSodium. It integrates the latest cryptography methods, such as AES, XChaCha20, Blake2b and X25519.
Symmetric Key
- Symmetric key. Symmetric key (XChaCha20 and Poly1305). With symmetric key, Bob and Alice have the same key. NaCl uses the XChaCha20 method, and which supports stream encryption (and which does not require padding as a block cipher does, and is also faster than block cipher modes). ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16 byte nonce. XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24 byte nonce. It has a lower propability of nonce misuse than ChaCha20.
- Encryption with a password. Symmetric Key with KDF. In symmetric key, we generate a secret key. This key is typically a random value or generated from a password and a salt value. If we use a password, we typically use a KDF (Key Derivation Function), and which uses a password and a salt value, in order to create a key of a given size. In this case we will use Argon2i, and which is memory resilent.
Hybrid Encryption
- Box. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Hashing
- Hashing and KDF (Argon2 and scrypt). Hashing and KDF. This case we will use PyNaCl (Networking and Cryptography) library, and which is a Python binding to libsodium. We will hash a password using SHA-256 and SHA-512, and also create a KDF (Key Derivation Function) using scrypt and Argon2.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
Ed25519
-
Ed25519. Ed25519. Using Ed25519 for digital signatures.
-
Finding Points on Ed25519. X25519 (Points).
In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 (Key Exchange)
- X25519 + BLAKE2b key-exchange. X25519. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
Curve 25519
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
Node.js

Node.js uses the JavaScript programming langauge as its base, and allows for code to be run on a server, rather than in the browser (such as with pure JavaScript). To run a node.js program, we run "node myfile.js", and use NPM to install libraries.
Symmetric key
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
RSA and public key
- RSA Opt imal Asymmetric Encryption Padding (OAEP) using Node.js. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
ECC Keys
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.

Hashing
- Hashing with node.js (All). Hashing. Hashing with node.js.
- Hashing with node.js (Selection). Hashing. Hashing with node.js.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- ECDSA with node.js. ECDSA. ECDSA with node.js.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
Key exchange
- Diffie-Hellman with node.js (random prime). DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method and uses a randomly generated prime number (press the button to generate a new prime).
- Diffie-Hellman with node.js. DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method. Each time the prime number will be fixed for the DH group selected.
- ECDH with node.js. ECDH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Elliptic Curve Diffie Hellman (ECDH) key exchange method.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
Key derivation
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
CryptoJS
- CryptoJS (in node.js). CryptoJS (Node.js). Various crypto methods in the browser.
Bulletproofs
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
Blockchain
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
Proxy encryption
- Proxy Encryption - Encrypting With Public Key, And Decrypt with Private Key. Proxy01. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This page just creates a key pair for Alice, and uses it to encrypt with the public key , and decrypt with the private key.
- Proxy Encryption. Proxy02. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This will go through the full use case of proxy re-encryption.
Tokens
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
Random
- Fortuna with node.js. Fortuna. Fortuna random numbers with node.js.
Other
- FPE with node.js. FPR. FPE with node.js.
- Puny with node.js. Puny. Puny character format with node.js.
Accumulators and Witnesses
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
PGP
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Password Entropy
- Password Entropy with Node.js. Password Entropy. Password entropy measures the strength of a password, and is measured as the number of bits which could represent all of the possibilities. An entropy score of less than 25 identifies a poor password, and between 25 and 50 is a weak password. For 50 to 75 we have a reasonable password, and between 75 and 100 is a very good password. Over 100 is an excellent password. The strength of the password relates to the number of characters used, and also the number of characters in the password.
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
- Homomorphic Encryption with Node.js and BGV. Homomorphic Encryption with Node.js and BFG. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BGV method.
Oblivious Transfer (OT)

Oblivious Transfer allows Bob to select data from Alice, but for Alice not to know which value has been selected.
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
OpenSSH

OpenSSH supports the usage of the SSH protocol. This allows for a remote login. One tool which is uses is ssh-keygen, and which allow for the generation of RSA, DSA and elliptic-curve keys that. These can be used for user and host authentication, such as for GitHub login and Cloud instance login.
OpenSSH
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here].
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
Outline

OpenSSL

OpenSSL is a standard library that implements cryptography.
Symmetric key (Command line)
-
Symmetric Key Encryption (OpenSSL 1.x) [here]. In this case we will create cipher text from OpenSSL 1.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 1.x) [here].In this case we will decrypt cipher text from OpenSSL 1.x using a key derived from a password
-
Symmetric Key Encryption (OpenSSL 3.x) [here]. In this case we will create cipher text from OpenSSL 3.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 3.x) [here].In this case we will decrypt cipher text from OpenSSL 3.x using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password.
Hashing
-
Hashing [here] OpenSSL supports a wide range of hashing methods including BLAKE2b, Gost, MD4, MD5, RMD-160, SHA-1, SHA-3, SHA-256 and SHA-512.
Libre OpenSSL
-
Symmetric Key Encryption using Libre OpenSSL [here]. In this case we will create cipher text from Libre OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption using Libre OpenSSL [here]. In this case we will decrypt ciphertext from Libre OpenSSL using a key derived from a password.
-
Hashing [here] Libre OpenSSL supports a wide range of hashing methods including Gost, MD4, MD5, RMD-160, SHA-1, SHA-256 and SHA-512.
Diffie-Hellman parameter generation
-
DH Parameters with OpenSSL [here]. The Diffie-Hellman (DH) method is perhaps one of the greatest inventions in Cybersecurity, and was created by Whitfield Diffie and Marty Hellman. With the DH method, Bob creates a random value (\(b\)) and Alice also creates a random value (\(a\)). Next Bob computes \(B=g^b \pmod p\) and sends it to Alice. Alice computes \(A=g^a \pmod p\) and sends this to Bob. Bob raises the value of \(A\) to the power of \(b\) and takes \(\pmod p\), and Alice raises \(B\) to the power of \(a\) and takes \(\pmod p\). In the end, they will have the same shared value: \(g^{ab} \pmod p\). This can then be used to derive an encryption key that they can use for a secure tunnel. Overall, \(p\) is the large prime number, and also known as the shared modulus between Bob and Alice.
Key derivation function
-
PBKDF2 key derivation with OpenSSL [here] PBKDF2 (Password Key Derivation Function 2) is a key derivation method. Overall it is relatively slow in its operation and where we take a password, a salt value, hashing method, and a number of iterations, in order to produce a given size of encryption key.
-
HKDF key derivation with OpenSSL [here] HKDF (HMAC Key Derivation function) is used to derive an encryption key from a pass phrase. Initially HKDF creates a pseudorandom key (PRK) using a pass phrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), andalong with a salt value. Next the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys.
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Passwords
-
Password example [here]. This page uses the OpenSSL library hash password generator, which is used in UNIX systems for the hashing of passwords which are contained in /etc/shadow and /etc/passwd. For newer passwords, the "-1" options is used to created the hashed value.
-
Hashed passwords with OpenSSL [here].
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
Public key
-
Generating an ECC key pair with OpenSSL [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)).
-
Generating an RSA key pair with OpenSSL [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2).
-
Generating an RSA key pair with OpenSSL with encryption [here]. This page implements RSA key pair generation with an encrypted key pair. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). In this case we will encrypt the key pair with either 3DES, 128-bit AES, 192-bit AES or 256-bit AES. The same password must be used to encrypt and decrypt.
-
Generate prime with OpenSSL [here]. Prime numbers are important in public key encrytion, and are used with RSA and ECC. For RSA, we generate two prime numbers (\(p\) and \(q\)) and which are multiplied together to create a modulus (\(N\)). If these prime numbers have 512 bit values, the modulus will be a 1,024 bit value. This defines the basic secure of RSA. With elliptic curve we use smaller prime numbers, such as 256-bit values for the secp256k1 curve.
ASN1 parsing
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). We will parse using asn1parse, and reveal the parameters.
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)) [RSA key pair]. We will parse using asn1parse, and reveal the parameters.
- DSA Parameters with asn1parse. DSA parameters with OpenSSL with asn1parse. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA (Digital Signature Algorithm)
- DSA Parameters. DSA parameters with OpenSSL. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
MAC (Message Authentication Code)
- HMAC with OpenSSL. MACs with OpenSSL. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authenticate both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2) and SHA-3. In this case we will use OpenSSL to generate the HMAC value.
- MACs with OpenSSL. MACs with OpenSSL. In the following we will generate MACs for HMAC, GMAC, CMAC, Blake2bmac, Blake2smac, KMAC128 and KMAC256. Overall, we will use an encryption key defined as a hex value for GMAC and CMAC, and a pass phrase for the others. The message is "hello".
Signing
- Digital signing a plaintext message with OpenSSL. Signing with OpenSSL. With digital signing, we can take a message, and create a signature. This normally involves signing with a private key and digital certificate. The signed message can be an a MIME format, and which can be integrated into an email message. In this can we have a 512-bit RSA key pair that will sign a plain text message.
Encrypting emails
- Encrypting an email message in OpenSSL. Encrypting messages with OpenSSL. With public key encryption, we can take a message, and encrypt it with the recipiant's public key. In this can we have a 512-bit RSA public key to encrypt a message.
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Random number generation with OpenSSL
-
Random number generator [here]. Random numbers are important in generating encryption keys and salt values. In this case OpenSSL generates a random number (in a Base64 format) for a given number of bytes.
Outline (C#/Python)
-
Symmetric Key Encryption (C#) [here]. This page uses the OpenSSL library through a C#/.NET wrapper. The DLLs it interfaces to are libeay32.dll and ssleay32.dll. OpenSSL supports a wide range of encryption methods, including 128-bit AES, 192-bit AES, 256-bit AES and Blowfish (bf). Different modes of ECB, CBC, and OFB are implemented. The examples use a default IV of "1234".
-
AES in Python with OpenSSL output [here]
-
Producing OpenSSL AES Encrypted String from C# [here]
Digital Certificates
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
Paillier - Partial Homomorphic Encryption

The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Fundamentals
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier).
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Using RSA
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
Applications
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Ed25519 signature using NaCl. eddsa. This page uses the NaCl port from libsodium.
- Ed25519 points using NaCl. eddsa. This page uses the NaCl port from libsodium to determine Ed25519 points.
Theory
With EdDSA, Alice will sign a message with her private key, and then Bob will use her public key to verify that she signed the message (and that the message has now changed):

Key generation
Alice generates a random 32-byte secret key (\(sk\)) and then creates a public key of:
\(pk=sk \cdot G\)
and where \(G\) is the base point of the curve.
Signing
Alice creates a SHA-512 hash of her private key:
\(h=\textrm{HASH}(sk)\)
Create \(r\) from the upper 32 bytes of hash and the message:
\( r = \textrm{HASH}(h[32:] \: || \: m))\)
And where "||" represents a concatenation of the byte array values. Next she matches \(r\) onto curve with:
\(R=r \cdot G\)
Next Alice computes \(s\) with:
\(s=r + (\textrm{HASH}(R \: || \: pk \: || \: m)) \cdot sk\)
The signature is (\(R,s\)). The values of \(R\) and \(s\) are 32 bytes long, and thus the signature is 64 bytes long.
Verifying
Bob creates \(S\) using \(R\), \(pk\) and \(m\):
\(S =\textrm{HASH}(R \: || \: pk \: || \: m) \)
And next creates two verification values:
\(v_1=s \cdot G\)
\(v_2=R+ pk \cdot S\)
If \(v_1==v_2\) the signature checks. This is because:
\( \begin{align} v_1&=s.G\\ &= (r + (\textrm{HASH}(R \: || \: pk \: || \: m)) \cdot sk) \cdot G \\ &= rG + sk \cdot G \cdot (\textrm{HASH}(R \: || \: pk \: || \: m)) \\ &= R+ pk \cdot S \\ &= v_2 \end{align} \)
ElGamal

Public key encryption is typically used to sign for things (and where we use the private key to encrypt something and prove this with the public key) and within key exchange methods. The core methods used are RSA and Elliptic Curve. But an alternative is to use discrete logarithms. One of the most interesting is ElGamal, and was created by Taher Elgamal in 1985.
ElGamal Method
- ElGamal. ElGamal. ElGamal is a public key method which uses discrete logarithms.
- ElGamal in Python. ElGamal in Python. ElGamal is a public key method which uses discrete logarithms.
- ElGamal in Python with variable prime sizes. ElGamal in Python for different prime sizes. ElGamal is a public key method which uses discrete logarithms.
- Selecting g in ElGamal. G in ElGamal. ElGamal is a public key method which uses discrete logarithms.
- Selecting g in discrete logs. g in discrete logs. This select a generator in discrete logs.
- Selecting g in discrete logs with random primes. g in discrete logs with random primes. This select a generator in discrete logs using random prime numbers which are define by a number of bits.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- Proving an Encrypted Shuffle With ElGamal and ECC. Shuffle. An encrypted shuffle with ElGamal.
- ElGamal encryption with Powershell. ElGamal encryption.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Commutative Encryption
- Commutative Encyption (Modified ElGamal). Commutative Encyption. Commutative Encyption allow Bob and Alice to encrypt a message, and then for the data to be decrypted usign any order of the keys.
ElGamal Signature
- ElGamal signatures. ElGamal. ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this.
- ElGamal signatures (alterative signing). ElGamal (Signing: s=ar + kh(m)). ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this. Normally we sign with \(s=k^{-1} (h(m)-ar) \pmod {p-1}\), but in this case we will use \(s=ar + kh(m))\).
- ElGamal signatures (alterative signing). ElGamal (Signing: s=ah(m) + kr). ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this. Normally we sign with \(s=k^{-1} (h(m)-ar) \pmod {p-1}\), but in this case we will use \(s=ah(m) + kr\).
- ElGamal signatures (alterative signing). ElGamal (Signing: r=as+kh(m)). ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this. Normally we sign with \(s=k^{-1} (h(m)-ar) \pmod {p-1}\), but in this case we will use \(r=as+kh(m)\).
- ElGamal signatures (alterative signing). ElGamal (Signing: r=ah(m) +ks). ElGamal is a public key method which uses discrete logarithms. This example generates a public key and a private key, and creates a signature (\(r,s\)) of a message, and then verifies this. Normally we sign with \(s=k^{-1} (h(m)-ar) \pmod {p-1}\), but in this case we will use \(r=ah(m) +ks\).
- ElGamal encryption with Go. ElGamal. This implements ElGamal encryption.
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
ElGamal Homomorphic Encryption
- ElGamal Homomorphic Cipher for Multiplication (Python). ElGamal. This outlines ElGamal Homomorphic multiplication with Python.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (Python). ElGamal. This outlines ElGamal Homomorphic division with Python.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (Python). ElGamal. This outlines ElGamal Homomorphic addition with Python.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (Python). ElGamal. This outlines ElGamal Homomorphic subtraction with Python.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
- ElGamal Homomorphic Cipher (Go). ElGamal. This outlines ElGamal Homomorphic cipher with Go.
- ElGamal Homomorphic Cipher (Go) - Divide. ElGamal. This outlines ElGamal Homomorphic cipher with Go with divide.
- ElGamal Homomorphic Cipher (Go) - Additive. ElGamal. This outlines ElGamal Homomorphic cipher with Go with addition.
ElGamal and ECC
- ElGamal with ECC. ElGamal with ECC. ElGamal using ECC.
- Proving an Encrypted Shuffle With ElGamal and ECC. Shuffle. An encrypted shuffle with ElGamal.
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- ElGamal - Applying Multiple Public Key Operations (ECC). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use elliptic curve methods, and using the Edwards 25519 curve.
ElGamal (Authenticated and Verified Encryption)
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenticated ciphertext.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
ElGamal (Encrypting with multiple public keys)
- ElGamal - Applying Multiple Public Key Operations (Discrete Logs). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use discrete logs.
- ElGamal - Applying Multiple Public Key Operations (ECC). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use elliptic curve methods, and using the Edwards 25519 curve.
Ethereum

This page outlines some examples of blockchain and cryptocurrency.
Test Network
- Math functions on Local Network. Go.
- Math functions on Test Network. Go.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- Storing State in a Smart Contract. Go.
- Deleting Data From A Smart Contract. Go.
- A Caesar Cipher Quiz Generator from a Smart Contract. Go.
- Hashing in a Smart Contract. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
- Dealing With Decimals In Smart Contracts. Go.
- Creating A Scrambled Alphabet Challenge Generator In Ethereum and Solidity. Go.
- Deploying a Scrambled Alphabet Generator To Ethereum (With Ganache and Ropsten). Go.
- Deploying a Scrambled Alphabet Generator To Ethereum (With Hardhat). Go.
- Pigpen, IPFS and Ethereum. Go.
- Proof of \(x\) from \(H(x)\) using zkSnarks. Go.
- Elliptic Curve Operations Within a Solidity Contract. Go.

Ethereum
- Creating Ethereum address with Python. Go.
- Creating Ethereum signing with Python. Go.
- ERC20 Tokens. Go.
- Ethereum address with Go. Addresses. This generates an Ethereum address.
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- PATRICIA trie. PATRICIA. Example of using PATRICIA (and which is used in Ethereum).
- Viewing Balance of account in Etheruem with Go. Balance. This views the balance of an account
- Viewing Block in Etheruem with Go. Block. This views a block.
- Viewing Cryptocurrency API with Python. Go.
- Viewing Ethereum blockchain with Python. Go.
- Viewing Transactions in Block in Etheruem with Go. Transactions. This views transactions.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
- Symmetric Key Encryption For Smart Contracts. Symmetric key. Solidity does not natively support symmetric key encryption, such as with AES. Overall, AES would consume too much gas and thus be expensive to implement. But, we can use hashing and X-OR methods to do the encryption. In this case, we will create a 256-bit random value, and then encrypt it with an encryption key, and then decrypt it.
Calling from Python
- Calling smart contracts with Python. Python.
Ethereum crypto
- ECIES with Go-Ethereum. Go.
Ethereum Blockchain
- IOTA Trytes. Trytes. `This outlines Trytes, as used in IOTA.
Ethereum Blockchain
- Blockchain: Adding Maths Functions. Go.
- Blockchain: Blocks, transactions and writing data. Go.
- Blockchain: Contracts and Addresses. Go.
- Blockchain: Getting transactions. Go.
- Blockchain: Hello World!. Go.
- Blockchain: Simple Purchasing System. Go.
- Blockchain: Viewing the blockchain. Go.
- Blockchain: Cracking Wallets. Go.
- Introduction to Blockchain. Go.
Presentations
Factorization

Many public key problems involve the difficulity in factorizing a value two its prime number factors. For example, in RSA, we have a public modulus \(N\) and which is equal to the multiplication of two prime numbers \(p\) and \(q\). If we can factorize the public modulus, we will be able to break the RSA cipher related to it.
RSA Crack
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA Factorization. RSA. This outlines the factorisation of the N value in the RSA method.
Methods
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Dixon. Go. Dixon Method.
- Rho factorization. Rho. Rho alogorithm.
- Smooth numbers. Go. Outline of smooth numbers.
Methods (Elliptic curve
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Quadratic residues
- Quadratic residue (mod p). Go. Outline of quadratic residue \(\pmod p\).
- Quadratic residue (mod p) using Legendre symbol. Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
Factorizing
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
Lenstra–Lenstra–Lovász (LLL) with lattices
- Crack ECDSA with weak nonces. ECDSA with weak nonces and using Lenstra–Lenstra–Lovász (LLL) method. This outlines ECDSA how the private key can be recovered with weak nonce values.
Network Forensics

These pages outlines some network forensics. This includes the understanding of the network stack, and with protocols such as Etherenet, IP, TCP, HTTP, and others.
Network Forensics (Theory)
- Network Forensics (Wireshark). Network Forensics. This provides information on how to detect threats through network forensics with Wireshark.
- Advanced Network Forensics. Network Forensics. This provides information on how to detect threats through network forensics.
Network Forensics (Practice)
- Advanced Network Forensics (Wireshark). Adv Network Forensics. This provides information on how to detect threats through network forensics with Wireshark.
- Network Forensics (PCAP). Network Forensics. This provides information on network forensics (reading PCAP files)
- Network Forensics (Text). Network Forensics. This provides information on network forensics (reading text files)
Tshark
-
Filters with TShark. TShark. This page runs Tshark with a given Pcap file and a defined filter.
Other
- Advanced Digital Forensics . Adv Digital Forensics. This provides information on how analyse disk based systems using open source forensics.
- Partition Analyser. MBR. This page will analyse the details of the partition details within the MBR (put one space between fields).
Presentations
Format Preserving Encryption

Format Preserving Encryption (FPE) is a method which allows the basic formatting of a message to stay in a similar format, and where the value itself is encrypted. It can be used to hide credit card details.
Methods
- Format Preserving Encryption. FPE. This outlines Format Preserving Encryption.
- FPE with Python. FPE. An implementation of Format Preserving Encryption (FPE) using Python.
- FPE with node.js. FPR. FPE with node.js.
- FPE and PKBKDF2 in Python. FPE and PKBKDF2 in Python. FPE using PKBDF2 to password generation.
FFX (Format-preserving, Feistel-based encryption)
- FPE with Go. FPE. An implementation of Format Preserving Encryption (FPE) for FFX1 and FFX3.
- FFX schemes. FFX. Within tokenization we can apply format preserving encryption (FPE) methods, which will convert our data into a format which still looks valid, but which cannot be mapped to the original value. For example, we could hide Bob's credit card detail into another valid credit card number, and which would not reveal his real number. A tokenization server could then convert the real credit card number into a format which still looked valid. For this we have a key which takes the data, and then converts it into a form which the same length as the original.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher in Python.
FFX in Rust
- FFX. FFX. This is an implementation of FFX in Rust.
Honey Encryption
- Honey Encryption. Honey. This outlines Honey encryption.
Crypto Principles

This page outlines some crypto principles.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Galois fields (polynomial operations)

This page outlines a few basic principles around the usage of Galois fields and polynomial operations. In 1832, Évariste Galois died of duelling wounds at the age of 20 but left a great legacy. While he was a teenager he worked on polynomials and laid down the principles of Galois theory, along with defining the concept of a finite field. In cryptography, the finite field is one of the major concepts and involves limiting the number of possible values to a limiting factor (\(p\)). The values of the field then range from 0 to p-1. Within a field, we can operate on values in the field using arithmetic operations. We can thus have an infinite field, and where we could include all of the possible integers. A finite field or Galois field of GF(\(2^n\)) has \(2^n\) elements. If \(n\) is four, we have 16 output values. Let’s say we have a number \(a∈{0, ... ,2^{n−1}}\), and represent it as a vector in the form of a polynomial:
\( a=a0+a_1 x+a_2 x^2 ... a_{n−1} x^{n−1}\)
If we use \(a_n∈{0,1}\), this is exactly the same as representing a binary number modulo \(2^n\). In this \(x^n\) represents bit position \(n\) and \(a_n\) is the value of the bit at position \(x^n\). If a bit is a zero at a given position, it will be not included in the polynomial equation. So, 1011 can be represented by \(x^3+x+1\) and 1010 is represented as \(x^3+x\). We can then perform arithmetic operations on these polynomial values. So, to add two values of 1010+1100 we can represent this as \((x^3+x)+(x^3+x^2)\) and which is \(x^2+x\) as we are using modulo 2 addition, and where \(x^3+x^3=0\). With modulo 2 addition, 0+0=0, 0+1=1, 1+0=1, and 1+1=1.
An example of Galois Fields is within AES (Advanced Encryption Standard) and which uses a finite field GF(\(2^8\)). With AES we operate on bytes (8 bits) in the form of \(b_7 b_6 b_5 b_4 b_3 b_2 b_1 b_0\) and which are operated on a a polynomial of \(b_7x^7+b_6x^6+b_5x^5+b_4x^4+b_3x^3+b_2x^2+b_1x^1+b_0\).
Galois fields (polynomial operations) - GF(\(p^n\))
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Additive Group Table for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Additive Group Table for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of addition. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the additive group table for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values.
- Multiplicative Group Table for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Multiplicative Group Table for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the additive group table for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values.
- Additive, Division and Multiplicative Group Table for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Additive, Division and Multiplicative Group Table for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the Additive, Division and Multiplicative Group Table for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values.
- Additive and Multiplicative Group Table for GF(\(2^2\)) and GF(\(2^3\)). Galois Fields Table for GF(2^m) with polynomials. This page implements Galois Fields GF(\(2^n\)) with Python and provides a table of additional and multiplication. It outlines GF(\(2^2\)) and GF(\(2^3\)), but also gives a program that can be used for others. Overall, we have the form of GF(\(p^n\)) and which provides use both an additive and a multiplicative group operations that provide all the possible outputs within the finite field. The value of \(p\) is a prime number, and \(n\) is any positive integer.
- Additive and Multiplicative Group Table for GF(\(2^2\)) and GF(\(2^3\)). Galois Fields Table for GF(2^m) with coefficient values. This page implements Galois Fields GF(\(2^n\)) with Python and provides a table of additional and multiplication. It outlines GF(\(2^2\)) and GF(\(2^3\)), but also gives a program that can be used for others. Overall, we have the form of GF(\(p^n\)) and which provides use both an additive and a multiplicative group operations that provide all the possible outputs within the finite field. The value of \(p\) is a prime number, and \(n\) is any positive integer. This version will show the polynomial coefficent values within the Galois Field.
- Additive and Multiplicative Group Table for GF(\(2^2\)) and GF(\(2^3\)). Galois Fields Table for GF(2^m) with integer values. This page implements Galois Fields GF(\(2^n\)) with Python and provides a table of additional and multiplication. It outlines GF(\(2^2\)) and GF(\(2^3\)), but also gives a program that can be used for others. Overall, we have the form of GF(\(p^n\)) and which provides use both an additive and a multiplicative group operations that provide all the possible outputs within the finite field. The value of \(p\) is a prime number, and \(n\) is any positive integer. This version will show the integer values within the Galois Field.
Irreducible polynomial for GF(p^n)
- Irreducible polynomial for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Irreducible polynomial for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the parameters for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values. This includes finding the irreducible polynomial for the Galois Field.
- Irreducible polynomial for GF(\(p^n\)) for a given \(p\) and for \(n\) values. Irreducible polynomial for GF(p^n) for a given p and for n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the parameters for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values. This includes finding the irreducible polynomial for the Galois Field. Other important parameters include the degree (the highest polynomial power) and the order (the number of possible output values).
- Conway and primitive polynomial GF(\(p^n\)). Conway and primitive polynomial GF(p^n). This page outlines Conway and primitive polynomials for GF(\(p^n\)).
Galois fields (polynomial operations) - GF(\(p\))
- Additive and Multiplicative Group mod n (\(Z_n\)). Additive and Multiplicative Group mod n. In finite fields, we have a \(\pmod n\) operation for a list of integers (\(\mathbb{Z}\)), and where \(n\) is a prime number. This works for our add (+) and multiply (\(\times\)) operations, and where: \( a \pmod n + b \pmod n = (a+b) \pmod n\); and \(a \pmod n \times b \pmod n = (a \times b) \pmod n\).
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Polynomial GF(2) Factoring and Irreducible Polynomials. Factors. This outlines the search for polynomial factors for GF(2).
Polynomial operations
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
Post-quantum
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Rust
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Sage
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Golang and Cryptography

The new scripted languages such as Python and Node.js are convenient. But, unfortunately, they can be slow as they are scripted, and not compiled. Each time the scripted code is run, the scripting engine must then convert each line of code to the required machine level code. This makes the code much slower than compiled languages, and also less robust. Thus many applications in cryptography are written in C and C++, as they allow for fast execution and give low level access. Unfortunately it can be complex to compile programs, as we often need to install binary libraries and then link these in. The Go programming language, though, has a similar code syntax to C/C++, but is small and efficient and allows access to low-level functions, such as as pointers. Go thus aims to “Code less, compile quicker, execute faster”. So let’s use Go to implement some cryptography methods, including symmetric key, hashing, public keys and zero-knowledge proofs (ZKPs). The slides related to these methods are included [here]. An introduction to Golang and Cryptography is [here].

Go ECDH
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret.
Go Hex and Base64
- Base64 and Hex in Go. Base64/Hex. Two common formats for representing binary data are hexademical and Base64.
Go symmetric key
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Reuse IV attack and AES. Reuse IV and GCM. This provides an implementation of a reuse IV against AES GCM.
- ASCON AEAD (Golang). ASCON AEAD (Golang). The outlines the usage of AEAD for ASCON using Golang.
Go HMAC and HKDF
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HKDF in Go. HKDF. Implementation ofHKDF, and where we dervice a key based on a given secret.
Go secret shares
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.

Go ZKP
- Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL). DLEQ. Create a non-interactive ZKP for discrete logs.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Fiat Shamir and ECC (Interative ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP with Kryptology. This implements a range proof using a Schnorr proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?

Go ECIES (Hybrid Encryption)
With this, we can use the power of public key encryption (to generate the encryption key) with symmetric key encryption (to actually encrypt and decrpyt the data):
- ECIES (Kryptology). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Coinbase Kryptology library.
- ECIES (CIRCL). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Cloudflare CIRCL library.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt and which is used in Contract Tracing for COVID-19.
Go ECDSA
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Go RSA
- RSA Principles. RSA Principles. The basics of RSA.
- RSA with Go. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA. RSA encryption with Go using OAEP.
- RSA Encryption with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
Go ElGamal
ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Proving an Encrypted Shuffle With ElGamal and ECC. Shuffle. An encrypted shuffle with ElGamal.
- ElGamal encryption with Go. ElGamal. This implements ElGamal encryption.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
- ElGamal - Applying Multiple Public Key Operations (ECC). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use elliptic curve methods, and using the Edwards 25519 curve.
Go PGP
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
Go Public key
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.

Go Hashing
- Hashing with Go. Hashing. Hashes with Go.
- GP Hashing with Go. GP Hashing. GP Hashes with Go.
- SHAKE with Go. SHAKE. This implements SHAKE in Go.
- libDisco with Go. libDisco. This implements libDisco.
- cSHAKE in Golang. cSHAKE. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS. With the SHA-3 hashing method, we have four different cryptographic hashing methods (SHA3-224, SHA3-256, SHA3-384, and SHA3-512) and two XOF functions (SHAKE128 and SHAKE256). With SHAKE128 and SHAKE256 we can integrate domain separation between different functions — and which are known as cSHAKE128 and cSHAKE256.
- Homomorphic Hashing with Golang. Homomorphic hashing. Normally with hashing methods, we need to take all the previous data and new data in order to create a new hash value for our data. In a homomorphic hashing method, we can basically take the previous hash, and then add on any new data values. We can also remove previous data values from our hash, too. This is more efficient in computing, as we do not have to process all of our data into a new hash, and can use simple homomorphic operations for the computation. The method we will use (LtHash) was initially defined by Bellare and Micciancio and updated Lewi et al at Facebook.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
Go ECC
- Hash to password with Go. Hash to password. Hash to password with Go.
- ECDH with Go. ECDH. ECDH with Go.
- Box with Go. Box. Box with Go.
- ECC with Go. ECC. ECC with Go.
- Curve 25519 with Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ElGamal with ECC. ElGamal with ECC. ElGamal using ECC.
- Curve 25519 with Go for test vectors. ECC. This does a test on some private keys to test the public key generation.
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Barebones Ed25519 with Go. ECC. This shows point addition and scalar multiply in Ed25519
- Barebones NIST P256 with Go. ECC. This shows point addition and scalar multiply in P256
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining \(n.G\) for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Points (Base Point and Others). Elliptic Curve points. Two common curves used in ECC (Elliptic Curve Cryptography) are secp256k1 (as used in Bitcoin and Ethereum) and P256 (secp256r1). The "k1" refers to the Kolbitz curve 1 (named after the creator of ECC). With these we have a base point which are can operate on. This is typically defined as \(G\). We can then operate on this with add and multiply operation. For example, \(2G=G+G\) and \(P=n.G\). In this following we will show the base point for a number of common curves, such as secp256r1, P256, Pallas, Curve 25519, BLS12381G1, BLS12381G2, BLS12377G1 and BLS12377G2.
Go Blockchain
- Ethereum address with Go. Addresses. This generates an Ethereum address.
- Viewing Balance of account in Etheruem with Go. Balance. This views the balance of an account
- Viewing Block in Etheruem with Go. Block. This views a block.
- Viewing Transactions in Block in Etheruem with Go. Transactions. This views transactions.

Go Homomorphic
- SIDH Go. SIDH. Post-quantum key exchange.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- NTP. NTP. An overview of NTP.
- BiBa. BiBa. An overview of BiBa One Time Signature.
Go DNS
- DNSSEC. DNSSEC. An overview of DNSSEC.
Go Signatures
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Go Signcryption
- Ahmad-Afzal-Iqbal (AAI) signcryption with Golang. Ahmad-Afzal-Iqbal (AAI). Ahmad-Afzal-Iqbal (AAI) signcryption with Golang.

Go Crypto pairing
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
Go Homomorphic
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add. HEAAN Add. HEAAN Add.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- Anonymous crypto. Anon. Anonymous crypto.
- Rho factorization. Rho. Rho alogorithm.
- Post-quantum signing (BLISS). BLISS. BLISS method.
Go Post quantum
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.

Go CIRCL
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- Ed448 with Go. X448. Ed448 with Go.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with FourQ (Cloudflare). FourQ.
- Verifiable Oblivious Pseudorandom Functions (VOPRF) with Cloudflare CIRCL. VOPRF. In our digital world, we give away too many of our secrets, especially where we just have to prove the knowledge of something, rather than actually revealing it. In many of the systems we use, we could just prove things in an oblivious way, and where we could pass a secret but in a blinded form. With this, a server does not discover our password and for us not to discover the identifier that a server holds on us. But, can we also provide a proof back that the right password has been used? Well, with Verifiable Oblivious Pseudorandom Functions (VOPRF), we can generate a random secret based on a key generated on the server (Alice), and which is based on Bob’s secret.
- Hash to Curve using Go (Cloudflare). Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). The method defined here is proposed an an Internet-Draft standard by the Internet Engineering Task Force (IETF) related to "Hashing to Elliptic Curves".
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
here Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
- eXtendable-Output Function (XOF) usign CIRCL. XOF. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS.

Go Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Google Tink (Golang) ECIES. Google Tink (ECIE5). This outlines ECIES encryption with public key and AES using Golang with Google Tink
Go Credentials
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.

Go Kryptology
- Public key points for curves. Simple. Display public key points for scalars.
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.

Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.

Principles
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Paillier
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
Go Format Preserving Encryption (FPE)
- FPE with Go. FPE. An implementation of Format Preserving Encryption (FPE) for FFX1 and FFX3.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
AWS Encryption
- AWS Symmetric Key Encryption. AWS (Symmetric key). Using symmetric key in AWS.
Go Oblivious Transfer
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Dragon Fly
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
Embedding data in an ECC point
- Embedding data in a point. Go. With Elliptic Curve Cryptography (ECC), we use points on an elliptic curve to represent our data. These are defined with (x,y) points. With this, it is possible to embedded a certain amount of data into the point - as long as it still gives us a valid point on the curve. This example will Curve 25519 to embed data, and is achieved by storing the length of the data in a single byte in the point, and then store the data as byte values in the point (followed by random data). To decode, we can then just read the first byte for the length of the message, and then reveal the data encoded into the point..
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Hashing (Cryptographic)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
Benchmarks and Password strength
The following are the tips related to hashing:
- Password strength. Test. This outlines the strength of various passwords types.
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
Theory
The following are the tips related to hashing:
- Balls in bins. BiBa. This implemented balls in bins.
- Birthday attack (with Big Integers). Calc. This provides a simple example of the birthday attack.
- Birthday attack. Calc. This provides a simple example of the birthday attack.
- Differential Cryptanalysis (Hashing). Cryptanalysis. This provides an implementation of differential cryptanalysis for hashing methods.
MD5, SHA-1
The following are the tips related to hashing:
- MD2 and MD4 MD2/4. The MD2 and MD4 hashing functions were developed by Prof Ronald Rivest in 1989 and 1990, respectively. They both produce a 128-bit hash, but have been shown be vulnerable to attack (see the Collision section in the page).
- MD5 and SHA-1 (to Base-64) with salt Salt. It is possible to add salt to the MD5 algorithm, to mix it up a little.
- MD5 and SHA-1 (to Base-64) Hash. MD5 and SHA-1 produces a hash signature, and the output is typically shown in a hex format or a Base-64. In this example the output is converted into a Base-64 format.
- MD5 and SHA-1. Hash. MD5 and SHA-1 methods produce a hash signature, and are the two of the most widely used methods. The MD5 algorithm has been shown to have weaknesses, and a collision of message hashes has been shown to occur in less than one day. An MD5 signature has 128 bits, an SHA-1 signature has 160 bits, and an SHA-256 signature has 256 bits.
- MD5 Cracking. Hash Cracker. MD5 has a 128-bit signature and can be cracked using rainbow tables. This page tries to crack the MD5 signature.
- Hashing with Go. Hashing. Hashes with Go.
- Detecting hash types. Hash type. This detects has values.
- OpenSSL hashing. Range of methods. Outlines the methods used in OpenSSL
- Hash. Hash. Hashing using JavaScript
- Hashing with node.js. Hashing. Hashing with node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Hashing methods
-
Hazmat Hashes. Hazmat Hashes. This includes the hashing methods in the Hazmat cryptography library. This includes Blake2p, Blake2s, MD5, SHA1, SHA224, SHA256, SGA384, SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHA512, SHA512-224, SHAKE128 and SHA256.
-
Hazmat Hashes. Hazmat Hashes. In this case we will implement Python code to determine SHA1, SHA2, SHA3, Blake2, MD5 and SM3 hashes.
OpenSSL Passwords
-
Password example [here]
-
Hashed passwords with OpenSSL [here]
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Blake 3 hashes
The following are the tips related to similarity hashing:
- Blake 3 in Python. Hashing. Blake 3 hashing.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
Other Hash functions
The following are the tips related to hashing:
- Bloom Filter Bloom filter. A Bloom filter goes a probabilistic method of determining if an element is in a data structure, using indexed hashing methods.
- Cuckoo Table Cuckoo filter. A Cockoo table uses two hash funtions.
- Chaffing. Chaffing. This produces a keyless system.
- GP Hashing with Go. GP Hashing. GP Hashes with Go.
- LDAP. LDAP. This produces a LDAP hash signature for a password.
- LM Hash. LM Hash. This is an LM Hash Calculator. LM Hash is used in many versions of Windows to store user passwords that are fewer than 15 characters long.
- Murmur and FNV Murmur and FNV. While hashing methods such as MD5 and SHA-1 use crypto methods, the Murmur and FNV hashes uses a non-cryptographic hash function. This can be used for general hash-based lookup and was designed by Austin Appleby. It has good performance compared with other hashing methods.
- Pearson. Pearson. This uses a non-crypto hash.
- phpass. phpass. This produces a phpass hash signature for a password.
- Tiger. Tiger. Tiger is a 192-bit hash function and was designed by Ross Anderson and Eli Biham in 1995. It is often used by clients within Gnutella file-sharing networks and does not suffer from known attacks on MD5 and SHA-0/SHA-1. Tiger2 is an addition, in which the message is padded with a byte of 0x80 (in a similar way to MD4, MD5, and SHA), whereas in Tiger it is 0x01. Otherwise, the two methods are the same in their operation.
- Whirlpool. Whirlpool. Whirlpool is a 512-bit cryptographic hash function and was created by Vincent Rijmen (one of the AES creators) and Paulo Barreto, in 2000.
- WPA-2 hash . WPA-2 hash. Implements SHA-2 hash.
- Reusable hash collisions. Reusable hash collisions. Reusable hash collisions.
- The Length Extension Attack. Length Extension Attack. The MD construct has many weaknesses, and one of the most serious is the length extension attack. With this an adversary (Eve) can take a hash for an unknown message, and then add additional data to produce a new valid hash. The hash methods which are at risk against the length extension attack are MD5, SHA-1 and SHA-256. Please follow the code link below to run an example.
- Consistent hashing. Consistent hash. This outlines the usage of Consistent hashes.
- ROR13 (Module and Function). ROR13. With ROR13 we take each 8-bit character and then convert to a unicode value (with 16 bits). Then for each character we rotate the bits right by thirteen places. The resultant hash is then just the accumuluation of the rotated values.
- ROR13 (Function). ROR13 (Function). With ROR13 we take each 8-bit character and then convert to a unicode value (with 16 bits). Then for each character we rotate the bits right by thirteen places. The resultant hash is then just the accumuluation of the rotated values.
- GOST, Streebog256 and Streebog512. GOST, Streebog256 and Streebog512. GOST94 is a hashing method developed with Euro-Asian Council for Standardization, Metrology and Certification (EASC). This has since been developed in the Streebog256 and Streebog512 hashing method. In this case, we will use Libre OpenSSL to convert data into a hashed value.
RIPEMD
- RIPEMD (RACE Integrity Primitives Evaluation Message Digest) and GOST. RIPEM160. RIPEMD is a 128-bit, 160-bit, 256-bit or 320-bit cryptographic hash function, and was created by Hans Dobbertin, Antoon Bosselaers, and Bart Preneel. It is used on TrueCrypt and is open source. The 160-bit version is seen as an alternative to SHA-1, and is part of ISO/IEC 10118
- RIPEMD160. RIPEM160. RIPEMD160 is a 160-bit cryptographic hash function, and was created by Hans Dobbertin, Antoon Bosselaers and Bart Preneel. RIPEMD160 is used in Bitcoin applications.
Chameleon hashes
The following are the tips related to Chameleon hashing:
- Chameleon hash in Golang Chameleon. With a Chameleon hash, we have a normal hash value which is resistant to collisions, but with a known secret we can easily create a collision. The concept was first defined by Krawcyk and Rabin.
Similarity hashes
The following are the tips related to similarity hashing:
- Similarity hash: SimHash (Charikar similarity) in Python Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash (Nilsimsa similarity) Nilsimsa. The Nilsimsa similarity is used to find similarities between spam emails.
- Minhash (Jaccard similarity) Jaccard similarity. The Minhash method is used to find similarities between strings, files and metadata.
- String enthropy String enthropy. Measurement of the entropy of strings.
- Counting identical elements (HyperLogLog) HyperLogLog. Counting the number of identical elements.
SHA-3 and SHA-3 contenders
The following are the tips related to Key derivation hashing:
- Blake and Blake 2. Blake. Implements Blake and Blake 2 (SHA-3 contender).
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
- Grøstl. Grøstl. Implements Grøstl (SHA-3 contender).
- KangarooTwelve. KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- SHA-3, Keccak and SHAKE . SHA-3. Implements SHA-3, Keccak and SHAKE (SHA-3 winner).
- SHA-3. SHA-3. SHA-3 was known as Keccak and is a hash function designed by Guido Bertoni, Joan Daemen, Michaël Peeters, and Gilles Van Assche. MD5 and SHA-0 have been shown to be susceptible to attacks, along with theoretical attacks on SHA-1. NIST thus defined there was a need for a new hashing method which did not use the existing methods for hashing, and setup a competition for competing algorithms. In October 2012, Keccak won the NIST hash function competition and is proposed as the SHA-3 standard. It should be noted that it is not replacement SHA-2, which is currently a secure method. Overall Keccak uses the sponge construction where the message blocks are XORed into the initial bits of the state, and then inevitably permuted.
- cSHAKE. cSHAKE. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS. With the SHA-3 hashing method, we have four different cryptographic hashing methods (SHA3-224, SHA3-256, SHA3-384, and SHA3-512) and two XOF functions (SHAKE128 and SHAKE256). With SHAKE128 and SHAKE256 we can integrate domain separation between different functions — and which are known as cSHAKE128 and cSHAKE256.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- Skein. Skein. Implements Skein (SHA-3 contender).
Key derivation hashing
The following are the tips related to Key derivation hashing:
- Argon2. Go. Outline of Argon2.
- Argon2 with NaCl. Go. Outline of Argon2 using NaCl.
- Balloon. Go. Outline of Balloon.
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- Double ratchet. Go. Outline of double ratcheting.
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- Scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat HKDF. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
Non-crypto/fast hashing
The following are the tips related to non-crypto hashing:
- A perfect hash Perfect hash. This is a non-crypto hash which optimizes the hash value.
- The universal hash Universal hash. This related to the concept of a universal hash.
- FNV. FNV. FNV is one of the fastest hashing methods.
- Murmur. Murmur. Murmur is one of the fastest hashing methods.
- Siphash. Siphash. Siphash is a fast hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- xxHash. xxHash. xxHash is one of the fastest hashing methods.
- Meow. Meow. Meow is one of the fastest hashing methods.
- o1Hash. o1Hash. o1Hash is one of the fastest hashing methods.
- CRC-32. CRC-32. CRC-32 is one of the fastest hashing methods.
- wyhash. wyhash. wyhash is one of the fastest hashing methods.
- CityHash. CityHash. CityHash is one of the fastest hashing methods, and is generally free of security problems.
- FarmHash. FarmHash. FarmHash is one of the fastest hashing methods, and is generally free of security problems.
- Non-crypto. Non-crypto. This includes a range of fast non-cryptography hashing methods.
- Non-crypto hashes (C++): Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro. Non-crypto hashes: Farm, City, xxHash, MUM, Spooky 2, Murmur, Metro and t1ha0. This includes a range of fast non-cryptography hashing methods for Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro using C++ methods.
- Pearson. Pearson. Pearson is one of the fastest hashing methods, and has been designed for 8-bit processors.
- C++: t1ha. t1ha. t1ha is one of the fastest hashing methods, and has been designed for 64-bit processors.
- C++: Spooky. Spooky. Spooky is one of the fastest hashing methods, and V2 has a 32-bit, 64-bit and 128-bit version.
- C++: xxHash. xxHash. xxHash is one of the fastest hashing methods, and has good performance for short data inputs.
- C++: MUM. MUM. MUM is one of the fastest hashing methods.
- C++: FNV 1/1a. FNV 1/1a. FNV 1/1a is one of the fastest hashing methods, and is particularily useful when there are small changes in strings, such as with IP addresses and URLs.
- C++: MetroHash. MetroHash. MetroHash is one of the fastest hashing methods.
- C++: CityHash. CityHash. CityHash was created by Google and is one of the fastest hashing methods. It was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Farm. FarmHash. FarmHash was created by Google and is one of the fastest hashing methods. It is an improvement to CityHash.
- C++: Murmur. Murmur. Murmur is one of the fastest hashing methods, but was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Halftime. Halftime. Halftime is one of the fastest hashing methods and was created by Jim Apple at Apache.
- C++: Highway. Highway. Highway is an ultra-fast keyed-hash, and is more than five times faster than SipHash. It was created by Jyrki Alakuijala, Bill Cox, Jan Wassenberg at Google.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
- C++: CLHash. CLHash. CLHash is an ultra-fast hashing method and focused on improving performance of the hashing of long strings.
- C++: FalkHash. FalkHash. FalkHash is an ultra-fast hashing method and beats most of the other non-cryptography methods for performance. It is focused on the x64 architecture and integrates with AES-NI.
- C++: wyHash. wyHash. wyHash is an ultra-fast hashing method.
- C++: Fibonacci. Fibonacci. Fibonacci is an ultra-fast hashing method.
- C++: Lookup3. Lookup3. Lookup3 is an ultra-fast hashing method.
Key-based hashing
The following are the tips related to Key-based hashing:
- SiphashSiphash. Siphash is a fast key-based hashing method.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
One Time Passwords/Time Stamps
The following are the tips related to hashing:
- One Time Passwords. One Time. This allows a new unique password to be created each instance, based on an initial seed.
- Timed One Time Password (TOTP). Timed One Time Password. This allows a new unique passcode to be created each instance, based on an initial seed for a given time window. We will use a five second window in this case, where a new passcode is generated every five seconds, based on an initial seed of a pass phrase.
- Hashed One Time Password (HOTP). Hashed One Time Password. This allows a new unique passcode to be created each instance, based on a counter value and an initial seed.
- Time Stamp Protocol. TSP. This creates a time stamp for data.
- HOTP and TOTP (Python). OTP. This creates hashed passwords.
eXtendable-Output Function (XOF)
- eXtendable-Output Function (XOF) usign CIRCL. XOF. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS.
SHAKE
The following are the tips related to hashing:
- SHAKE. SHAKE. Implements SHAKE and which is an Extendable Output Function (XOF).
- SHAKE with Go. SHAKE. This implements SHAKE in Go.
- libDisco with Go. libDisco. This implements libDisco.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify
the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods
such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC methods using the Python cryptography primitives for HMAC-MD5.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
Quantum-robust Public Key (Hash-based signature)
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
Hash to ECC point
- Hash to password with Go. Hash to password. Hash to password with Go.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve with libnum.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.

Password-hashing functions using Rust
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing (Non-cryptographic)

You might know those slow old hashing methods, such as MD5, SHA-1, and SHA-256. Well, they were designed to be fast, but also highly secure. But, if we just need a hashing method, such as for a hashtable or Bloom filter, we often don’t need all the security that comes with the main cryptography hashing methods. And so we have the non-cryptography hashing methods, and which are often ultra-fast and highly efficient. To show the difference, in a test, SHA-1 — one of the fastest cryptography hashing methods — managed a processing rate of 364.95 MiB/s, while t1ha was nearly a 100 times faster, at 34,636 MiB/s.
Non-crypto/fast hashing
The following are the tips related to non-crypto hashing:
- A perfect hash Perfect hash. This is a non-crypto hash which optimizes the hash value.
- The universal hash Universal hash. This related to the concept of a universal hash.
- FNV. FNV. FNV is one of the fastest hashing methods.
- Murmur. Murmur. Murmur is one of the fastest hashing methods.
- Siphash. Siphash. Siphash is a fast hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- xxHash. xxHash. xxHash is one of the fastest hashing methods.
- Meow. Meow. Meow is one of the fastest hashing methods.
- o1Hash. o1Hash. o1Hash is one of the fastest hashing methods.
- CRC-32. CRC-32. CRC-32 is one of the fastest hashing methods.
- wyhash. wyhash. wyhash is one of the fastest hashing methods.
- CityHash. CityHash. CityHash is one of the fastest hashing methods, and is generally free of security problems.
- FarmHash. FarmHash. FarmHash is one of the fastest hashing methods, and is generally free of security problems.
- Non-crypto. Non-crypto. This includes a range of fast non-cryptography hashing methods.
- Non-crypto hashes (C++): Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro. Non-crypto hashes: Farm, City, xxHash, MUM, Spooky 2, Murmur, Metro and t1ha0. This includes a range of fast non-cryptography hashing methods for Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro using C++ methods.
- Pearson. Pearson. Pearson is one of the fastest hashing methods, and has been designed for 8-bit processors.
- C++: t1ha. t1ha. t1ha is one of the fastest hashing methods, and has been designed for 64-bit processors.
- C++: Spooky. Spooky. Spooky is one of the fastest hashing methods, and V2 has a 32-bit, 64-bit and 128-bit version.
- C++: xxHash. xxHash. xxHash is one of the fastest hashing methods, and has good performance for short data inputs.
- C++: MUM. MUM. MUM is one of the fastest hashing methods.
- C++: FNV 1/1a. FNV 1/1a. FNV 1/1a is one of the fastest hashing methods, and is particularily useful when there are small changes in strings, such as with IP addresses and URLs.
- C++: MetroHash. MetroHash. MetroHash is one of the fastest hashing methods.
- C++: CityHash. CityHash. CityHash was created by Google and is one of the fastest hashing methods. It was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Farm. FarmHash. FarmHash was created by Google and is one of the fastest hashing methods. It is an improvement to CityHash.
- C++: Murmur. Murmur. Murmur is one of the fastest hashing methods, but was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Halftime. Halftime. Halftime is one of the fastest hashing methods and was created by Jim Apple at Apache.
- C++: Highway. Highway. Highway is an ultra-fast keyed-hash, and is more than five times faster than SipHash. It was created by Jyrki Alakuijala, Bill Cox, Jan Wassenberg at Google.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
- C++: CLHash. CLHash. CLHash is an ultra-fast hashing method and focused on improving performance of the hashing of long strings.
- C++: FalkHash. FalkHash. FalkHash is an ultra-fast hashing method and beats most of the other non-cryptography methods for performance. It is focused on the x64 architecture and integrates with AES-NI.
- C++: wyHash. wyHash. wyHash is an ultra-fast hashing method.
- C++: Fibonacci. Fibonacci. Fibonacci is an ultra-fast hashing method.
- C++: Lookup3. Lookup3. Lookup3 is an ultra-fast hashing method.
A fuller test with SMHasher gives [here]:
Hash function MiB/sec cycl./hash cycl./map Quality problems
------------------------------------------------------------------
o1hash 12439661.09 16.77 166.13 insecure, no seed, zeros, fails all tests
crc32_hw1 23208.73 46.74 179.70 insecure, 100% bias, collisions, distrib, BIC, machine-specific (x86 SSE4.2)
t1ha0_aes_noavx 22785.26 38.71 180.61 LongNeighbors, machine-specific (x86 AES-NI)
t1ha0_aes_avx1 22714.85 48.12 226.52 LongNeighbors, machine-specific (x64 AVX.txt)
t1ha0_aes_avx2 22345.33 44.38 556.47 LongNeighbors, machine-specific (x64 AVX2)
falkhash 20202.42 173.63 321.52 Sparse, LongNeighbors, machine-specific (x64 AES-NI)
MeowHash64low 17378.06 85.48 237.60 Sparse, invertible, machine-specific (x64 AES-NI)
MeowHash32low 17374.64 85.48 258.53 Sparse, invertible, machine-specific (x64 AES-NI)
MeowHash 17371.91 85.48 247.96 Sparse, invertible, machine-specific (x64 AES-NI)
FarmHash32 17112.05 47.7 214.71 machine-specific (x64 SSE4/AVX)
xxh3 16538.52 32.81 184.86 DiffDist bit 7 w. 36 bits, BIC
xxh3low 16462.36 32.77 199.79
farmhash32_c 16299.81 47.79 219.19 machine-specific (x64 SSE4/AVX)
xxh128low 15174.85 33.79 187.05
xxh128 15174.14 40.46 195.65
farsh32 14053.09 74.29 245.33 insecure: AppendedZeroes, collisions+bias, MomentChi2, LongNeighbors
metrohash64crc_2 14034.84 48.94 162.54 UB, Cyclic 8/8 byte, DiffDist, BIC, machine-specific (SSE4.2/NEON)
metrohash64crc_1 14000.5 49.08 150.54 UB, Cyclic 8/8 byte, DiffDist, BIC, MomentChi2, machine-specific (SSE4.2/NEON)
metrohash128crc_1 13948.67 65.2 168.08 UB, machine-specific (SSE4.2/NEON)
metrohash128crc_2 13920.19 65.12 176.70 UB, machine-specific (SSE4.2/NEON)
halftime_hash128 13478.23 97.79 252.14
wyhash32low 12911.09 29.59 205.43 2 bad seeds
wyhash 12879 30.35 196.77 2^33 bad seeds
CityCrc128 12343.43 74.5 209.75
fletcher2 12011.15 25.29 298.60 bad seed 0, UB, fails all tests
fletcher4 11928.55 25.27 293.49 bad seed 0, UB, fails all tests
halftime_hash256 11620.28 98.44 252.60
fibonacci 11339.87 26.33 705.64 UB, zeros, fails all tests
ahash64 9862.62 27.32 181.68 rust
Spooky128 9751.14 63.84 192.47 UB
Spooky64 9747.47 62.2 191.71 UB
Spooky32 9747.13 62.24 196.96 UB
t1ha1_64le 9723.86 34.39 176.91 Avalanche
cmetrohash64_1 9683.33 45.2 161.01 UB, LongNeighbors, BIC, MomentChi2
cmetrohash64_2 9669.95 44.75 149.67 LongNeighbors
metrohash64_2 9668.51 44.45 164.30 UB, LongNeighbors
metrohash64 9664.61 44.59 150.74 UB, LongNeighbors, BIC
metrohash64_1 9664.57 45.37 152.31 UB, LongNeighbors, BIC, MomentChi2
cmetrohash64_1o 9658.31 42.84 163.45 UB, LongNeighbors, BIC, MomentChi2
FNV1a_YT 9643.42 32.06 175.19 bad seed, UB, fails all tests
City128 9640.19 88.45 225.38
metrohash128_2 9584.94 59.1 167.43 UB, LongNeighbors
metrohash128 9569.16 58.68 167.53 UB, LongNeighbors
metrohash128_1 9558.17 59.04 175.94 UB, LongNeighbors
FarmHash128 9409.63 74.52 210.25
VHASH_32 9404.99 77.01 250.57 sanity, Seed, MomentChi2
VHASH_64 9392.39 74.72 227.92 sanity, Seed, MomentChi2
farmhash128_c 9244.13 79.08 209.44
t1ha2_atonce 9237.12 38.94 194.32 Zeroes low3
City64noSeed 9090.42 32.23 171.53 Avalanche, Sparse, TwoBytes, MomentChi2, Seed
City64low 9089.45 47.75 201.73
t1ha2_stream 9068.55 74.56 219.85 Sparse, Permutation, LongNeighbors
City64 9066.9 47.81 197.78 Sparse, TwoBytes
t1ha2_stream128 9065.5 93.19 236.50 Sparse, Permutation, LongNeighbors
xxHash64 8936.63 51.31 174.34
pengyhash 8744.48 85.31 222.45
farmhash64_c 8713.16 47.96 201.00
FarmHash64 8684.76 48.13 200.51
crc64_hw 8440.13 34.94 141.15 insecure, 100% bias, collisions, distrib, BIC, machine-specific (SSE4.2/NEON)
t1ha2_atonce128 8350.99 55.65 203.53 LongNeighbors
PMPML_64 8161.19 53.2 179.16 unseeded: Seed, MomentChi2, BIC
halftime_hash512 7681.62 125.81 274.01
tabulation 7621.75 42.19 179.93
t1ha1_64be 7481.37 38.16 193.22 Avalanche
MUMlow 7225.18 37.85 197.92 UB, 5 bad seeds
farsh64 7216.29 130.3 302.44 insecure: AppendedZeroes, collisions+bias, MomentChi2, LongNeighbors
MUM 7134.56 37.85 172.34 UB, too many bad seeds, machine-specific (32/64 differs)
nmhash32 7003.3 68.93 216.59
PMPML_32 6704.53 53.5 197.43 Avalanche >512, unseeded: Seed, BIC, MomentChi2, PerlinNoise
nmhash32x 6342.95 56.41 217.75
crc32_hw 6330.42 35.55 170.16 insecure, 100% bias, collisions, distrib, BIC, machine-specific (SSE4.2/NEON)
FNV2 6258.84 33.25 142.89 fails all tests
FNV1A_Pippip_Yurii 6258.46 28.19 184.41 UB, sanity, fails all tests
FNV1A_Totenschiff 6258.23 27.99 198.20 UB, zeros, fails all tests
HighwayHash64 6242.58 99.55 248.41
mx3 6146.02 52.48 173.09 UB
xxHash32 6040.87 51.77 177.91 LongNeighbors, collisions with 4bit diff, MomentChi2 220
prvhash64s_64 5481.48 170.05 325.39
mirhash 5413.73 39.68 154.47 UB, 2^36 bad seeds, LongNeighbors, machine-specific (32/64 differs)
mirhash32low 5412.76 39.79 182.13 UB, 4 bad seeds, Cyclic, LongNeighbors, machine-specific (32/64 differs)
Murmur3F 5226.4 52.18 175.85 UB
prvhash64s_128 5161.33 260.96 442.70
t1ha0_32le 5132.18 54.83 193.53 Sparse, LongNeighbors
halftime_hash64 4990.72 120.55 281.64
Murmur2B 4882.95 39.72 149.43 UB, 1.8% bias, collisions, 3.4% distrib, BIC
seahash32low 4801.33 58.54 227.31 PerlinNoise 32, !msvc
seahash 4796.97 58.55 201.58 PerlinNoise, !msvc
fasthash32 4737.61 45.32 181.86 UB, insecure
fasthash64 4737.21 42.79 164.87 UB, insecure, Moment Chi2 5159 !
umash32_hi 4662.92 54.22 214.20
umash64 4662.09 53.42 188.09
umash32 4633.19 53.42 216.33
t1ha0_32be 4585.59 55.98 183.45 Sparse, LongNeighbors
clhash 4472.31 82.72 229.73 PerlinNoise, machine-specific (x64 SSE4.2)
tabulation32 4317.34 35.45 197.20 collisions
Murmur2C 4092.99 51.84 164.65 UB, 2^32 bad seeds, 91% bias, collisions, distr, BIC, LongNeighbors
farsh128 3776.92 232.48 398.67
City32 3675.04 57.73 212.04
TSip 3228.14 57.96 211.71 !msvc
Murmur3C 3197.63 67.9 198.00 UB, LongNeighbors, Text, DiffDist
Crap8 3149.63 36.23 195.11 UB, 2.42% bias, collisions, 2% distrib
Murmur2 3146.91 41.87 187.89 UB, 1 bad seed, 1.7% bias, 81x coll, 1.7% distrib, BIC
Murmur2A 3146.79 46.87 191.96 UB, 1 bad seed, 12.7% bias, LongNeighbors
aesnihash 2963.39 71.24 217.73 fails many tests, machine-specific (x64 AES-NI)
BEBB4185 2951.62 222.03 343.63 UB, too many bad seeds, msvc-specific
jodyhash6 2848.42 29.99 164.36 bias, collisions, distr, BIC, LongNeighbors
wyhash32 2532.89 48.4 484.57 2 bad seeds, 32-bit
umash128 2427.46 70.6 197.29
Murmur3A 2413.88 53.36 182.37 UB, 1 bad seed, Moment Chi2 69
prvhash64_64m 2386.19 51.18 186.87
prvhash64_128 2383.57 103.44 246.45
prvhash64_64 2375.72 51.61 190.97
hasshe2 2372.52 68.64 216.74 Permutation,TwoBytes,Zeroes,Seed
PMurHash32 2344.78 58.48 196.43 1 bad seed, Moment Chi2 69
mirhashstrict32low 2218.87 65.48 190.59 1 bad seed, MomentChi2 9
mirhashstrict 2217.32 65.53 182.07
sha1ni 2019.96 135.84 564.40 insecure,sanity, Permutation, Zeroes, machine-specific
sha1ni_32 2019.94 136.82 589.46 machine-specific
superfast 1956.25 53.61 180.10 UB, bad seed 0, 91% bias, 5273.01x collisions, 37% distr, BIC
sha2ni-256_64 1910.34 146.06 595.16 Zeroes, machine-specific
sha2ni-256 1906.77 145.47 603.08 insecure,sanity, Permutation, Zeroes, machine-specific
farsh256 1895.77 459.86 575.95
SipHash13 1889.1 89 199.95 0.9% bias
Murmur1 1804.67 51.51 188.41 UB, 1 bad seed, 511x collisions, Diff, BIC
lookup3 1658.31 48.84 194.15 UB, 28% bias, collisions, 30% distr, BIC
pearsonbhash64 1486.34 104.32 185.03
poly_1_mersenne 1431.65 54.49 189.52 fails most tests
jodyhash32 1428.37 44.36 185.85 bias, collisions, distr, BIC LongNeighbors
pearsonbhash128 1347.03 121.75 214.84
poly_2_mersenne 1323.69 66.93 190.88
poly_3_mersenne 1323.59 74.86 206.77
poly_4_mersenne 1323.57 82.67 200.36
blake3_c 1285.91 340.01 552.63 no 32bit portability
GoodOAAT 1052 71.62 192.19
pearsonbhash256 998.9 167.05 261.29
SipHash 980.88 127.77 246.19
MicroOAAT 977.6 59.61 185.06 100% bias, distrib, BIC
FNV1a 791.84 69.69 177.84 bad seed, zeros, fails all tests
sdbm 791.84 67.69 177.06 bad seed 0, fails all tests
FNV64 791.82 70.24 159.29 fails all tests
bernstein 791.82 68.63 180.71 bad seed 0, fails all tests
beamsplitter 789.22 682.45 1150.3 UB, too many bad seeds
HalfSipHash 755.78 114.47 243.72 zeroes
chaskey 753.23 153.42 288.26 PerlinNoise
x17 527.9 98.78 184.09 99.98% bias, fails all tests
JenkinsOOAT_perl 452.49 118.78 194.78 bad seed 0, test FAIL
MurmurOAAT 452.49 113.07 197.83 bad seed 0, 1.5-11.5% bias, 7.2x collisions, BIC, LongNeighbors
JenkinsOOAT 452.48 142.85 213.93 bad seed 0, 1.5-11.5% bias, 7.2x collisions, BIC, LongNeighbors
crc32 392.1 131.62 204.58 insecure, 8590x collisions, distrib, PerlinNoise
sha1-160 364.95 1470.55 1794.1 Comb/Cyclic low32
rmd256 362.49 617.02 815.44 Bad seeds
blake2b-256_64 356.97 1222.76 1435.0
blake2b-224 356.59 1228.5 1425.87
blake2b-160 356.08 1236.84 1458.15
blake2b-256 355.97 1232.22 1443.31 Sparse high 32-bit
md5-128 353.76 638.29 803.39
md5_32a 353.64 629.85 799.56 Sparse high 32-bit
sha1_32a 353.03 1385.8 1759.9 Cyclic low32, 36.6% distrib
rmd128 334.36 659.03 838.32 Bad seeds
blake2s-128 295.3 698.09 1059.2
pearsonhash64 287.95 174.11 196.50 Avalanche, Seed, SSSE3 only. broken MSVC
pearsonhash128 287.95 171.72 194.61 Avalanche, Seed, SSSE3 only. broken MSVC
pearsonhash256 264.51 184.87 218.79 Avalanche, Seed, SSSE3 only. broken MSVC
blake2s-256 215.28 1014.88 1230.38
blake2s-160 215.01 1026.74 1239.54
blake2s-256_64 211.52 1044.22 1228.43
blake2s-224 207.06 1063.86 1236.50
rmd160 202.16 1045.79 1287.74 Bad seeds, Cyclic hi32
sha2-256_64 148.01 1376.34 1624.71 Bad seeds, Moment Chi2 7
sha2-256 147.8 1374.9 1606.06 Bad seeds, Moment Chi2 4
sha2-224_64 147.6 1360.1 1620.93 Bad seeds, Cyclic low32
sha2-224 147.13 1354.81 1589.92 Bad seeds, Comb low32
asconhashv12 144.98 885.02 1324.23
sha3-256 100.58 3877.18 4159.79 PerlinNoise
sha3-256_64 100.57 3909 4174.63 PerlinNoise
asconhashv12_64 86.73 684.02 606.93
floppsyhash 35.72 1868.92 1411.07
tifuhash_64 35.6 1679.52 1212.75 Cyclic low32
Problems include:
- Bad Seeds. A random seed is often used to initialise the hash. This problem relates to having a bad seed..
- Undefined behaviour (UB). This includes Misaligned, oob (Out of bounds), Signed integer overflow and Shift exponent overflow.
o1hash is the fastest, and a quick and dirty hashing method. It is generally not secure. t1h (Fast Positive Hash) requires AES-NI (Intel Advanced Encryption Standard Instructions) and is one of the fastest hashes at 22.785 Gbps. It has fairly good security levels. Meow comes in around 17.378 Gbps. We can see that SHA-1-160 runs as 364 Mbps, while Meow runs at 17.378 Gbps. Blake 3 is one of the fast cryptography hash and has a rate of 1.285 Gbps, and Blake 2 gives a rate around 215 Mbps. SHA-3 gives hashing rates of 100.58 Mbps.
Google recommend the following for 64-bit hashes without quality problems:
- xxh3low
-
wyhash
-
ahash64
-
t1ha2_atonce
-
FarmHash
-
halftime_hash128
-
Spooky32
-
pengyhash
-
nmhash32
-
mx3
-
MUM/mir
- fasthash32
Hash-based Signatures

With hash-based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature, unless we create a stateless method, such as SPHINCS+ [1]. Currently NIST have the final round for the Post Quantum Cryptography competition, and for digital signatures, SPHINCS+ is one of the alterative finalists (alongside Picnic).
Hash-based signature (theory)
- BiBa (Go). BiBa. An overview of BiBa One Time Signature [9]. Basically the method involves us taking a hash of a value using a standard hashing method, such as with SHA-256. There will then be \(2^{256}\) different hashing values. We aim to create a signature for a message, so Bob (the signer) selects a number of random values for his private key value and then publishes the hash of each of these (\(P_1\), \(P_2\), etc). He then sends these public keys to Alice. Now when Bob wants to sign a message, he will take one of his private key values, and then hashes it, and then determines the bin that it should be placed. In this case, we could use the \(\pmod N\) function on the hash, and where \(N\) is the number of bins. If we select \(2^{10}\) there will be 1,024 bins.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature [9].
Hash-based signature (stateful)
- BLISS - Post-quantum signing. BLISS. One of the alteratives to the usage of our existing public key methods is the usage of lattice cryptography, and especially in the usage of Ring Learning With Errors (RLWE). An important application is within digital signatures, and where Bob will sign something with his private key, and then Alice can prove that he signed it with his public key. One post-quantum signature method is BLISS (short for Bimodal Lattice Signature Scheme) [8]. It was created by Léo Ducas, Alain Durmus, Tancrède Lepoint and Vadim Lyubashevsky in 2013.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Hash to Obtain Random Subset (HORS) [3] is a quantum robust hashed-based one-time signature. With this we create a series of integers for our private keys and organise into an indexable form. Then we hash them to a sequence of public key values. Next we segment the hash of the message into a series of n-bit integer values. The signature is then achieved through a look-up of the value in the public key list.
- Lamport Signatures. Lamport. Outlines Lamport signatures [7]. When we sign a message we take its hash and then encrypt with our private key. The public key is then used to prove it, and will prove that we signed it with our private key. The Lamport signature uses 512 random hashes for the private key, and which are split into Set A and Set B. The public key is the hash of each of these values. The size of the private key is 16KB (2×256×256 bits) and the public key size is also 16 KB (512 hashes with each of 256 bits).
- Winternitz Signatures (W-OTS). Winternitz. Outlines Winternitz signatures [4, 5]. W-OTS uses relatively small key and signatures sizes, and is thought to be quantum robust. It generates 32x256 bit random private keys. We then hash these a number of times, and is defined by a parameter (w). If we use w=8, we hash the private keys by (2w). This creates 32x256 bits public keys. The signature is the created by taking eight bits at a time, and then the 8-bit binary int (n) is subtracted from 256 and the private key is the hashed 256-n times. The signature is then 32 hashes which are derived from random private keys. To verify the signature, the recipient parses the hash of the signature (using 8 bits at a time, and extracting the 8 bit int, n).
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method [6], and which is used within speeds-up of Hashing-based signature methods. Using methods such as SHA-1 and SHA-2 (aka SHA-256) will be inefficient as they tend to compress the data inputs through a number of stages. Haraka v2 [6] is different as focuses on inputs of just 256 bits (32 bytes) or 512 bits (64 bytes). This makes the method useful when we are dealing with key and hash values, and is especially useful for hash-based signatures. The output is 256 bits long, but where the input can be either be 256 bits (Haraka256) or 512 bits (Haraka512). These lengths are typically for the outputs of modern hashing applications. The Haraka method, too, has been optimized with AES instructions (AES-NI - Intel Advanced Encryption Standard New Instructions) and which are supported within the hardware of the processor. As Haraka is focused on short messages, the number of rounds within the hashing process has been reduced.
Hash-based signature (stateless)
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ digital signature. SPHINCS digital signature. Outline of the a SPHINCS stateless digital signature method [1].
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
Hash-based signature (Merkle-based)
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
Introduction
Many of the problems we see on the Internet relate to the lack of trust within transactions. The emails you receive and the Web sites that you visit often have very little trust built into them. For trust the email address of the sender, but anyone can fake that address. So increasingly we create a digital signature, and where we sign our messages. In this way, we can check for authentication, integrity and non-repudiation.
With the Alice creates a key-pair: a public key and a private key. She then takes a hash of the message, and then encrypts this hash with her private key, and passes the message and the signature to Bob. Bob then reads the message and takes a hash of it. He then decrypts Alice's signature with her public and checks the hashes. If they match, he knows that she signed and that it has not been changed along the way:
Currently, we often use RSA, DSA and ECDSA to sign our messages. These are based on the difficulty of finding out the factors of a number and on the processing of discrete logarithms. At the current time these methods are computationally hard problems, but with quantum computers, they become much easier. This was shown by Peter Shor who illustrated that it was possible to crack them in polynomial time.
Of all the methods that are being proposed, the hash-based methods look as if they have a good chance of success of creating quantum robust signatures. methods and code-based methods are being researched, but the usage of hashing methods is already well and could provide the best alternative to the existing methods. Hashing methods, too, often bring other advantages, such as forward secure, which means that a key which is cracked will not reveal all the previous keys.
Merkle trees
The root of hash-based methods isin Merkle trees, and which are a way of hashing is used in many applications, including with Bitcoin, Ethereum, Git distribution systems, No SQL, and in many P2P applications. With a Merkle tree we take our data elements, and then hash them, and take pairs of these hashes to create a new hash, and so we build a table. At the top of the tree is the root element (in this case Hash1234):

In this way, we can use the tree to see if we have matching data on systems.On a P2P network, we can transfer a file by splitting it into data segments and then distributing these segments across the network. A trusted source will have the complete Merkle tree for rebuilding the file, and a client can thus rebuild from the Merkle tree and determine the parts of the file which are still missing. Once transferred the root hash (and all the other hashes) will then match. In its core method, the Merkle Signature Scheme (MSS) has serious performance and memory issues, but enhanced methods such as XMSS create with much less of a performance hit.
One-time signatures (Lamport)
The core method used in hash-based signatures is that of the one-time signature, and where we create a new key pair for every method we need to create. If the keys were reused, an attacker could start to learn the private key, and thus spoof messages. One of the first methods was produced by Leslie Lamport and Whitfield Diffie, in 1979, and is defined as:
- We create two data sets with 256 random 256-bit numbers (Set A and Set B). These are the private key (512 values).
- we take the hash of each of the random numbers. This will give 512 hashes and will be the public key.
- We then hash the message using and then test each bit of the hash (0 ... 255). If it is a 0, we use the ith number in Set A, else we use the ith number from Set B.
- The signature is then 256 random numbers (taken from either Set A or Set B) and the public key is the 512 hashes (of Set A and Set B).
The public and private keys are then each 16KB in size. A demo of the method is here.

Figure 1: Lamport method
The major problem with the method is that a key pair for every message. also in 1979, found a solution with Merkle trees.
One-time signature (W-OTS)
To improve performance method (and which reduced key sizes), Merkle proposed Winternitz OTS (named after Robert Winternitz). With this method was possible to sign many bits at the same time. The method is:
- We create 32 256-bit random numbers. These 32 values will be our private key.
- We then hash each of these values 256 times. These 32 values will be our public key.
- We now take the message and hash it using SHA-256. This produces 32 8-bit values (N1, N2 ... N32).
- Next we take each 8-bit value in the hash of the message, and then hash 256-N times (where N is the value of the 8-bit value).
- To prove the signature, we take the message and hash it with SHA-256, and then take each 8-bit value. We then hash the 8-bit signature value by the number of times defined by the message hash value (N1, N2..). The result for each operation should equal the public key value.
This is illustrated below in Figure 2. A demo of the method is here.

Figure 2: W-OTS
Hash-based Signatures
The methods such as W-OTS and Lamport only provide for a one-time signature. In order to sign many messages, we can use the Merkel signature scheme (MSS). With this we take a hash of the keys and build these as the leaves of the tree. The root of the tree is then the public key - the verification key. We then just use the private key of the W-OTS method to create the signature. The sender also sends the authentication path, which is the neighbouring nodes within the path and which leads to the root of the tree. The recipient can then rebuild the tree using the verification key (which can be received a digital certificate) and the authentication path. For the next message we move onto another key pair and where the index of the key part is revealed.
In the following example we have our root as the public key, and then want to sign with Key3. We then show the authentication path which takes us to the root (as defined in the bold arrows):

Conclusions
Hashed-based methods look to be a strong contender for weaning us off RSA, DSA and ECDSA, but we will have to look at the stateful generation of keys. For this we will have to generate a bank of key pairs (2, 4, 8, 16, etc) and then create the public key from the root of the Merkle tree. We must then remember the keys we have used previously, and only use an unused one. Once we use our new key pair, we then show our working-out as to how the private key is integrated into our tree. It is a bit like a teacher marking a question correctly, and asking for the working out that go you to the answer.
References
[1] Bernstein, D. J., Hopwood, D., Hülsing, A., Lange, T., Niederhagen, R., Papachristodoulou, L., ... & Wilcox-O’Hearn, Z. (2015, April). SPHINCS: practical stateless hash-based signatures. In Annual international conference on the theory and applications of cryptographic techniques (pp. 368-397). Springer, Berlin, Heidelberg [paper].
[2] Bernstein, D. J., Hülsing, A., Kölbl, S., Niederhagen, R., Rijneveld, J., & Schwabe, P. (2019, November). The SPHINCS+ signature framework. In Proceedings of the 2019 ACM SIGSAC conference on computer and communications security (pp. 2129-2146) [paper].
[3] Reyzin, L., & Reyzin, N. (2002, July). Better than BiBa: Short one-time signatures with fast signing and verifying. In Australasian Conference on Information Security and Privacy (pp. 144-153). Springer, Berlin, Heidelberg [paper].
[4] Merkle, R. C. (1989, August). A certified digital signature. In Conference on the Theory and Application of Cryptology (pp. 218-238). Springer, New York, NY.
[5] Hülsing, A. (2013, June). W-OTS+–shorter signatures for hash-based signature schemes. In International Conference on Cryptology in Africa (pp. 173-188). Springer, Berlin, Heidelberg.
[6] Kölbl, S., Lauridsen, M. M., Mendel, F., & Rechberger, C. (2016). Haraka v2–efficient short-input hashing for post-quantum applications. IACR Transactions on Symmetric Cryptology, 1-29. [here]
[7] Lamport, L. (1979). Constructing digital signatures from a one-way function (Vol. 238). Technical Report CSL-98, SRI International. [paper]
[8] Ducas, L., Durmus, A., Lepoint, T., & Lyubashevsky, V. (2013, August). Lattice signatures and bimodal Gaussians. In Annual Cryptology Conference (pp. 40-56). Springer, Berlin, Heidelberg [paper].
[9] Perrig, A. (2001, November). The BiBa one-time signature and broadcast authentication protocol. In Proceedings of the 8th ACM Conference on Computer and Communications Security (pp. 28-37) [paper] .
Hashing (Simularity)

Similarity hashes allow for two data objects to be compared for their similarity.
Similarity assessment methods
The following relate to the basic methods used for string similarity:
- String similarity String similarity. This measures edit distance (including Levenshtein distance), Jaro (including Jaro-Winkler), and QGrams.
- String enthropy String enthropy. Measurement of the entropy of strings.
- Soundex Soundex. Soundex uses a phonetic algorithm to classify a sound as it is pronounced. It focuses on matching phrases which have minor spelling errors.
Similarity hashes
The following are the tips related to similarity hashing:
- Similarity hash: SimHash (Charikar similarity) in Python Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash (Nilsimsa similarity) Nilsimsa. The Nilsimsa similarity is used to find similarities between spam emails.
- Context Triggered Piecewise Hashes (CTPH): ssdeep CTPH similarity. Kornblum [6] created ssdeep and which computes fuzzy hashes. This aims to match similar byte sequences, no matter if there are differences between these sequences. For this we break a file up into fragments with a rolling hash function. We then produce a small hash for each of those fragments. These are then aggregated to produce the complete hash of a file. In comparing file signatures, we treat the resultant hash value as a string, and then uses an edit distance method to compare.
- TLSH (A Locality Sensitive Hash) TLSH similarity. In malware analysis and in text similarity, we often have to identify areas of data within files which are similar. One method is TLSH (A Locality Sensitive Hash), and which was defined by Oliver et al [7]. It is used - along with ssdeep - by VirusTotal to identify a hash value for malware.
- Minhash (Jaccard similarity) Jaccard similarity. The Minhash method is used to find similarities between strings, files and metadata.
- Counting identical elements (HyperLogLog) HyperLogLog. Counting the number of identical elements.
Hazmat cryptography

The Cryptography library in Python contains interfaces to common cryptographic algorithms, including symmetric key methods, hashing, public key, and key derivation functions. Many of these are contained with the Hazmat (Harzardous Material) primative setup.
Hashing, HMAC, CMAC, Poly1305 and HKDF
-
Hazmat Hashes. Hazmat Hashes. This includes the hashing methods in the Hazmat cryptography library. This includes Blake2p, Blake2s, MD5, SHA1, SHA224, SHA256, SGA384, SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHA512, SHA512-224, SHAKE128 and SHA256.
-
Hazmat Hashes. Hazmat Hashes. In this case we will implement Python code to determine SHA1, SHA2, SHA3, Blake2, MD5 and SM3 hashes.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
- Hazmat HKDF. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
- Hazmat CMAC. Hazmat CMAC. CMAC methods using the Python cryptography primitives.
- Hazmat Poly1305. Hazmat Poly1305. Poly1305 methods using the Python cryptography primitives.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
Symmetric key
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat. Implementation of ChaCha20/Poly1305 with a random key using Hazmat.
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat. Implementation of AES GCM with a random key using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hazmat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Hazmat Symmetric Key Padding. Symmetric key. This includes the coverage of padding with Hazmat.
- Hazmat Symmetric Key Padding. Symmetric key. This includes the coverage of padding with Hazmat.
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
- Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . With 3DES encryption, we use a 128-bit key and a 64-bit IV value. The two modes supported are ECB (without salt) and CBC (with salt). The DES algorithm has been around for a long time, and the 56-bit version is now easily crackable (in less than a day on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases, and splits the key into two. Overall the key size is typically 112 bits (with a combination of the three keys - of which two of the keys are the same). In this case we will use PKCS7 padding, and which fills the input data with a value that is equal to the number of padding bytes. Overall, DES has a 64-bit block size, and which equates to eight ASCII characters.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key . And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.
Asymmetric key
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- ECC key generaton with Hazmat. Elliptic Curve key gen. Creating ECC keys using Hazmat and Python.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- Hazmat RSA signing (with key values). RSA signing with Hazmat. RSA signing using Python and with Hazmat (with key values).
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here]
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Signatures. DSA Signatures. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. The ECDSA method is an extension of DSA, but implemented with elliptic curve (EC) methods. As with most public key signing methods, we take a hash of a message, and then apply a private key to create a signature (\(r,s\)). This is done by creating a random value (\(k\)) to produce the signature. The signature is then verified using the associated public key. This then verifies the creator of the signature and that the message has not been changed.
Digital Signature: ECDSA/EdDSA
- ECDSA with Hazmat. ECDSA wih Hazmat. This outlines ECDSA with Hazmat.
- Ed25519 for EdDSA signatures with Hazmat. EdDSA: Ed25519. This page uses the Hazmat primitives for the cryptography library.
- Ed448 for EdDSA signatures with Hazmat. EdDSA: Ed448. This page uses the Hazmat primitives for the cryptography library.
- Ed25519 using NaCl. Ed25519. This page uses the NaCl port from libsodium.
- ECDSA Signatures with Hazmat (SECP256R1, SECP384R1, SECP521R1, SECP224R1, SECP192R1, and SECP256K1). ECC Signatures. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and then creates an ECDSA signature for a given message.
Digital Signature: RSA
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
Key exchange: ECDH/X25519
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives and showing the byte values for the key.
Tokens
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
Homomorphic Encryption

Homomorphic encryption supports mathematical operations on encrypted values. Partial Homomorphic Encryption (PHE) supports a few arithmatic operations, while Full Homomorphic Encryption (FHE) supports add, subtract, multiply, and divide. Homomorphic encryption normally involves a public key to encrypt the data, and a private key to decrypt it. There have been four main generations of homomorphic encryption, and the most recent being the HEAAN method.
Simple
- Simple Homomorphic Cipher. Hom. This outlines a Simple Homomorphic cipher.
- Simple Homomorphic Cipher (Python). Hom. This outlines a Simple Homomorphic cipher with Python.
- Full Homomorphic Cipher with a Public Key. Public key. This outlines a Simple Homomorphic cipher using a public key
ElGamal
- ElGamal Homomorphic Cipher (Go). ElGamal. This outlines ElGamal Homomorphic cipher with Go.
- ElGamal Homomorphic Cipher (Go) - Divide. ElGamal. This outlines ElGamal Homomorphic cipher with Go with divide.
- ElGamal Homomorphic Cipher (Go) - Additive. ElGamal. This outlines ElGamal Homomorphic cipher with Go with addition.
- ElGamal Homomorphic Cipher for Multiplication (Python). ElGamal. This outlines ElGamal Homomorphic multiplication with Python.
- ElGamal Homomorphic Cipher for Division (Python). ElGamal. This outlines ElGamal Homomorphic division with Python.
- ElGamal Homomorphic Cipher for Addition (Python). ElGamal. This outlines ElGamal Homomorphic addition with Python.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (Python). ElGamal. This outlines ElGamal Homomorphic subtraction with Python.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
RSA
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
ZKP
- Full Homomorphic Cipher to determine if Bob is older. Older. This outlines a Simple Homomorphic cipher to determine if Bob is older than Alice.
- Full Homomorphic Cipher to determine matching password. Password. This outlines a Simple Homomorphic cipher to determine if a password matches
- Interactive ZKP With Probablistic Methods. ZKP. Interactive ZKP With Probablistic Methods using Python.
- Full Homomorphic Cipher for Millionaire's Problem. Millionaire. This outlines a Simple Homomorphic cipher for the Millionaire's Problem
Voting
- Trusted voting. Trusted. A trusted voting method.
Secret share
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Lattice
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
Full Homomorphic Cipher
- Full Homomorphic Cipher for 2-bit Adder. Adder. This outlines a Simple Homomorphic cipher for a 2-bit adder with DGHV.
- Full Homomorphic Cipher for Full Adder. Full Adder. This outlines a Simple Homomorphic cipher for a full adder with DGHV.
- Full Homomorphic Cipher for 4-bit Adder. Adder. This outlines a Simple Homomorphic cipher for a 4-bit adder with DGHV.
- Full Homomorphic Cipher for 4-bit Adder/Subtractor. Subtract. This outlines a Simple Homomorphic cipher for a 4-bit adder/subtractor with DGHV.
- Full Homomorphic Cipher to XOR two integers. X-OR. This outlines a Simple Homomorphic cipher to X-OR two integers
Paillier
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier) .
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Damgård-Jurik Homomorphic Encryption With Secret Shares. Damgård-Jurik Method. Two of the major areas of developments within cybersecurity will be the usage of homomorphic encryption, and in the usage of Shamir secret sharing. With homomorphic encryption, we can encrypt values, and then operate on them with arithmetic functions (such as add, subtract and multiply), and with Shamir secret sharing, we can split secrets into shares, and then distributed them over networks. These approaches will take privacy to new levels. So let’s look at the Damgård-Jurik method.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Learning with Errors (LWE)
- Learning With Errors . LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret key value (s) and another value (e). Next we select a number of values (t[]) and calculate g[] = t[] x s + e. The values of g[] and t[] become our public key.
- Public Key Encryption with Learning With Errors (LWE). LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret value (s) and which is our private key. We then create a public key which is based on random numbers (A), and then generate another set of numbers (B) which is based on A,s and random errors e. An example of encryption with multiple bits is given.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE)
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Others
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
- SIDH Go. SIDH. Post-quantum key exchange.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Anonymous crypto. Anon. Anonymous crypto.
- Rho factorization. Rho. Rho alogorithm.
- Post-quantum signing (BLISS). BLISS. BLISS method.
Homomorphic Encryption with Krytology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Homomorphic hashing
- Homomorphic Hashing with Golang. Homomorphic hashing. Normally with hashing methods, we need to take all the previous data and new data in order to create a new hash value for our data. In a homomorphic hashing method, we can basically take the previous hash, and then add on any new data values. We can also remove previous data values from our hash, too. This is more efficient in computing, as we do not have to process all of our data into a new hash, and can use simple homomorphic operations for the computation. The method we will use (LtHash) was initially defined by Bellare and Micciancio and updated Lewi et al at Facebook.
Identity Based Encryption (IBE)

This page outlines a few basic principles around the usage of IBE.
Identity Based Encryption (Pairing based)
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pair-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Identity Based Encryption (Others)
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Güther's implicitly certified identity-based public keys (IBE). Günther. This method allows Bob to generate Alices public key from her identity and publicly available parameters.
- Girault's self-certified public keys (IBE). Girault. This method allows Bob to generate Alices public key from her identity and publicly available parameters, and where we use an RSA key pair to self-certify Alice's public key.
Intrusion Detection Systems (IDS)
- Intrusion Detection Systems. Snort. This outlines some of the basics of IDS, including the requirement for Intrusion Detection Systems (IDSs), and where they are used.
- Advanced Network Forensics (Snort). Adv Network Forensics. This provides information on how to detect threats through network forensics with Snort
Snort

- Snort IDS. Snort. This is a Snort Analyser.
- Snort IDS 2 with rules editor. Snort. This provides information on how to detect threats through network forensics with Snort, and with an editing function for rules.
Presentation
IoT

The key objectives of this page are: Understand how a Pen Tester can generate vulnerabilities and test using the Metasploit framework; Define the options and payloads required to generate and use vulnerabilities; and Gaining remote access.
Devices
- Access the Wi-fi kettle. Go. This page outines how to access a wi-fi enabled kettle.
- Philips Hue Wireless Lighting. Go. This page shows how to use RESTful Web services to access to the Hue Led Lamps.
- Kali and R-PI. Go. This page shows the setup of a security testing infrastructure using a Raspberry Pi (R-PI) and a wifi access point.
- Kali, R-PI and RF electrical socket. Go. This page shows the control of an RF electical socket from a RPI.
- Capture from a Polar H10 heat rate sensor. Go. This page shows the capture of the Polar H10 heart sensor with an Ubertooth One.
- Trusted IoT: Linking IoT Devices to NFTs. Go. This page outlines a research paper which links a device to an NFT (Non-fungible Token).
Shodan Scanning
-
IoT Scan (Shodan). Go. This page includes a search of the Internet for key terms, such as for "apache", "mysql" and "cisco".
- IoT Banner Scan (Shodan). Go. This page includes a search of the Internet for key terms with the banner as a result (for the Top 10)
- Internet Services (Shodan). Go. This page includes a search of the Internet for key terms and display the IP address and port.
IoT Libraries
- libDisco with Go. libDisco. libdisco is a Golang library which can be used to create secure connections. It is based on the STROBE protocol framework. Symmetric cryptographic primitives rely on SHA-3 permutation, and asymmetric cryptographic primitives on X25519 and ed25519. STROBE defines a range of cryptographic protocols to integrate with IoT devices. In order to reduce processing, energy and memory requirements, it only uses Keccak (SHA-3) to encrypt and authenticate messages.
COSE/COBR
In computer security, we often have to represent binary data, in single values or groups of characters, bytes, words, long words, signed integers, floating-point values, double-precision floating-point values, and so on. This might be in the form of a data object, a signature or even encrypted content. For this, the ANS.1 DER format is often used, such as presenting digital certificates and signatures. An improvement on this for small messages with security is Concise Binary Object Representation (CBOR) — and which is defined in RFC8949 [1]. While JSON represents text-based data objects CBOR focuses on binary objects. It has been designed to create a lightweight encoder and decoder. This supports the use of CBOR within an IoT infrastructure. The data, also, does not require a data schema to be able to decode it, along with being extensible. CBOR defines the format of binary data with data objects and messages. We can then integrate security with CBOR Object Signing and Encryption (COSE), and which is defined in RFC8152 [2]. This includes signatures, message authentication codes (MACs), encryption and creating serialised objects.
- 128-bit AES GCM. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) can then build on this to include signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use a symmetric key to encrypt a message, and then decrypt it. In this case we will use AES GCM with a static 128-bit key ("0x000102030405060708090a0b0c0d0e0f").
- 256-bit AES GCM. Go. In this case we will use AES GCM using a random 256-bit key (32 bytes).
- EdDSA. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) [2] can then build on this to includes signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use EdDSA to create a signature for a message.
- ECDSA. Go. In this case we will use ECDSA to create a signature for a message.
- HMAC. Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT. Go. In this case we create a CWT token, and sign with an HMAC signature.
- ECDH. Go. In this case we create a symmetric key from ECDH. For this we will derive a shared key from the public key of Alice and Bob, and then define a single recipient which can derive the CEK (Content Encryption Key) using their private key. We will use the curves of P-256 (secp256r1), P-384 (secp384r1), P-521 (secp521r1) or SECP256K1 (as used with Bitcoin).
- RSA using COSE and CBOR. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\).
- RSA: dQ, dP and InvQ. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). The key pair also includes \(dQ\), \(dP\) and \(InvQ\), and these can be used with the Chinese remainder theory to optimize the decryption process.
Metasploit
- Armitage and Metasploit. Go.
- Exploiting Android with Metasploit. Go.
- Exploiting Android with Metasploit - Part 2. Go.
- Exploiting Windows/Mac OS X with Metasploit. Go.
- Remote Desktop Windows/Mac OS X with Metasploit. Go.
- Metasploit. Go.
- Internet of Things Security. Go.
- Metasploit (Enumeration and Scanning). Go.
- Metasploit (Malware). Go.
IP

 The following are a few interesting techniques around IP addresses:
The following are a few interesting techniques around IP addresses:
- Your details. IP. This shows your browser details.
- IP address analyser. IP. This involves converting an IP address to the host and network part of the address.
- IP subnet analyser. IP subnets. This involves converting an IP address to the host and network part of the address.
- IP address analyser. IP. This involves analysing IP addresses.
- Max subnets. Max subnets. This involves converting an IP address to the host and network part of the address.
- Route summarization. Summarization. This involves converting an IP address to the host and network part of the address.
- Whois. Whois. This does a basic Whois on a domain.
- URL Obfuscation. Obfuscation. This outlines URL obfuscation.
- HTTP Responses. Test. HTTP.
- Capturing Network Packets (Python). WinPCap. HTTP.
Cisco related
- Routing table. Routing table. This involves viewing a routing table for a Cisco device.
- ACL Generator. ACL. This involves a simple calculator for ACLs on network ranges.
- EIGRP metrics. EIGRP. Learn the basics of EIGRP metrics.
- VoIP B/W. VoIP. Calculate bandwidth for VoIP.
- Wild Card. Wild Card. On a Cisco device a wildcard mask is used to identify the parts of an IP address that need to be matched. It thus uses a wildcard mask, where a 0 in the bit position identifies that the device should match that bit, else a 1 shows that it should ignore it.
Protocols
- HTTP. HTTP. Show the request and response for HTTP.
- Ping analyser. IP. This involves converting a ping of a site.
IP Challenges
-
IP Test 1. IP Test. IP Classification test. This is a simple test which generates a range of IP addresses, and you must determine the IP address classification.
IP Subnet Challenge 1 Demo
-
IP Test 2. IP Test. IP Classification test Part 2. This test provides an address classification, and the user must find the addresses which are of this classification.
IP Subnet Challenge 2 Demo
-
IP Test 3. IP Test. IP Classification test Part 3. This test provides an address classification, where the network part of the address is determined.
IP Subnet Challenge 3 Demo
Subnet Challenges
- Subnet Test 1. Subnet Test. Subnet Test.
-
Subnet Test 2. Subnet Test. Subnet bits.
- Subnet Test 3. Subnet Test. Find the nth usable subnet. This test involves finding the nth usable subnet.
- Subnet Test 4. Subnet Test. Maximum subnets. This is a test page to determine the maximum number of subnets and hosts/subnet for IP classed addressing.
- Subnet Test 5. Subnet Test. Maximum host/subnet. This is a test page to determine the maximum number of hosts per subnet.
- Subnet Test 6. Subnet Test. Determine the required subnet mask for a given number of subnets. This is a test page to determine the required subnet mask for a given number of subnets and a given IP address classification.
- Subnet Test 7. Subnet Test. Determine the required subnet mask for a given number of host/subnet. This is a test page to determine the required subnet mask for a given number of hosts per subnet and a given IP address classification.
- Subnet Test 8. Subnet Test. Route summarization. This involves a calculation on route summarization.
- Subnet Test 9. Subnet Test. Binary to IP.
- Subnet Test 10. Subnet Test. Hex to IP.
-
Subnet Test 13. Subnet Test. Wild card mask network bits. Find the number of bits in the network part of the wild card mask. IP Wildcard challenge
- Subnet Test 14. Subnet Test. Wild card mask host bits. Find the number of bits in the host part of the wild card mask. IP Wildcard challenge
- Subnet Test 15. Subnet Test. Wild card mask ... find the network address. Find the network for the wild card mask. IP Wildcard challenge 2
- Subnet Test 16. Subnet Test. Find a matching IP address for a network and wild card mask. Find the IP for a network and a wild card mask.
- Subnet Test 17. Subnet Test. Find an address which is on a given network. Find an IP address on a network, for a given network address and subnet mask.
- Subnet Test 18. Subnet Test. Find an IP address on the same network. Find an IP address on the same subnet.
- Subnet Test 19. Subnet Test. Find subnet. Convert subnet mask.
- Megatest. Subnet Test. Challenging test for subnets.
JavaScript

JavaScript code allows execution within the browser, rather than on the server. It is often faster than code that runs on a server. Along with this we can also use Node.js, and which runs JavaScript code on a server.
Symmetric key
- AES. AES. In this example, we will use either a pre-generated key or a random one, and use AES (Rijndael) encryption.
- ChaCha20 and Poly1305. ChaCha. This page outlines Poly1305 and ChaCha20. ChaCha20 is a symmetric key method and Poly1305 is a message authentication code (MAC). They were created by Daniel J. Bernstein, and are alternatives to AES and HMAC.
- CMS (Padding). CMS. This page uses PKIJS encrypting on CMS. With CMS we can This document describes the Cryptographic Message Syntax (CMS). With this we can encapsulate an message within an encrypted entity.

Hashing
- Hash. Hash. This page defines a JavaScript Hash calculator. This uses a client-side JavaScript code to determine the hash signatures of a text value.
Signatures
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
- Boneh–Lynn–Shacham (BLS) signature. BLS. Boneh–Lynn–Shacham (BLS) signature method produces short signatures. They use elliptic curve pairing (and which are also known as bilinear maps).
Key exchange
- ECDH. ECDH. Elliptic Curve Diffie Hellman (ECDH) is used to generate a shared key. This implementation uses Elliptic Curve Cryptography (ECC) with JavaScript.
CryptoJS
- CryptoJS. CryptoJS. This page uses client-side JavaScript code to hashing, encrypt and sign, including for symmetric key (AES), streaming ciphers, hashing methods, and HMAC.
Blockchain
- PATRICIA trie. PATRICIA. In the following, we have the Top 2,500 Web sites in the world, and implemented with a Radix Trie (aka PATRICIA trie) In the following we have the Top 2,000 web sites on the Internet, and which have been indexed using the PATRICIA trie.
Public key
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
- RSA. RSA. RSA is an asymmetric encryption algorithm, which uses two keys, one to encrypt and the other to decrypt. It was created in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman, and is still one of the most widely used encryption methods. A typical application is in authenticating a sender, where the senders private key is used to encrypt a message, and then is decrypted by the receiver with the senders public key (which is known to anyone who wants it). It is also typically used for encrypting disks/files, such as for EFS.
Digital Certificates
- X.509 certificates in JavaScript. RSA and ECDSA Signed certificates. This page will generate either RSA and ECC key pairs, and then generate X.509 certificates, using either a signature of SHA1withRSA or SHA256withECDSA. For RSA signing we use an RSA private key to sign the certificate, and with ECDSA signing we use an ECC private key to sign the certificate.
Tokens
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
Random
- Random number generator. Rand. In the past, encryption and decryption had to be done through native code libraries, such as with Bouncy Castle and OpenSSL. With the increasing processing power of Web browsers, it is now possible to use encryption using JavaScript, which thus provides client-side processing of data. This Web page uses Javascript encryption, and generates a random 256-bit text key or a hex version. The 256-bit key is generated by generating 60 random numbers (from 0-25), and converting these to an ASCII character.
Malware obfuscation
- Malware obfuscation. Obfuscation. A malware writer will often hide certain keywords from the browser/human by encoding them in another format. This is typically done for hex coding (\xZZ), 16-bit unicoding (\uZZZZ) and octal coding (\ZZZ). To test, enter a value, and then press the button and it will convert encoded string.
Message Authentication Codes
- Chaskey (MAC). Chaskey. Chaskey Cipher is light-weight cryptography method for signing messages (MAC) using a 128-bit key. The hardware implementation only requires 3,334.33 gate equivalent with an operating clock frequency of 1 MHz (whereas Keccak requires 4,658 GE). In the page we create the Mac signature and also encrypt for CBC.
Other
- Password generation/hashing. Hashing. Linux can use salted passwords where the username, hashing method and hashed password are stored in a password file [More details]. The main methods are
Hashing

At times we need to generate secrets, such as encryption keys, from passwords or nonce values. A Key Derivation Function (KDF) is a verifiable way of doing this.
Key Derivation Functions (KDFs)
The following are the tips related to hashing:
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Password strength. Test. This outlines the strength of various passwords types.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
HKDF
The following are the tips related to Key derivation hashing:
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Hazmat HKDF for different hashing methods. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
-
HKDF key derivation with OpenSSL [
here]
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
PBKDF2
The following are the tips related to Key derivation hashing:
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- AES GCM (Python) with PBKDF2. AES GCM (Python) with PBKDF2.
- Fernet with PBKDF2 . AES GCM (Python) with PBKDF2.
- PBKDF2 key derivation. AES GCM (Python) with PBKDF2.
- Key Rotation with Fernet. AES GCM (Python) with PBKDF2.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Bcrypt
The following are the tips related to Key derivation hashing:
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- BCrypt. BCrypt. BCrypt with Rust.
-
Hash to password with Go. Hashing to Argon2, Scrypt and BCrypt. Hash to password with Go, including Argon2, Scrypt and BCrypt.
scrypt
- scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Argon 2
The following are the tips related to Key derivation hashing:
- Argon 2. Go. Outline of Argon2.
- Argon 2 with NaCl. Go. Outline of Argon2 using NaCl.
- Argon 2. Argon 2. Argon 2 with Rust.
- Balloon. Go. Outline of Balloon.
Other
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
- Double ratchet. Go. Outline of double ratcheting.
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
Outline
HMAC Key Derivation function (HKDF) is used to derive an encryption key from a passphrase. Initially, HKDF creates a pseudorandom key (PRK) using a passphrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), and along with a salt value. Next, the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys [RFC 5869][article]. In this case, we will use SHA-256.
The following shows how an encryption key can be generated using HKDF, and where we need a secret and a salt value. Both Bob and Alice have the same secret and salt.

With PBKDF2 (Password Based Key Derivation Function 2), we hash for a given number of rounds:

Key exchange

Key exchange is a way for Bob and Alice to communicate and for them to agree on a shared secret. The original method defined uses discrete logarithms (Diffie-Hellman), but most modern methods use elliptic curve techniques (ECDH). As quantum computers can crack both discrete log and elliptic curve methods, there are post quantum cryptography methods proposed. This includes SIDH, CSIDH, SIKE, and NewHope.
Key interchange/generation (Diffie-Hellman)
The following relates to key interchange:
- Selecting \(g\) in Diffie Hellman. G in Diffie Hellman. Picking a safe value of the generator \(g\) in discrete logarithms.
- Diffie-Hellman. Diffie-Hellman Calculation. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Real example). Diffie-Hellman Real. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Python). Diffie-Hellman. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (pre-compute). Diffie-Hellman (pre-compute). Many sites use the same prime numbers, which can then be cracked with a pre-computing attack.
- Key generation. Key gen. This will generate keys for different methods based on a passphrase.
- Diffie-Hellman (Man-in-the-middle). DF. This outlines the man-in-the-middle method for Diffie-Hellman.
- An Alternative Diffie-Hellman method. Alterative DH. This outlines an alternative Diffie-Hellman method.
Authenticated Key Exchange
The following are the tips related to Key derivation hashing:
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- MTI/A0. MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{ax+by} \pmod p\). MTI (Matsumoto, Takashima, Imai).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0. MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{x+y} \pmod p\)
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). The resultant key is \(xyG \)
- MTI/C0. MTI/C0. This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{xy} \pmod p\)
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG\).
- MTI/C1. MTI/C1. This outlines MTI/C1, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{abxy} \pmod p\).
- MQV (Menezes–Qu–Vanstone). MQV. MQV was created Alfred Menezes, Minghua Qu and Scott Vanstone in 1995 and is an authenticated key exchange method. Alice holds a key pair \((A,a)\) and Bob has a key pair \((B,b)\). With this \(a\) is Alice's private key, and \(A=aG\) is her public key. For Bob, his public key will be \(B=aG\) and a private key of \(b\), and where \(G\) is the base point on the elliptic curve.
- HMQV (Menezes–Qu–Vanstone). HMQV. HMQV builds on MQV and adds the identity of Bob and Alice.
- ECDH with X25519 and Blake2b. ECDH with X25519 and Blake2b. This uses PyNaCl to create an authenticated key exchange and uses X25519 and Blake2b.
Elliptic Curve (ECDH) - Python
The following are the tips related to ECC:
- Elliptic Curve. Elliptic Curve. Elliptic Curve is a public key method which can also be used to generate a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with simple parameters. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
Elliptic Curve (ECDH) - Golang and Node.js
The following are the tips related to ECC:
- ECDH with Go. ECDH. ECDH with Go.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with node.js. ECDH. ECDH with node.js.
- ECDH with JavaScript. ECDH. Elliptic Curve Diffie Hellman.
Password Authenticated Key Exchange (PAKE)
The following are the tips related to Key derivation hashing:
- SPAKE2. Go. Outline of SPAKE2.
- OPAQUE. Go. Outline of OPAQUE.
- SPEKE. Go. Outline of SPEKE (Simple Password Exponential Key Exchange).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
- J-PAKE. J-PAKE. This example generates a shared key based on a shared password.
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses discrete logs.
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
PQC NIST Finalists (Key Exchange)
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Key interchange/generation (Other)

The following relates to key interchange:
- Curve25519. Curve25519. This outlines Curve25519, which is used in the Tor network.
- Authenticated Key Exchange (Discrete logs). YAK. Key exchange with public keys and uses discrete logs.
- Authenticated Key Exchange (ECC). YAK. Key exchange with public keys and uses elliptic curve methods.
- Shamir No-key protocol. Shamir No Key. In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated.
- Shamir No-key protocol (sepc256k1). Shamir No Key (EC). In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated using the sepc256k1 elliptic curve.
- Conference keying (Burmester-Desmedt method). Conference keying. In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it.
- Conference keying (Burmester-Desmedt method) - Elliptic Curve (sepc256k1). Conference keying Elliptic Curve (sepc256k1). In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it, and uses the sepc256k1 elliptic curve.
Key exchange (with pairing)
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Kryptology

We need to build a new Internet. One that is build on mathematics and certainty, rather than the patchy version we have now. For this we need a layer of cryptography at the lowest level, and build software interfaces on top of this. Along with this we now have cryptographic methods which can now provide a foundation of trust, and which preserve privacy. And so the old libraries of OpenSSL are being squeezed out in favour of the new ones which are built on a solid foundation. The latest of these new "privacy-aware" libraries is Kryptology, and created by Coinbase. This library provides the APIs that developers need, in order to apply to areas of blockchain development. This library include BLS (Boneh-Lynn-Shacham) signatures, Zero-knowledge Proofs (ZKPs) and Shamir Secret Shares (SSS). With BLS we can digitally sign for data, but also preserve its privacy. Applications of this include group signatures, where multiple entities can merge their signing keys together and provide a single signature for a transaction. With SSS, we can split encryption keys up into shares, and then distribute them across a network. When required, we can call these shares back to reconstruct the key.
The focus for Coinbase seems to be the application of privacy coins, and where no tracking can be applied to the usage of these digital coins. This should support full anonymity for transactions, as opposed to Bitcoin which only supports pseudo-anonymity.

ECC Basics
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining n.G for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Points (Base Point and Others). Elliptic Curve points. Two common curves used in ECC (Elliptic Curve Cryptography) are secp256k1 (as used in Bitcoin and Ethereum) and P256 (secp256r1). The "k1" refers to the Kolbitz curve 1 (named after the creator of ECC). With these we have a base point which are can operate on. This is typically defined as \(G\). We can then operate on this with add and multiply operation. For example, \(2G=G+G\) and \(P=n.G\). In this following we will show the base point for a number of common curves, such as secp256r1, P256, Pallas, Curve 25519, BLS12381G1, BLS12381G2, BLS12377G1 and BLS12377G2.
ECDH
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret. We will use Golang and the Krytology library.
Simple ECC on curves
- Public key points for curves. Simple. Display public key points for scalars.
BLS Curve
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
Accumulator and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
Pallas Curve
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
Pairing-based Crypto
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
ElGamal and ECC
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a numerical input.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
Shamir Secret Shares
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Homomorphic Encryption
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Zero knowledge proofs
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
Verifiable Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Hash to scalar and point
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
CP-ABE
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Lattice cryptography

Latice cryptography is proposed as a post-quantum robust method for public key encryption, especially focused on digital signatures and key exchange mechanisms (KEMs).
Principles
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
NTRU
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- Lattice Encryption: NTRU Key Generation Python). NTRU. Outlines how NTRU operates for key generation.
Homomorphic
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Digital Signatures
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
Public-Key Encryption/Key Exchange
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
Light-weight cryptography

While AES and SHA work well together within computer systems, they struggle in an IoT/embedded world as they take up: too much processing power; too much physical space; and consume too much battery power. So NIST outlines a number of methods which can be used for light-weight cryptography, and which could be useful in IoT and RFID devices [1]. They define the device spectrum as:
- Conventional cryptography. Servers and Desktops. Tablets and smart phones.
- Light-weight cryptography. Embedded Systems. RFID and Sensor Networks.
With embedded systems, we commonly see 8-bit, 16-bit and 32-bit microcontrollers, and which would struggle to cope with real-time demands for conventional cryptography methods. And in the 40+ years since the first 4-bit processor, there is even a strong market for 4-bit processors. RFID and sensor network devices, especially, have limited numbers of gates available for security, and are often highly constrained with the power drain on the device.
So AES is typically a non-starter for many embedded devices. In light-weight cryptography, we often see smaller block size (typically 64 bits or 80 bits), smaller keys (often less than 90 bits) and less complex rounds (and where the S-boxes often just have 4-bits).
For light-weight cryptography the main constraints that we have are typically related to ener requirements, gate equivalents (GEs), and timing. With passive RFID devices, we do not have an associated battery for the power supply, and where the chip must power itself from energy coupled from the radio wave. An RFID device is thus likely to be severely constrained in the power drain associated with any cryptography functions, along with being constrained for the timing requirements and for the number of gates used. Even if an RFID device has an associated battery (active RFID), it may be difficult to recharge the battery, so the drain on power must often be minimised.
There is thus often a compromise between the cryptography method used and the overall security of the method. Thus often light-weight cryptography methods balance performance (throughput) against power drain and GE, and do not perform as well as main-stream cryptography standards (such as AES and SHA-256). Along with this the method must also have a low requirement for RAM (where the method requires the usage of running memory to perform its operation) and ROM (where the method is stored on the device). In order to assess the strengths of various methods we often define the area that the cryptography function will use on the device – and which is defined in \(µm^2\). The NIST finalists are defined in this [article]
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- GIFT AEAD. GIFT. GIFT is a light-weight block cipher. It is a (NIST Finalist)
- Elephant. Elephant. Elephant is a light-weight stream cipher. It is a (NIST Finalist).
- TinyJambu. TinyJambu. TinyJambu is a light-weight block cipher. It is a (NIST Finalist)
- Isap AEAD. Isap. Isap is a light-weight block cipher. It is a (NIST Finalist)
- PHOTON-Beetle AEAD. PHOTON-Beetle. PHOTON-Beetle is a light-weight block cipher. It is a (NIST Finalist)
- Romulus AEAD. Romulus. Romulus is a light-weight block cipher. It is a (NIST Finalist)
- Sparkle AEAD. Sparkle. Sparkle is a light-weight block cipher. It is a (NIST Finalist)
- CLEFIA. CLEFIA. CLEFIA is a light-weight block cipher.
- LED. LED. LED is a light-weight block cipher.
- Piccolo. Piccolo. Piccolo is an ultra light-weight block cipher.
- PRESENT. PRESENT. Present is a light-weight block cipher.
- Pyjamask. Pyjamask. Pyjamask is a light-weight block cipher.
- SIMON. SIMON. SIMON is a light-weight block cipher.
- SKINNY. SKINNY. SKINNEY is a light-weight block cipher.
- SPECK. SPECK. SPECK is a light-weight block cipher.
- XTEA. XTEA. XTEA is a light-weight block cipher.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encryption/Decryption. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.
Light-weight crypto (Other)
- Chaskey (MAC). Chaskey. Chaskey is a light-weight MAC function.
- Chaskey (MAC). Chaskey (Python). Chaskey is a light-weight MAC function.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (ASCON)
ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRFF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
Discrete Logs (Solving)

A discrete log problem is in the form of \(g^x \pmod p\) and where we know \(g\) and \(p\) and must solve for \(x\).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Message Authentication Code (MAC)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
HMAC
The following are the tips related to Key-based hashing:
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authentication both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2), Blake2b, SM3 and SHA-3. This page outlines the HMAC-MD5 methods using the Hazmat cryptography layer.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- HMAC (COSE). Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT with HMMAC. Go. In this case we create a CWT token, and sign with an HMAC signature.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- HMAC with Rust. HMAC. HMAC with Rust.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HMAC with OpenSSL. MACs with OpenSSL. HMAC in OpenSSL for a given input value, password and hashing method.
Cipher MACs
The following are the tips related to Key-based hashing:
- MACs with OpenSSL. MACs with OpenSSL. MAC methods implemented in OpenSSL, including CMAC and GMAC.
Key-based hashing
The following are the tips related to Key-based hashing:
- SipHash. Siphash. Siphash is a fast key-based hashing method.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Meow. Meow. Meow is one of the fastest hashing methods.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
Magic Numbers

This pages contains information related to magic numbers in file formats.
Network and File Forensics
- Magic numbers. Magic. This provides information on magic number for file forensics.
Graphics formats
- JPEG Analysis. JPEGs. This provides an analysis of JPEG files.
- GIF Analysis. GIFs. This provides an analysis of GIF files.
- TIF Analysis. TIFs. This provides an analysis of TIF files.
- PNG Analysis. PNGs. This provides an analysis of PNG files.
- BMP Analysis. BMPs. This provides an analysis of BMP files.
- PSD Analysis. PSDs. This provides an analysis of PSD files.
- WMF Analysis. WMF. This provides an analysis of WMF files.
- Adobe Illustrator Analysis. AI. This provides an analysis of AI files.
- Adobe In Design Analysis. INDD. This provides an analysis of INDD files.
- MIDI file. MIDI. This provides an analysis of MID files.
- ICO file. ICO. This provides an analysis of ICO files.
- PS file. PS. This provides an analysis of PS files.
- EPS file. EPS. This provides an analysis of EPS files.
- VSD file. VSD. This provides an analysis of Microsft Visio (VSD) files.
Video and audio formats
- MP3 Analysis. MP3s. This provides an analysis of MP3 files.
- AVI Analysis. AVIs. This provides an analysis of AVI files.
- Flash SWF Analysis. SWFs. This provides an analysis of Flash files.
- Flash FLV Analysis. FLVs. This provides an analysis of FLV files.
- MP4 Analysis. MP4. This provides an analysis of MP4 files.
- MOV Analysis. MOV. This provides an analysis of MOV files.
- WMV Analysis. WMV. This provides an analysis of WMV files.
- WMA Analysis. WMA. This provides an analysis of WMA files.
- JPEG 2000 Analysis. JPEG 2. This provides an analysis of JPEG 2000 files.
- WAV Analysis. WAV. This provides an analysis of WAV files.
Zips, Archives and Library files
- ZIP/Archive Analysis. ZIPs. This provides an analysis of ZIP/Achive files.
- GZ Analysis. GZ. This provides an analysis of GZip files.
- Tar Analysis. Tar. This provides an analysis of TAR files.
- MSI Analysis. MSI. This provides an analysis of MSI files.
- OBJ Analysis. OBJ. This provides an analysis of OBJ files.
- DLL Analysis. DLL. This provides an analysis of DLL files.
- CAB Analysis. CAB. This provides an analysis of CAB files.
- EXE Analysis. EXE. This provides an analysis of EXE files.
- RAR Analysis. RAR. This provides an analysis of RAR files.
- SYS Analysis. SYS. This provides an analysis of SYS files.
- HLP Analysis. HLP. This provides an analysis of HLP files.
- VMDK Analysis. VMDK. This provides an analysis of VMDK files (VMWare Virtual Disks).
- PST Analysis. PST. This provides an analysis of PST files (Outlook Email File).
- JAR Analysis. JAR. This provides an analysis of JAR files.
- SLN Analysis. SLN. This provides an analysis of Microsoft SLN files.
- Class Analysis. Class. This provides an analysis of Java Class files.
- Zlib. Zlib. This provides an analysis of Zlib files.
Documents
- PDF Analysis. PDFs. This provides an analysis of PDF files.
- DOC Analysis. DOCs. This provides an analysis of DOC files.
- RTF Analysis. RTFs. This provides an analysis of RTF files.
- XLS Analysis. XLSs. This provides an analysis of XLS files.
- PPT Analysis. PPTs. This provides an analysis of PPT files.
- MMP File. MMP. This provides an analysis of MMP files.
- DOCX Analysis. DOCX. This provides an analysis of DOCX files.
- XLSX Analysis. XLSX. This provides an analysis of XLSX files.
- PPTX Analysis. PPTX. This provides an analysis of PPTX files.
- MDB Analysis. MDB. This provides an analysis of MDB files.
- Outlook Message Analysis. MSG. This provides an analysis of MSG files.
Disk Image
- Raw disk format. RAW. This provides an analysis of the RAW disk format.
Tests
- File Forensics Test. File Test File Forensics Test.
- File Forensics Test (Fun). File Test (Fun) File Forensics Test.
Presentations
MIRACL Core Library

MIRACL Core is an open source library, and includes a wide range of public key encryption methods. It is especially focused on elliptic curve and pairing-friendly methods, but also supports a wide range of encryption methods, including RSA, AES and hashing. Overall, it can be ported onto a wide range of systems and supports C, C++, Go, Rust, Python, Java, Javascript and Swift. Along with this it supports limited capability devices such as the Arduino infrastructure. The GitHub repository is [here].
BN254
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.

Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- CL Signatures. CL. CL Signatures in Go using MIRACL.
- CL Signatures (advanced pairing). CL. CL Signatures in Go using MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages using MIRACL.
- PS Signatures. PS. Signatures using PS for short signatures using MIRACL.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures using MIRACL.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.

Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
Rust examples
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
NaCl

PyNaCl is a Python port of LibSodium. It integrates the latest cryptography methods, such as AES, XChaCha20, Blake2b and X25519.
Symmetric Key
- Symmetric key. Symmetric key (XChaCha20 and Poly1305). With symmetric key, Bob and Alice have the same key. NaCl uses the XChaCha20 method, and which supports stream encryption (and which does not require padding as a block cipher does, and is also faster than block cipher modes). ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16 byte nonce. XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24 byte nonce. It has a lower propability of nonce misuse than ChaCha20.
- Encryption with a password. Symmetric Key with KDF. In symmetric key, we generate a secret key. This key is typically a random value or generated from a password and a salt value. If we use a password, we typically use a KDF (Key Derivation Function), and which uses a password and a salt value, in order to create a key of a given size. In this case we will use Argon2i, and which is memory resilent.
Hybrid Encryption
- Box. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Hashing
- Hashing and KDF (Argon2 and scrypt). Hashing and KDF. This case we will use PyNaCl (Networking and Cryptography) library, and which is a Python binding to libsodium. We will hash a password using SHA-256 and SHA-512, and also create a KDF (Key Derivation Function) using scrypt and Argon2.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
Ed25519
-
Ed25519. Ed25519. Using Ed25519 for digital signatures.
-
Finding Points on Ed25519. X25519 (Points).
In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 (Key Exchange)
- X25519 + BLAKE2b key-exchange. X25519. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
Curve 25519
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
Node.js

Node.js uses the JavaScript programming langauge as its base, and allows for code to be run on a server, rather than in the browser (such as with pure JavaScript). To run a node.js program, we run "node myfile.js", and use NPM to install libraries.
Symmetric key
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
RSA and public key
- RSA Opt imal Asymmetric Encryption Padding (OAEP) using Node.js. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
ECC Keys
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.

Hashing
- Hashing with node.js (All). Hashing. Hashing with node.js.
- Hashing with node.js (Selection). Hashing. Hashing with node.js.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- ECDSA with node.js. ECDSA. ECDSA with node.js.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
Key exchange
- Diffie-Hellman with node.js (random prime). DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method and uses a randomly generated prime number (press the button to generate a new prime).
- Diffie-Hellman with node.js. DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method. Each time the prime number will be fixed for the DH group selected.
- ECDH with node.js. ECDH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Elliptic Curve Diffie Hellman (ECDH) key exchange method.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
Key derivation
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
CryptoJS
- CryptoJS (in node.js). CryptoJS (Node.js). Various crypto methods in the browser.
Bulletproofs
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
Blockchain
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
Proxy encryption
- Proxy Encryption - Encrypting With Public Key, And Decrypt with Private Key. Proxy01. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This page just creates a key pair for Alice, and uses it to encrypt with the public key , and decrypt with the private key.
- Proxy Encryption. Proxy02. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This will go through the full use case of proxy re-encryption.
Tokens
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
Random
- Fortuna with node.js. Fortuna. Fortuna random numbers with node.js.
Other
- FPE with node.js. FPR. FPE with node.js.
- Puny with node.js. Puny. Puny character format with node.js.
Accumulators and Witnesses
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
PGP
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Password Entropy
- Password Entropy with Node.js. Password Entropy. Password entropy measures the strength of a password, and is measured as the number of bits which could represent all of the possibilities. An entropy score of less than 25 identifies a poor password, and between 25 and 50 is a weak password. For 50 to 75 we have a reasonable password, and between 75 and 100 is a very good password. Over 100 is an excellent password. The strength of the password relates to the number of characters used, and also the number of characters in the password.
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
- Homomorphic Encryption with Node.js and BGV. Homomorphic Encryption with Node.js and BFG. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BGV method.
Oblivious Transfer (OT)

Oblivious Transfer allows Bob to select data from Alice, but for Alice not to know which value has been selected.
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
OpenSSH

OpenSSH supports the usage of the SSH protocol. This allows for a remote login. One tool which is uses is ssh-keygen, and which allow for the generation of RSA, DSA and elliptic-curve keys that. These can be used for user and host authentication, such as for GitHub login and Cloud instance login.
OpenSSH
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here].
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
Outline

OpenSSL

OpenSSL is a standard library that implements cryptography.
Symmetric key (Command line)
-
Symmetric Key Encryption (OpenSSL 1.x) [here]. In this case we will create cipher text from OpenSSL 1.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 1.x) [here].In this case we will decrypt cipher text from OpenSSL 1.x using a key derived from a password
-
Symmetric Key Encryption (OpenSSL 3.x) [here]. In this case we will create cipher text from OpenSSL 3.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 3.x) [here].In this case we will decrypt cipher text from OpenSSL 3.x using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password.
Hashing
-
Hashing [here] OpenSSL supports a wide range of hashing methods including BLAKE2b, Gost, MD4, MD5, RMD-160, SHA-1, SHA-3, SHA-256 and SHA-512.
Libre OpenSSL
-
Symmetric Key Encryption using Libre OpenSSL [here]. In this case we will create cipher text from Libre OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption using Libre OpenSSL [here]. In this case we will decrypt ciphertext from Libre OpenSSL using a key derived from a password.
-
Hashing [here] Libre OpenSSL supports a wide range of hashing methods including Gost, MD4, MD5, RMD-160, SHA-1, SHA-256 and SHA-512.
Diffie-Hellman parameter generation
-
DH Parameters with OpenSSL [here]. The Diffie-Hellman (DH) method is perhaps one of the greatest inventions in Cybersecurity, and was created by Whitfield Diffie and Marty Hellman. With the DH method, Bob creates a random value (\(b\)) and Alice also creates a random value (\(a\)). Next Bob computes \(B=g^b \pmod p\) and sends it to Alice. Alice computes \(A=g^a \pmod p\) and sends this to Bob. Bob raises the value of \(A\) to the power of \(b\) and takes \(\pmod p\), and Alice raises \(B\) to the power of \(a\) and takes \(\pmod p\). In the end, they will have the same shared value: \(g^{ab} \pmod p\). This can then be used to derive an encryption key that they can use for a secure tunnel. Overall, \(p\) is the large prime number, and also known as the shared modulus between Bob and Alice.
Key derivation function
-
PBKDF2 key derivation with OpenSSL [here] PBKDF2 (Password Key Derivation Function 2) is a key derivation method. Overall it is relatively slow in its operation and where we take a password, a salt value, hashing method, and a number of iterations, in order to produce a given size of encryption key.
-
HKDF key derivation with OpenSSL [here] HKDF (HMAC Key Derivation function) is used to derive an encryption key from a pass phrase. Initially HKDF creates a pseudorandom key (PRK) using a pass phrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), andalong with a salt value. Next the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys.
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Passwords
-
Password example [here]. This page uses the OpenSSL library hash password generator, which is used in UNIX systems for the hashing of passwords which are contained in /etc/shadow and /etc/passwd. For newer passwords, the "-1" options is used to created the hashed value.
-
Hashed passwords with OpenSSL [here].
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
Public key
-
Generating an ECC key pair with OpenSSL [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)).
-
Generating an RSA key pair with OpenSSL [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2).
-
Generating an RSA key pair with OpenSSL with encryption [here]. This page implements RSA key pair generation with an encrypted key pair. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). In this case we will encrypt the key pair with either 3DES, 128-bit AES, 192-bit AES or 256-bit AES. The same password must be used to encrypt and decrypt.
-
Generate prime with OpenSSL [here]. Prime numbers are important in public key encrytion, and are used with RSA and ECC. For RSA, we generate two prime numbers (\(p\) and \(q\)) and which are multiplied together to create a modulus (\(N\)). If these prime numbers have 512 bit values, the modulus will be a 1,024 bit value. This defines the basic secure of RSA. With elliptic curve we use smaller prime numbers, such as 256-bit values for the secp256k1 curve.
ASN1 parsing
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). We will parse using asn1parse, and reveal the parameters.
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)) [RSA key pair]. We will parse using asn1parse, and reveal the parameters.
- DSA Parameters with asn1parse. DSA parameters with OpenSSL with asn1parse. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA (Digital Signature Algorithm)
- DSA Parameters. DSA parameters with OpenSSL. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
MAC (Message Authentication Code)
- HMAC with OpenSSL. MACs with OpenSSL. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authenticate both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2) and SHA-3. In this case we will use OpenSSL to generate the HMAC value.
- MACs with OpenSSL. MACs with OpenSSL. In the following we will generate MACs for HMAC, GMAC, CMAC, Blake2bmac, Blake2smac, KMAC128 and KMAC256. Overall, we will use an encryption key defined as a hex value for GMAC and CMAC, and a pass phrase for the others. The message is "hello".
Signing
- Digital signing a plaintext message with OpenSSL. Signing with OpenSSL. With digital signing, we can take a message, and create a signature. This normally involves signing with a private key and digital certificate. The signed message can be an a MIME format, and which can be integrated into an email message. In this can we have a 512-bit RSA key pair that will sign a plain text message.
Encrypting emails
- Encrypting an email message in OpenSSL. Encrypting messages with OpenSSL. With public key encryption, we can take a message, and encrypt it with the recipiant's public key. In this can we have a 512-bit RSA public key to encrypt a message.
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Random number generation with OpenSSL
-
Random number generator [here]. Random numbers are important in generating encryption keys and salt values. In this case OpenSSL generates a random number (in a Base64 format) for a given number of bytes.
Outline (C#/Python)
-
Symmetric Key Encryption (C#) [here]. This page uses the OpenSSL library through a C#/.NET wrapper. The DLLs it interfaces to are libeay32.dll and ssleay32.dll. OpenSSL supports a wide range of encryption methods, including 128-bit AES, 192-bit AES, 256-bit AES and Blowfish (bf). Different modes of ECB, CBC, and OFB are implemented. The examples use a default IV of "1234".
-
AES in Python with OpenSSL output [here]
-
Producing OpenSSL AES Encrypted String from C# [here]
Digital Certificates
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
Paillier - Partial Homomorphic Encryption

The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Fundamentals
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier).
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Using RSA
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
Applications
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenticated ciphertext.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
ElGamal (Encrypting with multiple public keys)
- ElGamal - Applying Multiple Public Key Operations (Discrete Logs). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use discrete logs.
- ElGamal - Applying Multiple Public Key Operations (ECC). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use elliptic curve methods, and using the Edwards 25519 curve.
Ethereum

This page outlines some examples of blockchain and cryptocurrency.
Test Network
- Math functions on Local Network. Go.
- Math functions on Test Network. Go.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- Storing State in a Smart Contract. Go.
- Deleting Data From A Smart Contract. Go.
- A Caesar Cipher Quiz Generator from a Smart Contract. Go.
- Hashing in a Smart Contract. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
- Dealing With Decimals In Smart Contracts. Go.
- Creating A Scrambled Alphabet Challenge Generator In Ethereum and Solidity. Go.
- Deploying a Scrambled Alphabet Generator To Ethereum (With Ganache and Ropsten). Go.
- Deploying a Scrambled Alphabet Generator To Ethereum (With Hardhat). Go.
- Pigpen, IPFS and Ethereum. Go.
- Proof of \(x\) from \(H(x)\) using zkSnarks. Go.
- Elliptic Curve Operations Within a Solidity Contract. Go.

Ethereum
- Creating Ethereum address with Python. Go.
- Creating Ethereum signing with Python. Go.
- ERC20 Tokens. Go.
- Ethereum address with Go. Addresses. This generates an Ethereum address.
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- PATRICIA trie. PATRICIA. Example of using PATRICIA (and which is used in Ethereum).
- Viewing Balance of account in Etheruem with Go. Balance. This views the balance of an account
- Viewing Block in Etheruem with Go. Block. This views a block.
- Viewing Cryptocurrency API with Python. Go.
- Viewing Ethereum blockchain with Python. Go.
- Viewing Transactions in Block in Etheruem with Go. Transactions. This views transactions.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
- Symmetric Key Encryption For Smart Contracts. Symmetric key. Solidity does not natively support symmetric key encryption, such as with AES. Overall, AES would consume too much gas and thus be expensive to implement. But, we can use hashing and X-OR methods to do the encryption. In this case, we will create a 256-bit random value, and then encrypt it with an encryption key, and then decrypt it.
Calling from Python
- Calling smart contracts with Python. Python.
Ethereum crypto
- ECIES with Go-Ethereum. Go.
Ethereum Blockchain
- IOTA Trytes. Trytes. `This outlines Trytes, as used in IOTA.
Ethereum Blockchain
- Blockchain: Adding Maths Functions. Go.
- Blockchain: Blocks, transactions and writing data. Go.
- Blockchain: Contracts and Addresses. Go.
- Blockchain: Getting transactions. Go.
- Blockchain: Hello World!. Go.
- Blockchain: Simple Purchasing System. Go.
- Blockchain: Viewing the blockchain. Go.
- Blockchain: Cracking Wallets. Go.
- Introduction to Blockchain. Go.
Presentations
Factorization

Many public key problems involve the difficulity in factorizing a value two its prime number factors. For example, in RSA, we have a public modulus \(N\) and which is equal to the multiplication of two prime numbers \(p\) and \(q\). If we can factorize the public modulus, we will be able to break the RSA cipher related to it.
RSA Crack
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA Factorization. RSA. This outlines the factorisation of the N value in the RSA method.
Methods
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Dixon. Go. Dixon Method.
- Rho factorization. Rho. Rho alogorithm.
- Smooth numbers. Go. Outline of smooth numbers.
Methods (Elliptic curve
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Quadratic residues
- Quadratic residue (mod p). Go. Outline of quadratic residue \(\pmod p\).
- Quadratic residue (mod p) using Legendre symbol. Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
Factorizing
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
Lenstra–Lenstra–Lovász (LLL) with lattices
- Crack ECDSA with weak nonces. ECDSA with weak nonces and using Lenstra–Lenstra–Lovász (LLL) method. This outlines ECDSA how the private key can be recovered with weak nonce values.
Network Forensics

These pages outlines some network forensics. This includes the understanding of the network stack, and with protocols such as Etherenet, IP, TCP, HTTP, and others.
Network Forensics (Theory)
- Network Forensics (Wireshark). Network Forensics. This provides information on how to detect threats through network forensics with Wireshark.
- Advanced Network Forensics. Network Forensics. This provides information on how to detect threats through network forensics.
Network Forensics (Practice)
- Advanced Network Forensics (Wireshark). Adv Network Forensics. This provides information on how to detect threats through network forensics with Wireshark.
- Network Forensics (PCAP). Network Forensics. This provides information on network forensics (reading PCAP files)
- Network Forensics (Text). Network Forensics. This provides information on network forensics (reading text files)
Tshark
-
Filters with TShark. TShark. This page runs Tshark with a given Pcap file and a defined filter.
Other
- Advanced Digital Forensics . Adv Digital Forensics. This provides information on how analyse disk based systems using open source forensics.
- Partition Analyser. MBR. This page will analyse the details of the partition details within the MBR (put one space between fields).
Presentations
Format Preserving Encryption

Format Preserving Encryption (FPE) is a method which allows the basic formatting of a message to stay in a similar format, and where the value itself is encrypted. It can be used to hide credit card details.
Methods
- Format Preserving Encryption. FPE. This outlines Format Preserving Encryption.
- FPE with Python. FPE. An implementation of Format Preserving Encryption (FPE) using Python.
- FPE with node.js. FPR. FPE with node.js.
- FPE and PKBKDF2 in Python. FPE and PKBKDF2 in Python. FPE using PKBDF2 to password generation.
FFX (Format-preserving, Feistel-based encryption)
- FPE with Go. FPE. An implementation of Format Preserving Encryption (FPE) for FFX1 and FFX3.
- FFX schemes. FFX. Within tokenization we can apply format preserving encryption (FPE) methods, which will convert our data into a format which still looks valid, but which cannot be mapped to the original value. For example, we could hide Bob's credit card detail into another valid credit card number, and which would not reveal his real number. A tokenization server could then convert the real credit card number into a format which still looked valid. For this we have a key which takes the data, and then converts it into a form which the same length as the original.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher in Python.
FFX in Rust
- FFX. FFX. This is an implementation of FFX in Rust.
Honey Encryption
- Honey Encryption. Honey. This outlines Honey encryption.
Crypto Principles

This page outlines some crypto principles.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Galois fields (polynomial operations)

This page outlines a few basic principles around the usage of Galois fields and polynomial operations. In 1832, Évariste Galois died of duelling wounds at the age of 20 but left a great legacy. While he was a teenager he worked on polynomials and laid down the principles of Galois theory, along with defining the concept of a finite field. In cryptography, the finite field is one of the major concepts and involves limiting the number of possible values to a limiting factor (\(p\)). The values of the field then range from 0 to p-1. Within a field, we can operate on values in the field using arithmetic operations. We can thus have an infinite field, and where we could include all of the possible integers. A finite field or Galois field of GF(\(2^n\)) has \(2^n\) elements. If \(n\) is four, we have 16 output values. Let’s say we have a number \(a∈{0, ... ,2^{n−1}}\), and represent it as a vector in the form of a polynomial:
\( a=a0+a_1 x+a_2 x^2 ... a_{n−1} x^{n−1}\)
If we use \(a_n∈{0,1}\), this is exactly the same as representing a binary number modulo \(2^n\). In this \(x^n\) represents bit position \(n\) and \(a_n\) is the value of the bit at position \(x^n\). If a bit is a zero at a given position, it will be not included in the polynomial equation. So, 1011 can be represented by \(x^3+x+1\) and 1010 is represented as \(x^3+x\). We can then perform arithmetic operations on these polynomial values. So, to add two values of 1010+1100 we can represent this as \((x^3+x)+(x^3+x^2)\) and which is \(x^2+x\) as we are using modulo 2 addition, and where \(x^3+x^3=0\). With modulo 2 addition, 0+0=0, 0+1=1, 1+0=1, and 1+1=1.
An example of Galois Fields is within AES (Advanced Encryption Standard) and which uses a finite field GF(\(2^8\)). With AES we operate on bytes (8 bits) in the form of \(b_7 b_6 b_5 b_4 b_3 b_2 b_1 b_0\) and which are operated on a a polynomial of \(b_7x^7+b_6x^6+b_5x^5+b_4x^4+b_3x^3+b_2x^2+b_1x^1+b_0\).
Galois fields (polynomial operations) - GF(\(p^n\))
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Additive Group Table for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Additive Group Table for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of addition. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the additive group table for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values.
- Multiplicative Group Table for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Multiplicative Group Table for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the additive group table for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values.
- Additive, Division and Multiplicative Group Table for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Additive, Division and Multiplicative Group Table for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the Additive, Division and Multiplicative Group Table for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values.
- Additive and Multiplicative Group Table for GF(\(2^2\)) and GF(\(2^3\)). Galois Fields Table for GF(2^m) with polynomials. This page implements Galois Fields GF(\(2^n\)) with Python and provides a table of additional and multiplication. It outlines GF(\(2^2\)) and GF(\(2^3\)), but also gives a program that can be used for others. Overall, we have the form of GF(\(p^n\)) and which provides use both an additive and a multiplicative group operations that provide all the possible outputs within the finite field. The value of \(p\) is a prime number, and \(n\) is any positive integer.
- Additive and Multiplicative Group Table for GF(\(2^2\)) and GF(\(2^3\)). Galois Fields Table for GF(2^m) with coefficient values. This page implements Galois Fields GF(\(2^n\)) with Python and provides a table of additional and multiplication. It outlines GF(\(2^2\)) and GF(\(2^3\)), but also gives a program that can be used for others. Overall, we have the form of GF(\(p^n\)) and which provides use both an additive and a multiplicative group operations that provide all the possible outputs within the finite field. The value of \(p\) is a prime number, and \(n\) is any positive integer. This version will show the polynomial coefficent values within the Galois Field.
- Additive and Multiplicative Group Table for GF(\(2^2\)) and GF(\(2^3\)). Galois Fields Table for GF(2^m) with integer values. This page implements Galois Fields GF(\(2^n\)) with Python and provides a table of additional and multiplication. It outlines GF(\(2^2\)) and GF(\(2^3\)), but also gives a program that can be used for others. Overall, we have the form of GF(\(p^n\)) and which provides use both an additive and a multiplicative group operations that provide all the possible outputs within the finite field. The value of \(p\) is a prime number, and \(n\) is any positive integer. This version will show the integer values within the Galois Field.
Irreducible polynomial for GF(p^n)
- Irreducible polynomial for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Irreducible polynomial for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the parameters for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values. This includes finding the irreducible polynomial for the Galois Field.
- Irreducible polynomial for GF(\(p^n\)) for a given \(p\) and for \(n\) values. Irreducible polynomial for GF(p^n) for a given p and for n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the parameters for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values. This includes finding the irreducible polynomial for the Galois Field. Other important parameters include the degree (the highest polynomial power) and the order (the number of possible output values).
- Conway and primitive polynomial GF(\(p^n\)). Conway and primitive polynomial GF(p^n). This page outlines Conway and primitive polynomials for GF(\(p^n\)).
Galois fields (polynomial operations) - GF(\(p\))
- Additive and Multiplicative Group mod n (\(Z_n\)). Additive and Multiplicative Group mod n. In finite fields, we have a \(\pmod n\) operation for a list of integers (\(\mathbb{Z}\)), and where \(n\) is a prime number. This works for our add (+) and multiply (\(\times\)) operations, and where: \( a \pmod n + b \pmod n = (a+b) \pmod n\); and \(a \pmod n \times b \pmod n = (a \times b) \pmod n\).
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Polynomial GF(2) Factoring and Irreducible Polynomials. Factors. This outlines the search for polynomial factors for GF(2).
Polynomial operations
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
Post-quantum
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Rust
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Sage
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Golang and Cryptography

The new scripted languages such as Python and Node.js are convenient. But, unfortunately, they can be slow as they are scripted, and not compiled. Each time the scripted code is run, the scripting engine must then convert each line of code to the required machine level code. This makes the code much slower than compiled languages, and also less robust. Thus many applications in cryptography are written in C and C++, as they allow for fast execution and give low level access. Unfortunately it can be complex to compile programs, as we often need to install binary libraries and then link these in. The Go programming language, though, has a similar code syntax to C/C++, but is small and efficient and allows access to low-level functions, such as as pointers. Go thus aims to “Code less, compile quicker, execute faster”. So let’s use Go to implement some cryptography methods, including symmetric key, hashing, public keys and zero-knowledge proofs (ZKPs). The slides related to these methods are included [here]. An introduction to Golang and Cryptography is [here].

Go ECDH
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret.
Go Hex and Base64
- Base64 and Hex in Go. Base64/Hex. Two common formats for representing binary data are hexademical and Base64.
Go symmetric key
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Reuse IV attack and AES. Reuse IV and GCM. This provides an implementation of a reuse IV against AES GCM.
- ASCON AEAD (Golang). ASCON AEAD (Golang). The outlines the usage of AEAD for ASCON using Golang.
Go HMAC and HKDF
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HKDF in Go. HKDF. Implementation ofHKDF, and where we dervice a key based on a given secret.
Go secret shares
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.

Go ZKP
- Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL). DLEQ. Create a non-interactive ZKP for discrete logs.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Fiat Shamir and ECC (Interative ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP with Kryptology. This implements a range proof using a Schnorr proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?

Go ECIES (Hybrid Encryption)
With this, we can use the power of public key encryption (to generate the encryption key) with symmetric key encryption (to actually encrypt and decrpyt the data):
- ECIES (Kryptology). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Coinbase Kryptology library.
- ECIES (CIRCL). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Cloudflare CIRCL library.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt and which is used in Contract Tracing for COVID-19.
Go ECDSA
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Go RSA
- RSA Principles. RSA Principles. The basics of RSA.
- RSA with Go. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA. RSA encryption with Go using OAEP.
- RSA Encryption with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
Go ElGamal
ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Proving an Encrypted Shuffle With ElGamal and ECC. Shuffle. An encrypted shuffle with ElGamal.
- ElGamal encryption with Go. ElGamal. This implements ElGamal encryption.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
- ElGamal - Applying Multiple Public Key Operations (ECC). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use elliptic curve methods, and using the Edwards 25519 curve.
Go PGP
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
Go Public key
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.

Go Hashing
- Hashing with Go. Hashing. Hashes with Go.
- GP Hashing with Go. GP Hashing. GP Hashes with Go.
- SHAKE with Go. SHAKE. This implements SHAKE in Go.
- libDisco with Go. libDisco. This implements libDisco.
- cSHAKE in Golang. cSHAKE. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS. With the SHA-3 hashing method, we have four different cryptographic hashing methods (SHA3-224, SHA3-256, SHA3-384, and SHA3-512) and two XOF functions (SHAKE128 and SHAKE256). With SHAKE128 and SHAKE256 we can integrate domain separation between different functions — and which are known as cSHAKE128 and cSHAKE256.
- Homomorphic Hashing with Golang. Homomorphic hashing. Normally with hashing methods, we need to take all the previous data and new data in order to create a new hash value for our data. In a homomorphic hashing method, we can basically take the previous hash, and then add on any new data values. We can also remove previous data values from our hash, too. This is more efficient in computing, as we do not have to process all of our data into a new hash, and can use simple homomorphic operations for the computation. The method we will use (LtHash) was initially defined by Bellare and Micciancio and updated Lewi et al at Facebook.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
Go ECC
- Hash to password with Go. Hash to password. Hash to password with Go.
- ECDH with Go. ECDH. ECDH with Go.
- Box with Go. Box. Box with Go.
- ECC with Go. ECC. ECC with Go.
- Curve 25519 with Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ElGamal with ECC. ElGamal with ECC. ElGamal using ECC.
- Curve 25519 with Go for test vectors. ECC. This does a test on some private keys to test the public key generation.
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Barebones Ed25519 with Go. ECC. This shows point addition and scalar multiply in Ed25519
- Barebones NIST P256 with Go. ECC. This shows point addition and scalar multiply in P256
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining \(n.G\) for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Points (Base Point and Others). Elliptic Curve points. Two common curves used in ECC (Elliptic Curve Cryptography) are secp256k1 (as used in Bitcoin and Ethereum) and P256 (secp256r1). The "k1" refers to the Kolbitz curve 1 (named after the creator of ECC). With these we have a base point which are can operate on. This is typically defined as \(G\). We can then operate on this with add and multiply operation. For example, \(2G=G+G\) and \(P=n.G\). In this following we will show the base point for a number of common curves, such as secp256r1, P256, Pallas, Curve 25519, BLS12381G1, BLS12381G2, BLS12377G1 and BLS12377G2.
Go Blockchain
- Ethereum address with Go. Addresses. This generates an Ethereum address.
- Viewing Balance of account in Etheruem with Go. Balance. This views the balance of an account
- Viewing Block in Etheruem with Go. Block. This views a block.
- Viewing Transactions in Block in Etheruem with Go. Transactions. This views transactions.

Go Homomorphic
- SIDH Go. SIDH. Post-quantum key exchange.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- NTP. NTP. An overview of NTP.
- BiBa. BiBa. An overview of BiBa One Time Signature.
Go DNS
- DNSSEC. DNSSEC. An overview of DNSSEC.
Go Signatures
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Go Signcryption
- Ahmad-Afzal-Iqbal (AAI) signcryption with Golang. Ahmad-Afzal-Iqbal (AAI). Ahmad-Afzal-Iqbal (AAI) signcryption with Golang.

Go Crypto pairing
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
Go Homomorphic
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add. HEAAN Add. HEAAN Add.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- Anonymous crypto. Anon. Anonymous crypto.
- Rho factorization. Rho. Rho alogorithm.
- Post-quantum signing (BLISS). BLISS. BLISS method.
Go Post quantum
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.

Go CIRCL
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- Ed448 with Go. X448. Ed448 with Go.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with FourQ (Cloudflare). FourQ.
- Verifiable Oblivious Pseudorandom Functions (VOPRF) with Cloudflare CIRCL. VOPRF. In our digital world, we give away too many of our secrets, especially where we just have to prove the knowledge of something, rather than actually revealing it. In many of the systems we use, we could just prove things in an oblivious way, and where we could pass a secret but in a blinded form. With this, a server does not discover our password and for us not to discover the identifier that a server holds on us. But, can we also provide a proof back that the right password has been used? Well, with Verifiable Oblivious Pseudorandom Functions (VOPRF), we can generate a random secret based on a key generated on the server (Alice), and which is based on Bob’s secret.
- Hash to Curve using Go (Cloudflare). Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). The method defined here is proposed an an Internet-Draft standard by the Internet Engineering Task Force (IETF) related to "Hashing to Elliptic Curves".
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
here Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
- eXtendable-Output Function (XOF) usign CIRCL. XOF. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS.

Go Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Google Tink (Golang) ECIES. Google Tink (ECIE5). This outlines ECIES encryption with public key and AES using Golang with Google Tink
Go Credentials
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.

Go Kryptology
- Public key points for curves. Simple. Display public key points for scalars.
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.

Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.

Principles
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Paillier
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
Go Format Preserving Encryption (FPE)
- FPE with Go. FPE. An implementation of Format Preserving Encryption (FPE) for FFX1 and FFX3.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
AWS Encryption
- AWS Symmetric Key Encryption. AWS (Symmetric key). Using symmetric key in AWS.
Go Oblivious Transfer
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Dragon Fly
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
Embedding data in an ECC point
- Embedding data in a point. Go. With Elliptic Curve Cryptography (ECC), we use points on an elliptic curve to represent our data. These are defined with (x,y) points. With this, it is possible to embedded a certain amount of data into the point - as long as it still gives us a valid point on the curve. This example will Curve 25519 to embed data, and is achieved by storing the length of the data in a single byte in the point, and then store the data as byte values in the point (followed by random data). To decode, we can then just read the first byte for the length of the message, and then reveal the data encoded into the point..
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Hashing (Cryptographic)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
Benchmarks and Password strength
The following are the tips related to hashing:
- Password strength. Test. This outlines the strength of various passwords types.
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
Theory
The following are the tips related to hashing:
- Balls in bins. BiBa. This implemented balls in bins.
- Birthday attack (with Big Integers). Calc. This provides a simple example of the birthday attack.
- Birthday attack. Calc. This provides a simple example of the birthday attack.
- Differential Cryptanalysis (Hashing). Cryptanalysis. This provides an implementation of differential cryptanalysis for hashing methods.
MD5, SHA-1
The following are the tips related to hashing:
- MD2 and MD4 MD2/4. The MD2 and MD4 hashing functions were developed by Prof Ronald Rivest in 1989 and 1990, respectively. They both produce a 128-bit hash, but have been shown be vulnerable to attack (see the Collision section in the page).
- MD5 and SHA-1 (to Base-64) with salt Salt. It is possible to add salt to the MD5 algorithm, to mix it up a little.
- MD5 and SHA-1 (to Base-64) Hash. MD5 and SHA-1 produces a hash signature, and the output is typically shown in a hex format or a Base-64. In this example the output is converted into a Base-64 format.
- MD5 and SHA-1. Hash. MD5 and SHA-1 methods produce a hash signature, and are the two of the most widely used methods. The MD5 algorithm has been shown to have weaknesses, and a collision of message hashes has been shown to occur in less than one day. An MD5 signature has 128 bits, an SHA-1 signature has 160 bits, and an SHA-256 signature has 256 bits.
- MD5 Cracking. Hash Cracker. MD5 has a 128-bit signature and can be cracked using rainbow tables. This page tries to crack the MD5 signature.
- Hashing with Go. Hashing. Hashes with Go.
- Detecting hash types. Hash type. This detects has values.
- OpenSSL hashing. Range of methods. Outlines the methods used in OpenSSL
- Hash. Hash. Hashing using JavaScript
- Hashing with node.js. Hashing. Hashing with node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Hashing methods
-
Hazmat Hashes. Hazmat Hashes. This includes the hashing methods in the Hazmat cryptography library. This includes Blake2p, Blake2s, MD5, SHA1, SHA224, SHA256, SGA384, SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHA512, SHA512-224, SHAKE128 and SHA256.
-
Hazmat Hashes. Hazmat Hashes. In this case we will implement Python code to determine SHA1, SHA2, SHA3, Blake2, MD5 and SM3 hashes.
OpenSSL Passwords
-
Password example [here]
-
Hashed passwords with OpenSSL [here]
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Blake 3 hashes
The following are the tips related to similarity hashing:
- Blake 3 in Python. Hashing. Blake 3 hashing.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
Other Hash functions
The following are the tips related to hashing:
- Bloom Filter Bloom filter. A Bloom filter goes a probabilistic method of determining if an element is in a data structure, using indexed hashing methods.
- Cuckoo Table Cuckoo filter. A Cockoo table uses two hash funtions.
- Chaffing. Chaffing. This produces a keyless system.
- GP Hashing with Go. GP Hashing. GP Hashes with Go.
- LDAP. LDAP. This produces a LDAP hash signature for a password.
- LM Hash. LM Hash. This is an LM Hash Calculator. LM Hash is used in many versions of Windows to store user passwords that are fewer than 15 characters long.
- Murmur and FNV Murmur and FNV. While hashing methods such as MD5 and SHA-1 use crypto methods, the Murmur and FNV hashes uses a non-cryptographic hash function. This can be used for general hash-based lookup and was designed by Austin Appleby. It has good performance compared with other hashing methods.
- Pearson. Pearson. This uses a non-crypto hash.
- phpass. phpass. This produces a phpass hash signature for a password.
- Tiger. Tiger. Tiger is a 192-bit hash function and was designed by Ross Anderson and Eli Biham in 1995. It is often used by clients within Gnutella file-sharing networks and does not suffer from known attacks on MD5 and SHA-0/SHA-1. Tiger2 is an addition, in which the message is padded with a byte of 0x80 (in a similar way to MD4, MD5, and SHA), whereas in Tiger it is 0x01. Otherwise, the two methods are the same in their operation.
- Whirlpool. Whirlpool. Whirlpool is a 512-bit cryptographic hash function and was created by Vincent Rijmen (one of the AES creators) and Paulo Barreto, in 2000.
- WPA-2 hash . WPA-2 hash. Implements SHA-2 hash.
- Reusable hash collisions. Reusable hash collisions. Reusable hash collisions.
- The Length Extension Attack. Length Extension Attack. The MD construct has many weaknesses, and one of the most serious is the length extension attack. With this an adversary (Eve) can take a hash for an unknown message, and then add additional data to produce a new valid hash. The hash methods which are at risk against the length extension attack are MD5, SHA-1 and SHA-256. Please follow the code link below to run an example.
- Consistent hashing. Consistent hash. This outlines the usage of Consistent hashes.
- ROR13 (Module and Function). ROR13. With ROR13 we take each 8-bit character and then convert to a unicode value (with 16 bits). Then for each character we rotate the bits right by thirteen places. The resultant hash is then just the accumuluation of the rotated values.
- ROR13 (Function). ROR13 (Function). With ROR13 we take each 8-bit character and then convert to a unicode value (with 16 bits). Then for each character we rotate the bits right by thirteen places. The resultant hash is then just the accumuluation of the rotated values.
- GOST, Streebog256 and Streebog512. GOST, Streebog256 and Streebog512. GOST94 is a hashing method developed with Euro-Asian Council for Standardization, Metrology and Certification (EASC). This has since been developed in the Streebog256 and Streebog512 hashing method. In this case, we will use Libre OpenSSL to convert data into a hashed value.
RIPEMD
- RIPEMD (RACE Integrity Primitives Evaluation Message Digest) and GOST. RIPEM160. RIPEMD is a 128-bit, 160-bit, 256-bit or 320-bit cryptographic hash function, and was created by Hans Dobbertin, Antoon Bosselaers, and Bart Preneel. It is used on TrueCrypt and is open source. The 160-bit version is seen as an alternative to SHA-1, and is part of ISO/IEC 10118
- RIPEMD160. RIPEM160. RIPEMD160 is a 160-bit cryptographic hash function, and was created by Hans Dobbertin, Antoon Bosselaers and Bart Preneel. RIPEMD160 is used in Bitcoin applications.
Chameleon hashes
The following are the tips related to Chameleon hashing:
- Chameleon hash in Golang Chameleon. With a Chameleon hash, we have a normal hash value which is resistant to collisions, but with a known secret we can easily create a collision. The concept was first defined by Krawcyk and Rabin.
Similarity hashes
The following are the tips related to similarity hashing:
- Similarity hash: SimHash (Charikar similarity) in Python Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash (Nilsimsa similarity) Nilsimsa. The Nilsimsa similarity is used to find similarities between spam emails.
- Minhash (Jaccard similarity) Jaccard similarity. The Minhash method is used to find similarities between strings, files and metadata.
- String enthropy String enthropy. Measurement of the entropy of strings.
- Counting identical elements (HyperLogLog) HyperLogLog. Counting the number of identical elements.
SHA-3 and SHA-3 contenders
The following are the tips related to Key derivation hashing:
- Blake and Blake 2. Blake. Implements Blake and Blake 2 (SHA-3 contender).
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
- Grøstl. Grøstl. Implements Grøstl (SHA-3 contender).
- KangarooTwelve. KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- SHA-3, Keccak and SHAKE . SHA-3. Implements SHA-3, Keccak and SHAKE (SHA-3 winner).
- SHA-3. SHA-3. SHA-3 was known as Keccak and is a hash function designed by Guido Bertoni, Joan Daemen, Michaël Peeters, and Gilles Van Assche. MD5 and SHA-0 have been shown to be susceptible to attacks, along with theoretical attacks on SHA-1. NIST thus defined there was a need for a new hashing method which did not use the existing methods for hashing, and setup a competition for competing algorithms. In October 2012, Keccak won the NIST hash function competition and is proposed as the SHA-3 standard. It should be noted that it is not replacement SHA-2, which is currently a secure method. Overall Keccak uses the sponge construction where the message blocks are XORed into the initial bits of the state, and then inevitably permuted.
- cSHAKE. cSHAKE. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS. With the SHA-3 hashing method, we have four different cryptographic hashing methods (SHA3-224, SHA3-256, SHA3-384, and SHA3-512) and two XOF functions (SHAKE128 and SHAKE256). With SHAKE128 and SHAKE256 we can integrate domain separation between different functions — and which are known as cSHAKE128 and cSHAKE256.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- Skein. Skein. Implements Skein (SHA-3 contender).
Key derivation hashing
The following are the tips related to Key derivation hashing:
- Argon2. Go. Outline of Argon2.
- Argon2 with NaCl. Go. Outline of Argon2 using NaCl.
- Balloon. Go. Outline of Balloon.
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- Double ratchet. Go. Outline of double ratcheting.
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- Scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat HKDF. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
Non-crypto/fast hashing
The following are the tips related to non-crypto hashing:
- A perfect hash Perfect hash. This is a non-crypto hash which optimizes the hash value.
- The universal hash Universal hash. This related to the concept of a universal hash.
- FNV. FNV. FNV is one of the fastest hashing methods.
- Murmur. Murmur. Murmur is one of the fastest hashing methods.
- Siphash. Siphash. Siphash is a fast hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- xxHash. xxHash. xxHash is one of the fastest hashing methods.
- Meow. Meow. Meow is one of the fastest hashing methods.
- o1Hash. o1Hash. o1Hash is one of the fastest hashing methods.
- CRC-32. CRC-32. CRC-32 is one of the fastest hashing methods.
- wyhash. wyhash. wyhash is one of the fastest hashing methods.
- CityHash. CityHash. CityHash is one of the fastest hashing methods, and is generally free of security problems.
- FarmHash. FarmHash. FarmHash is one of the fastest hashing methods, and is generally free of security problems.
- Non-crypto. Non-crypto. This includes a range of fast non-cryptography hashing methods.
- Non-crypto hashes (C++): Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro. Non-crypto hashes: Farm, City, xxHash, MUM, Spooky 2, Murmur, Metro and t1ha0. This includes a range of fast non-cryptography hashing methods for Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro using C++ methods.
- Pearson. Pearson. Pearson is one of the fastest hashing methods, and has been designed for 8-bit processors.
- C++: t1ha. t1ha. t1ha is one of the fastest hashing methods, and has been designed for 64-bit processors.
- C++: Spooky. Spooky. Spooky is one of the fastest hashing methods, and V2 has a 32-bit, 64-bit and 128-bit version.
- C++: xxHash. xxHash. xxHash is one of the fastest hashing methods, and has good performance for short data inputs.
- C++: MUM. MUM. MUM is one of the fastest hashing methods.
- C++: FNV 1/1a. FNV 1/1a. FNV 1/1a is one of the fastest hashing methods, and is particularily useful when there are small changes in strings, such as with IP addresses and URLs.
- C++: MetroHash. MetroHash. MetroHash is one of the fastest hashing methods.
- C++: CityHash. CityHash. CityHash was created by Google and is one of the fastest hashing methods. It was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Farm. FarmHash. FarmHash was created by Google and is one of the fastest hashing methods. It is an improvement to CityHash.
- C++: Murmur. Murmur. Murmur is one of the fastest hashing methods, but was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Halftime. Halftime. Halftime is one of the fastest hashing methods and was created by Jim Apple at Apache.
- C++: Highway. Highway. Highway is an ultra-fast keyed-hash, and is more than five times faster than SipHash. It was created by Jyrki Alakuijala, Bill Cox, Jan Wassenberg at Google.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
- C++: CLHash. CLHash. CLHash is an ultra-fast hashing method and focused on improving performance of the hashing of long strings.
- C++: FalkHash. FalkHash. FalkHash is an ultra-fast hashing method and beats most of the other non-cryptography methods for performance. It is focused on the x64 architecture and integrates with AES-NI.
- C++: wyHash. wyHash. wyHash is an ultra-fast hashing method.
- C++: Fibonacci. Fibonacci. Fibonacci is an ultra-fast hashing method.
- C++: Lookup3. Lookup3. Lookup3 is an ultra-fast hashing method.
Key-based hashing
The following are the tips related to Key-based hashing:
- SiphashSiphash. Siphash is a fast key-based hashing method.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
One Time Passwords/Time Stamps
The following are the tips related to hashing:
- One Time Passwords. One Time. This allows a new unique password to be created each instance, based on an initial seed.
- Timed One Time Password (TOTP). Timed One Time Password. This allows a new unique passcode to be created each instance, based on an initial seed for a given time window. We will use a five second window in this case, where a new passcode is generated every five seconds, based on an initial seed of a pass phrase.
- Hashed One Time Password (HOTP). Hashed One Time Password. This allows a new unique passcode to be created each instance, based on a counter value and an initial seed.
- Time Stamp Protocol. TSP. This creates a time stamp for data.
- HOTP and TOTP (Python). OTP. This creates hashed passwords.
eXtendable-Output Function (XOF)
- eXtendable-Output Function (XOF) usign CIRCL. XOF. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS.
SHAKE
The following are the tips related to hashing:
- SHAKE. SHAKE. Implements SHAKE and which is an Extendable Output Function (XOF).
- SHAKE with Go. SHAKE. This implements SHAKE in Go.
- libDisco with Go. libDisco. This implements libDisco.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify
the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods
such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC methods using the Python cryptography primitives for HMAC-MD5.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
Quantum-robust Public Key (Hash-based signature)
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
Hash to ECC point
- Hash to password with Go. Hash to password. Hash to password with Go.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve with libnum.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.

Password-hashing functions using Rust
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing (Non-cryptographic)

You might know those slow old hashing methods, such as MD5, SHA-1, and SHA-256. Well, they were designed to be fast, but also highly secure. But, if we just need a hashing method, such as for a hashtable or Bloom filter, we often don’t need all the security that comes with the main cryptography hashing methods. And so we have the non-cryptography hashing methods, and which are often ultra-fast and highly efficient. To show the difference, in a test, SHA-1 — one of the fastest cryptography hashing methods — managed a processing rate of 364.95 MiB/s, while t1ha was nearly a 100 times faster, at 34,636 MiB/s.
Non-crypto/fast hashing
The following are the tips related to non-crypto hashing:
- A perfect hash Perfect hash. This is a non-crypto hash which optimizes the hash value.
- The universal hash Universal hash. This related to the concept of a universal hash.
- FNV. FNV. FNV is one of the fastest hashing methods.
- Murmur. Murmur. Murmur is one of the fastest hashing methods.
- Siphash. Siphash. Siphash is a fast hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- xxHash. xxHash. xxHash is one of the fastest hashing methods.
- Meow. Meow. Meow is one of the fastest hashing methods.
- o1Hash. o1Hash. o1Hash is one of the fastest hashing methods.
- CRC-32. CRC-32. CRC-32 is one of the fastest hashing methods.
- wyhash. wyhash. wyhash is one of the fastest hashing methods.
- CityHash. CityHash. CityHash is one of the fastest hashing methods, and is generally free of security problems.
- FarmHash. FarmHash. FarmHash is one of the fastest hashing methods, and is generally free of security problems.
- Non-crypto. Non-crypto. This includes a range of fast non-cryptography hashing methods.
- Non-crypto hashes (C++): Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro. Non-crypto hashes: Farm, City, xxHash, MUM, Spooky 2, Murmur, Metro and t1ha0. This includes a range of fast non-cryptography hashing methods for Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro using C++ methods.
- Pearson. Pearson. Pearson is one of the fastest hashing methods, and has been designed for 8-bit processors.
- C++: t1ha. t1ha. t1ha is one of the fastest hashing methods, and has been designed for 64-bit processors.
- C++: Spooky. Spooky. Spooky is one of the fastest hashing methods, and V2 has a 32-bit, 64-bit and 128-bit version.
- C++: xxHash. xxHash. xxHash is one of the fastest hashing methods, and has good performance for short data inputs.
- C++: MUM. MUM. MUM is one of the fastest hashing methods.
- C++: FNV 1/1a. FNV 1/1a. FNV 1/1a is one of the fastest hashing methods, and is particularily useful when there are small changes in strings, such as with IP addresses and URLs.
- C++: MetroHash. MetroHash. MetroHash is one of the fastest hashing methods.
- C++: CityHash. CityHash. CityHash was created by Google and is one of the fastest hashing methods. It was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Farm. FarmHash. FarmHash was created by Google and is one of the fastest hashing methods. It is an improvement to CityHash.
- C++: Murmur. Murmur. Murmur is one of the fastest hashing methods, but was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Halftime. Halftime. Halftime is one of the fastest hashing methods and was created by Jim Apple at Apache.
- C++: Highway. Highway. Highway is an ultra-fast keyed-hash, and is more than five times faster than SipHash. It was created by Jyrki Alakuijala, Bill Cox, Jan Wassenberg at Google.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
- C++: CLHash. CLHash. CLHash is an ultra-fast hashing method and focused on improving performance of the hashing of long strings.
- C++: FalkHash. FalkHash. FalkHash is an ultra-fast hashing method and beats most of the other non-cryptography methods for performance. It is focused on the x64 architecture and integrates with AES-NI.
- C++: wyHash. wyHash. wyHash is an ultra-fast hashing method.
- C++: Fibonacci. Fibonacci. Fibonacci is an ultra-fast hashing method.
- C++: Lookup3. Lookup3. Lookup3 is an ultra-fast hashing method.
A fuller test with SMHasher gives [here]:
Hash function MiB/sec cycl./hash cycl./map Quality problems
------------------------------------------------------------------
o1hash 12439661.09 16.77 166.13 insecure, no seed, zeros, fails all tests
crc32_hw1 23208.73 46.74 179.70 insecure, 100% bias, collisions, distrib, BIC, machine-specific (x86 SSE4.2)
t1ha0_aes_noavx 22785.26 38.71 180.61 LongNeighbors, machine-specific (x86 AES-NI)
t1ha0_aes_avx1 22714.85 48.12 226.52 LongNeighbors, machine-specific (x64 AVX.txt)
t1ha0_aes_avx2 22345.33 44.38 556.47 LongNeighbors, machine-specific (x64 AVX2)
falkhash 20202.42 173.63 321.52 Sparse, LongNeighbors, machine-specific (x64 AES-NI)
MeowHash64low 17378.06 85.48 237.60 Sparse, invertible, machine-specific (x64 AES-NI)
MeowHash32low 17374.64 85.48 258.53 Sparse, invertible, machine-specific (x64 AES-NI)
MeowHash 17371.91 85.48 247.96 Sparse, invertible, machine-specific (x64 AES-NI)
FarmHash32 17112.05 47.7 214.71 machine-specific (x64 SSE4/AVX)
xxh3 16538.52 32.81 184.86 DiffDist bit 7 w. 36 bits, BIC
xxh3low 16462.36 32.77 199.79
farmhash32_c 16299.81 47.79 219.19 machine-specific (x64 SSE4/AVX)
xxh128low 15174.85 33.79 187.05
xxh128 15174.14 40.46 195.65
farsh32 14053.09 74.29 245.33 insecure: AppendedZeroes, collisions+bias, MomentChi2, LongNeighbors
metrohash64crc_2 14034.84 48.94 162.54 UB, Cyclic 8/8 byte, DiffDist, BIC, machine-specific (SSE4.2/NEON)
metrohash64crc_1 14000.5 49.08 150.54 UB, Cyclic 8/8 byte, DiffDist, BIC, MomentChi2, machine-specific (SSE4.2/NEON)
metrohash128crc_1 13948.67 65.2 168.08 UB, machine-specific (SSE4.2/NEON)
metrohash128crc_2 13920.19 65.12 176.70 UB, machine-specific (SSE4.2/NEON)
halftime_hash128 13478.23 97.79 252.14
wyhash32low 12911.09 29.59 205.43 2 bad seeds
wyhash 12879 30.35 196.77 2^33 bad seeds
CityCrc128 12343.43 74.5 209.75
fletcher2 12011.15 25.29 298.60 bad seed 0, UB, fails all tests
fletcher4 11928.55 25.27 293.49 bad seed 0, UB, fails all tests
halftime_hash256 11620.28 98.44 252.60
fibonacci 11339.87 26.33 705.64 UB, zeros, fails all tests
ahash64 9862.62 27.32 181.68 rust
Spooky128 9751.14 63.84 192.47 UB
Spooky64 9747.47 62.2 191.71 UB
Spooky32 9747.13 62.24 196.96 UB
t1ha1_64le 9723.86 34.39 176.91 Avalanche
cmetrohash64_1 9683.33 45.2 161.01 UB, LongNeighbors, BIC, MomentChi2
cmetrohash64_2 9669.95 44.75 149.67 LongNeighbors
metrohash64_2 9668.51 44.45 164.30 UB, LongNeighbors
metrohash64 9664.61 44.59 150.74 UB, LongNeighbors, BIC
metrohash64_1 9664.57 45.37 152.31 UB, LongNeighbors, BIC, MomentChi2
cmetrohash64_1o 9658.31 42.84 163.45 UB, LongNeighbors, BIC, MomentChi2
FNV1a_YT 9643.42 32.06 175.19 bad seed, UB, fails all tests
City128 9640.19 88.45 225.38
metrohash128_2 9584.94 59.1 167.43 UB, LongNeighbors
metrohash128 9569.16 58.68 167.53 UB, LongNeighbors
metrohash128_1 9558.17 59.04 175.94 UB, LongNeighbors
FarmHash128 9409.63 74.52 210.25
VHASH_32 9404.99 77.01 250.57 sanity, Seed, MomentChi2
VHASH_64 9392.39 74.72 227.92 sanity, Seed, MomentChi2
farmhash128_c 9244.13 79.08 209.44
t1ha2_atonce 9237.12 38.94 194.32 Zeroes low3
City64noSeed 9090.42 32.23 171.53 Avalanche, Sparse, TwoBytes, MomentChi2, Seed
City64low 9089.45 47.75 201.73
t1ha2_stream 9068.55 74.56 219.85 Sparse, Permutation, LongNeighbors
City64 9066.9 47.81 197.78 Sparse, TwoBytes
t1ha2_stream128 9065.5 93.19 236.50 Sparse, Permutation, LongNeighbors
xxHash64 8936.63 51.31 174.34
pengyhash 8744.48 85.31 222.45
farmhash64_c 8713.16 47.96 201.00
FarmHash64 8684.76 48.13 200.51
crc64_hw 8440.13 34.94 141.15 insecure, 100% bias, collisions, distrib, BIC, machine-specific (SSE4.2/NEON)
t1ha2_atonce128 8350.99 55.65 203.53 LongNeighbors
PMPML_64 8161.19 53.2 179.16 unseeded: Seed, MomentChi2, BIC
halftime_hash512 7681.62 125.81 274.01
tabulation 7621.75 42.19 179.93
t1ha1_64be 7481.37 38.16 193.22 Avalanche
MUMlow 7225.18 37.85 197.92 UB, 5 bad seeds
farsh64 7216.29 130.3 302.44 insecure: AppendedZeroes, collisions+bias, MomentChi2, LongNeighbors
MUM 7134.56 37.85 172.34 UB, too many bad seeds, machine-specific (32/64 differs)
nmhash32 7003.3 68.93 216.59
PMPML_32 6704.53 53.5 197.43 Avalanche >512, unseeded: Seed, BIC, MomentChi2, PerlinNoise
nmhash32x 6342.95 56.41 217.75
crc32_hw 6330.42 35.55 170.16 insecure, 100% bias, collisions, distrib, BIC, machine-specific (SSE4.2/NEON)
FNV2 6258.84 33.25 142.89 fails all tests
FNV1A_Pippip_Yurii 6258.46 28.19 184.41 UB, sanity, fails all tests
FNV1A_Totenschiff 6258.23 27.99 198.20 UB, zeros, fails all tests
HighwayHash64 6242.58 99.55 248.41
mx3 6146.02 52.48 173.09 UB
xxHash32 6040.87 51.77 177.91 LongNeighbors, collisions with 4bit diff, MomentChi2 220
prvhash64s_64 5481.48 170.05 325.39
mirhash 5413.73 39.68 154.47 UB, 2^36 bad seeds, LongNeighbors, machine-specific (32/64 differs)
mirhash32low 5412.76 39.79 182.13 UB, 4 bad seeds, Cyclic, LongNeighbors, machine-specific (32/64 differs)
Murmur3F 5226.4 52.18 175.85 UB
prvhash64s_128 5161.33 260.96 442.70
t1ha0_32le 5132.18 54.83 193.53 Sparse, LongNeighbors
halftime_hash64 4990.72 120.55 281.64
Murmur2B 4882.95 39.72 149.43 UB, 1.8% bias, collisions, 3.4% distrib, BIC
seahash32low 4801.33 58.54 227.31 PerlinNoise 32, !msvc
seahash 4796.97 58.55 201.58 PerlinNoise, !msvc
fasthash32 4737.61 45.32 181.86 UB, insecure
fasthash64 4737.21 42.79 164.87 UB, insecure, Moment Chi2 5159 !
umash32_hi 4662.92 54.22 214.20
umash64 4662.09 53.42 188.09
umash32 4633.19 53.42 216.33
t1ha0_32be 4585.59 55.98 183.45 Sparse, LongNeighbors
clhash 4472.31 82.72 229.73 PerlinNoise, machine-specific (x64 SSE4.2)
tabulation32 4317.34 35.45 197.20 collisions
Murmur2C 4092.99 51.84 164.65 UB, 2^32 bad seeds, 91% bias, collisions, distr, BIC, LongNeighbors
farsh128 3776.92 232.48 398.67
City32 3675.04 57.73 212.04
TSip 3228.14 57.96 211.71 !msvc
Murmur3C 3197.63 67.9 198.00 UB, LongNeighbors, Text, DiffDist
Crap8 3149.63 36.23 195.11 UB, 2.42% bias, collisions, 2% distrib
Murmur2 3146.91 41.87 187.89 UB, 1 bad seed, 1.7% bias, 81x coll, 1.7% distrib, BIC
Murmur2A 3146.79 46.87 191.96 UB, 1 bad seed, 12.7% bias, LongNeighbors
aesnihash 2963.39 71.24 217.73 fails many tests, machine-specific (x64 AES-NI)
BEBB4185 2951.62 222.03 343.63 UB, too many bad seeds, msvc-specific
jodyhash6 2848.42 29.99 164.36 bias, collisions, distr, BIC, LongNeighbors
wyhash32 2532.89 48.4 484.57 2 bad seeds, 32-bit
umash128 2427.46 70.6 197.29
Murmur3A 2413.88 53.36 182.37 UB, 1 bad seed, Moment Chi2 69
prvhash64_64m 2386.19 51.18 186.87
prvhash64_128 2383.57 103.44 246.45
prvhash64_64 2375.72 51.61 190.97
hasshe2 2372.52 68.64 216.74 Permutation,TwoBytes,Zeroes,Seed
PMurHash32 2344.78 58.48 196.43 1 bad seed, Moment Chi2 69
mirhashstrict32low 2218.87 65.48 190.59 1 bad seed, MomentChi2 9
mirhashstrict 2217.32 65.53 182.07
sha1ni 2019.96 135.84 564.40 insecure,sanity, Permutation, Zeroes, machine-specific
sha1ni_32 2019.94 136.82 589.46 machine-specific
superfast 1956.25 53.61 180.10 UB, bad seed 0, 91% bias, 5273.01x collisions, 37% distr, BIC
sha2ni-256_64 1910.34 146.06 595.16 Zeroes, machine-specific
sha2ni-256 1906.77 145.47 603.08 insecure,sanity, Permutation, Zeroes, machine-specific
farsh256 1895.77 459.86 575.95
SipHash13 1889.1 89 199.95 0.9% bias
Murmur1 1804.67 51.51 188.41 UB, 1 bad seed, 511x collisions, Diff, BIC
lookup3 1658.31 48.84 194.15 UB, 28% bias, collisions, 30% distr, BIC
pearsonbhash64 1486.34 104.32 185.03
poly_1_mersenne 1431.65 54.49 189.52 fails most tests
jodyhash32 1428.37 44.36 185.85 bias, collisions, distr, BIC LongNeighbors
pearsonbhash128 1347.03 121.75 214.84
poly_2_mersenne 1323.69 66.93 190.88
poly_3_mersenne 1323.59 74.86 206.77
poly_4_mersenne 1323.57 82.67 200.36
blake3_c 1285.91 340.01 552.63 no 32bit portability
GoodOAAT 1052 71.62 192.19
pearsonbhash256 998.9 167.05 261.29
SipHash 980.88 127.77 246.19
MicroOAAT 977.6 59.61 185.06 100% bias, distrib, BIC
FNV1a 791.84 69.69 177.84 bad seed, zeros, fails all tests
sdbm 791.84 67.69 177.06 bad seed 0, fails all tests
FNV64 791.82 70.24 159.29 fails all tests
bernstein 791.82 68.63 180.71 bad seed 0, fails all tests
beamsplitter 789.22 682.45 1150.3 UB, too many bad seeds
HalfSipHash 755.78 114.47 243.72 zeroes
chaskey 753.23 153.42 288.26 PerlinNoise
x17 527.9 98.78 184.09 99.98% bias, fails all tests
JenkinsOOAT_perl 452.49 118.78 194.78 bad seed 0, test FAIL
MurmurOAAT 452.49 113.07 197.83 bad seed 0, 1.5-11.5% bias, 7.2x collisions, BIC, LongNeighbors
JenkinsOOAT 452.48 142.85 213.93 bad seed 0, 1.5-11.5% bias, 7.2x collisions, BIC, LongNeighbors
crc32 392.1 131.62 204.58 insecure, 8590x collisions, distrib, PerlinNoise
sha1-160 364.95 1470.55 1794.1 Comb/Cyclic low32
rmd256 362.49 617.02 815.44 Bad seeds
blake2b-256_64 356.97 1222.76 1435.0
blake2b-224 356.59 1228.5 1425.87
blake2b-160 356.08 1236.84 1458.15
blake2b-256 355.97 1232.22 1443.31 Sparse high 32-bit
md5-128 353.76 638.29 803.39
md5_32a 353.64 629.85 799.56 Sparse high 32-bit
sha1_32a 353.03 1385.8 1759.9 Cyclic low32, 36.6% distrib
rmd128 334.36 659.03 838.32 Bad seeds
blake2s-128 295.3 698.09 1059.2
pearsonhash64 287.95 174.11 196.50 Avalanche, Seed, SSSE3 only. broken MSVC
pearsonhash128 287.95 171.72 194.61 Avalanche, Seed, SSSE3 only. broken MSVC
pearsonhash256 264.51 184.87 218.79 Avalanche, Seed, SSSE3 only. broken MSVC
blake2s-256 215.28 1014.88 1230.38
blake2s-160 215.01 1026.74 1239.54
blake2s-256_64 211.52 1044.22 1228.43
blake2s-224 207.06 1063.86 1236.50
rmd160 202.16 1045.79 1287.74 Bad seeds, Cyclic hi32
sha2-256_64 148.01 1376.34 1624.71 Bad seeds, Moment Chi2 7
sha2-256 147.8 1374.9 1606.06 Bad seeds, Moment Chi2 4
sha2-224_64 147.6 1360.1 1620.93 Bad seeds, Cyclic low32
sha2-224 147.13 1354.81 1589.92 Bad seeds, Comb low32
asconhashv12 144.98 885.02 1324.23
sha3-256 100.58 3877.18 4159.79 PerlinNoise
sha3-256_64 100.57 3909 4174.63 PerlinNoise
asconhashv12_64 86.73 684.02 606.93
floppsyhash 35.72 1868.92 1411.07
tifuhash_64 35.6 1679.52 1212.75 Cyclic low32
Problems include:
- Bad Seeds. A random seed is often used to initialise the hash. This problem relates to having a bad seed..
- Undefined behaviour (UB). This includes Misaligned, oob (Out of bounds), Signed integer overflow and Shift exponent overflow.
o1hash is the fastest, and a quick and dirty hashing method. It is generally not secure. t1h (Fast Positive Hash) requires AES-NI (Intel Advanced Encryption Standard Instructions) and is one of the fastest hashes at 22.785 Gbps. It has fairly good security levels. Meow comes in around 17.378 Gbps. We can see that SHA-1-160 runs as 364 Mbps, while Meow runs at 17.378 Gbps. Blake 3 is one of the fast cryptography hash and has a rate of 1.285 Gbps, and Blake 2 gives a rate around 215 Mbps. SHA-3 gives hashing rates of 100.58 Mbps.
Google recommend the following for 64-bit hashes without quality problems:
- xxh3low
-
wyhash
-
ahash64
-
t1ha2_atonce
-
FarmHash
-
halftime_hash128
-
Spooky32
-
pengyhash
-
nmhash32
-
mx3
-
MUM/mir
- fasthash32
Hash-based Signatures

With hash-based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature, unless we create a stateless method, such as SPHINCS+ [1]. Currently NIST have the final round for the Post Quantum Cryptography competition, and for digital signatures, SPHINCS+ is one of the alterative finalists (alongside Picnic).
Hash-based signature (theory)
- BiBa (Go). BiBa. An overview of BiBa One Time Signature [9]. Basically the method involves us taking a hash of a value using a standard hashing method, such as with SHA-256. There will then be \(2^{256}\) different hashing values. We aim to create a signature for a message, so Bob (the signer) selects a number of random values for his private key value and then publishes the hash of each of these (\(P_1\), \(P_2\), etc). He then sends these public keys to Alice. Now when Bob wants to sign a message, he will take one of his private key values, and then hashes it, and then determines the bin that it should be placed. In this case, we could use the \(\pmod N\) function on the hash, and where \(N\) is the number of bins. If we select \(2^{10}\) there will be 1,024 bins.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature [9].
Hash-based signature (stateful)
- BLISS - Post-quantum signing. BLISS. One of the alteratives to the usage of our existing public key methods is the usage of lattice cryptography, and especially in the usage of Ring Learning With Errors (RLWE). An important application is within digital signatures, and where Bob will sign something with his private key, and then Alice can prove that he signed it with his public key. One post-quantum signature method is BLISS (short for Bimodal Lattice Signature Scheme) [8]. It was created by Léo Ducas, Alain Durmus, Tancrède Lepoint and Vadim Lyubashevsky in 2013.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Hash to Obtain Random Subset (HORS) [3] is a quantum robust hashed-based one-time signature. With this we create a series of integers for our private keys and organise into an indexable form. Then we hash them to a sequence of public key values. Next we segment the hash of the message into a series of n-bit integer values. The signature is then achieved through a look-up of the value in the public key list.
- Lamport Signatures. Lamport. Outlines Lamport signatures [7]. When we sign a message we take its hash and then encrypt with our private key. The public key is then used to prove it, and will prove that we signed it with our private key. The Lamport signature uses 512 random hashes for the private key, and which are split into Set A and Set B. The public key is the hash of each of these values. The size of the private key is 16KB (2×256×256 bits) and the public key size is also 16 KB (512 hashes with each of 256 bits).
- Winternitz Signatures (W-OTS). Winternitz. Outlines Winternitz signatures [4, 5]. W-OTS uses relatively small key and signatures sizes, and is thought to be quantum robust. It generates 32x256 bit random private keys. We then hash these a number of times, and is defined by a parameter (w). If we use w=8, we hash the private keys by (2w). This creates 32x256 bits public keys. The signature is the created by taking eight bits at a time, and then the 8-bit binary int (n) is subtracted from 256 and the private key is the hashed 256-n times. The signature is then 32 hashes which are derived from random private keys. To verify the signature, the recipient parses the hash of the signature (using 8 bits at a time, and extracting the 8 bit int, n).
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method [6], and which is used within speeds-up of Hashing-based signature methods. Using methods such as SHA-1 and SHA-2 (aka SHA-256) will be inefficient as they tend to compress the data inputs through a number of stages. Haraka v2 [6] is different as focuses on inputs of just 256 bits (32 bytes) or 512 bits (64 bytes). This makes the method useful when we are dealing with key and hash values, and is especially useful for hash-based signatures. The output is 256 bits long, but where the input can be either be 256 bits (Haraka256) or 512 bits (Haraka512). These lengths are typically for the outputs of modern hashing applications. The Haraka method, too, has been optimized with AES instructions (AES-NI - Intel Advanced Encryption Standard New Instructions) and which are supported within the hardware of the processor. As Haraka is focused on short messages, the number of rounds within the hashing process has been reduced.
Hash-based signature (stateless)
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ digital signature. SPHINCS digital signature. Outline of the a SPHINCS stateless digital signature method [1].
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
Hash-based signature (Merkle-based)
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
Introduction
Many of the problems we see on the Internet relate to the lack of trust within transactions. The emails you receive and the Web sites that you visit often have very little trust built into them. For trust the email address of the sender, but anyone can fake that address. So increasingly we create a digital signature, and where we sign our messages. In this way, we can check for authentication, integrity and non-repudiation.
With the Alice creates a key-pair: a public key and a private key. She then takes a hash of the message, and then encrypts this hash with her private key, and passes the message and the signature to Bob. Bob then reads the message and takes a hash of it. He then decrypts Alice's signature with her public and checks the hashes. If they match, he knows that she signed and that it has not been changed along the way:
Currently, we often use RSA, DSA and ECDSA to sign our messages. These are based on the difficulty of finding out the factors of a number and on the processing of discrete logarithms. At the current time these methods are computationally hard problems, but with quantum computers, they become much easier. This was shown by Peter Shor who illustrated that it was possible to crack them in polynomial time.
Of all the methods that are being proposed, the hash-based methods look as if they have a good chance of success of creating quantum robust signatures. methods and code-based methods are being researched, but the usage of hashing methods is already well and could provide the best alternative to the existing methods. Hashing methods, too, often bring other advantages, such as forward secure, which means that a key which is cracked will not reveal all the previous keys.
Merkle trees
The root of hash-based methods isin Merkle trees, and which are a way of hashing is used in many applications, including with Bitcoin, Ethereum, Git distribution systems, No SQL, and in many P2P applications. With a Merkle tree we take our data elements, and then hash them, and take pairs of these hashes to create a new hash, and so we build a table. At the top of the tree is the root element (in this case Hash1234):

In this way, we can use the tree to see if we have matching data on systems.On a P2P network, we can transfer a file by splitting it into data segments and then distributing these segments across the network. A trusted source will have the complete Merkle tree for rebuilding the file, and a client can thus rebuild from the Merkle tree and determine the parts of the file which are still missing. Once transferred the root hash (and all the other hashes) will then match. In its core method, the Merkle Signature Scheme (MSS) has serious performance and memory issues, but enhanced methods such as XMSS create with much less of a performance hit.
One-time signatures (Lamport)
The core method used in hash-based signatures is that of the one-time signature, and where we create a new key pair for every method we need to create. If the keys were reused, an attacker could start to learn the private key, and thus spoof messages. One of the first methods was produced by Leslie Lamport and Whitfield Diffie, in 1979, and is defined as:
- We create two data sets with 256 random 256-bit numbers (Set A and Set B). These are the private key (512 values).
- we take the hash of each of the random numbers. This will give 512 hashes and will be the public key.
- We then hash the message using and then test each bit of the hash (0 ... 255). If it is a 0, we use the ith number in Set A, else we use the ith number from Set B.
- The signature is then 256 random numbers (taken from either Set A or Set B) and the public key is the 512 hashes (of Set A and Set B).
The public and private keys are then each 16KB in size. A demo of the method is here.

Figure 1: Lamport method
The major problem with the method is that a key pair for every message. also in 1979, found a solution with Merkle trees.
One-time signature (W-OTS)
To improve performance method (and which reduced key sizes), Merkle proposed Winternitz OTS (named after Robert Winternitz). With this method was possible to sign many bits at the same time. The method is:
- We create 32 256-bit random numbers. These 32 values will be our private key.
- We then hash each of these values 256 times. These 32 values will be our public key.
- We now take the message and hash it using SHA-256. This produces 32 8-bit values (N1, N2 ... N32).
- Next we take each 8-bit value in the hash of the message, and then hash 256-N times (where N is the value of the 8-bit value).
- To prove the signature, we take the message and hash it with SHA-256, and then take each 8-bit value. We then hash the 8-bit signature value by the number of times defined by the message hash value (N1, N2..). The result for each operation should equal the public key value.
This is illustrated below in Figure 2. A demo of the method is here.

Figure 2: W-OTS
Hash-based Signatures
The methods such as W-OTS and Lamport only provide for a one-time signature. In order to sign many messages, we can use the Merkel signature scheme (MSS). With this we take a hash of the keys and build these as the leaves of the tree. The root of the tree is then the public key - the verification key. We then just use the private key of the W-OTS method to create the signature. The sender also sends the authentication path, which is the neighbouring nodes within the path and which leads to the root of the tree. The recipient can then rebuild the tree using the verification key (which can be received a digital certificate) and the authentication path. For the next message we move onto another key pair and where the index of the key part is revealed.
In the following example we have our root as the public key, and then want to sign with Key3. We then show the authentication path which takes us to the root (as defined in the bold arrows):

Conclusions
Hashed-based methods look to be a strong contender for weaning us off RSA, DSA and ECDSA, but we will have to look at the stateful generation of keys. For this we will have to generate a bank of key pairs (2, 4, 8, 16, etc) and then create the public key from the root of the Merkle tree. We must then remember the keys we have used previously, and only use an unused one. Once we use our new key pair, we then show our working-out as to how the private key is integrated into our tree. It is a bit like a teacher marking a question correctly, and asking for the working out that go you to the answer.
References
[1] Bernstein, D. J., Hopwood, D., Hülsing, A., Lange, T., Niederhagen, R., Papachristodoulou, L., ... & Wilcox-O’Hearn, Z. (2015, April). SPHINCS: practical stateless hash-based signatures. In Annual international conference on the theory and applications of cryptographic techniques (pp. 368-397). Springer, Berlin, Heidelberg [paper].
[2] Bernstein, D. J., Hülsing, A., Kölbl, S., Niederhagen, R., Rijneveld, J., & Schwabe, P. (2019, November). The SPHINCS+ signature framework. In Proceedings of the 2019 ACM SIGSAC conference on computer and communications security (pp. 2129-2146) [paper].
[3] Reyzin, L., & Reyzin, N. (2002, July). Better than BiBa: Short one-time signatures with fast signing and verifying. In Australasian Conference on Information Security and Privacy (pp. 144-153). Springer, Berlin, Heidelberg [paper].
[4] Merkle, R. C. (1989, August). A certified digital signature. In Conference on the Theory and Application of Cryptology (pp. 218-238). Springer, New York, NY.
[5] Hülsing, A. (2013, June). W-OTS+–shorter signatures for hash-based signature schemes. In International Conference on Cryptology in Africa (pp. 173-188). Springer, Berlin, Heidelberg.
[6] Kölbl, S., Lauridsen, M. M., Mendel, F., & Rechberger, C. (2016). Haraka v2–efficient short-input hashing for post-quantum applications. IACR Transactions on Symmetric Cryptology, 1-29. [here]
[7] Lamport, L. (1979). Constructing digital signatures from a one-way function (Vol. 238). Technical Report CSL-98, SRI International. [paper]
[8] Ducas, L., Durmus, A., Lepoint, T., & Lyubashevsky, V. (2013, August). Lattice signatures and bimodal Gaussians. In Annual Cryptology Conference (pp. 40-56). Springer, Berlin, Heidelberg [paper].
[9] Perrig, A. (2001, November). The BiBa one-time signature and broadcast authentication protocol. In Proceedings of the 8th ACM Conference on Computer and Communications Security (pp. 28-37) [paper] .
Hashing (Simularity)

Similarity hashes allow for two data objects to be compared for their similarity.
Similarity assessment methods
The following relate to the basic methods used for string similarity:
- String similarity String similarity. This measures edit distance (including Levenshtein distance), Jaro (including Jaro-Winkler), and QGrams.
- String enthropy String enthropy. Measurement of the entropy of strings.
- Soundex Soundex. Soundex uses a phonetic algorithm to classify a sound as it is pronounced. It focuses on matching phrases which have minor spelling errors.
Similarity hashes
The following are the tips related to similarity hashing:
- Similarity hash: SimHash (Charikar similarity) in Python Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash (Nilsimsa similarity) Nilsimsa. The Nilsimsa similarity is used to find similarities between spam emails.
- Context Triggered Piecewise Hashes (CTPH): ssdeep CTPH similarity. Kornblum [6] created ssdeep and which computes fuzzy hashes. This aims to match similar byte sequences, no matter if there are differences between these sequences. For this we break a file up into fragments with a rolling hash function. We then produce a small hash for each of those fragments. These are then aggregated to produce the complete hash of a file. In comparing file signatures, we treat the resultant hash value as a string, and then uses an edit distance method to compare.
- TLSH (A Locality Sensitive Hash) TLSH similarity. In malware analysis and in text similarity, we often have to identify areas of data within files which are similar. One method is TLSH (A Locality Sensitive Hash), and which was defined by Oliver et al [7]. It is used - along with ssdeep - by VirusTotal to identify a hash value for malware.
- Minhash (Jaccard similarity) Jaccard similarity. The Minhash method is used to find similarities between strings, files and metadata.
- Counting identical elements (HyperLogLog) HyperLogLog. Counting the number of identical elements.
Hazmat cryptography

The Cryptography library in Python contains interfaces to common cryptographic algorithms, including symmetric key methods, hashing, public key, and key derivation functions. Many of these are contained with the Hazmat (Harzardous Material) primative setup.
Hashing, HMAC, CMAC, Poly1305 and HKDF
-
Hazmat Hashes. Hazmat Hashes. This includes the hashing methods in the Hazmat cryptography library. This includes Blake2p, Blake2s, MD5, SHA1, SHA224, SHA256, SGA384, SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHA512, SHA512-224, SHAKE128 and SHA256.
-
Hazmat Hashes. Hazmat Hashes. In this case we will implement Python code to determine SHA1, SHA2, SHA3, Blake2, MD5 and SM3 hashes.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
- Hazmat HKDF. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
- Hazmat CMAC. Hazmat CMAC. CMAC methods using the Python cryptography primitives.
- Hazmat Poly1305. Hazmat Poly1305. Poly1305 methods using the Python cryptography primitives.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
Symmetric key
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat. Implementation of ChaCha20/Poly1305 with a random key using Hazmat.
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat. Implementation of AES GCM with a random key using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hazmat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Hazmat Symmetric Key Padding. Symmetric key. This includes the coverage of padding with Hazmat.
- Hazmat Symmetric Key Padding. Symmetric key. This includes the coverage of padding with Hazmat.
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
- Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . With 3DES encryption, we use a 128-bit key and a 64-bit IV value. The two modes supported are ECB (without salt) and CBC (with salt). The DES algorithm has been around for a long time, and the 56-bit version is now easily crackable (in less than a day on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases, and splits the key into two. Overall the key size is typically 112 bits (with a combination of the three keys - of which two of the keys are the same). In this case we will use PKCS7 padding, and which fills the input data with a value that is equal to the number of padding bytes. Overall, DES has a 64-bit block size, and which equates to eight ASCII characters.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key . And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.
Asymmetric key
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- ECC key generaton with Hazmat. Elliptic Curve key gen. Creating ECC keys using Hazmat and Python.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- Hazmat RSA signing (with key values). RSA signing with Hazmat. RSA signing using Python and with Hazmat (with key values).
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here]
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Signatures. DSA Signatures. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. The ECDSA method is an extension of DSA, but implemented with elliptic curve (EC) methods. As with most public key signing methods, we take a hash of a message, and then apply a private key to create a signature (\(r,s\)). This is done by creating a random value (\(k\)) to produce the signature. The signature is then verified using the associated public key. This then verifies the creator of the signature and that the message has not been changed.
Digital Signature: ECDSA/EdDSA
- ECDSA with Hazmat. ECDSA wih Hazmat. This outlines ECDSA with Hazmat.
- Ed25519 for EdDSA signatures with Hazmat. EdDSA: Ed25519. This page uses the Hazmat primitives for the cryptography library.
- Ed448 for EdDSA signatures with Hazmat. EdDSA: Ed448. This page uses the Hazmat primitives for the cryptography library.
- Ed25519 using NaCl. Ed25519. This page uses the NaCl port from libsodium.
- ECDSA Signatures with Hazmat (SECP256R1, SECP384R1, SECP521R1, SECP224R1, SECP192R1, and SECP256K1). ECC Signatures. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and then creates an ECDSA signature for a given message.
Digital Signature: RSA
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
Key exchange: ECDH/X25519
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives and showing the byte values for the key.
Tokens
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
Homomorphic Encryption

Homomorphic encryption supports mathematical operations on encrypted values. Partial Homomorphic Encryption (PHE) supports a few arithmatic operations, while Full Homomorphic Encryption (FHE) supports add, subtract, multiply, and divide. Homomorphic encryption normally involves a public key to encrypt the data, and a private key to decrypt it. There have been four main generations of homomorphic encryption, and the most recent being the HEAAN method.
Simple
- Simple Homomorphic Cipher. Hom. This outlines a Simple Homomorphic cipher.
- Simple Homomorphic Cipher (Python). Hom. This outlines a Simple Homomorphic cipher with Python.
- Full Homomorphic Cipher with a Public Key. Public key. This outlines a Simple Homomorphic cipher using a public key
ElGamal
- ElGamal Homomorphic Cipher (Go). ElGamal. This outlines ElGamal Homomorphic cipher with Go.
- ElGamal Homomorphic Cipher (Go) - Divide. ElGamal. This outlines ElGamal Homomorphic cipher with Go with divide.
- ElGamal Homomorphic Cipher (Go) - Additive. ElGamal. This outlines ElGamal Homomorphic cipher with Go with addition.
- ElGamal Homomorphic Cipher for Multiplication (Python). ElGamal. This outlines ElGamal Homomorphic multiplication with Python.
- ElGamal Homomorphic Cipher for Division (Python). ElGamal. This outlines ElGamal Homomorphic division with Python.
- ElGamal Homomorphic Cipher for Addition (Python). ElGamal. This outlines ElGamal Homomorphic addition with Python.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (Python). ElGamal. This outlines ElGamal Homomorphic subtraction with Python.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
RSA
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
ZKP
- Full Homomorphic Cipher to determine if Bob is older. Older. This outlines a Simple Homomorphic cipher to determine if Bob is older than Alice.
- Full Homomorphic Cipher to determine matching password. Password. This outlines a Simple Homomorphic cipher to determine if a password matches
- Interactive ZKP With Probablistic Methods. ZKP. Interactive ZKP With Probablistic Methods using Python.
- Full Homomorphic Cipher for Millionaire's Problem. Millionaire. This outlines a Simple Homomorphic cipher for the Millionaire's Problem
Voting
- Trusted voting. Trusted. A trusted voting method.
Secret share
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Lattice
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
Full Homomorphic Cipher
- Full Homomorphic Cipher for 2-bit Adder. Adder. This outlines a Simple Homomorphic cipher for a 2-bit adder with DGHV.
- Full Homomorphic Cipher for Full Adder. Full Adder. This outlines a Simple Homomorphic cipher for a full adder with DGHV.
- Full Homomorphic Cipher for 4-bit Adder. Adder. This outlines a Simple Homomorphic cipher for a 4-bit adder with DGHV.
- Full Homomorphic Cipher for 4-bit Adder/Subtractor. Subtract. This outlines a Simple Homomorphic cipher for a 4-bit adder/subtractor with DGHV.
- Full Homomorphic Cipher to XOR two integers. X-OR. This outlines a Simple Homomorphic cipher to X-OR two integers
Paillier
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier) .
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Damgård-Jurik Homomorphic Encryption With Secret Shares. Damgård-Jurik Method. Two of the major areas of developments within cybersecurity will be the usage of homomorphic encryption, and in the usage of Shamir secret sharing. With homomorphic encryption, we can encrypt values, and then operate on them with arithmetic functions (such as add, subtract and multiply), and with Shamir secret sharing, we can split secrets into shares, and then distributed them over networks. These approaches will take privacy to new levels. So let’s look at the Damgård-Jurik method.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Learning with Errors (LWE)
- Learning With Errors . LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret key value (s) and another value (e). Next we select a number of values (t[]) and calculate g[] = t[] x s + e. The values of g[] and t[] become our public key.
- Public Key Encryption with Learning With Errors (LWE). LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret value (s) and which is our private key. We then create a public key which is based on random numbers (A), and then generate another set of numbers (B) which is based on A,s and random errors e. An example of encryption with multiple bits is given.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE)
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Others
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
- SIDH Go. SIDH. Post-quantum key exchange.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Anonymous crypto. Anon. Anonymous crypto.
- Rho factorization. Rho. Rho alogorithm.
- Post-quantum signing (BLISS). BLISS. BLISS method.
Homomorphic Encryption with Krytology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Homomorphic hashing
- Homomorphic Hashing with Golang. Homomorphic hashing. Normally with hashing methods, we need to take all the previous data and new data in order to create a new hash value for our data. In a homomorphic hashing method, we can basically take the previous hash, and then add on any new data values. We can also remove previous data values from our hash, too. This is more efficient in computing, as we do not have to process all of our data into a new hash, and can use simple homomorphic operations for the computation. The method we will use (LtHash) was initially defined by Bellare and Micciancio and updated Lewi et al at Facebook.
Identity Based Encryption (IBE)

This page outlines a few basic principles around the usage of IBE.
Identity Based Encryption (Pairing based)
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pair-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Identity Based Encryption (Others)
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Güther's implicitly certified identity-based public keys (IBE). Günther. This method allows Bob to generate Alices public key from her identity and publicly available parameters.
- Girault's self-certified public keys (IBE). Girault. This method allows Bob to generate Alices public key from her identity and publicly available parameters, and where we use an RSA key pair to self-certify Alice's public key.
Intrusion Detection Systems (IDS)
- Intrusion Detection Systems. Snort. This outlines some of the basics of IDS, including the requirement for Intrusion Detection Systems (IDSs), and where they are used.
- Advanced Network Forensics (Snort). Adv Network Forensics. This provides information on how to detect threats through network forensics with Snort
Snort

- Snort IDS. Snort. This is a Snort Analyser.
- Snort IDS 2 with rules editor. Snort. This provides information on how to detect threats through network forensics with Snort, and with an editing function for rules.
Presentation
IoT

The key objectives of this page are: Understand how a Pen Tester can generate vulnerabilities and test using the Metasploit framework; Define the options and payloads required to generate and use vulnerabilities; and Gaining remote access.
Devices
- Access the Wi-fi kettle. Go. This page outines how to access a wi-fi enabled kettle.
- Philips Hue Wireless Lighting. Go. This page shows how to use RESTful Web services to access to the Hue Led Lamps.
- Kali and R-PI. Go. This page shows the setup of a security testing infrastructure using a Raspberry Pi (R-PI) and a wifi access point.
- Kali, R-PI and RF electrical socket. Go. This page shows the control of an RF electical socket from a RPI.
- Capture from a Polar H10 heat rate sensor. Go. This page shows the capture of the Polar H10 heart sensor with an Ubertooth One.
- Trusted IoT: Linking IoT Devices to NFTs. Go. This page outlines a research paper which links a device to an NFT (Non-fungible Token).
Shodan Scanning
-
IoT Scan (Shodan). Go. This page includes a search of the Internet for key terms, such as for "apache", "mysql" and "cisco".
- IoT Banner Scan (Shodan). Go. This page includes a search of the Internet for key terms with the banner as a result (for the Top 10)
- Internet Services (Shodan). Go. This page includes a search of the Internet for key terms and display the IP address and port.
IoT Libraries
- libDisco with Go. libDisco. libdisco is a Golang library which can be used to create secure connections. It is based on the STROBE protocol framework. Symmetric cryptographic primitives rely on SHA-3 permutation, and asymmetric cryptographic primitives on X25519 and ed25519. STROBE defines a range of cryptographic protocols to integrate with IoT devices. In order to reduce processing, energy and memory requirements, it only uses Keccak (SHA-3) to encrypt and authenticate messages.
COSE/COBR
In computer security, we often have to represent binary data, in single values or groups of characters, bytes, words, long words, signed integers, floating-point values, double-precision floating-point values, and so on. This might be in the form of a data object, a signature or even encrypted content. For this, the ANS.1 DER format is often used, such as presenting digital certificates and signatures. An improvement on this for small messages with security is Concise Binary Object Representation (CBOR) — and which is defined in RFC8949 [1]. While JSON represents text-based data objects CBOR focuses on binary objects. It has been designed to create a lightweight encoder and decoder. This supports the use of CBOR within an IoT infrastructure. The data, also, does not require a data schema to be able to decode it, along with being extensible. CBOR defines the format of binary data with data objects and messages. We can then integrate security with CBOR Object Signing and Encryption (COSE), and which is defined in RFC8152 [2]. This includes signatures, message authentication codes (MACs), encryption and creating serialised objects.
- 128-bit AES GCM. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) can then build on this to include signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use a symmetric key to encrypt a message, and then decrypt it. In this case we will use AES GCM with a static 128-bit key ("0x000102030405060708090a0b0c0d0e0f").
- 256-bit AES GCM. Go. In this case we will use AES GCM using a random 256-bit key (32 bytes).
- EdDSA. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) [2] can then build on this to includes signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use EdDSA to create a signature for a message.
- ECDSA. Go. In this case we will use ECDSA to create a signature for a message.
- HMAC. Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT. Go. In this case we create a CWT token, and sign with an HMAC signature.
- ECDH. Go. In this case we create a symmetric key from ECDH. For this we will derive a shared key from the public key of Alice and Bob, and then define a single recipient which can derive the CEK (Content Encryption Key) using their private key. We will use the curves of P-256 (secp256r1), P-384 (secp384r1), P-521 (secp521r1) or SECP256K1 (as used with Bitcoin).
- RSA using COSE and CBOR. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\).
- RSA: dQ, dP and InvQ. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). The key pair also includes \(dQ\), \(dP\) and \(InvQ\), and these can be used with the Chinese remainder theory to optimize the decryption process.
Metasploit
- Armitage and Metasploit. Go.
- Exploiting Android with Metasploit. Go.
- Exploiting Android with Metasploit - Part 2. Go.
- Exploiting Windows/Mac OS X with Metasploit. Go.
- Remote Desktop Windows/Mac OS X with Metasploit. Go.
- Metasploit. Go.
- Internet of Things Security. Go.
- Metasploit (Enumeration and Scanning). Go.
- Metasploit (Malware). Go.
IP

 The following are a few interesting techniques around IP addresses:
The following are a few interesting techniques around IP addresses:
- Your details. IP. This shows your browser details.
- IP address analyser. IP. This involves converting an IP address to the host and network part of the address.
- IP subnet analyser. IP subnets. This involves converting an IP address to the host and network part of the address.
- IP address analyser. IP. This involves analysing IP addresses.
- Max subnets. Max subnets. This involves converting an IP address to the host and network part of the address.
- Route summarization. Summarization. This involves converting an IP address to the host and network part of the address.
- Whois. Whois. This does a basic Whois on a domain.
- URL Obfuscation. Obfuscation. This outlines URL obfuscation.
- HTTP Responses. Test. HTTP.
- Capturing Network Packets (Python). WinPCap. HTTP.
Cisco related
- Routing table. Routing table. This involves viewing a routing table for a Cisco device.
- ACL Generator. ACL. This involves a simple calculator for ACLs on network ranges.
- EIGRP metrics. EIGRP. Learn the basics of EIGRP metrics.
- VoIP B/W. VoIP. Calculate bandwidth for VoIP.
- Wild Card. Wild Card. On a Cisco device a wildcard mask is used to identify the parts of an IP address that need to be matched. It thus uses a wildcard mask, where a 0 in the bit position identifies that the device should match that bit, else a 1 shows that it should ignore it.
Protocols
- HTTP. HTTP. Show the request and response for HTTP.
- Ping analyser. IP. This involves converting a ping of a site.
IP Challenges
-
IP Test 1. IP Test. IP Classification test. This is a simple test which generates a range of IP addresses, and you must determine the IP address classification.
IP Subnet Challenge 1 Demo
-
IP Test 2. IP Test. IP Classification test Part 2. This test provides an address classification, and the user must find the addresses which are of this classification.
IP Subnet Challenge 2 Demo
-
IP Test 3. IP Test. IP Classification test Part 3. This test provides an address classification, where the network part of the address is determined.
IP Subnet Challenge 3 Demo
Subnet Challenges
- Subnet Test 1. Subnet Test. Subnet Test.
-
Subnet Test 2. Subnet Test. Subnet bits.
- Subnet Test 3. Subnet Test. Find the nth usable subnet. This test involves finding the nth usable subnet.
- Subnet Test 4. Subnet Test. Maximum subnets. This is a test page to determine the maximum number of subnets and hosts/subnet for IP classed addressing.
- Subnet Test 5. Subnet Test. Maximum host/subnet. This is a test page to determine the maximum number of hosts per subnet.
- Subnet Test 6. Subnet Test. Determine the required subnet mask for a given number of subnets. This is a test page to determine the required subnet mask for a given number of subnets and a given IP address classification.
- Subnet Test 7. Subnet Test. Determine the required subnet mask for a given number of host/subnet. This is a test page to determine the required subnet mask for a given number of hosts per subnet and a given IP address classification.
- Subnet Test 8. Subnet Test. Route summarization. This involves a calculation on route summarization.
- Subnet Test 9. Subnet Test. Binary to IP.
- Subnet Test 10. Subnet Test. Hex to IP.
-
Subnet Test 13. Subnet Test. Wild card mask network bits. Find the number of bits in the network part of the wild card mask. IP Wildcard challenge
- Subnet Test 14. Subnet Test. Wild card mask host bits. Find the number of bits in the host part of the wild card mask. IP Wildcard challenge
- Subnet Test 15. Subnet Test. Wild card mask ... find the network address. Find the network for the wild card mask. IP Wildcard challenge 2
- Subnet Test 16. Subnet Test. Find a matching IP address for a network and wild card mask. Find the IP for a network and a wild card mask.
- Subnet Test 17. Subnet Test. Find an address which is on a given network. Find an IP address on a network, for a given network address and subnet mask.
- Subnet Test 18. Subnet Test. Find an IP address on the same network. Find an IP address on the same subnet.
- Subnet Test 19. Subnet Test. Find subnet. Convert subnet mask.
- Megatest. Subnet Test. Challenging test for subnets.
JavaScript

JavaScript code allows execution within the browser, rather than on the server. It is often faster than code that runs on a server. Along with this we can also use Node.js, and which runs JavaScript code on a server.
Symmetric key
- AES. AES. In this example, we will use either a pre-generated key or a random one, and use AES (Rijndael) encryption.
- ChaCha20 and Poly1305. ChaCha. This page outlines Poly1305 and ChaCha20. ChaCha20 is a symmetric key method and Poly1305 is a message authentication code (MAC). They were created by Daniel J. Bernstein, and are alternatives to AES and HMAC.
- CMS (Padding). CMS. This page uses PKIJS encrypting on CMS. With CMS we can This document describes the Cryptographic Message Syntax (CMS). With this we can encapsulate an message within an encrypted entity.

Hashing
- Hash. Hash. This page defines a JavaScript Hash calculator. This uses a client-side JavaScript code to determine the hash signatures of a text value.
Signatures
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
- Boneh–Lynn–Shacham (BLS) signature. BLS. Boneh–Lynn–Shacham (BLS) signature method produces short signatures. They use elliptic curve pairing (and which are also known as bilinear maps).
Key exchange
- ECDH. ECDH. Elliptic Curve Diffie Hellman (ECDH) is used to generate a shared key. This implementation uses Elliptic Curve Cryptography (ECC) with JavaScript.
CryptoJS
- CryptoJS. CryptoJS. This page uses client-side JavaScript code to hashing, encrypt and sign, including for symmetric key (AES), streaming ciphers, hashing methods, and HMAC.
Blockchain
- PATRICIA trie. PATRICIA. In the following, we have the Top 2,500 Web sites in the world, and implemented with a Radix Trie (aka PATRICIA trie) In the following we have the Top 2,000 web sites on the Internet, and which have been indexed using the PATRICIA trie.
Public key
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
- RSA. RSA. RSA is an asymmetric encryption algorithm, which uses two keys, one to encrypt and the other to decrypt. It was created in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman, and is still one of the most widely used encryption methods. A typical application is in authenticating a sender, where the senders private key is used to encrypt a message, and then is decrypted by the receiver with the senders public key (which is known to anyone who wants it). It is also typically used for encrypting disks/files, such as for EFS.
Digital Certificates
- X.509 certificates in JavaScript. RSA and ECDSA Signed certificates. This page will generate either RSA and ECC key pairs, and then generate X.509 certificates, using either a signature of SHA1withRSA or SHA256withECDSA. For RSA signing we use an RSA private key to sign the certificate, and with ECDSA signing we use an ECC private key to sign the certificate.
Tokens
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
Random
- Random number generator. Rand. In the past, encryption and decryption had to be done through native code libraries, such as with Bouncy Castle and OpenSSL. With the increasing processing power of Web browsers, it is now possible to use encryption using JavaScript, which thus provides client-side processing of data. This Web page uses Javascript encryption, and generates a random 256-bit text key or a hex version. The 256-bit key is generated by generating 60 random numbers (from 0-25), and converting these to an ASCII character.
Malware obfuscation
- Malware obfuscation. Obfuscation. A malware writer will often hide certain keywords from the browser/human by encoding them in another format. This is typically done for hex coding (\xZZ), 16-bit unicoding (\uZZZZ) and octal coding (\ZZZ). To test, enter a value, and then press the button and it will convert encoded string.
Message Authentication Codes
- Chaskey (MAC). Chaskey. Chaskey Cipher is light-weight cryptography method for signing messages (MAC) using a 128-bit key. The hardware implementation only requires 3,334.33 gate equivalent with an operating clock frequency of 1 MHz (whereas Keccak requires 4,658 GE). In the page we create the Mac signature and also encrypt for CBC.
Other
- Password generation/hashing. Hashing. Linux can use salted passwords where the username, hashing method and hashed password are stored in a password file [More details]. The main methods are
Hashing

At times we need to generate secrets, such as encryption keys, from passwords or nonce values. A Key Derivation Function (KDF) is a verifiable way of doing this.
Key Derivation Functions (KDFs)
The following are the tips related to hashing:
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Password strength. Test. This outlines the strength of various passwords types.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
HKDF
The following are the tips related to Key derivation hashing:
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Hazmat HKDF for different hashing methods. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
-
HKDF key derivation with OpenSSL [
here]
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
PBKDF2
The following are the tips related to Key derivation hashing:
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- AES GCM (Python) with PBKDF2. AES GCM (Python) with PBKDF2.
- Fernet with PBKDF2 . AES GCM (Python) with PBKDF2.
- PBKDF2 key derivation. AES GCM (Python) with PBKDF2.
- Key Rotation with Fernet. AES GCM (Python) with PBKDF2.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Bcrypt
The following are the tips related to Key derivation hashing:
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- BCrypt. BCrypt. BCrypt with Rust.
-
Hash to password with Go. Hashing to Argon2, Scrypt and BCrypt. Hash to password with Go, including Argon2, Scrypt and BCrypt.
scrypt
- scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Argon 2
The following are the tips related to Key derivation hashing:
- Argon 2. Go. Outline of Argon2.
- Argon 2 with NaCl. Go. Outline of Argon2 using NaCl.
- Argon 2. Argon 2. Argon 2 with Rust.
- Balloon. Go. Outline of Balloon.
Other
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
- Double ratchet. Go. Outline of double ratcheting.
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
Outline
HMAC Key Derivation function (HKDF) is used to derive an encryption key from a passphrase. Initially, HKDF creates a pseudorandom key (PRK) using a passphrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), and along with a salt value. Next, the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys [RFC 5869][article]. In this case, we will use SHA-256.
The following shows how an encryption key can be generated using HKDF, and where we need a secret and a salt value. Both Bob and Alice have the same secret and salt.

With PBKDF2 (Password Based Key Derivation Function 2), we hash for a given number of rounds:

Key exchange

Key exchange is a way for Bob and Alice to communicate and for them to agree on a shared secret. The original method defined uses discrete logarithms (Diffie-Hellman), but most modern methods use elliptic curve techniques (ECDH). As quantum computers can crack both discrete log and elliptic curve methods, there are post quantum cryptography methods proposed. This includes SIDH, CSIDH, SIKE, and NewHope.
Key interchange/generation (Diffie-Hellman)
The following relates to key interchange:
- Selecting \(g\) in Diffie Hellman. G in Diffie Hellman. Picking a safe value of the generator \(g\) in discrete logarithms.
- Diffie-Hellman. Diffie-Hellman Calculation. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Real example). Diffie-Hellman Real. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Python). Diffie-Hellman. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (pre-compute). Diffie-Hellman (pre-compute). Many sites use the same prime numbers, which can then be cracked with a pre-computing attack.
- Key generation. Key gen. This will generate keys for different methods based on a passphrase.
- Diffie-Hellman (Man-in-the-middle). DF. This outlines the man-in-the-middle method for Diffie-Hellman.
- An Alternative Diffie-Hellman method. Alterative DH. This outlines an alternative Diffie-Hellman method.
Authenticated Key Exchange
The following are the tips related to Key derivation hashing:
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- MTI/A0. MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{ax+by} \pmod p\). MTI (Matsumoto, Takashima, Imai).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0. MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{x+y} \pmod p\)
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). The resultant key is \(xyG \)
- MTI/C0. MTI/C0. This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{xy} \pmod p\)
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG\).
- MTI/C1. MTI/C1. This outlines MTI/C1, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{abxy} \pmod p\).
- MQV (Menezes–Qu–Vanstone). MQV. MQV was created Alfred Menezes, Minghua Qu and Scott Vanstone in 1995 and is an authenticated key exchange method. Alice holds a key pair \((A,a)\) and Bob has a key pair \((B,b)\). With this \(a\) is Alice's private key, and \(A=aG\) is her public key. For Bob, his public key will be \(B=aG\) and a private key of \(b\), and where \(G\) is the base point on the elliptic curve.
- HMQV (Menezes–Qu–Vanstone). HMQV. HMQV builds on MQV and adds the identity of Bob and Alice.
- ECDH with X25519 and Blake2b. ECDH with X25519 and Blake2b. This uses PyNaCl to create an authenticated key exchange and uses X25519 and Blake2b.
Elliptic Curve (ECDH) - Python
The following are the tips related to ECC:
- Elliptic Curve. Elliptic Curve. Elliptic Curve is a public key method which can also be used to generate a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with simple parameters. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
Elliptic Curve (ECDH) - Golang and Node.js
The following are the tips related to ECC:
- ECDH with Go. ECDH. ECDH with Go.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with node.js. ECDH. ECDH with node.js.
- ECDH with JavaScript. ECDH. Elliptic Curve Diffie Hellman.
Password Authenticated Key Exchange (PAKE)
The following are the tips related to Key derivation hashing:
- SPAKE2. Go. Outline of SPAKE2.
- OPAQUE. Go. Outline of OPAQUE.
- SPEKE. Go. Outline of SPEKE (Simple Password Exponential Key Exchange).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
- J-PAKE. J-PAKE. This example generates a shared key based on a shared password.
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses discrete logs.
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
PQC NIST Finalists (Key Exchange)
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Key interchange/generation (Other)

The following relates to key interchange:
- Curve25519. Curve25519. This outlines Curve25519, which is used in the Tor network.
- Authenticated Key Exchange (Discrete logs). YAK. Key exchange with public keys and uses discrete logs.
- Authenticated Key Exchange (ECC). YAK. Key exchange with public keys and uses elliptic curve methods.
- Shamir No-key protocol. Shamir No Key. In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated.
- Shamir No-key protocol (sepc256k1). Shamir No Key (EC). In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated using the sepc256k1 elliptic curve.
- Conference keying (Burmester-Desmedt method). Conference keying. In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it.
- Conference keying (Burmester-Desmedt method) - Elliptic Curve (sepc256k1). Conference keying Elliptic Curve (sepc256k1). In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it, and uses the sepc256k1 elliptic curve.
Key exchange (with pairing)
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Kryptology

We need to build a new Internet. One that is build on mathematics and certainty, rather than the patchy version we have now. For this we need a layer of cryptography at the lowest level, and build software interfaces on top of this. Along with this we now have cryptographic methods which can now provide a foundation of trust, and which preserve privacy. And so the old libraries of OpenSSL are being squeezed out in favour of the new ones which are built on a solid foundation. The latest of these new "privacy-aware" libraries is Kryptology, and created by Coinbase. This library provides the APIs that developers need, in order to apply to areas of blockchain development. This library include BLS (Boneh-Lynn-Shacham) signatures, Zero-knowledge Proofs (ZKPs) and Shamir Secret Shares (SSS). With BLS we can digitally sign for data, but also preserve its privacy. Applications of this include group signatures, where multiple entities can merge their signing keys together and provide a single signature for a transaction. With SSS, we can split encryption keys up into shares, and then distribute them across a network. When required, we can call these shares back to reconstruct the key.
The focus for Coinbase seems to be the application of privacy coins, and where no tracking can be applied to the usage of these digital coins. This should support full anonymity for transactions, as opposed to Bitcoin which only supports pseudo-anonymity.

ECC Basics
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining n.G for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Points (Base Point and Others). Elliptic Curve points. Two common curves used in ECC (Elliptic Curve Cryptography) are secp256k1 (as used in Bitcoin and Ethereum) and P256 (secp256r1). The "k1" refers to the Kolbitz curve 1 (named after the creator of ECC). With these we have a base point which are can operate on. This is typically defined as \(G\). We can then operate on this with add and multiply operation. For example, \(2G=G+G\) and \(P=n.G\). In this following we will show the base point for a number of common curves, such as secp256r1, P256, Pallas, Curve 25519, BLS12381G1, BLS12381G2, BLS12377G1 and BLS12377G2.
ECDH
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret. We will use Golang and the Krytology library.
Simple ECC on curves
- Public key points for curves. Simple. Display public key points for scalars.
BLS Curve
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
Accumulator and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
Pallas Curve
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
Pairing-based Crypto
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
ElGamal and ECC
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a numerical input.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
Shamir Secret Shares
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Homomorphic Encryption
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Zero knowledge proofs
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
Verifiable Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Hash to scalar and point
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
CP-ABE
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Lattice cryptography

Latice cryptography is proposed as a post-quantum robust method for public key encryption, especially focused on digital signatures and key exchange mechanisms (KEMs).
Principles
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
NTRU
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- Lattice Encryption: NTRU Key Generation Python). NTRU. Outlines how NTRU operates for key generation.
Homomorphic
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Digital Signatures
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
Public-Key Encryption/Key Exchange
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
Light-weight cryptography

While AES and SHA work well together within computer systems, they struggle in an IoT/embedded world as they take up: too much processing power; too much physical space; and consume too much battery power. So NIST outlines a number of methods which can be used for light-weight cryptography, and which could be useful in IoT and RFID devices [1]. They define the device spectrum as:
- Conventional cryptography. Servers and Desktops. Tablets and smart phones.
- Light-weight cryptography. Embedded Systems. RFID and Sensor Networks.
With embedded systems, we commonly see 8-bit, 16-bit and 32-bit microcontrollers, and which would struggle to cope with real-time demands for conventional cryptography methods. And in the 40+ years since the first 4-bit processor, there is even a strong market for 4-bit processors. RFID and sensor network devices, especially, have limited numbers of gates available for security, and are often highly constrained with the power drain on the device.
So AES is typically a non-starter for many embedded devices. In light-weight cryptography, we often see smaller block size (typically 64 bits or 80 bits), smaller keys (often less than 90 bits) and less complex rounds (and where the S-boxes often just have 4-bits).
For light-weight cryptography the main constraints that we have are typically related to ener requirements, gate equivalents (GEs), and timing. With passive RFID devices, we do not have an associated battery for the power supply, and where the chip must power itself from energy coupled from the radio wave. An RFID device is thus likely to be severely constrained in the power drain associated with any cryptography functions, along with being constrained for the timing requirements and for the number of gates used. Even if an RFID device has an associated battery (active RFID), it may be difficult to recharge the battery, so the drain on power must often be minimised.
There is thus often a compromise between the cryptography method used and the overall security of the method. Thus often light-weight cryptography methods balance performance (throughput) against power drain and GE, and do not perform as well as main-stream cryptography standards (such as AES and SHA-256). Along with this the method must also have a low requirement for RAM (where the method requires the usage of running memory to perform its operation) and ROM (where the method is stored on the device). In order to assess the strengths of various methods we often define the area that the cryptography function will use on the device – and which is defined in \(µm^2\). The NIST finalists are defined in this [article]
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- GIFT AEAD. GIFT. GIFT is a light-weight block cipher. It is a (NIST Finalist)
- Elephant. Elephant. Elephant is a light-weight stream cipher. It is a (NIST Finalist).
- TinyJambu. TinyJambu. TinyJambu is a light-weight block cipher. It is a (NIST Finalist)
- Isap AEAD. Isap. Isap is a light-weight block cipher. It is a (NIST Finalist)
- PHOTON-Beetle AEAD. PHOTON-Beetle. PHOTON-Beetle is a light-weight block cipher. It is a (NIST Finalist)
- Romulus AEAD. Romulus. Romulus is a light-weight block cipher. It is a (NIST Finalist)
- Sparkle AEAD. Sparkle. Sparkle is a light-weight block cipher. It is a (NIST Finalist)
- CLEFIA. CLEFIA. CLEFIA is a light-weight block cipher.
- LED. LED. LED is a light-weight block cipher.
- Piccolo. Piccolo. Piccolo is an ultra light-weight block cipher.
- PRESENT. PRESENT. Present is a light-weight block cipher.
- Pyjamask. Pyjamask. Pyjamask is a light-weight block cipher.
- SIMON. SIMON. SIMON is a light-weight block cipher.
- SKINNY. SKINNY. SKINNEY is a light-weight block cipher.
- SPECK. SPECK. SPECK is a light-weight block cipher.
- XTEA. XTEA. XTEA is a light-weight block cipher.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encryption/Decryption. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.
Light-weight crypto (Other)
- Chaskey (MAC). Chaskey. Chaskey is a light-weight MAC function.
- Chaskey (MAC). Chaskey (Python). Chaskey is a light-weight MAC function.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (ASCON)
ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRFF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
Discrete Logs (Solving)

A discrete log problem is in the form of \(g^x \pmod p\) and where we know \(g\) and \(p\) and must solve for \(x\).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Message Authentication Code (MAC)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
HMAC
The following are the tips related to Key-based hashing:
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authentication both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2), Blake2b, SM3 and SHA-3. This page outlines the HMAC-MD5 methods using the Hazmat cryptography layer.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- HMAC (COSE). Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT with HMMAC. Go. In this case we create a CWT token, and sign with an HMAC signature.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- HMAC with Rust. HMAC. HMAC with Rust.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HMAC with OpenSSL. MACs with OpenSSL. HMAC in OpenSSL for a given input value, password and hashing method.
Cipher MACs
The following are the tips related to Key-based hashing:
- MACs with OpenSSL. MACs with OpenSSL. MAC methods implemented in OpenSSL, including CMAC and GMAC.
Key-based hashing
The following are the tips related to Key-based hashing:
- SipHash. Siphash. Siphash is a fast key-based hashing method.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Meow. Meow. Meow is one of the fastest hashing methods.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
Magic Numbers

This pages contains information related to magic numbers in file formats.
Network and File Forensics
- Magic numbers. Magic. This provides information on magic number for file forensics.
Graphics formats
- JPEG Analysis. JPEGs. This provides an analysis of JPEG files.
- GIF Analysis. GIFs. This provides an analysis of GIF files.
- TIF Analysis. TIFs. This provides an analysis of TIF files.
- PNG Analysis. PNGs. This provides an analysis of PNG files.
- BMP Analysis. BMPs. This provides an analysis of BMP files.
- PSD Analysis. PSDs. This provides an analysis of PSD files.
- WMF Analysis. WMF. This provides an analysis of WMF files.
- Adobe Illustrator Analysis. AI. This provides an analysis of AI files.
- Adobe In Design Analysis. INDD. This provides an analysis of INDD files.
- MIDI file. MIDI. This provides an analysis of MID files.
- ICO file. ICO. This provides an analysis of ICO files.
- PS file. PS. This provides an analysis of PS files.
- EPS file. EPS. This provides an analysis of EPS files.
- VSD file. VSD. This provides an analysis of Microsft Visio (VSD) files.
Video and audio formats
- MP3 Analysis. MP3s. This provides an analysis of MP3 files.
- AVI Analysis. AVIs. This provides an analysis of AVI files.
- Flash SWF Analysis. SWFs. This provides an analysis of Flash files.
- Flash FLV Analysis. FLVs. This provides an analysis of FLV files.
- MP4 Analysis. MP4. This provides an analysis of MP4 files.
- MOV Analysis. MOV. This provides an analysis of MOV files.
- WMV Analysis. WMV. This provides an analysis of WMV files.
- WMA Analysis. WMA. This provides an analysis of WMA files.
- JPEG 2000 Analysis. JPEG 2. This provides an analysis of JPEG 2000 files.
- WAV Analysis. WAV. This provides an analysis of WAV files.
Zips, Archives and Library files
- ZIP/Archive Analysis. ZIPs. This provides an analysis of ZIP/Achive files.
- GZ Analysis. GZ. This provides an analysis of GZip files.
- Tar Analysis. Tar. This provides an analysis of TAR files.
- MSI Analysis. MSI. This provides an analysis of MSI files.
- OBJ Analysis. OBJ. This provides an analysis of OBJ files.
- DLL Analysis. DLL. This provides an analysis of DLL files.
- CAB Analysis. CAB. This provides an analysis of CAB files.
- EXE Analysis. EXE. This provides an analysis of EXE files.
- RAR Analysis. RAR. This provides an analysis of RAR files.
- SYS Analysis. SYS. This provides an analysis of SYS files.
- HLP Analysis. HLP. This provides an analysis of HLP files.
- VMDK Analysis. VMDK. This provides an analysis of VMDK files (VMWare Virtual Disks).
- PST Analysis. PST. This provides an analysis of PST files (Outlook Email File).
- JAR Analysis. JAR. This provides an analysis of JAR files.
- SLN Analysis. SLN. This provides an analysis of Microsoft SLN files.
- Class Analysis. Class. This provides an analysis of Java Class files.
- Zlib. Zlib. This provides an analysis of Zlib files.
Documents
- PDF Analysis. PDFs. This provides an analysis of PDF files.
- DOC Analysis. DOCs. This provides an analysis of DOC files.
- RTF Analysis. RTFs. This provides an analysis of RTF files.
- XLS Analysis. XLSs. This provides an analysis of XLS files.
- PPT Analysis. PPTs. This provides an analysis of PPT files.
- MMP File. MMP. This provides an analysis of MMP files.
- DOCX Analysis. DOCX. This provides an analysis of DOCX files.
- XLSX Analysis. XLSX. This provides an analysis of XLSX files.
- PPTX Analysis. PPTX. This provides an analysis of PPTX files.
- MDB Analysis. MDB. This provides an analysis of MDB files.
- Outlook Message Analysis. MSG. This provides an analysis of MSG files.
Disk Image
- Raw disk format. RAW. This provides an analysis of the RAW disk format.
Tests
- File Forensics Test. File Test File Forensics Test.
- File Forensics Test (Fun). File Test (Fun) File Forensics Test.
Presentations
MIRACL Core Library

MIRACL Core is an open source library, and includes a wide range of public key encryption methods. It is especially focused on elliptic curve and pairing-friendly methods, but also supports a wide range of encryption methods, including RSA, AES and hashing. Overall, it can be ported onto a wide range of systems and supports C, C++, Go, Rust, Python, Java, Javascript and Swift. Along with this it supports limited capability devices such as the Arduino infrastructure. The GitHub repository is [here].
BN254
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.

Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- CL Signatures. CL. CL Signatures in Go using MIRACL.
- CL Signatures (advanced pairing). CL. CL Signatures in Go using MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages using MIRACL.
- PS Signatures. PS. Signatures using PS for short signatures using MIRACL.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures using MIRACL.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.

Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
Rust examples
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
NaCl

PyNaCl is a Python port of LibSodium. It integrates the latest cryptography methods, such as AES, XChaCha20, Blake2b and X25519.
Symmetric Key
- Symmetric key. Symmetric key (XChaCha20 and Poly1305). With symmetric key, Bob and Alice have the same key. NaCl uses the XChaCha20 method, and which supports stream encryption (and which does not require padding as a block cipher does, and is also faster than block cipher modes). ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16 byte nonce. XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24 byte nonce. It has a lower propability of nonce misuse than ChaCha20.
- Encryption with a password. Symmetric Key with KDF. In symmetric key, we generate a secret key. This key is typically a random value or generated from a password and a salt value. If we use a password, we typically use a KDF (Key Derivation Function), and which uses a password and a salt value, in order to create a key of a given size. In this case we will use Argon2i, and which is memory resilent.
Hybrid Encryption
- Box. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Hashing
- Hashing and KDF (Argon2 and scrypt). Hashing and KDF. This case we will use PyNaCl (Networking and Cryptography) library, and which is a Python binding to libsodium. We will hash a password using SHA-256 and SHA-512, and also create a KDF (Key Derivation Function) using scrypt and Argon2.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
Ed25519
-
Ed25519. Ed25519. Using Ed25519 for digital signatures.
-
Finding Points on Ed25519. X25519 (Points).
In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 (Key Exchange)
- X25519 + BLAKE2b key-exchange. X25519. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
Curve 25519
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
Node.js

Node.js uses the JavaScript programming langauge as its base, and allows for code to be run on a server, rather than in the browser (such as with pure JavaScript). To run a node.js program, we run "node myfile.js", and use NPM to install libraries.
Symmetric key
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
RSA and public key
- RSA Opt imal Asymmetric Encryption Padding (OAEP) using Node.js. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
ECC Keys
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.

Hashing
- Hashing with node.js (All). Hashing. Hashing with node.js.
- Hashing with node.js (Selection). Hashing. Hashing with node.js.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- ECDSA with node.js. ECDSA. ECDSA with node.js.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
Key exchange
- Diffie-Hellman with node.js (random prime). DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method and uses a randomly generated prime number (press the button to generate a new prime).
- Diffie-Hellman with node.js. DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method. Each time the prime number will be fixed for the DH group selected.
- ECDH with node.js. ECDH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Elliptic Curve Diffie Hellman (ECDH) key exchange method.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
Key derivation
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
CryptoJS
- CryptoJS (in node.js). CryptoJS (Node.js). Various crypto methods in the browser.
Bulletproofs
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
Blockchain
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
Proxy encryption
- Proxy Encryption - Encrypting With Public Key, And Decrypt with Private Key. Proxy01. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This page just creates a key pair for Alice, and uses it to encrypt with the public key , and decrypt with the private key.
- Proxy Encryption. Proxy02. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This will go through the full use case of proxy re-encryption.
Tokens
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
Random
- Fortuna with node.js. Fortuna. Fortuna random numbers with node.js.
Other
- FPE with node.js. FPR. FPE with node.js.
- Puny with node.js. Puny. Puny character format with node.js.
Accumulators and Witnesses
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
PGP
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Password Entropy
- Password Entropy with Node.js. Password Entropy. Password entropy measures the strength of a password, and is measured as the number of bits which could represent all of the possibilities. An entropy score of less than 25 identifies a poor password, and between 25 and 50 is a weak password. For 50 to 75 we have a reasonable password, and between 75 and 100 is a very good password. Over 100 is an excellent password. The strength of the password relates to the number of characters used, and also the number of characters in the password.
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
- Homomorphic Encryption with Node.js and BGV. Homomorphic Encryption with Node.js and BFG. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BGV method.
Oblivious Transfer (OT)

Oblivious Transfer allows Bob to select data from Alice, but for Alice not to know which value has been selected.
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
OpenSSH

OpenSSH supports the usage of the SSH protocol. This allows for a remote login. One tool which is uses is ssh-keygen, and which allow for the generation of RSA, DSA and elliptic-curve keys that. These can be used for user and host authentication, such as for GitHub login and Cloud instance login.
OpenSSH
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here].
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
Outline

OpenSSL

OpenSSL is a standard library that implements cryptography.
Symmetric key (Command line)
-
Symmetric Key Encryption (OpenSSL 1.x) [here]. In this case we will create cipher text from OpenSSL 1.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 1.x) [here].In this case we will decrypt cipher text from OpenSSL 1.x using a key derived from a password
-
Symmetric Key Encryption (OpenSSL 3.x) [here]. In this case we will create cipher text from OpenSSL 3.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 3.x) [here].In this case we will decrypt cipher text from OpenSSL 3.x using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password.
Hashing
-
Hashing [here] OpenSSL supports a wide range of hashing methods including BLAKE2b, Gost, MD4, MD5, RMD-160, SHA-1, SHA-3, SHA-256 and SHA-512.
Libre OpenSSL
-
Symmetric Key Encryption using Libre OpenSSL [here]. In this case we will create cipher text from Libre OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption using Libre OpenSSL [here]. In this case we will decrypt ciphertext from Libre OpenSSL using a key derived from a password.
-
Hashing [here] Libre OpenSSL supports a wide range of hashing methods including Gost, MD4, MD5, RMD-160, SHA-1, SHA-256 and SHA-512.
Diffie-Hellman parameter generation
-
DH Parameters with OpenSSL [here]. The Diffie-Hellman (DH) method is perhaps one of the greatest inventions in Cybersecurity, and was created by Whitfield Diffie and Marty Hellman. With the DH method, Bob creates a random value (\(b\)) and Alice also creates a random value (\(a\)). Next Bob computes \(B=g^b \pmod p\) and sends it to Alice. Alice computes \(A=g^a \pmod p\) and sends this to Bob. Bob raises the value of \(A\) to the power of \(b\) and takes \(\pmod p\), and Alice raises \(B\) to the power of \(a\) and takes \(\pmod p\). In the end, they will have the same shared value: \(g^{ab} \pmod p\). This can then be used to derive an encryption key that they can use for a secure tunnel. Overall, \(p\) is the large prime number, and also known as the shared modulus between Bob and Alice.
Key derivation function
-
PBKDF2 key derivation with OpenSSL [here] PBKDF2 (Password Key Derivation Function 2) is a key derivation method. Overall it is relatively slow in its operation and where we take a password, a salt value, hashing method, and a number of iterations, in order to produce a given size of encryption key.
-
HKDF key derivation with OpenSSL [here] HKDF (HMAC Key Derivation function) is used to derive an encryption key from a pass phrase. Initially HKDF creates a pseudorandom key (PRK) using a pass phrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), andalong with a salt value. Next the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys.
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Passwords
-
Password example [here]. This page uses the OpenSSL library hash password generator, which is used in UNIX systems for the hashing of passwords which are contained in /etc/shadow and /etc/passwd. For newer passwords, the "-1" options is used to created the hashed value.
-
Hashed passwords with OpenSSL [here].
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
Public key
-
Generating an ECC key pair with OpenSSL [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)).
-
Generating an RSA key pair with OpenSSL [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2).
-
Generating an RSA key pair with OpenSSL with encryption [here]. This page implements RSA key pair generation with an encrypted key pair. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). In this case we will encrypt the key pair with either 3DES, 128-bit AES, 192-bit AES or 256-bit AES. The same password must be used to encrypt and decrypt.
-
Generate prime with OpenSSL [here]. Prime numbers are important in public key encrytion, and are used with RSA and ECC. For RSA, we generate two prime numbers (\(p\) and \(q\)) and which are multiplied together to create a modulus (\(N\)). If these prime numbers have 512 bit values, the modulus will be a 1,024 bit value. This defines the basic secure of RSA. With elliptic curve we use smaller prime numbers, such as 256-bit values for the secp256k1 curve.
ASN1 parsing
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). We will parse using asn1parse, and reveal the parameters.
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)) [RSA key pair]. We will parse using asn1parse, and reveal the parameters.
- DSA Parameters with asn1parse. DSA parameters with OpenSSL with asn1parse. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA (Digital Signature Algorithm)
- DSA Parameters. DSA parameters with OpenSSL. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
MAC (Message Authentication Code)
- HMAC with OpenSSL. MACs with OpenSSL. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authenticate both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2) and SHA-3. In this case we will use OpenSSL to generate the HMAC value.
- MACs with OpenSSL. MACs with OpenSSL. In the following we will generate MACs for HMAC, GMAC, CMAC, Blake2bmac, Blake2smac, KMAC128 and KMAC256. Overall, we will use an encryption key defined as a hex value for GMAC and CMAC, and a pass phrase for the others. The message is "hello".
Signing
- Digital signing a plaintext message with OpenSSL. Signing with OpenSSL. With digital signing, we can take a message, and create a signature. This normally involves signing with a private key and digital certificate. The signed message can be an a MIME format, and which can be integrated into an email message. In this can we have a 512-bit RSA key pair that will sign a plain text message.
Encrypting emails
- Encrypting an email message in OpenSSL. Encrypting messages with OpenSSL. With public key encryption, we can take a message, and encrypt it with the recipiant's public key. In this can we have a 512-bit RSA public key to encrypt a message.
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Random number generation with OpenSSL
-
Random number generator [here]. Random numbers are important in generating encryption keys and salt values. In this case OpenSSL generates a random number (in a Base64 format) for a given number of bytes.
Outline (C#/Python)
-
Symmetric Key Encryption (C#) [here]. This page uses the OpenSSL library through a C#/.NET wrapper. The DLLs it interfaces to are libeay32.dll and ssleay32.dll. OpenSSL supports a wide range of encryption methods, including 128-bit AES, 192-bit AES, 256-bit AES and Blowfish (bf). Different modes of ECB, CBC, and OFB are implemented. The examples use a default IV of "1234".
-
AES in Python with OpenSSL output [here]
-
Producing OpenSSL AES Encrypted String from C# [here]
Digital Certificates
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
Paillier - Partial Homomorphic Encryption

The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Fundamentals
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier).
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Using RSA
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
Applications
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- ElGamal - Applying Multiple Public Key Operations (Discrete Logs). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use discrete logs.
- ElGamal - Applying Multiple Public Key Operations (ECC). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use elliptic curve methods, and using the Edwards 25519 curve.
Ethereum

This page outlines some examples of blockchain and cryptocurrency.
Test Network
- Math functions on Local Network. Go.
- Math functions on Test Network. Go.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- Storing State in a Smart Contract. Go.
- Deleting Data From A Smart Contract. Go.
- A Caesar Cipher Quiz Generator from a Smart Contract. Go.
- Hashing in a Smart Contract. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
- Dealing With Decimals In Smart Contracts. Go.
- Creating A Scrambled Alphabet Challenge Generator In Ethereum and Solidity. Go.
- Deploying a Scrambled Alphabet Generator To Ethereum (With Ganache and Ropsten). Go.
- Deploying a Scrambled Alphabet Generator To Ethereum (With Hardhat). Go.
- Pigpen, IPFS and Ethereum. Go.
- Proof of \(x\) from \(H(x)\) using zkSnarks. Go.
- Elliptic Curve Operations Within a Solidity Contract. Go.

Ethereum
- Creating Ethereum address with Python. Go.
- Creating Ethereum signing with Python. Go.
- ERC20 Tokens. Go.
- Ethereum address with Go. Addresses. This generates an Ethereum address.
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- PATRICIA trie. PATRICIA. Example of using PATRICIA (and which is used in Ethereum).
- Viewing Balance of account in Etheruem with Go. Balance. This views the balance of an account
- Viewing Block in Etheruem with Go. Block. This views a block.
- Viewing Cryptocurrency API with Python. Go.
- Viewing Ethereum blockchain with Python. Go.
- Viewing Transactions in Block in Etheruem with Go. Transactions. This views transactions.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
- Symmetric Key Encryption For Smart Contracts. Symmetric key. Solidity does not natively support symmetric key encryption, such as with AES. Overall, AES would consume too much gas and thus be expensive to implement. But, we can use hashing and X-OR methods to do the encryption. In this case, we will create a 256-bit random value, and then encrypt it with an encryption key, and then decrypt it.
Calling from Python
- Calling smart contracts with Python. Python.
Ethereum crypto
- ECIES with Go-Ethereum. Go.
Ethereum Blockchain
- IOTA Trytes. Trytes. `This outlines Trytes, as used in IOTA.
Ethereum Blockchain
- Blockchain: Adding Maths Functions. Go.
- Blockchain: Blocks, transactions and writing data. Go.
- Blockchain: Contracts and Addresses. Go.
- Blockchain: Getting transactions. Go.
- Blockchain: Hello World!. Go.
- Blockchain: Simple Purchasing System. Go.
- Blockchain: Viewing the blockchain. Go.
- Blockchain: Cracking Wallets. Go.
- Introduction to Blockchain. Go.
Presentations
Factorization

Many public key problems involve the difficulity in factorizing a value two its prime number factors. For example, in RSA, we have a public modulus \(N\) and which is equal to the multiplication of two prime numbers \(p\) and \(q\). If we can factorize the public modulus, we will be able to break the RSA cipher related to it.
RSA Crack
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA Factorization. RSA. This outlines the factorisation of the N value in the RSA method.
Methods
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Dixon. Go. Dixon Method.
- Rho factorization. Rho. Rho alogorithm.
- Smooth numbers. Go. Outline of smooth numbers.
Methods (Elliptic curve
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Quadratic residues
- Quadratic residue (mod p). Go. Outline of quadratic residue \(\pmod p\).
- Quadratic residue (mod p) using Legendre symbol. Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
Factorizing
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
Lenstra–Lenstra–Lovász (LLL) with lattices
- Crack ECDSA with weak nonces. ECDSA with weak nonces and using Lenstra–Lenstra–Lovász (LLL) method. This outlines ECDSA how the private key can be recovered with weak nonce values.
Network Forensics

These pages outlines some network forensics. This includes the understanding of the network stack, and with protocols such as Etherenet, IP, TCP, HTTP, and others.
Network Forensics (Theory)
- Network Forensics (Wireshark). Network Forensics. This provides information on how to detect threats through network forensics with Wireshark.
- Advanced Network Forensics. Network Forensics. This provides information on how to detect threats through network forensics.
Network Forensics (Practice)
- Advanced Network Forensics (Wireshark). Adv Network Forensics. This provides information on how to detect threats through network forensics with Wireshark.
- Network Forensics (PCAP). Network Forensics. This provides information on network forensics (reading PCAP files)
- Network Forensics (Text). Network Forensics. This provides information on network forensics (reading text files)
Tshark
- Filters with TShark. TShark. This page runs Tshark with a given Pcap file and a defined filter.
Other
- Advanced Digital Forensics . Adv Digital Forensics. This provides information on how analyse disk based systems using open source forensics.
- Partition Analyser. MBR. This page will analyse the details of the partition details within the MBR (put one space between fields).
Presentations
Format Preserving Encryption

Format Preserving Encryption (FPE) is a method which allows the basic formatting of a message to stay in a similar format, and where the value itself is encrypted. It can be used to hide credit card details.
Methods
- Format Preserving Encryption. FPE. This outlines Format Preserving Encryption.
- FPE with Python. FPE. An implementation of Format Preserving Encryption (FPE) using Python.
- FPE with node.js. FPR. FPE with node.js.
- FPE and PKBKDF2 in Python. FPE and PKBKDF2 in Python. FPE using PKBDF2 to password generation.
FFX (Format-preserving, Feistel-based encryption)
- FPE with Go. FPE. An implementation of Format Preserving Encryption (FPE) for FFX1 and FFX3.
- FFX schemes. FFX. Within tokenization we can apply format preserving encryption (FPE) methods, which will convert our data into a format which still looks valid, but which cannot be mapped to the original value. For example, we could hide Bob's credit card detail into another valid credit card number, and which would not reveal his real number. A tokenization server could then convert the real credit card number into a format which still looked valid. For this we have a key which takes the data, and then converts it into a form which the same length as the original.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher in Python.
FFX in Rust
- FFX. FFX. This is an implementation of FFX in Rust.
Honey Encryption
- Honey Encryption. Honey. This outlines Honey encryption.
Crypto Principles

This page outlines some crypto principles.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Galois fields (polynomial operations)

This page outlines a few basic principles around the usage of Galois fields and polynomial operations. In 1832, Évariste Galois died of duelling wounds at the age of 20 but left a great legacy. While he was a teenager he worked on polynomials and laid down the principles of Galois theory, along with defining the concept of a finite field. In cryptography, the finite field is one of the major concepts and involves limiting the number of possible values to a limiting factor (\(p\)). The values of the field then range from 0 to p-1. Within a field, we can operate on values in the field using arithmetic operations. We can thus have an infinite field, and where we could include all of the possible integers. A finite field or Galois field of GF(\(2^n\)) has \(2^n\) elements. If \(n\) is four, we have 16 output values. Let’s say we have a number \(a∈{0, ... ,2^{n−1}}\), and represent it as a vector in the form of a polynomial:
\( a=a0+a_1 x+a_2 x^2 ... a_{n−1} x^{n−1}\)
If we use \(a_n∈{0,1}\), this is exactly the same as representing a binary number modulo \(2^n\). In this \(x^n\) represents bit position \(n\) and \(a_n\) is the value of the bit at position \(x^n\). If a bit is a zero at a given position, it will be not included in the polynomial equation. So, 1011 can be represented by \(x^3+x+1\) and 1010 is represented as \(x^3+x\). We can then perform arithmetic operations on these polynomial values. So, to add two values of 1010+1100 we can represent this as \((x^3+x)+(x^3+x^2)\) and which is \(x^2+x\) as we are using modulo 2 addition, and where \(x^3+x^3=0\). With modulo 2 addition, 0+0=0, 0+1=1, 1+0=1, and 1+1=1.
An example of Galois Fields is within AES (Advanced Encryption Standard) and which uses a finite field GF(\(2^8\)). With AES we operate on bytes (8 bits) in the form of \(b_7 b_6 b_5 b_4 b_3 b_2 b_1 b_0\) and which are operated on a a polynomial of \(b_7x^7+b_6x^6+b_5x^5+b_4x^4+b_3x^3+b_2x^2+b_1x^1+b_0\).
Galois fields (polynomial operations) - GF(\(p^n\))
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Additive Group Table for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Additive Group Table for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of addition. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the additive group table for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values.
- Multiplicative Group Table for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Multiplicative Group Table for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the additive group table for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values.
- Additive, Division and Multiplicative Group Table for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Additive, Division and Multiplicative Group Table for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the Additive, Division and Multiplicative Group Table for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values.
- Additive and Multiplicative Group Table for GF(\(2^2\)) and GF(\(2^3\)). Galois Fields Table for GF(2^m) with polynomials. This page implements Galois Fields GF(\(2^n\)) with Python and provides a table of additional and multiplication. It outlines GF(\(2^2\)) and GF(\(2^3\)), but also gives a program that can be used for others. Overall, we have the form of GF(\(p^n\)) and which provides use both an additive and a multiplicative group operations that provide all the possible outputs within the finite field. The value of \(p\) is a prime number, and \(n\) is any positive integer.
- Additive and Multiplicative Group Table for GF(\(2^2\)) and GF(\(2^3\)). Galois Fields Table for GF(2^m) with coefficient values. This page implements Galois Fields GF(\(2^n\)) with Python and provides a table of additional and multiplication. It outlines GF(\(2^2\)) and GF(\(2^3\)), but also gives a program that can be used for others. Overall, we have the form of GF(\(p^n\)) and which provides use both an additive and a multiplicative group operations that provide all the possible outputs within the finite field. The value of \(p\) is a prime number, and \(n\) is any positive integer. This version will show the polynomial coefficent values within the Galois Field.
- Additive and Multiplicative Group Table for GF(\(2^2\)) and GF(\(2^3\)). Galois Fields Table for GF(2^m) with integer values. This page implements Galois Fields GF(\(2^n\)) with Python and provides a table of additional and multiplication. It outlines GF(\(2^2\)) and GF(\(2^3\)), but also gives a program that can be used for others. Overall, we have the form of GF(\(p^n\)) and which provides use both an additive and a multiplicative group operations that provide all the possible outputs within the finite field. The value of \(p\) is a prime number, and \(n\) is any positive integer. This version will show the integer values within the Galois Field.
Irreducible polynomial for GF(p^n)
- Irreducible polynomial for GF(\(p^n\)) for a range of \(p\) and \(n\) values. Irreducible polynomial for GF(p^n) for a range of p and n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the parameters for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values. This includes finding the irreducible polynomial for the Galois Field.
- Irreducible polynomial for GF(\(p^n\)) for a given \(p\) and for \(n\) values. Irreducible polynomial for GF(p^n) for a given p and for n values. This page implements Galois Fields GF(\(p^n\)) with Python and provides a table of multiplication. With this \(p\) is a prime number and \(n\) ranges from 1 to \(n-1\). A GF(\(2^4\)) will have a range of outputs from 0 to 15. In this case, we will determine the parameters for for GF(\(2^3\)), GF(\(3^2\)), GF(\(5^2\)), and a range of other values. This includes finding the irreducible polynomial for the Galois Field. Other important parameters include the degree (the highest polynomial power) and the order (the number of possible output values).
- Conway and primitive polynomial GF(\(p^n\)). Conway and primitive polynomial GF(p^n). This page outlines Conway and primitive polynomials for GF(\(p^n\)).
Galois fields (polynomial operations) - GF(\(p\))
- Additive and Multiplicative Group mod n (\(Z_n\)). Additive and Multiplicative Group mod n. In finite fields, we have a \(\pmod n\) operation for a list of integers (\(\mathbb{Z}\)), and where \(n\) is a prime number. This works for our add (+) and multiply (\(\times\)) operations, and where: \( a \pmod n + b \pmod n = (a+b) \pmod n\); and \(a \pmod n \times b \pmod n = (a \times b) \pmod n\).
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Polynomial GF(2) Factoring and Irreducible Polynomials. Factors. This outlines the search for polynomial factors for GF(2).
Polynomial operations
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
Post-quantum
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Rust
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Sage
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Golang and Cryptography

The new scripted languages such as Python and Node.js are convenient. But, unfortunately, they can be slow as they are scripted, and not compiled. Each time the scripted code is run, the scripting engine must then convert each line of code to the required machine level code. This makes the code much slower than compiled languages, and also less robust. Thus many applications in cryptography are written in C and C++, as they allow for fast execution and give low level access. Unfortunately it can be complex to compile programs, as we often need to install binary libraries and then link these in. The Go programming language, though, has a similar code syntax to C/C++, but is small and efficient and allows access to low-level functions, such as as pointers. Go thus aims to “Code less, compile quicker, execute faster”. So let’s use Go to implement some cryptography methods, including symmetric key, hashing, public keys and zero-knowledge proofs (ZKPs). The slides related to these methods are included [here]. An introduction to Golang and Cryptography is [here].

Go ECDH
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret.
Go Hex and Base64
- Base64 and Hex in Go. Base64/Hex. Two common formats for representing binary data are hexademical and Base64.
Go symmetric key
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Reuse IV attack and AES. Reuse IV and GCM. This provides an implementation of a reuse IV against AES GCM.
- ASCON AEAD (Golang). ASCON AEAD (Golang). The outlines the usage of AEAD for ASCON using Golang.
Go HMAC and HKDF
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HKDF in Go. HKDF. Implementation ofHKDF, and where we dervice a key based on a given secret.
Go secret shares
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.

Go ZKP
- Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL). DLEQ. Create a non-interactive ZKP for discrete logs.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Fiat Shamir and ECC (Interative ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP with Kryptology. This implements a range proof using a Schnorr proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?

Go ECIES (Hybrid Encryption)
With this, we can use the power of public key encryption (to generate the encryption key) with symmetric key encryption (to actually encrypt and decrpyt the data):
- ECIES (Kryptology). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Coinbase Kryptology library.
- ECIES (CIRCL). ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt. We will use the Cloudflare CIRCL library.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt and which is used in Contract Tracing for COVID-19.
Go ECDSA
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Go RSA
- RSA Principles. RSA Principles. The basics of RSA.
- RSA with Go. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA. RSA encryption with Go using OAEP.
- RSA Encryption with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
Go ElGamal
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Proving an Encrypted Shuffle With ElGamal and ECC. Shuffle. An encrypted shuffle with ElGamal.
- ElGamal encryption with Go. ElGamal. This implements ElGamal encryption.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
- ElGamal - Applying Multiple Public Key Operations (ECC). Applying Multiple Public Key Operations. With the ElGamal method, we can modify the core method so that we can apply the public key multiple times, but only require a single decryption. This will use elliptic curve methods, and using the Edwards 25519 curve.
Go PGP
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
Go Public key
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.

Go Hashing
- Hashing with Go. Hashing. Hashes with Go.
- GP Hashing with Go. GP Hashing. GP Hashes with Go.
- SHAKE with Go. SHAKE. This implements SHAKE in Go.
- libDisco with Go. libDisco. This implements libDisco.
- cSHAKE in Golang. cSHAKE. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS. With the SHA-3 hashing method, we have four different cryptographic hashing methods (SHA3-224, SHA3-256, SHA3-384, and SHA3-512) and two XOF functions (SHAKE128 and SHAKE256). With SHAKE128 and SHAKE256 we can integrate domain separation between different functions — and which are known as cSHAKE128 and cSHAKE256.
- Homomorphic Hashing with Golang. Homomorphic hashing. Normally with hashing methods, we need to take all the previous data and new data in order to create a new hash value for our data. In a homomorphic hashing method, we can basically take the previous hash, and then add on any new data values. We can also remove previous data values from our hash, too. This is more efficient in computing, as we do not have to process all of our data into a new hash, and can use simple homomorphic operations for the computation. The method we will use (LtHash) was initially defined by Bellare and Micciancio and updated Lewi et al at Facebook.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
Go ECC
- Hash to password with Go. Hash to password. Hash to password with Go.
- ECDH with Go. ECDH. ECDH with Go.
- Box with Go. Box. Box with Go.
- ECC with Go. ECC. ECC with Go.
- Curve 25519 with Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ElGamal with ECC. ElGamal with ECC. ElGamal using ECC.
- Curve 25519 with Go for test vectors. ECC. This does a test on some private keys to test the public key generation.
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Barebones Ed25519 with Go. ECC. This shows point addition and scalar multiply in Ed25519
- Barebones NIST P256 with Go. ECC. This shows point addition and scalar multiply in P256
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining \(n.G\) for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Points (Base Point and Others). Elliptic Curve points. Two common curves used in ECC (Elliptic Curve Cryptography) are secp256k1 (as used in Bitcoin and Ethereum) and P256 (secp256r1). The "k1" refers to the Kolbitz curve 1 (named after the creator of ECC). With these we have a base point which are can operate on. This is typically defined as \(G\). We can then operate on this with add and multiply operation. For example, \(2G=G+G\) and \(P=n.G\). In this following we will show the base point for a number of common curves, such as secp256r1, P256, Pallas, Curve 25519, BLS12381G1, BLS12381G2, BLS12377G1 and BLS12377G2.
Go Blockchain
- Ethereum address with Go. Addresses. This generates an Ethereum address.
- Viewing Balance of account in Etheruem with Go. Balance. This views the balance of an account
- Viewing Block in Etheruem with Go. Block. This views a block.
- Viewing Transactions in Block in Etheruem with Go. Transactions. This views transactions.

Go Homomorphic
- SIDH Go. SIDH. Post-quantum key exchange.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- NTP. NTP. An overview of NTP.
- BiBa. BiBa. An overview of BiBa One Time Signature.
Go DNS
- DNSSEC. DNSSEC. An overview of DNSSEC.
Go Signatures
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Go Signcryption
- Ahmad-Afzal-Iqbal (AAI) signcryption with Golang. Ahmad-Afzal-Iqbal (AAI). Ahmad-Afzal-Iqbal (AAI) signcryption with Golang.

Go Crypto pairing
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
Go Homomorphic
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add. HEAAN Add. HEAAN Add.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- Anonymous crypto. Anon. Anonymous crypto.
- Rho factorization. Rho. Rho alogorithm.
- Post-quantum signing (BLISS). BLISS. BLISS method.
Go Post quantum
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.

Go CIRCL
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- Ed448 with Go. X448. Ed448 with Go.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with FourQ (Cloudflare). FourQ.
- Verifiable Oblivious Pseudorandom Functions (VOPRF) with Cloudflare CIRCL. VOPRF. In our digital world, we give away too many of our secrets, especially where we just have to prove the knowledge of something, rather than actually revealing it. In many of the systems we use, we could just prove things in an oblivious way, and where we could pass a secret but in a blinded form. With this, a server does not discover our password and for us not to discover the identifier that a server holds on us. But, can we also provide a proof back that the right password has been used? Well, with Verifiable Oblivious Pseudorandom Functions (VOPRF), we can generate a random secret based on a key generated on the server (Alice), and which is based on Bob’s secret.
- Hash to Curve using Go (Cloudflare). Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). The method defined here is proposed an an Internet-Draft standard by the Internet Engineering Task Force (IETF) related to "Hashing to Elliptic Curves".
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message. here Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
- eXtendable-Output Function (XOF) usign CIRCL. XOF. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS.

Go Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Google Tink (Golang) ECIES. Google Tink (ECIE5). This outlines ECIES encryption with public key and AES using Golang with Google Tink
Go Credentials
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.

Go Kryptology
- Public key points for curves. Simple. Display public key points for scalars.
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.

Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.

Principles
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Paillier
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
Go Format Preserving Encryption (FPE)
- FPE with Go. FPE. An implementation of Format Preserving Encryption (FPE) for FFX1 and FFX3.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
AWS Encryption
- AWS Symmetric Key Encryption. AWS (Symmetric key). Using symmetric key in AWS.
Go Oblivious Transfer
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Dragon Fly
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
Embedding data in an ECC point
- Embedding data in a point. Go. With Elliptic Curve Cryptography (ECC), we use points on an elliptic curve to represent our data. These are defined with (x,y) points. With this, it is possible to embedded a certain amount of data into the point - as long as it still gives us a valid point on the curve. This example will Curve 25519 to embed data, and is achieved by storing the length of the data in a single byte in the point, and then store the data as byte values in the point (followed by random data). To decode, we can then just read the first byte for the length of the message, and then reveal the data encoded into the point..
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Hashing (Cryptographic)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
Benchmarks and Password strength
The following are the tips related to hashing:
- Password strength. Test. This outlines the strength of various passwords types.
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
Theory
The following are the tips related to hashing:
- Balls in bins. BiBa. This implemented balls in bins.
- Birthday attack (with Big Integers). Calc. This provides a simple example of the birthday attack.
- Birthday attack. Calc. This provides a simple example of the birthday attack.
- Differential Cryptanalysis (Hashing). Cryptanalysis. This provides an implementation of differential cryptanalysis for hashing methods.
MD5, SHA-1
The following are the tips related to hashing:
- MD2 and MD4 MD2/4. The MD2 and MD4 hashing functions were developed by Prof Ronald Rivest in 1989 and 1990, respectively. They both produce a 128-bit hash, but have been shown be vulnerable to attack (see the Collision section in the page).
- MD5 and SHA-1 (to Base-64) with salt Salt. It is possible to add salt to the MD5 algorithm, to mix it up a little.
- MD5 and SHA-1 (to Base-64) Hash. MD5 and SHA-1 produces a hash signature, and the output is typically shown in a hex format or a Base-64. In this example the output is converted into a Base-64 format.
- MD5 and SHA-1. Hash. MD5 and SHA-1 methods produce a hash signature, and are the two of the most widely used methods. The MD5 algorithm has been shown to have weaknesses, and a collision of message hashes has been shown to occur in less than one day. An MD5 signature has 128 bits, an SHA-1 signature has 160 bits, and an SHA-256 signature has 256 bits.
- MD5 Cracking. Hash Cracker. MD5 has a 128-bit signature and can be cracked using rainbow tables. This page tries to crack the MD5 signature.
- Hashing with Go. Hashing. Hashes with Go.
- Detecting hash types. Hash type. This detects has values.
- OpenSSL hashing. Range of methods. Outlines the methods used in OpenSSL
- Hash. Hash. Hashing using JavaScript
- Hashing with node.js. Hashing. Hashing with node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Hashing methods
-
Hazmat Hashes. Hazmat Hashes. This includes the hashing methods in the Hazmat cryptography library. This includes Blake2p, Blake2s, MD5, SHA1, SHA224, SHA256, SGA384, SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHA512, SHA512-224, SHAKE128 and SHA256.
-
Hazmat Hashes. Hazmat Hashes. In this case we will implement Python code to determine SHA1, SHA2, SHA3, Blake2, MD5 and SM3 hashes.
OpenSSL Passwords
-
Password example [here]
-
Hashed passwords with OpenSSL [here]
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Blake 3 hashes
The following are the tips related to similarity hashing:
- Blake 3 in Python. Hashing. Blake 3 hashing.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
Other Hash functions
The following are the tips related to hashing:
- Bloom Filter Bloom filter. A Bloom filter goes a probabilistic method of determining if an element is in a data structure, using indexed hashing methods.
- Cuckoo Table Cuckoo filter. A Cockoo table uses two hash funtions.
- Chaffing. Chaffing. This produces a keyless system.
- GP Hashing with Go. GP Hashing. GP Hashes with Go.
- LDAP. LDAP. This produces a LDAP hash signature for a password.
- LM Hash. LM Hash. This is an LM Hash Calculator. LM Hash is used in many versions of Windows to store user passwords that are fewer than 15 characters long.
- Murmur and FNV Murmur and FNV. While hashing methods such as MD5 and SHA-1 use crypto methods, the Murmur and FNV hashes uses a non-cryptographic hash function. This can be used for general hash-based lookup and was designed by Austin Appleby. It has good performance compared with other hashing methods.
- Pearson. Pearson. This uses a non-crypto hash.
- phpass. phpass. This produces a phpass hash signature for a password.
- Tiger. Tiger. Tiger is a 192-bit hash function and was designed by Ross Anderson and Eli Biham in 1995. It is often used by clients within Gnutella file-sharing networks and does not suffer from known attacks on MD5 and SHA-0/SHA-1. Tiger2 is an addition, in which the message is padded with a byte of 0x80 (in a similar way to MD4, MD5, and SHA), whereas in Tiger it is 0x01. Otherwise, the two methods are the same in their operation.
- Whirlpool. Whirlpool. Whirlpool is a 512-bit cryptographic hash function and was created by Vincent Rijmen (one of the AES creators) and Paulo Barreto, in 2000.
- WPA-2 hash . WPA-2 hash. Implements SHA-2 hash.
- Reusable hash collisions. Reusable hash collisions. Reusable hash collisions.
- The Length Extension Attack. Length Extension Attack. The MD construct has many weaknesses, and one of the most serious is the length extension attack. With this an adversary (Eve) can take a hash for an unknown message, and then add additional data to produce a new valid hash. The hash methods which are at risk against the length extension attack are MD5, SHA-1 and SHA-256. Please follow the code link below to run an example.
- Consistent hashing. Consistent hash. This outlines the usage of Consistent hashes.
- ROR13 (Module and Function). ROR13. With ROR13 we take each 8-bit character and then convert to a unicode value (with 16 bits). Then for each character we rotate the bits right by thirteen places. The resultant hash is then just the accumuluation of the rotated values.
- ROR13 (Function). ROR13 (Function). With ROR13 we take each 8-bit character and then convert to a unicode value (with 16 bits). Then for each character we rotate the bits right by thirteen places. The resultant hash is then just the accumuluation of the rotated values.
- GOST, Streebog256 and Streebog512. GOST, Streebog256 and Streebog512. GOST94 is a hashing method developed with Euro-Asian Council for Standardization, Metrology and Certification (EASC). This has since been developed in the Streebog256 and Streebog512 hashing method. In this case, we will use Libre OpenSSL to convert data into a hashed value.
RIPEMD
- RIPEMD (RACE Integrity Primitives Evaluation Message Digest) and GOST. RIPEM160. RIPEMD is a 128-bit, 160-bit, 256-bit or 320-bit cryptographic hash function, and was created by Hans Dobbertin, Antoon Bosselaers, and Bart Preneel. It is used on TrueCrypt and is open source. The 160-bit version is seen as an alternative to SHA-1, and is part of ISO/IEC 10118
- RIPEMD160. RIPEM160. RIPEMD160 is a 160-bit cryptographic hash function, and was created by Hans Dobbertin, Antoon Bosselaers and Bart Preneel. RIPEMD160 is used in Bitcoin applications.
Chameleon hashes
The following are the tips related to Chameleon hashing:
- Chameleon hash in Golang Chameleon. With a Chameleon hash, we have a normal hash value which is resistant to collisions, but with a known secret we can easily create a collision. The concept was first defined by Krawcyk and Rabin.
Similarity hashes
The following are the tips related to similarity hashing:
- Similarity hash: SimHash (Charikar similarity) in Python Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash (Nilsimsa similarity) Nilsimsa. The Nilsimsa similarity is used to find similarities between spam emails.
- Minhash (Jaccard similarity) Jaccard similarity. The Minhash method is used to find similarities between strings, files and metadata.
- String enthropy String enthropy. Measurement of the entropy of strings.
- Counting identical elements (HyperLogLog) HyperLogLog. Counting the number of identical elements.
SHA-3 and SHA-3 contenders
The following are the tips related to Key derivation hashing:
- Blake and Blake 2. Blake. Implements Blake and Blake 2 (SHA-3 contender).
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
- Grøstl. Grøstl. Implements Grøstl (SHA-3 contender).
- KangarooTwelve. KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- SHA-3, Keccak and SHAKE . SHA-3. Implements SHA-3, Keccak and SHAKE (SHA-3 winner).
- SHA-3. SHA-3. SHA-3 was known as Keccak and is a hash function designed by Guido Bertoni, Joan Daemen, Michaël Peeters, and Gilles Van Assche. MD5 and SHA-0 have been shown to be susceptible to attacks, along with theoretical attacks on SHA-1. NIST thus defined there was a need for a new hashing method which did not use the existing methods for hashing, and setup a competition for competing algorithms. In October 2012, Keccak won the NIST hash function competition and is proposed as the SHA-3 standard. It should be noted that it is not replacement SHA-2, which is currently a secure method. Overall Keccak uses the sponge construction where the message blocks are XORed into the initial bits of the state, and then inevitably permuted.
- cSHAKE. cSHAKE. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS. With the SHA-3 hashing method, we have four different cryptographic hashing methods (SHA3-224, SHA3-256, SHA3-384, and SHA3-512) and two XOF functions (SHAKE128 and SHAKE256). With SHAKE128 and SHAKE256 we can integrate domain separation between different functions — and which are known as cSHAKE128 and cSHAKE256.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- Skein. Skein. Implements Skein (SHA-3 contender).
Key derivation hashing
The following are the tips related to Key derivation hashing:
- Argon2. Go. Outline of Argon2.
- Argon2 with NaCl. Go. Outline of Argon2 using NaCl.
- Balloon. Go. Outline of Balloon.
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- Double ratchet. Go. Outline of double ratcheting.
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- Scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat HKDF. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
Non-crypto/fast hashing
The following are the tips related to non-crypto hashing:
- A perfect hash Perfect hash. This is a non-crypto hash which optimizes the hash value.
- The universal hash Universal hash. This related to the concept of a universal hash.
- FNV. FNV. FNV is one of the fastest hashing methods.
- Murmur. Murmur. Murmur is one of the fastest hashing methods.
- Siphash. Siphash. Siphash is a fast hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- xxHash. xxHash. xxHash is one of the fastest hashing methods.
- Meow. Meow. Meow is one of the fastest hashing methods.
- o1Hash. o1Hash. o1Hash is one of the fastest hashing methods.
- CRC-32. CRC-32. CRC-32 is one of the fastest hashing methods.
- wyhash. wyhash. wyhash is one of the fastest hashing methods.
- CityHash. CityHash. CityHash is one of the fastest hashing methods, and is generally free of security problems.
- FarmHash. FarmHash. FarmHash is one of the fastest hashing methods, and is generally free of security problems.
- Non-crypto. Non-crypto. This includes a range of fast non-cryptography hashing methods.
- Non-crypto hashes (C++): Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro. Non-crypto hashes: Farm, City, xxHash, MUM, Spooky 2, Murmur, Metro and t1ha0. This includes a range of fast non-cryptography hashing methods for Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro using C++ methods.
- Pearson. Pearson. Pearson is one of the fastest hashing methods, and has been designed for 8-bit processors.
- C++: t1ha. t1ha. t1ha is one of the fastest hashing methods, and has been designed for 64-bit processors.
- C++: Spooky. Spooky. Spooky is one of the fastest hashing methods, and V2 has a 32-bit, 64-bit and 128-bit version.
- C++: xxHash. xxHash. xxHash is one of the fastest hashing methods, and has good performance for short data inputs.
- C++: MUM. MUM. MUM is one of the fastest hashing methods.
- C++: FNV 1/1a. FNV 1/1a. FNV 1/1a is one of the fastest hashing methods, and is particularily useful when there are small changes in strings, such as with IP addresses and URLs.
- C++: MetroHash. MetroHash. MetroHash is one of the fastest hashing methods.
- C++: CityHash. CityHash. CityHash was created by Google and is one of the fastest hashing methods. It was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Farm. FarmHash. FarmHash was created by Google and is one of the fastest hashing methods. It is an improvement to CityHash.
- C++: Murmur. Murmur. Murmur is one of the fastest hashing methods, but was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Halftime. Halftime. Halftime is one of the fastest hashing methods and was created by Jim Apple at Apache.
- C++: Highway. Highway. Highway is an ultra-fast keyed-hash, and is more than five times faster than SipHash. It was created by Jyrki Alakuijala, Bill Cox, Jan Wassenberg at Google.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
- C++: CLHash. CLHash. CLHash is an ultra-fast hashing method and focused on improving performance of the hashing of long strings.
- C++: FalkHash. FalkHash. FalkHash is an ultra-fast hashing method and beats most of the other non-cryptography methods for performance. It is focused on the x64 architecture and integrates with AES-NI.
- C++: wyHash. wyHash. wyHash is an ultra-fast hashing method.
- C++: Fibonacci. Fibonacci. Fibonacci is an ultra-fast hashing method.
- C++: Lookup3. Lookup3. Lookup3 is an ultra-fast hashing method.
Key-based hashing
The following are the tips related to Key-based hashing:
- SiphashSiphash. Siphash is a fast key-based hashing method.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
One Time Passwords/Time Stamps
The following are the tips related to hashing:
- One Time Passwords. One Time. This allows a new unique password to be created each instance, based on an initial seed.
- Timed One Time Password (TOTP). Timed One Time Password. This allows a new unique passcode to be created each instance, based on an initial seed for a given time window. We will use a five second window in this case, where a new passcode is generated every five seconds, based on an initial seed of a pass phrase.
- Hashed One Time Password (HOTP). Hashed One Time Password. This allows a new unique passcode to be created each instance, based on a counter value and an initial seed.
- Time Stamp Protocol. TSP. This creates a time stamp for data.
- HOTP and TOTP (Python). OTP. This creates hashed passwords.
eXtendable-Output Function (XOF)
- eXtendable-Output Function (XOF) usign CIRCL. XOF. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS.
SHAKE
The following are the tips related to hashing:
- SHAKE. SHAKE. Implements SHAKE and which is an Extendable Output Function (XOF).
- SHAKE with Go. SHAKE. This implements SHAKE in Go.
- libDisco with Go. libDisco. This implements libDisco.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify
the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods
such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC methods using the Python cryptography primitives for HMAC-MD5.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
Quantum-robust Public Key (Hash-based signature)
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
Hash to ECC point
- Hash to password with Go. Hash to password. Hash to password with Go.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve with libnum.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.

Password-hashing functions using Rust
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing (Non-cryptographic)

You might know those slow old hashing methods, such as MD5, SHA-1, and SHA-256. Well, they were designed to be fast, but also highly secure. But, if we just need a hashing method, such as for a hashtable or Bloom filter, we often don’t need all the security that comes with the main cryptography hashing methods. And so we have the non-cryptography hashing methods, and which are often ultra-fast and highly efficient. To show the difference, in a test, SHA-1 — one of the fastest cryptography hashing methods — managed a processing rate of 364.95 MiB/s, while t1ha was nearly a 100 times faster, at 34,636 MiB/s.
Non-crypto/fast hashing
The following are the tips related to non-crypto hashing:
- A perfect hash Perfect hash. This is a non-crypto hash which optimizes the hash value.
- The universal hash Universal hash. This related to the concept of a universal hash.
- FNV. FNV. FNV is one of the fastest hashing methods.
- Murmur. Murmur. Murmur is one of the fastest hashing methods.
- Siphash. Siphash. Siphash is a fast hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- xxHash. xxHash. xxHash is one of the fastest hashing methods.
- Meow. Meow. Meow is one of the fastest hashing methods.
- o1Hash. o1Hash. o1Hash is one of the fastest hashing methods.
- CRC-32. CRC-32. CRC-32 is one of the fastest hashing methods.
- wyhash. wyhash. wyhash is one of the fastest hashing methods.
- CityHash. CityHash. CityHash is one of the fastest hashing methods, and is generally free of security problems.
- FarmHash. FarmHash. FarmHash is one of the fastest hashing methods, and is generally free of security problems.
- Non-crypto. Non-crypto. This includes a range of fast non-cryptography hashing methods.
- Non-crypto hashes (C++): Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro. Non-crypto hashes: Farm, City, xxHash, MUM, Spooky 2, Murmur, Metro and t1ha0. This includes a range of fast non-cryptography hashing methods for Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro using C++ methods.
- Pearson. Pearson. Pearson is one of the fastest hashing methods, and has been designed for 8-bit processors.
- C++: t1ha. t1ha. t1ha is one of the fastest hashing methods, and has been designed for 64-bit processors.
- C++: Spooky. Spooky. Spooky is one of the fastest hashing methods, and V2 has a 32-bit, 64-bit and 128-bit version.
- C++: xxHash. xxHash. xxHash is one of the fastest hashing methods, and has good performance for short data inputs.
- C++: MUM. MUM. MUM is one of the fastest hashing methods.
- C++: FNV 1/1a. FNV 1/1a. FNV 1/1a is one of the fastest hashing methods, and is particularily useful when there are small changes in strings, such as with IP addresses and URLs.
- C++: MetroHash. MetroHash. MetroHash is one of the fastest hashing methods.
- C++: CityHash. CityHash. CityHash was created by Google and is one of the fastest hashing methods. It was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Farm. FarmHash. FarmHash was created by Google and is one of the fastest hashing methods. It is an improvement to CityHash.
- C++: Murmur. Murmur. Murmur is one of the fastest hashing methods, but was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Halftime. Halftime. Halftime is one of the fastest hashing methods and was created by Jim Apple at Apache.
- C++: Highway. Highway. Highway is an ultra-fast keyed-hash, and is more than five times faster than SipHash. It was created by Jyrki Alakuijala, Bill Cox, Jan Wassenberg at Google.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
- C++: CLHash. CLHash. CLHash is an ultra-fast hashing method and focused on improving performance of the hashing of long strings.
- C++: FalkHash. FalkHash. FalkHash is an ultra-fast hashing method and beats most of the other non-cryptography methods for performance. It is focused on the x64 architecture and integrates with AES-NI.
- C++: wyHash. wyHash. wyHash is an ultra-fast hashing method.
- C++: Fibonacci. Fibonacci. Fibonacci is an ultra-fast hashing method.
- C++: Lookup3. Lookup3. Lookup3 is an ultra-fast hashing method.
A fuller test with SMHasher gives [here]:
Hash function MiB/sec cycl./hash cycl./map Quality problems
------------------------------------------------------------------
o1hash 12439661.09 16.77 166.13 insecure, no seed, zeros, fails all tests
crc32_hw1 23208.73 46.74 179.70 insecure, 100% bias, collisions, distrib, BIC, machine-specific (x86 SSE4.2)
t1ha0_aes_noavx 22785.26 38.71 180.61 LongNeighbors, machine-specific (x86 AES-NI)
t1ha0_aes_avx1 22714.85 48.12 226.52 LongNeighbors, machine-specific (x64 AVX.txt)
t1ha0_aes_avx2 22345.33 44.38 556.47 LongNeighbors, machine-specific (x64 AVX2)
falkhash 20202.42 173.63 321.52 Sparse, LongNeighbors, machine-specific (x64 AES-NI)
MeowHash64low 17378.06 85.48 237.60 Sparse, invertible, machine-specific (x64 AES-NI)
MeowHash32low 17374.64 85.48 258.53 Sparse, invertible, machine-specific (x64 AES-NI)
MeowHash 17371.91 85.48 247.96 Sparse, invertible, machine-specific (x64 AES-NI)
FarmHash32 17112.05 47.7 214.71 machine-specific (x64 SSE4/AVX)
xxh3 16538.52 32.81 184.86 DiffDist bit 7 w. 36 bits, BIC
xxh3low 16462.36 32.77 199.79
farmhash32_c 16299.81 47.79 219.19 machine-specific (x64 SSE4/AVX)
xxh128low 15174.85 33.79 187.05
xxh128 15174.14 40.46 195.65
farsh32 14053.09 74.29 245.33 insecure: AppendedZeroes, collisions+bias, MomentChi2, LongNeighbors
metrohash64crc_2 14034.84 48.94 162.54 UB, Cyclic 8/8 byte, DiffDist, BIC, machine-specific (SSE4.2/NEON)
metrohash64crc_1 14000.5 49.08 150.54 UB, Cyclic 8/8 byte, DiffDist, BIC, MomentChi2, machine-specific (SSE4.2/NEON)
metrohash128crc_1 13948.67 65.2 168.08 UB, machine-specific (SSE4.2/NEON)
metrohash128crc_2 13920.19 65.12 176.70 UB, machine-specific (SSE4.2/NEON)
halftime_hash128 13478.23 97.79 252.14
wyhash32low 12911.09 29.59 205.43 2 bad seeds
wyhash 12879 30.35 196.77 2^33 bad seeds
CityCrc128 12343.43 74.5 209.75
fletcher2 12011.15 25.29 298.60 bad seed 0, UB, fails all tests
fletcher4 11928.55 25.27 293.49 bad seed 0, UB, fails all tests
halftime_hash256 11620.28 98.44 252.60
fibonacci 11339.87 26.33 705.64 UB, zeros, fails all tests
ahash64 9862.62 27.32 181.68 rust
Spooky128 9751.14 63.84 192.47 UB
Spooky64 9747.47 62.2 191.71 UB
Spooky32 9747.13 62.24 196.96 UB
t1ha1_64le 9723.86 34.39 176.91 Avalanche
cmetrohash64_1 9683.33 45.2 161.01 UB, LongNeighbors, BIC, MomentChi2
cmetrohash64_2 9669.95 44.75 149.67 LongNeighbors
metrohash64_2 9668.51 44.45 164.30 UB, LongNeighbors
metrohash64 9664.61 44.59 150.74 UB, LongNeighbors, BIC
metrohash64_1 9664.57 45.37 152.31 UB, LongNeighbors, BIC, MomentChi2
cmetrohash64_1o 9658.31 42.84 163.45 UB, LongNeighbors, BIC, MomentChi2
FNV1a_YT 9643.42 32.06 175.19 bad seed, UB, fails all tests
City128 9640.19 88.45 225.38
metrohash128_2 9584.94 59.1 167.43 UB, LongNeighbors
metrohash128 9569.16 58.68 167.53 UB, LongNeighbors
metrohash128_1 9558.17 59.04 175.94 UB, LongNeighbors
FarmHash128 9409.63 74.52 210.25
VHASH_32 9404.99 77.01 250.57 sanity, Seed, MomentChi2
VHASH_64 9392.39 74.72 227.92 sanity, Seed, MomentChi2
farmhash128_c 9244.13 79.08 209.44
t1ha2_atonce 9237.12 38.94 194.32 Zeroes low3
City64noSeed 9090.42 32.23 171.53 Avalanche, Sparse, TwoBytes, MomentChi2, Seed
City64low 9089.45 47.75 201.73
t1ha2_stream 9068.55 74.56 219.85 Sparse, Permutation, LongNeighbors
City64 9066.9 47.81 197.78 Sparse, TwoBytes
t1ha2_stream128 9065.5 93.19 236.50 Sparse, Permutation, LongNeighbors
xxHash64 8936.63 51.31 174.34
pengyhash 8744.48 85.31 222.45
farmhash64_c 8713.16 47.96 201.00
FarmHash64 8684.76 48.13 200.51
crc64_hw 8440.13 34.94 141.15 insecure, 100% bias, collisions, distrib, BIC, machine-specific (SSE4.2/NEON)
t1ha2_atonce128 8350.99 55.65 203.53 LongNeighbors
PMPML_64 8161.19 53.2 179.16 unseeded: Seed, MomentChi2, BIC
halftime_hash512 7681.62 125.81 274.01
tabulation 7621.75 42.19 179.93
t1ha1_64be 7481.37 38.16 193.22 Avalanche
MUMlow 7225.18 37.85 197.92 UB, 5 bad seeds
farsh64 7216.29 130.3 302.44 insecure: AppendedZeroes, collisions+bias, MomentChi2, LongNeighbors
MUM 7134.56 37.85 172.34 UB, too many bad seeds, machine-specific (32/64 differs)
nmhash32 7003.3 68.93 216.59
PMPML_32 6704.53 53.5 197.43 Avalanche >512, unseeded: Seed, BIC, MomentChi2, PerlinNoise
nmhash32x 6342.95 56.41 217.75
crc32_hw 6330.42 35.55 170.16 insecure, 100% bias, collisions, distrib, BIC, machine-specific (SSE4.2/NEON)
FNV2 6258.84 33.25 142.89 fails all tests
FNV1A_Pippip_Yurii 6258.46 28.19 184.41 UB, sanity, fails all tests
FNV1A_Totenschiff 6258.23 27.99 198.20 UB, zeros, fails all tests
HighwayHash64 6242.58 99.55 248.41
mx3 6146.02 52.48 173.09 UB
xxHash32 6040.87 51.77 177.91 LongNeighbors, collisions with 4bit diff, MomentChi2 220
prvhash64s_64 5481.48 170.05 325.39
mirhash 5413.73 39.68 154.47 UB, 2^36 bad seeds, LongNeighbors, machine-specific (32/64 differs)
mirhash32low 5412.76 39.79 182.13 UB, 4 bad seeds, Cyclic, LongNeighbors, machine-specific (32/64 differs)
Murmur3F 5226.4 52.18 175.85 UB
prvhash64s_128 5161.33 260.96 442.70
t1ha0_32le 5132.18 54.83 193.53 Sparse, LongNeighbors
halftime_hash64 4990.72 120.55 281.64
Murmur2B 4882.95 39.72 149.43 UB, 1.8% bias, collisions, 3.4% distrib, BIC
seahash32low 4801.33 58.54 227.31 PerlinNoise 32, !msvc
seahash 4796.97 58.55 201.58 PerlinNoise, !msvc
fasthash32 4737.61 45.32 181.86 UB, insecure
fasthash64 4737.21 42.79 164.87 UB, insecure, Moment Chi2 5159 !
umash32_hi 4662.92 54.22 214.20
umash64 4662.09 53.42 188.09
umash32 4633.19 53.42 216.33
t1ha0_32be 4585.59 55.98 183.45 Sparse, LongNeighbors
clhash 4472.31 82.72 229.73 PerlinNoise, machine-specific (x64 SSE4.2)
tabulation32 4317.34 35.45 197.20 collisions
Murmur2C 4092.99 51.84 164.65 UB, 2^32 bad seeds, 91% bias, collisions, distr, BIC, LongNeighbors
farsh128 3776.92 232.48 398.67
City32 3675.04 57.73 212.04
TSip 3228.14 57.96 211.71 !msvc
Murmur3C 3197.63 67.9 198.00 UB, LongNeighbors, Text, DiffDist
Crap8 3149.63 36.23 195.11 UB, 2.42% bias, collisions, 2% distrib
Murmur2 3146.91 41.87 187.89 UB, 1 bad seed, 1.7% bias, 81x coll, 1.7% distrib, BIC
Murmur2A 3146.79 46.87 191.96 UB, 1 bad seed, 12.7% bias, LongNeighbors
aesnihash 2963.39 71.24 217.73 fails many tests, machine-specific (x64 AES-NI)
BEBB4185 2951.62 222.03 343.63 UB, too many bad seeds, msvc-specific
jodyhash6 2848.42 29.99 164.36 bias, collisions, distr, BIC, LongNeighbors
wyhash32 2532.89 48.4 484.57 2 bad seeds, 32-bit
umash128 2427.46 70.6 197.29
Murmur3A 2413.88 53.36 182.37 UB, 1 bad seed, Moment Chi2 69
prvhash64_64m 2386.19 51.18 186.87
prvhash64_128 2383.57 103.44 246.45
prvhash64_64 2375.72 51.61 190.97
hasshe2 2372.52 68.64 216.74 Permutation,TwoBytes,Zeroes,Seed
PMurHash32 2344.78 58.48 196.43 1 bad seed, Moment Chi2 69
mirhashstrict32low 2218.87 65.48 190.59 1 bad seed, MomentChi2 9
mirhashstrict 2217.32 65.53 182.07
sha1ni 2019.96 135.84 564.40 insecure,sanity, Permutation, Zeroes, machine-specific
sha1ni_32 2019.94 136.82 589.46 machine-specific
superfast 1956.25 53.61 180.10 UB, bad seed 0, 91% bias, 5273.01x collisions, 37% distr, BIC
sha2ni-256_64 1910.34 146.06 595.16 Zeroes, machine-specific
sha2ni-256 1906.77 145.47 603.08 insecure,sanity, Permutation, Zeroes, machine-specific
farsh256 1895.77 459.86 575.95
SipHash13 1889.1 89 199.95 0.9% bias
Murmur1 1804.67 51.51 188.41 UB, 1 bad seed, 511x collisions, Diff, BIC
lookup3 1658.31 48.84 194.15 UB, 28% bias, collisions, 30% distr, BIC
pearsonbhash64 1486.34 104.32 185.03
poly_1_mersenne 1431.65 54.49 189.52 fails most tests
jodyhash32 1428.37 44.36 185.85 bias, collisions, distr, BIC LongNeighbors
pearsonbhash128 1347.03 121.75 214.84
poly_2_mersenne 1323.69 66.93 190.88
poly_3_mersenne 1323.59 74.86 206.77
poly_4_mersenne 1323.57 82.67 200.36
blake3_c 1285.91 340.01 552.63 no 32bit portability
GoodOAAT 1052 71.62 192.19
pearsonbhash256 998.9 167.05 261.29
SipHash 980.88 127.77 246.19
MicroOAAT 977.6 59.61 185.06 100% bias, distrib, BIC
FNV1a 791.84 69.69 177.84 bad seed, zeros, fails all tests
sdbm 791.84 67.69 177.06 bad seed 0, fails all tests
FNV64 791.82 70.24 159.29 fails all tests
bernstein 791.82 68.63 180.71 bad seed 0, fails all tests
beamsplitter 789.22 682.45 1150.3 UB, too many bad seeds
HalfSipHash 755.78 114.47 243.72 zeroes
chaskey 753.23 153.42 288.26 PerlinNoise
x17 527.9 98.78 184.09 99.98% bias, fails all tests
JenkinsOOAT_perl 452.49 118.78 194.78 bad seed 0, test FAIL
MurmurOAAT 452.49 113.07 197.83 bad seed 0, 1.5-11.5% bias, 7.2x collisions, BIC, LongNeighbors
JenkinsOOAT 452.48 142.85 213.93 bad seed 0, 1.5-11.5% bias, 7.2x collisions, BIC, LongNeighbors
crc32 392.1 131.62 204.58 insecure, 8590x collisions, distrib, PerlinNoise
sha1-160 364.95 1470.55 1794.1 Comb/Cyclic low32
rmd256 362.49 617.02 815.44 Bad seeds
blake2b-256_64 356.97 1222.76 1435.0
blake2b-224 356.59 1228.5 1425.87
blake2b-160 356.08 1236.84 1458.15
blake2b-256 355.97 1232.22 1443.31 Sparse high 32-bit
md5-128 353.76 638.29 803.39
md5_32a 353.64 629.85 799.56 Sparse high 32-bit
sha1_32a 353.03 1385.8 1759.9 Cyclic low32, 36.6% distrib
rmd128 334.36 659.03 838.32 Bad seeds
blake2s-128 295.3 698.09 1059.2
pearsonhash64 287.95 174.11 196.50 Avalanche, Seed, SSSE3 only. broken MSVC
pearsonhash128 287.95 171.72 194.61 Avalanche, Seed, SSSE3 only. broken MSVC
pearsonhash256 264.51 184.87 218.79 Avalanche, Seed, SSSE3 only. broken MSVC
blake2s-256 215.28 1014.88 1230.38
blake2s-160 215.01 1026.74 1239.54
blake2s-256_64 211.52 1044.22 1228.43
blake2s-224 207.06 1063.86 1236.50
rmd160 202.16 1045.79 1287.74 Bad seeds, Cyclic hi32
sha2-256_64 148.01 1376.34 1624.71 Bad seeds, Moment Chi2 7
sha2-256 147.8 1374.9 1606.06 Bad seeds, Moment Chi2 4
sha2-224_64 147.6 1360.1 1620.93 Bad seeds, Cyclic low32
sha2-224 147.13 1354.81 1589.92 Bad seeds, Comb low32
asconhashv12 144.98 885.02 1324.23
sha3-256 100.58 3877.18 4159.79 PerlinNoise
sha3-256_64 100.57 3909 4174.63 PerlinNoise
asconhashv12_64 86.73 684.02 606.93
floppsyhash 35.72 1868.92 1411.07
tifuhash_64 35.6 1679.52 1212.75 Cyclic low32
Problems include:
- Bad Seeds. A random seed is often used to initialise the hash. This problem relates to having a bad seed..
- Undefined behaviour (UB). This includes Misaligned, oob (Out of bounds), Signed integer overflow and Shift exponent overflow.
o1hash is the fastest, and a quick and dirty hashing method. It is generally not secure. t1h (Fast Positive Hash) requires AES-NI (Intel Advanced Encryption Standard Instructions) and is one of the fastest hashes at 22.785 Gbps. It has fairly good security levels. Meow comes in around 17.378 Gbps. We can see that SHA-1-160 runs as 364 Mbps, while Meow runs at 17.378 Gbps. Blake 3 is one of the fast cryptography hash and has a rate of 1.285 Gbps, and Blake 2 gives a rate around 215 Mbps. SHA-3 gives hashing rates of 100.58 Mbps.
Google recommend the following for 64-bit hashes without quality problems:
- xxh3low
-
wyhash
-
ahash64
-
t1ha2_atonce
-
FarmHash
-
halftime_hash128
-
Spooky32
-
pengyhash
-
nmhash32
-
mx3
-
MUM/mir
- fasthash32
Hash-based Signatures

With hash-based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature, unless we create a stateless method, such as SPHINCS+ [1]. Currently NIST have the final round for the Post Quantum Cryptography competition, and for digital signatures, SPHINCS+ is one of the alterative finalists (alongside Picnic).
Hash-based signature (theory)
- BiBa (Go). BiBa. An overview of BiBa One Time Signature [9]. Basically the method involves us taking a hash of a value using a standard hashing method, such as with SHA-256. There will then be \(2^{256}\) different hashing values. We aim to create a signature for a message, so Bob (the signer) selects a number of random values for his private key value and then publishes the hash of each of these (\(P_1\), \(P_2\), etc). He then sends these public keys to Alice. Now when Bob wants to sign a message, he will take one of his private key values, and then hashes it, and then determines the bin that it should be placed. In this case, we could use the \(\pmod N\) function on the hash, and where \(N\) is the number of bins. If we select \(2^{10}\) there will be 1,024 bins.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature [9].
Hash-based signature (stateful)
- BLISS - Post-quantum signing. BLISS. One of the alteratives to the usage of our existing public key methods is the usage of lattice cryptography, and especially in the usage of Ring Learning With Errors (RLWE). An important application is within digital signatures, and where Bob will sign something with his private key, and then Alice can prove that he signed it with his public key. One post-quantum signature method is BLISS (short for Bimodal Lattice Signature Scheme) [8]. It was created by Léo Ducas, Alain Durmus, Tancrède Lepoint and Vadim Lyubashevsky in 2013.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Hash to Obtain Random Subset (HORS) [3] is a quantum robust hashed-based one-time signature. With this we create a series of integers for our private keys and organise into an indexable form. Then we hash them to a sequence of public key values. Next we segment the hash of the message into a series of n-bit integer values. The signature is then achieved through a look-up of the value in the public key list.
- Lamport Signatures. Lamport. Outlines Lamport signatures [7]. When we sign a message we take its hash and then encrypt with our private key. The public key is then used to prove it, and will prove that we signed it with our private key. The Lamport signature uses 512 random hashes for the private key, and which are split into Set A and Set B. The public key is the hash of each of these values. The size of the private key is 16KB (2×256×256 bits) and the public key size is also 16 KB (512 hashes with each of 256 bits).
- Winternitz Signatures (W-OTS). Winternitz. Outlines Winternitz signatures [4, 5]. W-OTS uses relatively small key and signatures sizes, and is thought to be quantum robust. It generates 32x256 bit random private keys. We then hash these a number of times, and is defined by a parameter (w). If we use w=8, we hash the private keys by (2w). This creates 32x256 bits public keys. The signature is the created by taking eight bits at a time, and then the 8-bit binary int (n) is subtracted from 256 and the private key is the hashed 256-n times. The signature is then 32 hashes which are derived from random private keys. To verify the signature, the recipient parses the hash of the signature (using 8 bits at a time, and extracting the 8 bit int, n).
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method [6], and which is used within speeds-up of Hashing-based signature methods. Using methods such as SHA-1 and SHA-2 (aka SHA-256) will be inefficient as they tend to compress the data inputs through a number of stages. Haraka v2 [6] is different as focuses on inputs of just 256 bits (32 bytes) or 512 bits (64 bytes). This makes the method useful when we are dealing with key and hash values, and is especially useful for hash-based signatures. The output is 256 bits long, but where the input can be either be 256 bits (Haraka256) or 512 bits (Haraka512). These lengths are typically for the outputs of modern hashing applications. The Haraka method, too, has been optimized with AES instructions (AES-NI - Intel Advanced Encryption Standard New Instructions) and which are supported within the hardware of the processor. As Haraka is focused on short messages, the number of rounds within the hashing process has been reduced.
Hash-based signature (stateless)
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ digital signature. SPHINCS digital signature. Outline of the a SPHINCS stateless digital signature method [1].
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
Hash-based signature (Merkle-based)
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
Introduction
Many of the problems we see on the Internet relate to the lack of trust within transactions. The emails you receive and the Web sites that you visit often have very little trust built into them. For trust the email address of the sender, but anyone can fake that address. So increasingly we create a digital signature, and where we sign our messages. In this way, we can check for authentication, integrity and non-repudiation.
With the Alice creates a key-pair: a public key and a private key. She then takes a hash of the message, and then encrypts this hash with her private key, and passes the message and the signature to Bob. Bob then reads the message and takes a hash of it. He then decrypts Alice's signature with her public and checks the hashes. If they match, he knows that she signed and that it has not been changed along the way:
Currently, we often use RSA, DSA and ECDSA to sign our messages. These are based on the difficulty of finding out the factors of a number and on the processing of discrete logarithms. At the current time these methods are computationally hard problems, but with quantum computers, they become much easier. This was shown by Peter Shor who illustrated that it was possible to crack them in polynomial time.
Of all the methods that are being proposed, the hash-based methods look as if they have a good chance of success of creating quantum robust signatures. methods and code-based methods are being researched, but the usage of hashing methods is already well and could provide the best alternative to the existing methods. Hashing methods, too, often bring other advantages, such as forward secure, which means that a key which is cracked will not reveal all the previous keys.
Merkle trees
The root of hash-based methods isin Merkle trees, and which are a way of hashing is used in many applications, including with Bitcoin, Ethereum, Git distribution systems, No SQL, and in many P2P applications. With a Merkle tree we take our data elements, and then hash them, and take pairs of these hashes to create a new hash, and so we build a table. At the top of the tree is the root element (in this case Hash1234):

In this way, we can use the tree to see if we have matching data on systems.On a P2P network, we can transfer a file by splitting it into data segments and then distributing these segments across the network. A trusted source will have the complete Merkle tree for rebuilding the file, and a client can thus rebuild from the Merkle tree and determine the parts of the file which are still missing. Once transferred the root hash (and all the other hashes) will then match. In its core method, the Merkle Signature Scheme (MSS) has serious performance and memory issues, but enhanced methods such as XMSS create with much less of a performance hit.
One-time signatures (Lamport)
The core method used in hash-based signatures is that of the one-time signature, and where we create a new key pair for every method we need to create. If the keys were reused, an attacker could start to learn the private key, and thus spoof messages. One of the first methods was produced by Leslie Lamport and Whitfield Diffie, in 1979, and is defined as:
- We create two data sets with 256 random 256-bit numbers (Set A and Set B). These are the private key (512 values).
- we take the hash of each of the random numbers. This will give 512 hashes and will be the public key.
- We then hash the message using and then test each bit of the hash (0 ... 255). If it is a 0, we use the ith number in Set A, else we use the ith number from Set B.
- The signature is then 256 random numbers (taken from either Set A or Set B) and the public key is the 512 hashes (of Set A and Set B).
The public and private keys are then each 16KB in size. A demo of the method is here.

Figure 1: Lamport method
The major problem with the method is that a key pair for every message. also in 1979, found a solution with Merkle trees.
One-time signature (W-OTS)
To improve performance method (and which reduced key sizes), Merkle proposed Winternitz OTS (named after Robert Winternitz). With this method was possible to sign many bits at the same time. The method is:
- We create 32 256-bit random numbers. These 32 values will be our private key.
- We then hash each of these values 256 times. These 32 values will be our public key.
- We now take the message and hash it using SHA-256. This produces 32 8-bit values (N1, N2 ... N32).
- Next we take each 8-bit value in the hash of the message, and then hash 256-N times (where N is the value of the 8-bit value).
- To prove the signature, we take the message and hash it with SHA-256, and then take each 8-bit value. We then hash the 8-bit signature value by the number of times defined by the message hash value (N1, N2..). The result for each operation should equal the public key value.
This is illustrated below in Figure 2. A demo of the method is here.

Figure 2: W-OTS
Hash-based Signatures
The methods such as W-OTS and Lamport only provide for a one-time signature. In order to sign many messages, we can use the Merkel signature scheme (MSS). With this we take a hash of the keys and build these as the leaves of the tree. The root of the tree is then the public key - the verification key. We then just use the private key of the W-OTS method to create the signature. The sender also sends the authentication path, which is the neighbouring nodes within the path and which leads to the root of the tree. The recipient can then rebuild the tree using the verification key (which can be received a digital certificate) and the authentication path. For the next message we move onto another key pair and where the index of the key part is revealed.
In the following example we have our root as the public key, and then want to sign with Key3. We then show the authentication path which takes us to the root (as defined in the bold arrows):

Conclusions
Hashed-based methods look to be a strong contender for weaning us off RSA, DSA and ECDSA, but we will have to look at the stateful generation of keys. For this we will have to generate a bank of key pairs (2, 4, 8, 16, etc) and then create the public key from the root of the Merkle tree. We must then remember the keys we have used previously, and only use an unused one. Once we use our new key pair, we then show our working-out as to how the private key is integrated into our tree. It is a bit like a teacher marking a question correctly, and asking for the working out that go you to the answer.
References
[1] Bernstein, D. J., Hopwood, D., Hülsing, A., Lange, T., Niederhagen, R., Papachristodoulou, L., ... & Wilcox-O’Hearn, Z. (2015, April). SPHINCS: practical stateless hash-based signatures. In Annual international conference on the theory and applications of cryptographic techniques (pp. 368-397). Springer, Berlin, Heidelberg [paper].
[2] Bernstein, D. J., Hülsing, A., Kölbl, S., Niederhagen, R., Rijneveld, J., & Schwabe, P. (2019, November). The SPHINCS+ signature framework. In Proceedings of the 2019 ACM SIGSAC conference on computer and communications security (pp. 2129-2146) [paper].
[3] Reyzin, L., & Reyzin, N. (2002, July). Better than BiBa: Short one-time signatures with fast signing and verifying. In Australasian Conference on Information Security and Privacy (pp. 144-153). Springer, Berlin, Heidelberg [paper].
[4] Merkle, R. C. (1989, August). A certified digital signature. In Conference on the Theory and Application of Cryptology (pp. 218-238). Springer, New York, NY.
[5] Hülsing, A. (2013, June). W-OTS+–shorter signatures for hash-based signature schemes. In International Conference on Cryptology in Africa (pp. 173-188). Springer, Berlin, Heidelberg.
[6] Kölbl, S., Lauridsen, M. M., Mendel, F., & Rechberger, C. (2016). Haraka v2–efficient short-input hashing for post-quantum applications. IACR Transactions on Symmetric Cryptology, 1-29. [here]
[7] Lamport, L. (1979). Constructing digital signatures from a one-way function (Vol. 238). Technical Report CSL-98, SRI International. [paper]
[8] Ducas, L., Durmus, A., Lepoint, T., & Lyubashevsky, V. (2013, August). Lattice signatures and bimodal Gaussians. In Annual Cryptology Conference (pp. 40-56). Springer, Berlin, Heidelberg [paper].
[9] Perrig, A. (2001, November). The BiBa one-time signature and broadcast authentication protocol. In Proceedings of the 8th ACM Conference on Computer and Communications Security (pp. 28-37) [paper] .
Hashing (Simularity)

Similarity hashes allow for two data objects to be compared for their similarity.
Similarity assessment methods
The following relate to the basic methods used for string similarity:
- String similarity String similarity. This measures edit distance (including Levenshtein distance), Jaro (including Jaro-Winkler), and QGrams.
- String enthropy String enthropy. Measurement of the entropy of strings.
- Soundex Soundex. Soundex uses a phonetic algorithm to classify a sound as it is pronounced. It focuses on matching phrases which have minor spelling errors.
Similarity hashes
The following are the tips related to similarity hashing:
- Similarity hash: SimHash (Charikar similarity) in Python Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash (Nilsimsa similarity) Nilsimsa. The Nilsimsa similarity is used to find similarities between spam emails.
- Context Triggered Piecewise Hashes (CTPH): ssdeep CTPH similarity. Kornblum [6] created ssdeep and which computes fuzzy hashes. This aims to match similar byte sequences, no matter if there are differences between these sequences. For this we break a file up into fragments with a rolling hash function. We then produce a small hash for each of those fragments. These are then aggregated to produce the complete hash of a file. In comparing file signatures, we treat the resultant hash value as a string, and then uses an edit distance method to compare.
- TLSH (A Locality Sensitive Hash) TLSH similarity. In malware analysis and in text similarity, we often have to identify areas of data within files which are similar. One method is TLSH (A Locality Sensitive Hash), and which was defined by Oliver et al [7]. It is used - along with ssdeep - by VirusTotal to identify a hash value for malware.
- Minhash (Jaccard similarity) Jaccard similarity. The Minhash method is used to find similarities between strings, files and metadata.
- Counting identical elements (HyperLogLog) HyperLogLog. Counting the number of identical elements.
Hazmat cryptography

The Cryptography library in Python contains interfaces to common cryptographic algorithms, including symmetric key methods, hashing, public key, and key derivation functions. Many of these are contained with the Hazmat (Harzardous Material) primative setup.
Hashing, HMAC, CMAC, Poly1305 and HKDF
-
Hazmat Hashes. Hazmat Hashes. This includes the hashing methods in the Hazmat cryptography library. This includes Blake2p, Blake2s, MD5, SHA1, SHA224, SHA256, SGA384, SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHA512, SHA512-224, SHAKE128 and SHA256.
-
Hazmat Hashes. Hazmat Hashes. In this case we will implement Python code to determine SHA1, SHA2, SHA3, Blake2, MD5 and SM3 hashes.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
- Hazmat HKDF. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
- Hazmat CMAC. Hazmat CMAC. CMAC methods using the Python cryptography primitives.
- Hazmat Poly1305. Hazmat Poly1305. Poly1305 methods using the Python cryptography primitives.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
Symmetric key
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat. Implementation of ChaCha20/Poly1305 with a random key using Hazmat.
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat. Implementation of AES GCM with a random key using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hazmat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Hazmat Symmetric Key Padding. Symmetric key. This includes the coverage of padding with Hazmat.
- Hazmat Symmetric Key Padding. Symmetric key. This includes the coverage of padding with Hazmat.
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
- Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . With 3DES encryption, we use a 128-bit key and a 64-bit IV value. The two modes supported are ECB (without salt) and CBC (with salt). The DES algorithm has been around for a long time, and the 56-bit version is now easily crackable (in less than a day on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases, and splits the key into two. Overall the key size is typically 112 bits (with a combination of the three keys - of which two of the keys are the same). In this case we will use PKCS7 padding, and which fills the input data with a value that is equal to the number of padding bytes. Overall, DES has a 64-bit block size, and which equates to eight ASCII characters.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key . And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.
Asymmetric key
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- ECC key generaton with Hazmat. Elliptic Curve key gen. Creating ECC keys using Hazmat and Python.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- Hazmat RSA signing (with key values). RSA signing with Hazmat. RSA signing using Python and with Hazmat (with key values).
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here]
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Signatures. DSA Signatures. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. The ECDSA method is an extension of DSA, but implemented with elliptic curve (EC) methods. As with most public key signing methods, we take a hash of a message, and then apply a private key to create a signature (\(r,s\)). This is done by creating a random value (\(k\)) to produce the signature. The signature is then verified using the associated public key. This then verifies the creator of the signature and that the message has not been changed.
Digital Signature: ECDSA/EdDSA
- ECDSA with Hazmat. ECDSA wih Hazmat. This outlines ECDSA with Hazmat.
- Ed25519 for EdDSA signatures with Hazmat. EdDSA: Ed25519. This page uses the Hazmat primitives for the cryptography library.
- Ed448 for EdDSA signatures with Hazmat. EdDSA: Ed448. This page uses the Hazmat primitives for the cryptography library.
- Ed25519 using NaCl. Ed25519. This page uses the NaCl port from libsodium.
- ECDSA Signatures with Hazmat (SECP256R1, SECP384R1, SECP521R1, SECP224R1, SECP192R1, and SECP256K1). ECC Signatures. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and then creates an ECDSA signature for a given message.
Digital Signature: RSA
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
Key exchange: ECDH/X25519
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives and showing the byte values for the key.
Tokens
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
Homomorphic Encryption

Homomorphic encryption supports mathematical operations on encrypted values. Partial Homomorphic Encryption (PHE) supports a few arithmatic operations, while Full Homomorphic Encryption (FHE) supports add, subtract, multiply, and divide. Homomorphic encryption normally involves a public key to encrypt the data, and a private key to decrypt it. There have been four main generations of homomorphic encryption, and the most recent being the HEAAN method.
Simple
- Simple Homomorphic Cipher. Hom. This outlines a Simple Homomorphic cipher.
- Simple Homomorphic Cipher (Python). Hom. This outlines a Simple Homomorphic cipher with Python.
- Full Homomorphic Cipher with a Public Key. Public key. This outlines a Simple Homomorphic cipher using a public key
ElGamal
- ElGamal Homomorphic Cipher (Go). ElGamal. This outlines ElGamal Homomorphic cipher with Go.
- ElGamal Homomorphic Cipher (Go) - Divide. ElGamal. This outlines ElGamal Homomorphic cipher with Go with divide.
- ElGamal Homomorphic Cipher (Go) - Additive. ElGamal. This outlines ElGamal Homomorphic cipher with Go with addition.
- ElGamal Homomorphic Cipher for Multiplication (Python). ElGamal. This outlines ElGamal Homomorphic multiplication with Python.
- ElGamal Homomorphic Cipher for Division (Python). ElGamal. This outlines ElGamal Homomorphic division with Python.
- ElGamal Homomorphic Cipher for Addition (Python). ElGamal. This outlines ElGamal Homomorphic addition with Python.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (Python). ElGamal. This outlines ElGamal Homomorphic subtraction with Python.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
RSA
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
ZKP
- Full Homomorphic Cipher to determine if Bob is older. Older. This outlines a Simple Homomorphic cipher to determine if Bob is older than Alice.
- Full Homomorphic Cipher to determine matching password. Password. This outlines a Simple Homomorphic cipher to determine if a password matches
- Interactive ZKP With Probablistic Methods. ZKP. Interactive ZKP With Probablistic Methods using Python.
- Full Homomorphic Cipher for Millionaire's Problem. Millionaire. This outlines a Simple Homomorphic cipher for the Millionaire's Problem
Voting
- Trusted voting. Trusted. A trusted voting method.
Secret share
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Lattice
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
Full Homomorphic Cipher
- Full Homomorphic Cipher for 2-bit Adder. Adder. This outlines a Simple Homomorphic cipher for a 2-bit adder with DGHV.
- Full Homomorphic Cipher for Full Adder. Full Adder. This outlines a Simple Homomorphic cipher for a full adder with DGHV.
- Full Homomorphic Cipher for 4-bit Adder. Adder. This outlines a Simple Homomorphic cipher for a 4-bit adder with DGHV.
- Full Homomorphic Cipher for 4-bit Adder/Subtractor. Subtract. This outlines a Simple Homomorphic cipher for a 4-bit adder/subtractor with DGHV.
- Full Homomorphic Cipher to XOR two integers. X-OR. This outlines a Simple Homomorphic cipher to X-OR two integers
Paillier
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier) .
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Damgård-Jurik Homomorphic Encryption With Secret Shares. Damgård-Jurik Method. Two of the major areas of developments within cybersecurity will be the usage of homomorphic encryption, and in the usage of Shamir secret sharing. With homomorphic encryption, we can encrypt values, and then operate on them with arithmetic functions (such as add, subtract and multiply), and with Shamir secret sharing, we can split secrets into shares, and then distributed them over networks. These approaches will take privacy to new levels. So let’s look at the Damgård-Jurik method.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Learning with Errors (LWE)
- Learning With Errors . LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret key value (s) and another value (e). Next we select a number of values (t[]) and calculate g[] = t[] x s + e. The values of g[] and t[] become our public key.
- Public Key Encryption with Learning With Errors (LWE). LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret value (s) and which is our private key. We then create a public key which is based on random numbers (A), and then generate another set of numbers (B) which is based on A,s and random errors e. An example of encryption with multiple bits is given.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE)
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Others
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
- SIDH Go. SIDH. Post-quantum key exchange.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Anonymous crypto. Anon. Anonymous crypto.
- Rho factorization. Rho. Rho alogorithm.
- Post-quantum signing (BLISS). BLISS. BLISS method.
Homomorphic Encryption with Krytology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Homomorphic hashing
- Homomorphic Hashing with Golang. Homomorphic hashing. Normally with hashing methods, we need to take all the previous data and new data in order to create a new hash value for our data. In a homomorphic hashing method, we can basically take the previous hash, and then add on any new data values. We can also remove previous data values from our hash, too. This is more efficient in computing, as we do not have to process all of our data into a new hash, and can use simple homomorphic operations for the computation. The method we will use (LtHash) was initially defined by Bellare and Micciancio and updated Lewi et al at Facebook.
Identity Based Encryption (IBE)

This page outlines a few basic principles around the usage of IBE.
Identity Based Encryption (Pairing based)
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pair-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Identity Based Encryption (Others)
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Güther's implicitly certified identity-based public keys (IBE). Günther. This method allows Bob to generate Alices public key from her identity and publicly available parameters.
- Girault's self-certified public keys (IBE). Girault. This method allows Bob to generate Alices public key from her identity and publicly available parameters, and where we use an RSA key pair to self-certify Alice's public key.
Intrusion Detection Systems (IDS)
- Intrusion Detection Systems. Snort. This outlines some of the basics of IDS, including the requirement for Intrusion Detection Systems (IDSs), and where they are used.
- Advanced Network Forensics (Snort). Adv Network Forensics. This provides information on how to detect threats through network forensics with Snort
Snort

- Snort IDS. Snort. This is a Snort Analyser.
- Snort IDS 2 with rules editor. Snort. This provides information on how to detect threats through network forensics with Snort, and with an editing function for rules.
Presentation
IoT

The key objectives of this page are: Understand how a Pen Tester can generate vulnerabilities and test using the Metasploit framework; Define the options and payloads required to generate and use vulnerabilities; and Gaining remote access.
Devices
- Access the Wi-fi kettle. Go. This page outines how to access a wi-fi enabled kettle.
- Philips Hue Wireless Lighting. Go. This page shows how to use RESTful Web services to access to the Hue Led Lamps.
- Kali and R-PI. Go. This page shows the setup of a security testing infrastructure using a Raspberry Pi (R-PI) and a wifi access point.
- Kali, R-PI and RF electrical socket. Go. This page shows the control of an RF electical socket from a RPI.
- Capture from a Polar H10 heat rate sensor. Go. This page shows the capture of the Polar H10 heart sensor with an Ubertooth One.
- Trusted IoT: Linking IoT Devices to NFTs. Go. This page outlines a research paper which links a device to an NFT (Non-fungible Token).
Shodan Scanning
-
IoT Scan (Shodan). Go. This page includes a search of the Internet for key terms, such as for "apache", "mysql" and "cisco".
- IoT Banner Scan (Shodan). Go. This page includes a search of the Internet for key terms with the banner as a result (for the Top 10)
- Internet Services (Shodan). Go. This page includes a search of the Internet for key terms and display the IP address and port.
IoT Libraries
- libDisco with Go. libDisco. libdisco is a Golang library which can be used to create secure connections. It is based on the STROBE protocol framework. Symmetric cryptographic primitives rely on SHA-3 permutation, and asymmetric cryptographic primitives on X25519 and ed25519. STROBE defines a range of cryptographic protocols to integrate with IoT devices. In order to reduce processing, energy and memory requirements, it only uses Keccak (SHA-3) to encrypt and authenticate messages.
COSE/COBR
In computer security, we often have to represent binary data, in single values or groups of characters, bytes, words, long words, signed integers, floating-point values, double-precision floating-point values, and so on. This might be in the form of a data object, a signature or even encrypted content. For this, the ANS.1 DER format is often used, such as presenting digital certificates and signatures. An improvement on this for small messages with security is Concise Binary Object Representation (CBOR) — and which is defined in RFC8949 [1]. While JSON represents text-based data objects CBOR focuses on binary objects. It has been designed to create a lightweight encoder and decoder. This supports the use of CBOR within an IoT infrastructure. The data, also, does not require a data schema to be able to decode it, along with being extensible. CBOR defines the format of binary data with data objects and messages. We can then integrate security with CBOR Object Signing and Encryption (COSE), and which is defined in RFC8152 [2]. This includes signatures, message authentication codes (MACs), encryption and creating serialised objects.
- 128-bit AES GCM. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) can then build on this to include signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use a symmetric key to encrypt a message, and then decrypt it. In this case we will use AES GCM with a static 128-bit key ("0x000102030405060708090a0b0c0d0e0f").
- 256-bit AES GCM. Go. In this case we will use AES GCM using a random 256-bit key (32 bytes).
- EdDSA. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) [2] can then build on this to includes signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use EdDSA to create a signature for a message.
- ECDSA. Go. In this case we will use ECDSA to create a signature for a message.
- HMAC. Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT. Go. In this case we create a CWT token, and sign with an HMAC signature.
- ECDH. Go. In this case we create a symmetric key from ECDH. For this we will derive a shared key from the public key of Alice and Bob, and then define a single recipient which can derive the CEK (Content Encryption Key) using their private key. We will use the curves of P-256 (secp256r1), P-384 (secp384r1), P-521 (secp521r1) or SECP256K1 (as used with Bitcoin).
- RSA using COSE and CBOR. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\).
- RSA: dQ, dP and InvQ. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). The key pair also includes \(dQ\), \(dP\) and \(InvQ\), and these can be used with the Chinese remainder theory to optimize the decryption process.
Metasploit
- Armitage and Metasploit. Go.
- Exploiting Android with Metasploit. Go.
- Exploiting Android with Metasploit - Part 2. Go.
- Exploiting Windows/Mac OS X with Metasploit. Go.
- Remote Desktop Windows/Mac OS X with Metasploit. Go.
- Metasploit. Go.
- Internet of Things Security. Go.
- Metasploit (Enumeration and Scanning). Go.
- Metasploit (Malware). Go.
IP

 The following are a few interesting techniques around IP addresses:
The following are a few interesting techniques around IP addresses:
- Your details. IP. This shows your browser details.
- IP address analyser. IP. This involves converting an IP address to the host and network part of the address.
- IP subnet analyser. IP subnets. This involves converting an IP address to the host and network part of the address.
- IP address analyser. IP. This involves analysing IP addresses.
- Max subnets. Max subnets. This involves converting an IP address to the host and network part of the address.
- Route summarization. Summarization. This involves converting an IP address to the host and network part of the address.
- Whois. Whois. This does a basic Whois on a domain.
- URL Obfuscation. Obfuscation. This outlines URL obfuscation.
- HTTP Responses. Test. HTTP.
- Capturing Network Packets (Python). WinPCap. HTTP.
Cisco related
- Routing table. Routing table. This involves viewing a routing table for a Cisco device.
- ACL Generator. ACL. This involves a simple calculator for ACLs on network ranges.
- EIGRP metrics. EIGRP. Learn the basics of EIGRP metrics.
- VoIP B/W. VoIP. Calculate bandwidth for VoIP.
- Wild Card. Wild Card. On a Cisco device a wildcard mask is used to identify the parts of an IP address that need to be matched. It thus uses a wildcard mask, where a 0 in the bit position identifies that the device should match that bit, else a 1 shows that it should ignore it.
Protocols
- HTTP. HTTP. Show the request and response for HTTP.
- Ping analyser. IP. This involves converting a ping of a site.
IP Challenges
-
IP Test 1. IP Test. IP Classification test. This is a simple test which generates a range of IP addresses, and you must determine the IP address classification.
IP Subnet Challenge 1 Demo
-
IP Test 2. IP Test. IP Classification test Part 2. This test provides an address classification, and the user must find the addresses which are of this classification.
IP Subnet Challenge 2 Demo
-
IP Test 3. IP Test. IP Classification test Part 3. This test provides an address classification, where the network part of the address is determined.
IP Subnet Challenge 3 Demo
Subnet Challenges
- Subnet Test 1. Subnet Test. Subnet Test.
-
Subnet Test 2. Subnet Test. Subnet bits.
- Subnet Test 3. Subnet Test. Find the nth usable subnet. This test involves finding the nth usable subnet.
- Subnet Test 4. Subnet Test. Maximum subnets. This is a test page to determine the maximum number of subnets and hosts/subnet for IP classed addressing.
- Subnet Test 5. Subnet Test. Maximum host/subnet. This is a test page to determine the maximum number of hosts per subnet.
- Subnet Test 6. Subnet Test. Determine the required subnet mask for a given number of subnets. This is a test page to determine the required subnet mask for a given number of subnets and a given IP address classification.
- Subnet Test 7. Subnet Test. Determine the required subnet mask for a given number of host/subnet. This is a test page to determine the required subnet mask for a given number of hosts per subnet and a given IP address classification.
- Subnet Test 8. Subnet Test. Route summarization. This involves a calculation on route summarization.
- Subnet Test 9. Subnet Test. Binary to IP.
- Subnet Test 10. Subnet Test. Hex to IP.
-
Subnet Test 13. Subnet Test. Wild card mask network bits. Find the number of bits in the network part of the wild card mask. IP Wildcard challenge
- Subnet Test 14. Subnet Test. Wild card mask host bits. Find the number of bits in the host part of the wild card mask. IP Wildcard challenge
- Subnet Test 15. Subnet Test. Wild card mask ... find the network address. Find the network for the wild card mask. IP Wildcard challenge 2
- Subnet Test 16. Subnet Test. Find a matching IP address for a network and wild card mask. Find the IP for a network and a wild card mask.
- Subnet Test 17. Subnet Test. Find an address which is on a given network. Find an IP address on a network, for a given network address and subnet mask.
- Subnet Test 18. Subnet Test. Find an IP address on the same network. Find an IP address on the same subnet.
- Subnet Test 19. Subnet Test. Find subnet. Convert subnet mask.
- Megatest. Subnet Test. Challenging test for subnets.
JavaScript

JavaScript code allows execution within the browser, rather than on the server. It is often faster than code that runs on a server. Along with this we can also use Node.js, and which runs JavaScript code on a server.
Symmetric key
- AES. AES. In this example, we will use either a pre-generated key or a random one, and use AES (Rijndael) encryption.
- ChaCha20 and Poly1305. ChaCha. This page outlines Poly1305 and ChaCha20. ChaCha20 is a symmetric key method and Poly1305 is a message authentication code (MAC). They were created by Daniel J. Bernstein, and are alternatives to AES and HMAC.
- CMS (Padding). CMS. This page uses PKIJS encrypting on CMS. With CMS we can This document describes the Cryptographic Message Syntax (CMS). With this we can encapsulate an message within an encrypted entity.

Hashing
- Hash. Hash. This page defines a JavaScript Hash calculator. This uses a client-side JavaScript code to determine the hash signatures of a text value.
Signatures
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
- Boneh–Lynn–Shacham (BLS) signature. BLS. Boneh–Lynn–Shacham (BLS) signature method produces short signatures. They use elliptic curve pairing (and which are also known as bilinear maps).
Key exchange
- ECDH. ECDH. Elliptic Curve Diffie Hellman (ECDH) is used to generate a shared key. This implementation uses Elliptic Curve Cryptography (ECC) with JavaScript.
CryptoJS
- CryptoJS. CryptoJS. This page uses client-side JavaScript code to hashing, encrypt and sign, including for symmetric key (AES), streaming ciphers, hashing methods, and HMAC.
Blockchain
- PATRICIA trie. PATRICIA. In the following, we have the Top 2,500 Web sites in the world, and implemented with a Radix Trie (aka PATRICIA trie) In the following we have the Top 2,000 web sites on the Internet, and which have been indexed using the PATRICIA trie.
Public key
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
- RSA. RSA. RSA is an asymmetric encryption algorithm, which uses two keys, one to encrypt and the other to decrypt. It was created in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman, and is still one of the most widely used encryption methods. A typical application is in authenticating a sender, where the senders private key is used to encrypt a message, and then is decrypted by the receiver with the senders public key (which is known to anyone who wants it). It is also typically used for encrypting disks/files, such as for EFS.
Digital Certificates
- X.509 certificates in JavaScript. RSA and ECDSA Signed certificates. This page will generate either RSA and ECC key pairs, and then generate X.509 certificates, using either a signature of SHA1withRSA or SHA256withECDSA. For RSA signing we use an RSA private key to sign the certificate, and with ECDSA signing we use an ECC private key to sign the certificate.
Tokens
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
Random
- Random number generator. Rand. In the past, encryption and decryption had to be done through native code libraries, such as with Bouncy Castle and OpenSSL. With the increasing processing power of Web browsers, it is now possible to use encryption using JavaScript, which thus provides client-side processing of data. This Web page uses Javascript encryption, and generates a random 256-bit text key or a hex version. The 256-bit key is generated by generating 60 random numbers (from 0-25), and converting these to an ASCII character.
Malware obfuscation
- Malware obfuscation. Obfuscation. A malware writer will often hide certain keywords from the browser/human by encoding them in another format. This is typically done for hex coding (\xZZ), 16-bit unicoding (\uZZZZ) and octal coding (\ZZZ). To test, enter a value, and then press the button and it will convert encoded string.
Message Authentication Codes
- Chaskey (MAC). Chaskey. Chaskey Cipher is light-weight cryptography method for signing messages (MAC) using a 128-bit key. The hardware implementation only requires 3,334.33 gate equivalent with an operating clock frequency of 1 MHz (whereas Keccak requires 4,658 GE). In the page we create the Mac signature and also encrypt for CBC.
Other
- Password generation/hashing. Hashing. Linux can use salted passwords where the username, hashing method and hashed password are stored in a password file [More details]. The main methods are
Hashing

At times we need to generate secrets, such as encryption keys, from passwords or nonce values. A Key Derivation Function (KDF) is a verifiable way of doing this.
Key Derivation Functions (KDFs)
The following are the tips related to hashing:
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Password strength. Test. This outlines the strength of various passwords types.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
HKDF
The following are the tips related to Key derivation hashing:
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Hazmat HKDF for different hashing methods. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
-
HKDF key derivation with OpenSSL [
here]
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
PBKDF2
The following are the tips related to Key derivation hashing:
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- AES GCM (Python) with PBKDF2. AES GCM (Python) with PBKDF2.
- Fernet with PBKDF2 . AES GCM (Python) with PBKDF2.
- PBKDF2 key derivation. AES GCM (Python) with PBKDF2.
- Key Rotation with Fernet. AES GCM (Python) with PBKDF2.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Bcrypt
The following are the tips related to Key derivation hashing:
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- BCrypt. BCrypt. BCrypt with Rust.
-
Hash to password with Go. Hashing to Argon2, Scrypt and BCrypt. Hash to password with Go, including Argon2, Scrypt and BCrypt.
scrypt
- scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Argon 2
The following are the tips related to Key derivation hashing:
- Argon 2. Go. Outline of Argon2.
- Argon 2 with NaCl. Go. Outline of Argon2 using NaCl.
- Argon 2. Argon 2. Argon 2 with Rust.
- Balloon. Go. Outline of Balloon.
Other
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
- Double ratchet. Go. Outline of double ratcheting.
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
Outline
HMAC Key Derivation function (HKDF) is used to derive an encryption key from a passphrase. Initially, HKDF creates a pseudorandom key (PRK) using a passphrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), and along with a salt value. Next, the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys [RFC 5869][article]. In this case, we will use SHA-256.
The following shows how an encryption key can be generated using HKDF, and where we need a secret and a salt value. Both Bob and Alice have the same secret and salt.

With PBKDF2 (Password Based Key Derivation Function 2), we hash for a given number of rounds:

Key exchange

Key exchange is a way for Bob and Alice to communicate and for them to agree on a shared secret. The original method defined uses discrete logarithms (Diffie-Hellman), but most modern methods use elliptic curve techniques (ECDH). As quantum computers can crack both discrete log and elliptic curve methods, there are post quantum cryptography methods proposed. This includes SIDH, CSIDH, SIKE, and NewHope.
Key interchange/generation (Diffie-Hellman)
The following relates to key interchange:
- Selecting \(g\) in Diffie Hellman. G in Diffie Hellman. Picking a safe value of the generator \(g\) in discrete logarithms.
- Diffie-Hellman. Diffie-Hellman Calculation. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Real example). Diffie-Hellman Real. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Python). Diffie-Hellman. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (pre-compute). Diffie-Hellman (pre-compute). Many sites use the same prime numbers, which can then be cracked with a pre-computing attack.
- Key generation. Key gen. This will generate keys for different methods based on a passphrase.
- Diffie-Hellman (Man-in-the-middle). DF. This outlines the man-in-the-middle method for Diffie-Hellman.
- An Alternative Diffie-Hellman method. Alterative DH. This outlines an alternative Diffie-Hellman method.
Authenticated Key Exchange
The following are the tips related to Key derivation hashing:
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- MTI/A0. MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{ax+by} \pmod p\). MTI (Matsumoto, Takashima, Imai).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0. MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{x+y} \pmod p\)
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). The resultant key is \(xyG \)
- MTI/C0. MTI/C0. This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{xy} \pmod p\)
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG\).
- MTI/C1. MTI/C1. This outlines MTI/C1, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{abxy} \pmod p\).
- MQV (Menezes–Qu–Vanstone). MQV. MQV was created Alfred Menezes, Minghua Qu and Scott Vanstone in 1995 and is an authenticated key exchange method. Alice holds a key pair \((A,a)\) and Bob has a key pair \((B,b)\). With this \(a\) is Alice's private key, and \(A=aG\) is her public key. For Bob, his public key will be \(B=aG\) and a private key of \(b\), and where \(G\) is the base point on the elliptic curve.
- HMQV (Menezes–Qu–Vanstone). HMQV. HMQV builds on MQV and adds the identity of Bob and Alice.
- ECDH with X25519 and Blake2b. ECDH with X25519 and Blake2b. This uses PyNaCl to create an authenticated key exchange and uses X25519 and Blake2b.
Elliptic Curve (ECDH) - Python
The following are the tips related to ECC:
- Elliptic Curve. Elliptic Curve. Elliptic Curve is a public key method which can also be used to generate a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with simple parameters. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
Elliptic Curve (ECDH) - Golang and Node.js
The following are the tips related to ECC:
- ECDH with Go. ECDH. ECDH with Go.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with node.js. ECDH. ECDH with node.js.
- ECDH with JavaScript. ECDH. Elliptic Curve Diffie Hellman.
Password Authenticated Key Exchange (PAKE)
The following are the tips related to Key derivation hashing:
- SPAKE2. Go. Outline of SPAKE2.
- OPAQUE. Go. Outline of OPAQUE.
- SPEKE. Go. Outline of SPEKE (Simple Password Exponential Key Exchange).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
- J-PAKE. J-PAKE. This example generates a shared key based on a shared password.
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses discrete logs.
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
PQC NIST Finalists (Key Exchange)
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Key interchange/generation (Other)

The following relates to key interchange:
- Curve25519. Curve25519. This outlines Curve25519, which is used in the Tor network.
- Authenticated Key Exchange (Discrete logs). YAK. Key exchange with public keys and uses discrete logs.
- Authenticated Key Exchange (ECC). YAK. Key exchange with public keys and uses elliptic curve methods.
- Shamir No-key protocol. Shamir No Key. In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated.
- Shamir No-key protocol (sepc256k1). Shamir No Key (EC). In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated using the sepc256k1 elliptic curve.
- Conference keying (Burmester-Desmedt method). Conference keying. In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it.
- Conference keying (Burmester-Desmedt method) - Elliptic Curve (sepc256k1). Conference keying Elliptic Curve (sepc256k1). In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it, and uses the sepc256k1 elliptic curve.
Key exchange (with pairing)
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Kryptology

We need to build a new Internet. One that is build on mathematics and certainty, rather than the patchy version we have now. For this we need a layer of cryptography at the lowest level, and build software interfaces on top of this. Along with this we now have cryptographic methods which can now provide a foundation of trust, and which preserve privacy. And so the old libraries of OpenSSL are being squeezed out in favour of the new ones which are built on a solid foundation. The latest of these new "privacy-aware" libraries is Kryptology, and created by Coinbase. This library provides the APIs that developers need, in order to apply to areas of blockchain development. This library include BLS (Boneh-Lynn-Shacham) signatures, Zero-knowledge Proofs (ZKPs) and Shamir Secret Shares (SSS). With BLS we can digitally sign for data, but also preserve its privacy. Applications of this include group signatures, where multiple entities can merge their signing keys together and provide a single signature for a transaction. With SSS, we can split encryption keys up into shares, and then distribute them across a network. When required, we can call these shares back to reconstruct the key.
The focus for Coinbase seems to be the application of privacy coins, and where no tracking can be applied to the usage of these digital coins. This should support full anonymity for transactions, as opposed to Bitcoin which only supports pseudo-anonymity.

ECC Basics
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining n.G for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Points (Base Point and Others). Elliptic Curve points. Two common curves used in ECC (Elliptic Curve Cryptography) are secp256k1 (as used in Bitcoin and Ethereum) and P256 (secp256r1). The "k1" refers to the Kolbitz curve 1 (named after the creator of ECC). With these we have a base point which are can operate on. This is typically defined as \(G\). We can then operate on this with add and multiply operation. For example, \(2G=G+G\) and \(P=n.G\). In this following we will show the base point for a number of common curves, such as secp256r1, P256, Pallas, Curve 25519, BLS12381G1, BLS12381G2, BLS12377G1 and BLS12377G2.
ECDH
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret. We will use Golang and the Krytology library.
Simple ECC on curves
- Public key points for curves. Simple. Display public key points for scalars.
BLS Curve
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
Accumulator and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
Pallas Curve
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
Pairing-based Crypto
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
ElGamal and ECC
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a numerical input.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
Shamir Secret Shares
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Homomorphic Encryption
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Zero knowledge proofs
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
Verifiable Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Hash to scalar and point
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
CP-ABE
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Lattice cryptography

Latice cryptography is proposed as a post-quantum robust method for public key encryption, especially focused on digital signatures and key exchange mechanisms (KEMs).
Principles
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
NTRU
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- Lattice Encryption: NTRU Key Generation Python). NTRU. Outlines how NTRU operates for key generation.
Homomorphic
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Digital Signatures
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
Public-Key Encryption/Key Exchange
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
Light-weight cryptography

While AES and SHA work well together within computer systems, they struggle in an IoT/embedded world as they take up: too much processing power; too much physical space; and consume too much battery power. So NIST outlines a number of methods which can be used for light-weight cryptography, and which could be useful in IoT and RFID devices [1]. They define the device spectrum as:
- Conventional cryptography. Servers and Desktops. Tablets and smart phones.
- Light-weight cryptography. Embedded Systems. RFID and Sensor Networks.
With embedded systems, we commonly see 8-bit, 16-bit and 32-bit microcontrollers, and which would struggle to cope with real-time demands for conventional cryptography methods. And in the 40+ years since the first 4-bit processor, there is even a strong market for 4-bit processors. RFID and sensor network devices, especially, have limited numbers of gates available for security, and are often highly constrained with the power drain on the device.
So AES is typically a non-starter for many embedded devices. In light-weight cryptography, we often see smaller block size (typically 64 bits or 80 bits), smaller keys (often less than 90 bits) and less complex rounds (and where the S-boxes often just have 4-bits).
For light-weight cryptography the main constraints that we have are typically related to ener requirements, gate equivalents (GEs), and timing. With passive RFID devices, we do not have an associated battery for the power supply, and where the chip must power itself from energy coupled from the radio wave. An RFID device is thus likely to be severely constrained in the power drain associated with any cryptography functions, along with being constrained for the timing requirements and for the number of gates used. Even if an RFID device has an associated battery (active RFID), it may be difficult to recharge the battery, so the drain on power must often be minimised.
There is thus often a compromise between the cryptography method used and the overall security of the method. Thus often light-weight cryptography methods balance performance (throughput) against power drain and GE, and do not perform as well as main-stream cryptography standards (such as AES and SHA-256). Along with this the method must also have a low requirement for RAM (where the method requires the usage of running memory to perform its operation) and ROM (where the method is stored on the device). In order to assess the strengths of various methods we often define the area that the cryptography function will use on the device – and which is defined in \(µm^2\). The NIST finalists are defined in this [article]
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- GIFT AEAD. GIFT. GIFT is a light-weight block cipher. It is a (NIST Finalist)
- Elephant. Elephant. Elephant is a light-weight stream cipher. It is a (NIST Finalist).
- TinyJambu. TinyJambu. TinyJambu is a light-weight block cipher. It is a (NIST Finalist)
- Isap AEAD. Isap. Isap is a light-weight block cipher. It is a (NIST Finalist)
- PHOTON-Beetle AEAD. PHOTON-Beetle. PHOTON-Beetle is a light-weight block cipher. It is a (NIST Finalist)
- Romulus AEAD. Romulus. Romulus is a light-weight block cipher. It is a (NIST Finalist)
- Sparkle AEAD. Sparkle. Sparkle is a light-weight block cipher. It is a (NIST Finalist)
- CLEFIA. CLEFIA. CLEFIA is a light-weight block cipher.
- LED. LED. LED is a light-weight block cipher.
- Piccolo. Piccolo. Piccolo is an ultra light-weight block cipher.
- PRESENT. PRESENT. Present is a light-weight block cipher.
- Pyjamask. Pyjamask. Pyjamask is a light-weight block cipher.
- SIMON. SIMON. SIMON is a light-weight block cipher.
- SKINNY. SKINNY. SKINNEY is a light-weight block cipher.
- SPECK. SPECK. SPECK is a light-weight block cipher.
- XTEA. XTEA. XTEA is a light-weight block cipher.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encryption/Decryption. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.
Light-weight crypto (Other)
- Chaskey (MAC). Chaskey. Chaskey is a light-weight MAC function.
- Chaskey (MAC). Chaskey (Python). Chaskey is a light-weight MAC function.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (ASCON)
ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRFF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
Discrete Logs (Solving)

A discrete log problem is in the form of \(g^x \pmod p\) and where we know \(g\) and \(p\) and must solve for \(x\).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Message Authentication Code (MAC)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
HMAC
The following are the tips related to Key-based hashing:
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authentication both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2), Blake2b, SM3 and SHA-3. This page outlines the HMAC-MD5 methods using the Hazmat cryptography layer.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- HMAC (COSE). Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT with HMMAC. Go. In this case we create a CWT token, and sign with an HMAC signature.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- HMAC with Rust. HMAC. HMAC with Rust.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HMAC with OpenSSL. MACs with OpenSSL. HMAC in OpenSSL for a given input value, password and hashing method.
Cipher MACs
The following are the tips related to Key-based hashing:
- MACs with OpenSSL. MACs with OpenSSL. MAC methods implemented in OpenSSL, including CMAC and GMAC.
Key-based hashing
The following are the tips related to Key-based hashing:
- SipHash. Siphash. Siphash is a fast key-based hashing method.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Meow. Meow. Meow is one of the fastest hashing methods.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
Magic Numbers

This pages contains information related to magic numbers in file formats.
Network and File Forensics
- Magic numbers. Magic. This provides information on magic number for file forensics.
Graphics formats
- JPEG Analysis. JPEGs. This provides an analysis of JPEG files.
- GIF Analysis. GIFs. This provides an analysis of GIF files.
- TIF Analysis. TIFs. This provides an analysis of TIF files.
- PNG Analysis. PNGs. This provides an analysis of PNG files.
- BMP Analysis. BMPs. This provides an analysis of BMP files.
- PSD Analysis. PSDs. This provides an analysis of PSD files.
- WMF Analysis. WMF. This provides an analysis of WMF files.
- Adobe Illustrator Analysis. AI. This provides an analysis of AI files.
- Adobe In Design Analysis. INDD. This provides an analysis of INDD files.
- MIDI file. MIDI. This provides an analysis of MID files.
- ICO file. ICO. This provides an analysis of ICO files.
- PS file. PS. This provides an analysis of PS files.
- EPS file. EPS. This provides an analysis of EPS files.
- VSD file. VSD. This provides an analysis of Microsft Visio (VSD) files.
Video and audio formats
- MP3 Analysis. MP3s. This provides an analysis of MP3 files.
- AVI Analysis. AVIs. This provides an analysis of AVI files.
- Flash SWF Analysis. SWFs. This provides an analysis of Flash files.
- Flash FLV Analysis. FLVs. This provides an analysis of FLV files.
- MP4 Analysis. MP4. This provides an analysis of MP4 files.
- MOV Analysis. MOV. This provides an analysis of MOV files.
- WMV Analysis. WMV. This provides an analysis of WMV files.
- WMA Analysis. WMA. This provides an analysis of WMA files.
- JPEG 2000 Analysis. JPEG 2. This provides an analysis of JPEG 2000 files.
- WAV Analysis. WAV. This provides an analysis of WAV files.
Zips, Archives and Library files
- ZIP/Archive Analysis. ZIPs. This provides an analysis of ZIP/Achive files.
- GZ Analysis. GZ. This provides an analysis of GZip files.
- Tar Analysis. Tar. This provides an analysis of TAR files.
- MSI Analysis. MSI. This provides an analysis of MSI files.
- OBJ Analysis. OBJ. This provides an analysis of OBJ files.
- DLL Analysis. DLL. This provides an analysis of DLL files.
- CAB Analysis. CAB. This provides an analysis of CAB files.
- EXE Analysis. EXE. This provides an analysis of EXE files.
- RAR Analysis. RAR. This provides an analysis of RAR files.
- SYS Analysis. SYS. This provides an analysis of SYS files.
- HLP Analysis. HLP. This provides an analysis of HLP files.
- VMDK Analysis. VMDK. This provides an analysis of VMDK files (VMWare Virtual Disks).
- PST Analysis. PST. This provides an analysis of PST files (Outlook Email File).
- JAR Analysis. JAR. This provides an analysis of JAR files.
- SLN Analysis. SLN. This provides an analysis of Microsoft SLN files.
- Class Analysis. Class. This provides an analysis of Java Class files.
- Zlib. Zlib. This provides an analysis of Zlib files.
Documents
- PDF Analysis. PDFs. This provides an analysis of PDF files.
- DOC Analysis. DOCs. This provides an analysis of DOC files.
- RTF Analysis. RTFs. This provides an analysis of RTF files.
- XLS Analysis. XLSs. This provides an analysis of XLS files.
- PPT Analysis. PPTs. This provides an analysis of PPT files.
- MMP File. MMP. This provides an analysis of MMP files.
- DOCX Analysis. DOCX. This provides an analysis of DOCX files.
- XLSX Analysis. XLSX. This provides an analysis of XLSX files.
- PPTX Analysis. PPTX. This provides an analysis of PPTX files.
- MDB Analysis. MDB. This provides an analysis of MDB files.
- Outlook Message Analysis. MSG. This provides an analysis of MSG files.
Disk Image
- Raw disk format. RAW. This provides an analysis of the RAW disk format.
Tests
- File Forensics Test. File Test File Forensics Test.
- File Forensics Test (Fun). File Test (Fun) File Forensics Test.
Presentations
MIRACL Core Library

MIRACL Core is an open source library, and includes a wide range of public key encryption methods. It is especially focused on elliptic curve and pairing-friendly methods, but also supports a wide range of encryption methods, including RSA, AES and hashing. Overall, it can be ported onto a wide range of systems and supports C, C++, Go, Rust, Python, Java, Javascript and Swift. Along with this it supports limited capability devices such as the Arduino infrastructure. The GitHub repository is [here].
BN254
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.

Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- CL Signatures. CL. CL Signatures in Go using MIRACL.
- CL Signatures (advanced pairing). CL. CL Signatures in Go using MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages using MIRACL.
- PS Signatures. PS. Signatures using PS for short signatures using MIRACL.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures using MIRACL.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.

Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
Rust examples
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
NaCl

PyNaCl is a Python port of LibSodium. It integrates the latest cryptography methods, such as AES, XChaCha20, Blake2b and X25519.
Symmetric Key
- Symmetric key. Symmetric key (XChaCha20 and Poly1305). With symmetric key, Bob and Alice have the same key. NaCl uses the XChaCha20 method, and which supports stream encryption (and which does not require padding as a block cipher does, and is also faster than block cipher modes). ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16 byte nonce. XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24 byte nonce. It has a lower propability of nonce misuse than ChaCha20.
- Encryption with a password. Symmetric Key with KDF. In symmetric key, we generate a secret key. This key is typically a random value or generated from a password and a salt value. If we use a password, we typically use a KDF (Key Derivation Function), and which uses a password and a salt value, in order to create a key of a given size. In this case we will use Argon2i, and which is memory resilent.
Hybrid Encryption
- Box. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Hashing
- Hashing and KDF (Argon2 and scrypt). Hashing and KDF. This case we will use PyNaCl (Networking and Cryptography) library, and which is a Python binding to libsodium. We will hash a password using SHA-256 and SHA-512, and also create a KDF (Key Derivation Function) using scrypt and Argon2.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
Ed25519
-
Ed25519. Ed25519. Using Ed25519 for digital signatures.
-
Finding Points on Ed25519. X25519 (Points).
In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 (Key Exchange)
- X25519 + BLAKE2b key-exchange. X25519. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
Curve 25519
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
Node.js

Node.js uses the JavaScript programming langauge as its base, and allows for code to be run on a server, rather than in the browser (such as with pure JavaScript). To run a node.js program, we run "node myfile.js", and use NPM to install libraries.
Symmetric key
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
RSA and public key
- RSA Opt imal Asymmetric Encryption Padding (OAEP) using Node.js. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
ECC Keys
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.

Hashing
- Hashing with node.js (All). Hashing. Hashing with node.js.
- Hashing with node.js (Selection). Hashing. Hashing with node.js.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- ECDSA with node.js. ECDSA. ECDSA with node.js.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
Key exchange
- Diffie-Hellman with node.js (random prime). DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method and uses a randomly generated prime number (press the button to generate a new prime).
- Diffie-Hellman with node.js. DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method. Each time the prime number will be fixed for the DH group selected.
- ECDH with node.js. ECDH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Elliptic Curve Diffie Hellman (ECDH) key exchange method.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
Key derivation
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
CryptoJS
- CryptoJS (in node.js). CryptoJS (Node.js). Various crypto methods in the browser.
Bulletproofs
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
Blockchain
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
Proxy encryption
- Proxy Encryption - Encrypting With Public Key, And Decrypt with Private Key. Proxy01. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This page just creates a key pair for Alice, and uses it to encrypt with the public key , and decrypt with the private key.
- Proxy Encryption. Proxy02. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This will go through the full use case of proxy re-encryption.
Tokens
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
Random
- Fortuna with node.js. Fortuna. Fortuna random numbers with node.js.
Other
- FPE with node.js. FPR. FPE with node.js.
- Puny with node.js. Puny. Puny character format with node.js.
Accumulators and Witnesses
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
PGP
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Password Entropy
- Password Entropy with Node.js. Password Entropy. Password entropy measures the strength of a password, and is measured as the number of bits which could represent all of the possibilities. An entropy score of less than 25 identifies a poor password, and between 25 and 50 is a weak password. For 50 to 75 we have a reasonable password, and between 75 and 100 is a very good password. Over 100 is an excellent password. The strength of the password relates to the number of characters used, and also the number of characters in the password.
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
- Homomorphic Encryption with Node.js and BGV. Homomorphic Encryption with Node.js and BFG. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BGV method.
Oblivious Transfer (OT)

Oblivious Transfer allows Bob to select data from Alice, but for Alice not to know which value has been selected.
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
OpenSSH

OpenSSH supports the usage of the SSH protocol. This allows for a remote login. One tool which is uses is ssh-keygen, and which allow for the generation of RSA, DSA and elliptic-curve keys that. These can be used for user and host authentication, such as for GitHub login and Cloud instance login.
OpenSSH
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here].
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
Outline

OpenSSL

OpenSSL is a standard library that implements cryptography.
Symmetric key (Command line)
-
Symmetric Key Encryption (OpenSSL 1.x) [here]. In this case we will create cipher text from OpenSSL 1.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 1.x) [here].In this case we will decrypt cipher text from OpenSSL 1.x using a key derived from a password
-
Symmetric Key Encryption (OpenSSL 3.x) [here]. In this case we will create cipher text from OpenSSL 3.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 3.x) [here].In this case we will decrypt cipher text from OpenSSL 3.x using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password.
Hashing
-
Hashing [here] OpenSSL supports a wide range of hashing methods including BLAKE2b, Gost, MD4, MD5, RMD-160, SHA-1, SHA-3, SHA-256 and SHA-512.
Libre OpenSSL
-
Symmetric Key Encryption using Libre OpenSSL [here]. In this case we will create cipher text from Libre OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption using Libre OpenSSL [here]. In this case we will decrypt ciphertext from Libre OpenSSL using a key derived from a password.
-
Hashing [here] Libre OpenSSL supports a wide range of hashing methods including Gost, MD4, MD5, RMD-160, SHA-1, SHA-256 and SHA-512.
Diffie-Hellman parameter generation
-
DH Parameters with OpenSSL [here]. The Diffie-Hellman (DH) method is perhaps one of the greatest inventions in Cybersecurity, and was created by Whitfield Diffie and Marty Hellman. With the DH method, Bob creates a random value (\(b\)) and Alice also creates a random value (\(a\)). Next Bob computes \(B=g^b \pmod p\) and sends it to Alice. Alice computes \(A=g^a \pmod p\) and sends this to Bob. Bob raises the value of \(A\) to the power of \(b\) and takes \(\pmod p\), and Alice raises \(B\) to the power of \(a\) and takes \(\pmod p\). In the end, they will have the same shared value: \(g^{ab} \pmod p\). This can then be used to derive an encryption key that they can use for a secure tunnel. Overall, \(p\) is the large prime number, and also known as the shared modulus between Bob and Alice.
Key derivation function
-
PBKDF2 key derivation with OpenSSL [here] PBKDF2 (Password Key Derivation Function 2) is a key derivation method. Overall it is relatively slow in its operation and where we take a password, a salt value, hashing method, and a number of iterations, in order to produce a given size of encryption key.
-
HKDF key derivation with OpenSSL [here] HKDF (HMAC Key Derivation function) is used to derive an encryption key from a pass phrase. Initially HKDF creates a pseudorandom key (PRK) using a pass phrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), andalong with a salt value. Next the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys.
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Passwords
-
Password example [here]. This page uses the OpenSSL library hash password generator, which is used in UNIX systems for the hashing of passwords which are contained in /etc/shadow and /etc/passwd. For newer passwords, the "-1" options is used to created the hashed value.
-
Hashed passwords with OpenSSL [here].
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
Public key
-
Generating an ECC key pair with OpenSSL [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)).
-
Generating an RSA key pair with OpenSSL [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2).
-
Generating an RSA key pair with OpenSSL with encryption [here]. This page implements RSA key pair generation with an encrypted key pair. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). In this case we will encrypt the key pair with either 3DES, 128-bit AES, 192-bit AES or 256-bit AES. The same password must be used to encrypt and decrypt.
-
Generate prime with OpenSSL [here]. Prime numbers are important in public key encrytion, and are used with RSA and ECC. For RSA, we generate two prime numbers (\(p\) and \(q\)) and which are multiplied together to create a modulus (\(N\)). If these prime numbers have 512 bit values, the modulus will be a 1,024 bit value. This defines the basic secure of RSA. With elliptic curve we use smaller prime numbers, such as 256-bit values for the secp256k1 curve.
ASN1 parsing
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). We will parse using asn1parse, and reveal the parameters.
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)) [RSA key pair]. We will parse using asn1parse, and reveal the parameters.
- DSA Parameters with asn1parse. DSA parameters with OpenSSL with asn1parse. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA (Digital Signature Algorithm)
- DSA Parameters. DSA parameters with OpenSSL. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
MAC (Message Authentication Code)
- HMAC with OpenSSL. MACs with OpenSSL. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authenticate both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2) and SHA-3. In this case we will use OpenSSL to generate the HMAC value.
- MACs with OpenSSL. MACs with OpenSSL. In the following we will generate MACs for HMAC, GMAC, CMAC, Blake2bmac, Blake2smac, KMAC128 and KMAC256. Overall, we will use an encryption key defined as a hex value for GMAC and CMAC, and a pass phrase for the others. The message is "hello".
Signing
- Digital signing a plaintext message with OpenSSL. Signing with OpenSSL. With digital signing, we can take a message, and create a signature. This normally involves signing with a private key and digital certificate. The signed message can be an a MIME format, and which can be integrated into an email message. In this can we have a 512-bit RSA key pair that will sign a plain text message.
Encrypting emails
- Encrypting an email message in OpenSSL. Encrypting messages with OpenSSL. With public key encryption, we can take a message, and encrypt it with the recipiant's public key. In this can we have a 512-bit RSA public key to encrypt a message.
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Random number generation with OpenSSL
-
Random number generator [here]. Random numbers are important in generating encryption keys and salt values. In this case OpenSSL generates a random number (in a Base64 format) for a given number of bytes.
Outline (C#/Python)
-
Symmetric Key Encryption (C#) [here]. This page uses the OpenSSL library through a C#/.NET wrapper. The DLLs it interfaces to are libeay32.dll and ssleay32.dll. OpenSSL supports a wide range of encryption methods, including 128-bit AES, 192-bit AES, 256-bit AES and Blowfish (bf). Different modes of ECB, CBC, and OFB are implemented. The examples use a default IV of "1234".
-
AES in Python with OpenSSL output [here]
-
Producing OpenSSL AES Encrypted String from C# [here]
Digital Certificates
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
Paillier - Partial Homomorphic Encryption

The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Fundamentals
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier).
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Using RSA
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
Applications
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.

Go Kryptology
- Public key points for curves. Simple. Display public key points for scalars.
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.

Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.

Principles
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Paillier
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
Go Format Preserving Encryption (FPE)
- FPE with Go. FPE. An implementation of Format Preserving Encryption (FPE) for FFX1 and FFX3.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
AWS Encryption
- AWS Symmetric Key Encryption. AWS (Symmetric key). Using symmetric key in AWS.
Go Oblivious Transfer
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Dragon Fly
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
Embedding data in an ECC point
- Embedding data in a point. Go. With Elliptic Curve Cryptography (ECC), we use points on an elliptic curve to represent our data. These are defined with (x,y) points. With this, it is possible to embedded a certain amount of data into the point - as long as it still gives us a valid point on the curve. This example will Curve 25519 to embed data, and is achieved by storing the length of the data in a single byte in the point, and then store the data as byte values in the point (followed by random data). To decode, we can then just read the first byte for the length of the message, and then reveal the data encoded into the point..
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Hashing (Cryptographic)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
Benchmarks and Password strength
The following are the tips related to hashing:
- Password strength. Test. This outlines the strength of various passwords types.
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
Theory
The following are the tips related to hashing:
- Balls in bins. BiBa. This implemented balls in bins.
- Birthday attack (with Big Integers). Calc. This provides a simple example of the birthday attack.
- Birthday attack. Calc. This provides a simple example of the birthday attack.
- Differential Cryptanalysis (Hashing). Cryptanalysis. This provides an implementation of differential cryptanalysis for hashing methods.
MD5, SHA-1
The following are the tips related to hashing:
- MD2 and MD4 MD2/4. The MD2 and MD4 hashing functions were developed by Prof Ronald Rivest in 1989 and 1990, respectively. They both produce a 128-bit hash, but have been shown be vulnerable to attack (see the Collision section in the page).
- MD5 and SHA-1 (to Base-64) with salt Salt. It is possible to add salt to the MD5 algorithm, to mix it up a little.
- MD5 and SHA-1 (to Base-64) Hash. MD5 and SHA-1 produces a hash signature, and the output is typically shown in a hex format or a Base-64. In this example the output is converted into a Base-64 format.
- MD5 and SHA-1. Hash. MD5 and SHA-1 methods produce a hash signature, and are the two of the most widely used methods. The MD5 algorithm has been shown to have weaknesses, and a collision of message hashes has been shown to occur in less than one day. An MD5 signature has 128 bits, an SHA-1 signature has 160 bits, and an SHA-256 signature has 256 bits.
- MD5 Cracking. Hash Cracker. MD5 has a 128-bit signature and can be cracked using rainbow tables. This page tries to crack the MD5 signature.
- Hashing with Go. Hashing. Hashes with Go.
- Detecting hash types. Hash type. This detects has values.
- OpenSSL hashing. Range of methods. Outlines the methods used in OpenSSL
- Hash. Hash. Hashing using JavaScript
- Hashing with node.js. Hashing. Hashing with node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Hashing methods
-
Hazmat Hashes. Hazmat Hashes. This includes the hashing methods in the Hazmat cryptography library. This includes Blake2p, Blake2s, MD5, SHA1, SHA224, SHA256, SGA384, SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHA512, SHA512-224, SHAKE128 and SHA256.
-
Hazmat Hashes. Hazmat Hashes. In this case we will implement Python code to determine SHA1, SHA2, SHA3, Blake2, MD5 and SM3 hashes.
OpenSSL Passwords
-
Password example [here]
-
Hashed passwords with OpenSSL [here]
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Blake 3 hashes
The following are the tips related to similarity hashing:
- Blake 3 in Python. Hashing. Blake 3 hashing.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
Other Hash functions
The following are the tips related to hashing:
- Bloom Filter Bloom filter. A Bloom filter goes a probabilistic method of determining if an element is in a data structure, using indexed hashing methods.
- Cuckoo Table Cuckoo filter. A Cockoo table uses two hash funtions.
- Chaffing. Chaffing. This produces a keyless system.
- GP Hashing with Go. GP Hashing. GP Hashes with Go.
- LDAP. LDAP. This produces a LDAP hash signature for a password.
- LM Hash. LM Hash. This is an LM Hash Calculator. LM Hash is used in many versions of Windows to store user passwords that are fewer than 15 characters long.
- Murmur and FNV Murmur and FNV. While hashing methods such as MD5 and SHA-1 use crypto methods, the Murmur and FNV hashes uses a non-cryptographic hash function. This can be used for general hash-based lookup and was designed by Austin Appleby. It has good performance compared with other hashing methods.
- Pearson. Pearson. This uses a non-crypto hash.
- phpass. phpass. This produces a phpass hash signature for a password.
- Tiger. Tiger. Tiger is a 192-bit hash function and was designed by Ross Anderson and Eli Biham in 1995. It is often used by clients within Gnutella file-sharing networks and does not suffer from known attacks on MD5 and SHA-0/SHA-1. Tiger2 is an addition, in which the message is padded with a byte of 0x80 (in a similar way to MD4, MD5, and SHA), whereas in Tiger it is 0x01. Otherwise, the two methods are the same in their operation.
- Whirlpool. Whirlpool. Whirlpool is a 512-bit cryptographic hash function and was created by Vincent Rijmen (one of the AES creators) and Paulo Barreto, in 2000.
- WPA-2 hash . WPA-2 hash. Implements SHA-2 hash.
- Reusable hash collisions. Reusable hash collisions. Reusable hash collisions.
- The Length Extension Attack. Length Extension Attack. The MD construct has many weaknesses, and one of the most serious is the length extension attack. With this an adversary (Eve) can take a hash for an unknown message, and then add additional data to produce a new valid hash. The hash methods which are at risk against the length extension attack are MD5, SHA-1 and SHA-256. Please follow the code link below to run an example.
- Consistent hashing. Consistent hash. This outlines the usage of Consistent hashes.
- ROR13 (Module and Function). ROR13. With ROR13 we take each 8-bit character and then convert to a unicode value (with 16 bits). Then for each character we rotate the bits right by thirteen places. The resultant hash is then just the accumuluation of the rotated values.
- ROR13 (Function). ROR13 (Function). With ROR13 we take each 8-bit character and then convert to a unicode value (with 16 bits). Then for each character we rotate the bits right by thirteen places. The resultant hash is then just the accumuluation of the rotated values.
- GOST, Streebog256 and Streebog512. GOST, Streebog256 and Streebog512. GOST94 is a hashing method developed with Euro-Asian Council for Standardization, Metrology and Certification (EASC). This has since been developed in the Streebog256 and Streebog512 hashing method. In this case, we will use Libre OpenSSL to convert data into a hashed value.
RIPEMD
- RIPEMD (RACE Integrity Primitives Evaluation Message Digest) and GOST. RIPEM160. RIPEMD is a 128-bit, 160-bit, 256-bit or 320-bit cryptographic hash function, and was created by Hans Dobbertin, Antoon Bosselaers, and Bart Preneel. It is used on TrueCrypt and is open source. The 160-bit version is seen as an alternative to SHA-1, and is part of ISO/IEC 10118
- RIPEMD160. RIPEM160. RIPEMD160 is a 160-bit cryptographic hash function, and was created by Hans Dobbertin, Antoon Bosselaers and Bart Preneel. RIPEMD160 is used in Bitcoin applications.
Chameleon hashes
The following are the tips related to Chameleon hashing:
- Chameleon hash in Golang Chameleon. With a Chameleon hash, we have a normal hash value which is resistant to collisions, but with a known secret we can easily create a collision. The concept was first defined by Krawcyk and Rabin.
Similarity hashes
The following are the tips related to similarity hashing:
- Similarity hash: SimHash (Charikar similarity) in Python Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash (Nilsimsa similarity) Nilsimsa. The Nilsimsa similarity is used to find similarities between spam emails.
- Minhash (Jaccard similarity) Jaccard similarity. The Minhash method is used to find similarities between strings, files and metadata.
- String enthropy String enthropy. Measurement of the entropy of strings.
- Counting identical elements (HyperLogLog) HyperLogLog. Counting the number of identical elements.
SHA-3 and SHA-3 contenders
The following are the tips related to Key derivation hashing:
- Blake and Blake 2. Blake. Implements Blake and Blake 2 (SHA-3 contender).
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
- Grøstl. Grøstl. Implements Grøstl (SHA-3 contender).
- KangarooTwelve. KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- SHA-3, Keccak and SHAKE . SHA-3. Implements SHA-3, Keccak and SHAKE (SHA-3 winner).
- SHA-3. SHA-3. SHA-3 was known as Keccak and is a hash function designed by Guido Bertoni, Joan Daemen, Michaël Peeters, and Gilles Van Assche. MD5 and SHA-0 have been shown to be susceptible to attacks, along with theoretical attacks on SHA-1. NIST thus defined there was a need for a new hashing method which did not use the existing methods for hashing, and setup a competition for competing algorithms. In October 2012, Keccak won the NIST hash function competition and is proposed as the SHA-3 standard. It should be noted that it is not replacement SHA-2, which is currently a secure method. Overall Keccak uses the sponge construction where the message blocks are XORed into the initial bits of the state, and then inevitably permuted.
- cSHAKE. cSHAKE. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS. With the SHA-3 hashing method, we have four different cryptographic hashing methods (SHA3-224, SHA3-256, SHA3-384, and SHA3-512) and two XOF functions (SHAKE128 and SHAKE256). With SHAKE128 and SHAKE256 we can integrate domain separation between different functions — and which are known as cSHAKE128 and cSHAKE256.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- Skein. Skein. Implements Skein (SHA-3 contender).
Key derivation hashing
The following are the tips related to Key derivation hashing:
- Argon2. Go. Outline of Argon2.
- Argon2 with NaCl. Go. Outline of Argon2 using NaCl.
- Balloon. Go. Outline of Balloon.
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- Double ratchet. Go. Outline of double ratcheting.
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- Scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat HKDF. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
Non-crypto/fast hashing
The following are the tips related to non-crypto hashing:
- A perfect hash Perfect hash. This is a non-crypto hash which optimizes the hash value.
- The universal hash Universal hash. This related to the concept of a universal hash.
- FNV. FNV. FNV is one of the fastest hashing methods.
- Murmur. Murmur. Murmur is one of the fastest hashing methods.
- Siphash. Siphash. Siphash is a fast hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- xxHash. xxHash. xxHash is one of the fastest hashing methods.
- Meow. Meow. Meow is one of the fastest hashing methods.
- o1Hash. o1Hash. o1Hash is one of the fastest hashing methods.
- CRC-32. CRC-32. CRC-32 is one of the fastest hashing methods.
- wyhash. wyhash. wyhash is one of the fastest hashing methods.
- CityHash. CityHash. CityHash is one of the fastest hashing methods, and is generally free of security problems.
- FarmHash. FarmHash. FarmHash is one of the fastest hashing methods, and is generally free of security problems.
- Non-crypto. Non-crypto. This includes a range of fast non-cryptography hashing methods.
- Non-crypto hashes (C++): Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro. Non-crypto hashes: Farm, City, xxHash, MUM, Spooky 2, Murmur, Metro and t1ha0. This includes a range of fast non-cryptography hashing methods for Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro using C++ methods.
- Pearson. Pearson. Pearson is one of the fastest hashing methods, and has been designed for 8-bit processors.
- C++: t1ha. t1ha. t1ha is one of the fastest hashing methods, and has been designed for 64-bit processors.
- C++: Spooky. Spooky. Spooky is one of the fastest hashing methods, and V2 has a 32-bit, 64-bit and 128-bit version.
- C++: xxHash. xxHash. xxHash is one of the fastest hashing methods, and has good performance for short data inputs.
- C++: MUM. MUM. MUM is one of the fastest hashing methods.
- C++: FNV 1/1a. FNV 1/1a. FNV 1/1a is one of the fastest hashing methods, and is particularily useful when there are small changes in strings, such as with IP addresses and URLs.
- C++: MetroHash. MetroHash. MetroHash is one of the fastest hashing methods.
- C++: CityHash. CityHash. CityHash was created by Google and is one of the fastest hashing methods. It was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Farm. FarmHash. FarmHash was created by Google and is one of the fastest hashing methods. It is an improvement to CityHash.
- C++: Murmur. Murmur. Murmur is one of the fastest hashing methods, but was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Halftime. Halftime. Halftime is one of the fastest hashing methods and was created by Jim Apple at Apache.
- C++: Highway. Highway. Highway is an ultra-fast keyed-hash, and is more than five times faster than SipHash. It was created by Jyrki Alakuijala, Bill Cox, Jan Wassenberg at Google.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
- C++: CLHash. CLHash. CLHash is an ultra-fast hashing method and focused on improving performance of the hashing of long strings.
- C++: FalkHash. FalkHash. FalkHash is an ultra-fast hashing method and beats most of the other non-cryptography methods for performance. It is focused on the x64 architecture and integrates with AES-NI.
- C++: wyHash. wyHash. wyHash is an ultra-fast hashing method.
- C++: Fibonacci. Fibonacci. Fibonacci is an ultra-fast hashing method.
- C++: Lookup3. Lookup3. Lookup3 is an ultra-fast hashing method.
Key-based hashing
The following are the tips related to Key-based hashing:
- SiphashSiphash. Siphash is a fast key-based hashing method.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
One Time Passwords/Time Stamps
The following are the tips related to hashing:
- One Time Passwords. One Time. This allows a new unique password to be created each instance, based on an initial seed.
- Timed One Time Password (TOTP). Timed One Time Password. This allows a new unique passcode to be created each instance, based on an initial seed for a given time window. We will use a five second window in this case, where a new passcode is generated every five seconds, based on an initial seed of a pass phrase.
- Hashed One Time Password (HOTP). Hashed One Time Password. This allows a new unique passcode to be created each instance, based on a counter value and an initial seed.
- Time Stamp Protocol. TSP. This creates a time stamp for data.
- HOTP and TOTP (Python). OTP. This creates hashed passwords.
eXtendable-Output Function (XOF)
- eXtendable-Output Function (XOF) usign CIRCL. XOF. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS.
SHAKE
The following are the tips related to hashing:
- SHAKE. SHAKE. Implements SHAKE and which is an Extendable Output Function (XOF).
- SHAKE with Go. SHAKE. This implements SHAKE in Go.
- libDisco with Go. libDisco. This implements libDisco.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify
the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods
such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC methods using the Python cryptography primitives for HMAC-MD5.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
Quantum-robust Public Key (Hash-based signature)
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
Hash to ECC point
- Hash to password with Go. Hash to password. Hash to password with Go.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve with libnum.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.

Password-hashing functions using Rust
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing (Non-cryptographic)

You might know those slow old hashing methods, such as MD5, SHA-1, and SHA-256. Well, they were designed to be fast, but also highly secure. But, if we just need a hashing method, such as for a hashtable or Bloom filter, we often don’t need all the security that comes with the main cryptography hashing methods. And so we have the non-cryptography hashing methods, and which are often ultra-fast and highly efficient. To show the difference, in a test, SHA-1 — one of the fastest cryptography hashing methods — managed a processing rate of 364.95 MiB/s, while t1ha was nearly a 100 times faster, at 34,636 MiB/s.
Non-crypto/fast hashing
The following are the tips related to non-crypto hashing:
- A perfect hash Perfect hash. This is a non-crypto hash which optimizes the hash value.
- The universal hash Universal hash. This related to the concept of a universal hash.
- FNV. FNV. FNV is one of the fastest hashing methods.
- Murmur. Murmur. Murmur is one of the fastest hashing methods.
- Siphash. Siphash. Siphash is a fast hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- xxHash. xxHash. xxHash is one of the fastest hashing methods.
- Meow. Meow. Meow is one of the fastest hashing methods.
- o1Hash. o1Hash. o1Hash is one of the fastest hashing methods.
- CRC-32. CRC-32. CRC-32 is one of the fastest hashing methods.
- wyhash. wyhash. wyhash is one of the fastest hashing methods.
- CityHash. CityHash. CityHash is one of the fastest hashing methods, and is generally free of security problems.
- FarmHash. FarmHash. FarmHash is one of the fastest hashing methods, and is generally free of security problems.
- Non-crypto. Non-crypto. This includes a range of fast non-cryptography hashing methods.
- Non-crypto hashes (C++): Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro. Non-crypto hashes: Farm, City, xxHash, MUM, Spooky 2, Murmur, Metro and t1ha0. This includes a range of fast non-cryptography hashing methods for Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro using C++ methods.
- Pearson. Pearson. Pearson is one of the fastest hashing methods, and has been designed for 8-bit processors.
- C++: t1ha. t1ha. t1ha is one of the fastest hashing methods, and has been designed for 64-bit processors.
- C++: Spooky. Spooky. Spooky is one of the fastest hashing methods, and V2 has a 32-bit, 64-bit and 128-bit version.
- C++: xxHash. xxHash. xxHash is one of the fastest hashing methods, and has good performance for short data inputs.
- C++: MUM. MUM. MUM is one of the fastest hashing methods.
- C++: FNV 1/1a. FNV 1/1a. FNV 1/1a is one of the fastest hashing methods, and is particularily useful when there are small changes in strings, such as with IP addresses and URLs.
- C++: MetroHash. MetroHash. MetroHash is one of the fastest hashing methods.
- C++: CityHash. CityHash. CityHash was created by Google and is one of the fastest hashing methods. It was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Farm. FarmHash. FarmHash was created by Google and is one of the fastest hashing methods. It is an improvement to CityHash.
- C++: Murmur. Murmur. Murmur is one of the fastest hashing methods, but was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Halftime. Halftime. Halftime is one of the fastest hashing methods and was created by Jim Apple at Apache.
- C++: Highway. Highway. Highway is an ultra-fast keyed-hash, and is more than five times faster than SipHash. It was created by Jyrki Alakuijala, Bill Cox, Jan Wassenberg at Google.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
- C++: CLHash. CLHash. CLHash is an ultra-fast hashing method and focused on improving performance of the hashing of long strings.
- C++: FalkHash. FalkHash. FalkHash is an ultra-fast hashing method and beats most of the other non-cryptography methods for performance. It is focused on the x64 architecture and integrates with AES-NI.
- C++: wyHash. wyHash. wyHash is an ultra-fast hashing method.
- C++: Fibonacci. Fibonacci. Fibonacci is an ultra-fast hashing method.
- C++: Lookup3. Lookup3. Lookup3 is an ultra-fast hashing method.
A fuller test with SMHasher gives [here]:
Hash function MiB/sec cycl./hash cycl./map Quality problems
------------------------------------------------------------------
o1hash 12439661.09 16.77 166.13 insecure, no seed, zeros, fails all tests
crc32_hw1 23208.73 46.74 179.70 insecure, 100% bias, collisions, distrib, BIC, machine-specific (x86 SSE4.2)
t1ha0_aes_noavx 22785.26 38.71 180.61 LongNeighbors, machine-specific (x86 AES-NI)
t1ha0_aes_avx1 22714.85 48.12 226.52 LongNeighbors, machine-specific (x64 AVX.txt)
t1ha0_aes_avx2 22345.33 44.38 556.47 LongNeighbors, machine-specific (x64 AVX2)
falkhash 20202.42 173.63 321.52 Sparse, LongNeighbors, machine-specific (x64 AES-NI)
MeowHash64low 17378.06 85.48 237.60 Sparse, invertible, machine-specific (x64 AES-NI)
MeowHash32low 17374.64 85.48 258.53 Sparse, invertible, machine-specific (x64 AES-NI)
MeowHash 17371.91 85.48 247.96 Sparse, invertible, machine-specific (x64 AES-NI)
FarmHash32 17112.05 47.7 214.71 machine-specific (x64 SSE4/AVX)
xxh3 16538.52 32.81 184.86 DiffDist bit 7 w. 36 bits, BIC
xxh3low 16462.36 32.77 199.79
farmhash32_c 16299.81 47.79 219.19 machine-specific (x64 SSE4/AVX)
xxh128low 15174.85 33.79 187.05
xxh128 15174.14 40.46 195.65
farsh32 14053.09 74.29 245.33 insecure: AppendedZeroes, collisions+bias, MomentChi2, LongNeighbors
metrohash64crc_2 14034.84 48.94 162.54 UB, Cyclic 8/8 byte, DiffDist, BIC, machine-specific (SSE4.2/NEON)
metrohash64crc_1 14000.5 49.08 150.54 UB, Cyclic 8/8 byte, DiffDist, BIC, MomentChi2, machine-specific (SSE4.2/NEON)
metrohash128crc_1 13948.67 65.2 168.08 UB, machine-specific (SSE4.2/NEON)
metrohash128crc_2 13920.19 65.12 176.70 UB, machine-specific (SSE4.2/NEON)
halftime_hash128 13478.23 97.79 252.14
wyhash32low 12911.09 29.59 205.43 2 bad seeds
wyhash 12879 30.35 196.77 2^33 bad seeds
CityCrc128 12343.43 74.5 209.75
fletcher2 12011.15 25.29 298.60 bad seed 0, UB, fails all tests
fletcher4 11928.55 25.27 293.49 bad seed 0, UB, fails all tests
halftime_hash256 11620.28 98.44 252.60
fibonacci 11339.87 26.33 705.64 UB, zeros, fails all tests
ahash64 9862.62 27.32 181.68 rust
Spooky128 9751.14 63.84 192.47 UB
Spooky64 9747.47 62.2 191.71 UB
Spooky32 9747.13 62.24 196.96 UB
t1ha1_64le 9723.86 34.39 176.91 Avalanche
cmetrohash64_1 9683.33 45.2 161.01 UB, LongNeighbors, BIC, MomentChi2
cmetrohash64_2 9669.95 44.75 149.67 LongNeighbors
metrohash64_2 9668.51 44.45 164.30 UB, LongNeighbors
metrohash64 9664.61 44.59 150.74 UB, LongNeighbors, BIC
metrohash64_1 9664.57 45.37 152.31 UB, LongNeighbors, BIC, MomentChi2
cmetrohash64_1o 9658.31 42.84 163.45 UB, LongNeighbors, BIC, MomentChi2
FNV1a_YT 9643.42 32.06 175.19 bad seed, UB, fails all tests
City128 9640.19 88.45 225.38
metrohash128_2 9584.94 59.1 167.43 UB, LongNeighbors
metrohash128 9569.16 58.68 167.53 UB, LongNeighbors
metrohash128_1 9558.17 59.04 175.94 UB, LongNeighbors
FarmHash128 9409.63 74.52 210.25
VHASH_32 9404.99 77.01 250.57 sanity, Seed, MomentChi2
VHASH_64 9392.39 74.72 227.92 sanity, Seed, MomentChi2
farmhash128_c 9244.13 79.08 209.44
t1ha2_atonce 9237.12 38.94 194.32 Zeroes low3
City64noSeed 9090.42 32.23 171.53 Avalanche, Sparse, TwoBytes, MomentChi2, Seed
City64low 9089.45 47.75 201.73
t1ha2_stream 9068.55 74.56 219.85 Sparse, Permutation, LongNeighbors
City64 9066.9 47.81 197.78 Sparse, TwoBytes
t1ha2_stream128 9065.5 93.19 236.50 Sparse, Permutation, LongNeighbors
xxHash64 8936.63 51.31 174.34
pengyhash 8744.48 85.31 222.45
farmhash64_c 8713.16 47.96 201.00
FarmHash64 8684.76 48.13 200.51
crc64_hw 8440.13 34.94 141.15 insecure, 100% bias, collisions, distrib, BIC, machine-specific (SSE4.2/NEON)
t1ha2_atonce128 8350.99 55.65 203.53 LongNeighbors
PMPML_64 8161.19 53.2 179.16 unseeded: Seed, MomentChi2, BIC
halftime_hash512 7681.62 125.81 274.01
tabulation 7621.75 42.19 179.93
t1ha1_64be 7481.37 38.16 193.22 Avalanche
MUMlow 7225.18 37.85 197.92 UB, 5 bad seeds
farsh64 7216.29 130.3 302.44 insecure: AppendedZeroes, collisions+bias, MomentChi2, LongNeighbors
MUM 7134.56 37.85 172.34 UB, too many bad seeds, machine-specific (32/64 differs)
nmhash32 7003.3 68.93 216.59
PMPML_32 6704.53 53.5 197.43 Avalanche >512, unseeded: Seed, BIC, MomentChi2, PerlinNoise
nmhash32x 6342.95 56.41 217.75
crc32_hw 6330.42 35.55 170.16 insecure, 100% bias, collisions, distrib, BIC, machine-specific (SSE4.2/NEON)
FNV2 6258.84 33.25 142.89 fails all tests
FNV1A_Pippip_Yurii 6258.46 28.19 184.41 UB, sanity, fails all tests
FNV1A_Totenschiff 6258.23 27.99 198.20 UB, zeros, fails all tests
HighwayHash64 6242.58 99.55 248.41
mx3 6146.02 52.48 173.09 UB
xxHash32 6040.87 51.77 177.91 LongNeighbors, collisions with 4bit diff, MomentChi2 220
prvhash64s_64 5481.48 170.05 325.39
mirhash 5413.73 39.68 154.47 UB, 2^36 bad seeds, LongNeighbors, machine-specific (32/64 differs)
mirhash32low 5412.76 39.79 182.13 UB, 4 bad seeds, Cyclic, LongNeighbors, machine-specific (32/64 differs)
Murmur3F 5226.4 52.18 175.85 UB
prvhash64s_128 5161.33 260.96 442.70
t1ha0_32le 5132.18 54.83 193.53 Sparse, LongNeighbors
halftime_hash64 4990.72 120.55 281.64
Murmur2B 4882.95 39.72 149.43 UB, 1.8% bias, collisions, 3.4% distrib, BIC
seahash32low 4801.33 58.54 227.31 PerlinNoise 32, !msvc
seahash 4796.97 58.55 201.58 PerlinNoise, !msvc
fasthash32 4737.61 45.32 181.86 UB, insecure
fasthash64 4737.21 42.79 164.87 UB, insecure, Moment Chi2 5159 !
umash32_hi 4662.92 54.22 214.20
umash64 4662.09 53.42 188.09
umash32 4633.19 53.42 216.33
t1ha0_32be 4585.59 55.98 183.45 Sparse, LongNeighbors
clhash 4472.31 82.72 229.73 PerlinNoise, machine-specific (x64 SSE4.2)
tabulation32 4317.34 35.45 197.20 collisions
Murmur2C 4092.99 51.84 164.65 UB, 2^32 bad seeds, 91% bias, collisions, distr, BIC, LongNeighbors
farsh128 3776.92 232.48 398.67
City32 3675.04 57.73 212.04
TSip 3228.14 57.96 211.71 !msvc
Murmur3C 3197.63 67.9 198.00 UB, LongNeighbors, Text, DiffDist
Crap8 3149.63 36.23 195.11 UB, 2.42% bias, collisions, 2% distrib
Murmur2 3146.91 41.87 187.89 UB, 1 bad seed, 1.7% bias, 81x coll, 1.7% distrib, BIC
Murmur2A 3146.79 46.87 191.96 UB, 1 bad seed, 12.7% bias, LongNeighbors
aesnihash 2963.39 71.24 217.73 fails many tests, machine-specific (x64 AES-NI)
BEBB4185 2951.62 222.03 343.63 UB, too many bad seeds, msvc-specific
jodyhash6 2848.42 29.99 164.36 bias, collisions, distr, BIC, LongNeighbors
wyhash32 2532.89 48.4 484.57 2 bad seeds, 32-bit
umash128 2427.46 70.6 197.29
Murmur3A 2413.88 53.36 182.37 UB, 1 bad seed, Moment Chi2 69
prvhash64_64m 2386.19 51.18 186.87
prvhash64_128 2383.57 103.44 246.45
prvhash64_64 2375.72 51.61 190.97
hasshe2 2372.52 68.64 216.74 Permutation,TwoBytes,Zeroes,Seed
PMurHash32 2344.78 58.48 196.43 1 bad seed, Moment Chi2 69
mirhashstrict32low 2218.87 65.48 190.59 1 bad seed, MomentChi2 9
mirhashstrict 2217.32 65.53 182.07
sha1ni 2019.96 135.84 564.40 insecure,sanity, Permutation, Zeroes, machine-specific
sha1ni_32 2019.94 136.82 589.46 machine-specific
superfast 1956.25 53.61 180.10 UB, bad seed 0, 91% bias, 5273.01x collisions, 37% distr, BIC
sha2ni-256_64 1910.34 146.06 595.16 Zeroes, machine-specific
sha2ni-256 1906.77 145.47 603.08 insecure,sanity, Permutation, Zeroes, machine-specific
farsh256 1895.77 459.86 575.95
SipHash13 1889.1 89 199.95 0.9% bias
Murmur1 1804.67 51.51 188.41 UB, 1 bad seed, 511x collisions, Diff, BIC
lookup3 1658.31 48.84 194.15 UB, 28% bias, collisions, 30% distr, BIC
pearsonbhash64 1486.34 104.32 185.03
poly_1_mersenne 1431.65 54.49 189.52 fails most tests
jodyhash32 1428.37 44.36 185.85 bias, collisions, distr, BIC LongNeighbors
pearsonbhash128 1347.03 121.75 214.84
poly_2_mersenne 1323.69 66.93 190.88
poly_3_mersenne 1323.59 74.86 206.77
poly_4_mersenne 1323.57 82.67 200.36
blake3_c 1285.91 340.01 552.63 no 32bit portability
GoodOAAT 1052 71.62 192.19
pearsonbhash256 998.9 167.05 261.29
SipHash 980.88 127.77 246.19
MicroOAAT 977.6 59.61 185.06 100% bias, distrib, BIC
FNV1a 791.84 69.69 177.84 bad seed, zeros, fails all tests
sdbm 791.84 67.69 177.06 bad seed 0, fails all tests
FNV64 791.82 70.24 159.29 fails all tests
bernstein 791.82 68.63 180.71 bad seed 0, fails all tests
beamsplitter 789.22 682.45 1150.3 UB, too many bad seeds
HalfSipHash 755.78 114.47 243.72 zeroes
chaskey 753.23 153.42 288.26 PerlinNoise
x17 527.9 98.78 184.09 99.98% bias, fails all tests
JenkinsOOAT_perl 452.49 118.78 194.78 bad seed 0, test FAIL
MurmurOAAT 452.49 113.07 197.83 bad seed 0, 1.5-11.5% bias, 7.2x collisions, BIC, LongNeighbors
JenkinsOOAT 452.48 142.85 213.93 bad seed 0, 1.5-11.5% bias, 7.2x collisions, BIC, LongNeighbors
crc32 392.1 131.62 204.58 insecure, 8590x collisions, distrib, PerlinNoise
sha1-160 364.95 1470.55 1794.1 Comb/Cyclic low32
rmd256 362.49 617.02 815.44 Bad seeds
blake2b-256_64 356.97 1222.76 1435.0
blake2b-224 356.59 1228.5 1425.87
blake2b-160 356.08 1236.84 1458.15
blake2b-256 355.97 1232.22 1443.31 Sparse high 32-bit
md5-128 353.76 638.29 803.39
md5_32a 353.64 629.85 799.56 Sparse high 32-bit
sha1_32a 353.03 1385.8 1759.9 Cyclic low32, 36.6% distrib
rmd128 334.36 659.03 838.32 Bad seeds
blake2s-128 295.3 698.09 1059.2
pearsonhash64 287.95 174.11 196.50 Avalanche, Seed, SSSE3 only. broken MSVC
pearsonhash128 287.95 171.72 194.61 Avalanche, Seed, SSSE3 only. broken MSVC
pearsonhash256 264.51 184.87 218.79 Avalanche, Seed, SSSE3 only. broken MSVC
blake2s-256 215.28 1014.88 1230.38
blake2s-160 215.01 1026.74 1239.54
blake2s-256_64 211.52 1044.22 1228.43
blake2s-224 207.06 1063.86 1236.50
rmd160 202.16 1045.79 1287.74 Bad seeds, Cyclic hi32
sha2-256_64 148.01 1376.34 1624.71 Bad seeds, Moment Chi2 7
sha2-256 147.8 1374.9 1606.06 Bad seeds, Moment Chi2 4
sha2-224_64 147.6 1360.1 1620.93 Bad seeds, Cyclic low32
sha2-224 147.13 1354.81 1589.92 Bad seeds, Comb low32
asconhashv12 144.98 885.02 1324.23
sha3-256 100.58 3877.18 4159.79 PerlinNoise
sha3-256_64 100.57 3909 4174.63 PerlinNoise
asconhashv12_64 86.73 684.02 606.93
floppsyhash 35.72 1868.92 1411.07
tifuhash_64 35.6 1679.52 1212.75 Cyclic low32
Problems include:
- Bad Seeds. A random seed is often used to initialise the hash. This problem relates to having a bad seed..
- Undefined behaviour (UB). This includes Misaligned, oob (Out of bounds), Signed integer overflow and Shift exponent overflow.
o1hash is the fastest, and a quick and dirty hashing method. It is generally not secure. t1h (Fast Positive Hash) requires AES-NI (Intel Advanced Encryption Standard Instructions) and is one of the fastest hashes at 22.785 Gbps. It has fairly good security levels. Meow comes in around 17.378 Gbps. We can see that SHA-1-160 runs as 364 Mbps, while Meow runs at 17.378 Gbps. Blake 3 is one of the fast cryptography hash and has a rate of 1.285 Gbps, and Blake 2 gives a rate around 215 Mbps. SHA-3 gives hashing rates of 100.58 Mbps.
Google recommend the following for 64-bit hashes without quality problems:
- xxh3low
-
wyhash
-
ahash64
-
t1ha2_atonce
-
FarmHash
-
halftime_hash128
-
Spooky32
-
pengyhash
-
nmhash32
-
mx3
-
MUM/mir
- fasthash32
Hash-based Signatures

With hash-based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature, unless we create a stateless method, such as SPHINCS+ [1]. Currently NIST have the final round for the Post Quantum Cryptography competition, and for digital signatures, SPHINCS+ is one of the alterative finalists (alongside Picnic).
Hash-based signature (theory)
- BiBa (Go). BiBa. An overview of BiBa One Time Signature [9]. Basically the method involves us taking a hash of a value using a standard hashing method, such as with SHA-256. There will then be \(2^{256}\) different hashing values. We aim to create a signature for a message, so Bob (the signer) selects a number of random values for his private key value and then publishes the hash of each of these (\(P_1\), \(P_2\), etc). He then sends these public keys to Alice. Now when Bob wants to sign a message, he will take one of his private key values, and then hashes it, and then determines the bin that it should be placed. In this case, we could use the \(\pmod N\) function on the hash, and where \(N\) is the number of bins. If we select \(2^{10}\) there will be 1,024 bins.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature [9].
Hash-based signature (stateful)
- BLISS - Post-quantum signing. BLISS. One of the alteratives to the usage of our existing public key methods is the usage of lattice cryptography, and especially in the usage of Ring Learning With Errors (RLWE). An important application is within digital signatures, and where Bob will sign something with his private key, and then Alice can prove that he signed it with his public key. One post-quantum signature method is BLISS (short for Bimodal Lattice Signature Scheme) [8]. It was created by Léo Ducas, Alain Durmus, Tancrède Lepoint and Vadim Lyubashevsky in 2013.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Hash to Obtain Random Subset (HORS) [3] is a quantum robust hashed-based one-time signature. With this we create a series of integers for our private keys and organise into an indexable form. Then we hash them to a sequence of public key values. Next we segment the hash of the message into a series of n-bit integer values. The signature is then achieved through a look-up of the value in the public key list.
- Lamport Signatures. Lamport. Outlines Lamport signatures [7]. When we sign a message we take its hash and then encrypt with our private key. The public key is then used to prove it, and will prove that we signed it with our private key. The Lamport signature uses 512 random hashes for the private key, and which are split into Set A and Set B. The public key is the hash of each of these values. The size of the private key is 16KB (2×256×256 bits) and the public key size is also 16 KB (512 hashes with each of 256 bits).
- Winternitz Signatures (W-OTS). Winternitz. Outlines Winternitz signatures [4, 5]. W-OTS uses relatively small key and signatures sizes, and is thought to be quantum robust. It generates 32x256 bit random private keys. We then hash these a number of times, and is defined by a parameter (w). If we use w=8, we hash the private keys by (2w). This creates 32x256 bits public keys. The signature is the created by taking eight bits at a time, and then the 8-bit binary int (n) is subtracted from 256 and the private key is the hashed 256-n times. The signature is then 32 hashes which are derived from random private keys. To verify the signature, the recipient parses the hash of the signature (using 8 bits at a time, and extracting the 8 bit int, n).
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method [6], and which is used within speeds-up of Hashing-based signature methods. Using methods such as SHA-1 and SHA-2 (aka SHA-256) will be inefficient as they tend to compress the data inputs through a number of stages. Haraka v2 [6] is different as focuses on inputs of just 256 bits (32 bytes) or 512 bits (64 bytes). This makes the method useful when we are dealing with key and hash values, and is especially useful for hash-based signatures. The output is 256 bits long, but where the input can be either be 256 bits (Haraka256) or 512 bits (Haraka512). These lengths are typically for the outputs of modern hashing applications. The Haraka method, too, has been optimized with AES instructions (AES-NI - Intel Advanced Encryption Standard New Instructions) and which are supported within the hardware of the processor. As Haraka is focused on short messages, the number of rounds within the hashing process has been reduced.
Hash-based signature (stateless)
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ digital signature. SPHINCS digital signature. Outline of the a SPHINCS stateless digital signature method [1].
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
Hash-based signature (Merkle-based)
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
Introduction
Many of the problems we see on the Internet relate to the lack of trust within transactions. The emails you receive and the Web sites that you visit often have very little trust built into them. For trust the email address of the sender, but anyone can fake that address. So increasingly we create a digital signature, and where we sign our messages. In this way, we can check for authentication, integrity and non-repudiation.
With the Alice creates a key-pair: a public key and a private key. She then takes a hash of the message, and then encrypts this hash with her private key, and passes the message and the signature to Bob. Bob then reads the message and takes a hash of it. He then decrypts Alice's signature with her public and checks the hashes. If they match, he knows that she signed and that it has not been changed along the way:
Currently, we often use RSA, DSA and ECDSA to sign our messages. These are based on the difficulty of finding out the factors of a number and on the processing of discrete logarithms. At the current time these methods are computationally hard problems, but with quantum computers, they become much easier. This was shown by Peter Shor who illustrated that it was possible to crack them in polynomial time.
Of all the methods that are being proposed, the hash-based methods look as if they have a good chance of success of creating quantum robust signatures. methods and code-based methods are being researched, but the usage of hashing methods is already well and could provide the best alternative to the existing methods. Hashing methods, too, often bring other advantages, such as forward secure, which means that a key which is cracked will not reveal all the previous keys.
Merkle trees
The root of hash-based methods isin Merkle trees, and which are a way of hashing is used in many applications, including with Bitcoin, Ethereum, Git distribution systems, No SQL, and in many P2P applications. With a Merkle tree we take our data elements, and then hash them, and take pairs of these hashes to create a new hash, and so we build a table. At the top of the tree is the root element (in this case Hash1234):

In this way, we can use the tree to see if we have matching data on systems.On a P2P network, we can transfer a file by splitting it into data segments and then distributing these segments across the network. A trusted source will have the complete Merkle tree for rebuilding the file, and a client can thus rebuild from the Merkle tree and determine the parts of the file which are still missing. Once transferred the root hash (and all the other hashes) will then match. In its core method, the Merkle Signature Scheme (MSS) has serious performance and memory issues, but enhanced methods such as XMSS create with much less of a performance hit.
One-time signatures (Lamport)
The core method used in hash-based signatures is that of the one-time signature, and where we create a new key pair for every method we need to create. If the keys were reused, an attacker could start to learn the private key, and thus spoof messages. One of the first methods was produced by Leslie Lamport and Whitfield Diffie, in 1979, and is defined as:
- We create two data sets with 256 random 256-bit numbers (Set A and Set B). These are the private key (512 values).
- we take the hash of each of the random numbers. This will give 512 hashes and will be the public key.
- We then hash the message using and then test each bit of the hash (0 ... 255). If it is a 0, we use the ith number in Set A, else we use the ith number from Set B.
- The signature is then 256 random numbers (taken from either Set A or Set B) and the public key is the 512 hashes (of Set A and Set B).
The public and private keys are then each 16KB in size. A demo of the method is here.

Figure 1: Lamport method
The major problem with the method is that a key pair for every message. also in 1979, found a solution with Merkle trees.
One-time signature (W-OTS)
To improve performance method (and which reduced key sizes), Merkle proposed Winternitz OTS (named after Robert Winternitz). With this method was possible to sign many bits at the same time. The method is:
- We create 32 256-bit random numbers. These 32 values will be our private key.
- We then hash each of these values 256 times. These 32 values will be our public key.
- We now take the message and hash it using SHA-256. This produces 32 8-bit values (N1, N2 ... N32).
- Next we take each 8-bit value in the hash of the message, and then hash 256-N times (where N is the value of the 8-bit value).
- To prove the signature, we take the message and hash it with SHA-256, and then take each 8-bit value. We then hash the 8-bit signature value by the number of times defined by the message hash value (N1, N2..). The result for each operation should equal the public key value.
This is illustrated below in Figure 2. A demo of the method is here.

Figure 2: W-OTS
Hash-based Signatures
The methods such as W-OTS and Lamport only provide for a one-time signature. In order to sign many messages, we can use the Merkel signature scheme (MSS). With this we take a hash of the keys and build these as the leaves of the tree. The root of the tree is then the public key - the verification key. We then just use the private key of the W-OTS method to create the signature. The sender also sends the authentication path, which is the neighbouring nodes within the path and which leads to the root of the tree. The recipient can then rebuild the tree using the verification key (which can be received a digital certificate) and the authentication path. For the next message we move onto another key pair and where the index of the key part is revealed.
In the following example we have our root as the public key, and then want to sign with Key3. We then show the authentication path which takes us to the root (as defined in the bold arrows):

Conclusions
Hashed-based methods look to be a strong contender for weaning us off RSA, DSA and ECDSA, but we will have to look at the stateful generation of keys. For this we will have to generate a bank of key pairs (2, 4, 8, 16, etc) and then create the public key from the root of the Merkle tree. We must then remember the keys we have used previously, and only use an unused one. Once we use our new key pair, we then show our working-out as to how the private key is integrated into our tree. It is a bit like a teacher marking a question correctly, and asking for the working out that go you to the answer.
References
[1] Bernstein, D. J., Hopwood, D., Hülsing, A., Lange, T., Niederhagen, R., Papachristodoulou, L., ... & Wilcox-O’Hearn, Z. (2015, April). SPHINCS: practical stateless hash-based signatures. In Annual international conference on the theory and applications of cryptographic techniques (pp. 368-397). Springer, Berlin, Heidelberg [paper].
[2] Bernstein, D. J., Hülsing, A., Kölbl, S., Niederhagen, R., Rijneveld, J., & Schwabe, P. (2019, November). The SPHINCS+ signature framework. In Proceedings of the 2019 ACM SIGSAC conference on computer and communications security (pp. 2129-2146) [paper].
[3] Reyzin, L., & Reyzin, N. (2002, July). Better than BiBa: Short one-time signatures with fast signing and verifying. In Australasian Conference on Information Security and Privacy (pp. 144-153). Springer, Berlin, Heidelberg [paper].
[4] Merkle, R. C. (1989, August). A certified digital signature. In Conference on the Theory and Application of Cryptology (pp. 218-238). Springer, New York, NY.
[5] Hülsing, A. (2013, June). W-OTS+–shorter signatures for hash-based signature schemes. In International Conference on Cryptology in Africa (pp. 173-188). Springer, Berlin, Heidelberg.
[6] Kölbl, S., Lauridsen, M. M., Mendel, F., & Rechberger, C. (2016). Haraka v2–efficient short-input hashing for post-quantum applications. IACR Transactions on Symmetric Cryptology, 1-29. [here]
[7] Lamport, L. (1979). Constructing digital signatures from a one-way function (Vol. 238). Technical Report CSL-98, SRI International. [paper]
[8] Ducas, L., Durmus, A., Lepoint, T., & Lyubashevsky, V. (2013, August). Lattice signatures and bimodal Gaussians. In Annual Cryptology Conference (pp. 40-56). Springer, Berlin, Heidelberg [paper].
[9] Perrig, A. (2001, November). The BiBa one-time signature and broadcast authentication protocol. In Proceedings of the 8th ACM Conference on Computer and Communications Security (pp. 28-37) [paper] .
Hashing (Simularity)

Similarity hashes allow for two data objects to be compared for their similarity.
Similarity assessment methods
The following relate to the basic methods used for string similarity:
- String similarity String similarity. This measures edit distance (including Levenshtein distance), Jaro (including Jaro-Winkler), and QGrams.
- String enthropy String enthropy. Measurement of the entropy of strings.
- Soundex Soundex. Soundex uses a phonetic algorithm to classify a sound as it is pronounced. It focuses on matching phrases which have minor spelling errors.
Similarity hashes
The following are the tips related to similarity hashing:
- Similarity hash: SimHash (Charikar similarity) in Python Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash (Nilsimsa similarity) Nilsimsa. The Nilsimsa similarity is used to find similarities between spam emails.
- Context Triggered Piecewise Hashes (CTPH): ssdeep CTPH similarity. Kornblum [6] created ssdeep and which computes fuzzy hashes. This aims to match similar byte sequences, no matter if there are differences between these sequences. For this we break a file up into fragments with a rolling hash function. We then produce a small hash for each of those fragments. These are then aggregated to produce the complete hash of a file. In comparing file signatures, we treat the resultant hash value as a string, and then uses an edit distance method to compare.
- TLSH (A Locality Sensitive Hash) TLSH similarity. In malware analysis and in text similarity, we often have to identify areas of data within files which are similar. One method is TLSH (A Locality Sensitive Hash), and which was defined by Oliver et al [7]. It is used - along with ssdeep - by VirusTotal to identify a hash value for malware.
- Minhash (Jaccard similarity) Jaccard similarity. The Minhash method is used to find similarities between strings, files and metadata.
- Counting identical elements (HyperLogLog) HyperLogLog. Counting the number of identical elements.
Hazmat cryptography

The Cryptography library in Python contains interfaces to common cryptographic algorithms, including symmetric key methods, hashing, public key, and key derivation functions. Many of these are contained with the Hazmat (Harzardous Material) primative setup.
Hashing, HMAC, CMAC, Poly1305 and HKDF
-
Hazmat Hashes. Hazmat Hashes. This includes the hashing methods in the Hazmat cryptography library. This includes Blake2p, Blake2s, MD5, SHA1, SHA224, SHA256, SGA384, SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHA512, SHA512-224, SHAKE128 and SHA256.
-
Hazmat Hashes. Hazmat Hashes. In this case we will implement Python code to determine SHA1, SHA2, SHA3, Blake2, MD5 and SM3 hashes.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
- Hazmat HKDF. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
- Hazmat CMAC. Hazmat CMAC. CMAC methods using the Python cryptography primitives.
- Hazmat Poly1305. Hazmat Poly1305. Poly1305 methods using the Python cryptography primitives.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
Symmetric key
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat. Implementation of ChaCha20/Poly1305 with a random key using Hazmat.
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat. Implementation of AES GCM with a random key using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hazmat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Hazmat Symmetric Key Padding. Symmetric key. This includes the coverage of padding with Hazmat.
- Hazmat Symmetric Key Padding. Symmetric key. This includes the coverage of padding with Hazmat.
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
- Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . With 3DES encryption, we use a 128-bit key and a 64-bit IV value. The two modes supported are ECB (without salt) and CBC (with salt). The DES algorithm has been around for a long time, and the 56-bit version is now easily crackable (in less than a day on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases, and splits the key into two. Overall the key size is typically 112 bits (with a combination of the three keys - of which two of the keys are the same). In this case we will use PKCS7 padding, and which fills the input data with a value that is equal to the number of padding bytes. Overall, DES has a 64-bit block size, and which equates to eight ASCII characters.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key . And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.
Asymmetric key
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- ECC key generaton with Hazmat. Elliptic Curve key gen. Creating ECC keys using Hazmat and Python.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- Hazmat RSA signing (with key values). RSA signing with Hazmat. RSA signing using Python and with Hazmat (with key values).
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here]
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Signatures. DSA Signatures. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. The ECDSA method is an extension of DSA, but implemented with elliptic curve (EC) methods. As with most public key signing methods, we take a hash of a message, and then apply a private key to create a signature (\(r,s\)). This is done by creating a random value (\(k\)) to produce the signature. The signature is then verified using the associated public key. This then verifies the creator of the signature and that the message has not been changed.
Digital Signature: ECDSA/EdDSA
- ECDSA with Hazmat. ECDSA wih Hazmat. This outlines ECDSA with Hazmat.
- Ed25519 for EdDSA signatures with Hazmat. EdDSA: Ed25519. This page uses the Hazmat primitives for the cryptography library.
- Ed448 for EdDSA signatures with Hazmat. EdDSA: Ed448. This page uses the Hazmat primitives for the cryptography library.
- Ed25519 using NaCl. Ed25519. This page uses the NaCl port from libsodium.
- ECDSA Signatures with Hazmat (SECP256R1, SECP384R1, SECP521R1, SECP224R1, SECP192R1, and SECP256K1). ECC Signatures. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and then creates an ECDSA signature for a given message.
Digital Signature: RSA
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
Key exchange: ECDH/X25519
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives and showing the byte values for the key.
Tokens
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
Homomorphic Encryption

Homomorphic encryption supports mathematical operations on encrypted values. Partial Homomorphic Encryption (PHE) supports a few arithmatic operations, while Full Homomorphic Encryption (FHE) supports add, subtract, multiply, and divide. Homomorphic encryption normally involves a public key to encrypt the data, and a private key to decrypt it. There have been four main generations of homomorphic encryption, and the most recent being the HEAAN method.
Simple
- Simple Homomorphic Cipher. Hom. This outlines a Simple Homomorphic cipher.
- Simple Homomorphic Cipher (Python). Hom. This outlines a Simple Homomorphic cipher with Python.
- Full Homomorphic Cipher with a Public Key. Public key. This outlines a Simple Homomorphic cipher using a public key
ElGamal
- ElGamal Homomorphic Cipher (Go). ElGamal. This outlines ElGamal Homomorphic cipher with Go.
- ElGamal Homomorphic Cipher (Go) - Divide. ElGamal. This outlines ElGamal Homomorphic cipher with Go with divide.
- ElGamal Homomorphic Cipher (Go) - Additive. ElGamal. This outlines ElGamal Homomorphic cipher with Go with addition.
- ElGamal Homomorphic Cipher for Multiplication (Python). ElGamal. This outlines ElGamal Homomorphic multiplication with Python.
- ElGamal Homomorphic Cipher for Division (Python). ElGamal. This outlines ElGamal Homomorphic division with Python.
- ElGamal Homomorphic Cipher for Addition (Python). ElGamal. This outlines ElGamal Homomorphic addition with Python.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (Python). ElGamal. This outlines ElGamal Homomorphic subtraction with Python.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
RSA
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
ZKP
- Full Homomorphic Cipher to determine if Bob is older. Older. This outlines a Simple Homomorphic cipher to determine if Bob is older than Alice.
- Full Homomorphic Cipher to determine matching password. Password. This outlines a Simple Homomorphic cipher to determine if a password matches
- Interactive ZKP With Probablistic Methods. ZKP. Interactive ZKP With Probablistic Methods using Python.
- Full Homomorphic Cipher for Millionaire's Problem. Millionaire. This outlines a Simple Homomorphic cipher for the Millionaire's Problem
Voting
- Trusted voting. Trusted. A trusted voting method.
Secret share
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Lattice
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
Full Homomorphic Cipher
- Full Homomorphic Cipher for 2-bit Adder. Adder. This outlines a Simple Homomorphic cipher for a 2-bit adder with DGHV.
- Full Homomorphic Cipher for Full Adder. Full Adder. This outlines a Simple Homomorphic cipher for a full adder with DGHV.
- Full Homomorphic Cipher for 4-bit Adder. Adder. This outlines a Simple Homomorphic cipher for a 4-bit adder with DGHV.
- Full Homomorphic Cipher for 4-bit Adder/Subtractor. Subtract. This outlines a Simple Homomorphic cipher for a 4-bit adder/subtractor with DGHV.
- Full Homomorphic Cipher to XOR two integers. X-OR. This outlines a Simple Homomorphic cipher to X-OR two integers
Paillier
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier) .
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Damgård-Jurik Homomorphic Encryption With Secret Shares. Damgård-Jurik Method. Two of the major areas of developments within cybersecurity will be the usage of homomorphic encryption, and in the usage of Shamir secret sharing. With homomorphic encryption, we can encrypt values, and then operate on them with arithmetic functions (such as add, subtract and multiply), and with Shamir secret sharing, we can split secrets into shares, and then distributed them over networks. These approaches will take privacy to new levels. So let’s look at the Damgård-Jurik method.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Learning with Errors (LWE)
- Learning With Errors . LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret key value (s) and another value (e). Next we select a number of values (t[]) and calculate g[] = t[] x s + e. The values of g[] and t[] become our public key.
- Public Key Encryption with Learning With Errors (LWE). LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret value (s) and which is our private key. We then create a public key which is based on random numbers (A), and then generate another set of numbers (B) which is based on A,s and random errors e. An example of encryption with multiple bits is given.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE)
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Others
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
- SIDH Go. SIDH. Post-quantum key exchange.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Anonymous crypto. Anon. Anonymous crypto.
- Rho factorization. Rho. Rho alogorithm.
- Post-quantum signing (BLISS). BLISS. BLISS method.
Homomorphic Encryption with Krytology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Homomorphic hashing
- Homomorphic Hashing with Golang. Homomorphic hashing. Normally with hashing methods, we need to take all the previous data and new data in order to create a new hash value for our data. In a homomorphic hashing method, we can basically take the previous hash, and then add on any new data values. We can also remove previous data values from our hash, too. This is more efficient in computing, as we do not have to process all of our data into a new hash, and can use simple homomorphic operations for the computation. The method we will use (LtHash) was initially defined by Bellare and Micciancio and updated Lewi et al at Facebook.
Identity Based Encryption (IBE)

This page outlines a few basic principles around the usage of IBE.
Identity Based Encryption (Pairing based)
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pair-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Identity Based Encryption (Others)
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Güther's implicitly certified identity-based public keys (IBE). Günther. This method allows Bob to generate Alices public key from her identity and publicly available parameters.
- Girault's self-certified public keys (IBE). Girault. This method allows Bob to generate Alices public key from her identity and publicly available parameters, and where we use an RSA key pair to self-certify Alice's public key.
Intrusion Detection Systems (IDS)
- Intrusion Detection Systems. Snort. This outlines some of the basics of IDS, including the requirement for Intrusion Detection Systems (IDSs), and where they are used.
- Advanced Network Forensics (Snort). Adv Network Forensics. This provides information on how to detect threats through network forensics with Snort
Snort

- Snort IDS. Snort. This is a Snort Analyser.
- Snort IDS 2 with rules editor. Snort. This provides information on how to detect threats through network forensics with Snort, and with an editing function for rules.
Presentation
IoT

The key objectives of this page are: Understand how a Pen Tester can generate vulnerabilities and test using the Metasploit framework; Define the options and payloads required to generate and use vulnerabilities; and Gaining remote access.
Devices
- Access the Wi-fi kettle. Go. This page outines how to access a wi-fi enabled kettle.
- Philips Hue Wireless Lighting. Go. This page shows how to use RESTful Web services to access to the Hue Led Lamps.
- Kali and R-PI. Go. This page shows the setup of a security testing infrastructure using a Raspberry Pi (R-PI) and a wifi access point.
- Kali, R-PI and RF electrical socket. Go. This page shows the control of an RF electical socket from a RPI.
- Capture from a Polar H10 heat rate sensor. Go. This page shows the capture of the Polar H10 heart sensor with an Ubertooth One.
- Trusted IoT: Linking IoT Devices to NFTs. Go. This page outlines a research paper which links a device to an NFT (Non-fungible Token).
Shodan Scanning
-
IoT Scan (Shodan). Go. This page includes a search of the Internet for key terms, such as for "apache", "mysql" and "cisco".
- IoT Banner Scan (Shodan). Go. This page includes a search of the Internet for key terms with the banner as a result (for the Top 10)
- Internet Services (Shodan). Go. This page includes a search of the Internet for key terms and display the IP address and port.
IoT Libraries
- libDisco with Go. libDisco. libdisco is a Golang library which can be used to create secure connections. It is based on the STROBE protocol framework. Symmetric cryptographic primitives rely on SHA-3 permutation, and asymmetric cryptographic primitives on X25519 and ed25519. STROBE defines a range of cryptographic protocols to integrate with IoT devices. In order to reduce processing, energy and memory requirements, it only uses Keccak (SHA-3) to encrypt and authenticate messages.
COSE/COBR
In computer security, we often have to represent binary data, in single values or groups of characters, bytes, words, long words, signed integers, floating-point values, double-precision floating-point values, and so on. This might be in the form of a data object, a signature or even encrypted content. For this, the ANS.1 DER format is often used, such as presenting digital certificates and signatures. An improvement on this for small messages with security is Concise Binary Object Representation (CBOR) — and which is defined in RFC8949 [1]. While JSON represents text-based data objects CBOR focuses on binary objects. It has been designed to create a lightweight encoder and decoder. This supports the use of CBOR within an IoT infrastructure. The data, also, does not require a data schema to be able to decode it, along with being extensible. CBOR defines the format of binary data with data objects and messages. We can then integrate security with CBOR Object Signing and Encryption (COSE), and which is defined in RFC8152 [2]. This includes signatures, message authentication codes (MACs), encryption and creating serialised objects.
- 128-bit AES GCM. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) can then build on this to include signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use a symmetric key to encrypt a message, and then decrypt it. In this case we will use AES GCM with a static 128-bit key ("0x000102030405060708090a0b0c0d0e0f").
- 256-bit AES GCM. Go. In this case we will use AES GCM using a random 256-bit key (32 bytes).
- EdDSA. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) [2] can then build on this to includes signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use EdDSA to create a signature for a message.
- ECDSA. Go. In this case we will use ECDSA to create a signature for a message.
- HMAC. Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT. Go. In this case we create a CWT token, and sign with an HMAC signature.
- ECDH. Go. In this case we create a symmetric key from ECDH. For this we will derive a shared key from the public key of Alice and Bob, and then define a single recipient which can derive the CEK (Content Encryption Key) using their private key. We will use the curves of P-256 (secp256r1), P-384 (secp384r1), P-521 (secp521r1) or SECP256K1 (as used with Bitcoin).
- RSA using COSE and CBOR. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\).
- RSA: dQ, dP and InvQ. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). The key pair also includes \(dQ\), \(dP\) and \(InvQ\), and these can be used with the Chinese remainder theory to optimize the decryption process.
Metasploit
- Armitage and Metasploit. Go.
- Exploiting Android with Metasploit. Go.
- Exploiting Android with Metasploit - Part 2. Go.
- Exploiting Windows/Mac OS X with Metasploit. Go.
- Remote Desktop Windows/Mac OS X with Metasploit. Go.
- Metasploit. Go.
- Internet of Things Security. Go.
- Metasploit (Enumeration and Scanning). Go.
- Metasploit (Malware). Go.
IP

 The following are a few interesting techniques around IP addresses:
The following are a few interesting techniques around IP addresses:
- Your details. IP. This shows your browser details.
- IP address analyser. IP. This involves converting an IP address to the host and network part of the address.
- IP subnet analyser. IP subnets. This involves converting an IP address to the host and network part of the address.
- IP address analyser. IP. This involves analysing IP addresses.
- Max subnets. Max subnets. This involves converting an IP address to the host and network part of the address.
- Route summarization. Summarization. This involves converting an IP address to the host and network part of the address.
- Whois. Whois. This does a basic Whois on a domain.
- URL Obfuscation. Obfuscation. This outlines URL obfuscation.
- HTTP Responses. Test. HTTP.
- Capturing Network Packets (Python). WinPCap. HTTP.
Cisco related
- Routing table. Routing table. This involves viewing a routing table for a Cisco device.
- ACL Generator. ACL. This involves a simple calculator for ACLs on network ranges.
- EIGRP metrics. EIGRP. Learn the basics of EIGRP metrics.
- VoIP B/W. VoIP. Calculate bandwidth for VoIP.
- Wild Card. Wild Card. On a Cisco device a wildcard mask is used to identify the parts of an IP address that need to be matched. It thus uses a wildcard mask, where a 0 in the bit position identifies that the device should match that bit, else a 1 shows that it should ignore it.
Protocols
- HTTP. HTTP. Show the request and response for HTTP.
- Ping analyser. IP. This involves converting a ping of a site.
IP Challenges
-
IP Test 1. IP Test. IP Classification test. This is a simple test which generates a range of IP addresses, and you must determine the IP address classification.
IP Subnet Challenge 1 Demo
-
IP Test 2. IP Test. IP Classification test Part 2. This test provides an address classification, and the user must find the addresses which are of this classification.
IP Subnet Challenge 2 Demo
-
IP Test 3. IP Test. IP Classification test Part 3. This test provides an address classification, where the network part of the address is determined.
IP Subnet Challenge 3 Demo
Subnet Challenges
- Subnet Test 1. Subnet Test. Subnet Test.
-
Subnet Test 2. Subnet Test. Subnet bits.
- Subnet Test 3. Subnet Test. Find the nth usable subnet. This test involves finding the nth usable subnet.
- Subnet Test 4. Subnet Test. Maximum subnets. This is a test page to determine the maximum number of subnets and hosts/subnet for IP classed addressing.
- Subnet Test 5. Subnet Test. Maximum host/subnet. This is a test page to determine the maximum number of hosts per subnet.
- Subnet Test 6. Subnet Test. Determine the required subnet mask for a given number of subnets. This is a test page to determine the required subnet mask for a given number of subnets and a given IP address classification.
- Subnet Test 7. Subnet Test. Determine the required subnet mask for a given number of host/subnet. This is a test page to determine the required subnet mask for a given number of hosts per subnet and a given IP address classification.
- Subnet Test 8. Subnet Test. Route summarization. This involves a calculation on route summarization.
- Subnet Test 9. Subnet Test. Binary to IP.
- Subnet Test 10. Subnet Test. Hex to IP.
-
Subnet Test 13. Subnet Test. Wild card mask network bits. Find the number of bits in the network part of the wild card mask. IP Wildcard challenge
- Subnet Test 14. Subnet Test. Wild card mask host bits. Find the number of bits in the host part of the wild card mask. IP Wildcard challenge
- Subnet Test 15. Subnet Test. Wild card mask ... find the network address. Find the network for the wild card mask. IP Wildcard challenge 2
- Subnet Test 16. Subnet Test. Find a matching IP address for a network and wild card mask. Find the IP for a network and a wild card mask.
- Subnet Test 17. Subnet Test. Find an address which is on a given network. Find an IP address on a network, for a given network address and subnet mask.
- Subnet Test 18. Subnet Test. Find an IP address on the same network. Find an IP address on the same subnet.
- Subnet Test 19. Subnet Test. Find subnet. Convert subnet mask.
- Megatest. Subnet Test. Challenging test for subnets.
JavaScript

JavaScript code allows execution within the browser, rather than on the server. It is often faster than code that runs on a server. Along with this we can also use Node.js, and which runs JavaScript code on a server.
Symmetric key
- AES. AES. In this example, we will use either a pre-generated key or a random one, and use AES (Rijndael) encryption.
- ChaCha20 and Poly1305. ChaCha. This page outlines Poly1305 and ChaCha20. ChaCha20 is a symmetric key method and Poly1305 is a message authentication code (MAC). They were created by Daniel J. Bernstein, and are alternatives to AES and HMAC.
- CMS (Padding). CMS. This page uses PKIJS encrypting on CMS. With CMS we can This document describes the Cryptographic Message Syntax (CMS). With this we can encapsulate an message within an encrypted entity.

Hashing
- Hash. Hash. This page defines a JavaScript Hash calculator. This uses a client-side JavaScript code to determine the hash signatures of a text value.
Signatures
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
- Boneh–Lynn–Shacham (BLS) signature. BLS. Boneh–Lynn–Shacham (BLS) signature method produces short signatures. They use elliptic curve pairing (and which are also known as bilinear maps).
Key exchange
- ECDH. ECDH. Elliptic Curve Diffie Hellman (ECDH) is used to generate a shared key. This implementation uses Elliptic Curve Cryptography (ECC) with JavaScript.
CryptoJS
- CryptoJS. CryptoJS. This page uses client-side JavaScript code to hashing, encrypt and sign, including for symmetric key (AES), streaming ciphers, hashing methods, and HMAC.
Blockchain
- PATRICIA trie. PATRICIA. In the following, we have the Top 2,500 Web sites in the world, and implemented with a Radix Trie (aka PATRICIA trie) In the following we have the Top 2,000 web sites on the Internet, and which have been indexed using the PATRICIA trie.
Public key
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
- RSA. RSA. RSA is an asymmetric encryption algorithm, which uses two keys, one to encrypt and the other to decrypt. It was created in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman, and is still one of the most widely used encryption methods. A typical application is in authenticating a sender, where the senders private key is used to encrypt a message, and then is decrypted by the receiver with the senders public key (which is known to anyone who wants it). It is also typically used for encrypting disks/files, such as for EFS.
Digital Certificates
- X.509 certificates in JavaScript. RSA and ECDSA Signed certificates. This page will generate either RSA and ECC key pairs, and then generate X.509 certificates, using either a signature of SHA1withRSA or SHA256withECDSA. For RSA signing we use an RSA private key to sign the certificate, and with ECDSA signing we use an ECC private key to sign the certificate.
Tokens
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
Random
- Random number generator. Rand. In the past, encryption and decryption had to be done through native code libraries, such as with Bouncy Castle and OpenSSL. With the increasing processing power of Web browsers, it is now possible to use encryption using JavaScript, which thus provides client-side processing of data. This Web page uses Javascript encryption, and generates a random 256-bit text key or a hex version. The 256-bit key is generated by generating 60 random numbers (from 0-25), and converting these to an ASCII character.
Malware obfuscation
- Malware obfuscation. Obfuscation. A malware writer will often hide certain keywords from the browser/human by encoding them in another format. This is typically done for hex coding (\xZZ), 16-bit unicoding (\uZZZZ) and octal coding (\ZZZ). To test, enter a value, and then press the button and it will convert encoded string.
Message Authentication Codes
- Chaskey (MAC). Chaskey. Chaskey Cipher is light-weight cryptography method for signing messages (MAC) using a 128-bit key. The hardware implementation only requires 3,334.33 gate equivalent with an operating clock frequency of 1 MHz (whereas Keccak requires 4,658 GE). In the page we create the Mac signature and also encrypt for CBC.
Other
- Password generation/hashing. Hashing. Linux can use salted passwords where the username, hashing method and hashed password are stored in a password file [More details]. The main methods are
Hashing

At times we need to generate secrets, such as encryption keys, from passwords or nonce values. A Key Derivation Function (KDF) is a verifiable way of doing this.
Key Derivation Functions (KDFs)
The following are the tips related to hashing:
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Password strength. Test. This outlines the strength of various passwords types.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
HKDF
The following are the tips related to Key derivation hashing:
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Hazmat HKDF for different hashing methods. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
-
HKDF key derivation with OpenSSL [
here]
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
PBKDF2
The following are the tips related to Key derivation hashing:
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- AES GCM (Python) with PBKDF2. AES GCM (Python) with PBKDF2.
- Fernet with PBKDF2 . AES GCM (Python) with PBKDF2.
- PBKDF2 key derivation. AES GCM (Python) with PBKDF2.
- Key Rotation with Fernet. AES GCM (Python) with PBKDF2.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Bcrypt
The following are the tips related to Key derivation hashing:
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- BCrypt. BCrypt. BCrypt with Rust.
-
Hash to password with Go. Hashing to Argon2, Scrypt and BCrypt. Hash to password with Go, including Argon2, Scrypt and BCrypt.
scrypt
- scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Argon 2
The following are the tips related to Key derivation hashing:
- Argon 2. Go. Outline of Argon2.
- Argon 2 with NaCl. Go. Outline of Argon2 using NaCl.
- Argon 2. Argon 2. Argon 2 with Rust.
- Balloon. Go. Outline of Balloon.
Other
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
- Double ratchet. Go. Outline of double ratcheting.
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
Outline
HMAC Key Derivation function (HKDF) is used to derive an encryption key from a passphrase. Initially, HKDF creates a pseudorandom key (PRK) using a passphrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), and along with a salt value. Next, the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys [RFC 5869][article]. In this case, we will use SHA-256.
The following shows how an encryption key can be generated using HKDF, and where we need a secret and a salt value. Both Bob and Alice have the same secret and salt.

With PBKDF2 (Password Based Key Derivation Function 2), we hash for a given number of rounds:

Key exchange

Key exchange is a way for Bob and Alice to communicate and for them to agree on a shared secret. The original method defined uses discrete logarithms (Diffie-Hellman), but most modern methods use elliptic curve techniques (ECDH). As quantum computers can crack both discrete log and elliptic curve methods, there are post quantum cryptography methods proposed. This includes SIDH, CSIDH, SIKE, and NewHope.
Key interchange/generation (Diffie-Hellman)
The following relates to key interchange:
- Selecting \(g\) in Diffie Hellman. G in Diffie Hellman. Picking a safe value of the generator \(g\) in discrete logarithms.
- Diffie-Hellman. Diffie-Hellman Calculation. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Real example). Diffie-Hellman Real. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Python). Diffie-Hellman. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (pre-compute). Diffie-Hellman (pre-compute). Many sites use the same prime numbers, which can then be cracked with a pre-computing attack.
- Key generation. Key gen. This will generate keys for different methods based on a passphrase.
- Diffie-Hellman (Man-in-the-middle). DF. This outlines the man-in-the-middle method for Diffie-Hellman.
- An Alternative Diffie-Hellman method. Alterative DH. This outlines an alternative Diffie-Hellman method.
Authenticated Key Exchange
The following are the tips related to Key derivation hashing:
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- MTI/A0. MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{ax+by} \pmod p\). MTI (Matsumoto, Takashima, Imai).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0. MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{x+y} \pmod p\)
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). The resultant key is \(xyG \)
- MTI/C0. MTI/C0. This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{xy} \pmod p\)
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG\).
- MTI/C1. MTI/C1. This outlines MTI/C1, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{abxy} \pmod p\).
- MQV (Menezes–Qu–Vanstone). MQV. MQV was created Alfred Menezes, Minghua Qu and Scott Vanstone in 1995 and is an authenticated key exchange method. Alice holds a key pair \((A,a)\) and Bob has a key pair \((B,b)\). With this \(a\) is Alice's private key, and \(A=aG\) is her public key. For Bob, his public key will be \(B=aG\) and a private key of \(b\), and where \(G\) is the base point on the elliptic curve.
- HMQV (Menezes–Qu–Vanstone). HMQV. HMQV builds on MQV and adds the identity of Bob and Alice.
- ECDH with X25519 and Blake2b. ECDH with X25519 and Blake2b. This uses PyNaCl to create an authenticated key exchange and uses X25519 and Blake2b.
Elliptic Curve (ECDH) - Python
The following are the tips related to ECC:
- Elliptic Curve. Elliptic Curve. Elliptic Curve is a public key method which can also be used to generate a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with simple parameters. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
Elliptic Curve (ECDH) - Golang and Node.js
The following are the tips related to ECC:
- ECDH with Go. ECDH. ECDH with Go.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with node.js. ECDH. ECDH with node.js.
- ECDH with JavaScript. ECDH. Elliptic Curve Diffie Hellman.
Password Authenticated Key Exchange (PAKE)
The following are the tips related to Key derivation hashing:
- SPAKE2. Go. Outline of SPAKE2.
- OPAQUE. Go. Outline of OPAQUE.
- SPEKE. Go. Outline of SPEKE (Simple Password Exponential Key Exchange).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
- J-PAKE. J-PAKE. This example generates a shared key based on a shared password.
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses discrete logs.
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
PQC NIST Finalists (Key Exchange)
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Key interchange/generation (Other)

The following relates to key interchange:
- Curve25519. Curve25519. This outlines Curve25519, which is used in the Tor network.
- Authenticated Key Exchange (Discrete logs). YAK. Key exchange with public keys and uses discrete logs.
- Authenticated Key Exchange (ECC). YAK. Key exchange with public keys and uses elliptic curve methods.
- Shamir No-key protocol. Shamir No Key. In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated.
- Shamir No-key protocol (sepc256k1). Shamir No Key (EC). In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated using the sepc256k1 elliptic curve.
- Conference keying (Burmester-Desmedt method). Conference keying. In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it.
- Conference keying (Burmester-Desmedt method) - Elliptic Curve (sepc256k1). Conference keying Elliptic Curve (sepc256k1). In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it, and uses the sepc256k1 elliptic curve.
Key exchange (with pairing)
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Kryptology

We need to build a new Internet. One that is build on mathematics and certainty, rather than the patchy version we have now. For this we need a layer of cryptography at the lowest level, and build software interfaces on top of this. Along with this we now have cryptographic methods which can now provide a foundation of trust, and which preserve privacy. And so the old libraries of OpenSSL are being squeezed out in favour of the new ones which are built on a solid foundation. The latest of these new "privacy-aware" libraries is Kryptology, and created by Coinbase. This library provides the APIs that developers need, in order to apply to areas of blockchain development. This library include BLS (Boneh-Lynn-Shacham) signatures, Zero-knowledge Proofs (ZKPs) and Shamir Secret Shares (SSS). With BLS we can digitally sign for data, but also preserve its privacy. Applications of this include group signatures, where multiple entities can merge their signing keys together and provide a single signature for a transaction. With SSS, we can split encryption keys up into shares, and then distribute them across a network. When required, we can call these shares back to reconstruct the key.
The focus for Coinbase seems to be the application of privacy coins, and where no tracking can be applied to the usage of these digital coins. This should support full anonymity for transactions, as opposed to Bitcoin which only supports pseudo-anonymity.

ECC Basics
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining n.G for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Points (Base Point and Others). Elliptic Curve points. Two common curves used in ECC (Elliptic Curve Cryptography) are secp256k1 (as used in Bitcoin and Ethereum) and P256 (secp256r1). The "k1" refers to the Kolbitz curve 1 (named after the creator of ECC). With these we have a base point which are can operate on. This is typically defined as \(G\). We can then operate on this with add and multiply operation. For example, \(2G=G+G\) and \(P=n.G\). In this following we will show the base point for a number of common curves, such as secp256r1, P256, Pallas, Curve 25519, BLS12381G1, BLS12381G2, BLS12377G1 and BLS12377G2.
ECDH
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret. We will use Golang and the Krytology library.
Simple ECC on curves
- Public key points for curves. Simple. Display public key points for scalars.
BLS Curve
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
Accumulator and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
Pallas Curve
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
Pairing-based Crypto
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
ElGamal and ECC
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a numerical input.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
Shamir Secret Shares
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Homomorphic Encryption
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Zero knowledge proofs
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
Verifiable Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Hash to scalar and point
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
CP-ABE
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Lattice cryptography

Latice cryptography is proposed as a post-quantum robust method for public key encryption, especially focused on digital signatures and key exchange mechanisms (KEMs).
Principles
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
NTRU
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- Lattice Encryption: NTRU Key Generation Python). NTRU. Outlines how NTRU operates for key generation.
Homomorphic
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Digital Signatures
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
Public-Key Encryption/Key Exchange
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
Light-weight cryptography

While AES and SHA work well together within computer systems, they struggle in an IoT/embedded world as they take up: too much processing power; too much physical space; and consume too much battery power. So NIST outlines a number of methods which can be used for light-weight cryptography, and which could be useful in IoT and RFID devices [1]. They define the device spectrum as:
- Conventional cryptography. Servers and Desktops. Tablets and smart phones.
- Light-weight cryptography. Embedded Systems. RFID and Sensor Networks.
With embedded systems, we commonly see 8-bit, 16-bit and 32-bit microcontrollers, and which would struggle to cope with real-time demands for conventional cryptography methods. And in the 40+ years since the first 4-bit processor, there is even a strong market for 4-bit processors. RFID and sensor network devices, especially, have limited numbers of gates available for security, and are often highly constrained with the power drain on the device.
So AES is typically a non-starter for many embedded devices. In light-weight cryptography, we often see smaller block size (typically 64 bits or 80 bits), smaller keys (often less than 90 bits) and less complex rounds (and where the S-boxes often just have 4-bits).
For light-weight cryptography the main constraints that we have are typically related to ener requirements, gate equivalents (GEs), and timing. With passive RFID devices, we do not have an associated battery for the power supply, and where the chip must power itself from energy coupled from the radio wave. An RFID device is thus likely to be severely constrained in the power drain associated with any cryptography functions, along with being constrained for the timing requirements and for the number of gates used. Even if an RFID device has an associated battery (active RFID), it may be difficult to recharge the battery, so the drain on power must often be minimised.
There is thus often a compromise between the cryptography method used and the overall security of the method. Thus often light-weight cryptography methods balance performance (throughput) against power drain and GE, and do not perform as well as main-stream cryptography standards (such as AES and SHA-256). Along with this the method must also have a low requirement for RAM (where the method requires the usage of running memory to perform its operation) and ROM (where the method is stored on the device). In order to assess the strengths of various methods we often define the area that the cryptography function will use on the device – and which is defined in \(µm^2\). The NIST finalists are defined in this [article]
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- GIFT AEAD. GIFT. GIFT is a light-weight block cipher. It is a (NIST Finalist)
- Elephant. Elephant. Elephant is a light-weight stream cipher. It is a (NIST Finalist).
- TinyJambu. TinyJambu. TinyJambu is a light-weight block cipher. It is a (NIST Finalist)
- Isap AEAD. Isap. Isap is a light-weight block cipher. It is a (NIST Finalist)
- PHOTON-Beetle AEAD. PHOTON-Beetle. PHOTON-Beetle is a light-weight block cipher. It is a (NIST Finalist)
- Romulus AEAD. Romulus. Romulus is a light-weight block cipher. It is a (NIST Finalist)
- Sparkle AEAD. Sparkle. Sparkle is a light-weight block cipher. It is a (NIST Finalist)
- CLEFIA. CLEFIA. CLEFIA is a light-weight block cipher.
- LED. LED. LED is a light-weight block cipher.
- Piccolo. Piccolo. Piccolo is an ultra light-weight block cipher.
- PRESENT. PRESENT. Present is a light-weight block cipher.
- Pyjamask. Pyjamask. Pyjamask is a light-weight block cipher.
- SIMON. SIMON. SIMON is a light-weight block cipher.
- SKINNY. SKINNY. SKINNEY is a light-weight block cipher.
- SPECK. SPECK. SPECK is a light-weight block cipher.
- XTEA. XTEA. XTEA is a light-weight block cipher.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encryption/Decryption. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.
Light-weight crypto (Other)
- Chaskey (MAC). Chaskey. Chaskey is a light-weight MAC function.
- Chaskey (MAC). Chaskey (Python). Chaskey is a light-weight MAC function.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (ASCON)
ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRFF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
Discrete Logs (Solving)

A discrete log problem is in the form of \(g^x \pmod p\) and where we know \(g\) and \(p\) and must solve for \(x\).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Message Authentication Code (MAC)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
HMAC
The following are the tips related to Key-based hashing:
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authentication both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2), Blake2b, SM3 and SHA-3. This page outlines the HMAC-MD5 methods using the Hazmat cryptography layer.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- HMAC (COSE). Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT with HMMAC. Go. In this case we create a CWT token, and sign with an HMAC signature.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- HMAC with Rust. HMAC. HMAC with Rust.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HMAC with OpenSSL. MACs with OpenSSL. HMAC in OpenSSL for a given input value, password and hashing method.
Cipher MACs
The following are the tips related to Key-based hashing:
- MACs with OpenSSL. MACs with OpenSSL. MAC methods implemented in OpenSSL, including CMAC and GMAC.
Key-based hashing
The following are the tips related to Key-based hashing:
- SipHash. Siphash. Siphash is a fast key-based hashing method.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Meow. Meow. Meow is one of the fastest hashing methods.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
Magic Numbers

This pages contains information related to magic numbers in file formats.
Network and File Forensics
- Magic numbers. Magic. This provides information on magic number for file forensics.
Graphics formats
- JPEG Analysis. JPEGs. This provides an analysis of JPEG files.
- GIF Analysis. GIFs. This provides an analysis of GIF files.
- TIF Analysis. TIFs. This provides an analysis of TIF files.
- PNG Analysis. PNGs. This provides an analysis of PNG files.
- BMP Analysis. BMPs. This provides an analysis of BMP files.
- PSD Analysis. PSDs. This provides an analysis of PSD files.
- WMF Analysis. WMF. This provides an analysis of WMF files.
- Adobe Illustrator Analysis. AI. This provides an analysis of AI files.
- Adobe In Design Analysis. INDD. This provides an analysis of INDD files.
- MIDI file. MIDI. This provides an analysis of MID files.
- ICO file. ICO. This provides an analysis of ICO files.
- PS file. PS. This provides an analysis of PS files.
- EPS file. EPS. This provides an analysis of EPS files.
- VSD file. VSD. This provides an analysis of Microsft Visio (VSD) files.
Video and audio formats
- MP3 Analysis. MP3s. This provides an analysis of MP3 files.
- AVI Analysis. AVIs. This provides an analysis of AVI files.
- Flash SWF Analysis. SWFs. This provides an analysis of Flash files.
- Flash FLV Analysis. FLVs. This provides an analysis of FLV files.
- MP4 Analysis. MP4. This provides an analysis of MP4 files.
- MOV Analysis. MOV. This provides an analysis of MOV files.
- WMV Analysis. WMV. This provides an analysis of WMV files.
- WMA Analysis. WMA. This provides an analysis of WMA files.
- JPEG 2000 Analysis. JPEG 2. This provides an analysis of JPEG 2000 files.
- WAV Analysis. WAV. This provides an analysis of WAV files.
Zips, Archives and Library files
- ZIP/Archive Analysis. ZIPs. This provides an analysis of ZIP/Achive files.
- GZ Analysis. GZ. This provides an analysis of GZip files.
- Tar Analysis. Tar. This provides an analysis of TAR files.
- MSI Analysis. MSI. This provides an analysis of MSI files.
- OBJ Analysis. OBJ. This provides an analysis of OBJ files.
- DLL Analysis. DLL. This provides an analysis of DLL files.
- CAB Analysis. CAB. This provides an analysis of CAB files.
- EXE Analysis. EXE. This provides an analysis of EXE files.
- RAR Analysis. RAR. This provides an analysis of RAR files.
- SYS Analysis. SYS. This provides an analysis of SYS files.
- HLP Analysis. HLP. This provides an analysis of HLP files.
- VMDK Analysis. VMDK. This provides an analysis of VMDK files (VMWare Virtual Disks).
- PST Analysis. PST. This provides an analysis of PST files (Outlook Email File).
- JAR Analysis. JAR. This provides an analysis of JAR files.
- SLN Analysis. SLN. This provides an analysis of Microsoft SLN files.
- Class Analysis. Class. This provides an analysis of Java Class files.
- Zlib. Zlib. This provides an analysis of Zlib files.
Documents
- PDF Analysis. PDFs. This provides an analysis of PDF files.
- DOC Analysis. DOCs. This provides an analysis of DOC files.
- RTF Analysis. RTFs. This provides an analysis of RTF files.
- XLS Analysis. XLSs. This provides an analysis of XLS files.
- PPT Analysis. PPTs. This provides an analysis of PPT files.
- MMP File. MMP. This provides an analysis of MMP files.
- DOCX Analysis. DOCX. This provides an analysis of DOCX files.
- XLSX Analysis. XLSX. This provides an analysis of XLSX files.
- PPTX Analysis. PPTX. This provides an analysis of PPTX files.
- MDB Analysis. MDB. This provides an analysis of MDB files.
- Outlook Message Analysis. MSG. This provides an analysis of MSG files.
Disk Image
- Raw disk format. RAW. This provides an analysis of the RAW disk format.
Tests
- File Forensics Test. File Test File Forensics Test.
- File Forensics Test (Fun). File Test (Fun) File Forensics Test.
Presentations
MIRACL Core Library

MIRACL Core is an open source library, and includes a wide range of public key encryption methods. It is especially focused on elliptic curve and pairing-friendly methods, but also supports a wide range of encryption methods, including RSA, AES and hashing. Overall, it can be ported onto a wide range of systems and supports C, C++, Go, Rust, Python, Java, Javascript and Swift. Along with this it supports limited capability devices such as the Arduino infrastructure. The GitHub repository is [here].
BN254
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.

Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- CL Signatures. CL. CL Signatures in Go using MIRACL.
- CL Signatures (advanced pairing). CL. CL Signatures in Go using MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages using MIRACL.
- PS Signatures. PS. Signatures using PS for short signatures using MIRACL.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures using MIRACL.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.

Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
Rust examples
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
NaCl

PyNaCl is a Python port of LibSodium. It integrates the latest cryptography methods, such as AES, XChaCha20, Blake2b and X25519.
Symmetric Key
- Symmetric key. Symmetric key (XChaCha20 and Poly1305). With symmetric key, Bob and Alice have the same key. NaCl uses the XChaCha20 method, and which supports stream encryption (and which does not require padding as a block cipher does, and is also faster than block cipher modes). ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16 byte nonce. XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24 byte nonce. It has a lower propability of nonce misuse than ChaCha20.
- Encryption with a password. Symmetric Key with KDF. In symmetric key, we generate a secret key. This key is typically a random value or generated from a password and a salt value. If we use a password, we typically use a KDF (Key Derivation Function), and which uses a password and a salt value, in order to create a key of a given size. In this case we will use Argon2i, and which is memory resilent.
Hybrid Encryption
- Box. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Hashing
- Hashing and KDF (Argon2 and scrypt). Hashing and KDF. This case we will use PyNaCl (Networking and Cryptography) library, and which is a Python binding to libsodium. We will hash a password using SHA-256 and SHA-512, and also create a KDF (Key Derivation Function) using scrypt and Argon2.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
Ed25519
-
Ed25519. Ed25519. Using Ed25519 for digital signatures.
-
Finding Points on Ed25519. X25519 (Points).
In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 (Key Exchange)
- X25519 + BLAKE2b key-exchange. X25519. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
Curve 25519
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
Node.js

Node.js uses the JavaScript programming langauge as its base, and allows for code to be run on a server, rather than in the browser (such as with pure JavaScript). To run a node.js program, we run "node myfile.js", and use NPM to install libraries.
Symmetric key
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
RSA and public key
- RSA Opt imal Asymmetric Encryption Padding (OAEP) using Node.js. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
ECC Keys
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.

Hashing
- Hashing with node.js (All). Hashing. Hashing with node.js.
- Hashing with node.js (Selection). Hashing. Hashing with node.js.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- ECDSA with node.js. ECDSA. ECDSA with node.js.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
Key exchange
- Diffie-Hellman with node.js (random prime). DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method and uses a randomly generated prime number (press the button to generate a new prime).
- Diffie-Hellman with node.js. DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method. Each time the prime number will be fixed for the DH group selected.
- ECDH with node.js. ECDH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Elliptic Curve Diffie Hellman (ECDH) key exchange method.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
Key derivation
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
CryptoJS
- CryptoJS (in node.js). CryptoJS (Node.js). Various crypto methods in the browser.
Bulletproofs
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
Blockchain
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
Proxy encryption
- Proxy Encryption - Encrypting With Public Key, And Decrypt with Private Key. Proxy01. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This page just creates a key pair for Alice, and uses it to encrypt with the public key , and decrypt with the private key.
- Proxy Encryption. Proxy02. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This will go through the full use case of proxy re-encryption.
Tokens
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
Random
- Fortuna with node.js. Fortuna. Fortuna random numbers with node.js.
Other
- FPE with node.js. FPR. FPE with node.js.
- Puny with node.js. Puny. Puny character format with node.js.
Accumulators and Witnesses
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
PGP
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Password Entropy
- Password Entropy with Node.js. Password Entropy. Password entropy measures the strength of a password, and is measured as the number of bits which could represent all of the possibilities. An entropy score of less than 25 identifies a poor password, and between 25 and 50 is a weak password. For 50 to 75 we have a reasonable password, and between 75 and 100 is a very good password. Over 100 is an excellent password. The strength of the password relates to the number of characters used, and also the number of characters in the password.
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
- Homomorphic Encryption with Node.js and BGV. Homomorphic Encryption with Node.js and BFG. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BGV method.
Oblivious Transfer (OT)

Oblivious Transfer allows Bob to select data from Alice, but for Alice not to know which value has been selected.
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
OpenSSH

OpenSSH supports the usage of the SSH protocol. This allows for a remote login. One tool which is uses is ssh-keygen, and which allow for the generation of RSA, DSA and elliptic-curve keys that. These can be used for user and host authentication, such as for GitHub login and Cloud instance login.
OpenSSH
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here].
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
Outline

OpenSSL

OpenSSL is a standard library that implements cryptography.
Symmetric key (Command line)
-
Symmetric Key Encryption (OpenSSL 1.x) [here]. In this case we will create cipher text from OpenSSL 1.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 1.x) [here].In this case we will decrypt cipher text from OpenSSL 1.x using a key derived from a password
-
Symmetric Key Encryption (OpenSSL 3.x) [here]. In this case we will create cipher text from OpenSSL 3.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 3.x) [here].In this case we will decrypt cipher text from OpenSSL 3.x using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password.
Hashing
-
Hashing [here] OpenSSL supports a wide range of hashing methods including BLAKE2b, Gost, MD4, MD5, RMD-160, SHA-1, SHA-3, SHA-256 and SHA-512.
Libre OpenSSL
-
Symmetric Key Encryption using Libre OpenSSL [here]. In this case we will create cipher text from Libre OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption using Libre OpenSSL [here]. In this case we will decrypt ciphertext from Libre OpenSSL using a key derived from a password.
-
Hashing [here] Libre OpenSSL supports a wide range of hashing methods including Gost, MD4, MD5, RMD-160, SHA-1, SHA-256 and SHA-512.
Diffie-Hellman parameter generation
-
DH Parameters with OpenSSL [here]. The Diffie-Hellman (DH) method is perhaps one of the greatest inventions in Cybersecurity, and was created by Whitfield Diffie and Marty Hellman. With the DH method, Bob creates a random value (\(b\)) and Alice also creates a random value (\(a\)). Next Bob computes \(B=g^b \pmod p\) and sends it to Alice. Alice computes \(A=g^a \pmod p\) and sends this to Bob. Bob raises the value of \(A\) to the power of \(b\) and takes \(\pmod p\), and Alice raises \(B\) to the power of \(a\) and takes \(\pmod p\). In the end, they will have the same shared value: \(g^{ab} \pmod p\). This can then be used to derive an encryption key that they can use for a secure tunnel. Overall, \(p\) is the large prime number, and also known as the shared modulus between Bob and Alice.
Key derivation function
-
PBKDF2 key derivation with OpenSSL [here] PBKDF2 (Password Key Derivation Function 2) is a key derivation method. Overall it is relatively slow in its operation and where we take a password, a salt value, hashing method, and a number of iterations, in order to produce a given size of encryption key.
-
HKDF key derivation with OpenSSL [here] HKDF (HMAC Key Derivation function) is used to derive an encryption key from a pass phrase. Initially HKDF creates a pseudorandom key (PRK) using a pass phrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), andalong with a salt value. Next the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys.
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Passwords
-
Password example [here]. This page uses the OpenSSL library hash password generator, which is used in UNIX systems for the hashing of passwords which are contained in /etc/shadow and /etc/passwd. For newer passwords, the "-1" options is used to created the hashed value.
-
Hashed passwords with OpenSSL [here].
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
Public key
-
Generating an ECC key pair with OpenSSL [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)).
-
Generating an RSA key pair with OpenSSL [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2).
-
Generating an RSA key pair with OpenSSL with encryption [here]. This page implements RSA key pair generation with an encrypted key pair. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). In this case we will encrypt the key pair with either 3DES, 128-bit AES, 192-bit AES or 256-bit AES. The same password must be used to encrypt and decrypt.
-
Generate prime with OpenSSL [here]. Prime numbers are important in public key encrytion, and are used with RSA and ECC. For RSA, we generate two prime numbers (\(p\) and \(q\)) and which are multiplied together to create a modulus (\(N\)). If these prime numbers have 512 bit values, the modulus will be a 1,024 bit value. This defines the basic secure of RSA. With elliptic curve we use smaller prime numbers, such as 256-bit values for the secp256k1 curve.
ASN1 parsing
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). We will parse using asn1parse, and reveal the parameters.
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)) [RSA key pair]. We will parse using asn1parse, and reveal the parameters.
- DSA Parameters with asn1parse. DSA parameters with OpenSSL with asn1parse. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA (Digital Signature Algorithm)
- DSA Parameters. DSA parameters with OpenSSL. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
MAC (Message Authentication Code)
- HMAC with OpenSSL. MACs with OpenSSL. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authenticate both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2) and SHA-3. In this case we will use OpenSSL to generate the HMAC value.
- MACs with OpenSSL. MACs with OpenSSL. In the following we will generate MACs for HMAC, GMAC, CMAC, Blake2bmac, Blake2smac, KMAC128 and KMAC256. Overall, we will use an encryption key defined as a hex value for GMAC and CMAC, and a pass phrase for the others. The message is "hello".
Signing
- Digital signing a plaintext message with OpenSSL. Signing with OpenSSL. With digital signing, we can take a message, and create a signature. This normally involves signing with a private key and digital certificate. The signed message can be an a MIME format, and which can be integrated into an email message. In this can we have a 512-bit RSA key pair that will sign a plain text message.
Encrypting emails
- Encrypting an email message in OpenSSL. Encrypting messages with OpenSSL. With public key encryption, we can take a message, and encrypt it with the recipiant's public key. In this can we have a 512-bit RSA public key to encrypt a message.
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Random number generation with OpenSSL
-
Random number generator [here]. Random numbers are important in generating encryption keys and salt values. In this case OpenSSL generates a random number (in a Base64 format) for a given number of bytes.
Outline (C#/Python)
-
Symmetric Key Encryption (C#) [here]. This page uses the OpenSSL library through a C#/.NET wrapper. The DLLs it interfaces to are libeay32.dll and ssleay32.dll. OpenSSL supports a wide range of encryption methods, including 128-bit AES, 192-bit AES, 256-bit AES and Blowfish (bf). Different modes of ECB, CBC, and OFB are implemented. The examples use a default IV of "1234".
-
AES in Python with OpenSSL output [here]
-
Producing OpenSSL AES Encrypted String from C# [here]
Digital Certificates
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
Paillier - Partial Homomorphic Encryption

The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Fundamentals
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier).
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Using RSA
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
Applications
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Public key points for curves. Simple. Display public key points for scalars.
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.

Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.

Principles
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Paillier
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
Go Format Preserving Encryption (FPE)
- FPE with Go. FPE. An implementation of Format Preserving Encryption (FPE) for FFX1 and FFX3.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
AWS Encryption
- AWS Symmetric Key Encryption. AWS (Symmetric key). Using symmetric key in AWS.
Go Oblivious Transfer
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Dragon Fly
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
Embedding data in an ECC point
- Embedding data in a point. Go. With Elliptic Curve Cryptography (ECC), we use points on an elliptic curve to represent our data. These are defined with (x,y) points. With this, it is possible to embedded a certain amount of data into the point - as long as it still gives us a valid point on the curve. This example will Curve 25519 to embed data, and is achieved by storing the length of the data in a single byte in the point, and then store the data as byte values in the point (followed by random data). To decode, we can then just read the first byte for the length of the message, and then reveal the data encoded into the point..
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Hashing (Cryptographic)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
Benchmarks and Password strength
The following are the tips related to hashing:
- Password strength. Test. This outlines the strength of various passwords types.
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
Theory
The following are the tips related to hashing:
- Balls in bins. BiBa. This implemented balls in bins.
- Birthday attack (with Big Integers). Calc. This provides a simple example of the birthday attack.
- Birthday attack. Calc. This provides a simple example of the birthday attack.
- Differential Cryptanalysis (Hashing). Cryptanalysis. This provides an implementation of differential cryptanalysis for hashing methods.
MD5, SHA-1
The following are the tips related to hashing:
- MD2 and MD4 MD2/4. The MD2 and MD4 hashing functions were developed by Prof Ronald Rivest in 1989 and 1990, respectively. They both produce a 128-bit hash, but have been shown be vulnerable to attack (see the Collision section in the page).
- MD5 and SHA-1 (to Base-64) with salt Salt. It is possible to add salt to the MD5 algorithm, to mix it up a little.
- MD5 and SHA-1 (to Base-64) Hash. MD5 and SHA-1 produces a hash signature, and the output is typically shown in a hex format or a Base-64. In this example the output is converted into a Base-64 format.
- MD5 and SHA-1. Hash. MD5 and SHA-1 methods produce a hash signature, and are the two of the most widely used methods. The MD5 algorithm has been shown to have weaknesses, and a collision of message hashes has been shown to occur in less than one day. An MD5 signature has 128 bits, an SHA-1 signature has 160 bits, and an SHA-256 signature has 256 bits.
- MD5 Cracking. Hash Cracker. MD5 has a 128-bit signature and can be cracked using rainbow tables. This page tries to crack the MD5 signature.
- Hashing with Go. Hashing. Hashes with Go.
- Detecting hash types. Hash type. This detects has values.
- OpenSSL hashing. Range of methods. Outlines the methods used in OpenSSL
- Hash. Hash. Hashing using JavaScript
- Hashing with node.js. Hashing. Hashing with node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Hashing methods
-
Hazmat Hashes. Hazmat Hashes. This includes the hashing methods in the Hazmat cryptography library. This includes Blake2p, Blake2s, MD5, SHA1, SHA224, SHA256, SGA384, SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHA512, SHA512-224, SHAKE128 and SHA256.
-
Hazmat Hashes. Hazmat Hashes. In this case we will implement Python code to determine SHA1, SHA2, SHA3, Blake2, MD5 and SM3 hashes.
OpenSSL Passwords
-
Password example [here]
-
Hashed passwords with OpenSSL [here]
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Blake 3 hashes
The following are the tips related to similarity hashing:
- Blake 3 in Python. Hashing. Blake 3 hashing.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
Other Hash functions
The following are the tips related to hashing:
- Bloom Filter Bloom filter. A Bloom filter goes a probabilistic method of determining if an element is in a data structure, using indexed hashing methods.
- Cuckoo Table Cuckoo filter. A Cockoo table uses two hash funtions.
- Chaffing. Chaffing. This produces a keyless system.
- GP Hashing with Go. GP Hashing. GP Hashes with Go.
- LDAP. LDAP. This produces a LDAP hash signature for a password.
- LM Hash. LM Hash. This is an LM Hash Calculator. LM Hash is used in many versions of Windows to store user passwords that are fewer than 15 characters long.
- Murmur and FNV Murmur and FNV. While hashing methods such as MD5 and SHA-1 use crypto methods, the Murmur and FNV hashes uses a non-cryptographic hash function. This can be used for general hash-based lookup and was designed by Austin Appleby. It has good performance compared with other hashing methods.
- Pearson. Pearson. This uses a non-crypto hash.
- phpass. phpass. This produces a phpass hash signature for a password.
- Tiger. Tiger. Tiger is a 192-bit hash function and was designed by Ross Anderson and Eli Biham in 1995. It is often used by clients within Gnutella file-sharing networks and does not suffer from known attacks on MD5 and SHA-0/SHA-1. Tiger2 is an addition, in which the message is padded with a byte of 0x80 (in a similar way to MD4, MD5, and SHA), whereas in Tiger it is 0x01. Otherwise, the two methods are the same in their operation.
- Whirlpool. Whirlpool. Whirlpool is a 512-bit cryptographic hash function and was created by Vincent Rijmen (one of the AES creators) and Paulo Barreto, in 2000.
- WPA-2 hash . WPA-2 hash. Implements SHA-2 hash.
- Reusable hash collisions. Reusable hash collisions. Reusable hash collisions.
- The Length Extension Attack. Length Extension Attack. The MD construct has many weaknesses, and one of the most serious is the length extension attack. With this an adversary (Eve) can take a hash for an unknown message, and then add additional data to produce a new valid hash. The hash methods which are at risk against the length extension attack are MD5, SHA-1 and SHA-256. Please follow the code link below to run an example.
- Consistent hashing. Consistent hash. This outlines the usage of Consistent hashes.
- ROR13 (Module and Function). ROR13. With ROR13 we take each 8-bit character and then convert to a unicode value (with 16 bits). Then for each character we rotate the bits right by thirteen places. The resultant hash is then just the accumuluation of the rotated values.
- ROR13 (Function). ROR13 (Function). With ROR13 we take each 8-bit character and then convert to a unicode value (with 16 bits). Then for each character we rotate the bits right by thirteen places. The resultant hash is then just the accumuluation of the rotated values.
- GOST, Streebog256 and Streebog512. GOST, Streebog256 and Streebog512. GOST94 is a hashing method developed with Euro-Asian Council for Standardization, Metrology and Certification (EASC). This has since been developed in the Streebog256 and Streebog512 hashing method. In this case, we will use Libre OpenSSL to convert data into a hashed value.
RIPEMD
- RIPEMD (RACE Integrity Primitives Evaluation Message Digest) and GOST. RIPEM160. RIPEMD is a 128-bit, 160-bit, 256-bit or 320-bit cryptographic hash function, and was created by Hans Dobbertin, Antoon Bosselaers, and Bart Preneel. It is used on TrueCrypt and is open source. The 160-bit version is seen as an alternative to SHA-1, and is part of ISO/IEC 10118
- RIPEMD160. RIPEM160. RIPEMD160 is a 160-bit cryptographic hash function, and was created by Hans Dobbertin, Antoon Bosselaers and Bart Preneel. RIPEMD160 is used in Bitcoin applications.
Chameleon hashes
The following are the tips related to Chameleon hashing:
- Chameleon hash in Golang Chameleon. With a Chameleon hash, we have a normal hash value which is resistant to collisions, but with a known secret we can easily create a collision. The concept was first defined by Krawcyk and Rabin.
Similarity hashes
The following are the tips related to similarity hashing:
- Similarity hash: SimHash (Charikar similarity) in Python Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash (Nilsimsa similarity) Nilsimsa. The Nilsimsa similarity is used to find similarities between spam emails.
- Minhash (Jaccard similarity) Jaccard similarity. The Minhash method is used to find similarities between strings, files and metadata.
- String enthropy String enthropy. Measurement of the entropy of strings.
- Counting identical elements (HyperLogLog) HyperLogLog. Counting the number of identical elements.
SHA-3 and SHA-3 contenders
The following are the tips related to Key derivation hashing:
- Blake and Blake 2. Blake. Implements Blake and Blake 2 (SHA-3 contender).
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
- Grøstl. Grøstl. Implements Grøstl (SHA-3 contender).
- KangarooTwelve. KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- SHA-3, Keccak and SHAKE . SHA-3. Implements SHA-3, Keccak and SHAKE (SHA-3 winner).
- SHA-3. SHA-3. SHA-3 was known as Keccak and is a hash function designed by Guido Bertoni, Joan Daemen, Michaël Peeters, and Gilles Van Assche. MD5 and SHA-0 have been shown to be susceptible to attacks, along with theoretical attacks on SHA-1. NIST thus defined there was a need for a new hashing method which did not use the existing methods for hashing, and setup a competition for competing algorithms. In October 2012, Keccak won the NIST hash function competition and is proposed as the SHA-3 standard. It should be noted that it is not replacement SHA-2, which is currently a secure method. Overall Keccak uses the sponge construction where the message blocks are XORed into the initial bits of the state, and then inevitably permuted.
- cSHAKE. cSHAKE. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS. With the SHA-3 hashing method, we have four different cryptographic hashing methods (SHA3-224, SHA3-256, SHA3-384, and SHA3-512) and two XOF functions (SHAKE128 and SHAKE256). With SHAKE128 and SHAKE256 we can integrate domain separation between different functions — and which are known as cSHAKE128 and cSHAKE256.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- Skein. Skein. Implements Skein (SHA-3 contender).
Key derivation hashing
The following are the tips related to Key derivation hashing:
- Argon2. Go. Outline of Argon2.
- Argon2 with NaCl. Go. Outline of Argon2 using NaCl.
- Balloon. Go. Outline of Balloon.
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- Double ratchet. Go. Outline of double ratcheting.
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- Scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat HKDF. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
Non-crypto/fast hashing
The following are the tips related to non-crypto hashing:
- A perfect hash Perfect hash. This is a non-crypto hash which optimizes the hash value.
- The universal hash Universal hash. This related to the concept of a universal hash.
- FNV. FNV. FNV is one of the fastest hashing methods.
- Murmur. Murmur. Murmur is one of the fastest hashing methods.
- Siphash. Siphash. Siphash is a fast hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- xxHash. xxHash. xxHash is one of the fastest hashing methods.
- Meow. Meow. Meow is one of the fastest hashing methods.
- o1Hash. o1Hash. o1Hash is one of the fastest hashing methods.
- CRC-32. CRC-32. CRC-32 is one of the fastest hashing methods.
- wyhash. wyhash. wyhash is one of the fastest hashing methods.
- CityHash. CityHash. CityHash is one of the fastest hashing methods, and is generally free of security problems.
- FarmHash. FarmHash. FarmHash is one of the fastest hashing methods, and is generally free of security problems.
- Non-crypto. Non-crypto. This includes a range of fast non-cryptography hashing methods.
- Non-crypto hashes (C++): Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro. Non-crypto hashes: Farm, City, xxHash, MUM, Spooky 2, Murmur, Metro and t1ha0. This includes a range of fast non-cryptography hashing methods for Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro using C++ methods.
- Pearson. Pearson. Pearson is one of the fastest hashing methods, and has been designed for 8-bit processors.
- C++: t1ha. t1ha. t1ha is one of the fastest hashing methods, and has been designed for 64-bit processors.
- C++: Spooky. Spooky. Spooky is one of the fastest hashing methods, and V2 has a 32-bit, 64-bit and 128-bit version.
- C++: xxHash. xxHash. xxHash is one of the fastest hashing methods, and has good performance for short data inputs.
- C++: MUM. MUM. MUM is one of the fastest hashing methods.
- C++: FNV 1/1a. FNV 1/1a. FNV 1/1a is one of the fastest hashing methods, and is particularily useful when there are small changes in strings, such as with IP addresses and URLs.
- C++: MetroHash. MetroHash. MetroHash is one of the fastest hashing methods.
- C++: CityHash. CityHash. CityHash was created by Google and is one of the fastest hashing methods. It was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Farm. FarmHash. FarmHash was created by Google and is one of the fastest hashing methods. It is an improvement to CityHash.
- C++: Murmur. Murmur. Murmur is one of the fastest hashing methods, but was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Halftime. Halftime. Halftime is one of the fastest hashing methods and was created by Jim Apple at Apache.
- C++: Highway. Highway. Highway is an ultra-fast keyed-hash, and is more than five times faster than SipHash. It was created by Jyrki Alakuijala, Bill Cox, Jan Wassenberg at Google.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
- C++: CLHash. CLHash. CLHash is an ultra-fast hashing method and focused on improving performance of the hashing of long strings.
- C++: FalkHash. FalkHash. FalkHash is an ultra-fast hashing method and beats most of the other non-cryptography methods for performance. It is focused on the x64 architecture and integrates with AES-NI.
- C++: wyHash. wyHash. wyHash is an ultra-fast hashing method.
- C++: Fibonacci. Fibonacci. Fibonacci is an ultra-fast hashing method.
- C++: Lookup3. Lookup3. Lookup3 is an ultra-fast hashing method.
Key-based hashing
The following are the tips related to Key-based hashing:
- SiphashSiphash. Siphash is a fast key-based hashing method.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
One Time Passwords/Time Stamps
The following are the tips related to hashing:
- One Time Passwords. One Time. This allows a new unique password to be created each instance, based on an initial seed.
- Timed One Time Password (TOTP). Timed One Time Password. This allows a new unique passcode to be created each instance, based on an initial seed for a given time window. We will use a five second window in this case, where a new passcode is generated every five seconds, based on an initial seed of a pass phrase.
- Hashed One Time Password (HOTP). Hashed One Time Password. This allows a new unique passcode to be created each instance, based on a counter value and an initial seed.
- Time Stamp Protocol. TSP. This creates a time stamp for data.
- HOTP and TOTP (Python). OTP. This creates hashed passwords.
eXtendable-Output Function (XOF)
- eXtendable-Output Function (XOF) usign CIRCL. XOF. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS.
SHAKE
The following are the tips related to hashing:
- SHAKE. SHAKE. Implements SHAKE and which is an Extendable Output Function (XOF).
- SHAKE with Go. SHAKE. This implements SHAKE in Go.
- libDisco with Go. libDisco. This implements libDisco.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify
the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods
such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC methods using the Python cryptography primitives for HMAC-MD5.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
Quantum-robust Public Key (Hash-based signature)
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
Hash to ECC point
- Hash to password with Go. Hash to password. Hash to password with Go.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve with libnum.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.

Password-hashing functions using Rust
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing (Non-cryptographic)

You might know those slow old hashing methods, such as MD5, SHA-1, and SHA-256. Well, they were designed to be fast, but also highly secure. But, if we just need a hashing method, such as for a hashtable or Bloom filter, we often don’t need all the security that comes with the main cryptography hashing methods. And so we have the non-cryptography hashing methods, and which are often ultra-fast and highly efficient. To show the difference, in a test, SHA-1 — one of the fastest cryptography hashing methods — managed a processing rate of 364.95 MiB/s, while t1ha was nearly a 100 times faster, at 34,636 MiB/s.
Non-crypto/fast hashing
The following are the tips related to non-crypto hashing:
- A perfect hash Perfect hash. This is a non-crypto hash which optimizes the hash value.
- The universal hash Universal hash. This related to the concept of a universal hash.
- FNV. FNV. FNV is one of the fastest hashing methods.
- Murmur. Murmur. Murmur is one of the fastest hashing methods.
- Siphash. Siphash. Siphash is a fast hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- xxHash. xxHash. xxHash is one of the fastest hashing methods.
- Meow. Meow. Meow is one of the fastest hashing methods.
- o1Hash. o1Hash. o1Hash is one of the fastest hashing methods.
- CRC-32. CRC-32. CRC-32 is one of the fastest hashing methods.
- wyhash. wyhash. wyhash is one of the fastest hashing methods.
- CityHash. CityHash. CityHash is one of the fastest hashing methods, and is generally free of security problems.
- FarmHash. FarmHash. FarmHash is one of the fastest hashing methods, and is generally free of security problems.
- Non-crypto. Non-crypto. This includes a range of fast non-cryptography hashing methods.
- Non-crypto hashes (C++): Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro. Non-crypto hashes: Farm, City, xxHash, MUM, Spooky 2, Murmur, Metro and t1ha0. This includes a range of fast non-cryptography hashing methods for Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro using C++ methods.
- Pearson. Pearson. Pearson is one of the fastest hashing methods, and has been designed for 8-bit processors.
- C++: t1ha. t1ha. t1ha is one of the fastest hashing methods, and has been designed for 64-bit processors.
- C++: Spooky. Spooky. Spooky is one of the fastest hashing methods, and V2 has a 32-bit, 64-bit and 128-bit version.
- C++: xxHash. xxHash. xxHash is one of the fastest hashing methods, and has good performance for short data inputs.
- C++: MUM. MUM. MUM is one of the fastest hashing methods.
- C++: FNV 1/1a. FNV 1/1a. FNV 1/1a is one of the fastest hashing methods, and is particularily useful when there are small changes in strings, such as with IP addresses and URLs.
- C++: MetroHash. MetroHash. MetroHash is one of the fastest hashing methods.
- C++: CityHash. CityHash. CityHash was created by Google and is one of the fastest hashing methods. It was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Farm. FarmHash. FarmHash was created by Google and is one of the fastest hashing methods. It is an improvement to CityHash.
- C++: Murmur. Murmur. Murmur is one of the fastest hashing methods, but was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Halftime. Halftime. Halftime is one of the fastest hashing methods and was created by Jim Apple at Apache.
- C++: Highway. Highway. Highway is an ultra-fast keyed-hash, and is more than five times faster than SipHash. It was created by Jyrki Alakuijala, Bill Cox, Jan Wassenberg at Google.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
- C++: CLHash. CLHash. CLHash is an ultra-fast hashing method and focused on improving performance of the hashing of long strings.
- C++: FalkHash. FalkHash. FalkHash is an ultra-fast hashing method and beats most of the other non-cryptography methods for performance. It is focused on the x64 architecture and integrates with AES-NI.
- C++: wyHash. wyHash. wyHash is an ultra-fast hashing method.
- C++: Fibonacci. Fibonacci. Fibonacci is an ultra-fast hashing method.
- C++: Lookup3. Lookup3. Lookup3 is an ultra-fast hashing method.
A fuller test with SMHasher gives [here]:
Hash function MiB/sec cycl./hash cycl./map Quality problems
------------------------------------------------------------------
o1hash 12439661.09 16.77 166.13 insecure, no seed, zeros, fails all tests
crc32_hw1 23208.73 46.74 179.70 insecure, 100% bias, collisions, distrib, BIC, machine-specific (x86 SSE4.2)
t1ha0_aes_noavx 22785.26 38.71 180.61 LongNeighbors, machine-specific (x86 AES-NI)
t1ha0_aes_avx1 22714.85 48.12 226.52 LongNeighbors, machine-specific (x64 AVX.txt)
t1ha0_aes_avx2 22345.33 44.38 556.47 LongNeighbors, machine-specific (x64 AVX2)
falkhash 20202.42 173.63 321.52 Sparse, LongNeighbors, machine-specific (x64 AES-NI)
MeowHash64low 17378.06 85.48 237.60 Sparse, invertible, machine-specific (x64 AES-NI)
MeowHash32low 17374.64 85.48 258.53 Sparse, invertible, machine-specific (x64 AES-NI)
MeowHash 17371.91 85.48 247.96 Sparse, invertible, machine-specific (x64 AES-NI)
FarmHash32 17112.05 47.7 214.71 machine-specific (x64 SSE4/AVX)
xxh3 16538.52 32.81 184.86 DiffDist bit 7 w. 36 bits, BIC
xxh3low 16462.36 32.77 199.79
farmhash32_c 16299.81 47.79 219.19 machine-specific (x64 SSE4/AVX)
xxh128low 15174.85 33.79 187.05
xxh128 15174.14 40.46 195.65
farsh32 14053.09 74.29 245.33 insecure: AppendedZeroes, collisions+bias, MomentChi2, LongNeighbors
metrohash64crc_2 14034.84 48.94 162.54 UB, Cyclic 8/8 byte, DiffDist, BIC, machine-specific (SSE4.2/NEON)
metrohash64crc_1 14000.5 49.08 150.54 UB, Cyclic 8/8 byte, DiffDist, BIC, MomentChi2, machine-specific (SSE4.2/NEON)
metrohash128crc_1 13948.67 65.2 168.08 UB, machine-specific (SSE4.2/NEON)
metrohash128crc_2 13920.19 65.12 176.70 UB, machine-specific (SSE4.2/NEON)
halftime_hash128 13478.23 97.79 252.14
wyhash32low 12911.09 29.59 205.43 2 bad seeds
wyhash 12879 30.35 196.77 2^33 bad seeds
CityCrc128 12343.43 74.5 209.75
fletcher2 12011.15 25.29 298.60 bad seed 0, UB, fails all tests
fletcher4 11928.55 25.27 293.49 bad seed 0, UB, fails all tests
halftime_hash256 11620.28 98.44 252.60
fibonacci 11339.87 26.33 705.64 UB, zeros, fails all tests
ahash64 9862.62 27.32 181.68 rust
Spooky128 9751.14 63.84 192.47 UB
Spooky64 9747.47 62.2 191.71 UB
Spooky32 9747.13 62.24 196.96 UB
t1ha1_64le 9723.86 34.39 176.91 Avalanche
cmetrohash64_1 9683.33 45.2 161.01 UB, LongNeighbors, BIC, MomentChi2
cmetrohash64_2 9669.95 44.75 149.67 LongNeighbors
metrohash64_2 9668.51 44.45 164.30 UB, LongNeighbors
metrohash64 9664.61 44.59 150.74 UB, LongNeighbors, BIC
metrohash64_1 9664.57 45.37 152.31 UB, LongNeighbors, BIC, MomentChi2
cmetrohash64_1o 9658.31 42.84 163.45 UB, LongNeighbors, BIC, MomentChi2
FNV1a_YT 9643.42 32.06 175.19 bad seed, UB, fails all tests
City128 9640.19 88.45 225.38
metrohash128_2 9584.94 59.1 167.43 UB, LongNeighbors
metrohash128 9569.16 58.68 167.53 UB, LongNeighbors
metrohash128_1 9558.17 59.04 175.94 UB, LongNeighbors
FarmHash128 9409.63 74.52 210.25
VHASH_32 9404.99 77.01 250.57 sanity, Seed, MomentChi2
VHASH_64 9392.39 74.72 227.92 sanity, Seed, MomentChi2
farmhash128_c 9244.13 79.08 209.44
t1ha2_atonce 9237.12 38.94 194.32 Zeroes low3
City64noSeed 9090.42 32.23 171.53 Avalanche, Sparse, TwoBytes, MomentChi2, Seed
City64low 9089.45 47.75 201.73
t1ha2_stream 9068.55 74.56 219.85 Sparse, Permutation, LongNeighbors
City64 9066.9 47.81 197.78 Sparse, TwoBytes
t1ha2_stream128 9065.5 93.19 236.50 Sparse, Permutation, LongNeighbors
xxHash64 8936.63 51.31 174.34
pengyhash 8744.48 85.31 222.45
farmhash64_c 8713.16 47.96 201.00
FarmHash64 8684.76 48.13 200.51
crc64_hw 8440.13 34.94 141.15 insecure, 100% bias, collisions, distrib, BIC, machine-specific (SSE4.2/NEON)
t1ha2_atonce128 8350.99 55.65 203.53 LongNeighbors
PMPML_64 8161.19 53.2 179.16 unseeded: Seed, MomentChi2, BIC
halftime_hash512 7681.62 125.81 274.01
tabulation 7621.75 42.19 179.93
t1ha1_64be 7481.37 38.16 193.22 Avalanche
MUMlow 7225.18 37.85 197.92 UB, 5 bad seeds
farsh64 7216.29 130.3 302.44 insecure: AppendedZeroes, collisions+bias, MomentChi2, LongNeighbors
MUM 7134.56 37.85 172.34 UB, too many bad seeds, machine-specific (32/64 differs)
nmhash32 7003.3 68.93 216.59
PMPML_32 6704.53 53.5 197.43 Avalanche >512, unseeded: Seed, BIC, MomentChi2, PerlinNoise
nmhash32x 6342.95 56.41 217.75
crc32_hw 6330.42 35.55 170.16 insecure, 100% bias, collisions, distrib, BIC, machine-specific (SSE4.2/NEON)
FNV2 6258.84 33.25 142.89 fails all tests
FNV1A_Pippip_Yurii 6258.46 28.19 184.41 UB, sanity, fails all tests
FNV1A_Totenschiff 6258.23 27.99 198.20 UB, zeros, fails all tests
HighwayHash64 6242.58 99.55 248.41
mx3 6146.02 52.48 173.09 UB
xxHash32 6040.87 51.77 177.91 LongNeighbors, collisions with 4bit diff, MomentChi2 220
prvhash64s_64 5481.48 170.05 325.39
mirhash 5413.73 39.68 154.47 UB, 2^36 bad seeds, LongNeighbors, machine-specific (32/64 differs)
mirhash32low 5412.76 39.79 182.13 UB, 4 bad seeds, Cyclic, LongNeighbors, machine-specific (32/64 differs)
Murmur3F 5226.4 52.18 175.85 UB
prvhash64s_128 5161.33 260.96 442.70
t1ha0_32le 5132.18 54.83 193.53 Sparse, LongNeighbors
halftime_hash64 4990.72 120.55 281.64
Murmur2B 4882.95 39.72 149.43 UB, 1.8% bias, collisions, 3.4% distrib, BIC
seahash32low 4801.33 58.54 227.31 PerlinNoise 32, !msvc
seahash 4796.97 58.55 201.58 PerlinNoise, !msvc
fasthash32 4737.61 45.32 181.86 UB, insecure
fasthash64 4737.21 42.79 164.87 UB, insecure, Moment Chi2 5159 !
umash32_hi 4662.92 54.22 214.20
umash64 4662.09 53.42 188.09
umash32 4633.19 53.42 216.33
t1ha0_32be 4585.59 55.98 183.45 Sparse, LongNeighbors
clhash 4472.31 82.72 229.73 PerlinNoise, machine-specific (x64 SSE4.2)
tabulation32 4317.34 35.45 197.20 collisions
Murmur2C 4092.99 51.84 164.65 UB, 2^32 bad seeds, 91% bias, collisions, distr, BIC, LongNeighbors
farsh128 3776.92 232.48 398.67
City32 3675.04 57.73 212.04
TSip 3228.14 57.96 211.71 !msvc
Murmur3C 3197.63 67.9 198.00 UB, LongNeighbors, Text, DiffDist
Crap8 3149.63 36.23 195.11 UB, 2.42% bias, collisions, 2% distrib
Murmur2 3146.91 41.87 187.89 UB, 1 bad seed, 1.7% bias, 81x coll, 1.7% distrib, BIC
Murmur2A 3146.79 46.87 191.96 UB, 1 bad seed, 12.7% bias, LongNeighbors
aesnihash 2963.39 71.24 217.73 fails many tests, machine-specific (x64 AES-NI)
BEBB4185 2951.62 222.03 343.63 UB, too many bad seeds, msvc-specific
jodyhash6 2848.42 29.99 164.36 bias, collisions, distr, BIC, LongNeighbors
wyhash32 2532.89 48.4 484.57 2 bad seeds, 32-bit
umash128 2427.46 70.6 197.29
Murmur3A 2413.88 53.36 182.37 UB, 1 bad seed, Moment Chi2 69
prvhash64_64m 2386.19 51.18 186.87
prvhash64_128 2383.57 103.44 246.45
prvhash64_64 2375.72 51.61 190.97
hasshe2 2372.52 68.64 216.74 Permutation,TwoBytes,Zeroes,Seed
PMurHash32 2344.78 58.48 196.43 1 bad seed, Moment Chi2 69
mirhashstrict32low 2218.87 65.48 190.59 1 bad seed, MomentChi2 9
mirhashstrict 2217.32 65.53 182.07
sha1ni 2019.96 135.84 564.40 insecure,sanity, Permutation, Zeroes, machine-specific
sha1ni_32 2019.94 136.82 589.46 machine-specific
superfast 1956.25 53.61 180.10 UB, bad seed 0, 91% bias, 5273.01x collisions, 37% distr, BIC
sha2ni-256_64 1910.34 146.06 595.16 Zeroes, machine-specific
sha2ni-256 1906.77 145.47 603.08 insecure,sanity, Permutation, Zeroes, machine-specific
farsh256 1895.77 459.86 575.95
SipHash13 1889.1 89 199.95 0.9% bias
Murmur1 1804.67 51.51 188.41 UB, 1 bad seed, 511x collisions, Diff, BIC
lookup3 1658.31 48.84 194.15 UB, 28% bias, collisions, 30% distr, BIC
pearsonbhash64 1486.34 104.32 185.03
poly_1_mersenne 1431.65 54.49 189.52 fails most tests
jodyhash32 1428.37 44.36 185.85 bias, collisions, distr, BIC LongNeighbors
pearsonbhash128 1347.03 121.75 214.84
poly_2_mersenne 1323.69 66.93 190.88
poly_3_mersenne 1323.59 74.86 206.77
poly_4_mersenne 1323.57 82.67 200.36
blake3_c 1285.91 340.01 552.63 no 32bit portability
GoodOAAT 1052 71.62 192.19
pearsonbhash256 998.9 167.05 261.29
SipHash 980.88 127.77 246.19
MicroOAAT 977.6 59.61 185.06 100% bias, distrib, BIC
FNV1a 791.84 69.69 177.84 bad seed, zeros, fails all tests
sdbm 791.84 67.69 177.06 bad seed 0, fails all tests
FNV64 791.82 70.24 159.29 fails all tests
bernstein 791.82 68.63 180.71 bad seed 0, fails all tests
beamsplitter 789.22 682.45 1150.3 UB, too many bad seeds
HalfSipHash 755.78 114.47 243.72 zeroes
chaskey 753.23 153.42 288.26 PerlinNoise
x17 527.9 98.78 184.09 99.98% bias, fails all tests
JenkinsOOAT_perl 452.49 118.78 194.78 bad seed 0, test FAIL
MurmurOAAT 452.49 113.07 197.83 bad seed 0, 1.5-11.5% bias, 7.2x collisions, BIC, LongNeighbors
JenkinsOOAT 452.48 142.85 213.93 bad seed 0, 1.5-11.5% bias, 7.2x collisions, BIC, LongNeighbors
crc32 392.1 131.62 204.58 insecure, 8590x collisions, distrib, PerlinNoise
sha1-160 364.95 1470.55 1794.1 Comb/Cyclic low32
rmd256 362.49 617.02 815.44 Bad seeds
blake2b-256_64 356.97 1222.76 1435.0
blake2b-224 356.59 1228.5 1425.87
blake2b-160 356.08 1236.84 1458.15
blake2b-256 355.97 1232.22 1443.31 Sparse high 32-bit
md5-128 353.76 638.29 803.39
md5_32a 353.64 629.85 799.56 Sparse high 32-bit
sha1_32a 353.03 1385.8 1759.9 Cyclic low32, 36.6% distrib
rmd128 334.36 659.03 838.32 Bad seeds
blake2s-128 295.3 698.09 1059.2
pearsonhash64 287.95 174.11 196.50 Avalanche, Seed, SSSE3 only. broken MSVC
pearsonhash128 287.95 171.72 194.61 Avalanche, Seed, SSSE3 only. broken MSVC
pearsonhash256 264.51 184.87 218.79 Avalanche, Seed, SSSE3 only. broken MSVC
blake2s-256 215.28 1014.88 1230.38
blake2s-160 215.01 1026.74 1239.54
blake2s-256_64 211.52 1044.22 1228.43
blake2s-224 207.06 1063.86 1236.50
rmd160 202.16 1045.79 1287.74 Bad seeds, Cyclic hi32
sha2-256_64 148.01 1376.34 1624.71 Bad seeds, Moment Chi2 7
sha2-256 147.8 1374.9 1606.06 Bad seeds, Moment Chi2 4
sha2-224_64 147.6 1360.1 1620.93 Bad seeds, Cyclic low32
sha2-224 147.13 1354.81 1589.92 Bad seeds, Comb low32
asconhashv12 144.98 885.02 1324.23
sha3-256 100.58 3877.18 4159.79 PerlinNoise
sha3-256_64 100.57 3909 4174.63 PerlinNoise
asconhashv12_64 86.73 684.02 606.93
floppsyhash 35.72 1868.92 1411.07
tifuhash_64 35.6 1679.52 1212.75 Cyclic low32
Problems include:
- Bad Seeds. A random seed is often used to initialise the hash. This problem relates to having a bad seed..
- Undefined behaviour (UB). This includes Misaligned, oob (Out of bounds), Signed integer overflow and Shift exponent overflow.
o1hash is the fastest, and a quick and dirty hashing method. It is generally not secure. t1h (Fast Positive Hash) requires AES-NI (Intel Advanced Encryption Standard Instructions) and is one of the fastest hashes at 22.785 Gbps. It has fairly good security levels. Meow comes in around 17.378 Gbps. We can see that SHA-1-160 runs as 364 Mbps, while Meow runs at 17.378 Gbps. Blake 3 is one of the fast cryptography hash and has a rate of 1.285 Gbps, and Blake 2 gives a rate around 215 Mbps. SHA-3 gives hashing rates of 100.58 Mbps.
Google recommend the following for 64-bit hashes without quality problems:
- xxh3low
-
wyhash
-
ahash64
-
t1ha2_atonce
-
FarmHash
-
halftime_hash128
-
Spooky32
-
pengyhash
-
nmhash32
-
mx3
-
MUM/mir
- fasthash32
Hash-based Signatures

With hash-based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature, unless we create a stateless method, such as SPHINCS+ [1]. Currently NIST have the final round for the Post Quantum Cryptography competition, and for digital signatures, SPHINCS+ is one of the alterative finalists (alongside Picnic).
Hash-based signature (theory)
- BiBa (Go). BiBa. An overview of BiBa One Time Signature [9]. Basically the method involves us taking a hash of a value using a standard hashing method, such as with SHA-256. There will then be \(2^{256}\) different hashing values. We aim to create a signature for a message, so Bob (the signer) selects a number of random values for his private key value and then publishes the hash of each of these (\(P_1\), \(P_2\), etc). He then sends these public keys to Alice. Now when Bob wants to sign a message, he will take one of his private key values, and then hashes it, and then determines the bin that it should be placed. In this case, we could use the \(\pmod N\) function on the hash, and where \(N\) is the number of bins. If we select \(2^{10}\) there will be 1,024 bins.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature [9].
Hash-based signature (stateful)
- BLISS - Post-quantum signing. BLISS. One of the alteratives to the usage of our existing public key methods is the usage of lattice cryptography, and especially in the usage of Ring Learning With Errors (RLWE). An important application is within digital signatures, and where Bob will sign something with his private key, and then Alice can prove that he signed it with his public key. One post-quantum signature method is BLISS (short for Bimodal Lattice Signature Scheme) [8]. It was created by Léo Ducas, Alain Durmus, Tancrède Lepoint and Vadim Lyubashevsky in 2013.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Hash to Obtain Random Subset (HORS) [3] is a quantum robust hashed-based one-time signature. With this we create a series of integers for our private keys and organise into an indexable form. Then we hash them to a sequence of public key values. Next we segment the hash of the message into a series of n-bit integer values. The signature is then achieved through a look-up of the value in the public key list.
- Lamport Signatures. Lamport. Outlines Lamport signatures [7]. When we sign a message we take its hash and then encrypt with our private key. The public key is then used to prove it, and will prove that we signed it with our private key. The Lamport signature uses 512 random hashes for the private key, and which are split into Set A and Set B. The public key is the hash of each of these values. The size of the private key is 16KB (2×256×256 bits) and the public key size is also 16 KB (512 hashes with each of 256 bits).
- Winternitz Signatures (W-OTS). Winternitz. Outlines Winternitz signatures [4, 5]. W-OTS uses relatively small key and signatures sizes, and is thought to be quantum robust. It generates 32x256 bit random private keys. We then hash these a number of times, and is defined by a parameter (w). If we use w=8, we hash the private keys by (2w). This creates 32x256 bits public keys. The signature is the created by taking eight bits at a time, and then the 8-bit binary int (n) is subtracted from 256 and the private key is the hashed 256-n times. The signature is then 32 hashes which are derived from random private keys. To verify the signature, the recipient parses the hash of the signature (using 8 bits at a time, and extracting the 8 bit int, n).
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method [6], and which is used within speeds-up of Hashing-based signature methods. Using methods such as SHA-1 and SHA-2 (aka SHA-256) will be inefficient as they tend to compress the data inputs through a number of stages. Haraka v2 [6] is different as focuses on inputs of just 256 bits (32 bytes) or 512 bits (64 bytes). This makes the method useful when we are dealing with key and hash values, and is especially useful for hash-based signatures. The output is 256 bits long, but where the input can be either be 256 bits (Haraka256) or 512 bits (Haraka512). These lengths are typically for the outputs of modern hashing applications. The Haraka method, too, has been optimized with AES instructions (AES-NI - Intel Advanced Encryption Standard New Instructions) and which are supported within the hardware of the processor. As Haraka is focused on short messages, the number of rounds within the hashing process has been reduced.
Hash-based signature (stateless)
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ digital signature. SPHINCS digital signature. Outline of the a SPHINCS stateless digital signature method [1].
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
Hash-based signature (Merkle-based)
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
Introduction
Many of the problems we see on the Internet relate to the lack of trust within transactions. The emails you receive and the Web sites that you visit often have very little trust built into them. For trust the email address of the sender, but anyone can fake that address. So increasingly we create a digital signature, and where we sign our messages. In this way, we can check for authentication, integrity and non-repudiation.
With the Alice creates a key-pair: a public key and a private key. She then takes a hash of the message, and then encrypts this hash with her private key, and passes the message and the signature to Bob. Bob then reads the message and takes a hash of it. He then decrypts Alice's signature with her public and checks the hashes. If they match, he knows that she signed and that it has not been changed along the way:
Currently, we often use RSA, DSA and ECDSA to sign our messages. These are based on the difficulty of finding out the factors of a number and on the processing of discrete logarithms. At the current time these methods are computationally hard problems, but with quantum computers, they become much easier. This was shown by Peter Shor who illustrated that it was possible to crack them in polynomial time.
Of all the methods that are being proposed, the hash-based methods look as if they have a good chance of success of creating quantum robust signatures. methods and code-based methods are being researched, but the usage of hashing methods is already well and could provide the best alternative to the existing methods. Hashing methods, too, often bring other advantages, such as forward secure, which means that a key which is cracked will not reveal all the previous keys.
Merkle trees
The root of hash-based methods isin Merkle trees, and which are a way of hashing is used in many applications, including with Bitcoin, Ethereum, Git distribution systems, No SQL, and in many P2P applications. With a Merkle tree we take our data elements, and then hash them, and take pairs of these hashes to create a new hash, and so we build a table. At the top of the tree is the root element (in this case Hash1234):

In this way, we can use the tree to see if we have matching data on systems.On a P2P network, we can transfer a file by splitting it into data segments and then distributing these segments across the network. A trusted source will have the complete Merkle tree for rebuilding the file, and a client can thus rebuild from the Merkle tree and determine the parts of the file which are still missing. Once transferred the root hash (and all the other hashes) will then match. In its core method, the Merkle Signature Scheme (MSS) has serious performance and memory issues, but enhanced methods such as XMSS create with much less of a performance hit.
One-time signatures (Lamport)
The core method used in hash-based signatures is that of the one-time signature, and where we create a new key pair for every method we need to create. If the keys were reused, an attacker could start to learn the private key, and thus spoof messages. One of the first methods was produced by Leslie Lamport and Whitfield Diffie, in 1979, and is defined as:
- We create two data sets with 256 random 256-bit numbers (Set A and Set B). These are the private key (512 values).
- we take the hash of each of the random numbers. This will give 512 hashes and will be the public key.
- We then hash the message using and then test each bit of the hash (0 ... 255). If it is a 0, we use the ith number in Set A, else we use the ith number from Set B.
- The signature is then 256 random numbers (taken from either Set A or Set B) and the public key is the 512 hashes (of Set A and Set B).
The public and private keys are then each 16KB in size. A demo of the method is here.

Figure 1: Lamport method
The major problem with the method is that a key pair for every message. also in 1979, found a solution with Merkle trees.
One-time signature (W-OTS)
To improve performance method (and which reduced key sizes), Merkle proposed Winternitz OTS (named after Robert Winternitz). With this method was possible to sign many bits at the same time. The method is:
- We create 32 256-bit random numbers. These 32 values will be our private key.
- We then hash each of these values 256 times. These 32 values will be our public key.
- We now take the message and hash it using SHA-256. This produces 32 8-bit values (N1, N2 ... N32).
- Next we take each 8-bit value in the hash of the message, and then hash 256-N times (where N is the value of the 8-bit value).
- To prove the signature, we take the message and hash it with SHA-256, and then take each 8-bit value. We then hash the 8-bit signature value by the number of times defined by the message hash value (N1, N2..). The result for each operation should equal the public key value.
This is illustrated below in Figure 2. A demo of the method is here.

Figure 2: W-OTS
Hash-based Signatures
The methods such as W-OTS and Lamport only provide for a one-time signature. In order to sign many messages, we can use the Merkel signature scheme (MSS). With this we take a hash of the keys and build these as the leaves of the tree. The root of the tree is then the public key - the verification key. We then just use the private key of the W-OTS method to create the signature. The sender also sends the authentication path, which is the neighbouring nodes within the path and which leads to the root of the tree. The recipient can then rebuild the tree using the verification key (which can be received a digital certificate) and the authentication path. For the next message we move onto another key pair and where the index of the key part is revealed.
In the following example we have our root as the public key, and then want to sign with Key3. We then show the authentication path which takes us to the root (as defined in the bold arrows):

Conclusions
Hashed-based methods look to be a strong contender for weaning us off RSA, DSA and ECDSA, but we will have to look at the stateful generation of keys. For this we will have to generate a bank of key pairs (2, 4, 8, 16, etc) and then create the public key from the root of the Merkle tree. We must then remember the keys we have used previously, and only use an unused one. Once we use our new key pair, we then show our working-out as to how the private key is integrated into our tree. It is a bit like a teacher marking a question correctly, and asking for the working out that go you to the answer.
References
[1] Bernstein, D. J., Hopwood, D., Hülsing, A., Lange, T., Niederhagen, R., Papachristodoulou, L., ... & Wilcox-O’Hearn, Z. (2015, April). SPHINCS: practical stateless hash-based signatures. In Annual international conference on the theory and applications of cryptographic techniques (pp. 368-397). Springer, Berlin, Heidelberg [paper].
[2] Bernstein, D. J., Hülsing, A., Kölbl, S., Niederhagen, R., Rijneveld, J., & Schwabe, P. (2019, November). The SPHINCS+ signature framework. In Proceedings of the 2019 ACM SIGSAC conference on computer and communications security (pp. 2129-2146) [paper].
[3] Reyzin, L., & Reyzin, N. (2002, July). Better than BiBa: Short one-time signatures with fast signing and verifying. In Australasian Conference on Information Security and Privacy (pp. 144-153). Springer, Berlin, Heidelberg [paper].
[4] Merkle, R. C. (1989, August). A certified digital signature. In Conference on the Theory and Application of Cryptology (pp. 218-238). Springer, New York, NY.
[5] Hülsing, A. (2013, June). W-OTS+–shorter signatures for hash-based signature schemes. In International Conference on Cryptology in Africa (pp. 173-188). Springer, Berlin, Heidelberg.
[6] Kölbl, S., Lauridsen, M. M., Mendel, F., & Rechberger, C. (2016). Haraka v2–efficient short-input hashing for post-quantum applications. IACR Transactions on Symmetric Cryptology, 1-29. [here]
[7] Lamport, L. (1979). Constructing digital signatures from a one-way function (Vol. 238). Technical Report CSL-98, SRI International. [paper]
[8] Ducas, L., Durmus, A., Lepoint, T., & Lyubashevsky, V. (2013, August). Lattice signatures and bimodal Gaussians. In Annual Cryptology Conference (pp. 40-56). Springer, Berlin, Heidelberg [paper].
[9] Perrig, A. (2001, November). The BiBa one-time signature and broadcast authentication protocol. In Proceedings of the 8th ACM Conference on Computer and Communications Security (pp. 28-37) [paper] .
Hashing (Simularity)

Similarity hashes allow for two data objects to be compared for their similarity.
Similarity assessment methods
The following relate to the basic methods used for string similarity:
- String similarity String similarity. This measures edit distance (including Levenshtein distance), Jaro (including Jaro-Winkler), and QGrams.
- String enthropy String enthropy. Measurement of the entropy of strings.
- Soundex Soundex. Soundex uses a phonetic algorithm to classify a sound as it is pronounced. It focuses on matching phrases which have minor spelling errors.
Similarity hashes
The following are the tips related to similarity hashing:
- Similarity hash: SimHash (Charikar similarity) in Python Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash (Nilsimsa similarity) Nilsimsa. The Nilsimsa similarity is used to find similarities between spam emails.
- Context Triggered Piecewise Hashes (CTPH): ssdeep CTPH similarity. Kornblum [6] created ssdeep and which computes fuzzy hashes. This aims to match similar byte sequences, no matter if there are differences between these sequences. For this we break a file up into fragments with a rolling hash function. We then produce a small hash for each of those fragments. These are then aggregated to produce the complete hash of a file. In comparing file signatures, we treat the resultant hash value as a string, and then uses an edit distance method to compare.
- TLSH (A Locality Sensitive Hash) TLSH similarity. In malware analysis and in text similarity, we often have to identify areas of data within files which are similar. One method is TLSH (A Locality Sensitive Hash), and which was defined by Oliver et al [7]. It is used - along with ssdeep - by VirusTotal to identify a hash value for malware.
- Minhash (Jaccard similarity) Jaccard similarity. The Minhash method is used to find similarities between strings, files and metadata.
- Counting identical elements (HyperLogLog) HyperLogLog. Counting the number of identical elements.
Hazmat cryptography

The Cryptography library in Python contains interfaces to common cryptographic algorithms, including symmetric key methods, hashing, public key, and key derivation functions. Many of these are contained with the Hazmat (Harzardous Material) primative setup.
Hashing, HMAC, CMAC, Poly1305 and HKDF
-
Hazmat Hashes. Hazmat Hashes. This includes the hashing methods in the Hazmat cryptography library. This includes Blake2p, Blake2s, MD5, SHA1, SHA224, SHA256, SGA384, SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHA512, SHA512-224, SHAKE128 and SHA256.
-
Hazmat Hashes. Hazmat Hashes. In this case we will implement Python code to determine SHA1, SHA2, SHA3, Blake2, MD5 and SM3 hashes.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
- Hazmat HKDF. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
- Hazmat CMAC. Hazmat CMAC. CMAC methods using the Python cryptography primitives.
- Hazmat Poly1305. Hazmat Poly1305. Poly1305 methods using the Python cryptography primitives.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
Symmetric key
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat. Implementation of ChaCha20/Poly1305 with a random key using Hazmat.
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat. Implementation of AES GCM with a random key using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hazmat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Hazmat Symmetric Key Padding. Symmetric key. This includes the coverage of padding with Hazmat.
- Hazmat Symmetric Key Padding. Symmetric key. This includes the coverage of padding with Hazmat.
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
- Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . With 3DES encryption, we use a 128-bit key and a 64-bit IV value. The two modes supported are ECB (without salt) and CBC (with salt). The DES algorithm has been around for a long time, and the 56-bit version is now easily crackable (in less than a day on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases, and splits the key into two. Overall the key size is typically 112 bits (with a combination of the three keys - of which two of the keys are the same). In this case we will use PKCS7 padding, and which fills the input data with a value that is equal to the number of padding bytes. Overall, DES has a 64-bit block size, and which equates to eight ASCII characters.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key . And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.
Asymmetric key
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- ECC key generaton with Hazmat. Elliptic Curve key gen. Creating ECC keys using Hazmat and Python.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- Hazmat RSA signing (with key values). RSA signing with Hazmat. RSA signing using Python and with Hazmat (with key values).
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here]
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Signatures. DSA Signatures. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. The ECDSA method is an extension of DSA, but implemented with elliptic curve (EC) methods. As with most public key signing methods, we take a hash of a message, and then apply a private key to create a signature (\(r,s\)). This is done by creating a random value (\(k\)) to produce the signature. The signature is then verified using the associated public key. This then verifies the creator of the signature and that the message has not been changed.
Digital Signature: ECDSA/EdDSA
- ECDSA with Hazmat. ECDSA wih Hazmat. This outlines ECDSA with Hazmat.
- Ed25519 for EdDSA signatures with Hazmat. EdDSA: Ed25519. This page uses the Hazmat primitives for the cryptography library.
- Ed448 for EdDSA signatures with Hazmat. EdDSA: Ed448. This page uses the Hazmat primitives for the cryptography library.
- Ed25519 using NaCl. Ed25519. This page uses the NaCl port from libsodium.
- ECDSA Signatures with Hazmat (SECP256R1, SECP384R1, SECP521R1, SECP224R1, SECP192R1, and SECP256K1). ECC Signatures. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and then creates an ECDSA signature for a given message.
Digital Signature: RSA
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
Key exchange: ECDH/X25519
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives and showing the byte values for the key.
Tokens
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
Homomorphic Encryption

Homomorphic encryption supports mathematical operations on encrypted values. Partial Homomorphic Encryption (PHE) supports a few arithmatic operations, while Full Homomorphic Encryption (FHE) supports add, subtract, multiply, and divide. Homomorphic encryption normally involves a public key to encrypt the data, and a private key to decrypt it. There have been four main generations of homomorphic encryption, and the most recent being the HEAAN method.
Simple
- Simple Homomorphic Cipher. Hom. This outlines a Simple Homomorphic cipher.
- Simple Homomorphic Cipher (Python). Hom. This outlines a Simple Homomorphic cipher with Python.
- Full Homomorphic Cipher with a Public Key. Public key. This outlines a Simple Homomorphic cipher using a public key
ElGamal
- ElGamal Homomorphic Cipher (Go). ElGamal. This outlines ElGamal Homomorphic cipher with Go.
- ElGamal Homomorphic Cipher (Go) - Divide. ElGamal. This outlines ElGamal Homomorphic cipher with Go with divide.
- ElGamal Homomorphic Cipher (Go) - Additive. ElGamal. This outlines ElGamal Homomorphic cipher with Go with addition.
- ElGamal Homomorphic Cipher for Multiplication (Python). ElGamal. This outlines ElGamal Homomorphic multiplication with Python.
- ElGamal Homomorphic Cipher for Division (Python). ElGamal. This outlines ElGamal Homomorphic division with Python.
- ElGamal Homomorphic Cipher for Addition (Python). ElGamal. This outlines ElGamal Homomorphic addition with Python.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (Python). ElGamal. This outlines ElGamal Homomorphic subtraction with Python.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
RSA
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
ZKP
- Full Homomorphic Cipher to determine if Bob is older. Older. This outlines a Simple Homomorphic cipher to determine if Bob is older than Alice.
- Full Homomorphic Cipher to determine matching password. Password. This outlines a Simple Homomorphic cipher to determine if a password matches
- Interactive ZKP With Probablistic Methods. ZKP. Interactive ZKP With Probablistic Methods using Python.
- Full Homomorphic Cipher for Millionaire's Problem. Millionaire. This outlines a Simple Homomorphic cipher for the Millionaire's Problem
Voting
- Trusted voting. Trusted. A trusted voting method.
Secret share
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Lattice
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
Full Homomorphic Cipher
- Full Homomorphic Cipher for 2-bit Adder. Adder. This outlines a Simple Homomorphic cipher for a 2-bit adder with DGHV.
- Full Homomorphic Cipher for Full Adder. Full Adder. This outlines a Simple Homomorphic cipher for a full adder with DGHV.
- Full Homomorphic Cipher for 4-bit Adder. Adder. This outlines a Simple Homomorphic cipher for a 4-bit adder with DGHV.
- Full Homomorphic Cipher for 4-bit Adder/Subtractor. Subtract. This outlines a Simple Homomorphic cipher for a 4-bit adder/subtractor with DGHV.
- Full Homomorphic Cipher to XOR two integers. X-OR. This outlines a Simple Homomorphic cipher to X-OR two integers
Paillier
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier) .
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Damgård-Jurik Homomorphic Encryption With Secret Shares. Damgård-Jurik Method. Two of the major areas of developments within cybersecurity will be the usage of homomorphic encryption, and in the usage of Shamir secret sharing. With homomorphic encryption, we can encrypt values, and then operate on them with arithmetic functions (such as add, subtract and multiply), and with Shamir secret sharing, we can split secrets into shares, and then distributed them over networks. These approaches will take privacy to new levels. So let’s look at the Damgård-Jurik method.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Learning with Errors (LWE)
- Learning With Errors . LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret key value (s) and another value (e). Next we select a number of values (t[]) and calculate g[] = t[] x s + e. The values of g[] and t[] become our public key.
- Public Key Encryption with Learning With Errors (LWE). LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret value (s) and which is our private key. We then create a public key which is based on random numbers (A), and then generate another set of numbers (B) which is based on A,s and random errors e. An example of encryption with multiple bits is given.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE)
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Others
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
- SIDH Go. SIDH. Post-quantum key exchange.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Anonymous crypto. Anon. Anonymous crypto.
- Rho factorization. Rho. Rho alogorithm.
- Post-quantum signing (BLISS). BLISS. BLISS method.
Homomorphic Encryption with Krytology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Homomorphic hashing
- Homomorphic Hashing with Golang. Homomorphic hashing. Normally with hashing methods, we need to take all the previous data and new data in order to create a new hash value for our data. In a homomorphic hashing method, we can basically take the previous hash, and then add on any new data values. We can also remove previous data values from our hash, too. This is more efficient in computing, as we do not have to process all of our data into a new hash, and can use simple homomorphic operations for the computation. The method we will use (LtHash) was initially defined by Bellare and Micciancio and updated Lewi et al at Facebook.
Identity Based Encryption (IBE)

This page outlines a few basic principles around the usage of IBE.
Identity Based Encryption (Pairing based)
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pair-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Identity Based Encryption (Others)
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Güther's implicitly certified identity-based public keys (IBE). Günther. This method allows Bob to generate Alices public key from her identity and publicly available parameters.
- Girault's self-certified public keys (IBE). Girault. This method allows Bob to generate Alices public key from her identity and publicly available parameters, and where we use an RSA key pair to self-certify Alice's public key.
Intrusion Detection Systems (IDS)
- Intrusion Detection Systems. Snort. This outlines some of the basics of IDS, including the requirement for Intrusion Detection Systems (IDSs), and where they are used.
- Advanced Network Forensics (Snort). Adv Network Forensics. This provides information on how to detect threats through network forensics with Snort
Snort

- Snort IDS. Snort. This is a Snort Analyser.
- Snort IDS 2 with rules editor. Snort. This provides information on how to detect threats through network forensics with Snort, and with an editing function for rules.
Presentation
IoT

The key objectives of this page are: Understand how a Pen Tester can generate vulnerabilities and test using the Metasploit framework; Define the options and payloads required to generate and use vulnerabilities; and Gaining remote access.
Devices
- Access the Wi-fi kettle. Go. This page outines how to access a wi-fi enabled kettle.
- Philips Hue Wireless Lighting. Go. This page shows how to use RESTful Web services to access to the Hue Led Lamps.
- Kali and R-PI. Go. This page shows the setup of a security testing infrastructure using a Raspberry Pi (R-PI) and a wifi access point.
- Kali, R-PI and RF electrical socket. Go. This page shows the control of an RF electical socket from a RPI.
- Capture from a Polar H10 heat rate sensor. Go. This page shows the capture of the Polar H10 heart sensor with an Ubertooth One.
- Trusted IoT: Linking IoT Devices to NFTs. Go. This page outlines a research paper which links a device to an NFT (Non-fungible Token).
Shodan Scanning
-
IoT Scan (Shodan). Go. This page includes a search of the Internet for key terms, such as for "apache", "mysql" and "cisco".
- IoT Banner Scan (Shodan). Go. This page includes a search of the Internet for key terms with the banner as a result (for the Top 10)
- Internet Services (Shodan). Go. This page includes a search of the Internet for key terms and display the IP address and port.
IoT Libraries
- libDisco with Go. libDisco. libdisco is a Golang library which can be used to create secure connections. It is based on the STROBE protocol framework. Symmetric cryptographic primitives rely on SHA-3 permutation, and asymmetric cryptographic primitives on X25519 and ed25519. STROBE defines a range of cryptographic protocols to integrate with IoT devices. In order to reduce processing, energy and memory requirements, it only uses Keccak (SHA-3) to encrypt and authenticate messages.
COSE/COBR
In computer security, we often have to represent binary data, in single values or groups of characters, bytes, words, long words, signed integers, floating-point values, double-precision floating-point values, and so on. This might be in the form of a data object, a signature or even encrypted content. For this, the ANS.1 DER format is often used, such as presenting digital certificates and signatures. An improvement on this for small messages with security is Concise Binary Object Representation (CBOR) — and which is defined in RFC8949 [1]. While JSON represents text-based data objects CBOR focuses on binary objects. It has been designed to create a lightweight encoder and decoder. This supports the use of CBOR within an IoT infrastructure. The data, also, does not require a data schema to be able to decode it, along with being extensible. CBOR defines the format of binary data with data objects and messages. We can then integrate security with CBOR Object Signing and Encryption (COSE), and which is defined in RFC8152 [2]. This includes signatures, message authentication codes (MACs), encryption and creating serialised objects.
- 128-bit AES GCM. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) can then build on this to include signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use a symmetric key to encrypt a message, and then decrypt it. In this case we will use AES GCM with a static 128-bit key ("0x000102030405060708090a0b0c0d0e0f").
- 256-bit AES GCM. Go. In this case we will use AES GCM using a random 256-bit key (32 bytes).
- EdDSA. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) [2] can then build on this to includes signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use EdDSA to create a signature for a message.
- ECDSA. Go. In this case we will use ECDSA to create a signature for a message.
- HMAC. Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT. Go. In this case we create a CWT token, and sign with an HMAC signature.
- ECDH. Go. In this case we create a symmetric key from ECDH. For this we will derive a shared key from the public key of Alice and Bob, and then define a single recipient which can derive the CEK (Content Encryption Key) using their private key. We will use the curves of P-256 (secp256r1), P-384 (secp384r1), P-521 (secp521r1) or SECP256K1 (as used with Bitcoin).
- RSA using COSE and CBOR. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\).
- RSA: dQ, dP and InvQ. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). The key pair also includes \(dQ\), \(dP\) and \(InvQ\), and these can be used with the Chinese remainder theory to optimize the decryption process.
Metasploit
- Armitage and Metasploit. Go.
- Exploiting Android with Metasploit. Go.
- Exploiting Android with Metasploit - Part 2. Go.
- Exploiting Windows/Mac OS X with Metasploit. Go.
- Remote Desktop Windows/Mac OS X with Metasploit. Go.
- Metasploit. Go.
- Internet of Things Security. Go.
- Metasploit (Enumeration and Scanning). Go.
- Metasploit (Malware). Go.
IP

 The following are a few interesting techniques around IP addresses:
The following are a few interesting techniques around IP addresses:
- Your details. IP. This shows your browser details.
- IP address analyser. IP. This involves converting an IP address to the host and network part of the address.
- IP subnet analyser. IP subnets. This involves converting an IP address to the host and network part of the address.
- IP address analyser. IP. This involves analysing IP addresses.
- Max subnets. Max subnets. This involves converting an IP address to the host and network part of the address.
- Route summarization. Summarization. This involves converting an IP address to the host and network part of the address.
- Whois. Whois. This does a basic Whois on a domain.
- URL Obfuscation. Obfuscation. This outlines URL obfuscation.
- HTTP Responses. Test. HTTP.
- Capturing Network Packets (Python). WinPCap. HTTP.
Cisco related
- Routing table. Routing table. This involves viewing a routing table for a Cisco device.
- ACL Generator. ACL. This involves a simple calculator for ACLs on network ranges.
- EIGRP metrics. EIGRP. Learn the basics of EIGRP metrics.
- VoIP B/W. VoIP. Calculate bandwidth for VoIP.
- Wild Card. Wild Card. On a Cisco device a wildcard mask is used to identify the parts of an IP address that need to be matched. It thus uses a wildcard mask, where a 0 in the bit position identifies that the device should match that bit, else a 1 shows that it should ignore it.
Protocols
- HTTP. HTTP. Show the request and response for HTTP.
- Ping analyser. IP. This involves converting a ping of a site.
IP Challenges
-
IP Test 1. IP Test. IP Classification test. This is a simple test which generates a range of IP addresses, and you must determine the IP address classification.
IP Subnet Challenge 1 Demo
-
IP Test 2. IP Test. IP Classification test Part 2. This test provides an address classification, and the user must find the addresses which are of this classification.
IP Subnet Challenge 2 Demo
-
IP Test 3. IP Test. IP Classification test Part 3. This test provides an address classification, where the network part of the address is determined.
IP Subnet Challenge 3 Demo
Subnet Challenges
- Subnet Test 1. Subnet Test. Subnet Test.
-
Subnet Test 2. Subnet Test. Subnet bits.
- Subnet Test 3. Subnet Test. Find the nth usable subnet. This test involves finding the nth usable subnet.
- Subnet Test 4. Subnet Test. Maximum subnets. This is a test page to determine the maximum number of subnets and hosts/subnet for IP classed addressing.
- Subnet Test 5. Subnet Test. Maximum host/subnet. This is a test page to determine the maximum number of hosts per subnet.
- Subnet Test 6. Subnet Test. Determine the required subnet mask for a given number of subnets. This is a test page to determine the required subnet mask for a given number of subnets and a given IP address classification.
- Subnet Test 7. Subnet Test. Determine the required subnet mask for a given number of host/subnet. This is a test page to determine the required subnet mask for a given number of hosts per subnet and a given IP address classification.
- Subnet Test 8. Subnet Test. Route summarization. This involves a calculation on route summarization.
- Subnet Test 9. Subnet Test. Binary to IP.
- Subnet Test 10. Subnet Test. Hex to IP.
-
Subnet Test 13. Subnet Test. Wild card mask network bits. Find the number of bits in the network part of the wild card mask. IP Wildcard challenge
- Subnet Test 14. Subnet Test. Wild card mask host bits. Find the number of bits in the host part of the wild card mask. IP Wildcard challenge
- Subnet Test 15. Subnet Test. Wild card mask ... find the network address. Find the network for the wild card mask. IP Wildcard challenge 2
- Subnet Test 16. Subnet Test. Find a matching IP address for a network and wild card mask. Find the IP for a network and a wild card mask.
- Subnet Test 17. Subnet Test. Find an address which is on a given network. Find an IP address on a network, for a given network address and subnet mask.
- Subnet Test 18. Subnet Test. Find an IP address on the same network. Find an IP address on the same subnet.
- Subnet Test 19. Subnet Test. Find subnet. Convert subnet mask.
- Megatest. Subnet Test. Challenging test for subnets.
JavaScript

JavaScript code allows execution within the browser, rather than on the server. It is often faster than code that runs on a server. Along with this we can also use Node.js, and which runs JavaScript code on a server.
Symmetric key
- AES. AES. In this example, we will use either a pre-generated key or a random one, and use AES (Rijndael) encryption.
- ChaCha20 and Poly1305. ChaCha. This page outlines Poly1305 and ChaCha20. ChaCha20 is a symmetric key method and Poly1305 is a message authentication code (MAC). They were created by Daniel J. Bernstein, and are alternatives to AES and HMAC.
- CMS (Padding). CMS. This page uses PKIJS encrypting on CMS. With CMS we can This document describes the Cryptographic Message Syntax (CMS). With this we can encapsulate an message within an encrypted entity.

Hashing
- Hash. Hash. This page defines a JavaScript Hash calculator. This uses a client-side JavaScript code to determine the hash signatures of a text value.
Signatures
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
- Boneh–Lynn–Shacham (BLS) signature. BLS. Boneh–Lynn–Shacham (BLS) signature method produces short signatures. They use elliptic curve pairing (and which are also known as bilinear maps).
Key exchange
- ECDH. ECDH. Elliptic Curve Diffie Hellman (ECDH) is used to generate a shared key. This implementation uses Elliptic Curve Cryptography (ECC) with JavaScript.
CryptoJS
- CryptoJS. CryptoJS. This page uses client-side JavaScript code to hashing, encrypt and sign, including for symmetric key (AES), streaming ciphers, hashing methods, and HMAC.
Blockchain
- PATRICIA trie. PATRICIA. In the following, we have the Top 2,500 Web sites in the world, and implemented with a Radix Trie (aka PATRICIA trie) In the following we have the Top 2,000 web sites on the Internet, and which have been indexed using the PATRICIA trie.
Public key
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
- RSA. RSA. RSA is an asymmetric encryption algorithm, which uses two keys, one to encrypt and the other to decrypt. It was created in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman, and is still one of the most widely used encryption methods. A typical application is in authenticating a sender, where the senders private key is used to encrypt a message, and then is decrypted by the receiver with the senders public key (which is known to anyone who wants it). It is also typically used for encrypting disks/files, such as for EFS.
Digital Certificates
- X.509 certificates in JavaScript. RSA and ECDSA Signed certificates. This page will generate either RSA and ECC key pairs, and then generate X.509 certificates, using either a signature of SHA1withRSA or SHA256withECDSA. For RSA signing we use an RSA private key to sign the certificate, and with ECDSA signing we use an ECC private key to sign the certificate.
Tokens
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
Random
- Random number generator. Rand. In the past, encryption and decryption had to be done through native code libraries, such as with Bouncy Castle and OpenSSL. With the increasing processing power of Web browsers, it is now possible to use encryption using JavaScript, which thus provides client-side processing of data. This Web page uses Javascript encryption, and generates a random 256-bit text key or a hex version. The 256-bit key is generated by generating 60 random numbers (from 0-25), and converting these to an ASCII character.
Malware obfuscation
- Malware obfuscation. Obfuscation. A malware writer will often hide certain keywords from the browser/human by encoding them in another format. This is typically done for hex coding (\xZZ), 16-bit unicoding (\uZZZZ) and octal coding (\ZZZ). To test, enter a value, and then press the button and it will convert encoded string.
Message Authentication Codes
- Chaskey (MAC). Chaskey. Chaskey Cipher is light-weight cryptography method for signing messages (MAC) using a 128-bit key. The hardware implementation only requires 3,334.33 gate equivalent with an operating clock frequency of 1 MHz (whereas Keccak requires 4,658 GE). In the page we create the Mac signature and also encrypt for CBC.
Other
- Password generation/hashing. Hashing. Linux can use salted passwords where the username, hashing method and hashed password are stored in a password file [More details]. The main methods are
Hashing

At times we need to generate secrets, such as encryption keys, from passwords or nonce values. A Key Derivation Function (KDF) is a verifiable way of doing this.
Key Derivation Functions (KDFs)
The following are the tips related to hashing:
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Password strength. Test. This outlines the strength of various passwords types.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
HKDF
The following are the tips related to Key derivation hashing:
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Hazmat HKDF for different hashing methods. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
-
HKDF key derivation with OpenSSL [
here]
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
PBKDF2
The following are the tips related to Key derivation hashing:
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- AES GCM (Python) with PBKDF2. AES GCM (Python) with PBKDF2.
- Fernet with PBKDF2 . AES GCM (Python) with PBKDF2.
- PBKDF2 key derivation. AES GCM (Python) with PBKDF2.
- Key Rotation with Fernet. AES GCM (Python) with PBKDF2.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Bcrypt
The following are the tips related to Key derivation hashing:
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- BCrypt. BCrypt. BCrypt with Rust.
-
Hash to password with Go. Hashing to Argon2, Scrypt and BCrypt. Hash to password with Go, including Argon2, Scrypt and BCrypt.
scrypt
- scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Argon 2
The following are the tips related to Key derivation hashing:
- Argon 2. Go. Outline of Argon2.
- Argon 2 with NaCl. Go. Outline of Argon2 using NaCl.
- Argon 2. Argon 2. Argon 2 with Rust.
- Balloon. Go. Outline of Balloon.
Other
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
- Double ratchet. Go. Outline of double ratcheting.
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
Outline
HMAC Key Derivation function (HKDF) is used to derive an encryption key from a passphrase. Initially, HKDF creates a pseudorandom key (PRK) using a passphrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), and along with a salt value. Next, the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys [RFC 5869][article]. In this case, we will use SHA-256.
The following shows how an encryption key can be generated using HKDF, and where we need a secret and a salt value. Both Bob and Alice have the same secret and salt.

With PBKDF2 (Password Based Key Derivation Function 2), we hash for a given number of rounds:

Key exchange

Key exchange is a way for Bob and Alice to communicate and for them to agree on a shared secret. The original method defined uses discrete logarithms (Diffie-Hellman), but most modern methods use elliptic curve techniques (ECDH). As quantum computers can crack both discrete log and elliptic curve methods, there are post quantum cryptography methods proposed. This includes SIDH, CSIDH, SIKE, and NewHope.
Key interchange/generation (Diffie-Hellman)
The following relates to key interchange:
- Selecting \(g\) in Diffie Hellman. G in Diffie Hellman. Picking a safe value of the generator \(g\) in discrete logarithms.
- Diffie-Hellman. Diffie-Hellman Calculation. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Real example). Diffie-Hellman Real. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Python). Diffie-Hellman. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (pre-compute). Diffie-Hellman (pre-compute). Many sites use the same prime numbers, which can then be cracked with a pre-computing attack.
- Key generation. Key gen. This will generate keys for different methods based on a passphrase.
- Diffie-Hellman (Man-in-the-middle). DF. This outlines the man-in-the-middle method for Diffie-Hellman.
- An Alternative Diffie-Hellman method. Alterative DH. This outlines an alternative Diffie-Hellman method.
Authenticated Key Exchange
The following are the tips related to Key derivation hashing:
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- MTI/A0. MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{ax+by} \pmod p\). MTI (Matsumoto, Takashima, Imai).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0. MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{x+y} \pmod p\)
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). The resultant key is \(xyG \)
- MTI/C0. MTI/C0. This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{xy} \pmod p\)
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG\).
- MTI/C1. MTI/C1. This outlines MTI/C1, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{abxy} \pmod p\).
- MQV (Menezes–Qu–Vanstone). MQV. MQV was created Alfred Menezes, Minghua Qu and Scott Vanstone in 1995 and is an authenticated key exchange method. Alice holds a key pair \((A,a)\) and Bob has a key pair \((B,b)\). With this \(a\) is Alice's private key, and \(A=aG\) is her public key. For Bob, his public key will be \(B=aG\) and a private key of \(b\), and where \(G\) is the base point on the elliptic curve.
- HMQV (Menezes–Qu–Vanstone). HMQV. HMQV builds on MQV and adds the identity of Bob and Alice.
- ECDH with X25519 and Blake2b. ECDH with X25519 and Blake2b. This uses PyNaCl to create an authenticated key exchange and uses X25519 and Blake2b.
Elliptic Curve (ECDH) - Python
The following are the tips related to ECC:
- Elliptic Curve. Elliptic Curve. Elliptic Curve is a public key method which can also be used to generate a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with simple parameters. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
Elliptic Curve (ECDH) - Golang and Node.js
The following are the tips related to ECC:
- ECDH with Go. ECDH. ECDH with Go.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with node.js. ECDH. ECDH with node.js.
- ECDH with JavaScript. ECDH. Elliptic Curve Diffie Hellman.
Password Authenticated Key Exchange (PAKE)
The following are the tips related to Key derivation hashing:
- SPAKE2. Go. Outline of SPAKE2.
- OPAQUE. Go. Outline of OPAQUE.
- SPEKE. Go. Outline of SPEKE (Simple Password Exponential Key Exchange).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
- J-PAKE. J-PAKE. This example generates a shared key based on a shared password.
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses discrete logs.
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
PQC NIST Finalists (Key Exchange)
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Key interchange/generation (Other)

The following relates to key interchange:
- Curve25519. Curve25519. This outlines Curve25519, which is used in the Tor network.
- Authenticated Key Exchange (Discrete logs). YAK. Key exchange with public keys and uses discrete logs.
- Authenticated Key Exchange (ECC). YAK. Key exchange with public keys and uses elliptic curve methods.
- Shamir No-key protocol. Shamir No Key. In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated.
- Shamir No-key protocol (sepc256k1). Shamir No Key (EC). In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated using the sepc256k1 elliptic curve.
- Conference keying (Burmester-Desmedt method). Conference keying. In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it.
- Conference keying (Burmester-Desmedt method) - Elliptic Curve (sepc256k1). Conference keying Elliptic Curve (sepc256k1). In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it, and uses the sepc256k1 elliptic curve.
Key exchange (with pairing)
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Kryptology

We need to build a new Internet. One that is build on mathematics and certainty, rather than the patchy version we have now. For this we need a layer of cryptography at the lowest level, and build software interfaces on top of this. Along with this we now have cryptographic methods which can now provide a foundation of trust, and which preserve privacy. And so the old libraries of OpenSSL are being squeezed out in favour of the new ones which are built on a solid foundation. The latest of these new "privacy-aware" libraries is Kryptology, and created by Coinbase. This library provides the APIs that developers need, in order to apply to areas of blockchain development. This library include BLS (Boneh-Lynn-Shacham) signatures, Zero-knowledge Proofs (ZKPs) and Shamir Secret Shares (SSS). With BLS we can digitally sign for data, but also preserve its privacy. Applications of this include group signatures, where multiple entities can merge their signing keys together and provide a single signature for a transaction. With SSS, we can split encryption keys up into shares, and then distribute them across a network. When required, we can call these shares back to reconstruct the key.
The focus for Coinbase seems to be the application of privacy coins, and where no tracking can be applied to the usage of these digital coins. This should support full anonymity for transactions, as opposed to Bitcoin which only supports pseudo-anonymity.

ECC Basics
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining n.G for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Points (Base Point and Others). Elliptic Curve points. Two common curves used in ECC (Elliptic Curve Cryptography) are secp256k1 (as used in Bitcoin and Ethereum) and P256 (secp256r1). The "k1" refers to the Kolbitz curve 1 (named after the creator of ECC). With these we have a base point which are can operate on. This is typically defined as \(G\). We can then operate on this with add and multiply operation. For example, \(2G=G+G\) and \(P=n.G\). In this following we will show the base point for a number of common curves, such as secp256r1, P256, Pallas, Curve 25519, BLS12381G1, BLS12381G2, BLS12377G1 and BLS12377G2.
ECDH
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret. We will use Golang and the Krytology library.
Simple ECC on curves
- Public key points for curves. Simple. Display public key points for scalars.
BLS Curve
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
Accumulator and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
Pallas Curve
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
Pairing-based Crypto
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
ElGamal and ECC
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a numerical input.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
Shamir Secret Shares
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Homomorphic Encryption
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Zero knowledge proofs
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
Verifiable Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Hash to scalar and point
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
CP-ABE
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Lattice cryptography

Latice cryptography is proposed as a post-quantum robust method for public key encryption, especially focused on digital signatures and key exchange mechanisms (KEMs).
Principles
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
NTRU
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- Lattice Encryption: NTRU Key Generation Python). NTRU. Outlines how NTRU operates for key generation.
Homomorphic
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Digital Signatures
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
Public-Key Encryption/Key Exchange
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
Light-weight cryptography

While AES and SHA work well together within computer systems, they struggle in an IoT/embedded world as they take up: too much processing power; too much physical space; and consume too much battery power. So NIST outlines a number of methods which can be used for light-weight cryptography, and which could be useful in IoT and RFID devices [1]. They define the device spectrum as:
- Conventional cryptography. Servers and Desktops. Tablets and smart phones.
- Light-weight cryptography. Embedded Systems. RFID and Sensor Networks.
With embedded systems, we commonly see 8-bit, 16-bit and 32-bit microcontrollers, and which would struggle to cope with real-time demands for conventional cryptography methods. And in the 40+ years since the first 4-bit processor, there is even a strong market for 4-bit processors. RFID and sensor network devices, especially, have limited numbers of gates available for security, and are often highly constrained with the power drain on the device.
So AES is typically a non-starter for many embedded devices. In light-weight cryptography, we often see smaller block size (typically 64 bits or 80 bits), smaller keys (often less than 90 bits) and less complex rounds (and where the S-boxes often just have 4-bits).
For light-weight cryptography the main constraints that we have are typically related to ener requirements, gate equivalents (GEs), and timing. With passive RFID devices, we do not have an associated battery for the power supply, and where the chip must power itself from energy coupled from the radio wave. An RFID device is thus likely to be severely constrained in the power drain associated with any cryptography functions, along with being constrained for the timing requirements and for the number of gates used. Even if an RFID device has an associated battery (active RFID), it may be difficult to recharge the battery, so the drain on power must often be minimised.
There is thus often a compromise between the cryptography method used and the overall security of the method. Thus often light-weight cryptography methods balance performance (throughput) against power drain and GE, and do not perform as well as main-stream cryptography standards (such as AES and SHA-256). Along with this the method must also have a low requirement for RAM (where the method requires the usage of running memory to perform its operation) and ROM (where the method is stored on the device). In order to assess the strengths of various methods we often define the area that the cryptography function will use on the device – and which is defined in \(µm^2\). The NIST finalists are defined in this [article]
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- GIFT AEAD. GIFT. GIFT is a light-weight block cipher. It is a (NIST Finalist)
- Elephant. Elephant. Elephant is a light-weight stream cipher. It is a (NIST Finalist).
- TinyJambu. TinyJambu. TinyJambu is a light-weight block cipher. It is a (NIST Finalist)
- Isap AEAD. Isap. Isap is a light-weight block cipher. It is a (NIST Finalist)
- PHOTON-Beetle AEAD. PHOTON-Beetle. PHOTON-Beetle is a light-weight block cipher. It is a (NIST Finalist)
- Romulus AEAD. Romulus. Romulus is a light-weight block cipher. It is a (NIST Finalist)
- Sparkle AEAD. Sparkle. Sparkle is a light-weight block cipher. It is a (NIST Finalist)
- CLEFIA. CLEFIA. CLEFIA is a light-weight block cipher.
- LED. LED. LED is a light-weight block cipher.
- Piccolo. Piccolo. Piccolo is an ultra light-weight block cipher.
- PRESENT. PRESENT. Present is a light-weight block cipher.
- Pyjamask. Pyjamask. Pyjamask is a light-weight block cipher.
- SIMON. SIMON. SIMON is a light-weight block cipher.
- SKINNY. SKINNY. SKINNEY is a light-weight block cipher.
- SPECK. SPECK. SPECK is a light-weight block cipher.
- XTEA. XTEA. XTEA is a light-weight block cipher.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encryption/Decryption. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.
Light-weight crypto (Other)
- Chaskey (MAC). Chaskey. Chaskey is a light-weight MAC function.
- Chaskey (MAC). Chaskey (Python). Chaskey is a light-weight MAC function.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (ASCON)
ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRFF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
Discrete Logs (Solving)

A discrete log problem is in the form of \(g^x \pmod p\) and where we know \(g\) and \(p\) and must solve for \(x\).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Message Authentication Code (MAC)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
HMAC
The following are the tips related to Key-based hashing:
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authentication both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2), Blake2b, SM3 and SHA-3. This page outlines the HMAC-MD5 methods using the Hazmat cryptography layer.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- HMAC (COSE). Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT with HMMAC. Go. In this case we create a CWT token, and sign with an HMAC signature.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- HMAC with Rust. HMAC. HMAC with Rust.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HMAC with OpenSSL. MACs with OpenSSL. HMAC in OpenSSL for a given input value, password and hashing method.
Cipher MACs
The following are the tips related to Key-based hashing:
- MACs with OpenSSL. MACs with OpenSSL. MAC methods implemented in OpenSSL, including CMAC and GMAC.
Key-based hashing
The following are the tips related to Key-based hashing:
- SipHash. Siphash. Siphash is a fast key-based hashing method.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Meow. Meow. Meow is one of the fastest hashing methods.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
Magic Numbers

This pages contains information related to magic numbers in file formats.
Network and File Forensics
- Magic numbers. Magic. This provides information on magic number for file forensics.
Graphics formats
- JPEG Analysis. JPEGs. This provides an analysis of JPEG files.
- GIF Analysis. GIFs. This provides an analysis of GIF files.
- TIF Analysis. TIFs. This provides an analysis of TIF files.
- PNG Analysis. PNGs. This provides an analysis of PNG files.
- BMP Analysis. BMPs. This provides an analysis of BMP files.
- PSD Analysis. PSDs. This provides an analysis of PSD files.
- WMF Analysis. WMF. This provides an analysis of WMF files.
- Adobe Illustrator Analysis. AI. This provides an analysis of AI files.
- Adobe In Design Analysis. INDD. This provides an analysis of INDD files.
- MIDI file. MIDI. This provides an analysis of MID files.
- ICO file. ICO. This provides an analysis of ICO files.
- PS file. PS. This provides an analysis of PS files.
- EPS file. EPS. This provides an analysis of EPS files.
- VSD file. VSD. This provides an analysis of Microsft Visio (VSD) files.
Video and audio formats
- MP3 Analysis. MP3s. This provides an analysis of MP3 files.
- AVI Analysis. AVIs. This provides an analysis of AVI files.
- Flash SWF Analysis. SWFs. This provides an analysis of Flash files.
- Flash FLV Analysis. FLVs. This provides an analysis of FLV files.
- MP4 Analysis. MP4. This provides an analysis of MP4 files.
- MOV Analysis. MOV. This provides an analysis of MOV files.
- WMV Analysis. WMV. This provides an analysis of WMV files.
- WMA Analysis. WMA. This provides an analysis of WMA files.
- JPEG 2000 Analysis. JPEG 2. This provides an analysis of JPEG 2000 files.
- WAV Analysis. WAV. This provides an analysis of WAV files.
Zips, Archives and Library files
- ZIP/Archive Analysis. ZIPs. This provides an analysis of ZIP/Achive files.
- GZ Analysis. GZ. This provides an analysis of GZip files.
- Tar Analysis. Tar. This provides an analysis of TAR files.
- MSI Analysis. MSI. This provides an analysis of MSI files.
- OBJ Analysis. OBJ. This provides an analysis of OBJ files.
- DLL Analysis. DLL. This provides an analysis of DLL files.
- CAB Analysis. CAB. This provides an analysis of CAB files.
- EXE Analysis. EXE. This provides an analysis of EXE files.
- RAR Analysis. RAR. This provides an analysis of RAR files.
- SYS Analysis. SYS. This provides an analysis of SYS files.
- HLP Analysis. HLP. This provides an analysis of HLP files.
- VMDK Analysis. VMDK. This provides an analysis of VMDK files (VMWare Virtual Disks).
- PST Analysis. PST. This provides an analysis of PST files (Outlook Email File).
- JAR Analysis. JAR. This provides an analysis of JAR files.
- SLN Analysis. SLN. This provides an analysis of Microsoft SLN files.
- Class Analysis. Class. This provides an analysis of Java Class files.
- Zlib. Zlib. This provides an analysis of Zlib files.
Documents
- PDF Analysis. PDFs. This provides an analysis of PDF files.
- DOC Analysis. DOCs. This provides an analysis of DOC files.
- RTF Analysis. RTFs. This provides an analysis of RTF files.
- XLS Analysis. XLSs. This provides an analysis of XLS files.
- PPT Analysis. PPTs. This provides an analysis of PPT files.
- MMP File. MMP. This provides an analysis of MMP files.
- DOCX Analysis. DOCX. This provides an analysis of DOCX files.
- XLSX Analysis. XLSX. This provides an analysis of XLSX files.
- PPTX Analysis. PPTX. This provides an analysis of PPTX files.
- MDB Analysis. MDB. This provides an analysis of MDB files.
- Outlook Message Analysis. MSG. This provides an analysis of MSG files.
Disk Image
- Raw disk format. RAW. This provides an analysis of the RAW disk format.
Tests
- File Forensics Test. File Test File Forensics Test.
- File Forensics Test (Fun). File Test (Fun) File Forensics Test.
Presentations
MIRACL Core Library

MIRACL Core is an open source library, and includes a wide range of public key encryption methods. It is especially focused on elliptic curve and pairing-friendly methods, but also supports a wide range of encryption methods, including RSA, AES and hashing. Overall, it can be ported onto a wide range of systems and supports C, C++, Go, Rust, Python, Java, Javascript and Swift. Along with this it supports limited capability devices such as the Arduino infrastructure. The GitHub repository is [here].
BN254
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.

Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- CL Signatures. CL. CL Signatures in Go using MIRACL.
- CL Signatures (advanced pairing). CL. CL Signatures in Go using MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages using MIRACL.
- PS Signatures. PS. Signatures using PS for short signatures using MIRACL.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures using MIRACL.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.

Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
Rust examples
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
NaCl

PyNaCl is a Python port of LibSodium. It integrates the latest cryptography methods, such as AES, XChaCha20, Blake2b and X25519.
Symmetric Key
- Symmetric key. Symmetric key (XChaCha20 and Poly1305). With symmetric key, Bob and Alice have the same key. NaCl uses the XChaCha20 method, and which supports stream encryption (and which does not require padding as a block cipher does, and is also faster than block cipher modes). ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16 byte nonce. XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24 byte nonce. It has a lower propability of nonce misuse than ChaCha20.
- Encryption with a password. Symmetric Key with KDF. In symmetric key, we generate a secret key. This key is typically a random value or generated from a password and a salt value. If we use a password, we typically use a KDF (Key Derivation Function), and which uses a password and a salt value, in order to create a key of a given size. In this case we will use Argon2i, and which is memory resilent.
Hybrid Encryption
- Box. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Hashing
- Hashing and KDF (Argon2 and scrypt). Hashing and KDF. This case we will use PyNaCl (Networking and Cryptography) library, and which is a Python binding to libsodium. We will hash a password using SHA-256 and SHA-512, and also create a KDF (Key Derivation Function) using scrypt and Argon2.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
Ed25519
-
Ed25519. Ed25519. Using Ed25519 for digital signatures.
-
Finding Points on Ed25519. X25519 (Points).
In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 (Key Exchange)
- X25519 + BLAKE2b key-exchange. X25519. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
Curve 25519
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
Node.js

Node.js uses the JavaScript programming langauge as its base, and allows for code to be run on a server, rather than in the browser (such as with pure JavaScript). To run a node.js program, we run "node myfile.js", and use NPM to install libraries.
Symmetric key
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
RSA and public key
- RSA Opt imal Asymmetric Encryption Padding (OAEP) using Node.js. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
ECC Keys
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.

Hashing
- Hashing with node.js (All). Hashing. Hashing with node.js.
- Hashing with node.js (Selection). Hashing. Hashing with node.js.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- ECDSA with node.js. ECDSA. ECDSA with node.js.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
Key exchange
- Diffie-Hellman with node.js (random prime). DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method and uses a randomly generated prime number (press the button to generate a new prime).
- Diffie-Hellman with node.js. DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method. Each time the prime number will be fixed for the DH group selected.
- ECDH with node.js. ECDH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Elliptic Curve Diffie Hellman (ECDH) key exchange method.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
Key derivation
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
CryptoJS
- CryptoJS (in node.js). CryptoJS (Node.js). Various crypto methods in the browser.
Bulletproofs
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
Blockchain
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
Proxy encryption
- Proxy Encryption - Encrypting With Public Key, And Decrypt with Private Key. Proxy01. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This page just creates a key pair for Alice, and uses it to encrypt with the public key , and decrypt with the private key.
- Proxy Encryption. Proxy02. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This will go through the full use case of proxy re-encryption.
Tokens
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
Random
- Fortuna with node.js. Fortuna. Fortuna random numbers with node.js.
Other
- FPE with node.js. FPR. FPE with node.js.
- Puny with node.js. Puny. Puny character format with node.js.
Accumulators and Witnesses
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
PGP
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Password Entropy
- Password Entropy with Node.js. Password Entropy. Password entropy measures the strength of a password, and is measured as the number of bits which could represent all of the possibilities. An entropy score of less than 25 identifies a poor password, and between 25 and 50 is a weak password. For 50 to 75 we have a reasonable password, and between 75 and 100 is a very good password. Over 100 is an excellent password. The strength of the password relates to the number of characters used, and also the number of characters in the password.
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
- Homomorphic Encryption with Node.js and BGV. Homomorphic Encryption with Node.js and BFG. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BGV method.
Oblivious Transfer (OT)

Oblivious Transfer allows Bob to select data from Alice, but for Alice not to know which value has been selected.
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
OpenSSH

OpenSSH supports the usage of the SSH protocol. This allows for a remote login. One tool which is uses is ssh-keygen, and which allow for the generation of RSA, DSA and elliptic-curve keys that. These can be used for user and host authentication, such as for GitHub login and Cloud instance login.
OpenSSH
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here].
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
Outline

OpenSSL

OpenSSL is a standard library that implements cryptography.
Symmetric key (Command line)
-
Symmetric Key Encryption (OpenSSL 1.x) [here]. In this case we will create cipher text from OpenSSL 1.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 1.x) [here].In this case we will decrypt cipher text from OpenSSL 1.x using a key derived from a password
-
Symmetric Key Encryption (OpenSSL 3.x) [here]. In this case we will create cipher text from OpenSSL 3.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 3.x) [here].In this case we will decrypt cipher text from OpenSSL 3.x using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password.
Hashing
-
Hashing [here] OpenSSL supports a wide range of hashing methods including BLAKE2b, Gost, MD4, MD5, RMD-160, SHA-1, SHA-3, SHA-256 and SHA-512.
Libre OpenSSL
-
Symmetric Key Encryption using Libre OpenSSL [here]. In this case we will create cipher text from Libre OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption using Libre OpenSSL [here]. In this case we will decrypt ciphertext from Libre OpenSSL using a key derived from a password.
-
Hashing [here] Libre OpenSSL supports a wide range of hashing methods including Gost, MD4, MD5, RMD-160, SHA-1, SHA-256 and SHA-512.
Diffie-Hellman parameter generation
-
DH Parameters with OpenSSL [here]. The Diffie-Hellman (DH) method is perhaps one of the greatest inventions in Cybersecurity, and was created by Whitfield Diffie and Marty Hellman. With the DH method, Bob creates a random value (\(b\)) and Alice also creates a random value (\(a\)). Next Bob computes \(B=g^b \pmod p\) and sends it to Alice. Alice computes \(A=g^a \pmod p\) and sends this to Bob. Bob raises the value of \(A\) to the power of \(b\) and takes \(\pmod p\), and Alice raises \(B\) to the power of \(a\) and takes \(\pmod p\). In the end, they will have the same shared value: \(g^{ab} \pmod p\). This can then be used to derive an encryption key that they can use for a secure tunnel. Overall, \(p\) is the large prime number, and also known as the shared modulus between Bob and Alice.
Key derivation function
-
PBKDF2 key derivation with OpenSSL [here] PBKDF2 (Password Key Derivation Function 2) is a key derivation method. Overall it is relatively slow in its operation and where we take a password, a salt value, hashing method, and a number of iterations, in order to produce a given size of encryption key.
-
HKDF key derivation with OpenSSL [here] HKDF (HMAC Key Derivation function) is used to derive an encryption key from a pass phrase. Initially HKDF creates a pseudorandom key (PRK) using a pass phrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), andalong with a salt value. Next the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys.
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Passwords
-
Password example [here]. This page uses the OpenSSL library hash password generator, which is used in UNIX systems for the hashing of passwords which are contained in /etc/shadow and /etc/passwd. For newer passwords, the "-1" options is used to created the hashed value.
-
Hashed passwords with OpenSSL [here].
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
Public key
-
Generating an ECC key pair with OpenSSL [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)).
-
Generating an RSA key pair with OpenSSL [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2).
-
Generating an RSA key pair with OpenSSL with encryption [here]. This page implements RSA key pair generation with an encrypted key pair. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). In this case we will encrypt the key pair with either 3DES, 128-bit AES, 192-bit AES or 256-bit AES. The same password must be used to encrypt and decrypt.
-
Generate prime with OpenSSL [here]. Prime numbers are important in public key encrytion, and are used with RSA and ECC. For RSA, we generate two prime numbers (\(p\) and \(q\)) and which are multiplied together to create a modulus (\(N\)). If these prime numbers have 512 bit values, the modulus will be a 1,024 bit value. This defines the basic secure of RSA. With elliptic curve we use smaller prime numbers, such as 256-bit values for the secp256k1 curve.
ASN1 parsing
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). We will parse using asn1parse, and reveal the parameters.
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)) [RSA key pair]. We will parse using asn1parse, and reveal the parameters.
- DSA Parameters with asn1parse. DSA parameters with OpenSSL with asn1parse. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA (Digital Signature Algorithm)
- DSA Parameters. DSA parameters with OpenSSL. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
MAC (Message Authentication Code)
- HMAC with OpenSSL. MACs with OpenSSL. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authenticate both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2) and SHA-3. In this case we will use OpenSSL to generate the HMAC value.
- MACs with OpenSSL. MACs with OpenSSL. In the following we will generate MACs for HMAC, GMAC, CMAC, Blake2bmac, Blake2smac, KMAC128 and KMAC256. Overall, we will use an encryption key defined as a hex value for GMAC and CMAC, and a pass phrase for the others. The message is "hello".
Signing
- Digital signing a plaintext message with OpenSSL. Signing with OpenSSL. With digital signing, we can take a message, and create a signature. This normally involves signing with a private key and digital certificate. The signed message can be an a MIME format, and which can be integrated into an email message. In this can we have a 512-bit RSA key pair that will sign a plain text message.
Encrypting emails
- Encrypting an email message in OpenSSL. Encrypting messages with OpenSSL. With public key encryption, we can take a message, and encrypt it with the recipiant's public key. In this can we have a 512-bit RSA public key to encrypt a message.
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Random number generation with OpenSSL
-
Random number generator [here]. Random numbers are important in generating encryption keys and salt values. In this case OpenSSL generates a random number (in a Base64 format) for a given number of bytes.
Outline (C#/Python)
-
Symmetric Key Encryption (C#) [here]. This page uses the OpenSSL library through a C#/.NET wrapper. The DLLs it interfaces to are libeay32.dll and ssleay32.dll. OpenSSL supports a wide range of encryption methods, including 128-bit AES, 192-bit AES, 256-bit AES and Blowfish (bf). Different modes of ECB, CBC, and OFB are implemented. The examples use a default IV of "1234".
-
AES in Python with OpenSSL output [here]
-
Producing OpenSSL AES Encrypted String from C# [here]
Digital Certificates
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
Paillier - Partial Homomorphic Encryption

The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Fundamentals
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier).
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Using RSA
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
Applications
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Paillier
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
Go Format Preserving Encryption (FPE)
- FPE with Go. FPE. An implementation of Format Preserving Encryption (FPE) for FFX1 and FFX3.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
AWS Encryption
- AWS Symmetric Key Encryption. AWS (Symmetric key). Using symmetric key in AWS.
Go Oblivious Transfer
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Dragon Fly
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
Embedding data in an ECC point
- Embedding data in a point. Go. With Elliptic Curve Cryptography (ECC), we use points on an elliptic curve to represent our data. These are defined with (x,y) points. With this, it is possible to embedded a certain amount of data into the point - as long as it still gives us a valid point on the curve. This example will Curve 25519 to embed data, and is achieved by storing the length of the data in a single byte in the point, and then store the data as byte values in the point (followed by random data). To decode, we can then just read the first byte for the length of the message, and then reveal the data encoded into the point..
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Hashing (Cryptographic)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
Benchmarks and Password strength
The following are the tips related to hashing:
- Password strength. Test. This outlines the strength of various passwords types.
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
Theory
The following are the tips related to hashing:
- Balls in bins. BiBa. This implemented balls in bins.
- Birthday attack (with Big Integers). Calc. This provides a simple example of the birthday attack.
- Birthday attack. Calc. This provides a simple example of the birthday attack.
- Differential Cryptanalysis (Hashing). Cryptanalysis. This provides an implementation of differential cryptanalysis for hashing methods.
MD5, SHA-1
The following are the tips related to hashing:
- MD2 and MD4 MD2/4. The MD2 and MD4 hashing functions were developed by Prof Ronald Rivest in 1989 and 1990, respectively. They both produce a 128-bit hash, but have been shown be vulnerable to attack (see the Collision section in the page).
- MD5 and SHA-1 (to Base-64) with salt Salt. It is possible to add salt to the MD5 algorithm, to mix it up a little.
- MD5 and SHA-1 (to Base-64) Hash. MD5 and SHA-1 produces a hash signature, and the output is typically shown in a hex format or a Base-64. In this example the output is converted into a Base-64 format.
- MD5 and SHA-1. Hash. MD5 and SHA-1 methods produce a hash signature, and are the two of the most widely used methods. The MD5 algorithm has been shown to have weaknesses, and a collision of message hashes has been shown to occur in less than one day. An MD5 signature has 128 bits, an SHA-1 signature has 160 bits, and an SHA-256 signature has 256 bits.
- MD5 Cracking. Hash Cracker. MD5 has a 128-bit signature and can be cracked using rainbow tables. This page tries to crack the MD5 signature.
- Hashing with Go. Hashing. Hashes with Go.
- Detecting hash types. Hash type. This detects has values.
- OpenSSL hashing. Range of methods. Outlines the methods used in OpenSSL
- Hash. Hash. Hashing using JavaScript
- Hashing with node.js. Hashing. Hashing with node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Hashing methods
-
Hazmat Hashes. Hazmat Hashes. This includes the hashing methods in the Hazmat cryptography library. This includes Blake2p, Blake2s, MD5, SHA1, SHA224, SHA256, SGA384, SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHA512, SHA512-224, SHAKE128 and SHA256.
-
Hazmat Hashes. Hazmat Hashes. In this case we will implement Python code to determine SHA1, SHA2, SHA3, Blake2, MD5 and SM3 hashes.
OpenSSL Passwords
-
Password example [here]
-
Hashed passwords with OpenSSL [here]
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Blake 3 hashes
The following are the tips related to similarity hashing:
- Blake 3 in Python. Hashing. Blake 3 hashing.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
Other Hash functions
The following are the tips related to hashing:
- Bloom Filter Bloom filter. A Bloom filter goes a probabilistic method of determining if an element is in a data structure, using indexed hashing methods.
- Cuckoo Table Cuckoo filter. A Cockoo table uses two hash funtions.
- Chaffing. Chaffing. This produces a keyless system.
- GP Hashing with Go. GP Hashing. GP Hashes with Go.
- LDAP. LDAP. This produces a LDAP hash signature for a password.
- LM Hash. LM Hash. This is an LM Hash Calculator. LM Hash is used in many versions of Windows to store user passwords that are fewer than 15 characters long.
- Murmur and FNV Murmur and FNV. While hashing methods such as MD5 and SHA-1 use crypto methods, the Murmur and FNV hashes uses a non-cryptographic hash function. This can be used for general hash-based lookup and was designed by Austin Appleby. It has good performance compared with other hashing methods.
- Pearson. Pearson. This uses a non-crypto hash.
- phpass. phpass. This produces a phpass hash signature for a password.
- Tiger. Tiger. Tiger is a 192-bit hash function and was designed by Ross Anderson and Eli Biham in 1995. It is often used by clients within Gnutella file-sharing networks and does not suffer from known attacks on MD5 and SHA-0/SHA-1. Tiger2 is an addition, in which the message is padded with a byte of 0x80 (in a similar way to MD4, MD5, and SHA), whereas in Tiger it is 0x01. Otherwise, the two methods are the same in their operation.
- Whirlpool. Whirlpool. Whirlpool is a 512-bit cryptographic hash function and was created by Vincent Rijmen (one of the AES creators) and Paulo Barreto, in 2000.
- WPA-2 hash . WPA-2 hash. Implements SHA-2 hash.
- Reusable hash collisions. Reusable hash collisions. Reusable hash collisions.
- The Length Extension Attack. Length Extension Attack. The MD construct has many weaknesses, and one of the most serious is the length extension attack. With this an adversary (Eve) can take a hash for an unknown message, and then add additional data to produce a new valid hash. The hash methods which are at risk against the length extension attack are MD5, SHA-1 and SHA-256. Please follow the code link below to run an example.
- Consistent hashing. Consistent hash. This outlines the usage of Consistent hashes.
- ROR13 (Module and Function). ROR13. With ROR13 we take each 8-bit character and then convert to a unicode value (with 16 bits). Then for each character we rotate the bits right by thirteen places. The resultant hash is then just the accumuluation of the rotated values.
- ROR13 (Function). ROR13 (Function). With ROR13 we take each 8-bit character and then convert to a unicode value (with 16 bits). Then for each character we rotate the bits right by thirteen places. The resultant hash is then just the accumuluation of the rotated values.
- GOST, Streebog256 and Streebog512. GOST, Streebog256 and Streebog512. GOST94 is a hashing method developed with Euro-Asian Council for Standardization, Metrology and Certification (EASC). This has since been developed in the Streebog256 and Streebog512 hashing method. In this case, we will use Libre OpenSSL to convert data into a hashed value.
RIPEMD
- RIPEMD (RACE Integrity Primitives Evaluation Message Digest) and GOST. RIPEM160. RIPEMD is a 128-bit, 160-bit, 256-bit or 320-bit cryptographic hash function, and was created by Hans Dobbertin, Antoon Bosselaers, and Bart Preneel. It is used on TrueCrypt and is open source. The 160-bit version is seen as an alternative to SHA-1, and is part of ISO/IEC 10118
- RIPEMD160. RIPEM160. RIPEMD160 is a 160-bit cryptographic hash function, and was created by Hans Dobbertin, Antoon Bosselaers and Bart Preneel. RIPEMD160 is used in Bitcoin applications.
Chameleon hashes
The following are the tips related to Chameleon hashing:
- Chameleon hash in Golang Chameleon. With a Chameleon hash, we have a normal hash value which is resistant to collisions, but with a known secret we can easily create a collision. The concept was first defined by Krawcyk and Rabin.
Similarity hashes
The following are the tips related to similarity hashing:
- Similarity hash: SimHash (Charikar similarity) in Python Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash (Nilsimsa similarity) Nilsimsa. The Nilsimsa similarity is used to find similarities between spam emails.
- Minhash (Jaccard similarity) Jaccard similarity. The Minhash method is used to find similarities between strings, files and metadata.
- String enthropy String enthropy. Measurement of the entropy of strings.
- Counting identical elements (HyperLogLog) HyperLogLog. Counting the number of identical elements.
SHA-3 and SHA-3 contenders
The following are the tips related to Key derivation hashing:
- Blake and Blake 2. Blake. Implements Blake and Blake 2 (SHA-3 contender).
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
- Grøstl. Grøstl. Implements Grøstl (SHA-3 contender).
- KangarooTwelve. KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- SHA-3, Keccak and SHAKE . SHA-3. Implements SHA-3, Keccak and SHAKE (SHA-3 winner).
- SHA-3. SHA-3. SHA-3 was known as Keccak and is a hash function designed by Guido Bertoni, Joan Daemen, Michaël Peeters, and Gilles Van Assche. MD5 and SHA-0 have been shown to be susceptible to attacks, along with theoretical attacks on SHA-1. NIST thus defined there was a need for a new hashing method which did not use the existing methods for hashing, and setup a competition for competing algorithms. In October 2012, Keccak won the NIST hash function competition and is proposed as the SHA-3 standard. It should be noted that it is not replacement SHA-2, which is currently a secure method. Overall Keccak uses the sponge construction where the message blocks are XORed into the initial bits of the state, and then inevitably permuted.
- cSHAKE. cSHAKE. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS. With the SHA-3 hashing method, we have four different cryptographic hashing methods (SHA3-224, SHA3-256, SHA3-384, and SHA3-512) and two XOF functions (SHAKE128 and SHAKE256). With SHAKE128 and SHAKE256 we can integrate domain separation between different functions — and which are known as cSHAKE128 and cSHAKE256.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- Skein. Skein. Implements Skein (SHA-3 contender).
Key derivation hashing
The following are the tips related to Key derivation hashing:
- Argon2. Go. Outline of Argon2.
- Argon2 with NaCl. Go. Outline of Argon2 using NaCl.
- Balloon. Go. Outline of Balloon.
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- Double ratchet. Go. Outline of double ratcheting.
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- Scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat HKDF. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
Non-crypto/fast hashing
The following are the tips related to non-crypto hashing:
- A perfect hash Perfect hash. This is a non-crypto hash which optimizes the hash value.
- The universal hash Universal hash. This related to the concept of a universal hash.
- FNV. FNV. FNV is one of the fastest hashing methods.
- Murmur. Murmur. Murmur is one of the fastest hashing methods.
- Siphash. Siphash. Siphash is a fast hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- xxHash. xxHash. xxHash is one of the fastest hashing methods.
- Meow. Meow. Meow is one of the fastest hashing methods.
- o1Hash. o1Hash. o1Hash is one of the fastest hashing methods.
- CRC-32. CRC-32. CRC-32 is one of the fastest hashing methods.
- wyhash. wyhash. wyhash is one of the fastest hashing methods.
- CityHash. CityHash. CityHash is one of the fastest hashing methods, and is generally free of security problems.
- FarmHash. FarmHash. FarmHash is one of the fastest hashing methods, and is generally free of security problems.
- Non-crypto. Non-crypto. This includes a range of fast non-cryptography hashing methods.
- Non-crypto hashes (C++): Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro. Non-crypto hashes: Farm, City, xxHash, MUM, Spooky 2, Murmur, Metro and t1ha0. This includes a range of fast non-cryptography hashing methods for Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro using C++ methods.
- Pearson. Pearson. Pearson is one of the fastest hashing methods, and has been designed for 8-bit processors.
- C++: t1ha. t1ha. t1ha is one of the fastest hashing methods, and has been designed for 64-bit processors.
- C++: Spooky. Spooky. Spooky is one of the fastest hashing methods, and V2 has a 32-bit, 64-bit and 128-bit version.
- C++: xxHash. xxHash. xxHash is one of the fastest hashing methods, and has good performance for short data inputs.
- C++: MUM. MUM. MUM is one of the fastest hashing methods.
- C++: FNV 1/1a. FNV 1/1a. FNV 1/1a is one of the fastest hashing methods, and is particularily useful when there are small changes in strings, such as with IP addresses and URLs.
- C++: MetroHash. MetroHash. MetroHash is one of the fastest hashing methods.
- C++: CityHash. CityHash. CityHash was created by Google and is one of the fastest hashing methods. It was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Farm. FarmHash. FarmHash was created by Google and is one of the fastest hashing methods. It is an improvement to CityHash.
- C++: Murmur. Murmur. Murmur is one of the fastest hashing methods, but was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Halftime. Halftime. Halftime is one of the fastest hashing methods and was created by Jim Apple at Apache.
- C++: Highway. Highway. Highway is an ultra-fast keyed-hash, and is more than five times faster than SipHash. It was created by Jyrki Alakuijala, Bill Cox, Jan Wassenberg at Google.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
- C++: CLHash. CLHash. CLHash is an ultra-fast hashing method and focused on improving performance of the hashing of long strings.
- C++: FalkHash. FalkHash. FalkHash is an ultra-fast hashing method and beats most of the other non-cryptography methods for performance. It is focused on the x64 architecture and integrates with AES-NI.
- C++: wyHash. wyHash. wyHash is an ultra-fast hashing method.
- C++: Fibonacci. Fibonacci. Fibonacci is an ultra-fast hashing method.
- C++: Lookup3. Lookup3. Lookup3 is an ultra-fast hashing method.
Key-based hashing
The following are the tips related to Key-based hashing:
- SiphashSiphash. Siphash is a fast key-based hashing method.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
One Time Passwords/Time Stamps
The following are the tips related to hashing:
- One Time Passwords. One Time. This allows a new unique password to be created each instance, based on an initial seed.
- Timed One Time Password (TOTP). Timed One Time Password. This allows a new unique passcode to be created each instance, based on an initial seed for a given time window. We will use a five second window in this case, where a new passcode is generated every five seconds, based on an initial seed of a pass phrase.
- Hashed One Time Password (HOTP). Hashed One Time Password. This allows a new unique passcode to be created each instance, based on a counter value and an initial seed.
- Time Stamp Protocol. TSP. This creates a time stamp for data.
- HOTP and TOTP (Python). OTP. This creates hashed passwords.
eXtendable-Output Function (XOF)
- eXtendable-Output Function (XOF) usign CIRCL. XOF. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS.
SHAKE
The following are the tips related to hashing:
- SHAKE. SHAKE. Implements SHAKE and which is an Extendable Output Function (XOF).
- SHAKE with Go. SHAKE. This implements SHAKE in Go.
- libDisco with Go. libDisco. This implements libDisco.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify
the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods
such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC methods using the Python cryptography primitives for HMAC-MD5.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
Quantum-robust Public Key (Hash-based signature)
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
Hash to ECC point
- Hash to password with Go. Hash to password. Hash to password with Go.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve with libnum.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.

Password-hashing functions using Rust
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing (Non-cryptographic)

You might know those slow old hashing methods, such as MD5, SHA-1, and SHA-256. Well, they were designed to be fast, but also highly secure. But, if we just need a hashing method, such as for a hashtable or Bloom filter, we often don’t need all the security that comes with the main cryptography hashing methods. And so we have the non-cryptography hashing methods, and which are often ultra-fast and highly efficient. To show the difference, in a test, SHA-1 — one of the fastest cryptography hashing methods — managed a processing rate of 364.95 MiB/s, while t1ha was nearly a 100 times faster, at 34,636 MiB/s.
Non-crypto/fast hashing
The following are the tips related to non-crypto hashing:
- A perfect hash Perfect hash. This is a non-crypto hash which optimizes the hash value.
- The universal hash Universal hash. This related to the concept of a universal hash.
- FNV. FNV. FNV is one of the fastest hashing methods.
- Murmur. Murmur. Murmur is one of the fastest hashing methods.
- Siphash. Siphash. Siphash is a fast hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- xxHash. xxHash. xxHash is one of the fastest hashing methods.
- Meow. Meow. Meow is one of the fastest hashing methods.
- o1Hash. o1Hash. o1Hash is one of the fastest hashing methods.
- CRC-32. CRC-32. CRC-32 is one of the fastest hashing methods.
- wyhash. wyhash. wyhash is one of the fastest hashing methods.
- CityHash. CityHash. CityHash is one of the fastest hashing methods, and is generally free of security problems.
- FarmHash. FarmHash. FarmHash is one of the fastest hashing methods, and is generally free of security problems.
- Non-crypto. Non-crypto. This includes a range of fast non-cryptography hashing methods.
- Non-crypto hashes (C++): Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro. Non-crypto hashes: Farm, City, xxHash, MUM, Spooky 2, Murmur, Metro and t1ha0. This includes a range of fast non-cryptography hashing methods for Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro using C++ methods.
- Pearson. Pearson. Pearson is one of the fastest hashing methods, and has been designed for 8-bit processors.
- C++: t1ha. t1ha. t1ha is one of the fastest hashing methods, and has been designed for 64-bit processors.
- C++: Spooky. Spooky. Spooky is one of the fastest hashing methods, and V2 has a 32-bit, 64-bit and 128-bit version.
- C++: xxHash. xxHash. xxHash is one of the fastest hashing methods, and has good performance for short data inputs.
- C++: MUM. MUM. MUM is one of the fastest hashing methods.
- C++: FNV 1/1a. FNV 1/1a. FNV 1/1a is one of the fastest hashing methods, and is particularily useful when there are small changes in strings, such as with IP addresses and URLs.
- C++: MetroHash. MetroHash. MetroHash is one of the fastest hashing methods.
- C++: CityHash. CityHash. CityHash was created by Google and is one of the fastest hashing methods. It was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Farm. FarmHash. FarmHash was created by Google and is one of the fastest hashing methods. It is an improvement to CityHash.
- C++: Murmur. Murmur. Murmur is one of the fastest hashing methods, but was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Halftime. Halftime. Halftime is one of the fastest hashing methods and was created by Jim Apple at Apache.
- C++: Highway. Highway. Highway is an ultra-fast keyed-hash, and is more than five times faster than SipHash. It was created by Jyrki Alakuijala, Bill Cox, Jan Wassenberg at Google.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
- C++: CLHash. CLHash. CLHash is an ultra-fast hashing method and focused on improving performance of the hashing of long strings.
- C++: FalkHash. FalkHash. FalkHash is an ultra-fast hashing method and beats most of the other non-cryptography methods for performance. It is focused on the x64 architecture and integrates with AES-NI.
- C++: wyHash. wyHash. wyHash is an ultra-fast hashing method.
- C++: Fibonacci. Fibonacci. Fibonacci is an ultra-fast hashing method.
- C++: Lookup3. Lookup3. Lookup3 is an ultra-fast hashing method.
A fuller test with SMHasher gives [here]:
Hash function MiB/sec cycl./hash cycl./map Quality problems
------------------------------------------------------------------
o1hash 12439661.09 16.77 166.13 insecure, no seed, zeros, fails all tests
crc32_hw1 23208.73 46.74 179.70 insecure, 100% bias, collisions, distrib, BIC, machine-specific (x86 SSE4.2)
t1ha0_aes_noavx 22785.26 38.71 180.61 LongNeighbors, machine-specific (x86 AES-NI)
t1ha0_aes_avx1 22714.85 48.12 226.52 LongNeighbors, machine-specific (x64 AVX.txt)
t1ha0_aes_avx2 22345.33 44.38 556.47 LongNeighbors, machine-specific (x64 AVX2)
falkhash 20202.42 173.63 321.52 Sparse, LongNeighbors, machine-specific (x64 AES-NI)
MeowHash64low 17378.06 85.48 237.60 Sparse, invertible, machine-specific (x64 AES-NI)
MeowHash32low 17374.64 85.48 258.53 Sparse, invertible, machine-specific (x64 AES-NI)
MeowHash 17371.91 85.48 247.96 Sparse, invertible, machine-specific (x64 AES-NI)
FarmHash32 17112.05 47.7 214.71 machine-specific (x64 SSE4/AVX)
xxh3 16538.52 32.81 184.86 DiffDist bit 7 w. 36 bits, BIC
xxh3low 16462.36 32.77 199.79
farmhash32_c 16299.81 47.79 219.19 machine-specific (x64 SSE4/AVX)
xxh128low 15174.85 33.79 187.05
xxh128 15174.14 40.46 195.65
farsh32 14053.09 74.29 245.33 insecure: AppendedZeroes, collisions+bias, MomentChi2, LongNeighbors
metrohash64crc_2 14034.84 48.94 162.54 UB, Cyclic 8/8 byte, DiffDist, BIC, machine-specific (SSE4.2/NEON)
metrohash64crc_1 14000.5 49.08 150.54 UB, Cyclic 8/8 byte, DiffDist, BIC, MomentChi2, machine-specific (SSE4.2/NEON)
metrohash128crc_1 13948.67 65.2 168.08 UB, machine-specific (SSE4.2/NEON)
metrohash128crc_2 13920.19 65.12 176.70 UB, machine-specific (SSE4.2/NEON)
halftime_hash128 13478.23 97.79 252.14
wyhash32low 12911.09 29.59 205.43 2 bad seeds
wyhash 12879 30.35 196.77 2^33 bad seeds
CityCrc128 12343.43 74.5 209.75
fletcher2 12011.15 25.29 298.60 bad seed 0, UB, fails all tests
fletcher4 11928.55 25.27 293.49 bad seed 0, UB, fails all tests
halftime_hash256 11620.28 98.44 252.60
fibonacci 11339.87 26.33 705.64 UB, zeros, fails all tests
ahash64 9862.62 27.32 181.68 rust
Spooky128 9751.14 63.84 192.47 UB
Spooky64 9747.47 62.2 191.71 UB
Spooky32 9747.13 62.24 196.96 UB
t1ha1_64le 9723.86 34.39 176.91 Avalanche
cmetrohash64_1 9683.33 45.2 161.01 UB, LongNeighbors, BIC, MomentChi2
cmetrohash64_2 9669.95 44.75 149.67 LongNeighbors
metrohash64_2 9668.51 44.45 164.30 UB, LongNeighbors
metrohash64 9664.61 44.59 150.74 UB, LongNeighbors, BIC
metrohash64_1 9664.57 45.37 152.31 UB, LongNeighbors, BIC, MomentChi2
cmetrohash64_1o 9658.31 42.84 163.45 UB, LongNeighbors, BIC, MomentChi2
FNV1a_YT 9643.42 32.06 175.19 bad seed, UB, fails all tests
City128 9640.19 88.45 225.38
metrohash128_2 9584.94 59.1 167.43 UB, LongNeighbors
metrohash128 9569.16 58.68 167.53 UB, LongNeighbors
metrohash128_1 9558.17 59.04 175.94 UB, LongNeighbors
FarmHash128 9409.63 74.52 210.25
VHASH_32 9404.99 77.01 250.57 sanity, Seed, MomentChi2
VHASH_64 9392.39 74.72 227.92 sanity, Seed, MomentChi2
farmhash128_c 9244.13 79.08 209.44
t1ha2_atonce 9237.12 38.94 194.32 Zeroes low3
City64noSeed 9090.42 32.23 171.53 Avalanche, Sparse, TwoBytes, MomentChi2, Seed
City64low 9089.45 47.75 201.73
t1ha2_stream 9068.55 74.56 219.85 Sparse, Permutation, LongNeighbors
City64 9066.9 47.81 197.78 Sparse, TwoBytes
t1ha2_stream128 9065.5 93.19 236.50 Sparse, Permutation, LongNeighbors
xxHash64 8936.63 51.31 174.34
pengyhash 8744.48 85.31 222.45
farmhash64_c 8713.16 47.96 201.00
FarmHash64 8684.76 48.13 200.51
crc64_hw 8440.13 34.94 141.15 insecure, 100% bias, collisions, distrib, BIC, machine-specific (SSE4.2/NEON)
t1ha2_atonce128 8350.99 55.65 203.53 LongNeighbors
PMPML_64 8161.19 53.2 179.16 unseeded: Seed, MomentChi2, BIC
halftime_hash512 7681.62 125.81 274.01
tabulation 7621.75 42.19 179.93
t1ha1_64be 7481.37 38.16 193.22 Avalanche
MUMlow 7225.18 37.85 197.92 UB, 5 bad seeds
farsh64 7216.29 130.3 302.44 insecure: AppendedZeroes, collisions+bias, MomentChi2, LongNeighbors
MUM 7134.56 37.85 172.34 UB, too many bad seeds, machine-specific (32/64 differs)
nmhash32 7003.3 68.93 216.59
PMPML_32 6704.53 53.5 197.43 Avalanche >512, unseeded: Seed, BIC, MomentChi2, PerlinNoise
nmhash32x 6342.95 56.41 217.75
crc32_hw 6330.42 35.55 170.16 insecure, 100% bias, collisions, distrib, BIC, machine-specific (SSE4.2/NEON)
FNV2 6258.84 33.25 142.89 fails all tests
FNV1A_Pippip_Yurii 6258.46 28.19 184.41 UB, sanity, fails all tests
FNV1A_Totenschiff 6258.23 27.99 198.20 UB, zeros, fails all tests
HighwayHash64 6242.58 99.55 248.41
mx3 6146.02 52.48 173.09 UB
xxHash32 6040.87 51.77 177.91 LongNeighbors, collisions with 4bit diff, MomentChi2 220
prvhash64s_64 5481.48 170.05 325.39
mirhash 5413.73 39.68 154.47 UB, 2^36 bad seeds, LongNeighbors, machine-specific (32/64 differs)
mirhash32low 5412.76 39.79 182.13 UB, 4 bad seeds, Cyclic, LongNeighbors, machine-specific (32/64 differs)
Murmur3F 5226.4 52.18 175.85 UB
prvhash64s_128 5161.33 260.96 442.70
t1ha0_32le 5132.18 54.83 193.53 Sparse, LongNeighbors
halftime_hash64 4990.72 120.55 281.64
Murmur2B 4882.95 39.72 149.43 UB, 1.8% bias, collisions, 3.4% distrib, BIC
seahash32low 4801.33 58.54 227.31 PerlinNoise 32, !msvc
seahash 4796.97 58.55 201.58 PerlinNoise, !msvc
fasthash32 4737.61 45.32 181.86 UB, insecure
fasthash64 4737.21 42.79 164.87 UB, insecure, Moment Chi2 5159 !
umash32_hi 4662.92 54.22 214.20
umash64 4662.09 53.42 188.09
umash32 4633.19 53.42 216.33
t1ha0_32be 4585.59 55.98 183.45 Sparse, LongNeighbors
clhash 4472.31 82.72 229.73 PerlinNoise, machine-specific (x64 SSE4.2)
tabulation32 4317.34 35.45 197.20 collisions
Murmur2C 4092.99 51.84 164.65 UB, 2^32 bad seeds, 91% bias, collisions, distr, BIC, LongNeighbors
farsh128 3776.92 232.48 398.67
City32 3675.04 57.73 212.04
TSip 3228.14 57.96 211.71 !msvc
Murmur3C 3197.63 67.9 198.00 UB, LongNeighbors, Text, DiffDist
Crap8 3149.63 36.23 195.11 UB, 2.42% bias, collisions, 2% distrib
Murmur2 3146.91 41.87 187.89 UB, 1 bad seed, 1.7% bias, 81x coll, 1.7% distrib, BIC
Murmur2A 3146.79 46.87 191.96 UB, 1 bad seed, 12.7% bias, LongNeighbors
aesnihash 2963.39 71.24 217.73 fails many tests, machine-specific (x64 AES-NI)
BEBB4185 2951.62 222.03 343.63 UB, too many bad seeds, msvc-specific
jodyhash6 2848.42 29.99 164.36 bias, collisions, distr, BIC, LongNeighbors
wyhash32 2532.89 48.4 484.57 2 bad seeds, 32-bit
umash128 2427.46 70.6 197.29
Murmur3A 2413.88 53.36 182.37 UB, 1 bad seed, Moment Chi2 69
prvhash64_64m 2386.19 51.18 186.87
prvhash64_128 2383.57 103.44 246.45
prvhash64_64 2375.72 51.61 190.97
hasshe2 2372.52 68.64 216.74 Permutation,TwoBytes,Zeroes,Seed
PMurHash32 2344.78 58.48 196.43 1 bad seed, Moment Chi2 69
mirhashstrict32low 2218.87 65.48 190.59 1 bad seed, MomentChi2 9
mirhashstrict 2217.32 65.53 182.07
sha1ni 2019.96 135.84 564.40 insecure,sanity, Permutation, Zeroes, machine-specific
sha1ni_32 2019.94 136.82 589.46 machine-specific
superfast 1956.25 53.61 180.10 UB, bad seed 0, 91% bias, 5273.01x collisions, 37% distr, BIC
sha2ni-256_64 1910.34 146.06 595.16 Zeroes, machine-specific
sha2ni-256 1906.77 145.47 603.08 insecure,sanity, Permutation, Zeroes, machine-specific
farsh256 1895.77 459.86 575.95
SipHash13 1889.1 89 199.95 0.9% bias
Murmur1 1804.67 51.51 188.41 UB, 1 bad seed, 511x collisions, Diff, BIC
lookup3 1658.31 48.84 194.15 UB, 28% bias, collisions, 30% distr, BIC
pearsonbhash64 1486.34 104.32 185.03
poly_1_mersenne 1431.65 54.49 189.52 fails most tests
jodyhash32 1428.37 44.36 185.85 bias, collisions, distr, BIC LongNeighbors
pearsonbhash128 1347.03 121.75 214.84
poly_2_mersenne 1323.69 66.93 190.88
poly_3_mersenne 1323.59 74.86 206.77
poly_4_mersenne 1323.57 82.67 200.36
blake3_c 1285.91 340.01 552.63 no 32bit portability
GoodOAAT 1052 71.62 192.19
pearsonbhash256 998.9 167.05 261.29
SipHash 980.88 127.77 246.19
MicroOAAT 977.6 59.61 185.06 100% bias, distrib, BIC
FNV1a 791.84 69.69 177.84 bad seed, zeros, fails all tests
sdbm 791.84 67.69 177.06 bad seed 0, fails all tests
FNV64 791.82 70.24 159.29 fails all tests
bernstein 791.82 68.63 180.71 bad seed 0, fails all tests
beamsplitter 789.22 682.45 1150.3 UB, too many bad seeds
HalfSipHash 755.78 114.47 243.72 zeroes
chaskey 753.23 153.42 288.26 PerlinNoise
x17 527.9 98.78 184.09 99.98% bias, fails all tests
JenkinsOOAT_perl 452.49 118.78 194.78 bad seed 0, test FAIL
MurmurOAAT 452.49 113.07 197.83 bad seed 0, 1.5-11.5% bias, 7.2x collisions, BIC, LongNeighbors
JenkinsOOAT 452.48 142.85 213.93 bad seed 0, 1.5-11.5% bias, 7.2x collisions, BIC, LongNeighbors
crc32 392.1 131.62 204.58 insecure, 8590x collisions, distrib, PerlinNoise
sha1-160 364.95 1470.55 1794.1 Comb/Cyclic low32
rmd256 362.49 617.02 815.44 Bad seeds
blake2b-256_64 356.97 1222.76 1435.0
blake2b-224 356.59 1228.5 1425.87
blake2b-160 356.08 1236.84 1458.15
blake2b-256 355.97 1232.22 1443.31 Sparse high 32-bit
md5-128 353.76 638.29 803.39
md5_32a 353.64 629.85 799.56 Sparse high 32-bit
sha1_32a 353.03 1385.8 1759.9 Cyclic low32, 36.6% distrib
rmd128 334.36 659.03 838.32 Bad seeds
blake2s-128 295.3 698.09 1059.2
pearsonhash64 287.95 174.11 196.50 Avalanche, Seed, SSSE3 only. broken MSVC
pearsonhash128 287.95 171.72 194.61 Avalanche, Seed, SSSE3 only. broken MSVC
pearsonhash256 264.51 184.87 218.79 Avalanche, Seed, SSSE3 only. broken MSVC
blake2s-256 215.28 1014.88 1230.38
blake2s-160 215.01 1026.74 1239.54
blake2s-256_64 211.52 1044.22 1228.43
blake2s-224 207.06 1063.86 1236.50
rmd160 202.16 1045.79 1287.74 Bad seeds, Cyclic hi32
sha2-256_64 148.01 1376.34 1624.71 Bad seeds, Moment Chi2 7
sha2-256 147.8 1374.9 1606.06 Bad seeds, Moment Chi2 4
sha2-224_64 147.6 1360.1 1620.93 Bad seeds, Cyclic low32
sha2-224 147.13 1354.81 1589.92 Bad seeds, Comb low32
asconhashv12 144.98 885.02 1324.23
sha3-256 100.58 3877.18 4159.79 PerlinNoise
sha3-256_64 100.57 3909 4174.63 PerlinNoise
asconhashv12_64 86.73 684.02 606.93
floppsyhash 35.72 1868.92 1411.07
tifuhash_64 35.6 1679.52 1212.75 Cyclic low32
Problems include:
- Bad Seeds. A random seed is often used to initialise the hash. This problem relates to having a bad seed..
- Undefined behaviour (UB). This includes Misaligned, oob (Out of bounds), Signed integer overflow and Shift exponent overflow.
o1hash is the fastest, and a quick and dirty hashing method. It is generally not secure. t1h (Fast Positive Hash) requires AES-NI (Intel Advanced Encryption Standard Instructions) and is one of the fastest hashes at 22.785 Gbps. It has fairly good security levels. Meow comes in around 17.378 Gbps. We can see that SHA-1-160 runs as 364 Mbps, while Meow runs at 17.378 Gbps. Blake 3 is one of the fast cryptography hash and has a rate of 1.285 Gbps, and Blake 2 gives a rate around 215 Mbps. SHA-3 gives hashing rates of 100.58 Mbps.
Google recommend the following for 64-bit hashes without quality problems:
- xxh3low
-
wyhash
-
ahash64
-
t1ha2_atonce
-
FarmHash
-
halftime_hash128
-
Spooky32
-
pengyhash
-
nmhash32
-
mx3
-
MUM/mir
- fasthash32
Hash-based Signatures

With hash-based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature, unless we create a stateless method, such as SPHINCS+ [1]. Currently NIST have the final round for the Post Quantum Cryptography competition, and for digital signatures, SPHINCS+ is one of the alterative finalists (alongside Picnic).
Hash-based signature (theory)
- BiBa (Go). BiBa. An overview of BiBa One Time Signature [9]. Basically the method involves us taking a hash of a value using a standard hashing method, such as with SHA-256. There will then be \(2^{256}\) different hashing values. We aim to create a signature for a message, so Bob (the signer) selects a number of random values for his private key value and then publishes the hash of each of these (\(P_1\), \(P_2\), etc). He then sends these public keys to Alice. Now when Bob wants to sign a message, he will take one of his private key values, and then hashes it, and then determines the bin that it should be placed. In this case, we could use the \(\pmod N\) function on the hash, and where \(N\) is the number of bins. If we select \(2^{10}\) there will be 1,024 bins.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature [9].
Hash-based signature (stateful)
- BLISS - Post-quantum signing. BLISS. One of the alteratives to the usage of our existing public key methods is the usage of lattice cryptography, and especially in the usage of Ring Learning With Errors (RLWE). An important application is within digital signatures, and where Bob will sign something with his private key, and then Alice can prove that he signed it with his public key. One post-quantum signature method is BLISS (short for Bimodal Lattice Signature Scheme) [8]. It was created by Léo Ducas, Alain Durmus, Tancrède Lepoint and Vadim Lyubashevsky in 2013.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Hash to Obtain Random Subset (HORS) [3] is a quantum robust hashed-based one-time signature. With this we create a series of integers for our private keys and organise into an indexable form. Then we hash them to a sequence of public key values. Next we segment the hash of the message into a series of n-bit integer values. The signature is then achieved through a look-up of the value in the public key list.
- Lamport Signatures. Lamport. Outlines Lamport signatures [7]. When we sign a message we take its hash and then encrypt with our private key. The public key is then used to prove it, and will prove that we signed it with our private key. The Lamport signature uses 512 random hashes for the private key, and which are split into Set A and Set B. The public key is the hash of each of these values. The size of the private key is 16KB (2×256×256 bits) and the public key size is also 16 KB (512 hashes with each of 256 bits).
- Winternitz Signatures (W-OTS). Winternitz. Outlines Winternitz signatures [4, 5]. W-OTS uses relatively small key and signatures sizes, and is thought to be quantum robust. It generates 32x256 bit random private keys. We then hash these a number of times, and is defined by a parameter (w). If we use w=8, we hash the private keys by (2w). This creates 32x256 bits public keys. The signature is the created by taking eight bits at a time, and then the 8-bit binary int (n) is subtracted from 256 and the private key is the hashed 256-n times. The signature is then 32 hashes which are derived from random private keys. To verify the signature, the recipient parses the hash of the signature (using 8 bits at a time, and extracting the 8 bit int, n).
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method [6], and which is used within speeds-up of Hashing-based signature methods. Using methods such as SHA-1 and SHA-2 (aka SHA-256) will be inefficient as they tend to compress the data inputs through a number of stages. Haraka v2 [6] is different as focuses on inputs of just 256 bits (32 bytes) or 512 bits (64 bytes). This makes the method useful when we are dealing with key and hash values, and is especially useful for hash-based signatures. The output is 256 bits long, but where the input can be either be 256 bits (Haraka256) or 512 bits (Haraka512). These lengths are typically for the outputs of modern hashing applications. The Haraka method, too, has been optimized with AES instructions (AES-NI - Intel Advanced Encryption Standard New Instructions) and which are supported within the hardware of the processor. As Haraka is focused on short messages, the number of rounds within the hashing process has been reduced.
Hash-based signature (stateless)
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ digital signature. SPHINCS digital signature. Outline of the a SPHINCS stateless digital signature method [1].
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
Hash-based signature (Merkle-based)
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
Introduction
Many of the problems we see on the Internet relate to the lack of trust within transactions. The emails you receive and the Web sites that you visit often have very little trust built into them. For trust the email address of the sender, but anyone can fake that address. So increasingly we create a digital signature, and where we sign our messages. In this way, we can check for authentication, integrity and non-repudiation.
With the Alice creates a key-pair: a public key and a private key. She then takes a hash of the message, and then encrypts this hash with her private key, and passes the message and the signature to Bob. Bob then reads the message and takes a hash of it. He then decrypts Alice's signature with her public and checks the hashes. If they match, he knows that she signed and that it has not been changed along the way:
Currently, we often use RSA, DSA and ECDSA to sign our messages. These are based on the difficulty of finding out the factors of a number and on the processing of discrete logarithms. At the current time these methods are computationally hard problems, but with quantum computers, they become much easier. This was shown by Peter Shor who illustrated that it was possible to crack them in polynomial time.
Of all the methods that are being proposed, the hash-based methods look as if they have a good chance of success of creating quantum robust signatures. methods and code-based methods are being researched, but the usage of hashing methods is already well and could provide the best alternative to the existing methods. Hashing methods, too, often bring other advantages, such as forward secure, which means that a key which is cracked will not reveal all the previous keys.
Merkle trees
The root of hash-based methods isin Merkle trees, and which are a way of hashing is used in many applications, including with Bitcoin, Ethereum, Git distribution systems, No SQL, and in many P2P applications. With a Merkle tree we take our data elements, and then hash them, and take pairs of these hashes to create a new hash, and so we build a table. At the top of the tree is the root element (in this case Hash1234):

In this way, we can use the tree to see if we have matching data on systems.On a P2P network, we can transfer a file by splitting it into data segments and then distributing these segments across the network. A trusted source will have the complete Merkle tree for rebuilding the file, and a client can thus rebuild from the Merkle tree and determine the parts of the file which are still missing. Once transferred the root hash (and all the other hashes) will then match. In its core method, the Merkle Signature Scheme (MSS) has serious performance and memory issues, but enhanced methods such as XMSS create with much less of a performance hit.
One-time signatures (Lamport)
The core method used in hash-based signatures is that of the one-time signature, and where we create a new key pair for every method we need to create. If the keys were reused, an attacker could start to learn the private key, and thus spoof messages. One of the first methods was produced by Leslie Lamport and Whitfield Diffie, in 1979, and is defined as:
- We create two data sets with 256 random 256-bit numbers (Set A and Set B). These are the private key (512 values).
- we take the hash of each of the random numbers. This will give 512 hashes and will be the public key.
- We then hash the message using and then test each bit of the hash (0 ... 255). If it is a 0, we use the ith number in Set A, else we use the ith number from Set B.
- The signature is then 256 random numbers (taken from either Set A or Set B) and the public key is the 512 hashes (of Set A and Set B).
The public and private keys are then each 16KB in size. A demo of the method is here.

Figure 1: Lamport method
The major problem with the method is that a key pair for every message. also in 1979, found a solution with Merkle trees.
One-time signature (W-OTS)
To improve performance method (and which reduced key sizes), Merkle proposed Winternitz OTS (named after Robert Winternitz). With this method was possible to sign many bits at the same time. The method is:
- We create 32 256-bit random numbers. These 32 values will be our private key.
- We then hash each of these values 256 times. These 32 values will be our public key.
- We now take the message and hash it using SHA-256. This produces 32 8-bit values (N1, N2 ... N32).
- Next we take each 8-bit value in the hash of the message, and then hash 256-N times (where N is the value of the 8-bit value).
- To prove the signature, we take the message and hash it with SHA-256, and then take each 8-bit value. We then hash the 8-bit signature value by the number of times defined by the message hash value (N1, N2..). The result for each operation should equal the public key value.
This is illustrated below in Figure 2. A demo of the method is here.

Figure 2: W-OTS
Hash-based Signatures
The methods such as W-OTS and Lamport only provide for a one-time signature. In order to sign many messages, we can use the Merkel signature scheme (MSS). With this we take a hash of the keys and build these as the leaves of the tree. The root of the tree is then the public key - the verification key. We then just use the private key of the W-OTS method to create the signature. The sender also sends the authentication path, which is the neighbouring nodes within the path and which leads to the root of the tree. The recipient can then rebuild the tree using the verification key (which can be received a digital certificate) and the authentication path. For the next message we move onto another key pair and where the index of the key part is revealed.
In the following example we have our root as the public key, and then want to sign with Key3. We then show the authentication path which takes us to the root (as defined in the bold arrows):

Conclusions
Hashed-based methods look to be a strong contender for weaning us off RSA, DSA and ECDSA, but we will have to look at the stateful generation of keys. For this we will have to generate a bank of key pairs (2, 4, 8, 16, etc) and then create the public key from the root of the Merkle tree. We must then remember the keys we have used previously, and only use an unused one. Once we use our new key pair, we then show our working-out as to how the private key is integrated into our tree. It is a bit like a teacher marking a question correctly, and asking for the working out that go you to the answer.
References
[1] Bernstein, D. J., Hopwood, D., Hülsing, A., Lange, T., Niederhagen, R., Papachristodoulou, L., ... & Wilcox-O’Hearn, Z. (2015, April). SPHINCS: practical stateless hash-based signatures. In Annual international conference on the theory and applications of cryptographic techniques (pp. 368-397). Springer, Berlin, Heidelberg [paper].
[2] Bernstein, D. J., Hülsing, A., Kölbl, S., Niederhagen, R., Rijneveld, J., & Schwabe, P. (2019, November). The SPHINCS+ signature framework. In Proceedings of the 2019 ACM SIGSAC conference on computer and communications security (pp. 2129-2146) [paper].
[3] Reyzin, L., & Reyzin, N. (2002, July). Better than BiBa: Short one-time signatures with fast signing and verifying. In Australasian Conference on Information Security and Privacy (pp. 144-153). Springer, Berlin, Heidelberg [paper].
[4] Merkle, R. C. (1989, August). A certified digital signature. In Conference on the Theory and Application of Cryptology (pp. 218-238). Springer, New York, NY.
[5] Hülsing, A. (2013, June). W-OTS+–shorter signatures for hash-based signature schemes. In International Conference on Cryptology in Africa (pp. 173-188). Springer, Berlin, Heidelberg.
[6] Kölbl, S., Lauridsen, M. M., Mendel, F., & Rechberger, C. (2016). Haraka v2–efficient short-input hashing for post-quantum applications. IACR Transactions on Symmetric Cryptology, 1-29. [here]
[7] Lamport, L. (1979). Constructing digital signatures from a one-way function (Vol. 238). Technical Report CSL-98, SRI International. [paper]
[8] Ducas, L., Durmus, A., Lepoint, T., & Lyubashevsky, V. (2013, August). Lattice signatures and bimodal Gaussians. In Annual Cryptology Conference (pp. 40-56). Springer, Berlin, Heidelberg [paper].
[9] Perrig, A. (2001, November). The BiBa one-time signature and broadcast authentication protocol. In Proceedings of the 8th ACM Conference on Computer and Communications Security (pp. 28-37) [paper] .
Hashing (Simularity)

Similarity hashes allow for two data objects to be compared for their similarity.
Similarity assessment methods
The following relate to the basic methods used for string similarity:
- String similarity String similarity. This measures edit distance (including Levenshtein distance), Jaro (including Jaro-Winkler), and QGrams.
- String enthropy String enthropy. Measurement of the entropy of strings.
- Soundex Soundex. Soundex uses a phonetic algorithm to classify a sound as it is pronounced. It focuses on matching phrases which have minor spelling errors.
Similarity hashes
The following are the tips related to similarity hashing:
- Similarity hash: SimHash (Charikar similarity) in Python Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash (Nilsimsa similarity) Nilsimsa. The Nilsimsa similarity is used to find similarities between spam emails.
- Context Triggered Piecewise Hashes (CTPH): ssdeep CTPH similarity. Kornblum [6] created ssdeep and which computes fuzzy hashes. This aims to match similar byte sequences, no matter if there are differences between these sequences. For this we break a file up into fragments with a rolling hash function. We then produce a small hash for each of those fragments. These are then aggregated to produce the complete hash of a file. In comparing file signatures, we treat the resultant hash value as a string, and then uses an edit distance method to compare.
- TLSH (A Locality Sensitive Hash) TLSH similarity. In malware analysis and in text similarity, we often have to identify areas of data within files which are similar. One method is TLSH (A Locality Sensitive Hash), and which was defined by Oliver et al [7]. It is used - along with ssdeep - by VirusTotal to identify a hash value for malware.
- Minhash (Jaccard similarity) Jaccard similarity. The Minhash method is used to find similarities between strings, files and metadata.
- Counting identical elements (HyperLogLog) HyperLogLog. Counting the number of identical elements.
Hazmat cryptography

The Cryptography library in Python contains interfaces to common cryptographic algorithms, including symmetric key methods, hashing, public key, and key derivation functions. Many of these are contained with the Hazmat (Harzardous Material) primative setup.
Hashing, HMAC, CMAC, Poly1305 and HKDF
-
Hazmat Hashes. Hazmat Hashes. This includes the hashing methods in the Hazmat cryptography library. This includes Blake2p, Blake2s, MD5, SHA1, SHA224, SHA256, SGA384, SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHA512, SHA512-224, SHAKE128 and SHA256.
-
Hazmat Hashes. Hazmat Hashes. In this case we will implement Python code to determine SHA1, SHA2, SHA3, Blake2, MD5 and SM3 hashes.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
- Hazmat HKDF. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
- Hazmat CMAC. Hazmat CMAC. CMAC methods using the Python cryptography primitives.
- Hazmat Poly1305. Hazmat Poly1305. Poly1305 methods using the Python cryptography primitives.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
Symmetric key
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat. Implementation of ChaCha20/Poly1305 with a random key using Hazmat.
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat. Implementation of AES GCM with a random key using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hazmat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Hazmat Symmetric Key Padding. Symmetric key. This includes the coverage of padding with Hazmat.
- Hazmat Symmetric Key Padding. Symmetric key. This includes the coverage of padding with Hazmat.
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
- Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . With 3DES encryption, we use a 128-bit key and a 64-bit IV value. The two modes supported are ECB (without salt) and CBC (with salt). The DES algorithm has been around for a long time, and the 56-bit version is now easily crackable (in less than a day on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases, and splits the key into two. Overall the key size is typically 112 bits (with a combination of the three keys - of which two of the keys are the same). In this case we will use PKCS7 padding, and which fills the input data with a value that is equal to the number of padding bytes. Overall, DES has a 64-bit block size, and which equates to eight ASCII characters.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key . And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.
Asymmetric key
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- ECC key generaton with Hazmat. Elliptic Curve key gen. Creating ECC keys using Hazmat and Python.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- Hazmat RSA signing (with key values). RSA signing with Hazmat. RSA signing using Python and with Hazmat (with key values).
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here]
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Signatures. DSA Signatures. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. The ECDSA method is an extension of DSA, but implemented with elliptic curve (EC) methods. As with most public key signing methods, we take a hash of a message, and then apply a private key to create a signature (\(r,s\)). This is done by creating a random value (\(k\)) to produce the signature. The signature is then verified using the associated public key. This then verifies the creator of the signature and that the message has not been changed.
Digital Signature: ECDSA/EdDSA
- ECDSA with Hazmat. ECDSA wih Hazmat. This outlines ECDSA with Hazmat.
- Ed25519 for EdDSA signatures with Hazmat. EdDSA: Ed25519. This page uses the Hazmat primitives for the cryptography library.
- Ed448 for EdDSA signatures with Hazmat. EdDSA: Ed448. This page uses the Hazmat primitives for the cryptography library.
- Ed25519 using NaCl. Ed25519. This page uses the NaCl port from libsodium.
- ECDSA Signatures with Hazmat (SECP256R1, SECP384R1, SECP521R1, SECP224R1, SECP192R1, and SECP256K1). ECC Signatures. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and then creates an ECDSA signature for a given message.
Digital Signature: RSA
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
Key exchange: ECDH/X25519
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives and showing the byte values for the key.
Tokens
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
Homomorphic Encryption

Homomorphic encryption supports mathematical operations on encrypted values. Partial Homomorphic Encryption (PHE) supports a few arithmatic operations, while Full Homomorphic Encryption (FHE) supports add, subtract, multiply, and divide. Homomorphic encryption normally involves a public key to encrypt the data, and a private key to decrypt it. There have been four main generations of homomorphic encryption, and the most recent being the HEAAN method.
Simple
- Simple Homomorphic Cipher. Hom. This outlines a Simple Homomorphic cipher.
- Simple Homomorphic Cipher (Python). Hom. This outlines a Simple Homomorphic cipher with Python.
- Full Homomorphic Cipher with a Public Key. Public key. This outlines a Simple Homomorphic cipher using a public key
ElGamal
- ElGamal Homomorphic Cipher (Go). ElGamal. This outlines ElGamal Homomorphic cipher with Go.
- ElGamal Homomorphic Cipher (Go) - Divide. ElGamal. This outlines ElGamal Homomorphic cipher with Go with divide.
- ElGamal Homomorphic Cipher (Go) - Additive. ElGamal. This outlines ElGamal Homomorphic cipher with Go with addition.
- ElGamal Homomorphic Cipher for Multiplication (Python). ElGamal. This outlines ElGamal Homomorphic multiplication with Python.
- ElGamal Homomorphic Cipher for Division (Python). ElGamal. This outlines ElGamal Homomorphic division with Python.
- ElGamal Homomorphic Cipher for Addition (Python). ElGamal. This outlines ElGamal Homomorphic addition with Python.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (Python). ElGamal. This outlines ElGamal Homomorphic subtraction with Python.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
RSA
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
ZKP
- Full Homomorphic Cipher to determine if Bob is older. Older. This outlines a Simple Homomorphic cipher to determine if Bob is older than Alice.
- Full Homomorphic Cipher to determine matching password. Password. This outlines a Simple Homomorphic cipher to determine if a password matches
- Interactive ZKP With Probablistic Methods. ZKP. Interactive ZKP With Probablistic Methods using Python.
- Full Homomorphic Cipher for Millionaire's Problem. Millionaire. This outlines a Simple Homomorphic cipher for the Millionaire's Problem
Voting
- Trusted voting. Trusted. A trusted voting method.
Secret share
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Lattice
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
Full Homomorphic Cipher
- Full Homomorphic Cipher for 2-bit Adder. Adder. This outlines a Simple Homomorphic cipher for a 2-bit adder with DGHV.
- Full Homomorphic Cipher for Full Adder. Full Adder. This outlines a Simple Homomorphic cipher for a full adder with DGHV.
- Full Homomorphic Cipher for 4-bit Adder. Adder. This outlines a Simple Homomorphic cipher for a 4-bit adder with DGHV.
- Full Homomorphic Cipher for 4-bit Adder/Subtractor. Subtract. This outlines a Simple Homomorphic cipher for a 4-bit adder/subtractor with DGHV.
- Full Homomorphic Cipher to XOR two integers. X-OR. This outlines a Simple Homomorphic cipher to X-OR two integers
Paillier
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier) .
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Damgård-Jurik Homomorphic Encryption With Secret Shares. Damgård-Jurik Method. Two of the major areas of developments within cybersecurity will be the usage of homomorphic encryption, and in the usage of Shamir secret sharing. With homomorphic encryption, we can encrypt values, and then operate on them with arithmetic functions (such as add, subtract and multiply), and with Shamir secret sharing, we can split secrets into shares, and then distributed them over networks. These approaches will take privacy to new levels. So let’s look at the Damgård-Jurik method.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Learning with Errors (LWE)
- Learning With Errors . LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret key value (s) and another value (e). Next we select a number of values (t[]) and calculate g[] = t[] x s + e. The values of g[] and t[] become our public key.
- Public Key Encryption with Learning With Errors (LWE). LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret value (s) and which is our private key. We then create a public key which is based on random numbers (A), and then generate another set of numbers (B) which is based on A,s and random errors e. An example of encryption with multiple bits is given.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE)
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Others
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
- SIDH Go. SIDH. Post-quantum key exchange.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Anonymous crypto. Anon. Anonymous crypto.
- Rho factorization. Rho. Rho alogorithm.
- Post-quantum signing (BLISS). BLISS. BLISS method.
Homomorphic Encryption with Krytology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Homomorphic hashing
- Homomorphic Hashing with Golang. Homomorphic hashing. Normally with hashing methods, we need to take all the previous data and new data in order to create a new hash value for our data. In a homomorphic hashing method, we can basically take the previous hash, and then add on any new data values. We can also remove previous data values from our hash, too. This is more efficient in computing, as we do not have to process all of our data into a new hash, and can use simple homomorphic operations for the computation. The method we will use (LtHash) was initially defined by Bellare and Micciancio and updated Lewi et al at Facebook.
Identity Based Encryption (IBE)

This page outlines a few basic principles around the usage of IBE.
Identity Based Encryption (Pairing based)
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pair-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Identity Based Encryption (Others)
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Güther's implicitly certified identity-based public keys (IBE). Günther. This method allows Bob to generate Alices public key from her identity and publicly available parameters.
- Girault's self-certified public keys (IBE). Girault. This method allows Bob to generate Alices public key from her identity and publicly available parameters, and where we use an RSA key pair to self-certify Alice's public key.
Intrusion Detection Systems (IDS)
- Intrusion Detection Systems. Snort. This outlines some of the basics of IDS, including the requirement for Intrusion Detection Systems (IDSs), and where they are used.
- Advanced Network Forensics (Snort). Adv Network Forensics. This provides information on how to detect threats through network forensics with Snort
Snort

- Snort IDS. Snort. This is a Snort Analyser.
- Snort IDS 2 with rules editor. Snort. This provides information on how to detect threats through network forensics with Snort, and with an editing function for rules.
Presentation
IoT

The key objectives of this page are: Understand how a Pen Tester can generate vulnerabilities and test using the Metasploit framework; Define the options and payloads required to generate and use vulnerabilities; and Gaining remote access.
Devices
- Access the Wi-fi kettle. Go. This page outines how to access a wi-fi enabled kettle.
- Philips Hue Wireless Lighting. Go. This page shows how to use RESTful Web services to access to the Hue Led Lamps.
- Kali and R-PI. Go. This page shows the setup of a security testing infrastructure using a Raspberry Pi (R-PI) and a wifi access point.
- Kali, R-PI and RF electrical socket. Go. This page shows the control of an RF electical socket from a RPI.
- Capture from a Polar H10 heat rate sensor. Go. This page shows the capture of the Polar H10 heart sensor with an Ubertooth One.
- Trusted IoT: Linking IoT Devices to NFTs. Go. This page outlines a research paper which links a device to an NFT (Non-fungible Token).
Shodan Scanning
-
IoT Scan (Shodan). Go. This page includes a search of the Internet for key terms, such as for "apache", "mysql" and "cisco".
- IoT Banner Scan (Shodan). Go. This page includes a search of the Internet for key terms with the banner as a result (for the Top 10)
- Internet Services (Shodan). Go. This page includes a search of the Internet for key terms and display the IP address and port.
IoT Libraries
- libDisco with Go. libDisco. libdisco is a Golang library which can be used to create secure connections. It is based on the STROBE protocol framework. Symmetric cryptographic primitives rely on SHA-3 permutation, and asymmetric cryptographic primitives on X25519 and ed25519. STROBE defines a range of cryptographic protocols to integrate with IoT devices. In order to reduce processing, energy and memory requirements, it only uses Keccak (SHA-3) to encrypt and authenticate messages.
COSE/COBR
In computer security, we often have to represent binary data, in single values or groups of characters, bytes, words, long words, signed integers, floating-point values, double-precision floating-point values, and so on. This might be in the form of a data object, a signature or even encrypted content. For this, the ANS.1 DER format is often used, such as presenting digital certificates and signatures. An improvement on this for small messages with security is Concise Binary Object Representation (CBOR) — and which is defined in RFC8949 [1]. While JSON represents text-based data objects CBOR focuses on binary objects. It has been designed to create a lightweight encoder and decoder. This supports the use of CBOR within an IoT infrastructure. The data, also, does not require a data schema to be able to decode it, along with being extensible. CBOR defines the format of binary data with data objects and messages. We can then integrate security with CBOR Object Signing and Encryption (COSE), and which is defined in RFC8152 [2]. This includes signatures, message authentication codes (MACs), encryption and creating serialised objects.
- 128-bit AES GCM. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) can then build on this to include signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use a symmetric key to encrypt a message, and then decrypt it. In this case we will use AES GCM with a static 128-bit key ("0x000102030405060708090a0b0c0d0e0f").
- 256-bit AES GCM. Go. In this case we will use AES GCM using a random 256-bit key (32 bytes).
- EdDSA. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) [2] can then build on this to includes signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use EdDSA to create a signature for a message.
- ECDSA. Go. In this case we will use ECDSA to create a signature for a message.
- HMAC. Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT. Go. In this case we create a CWT token, and sign with an HMAC signature.
- ECDH. Go. In this case we create a symmetric key from ECDH. For this we will derive a shared key from the public key of Alice and Bob, and then define a single recipient which can derive the CEK (Content Encryption Key) using their private key. We will use the curves of P-256 (secp256r1), P-384 (secp384r1), P-521 (secp521r1) or SECP256K1 (as used with Bitcoin).
- RSA using COSE and CBOR. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\).
- RSA: dQ, dP and InvQ. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). The key pair also includes \(dQ\), \(dP\) and \(InvQ\), and these can be used with the Chinese remainder theory to optimize the decryption process.
Metasploit
- Armitage and Metasploit. Go.
- Exploiting Android with Metasploit. Go.
- Exploiting Android with Metasploit - Part 2. Go.
- Exploiting Windows/Mac OS X with Metasploit. Go.
- Remote Desktop Windows/Mac OS X with Metasploit. Go.
- Metasploit. Go.
- Internet of Things Security. Go.
- Metasploit (Enumeration and Scanning). Go.
- Metasploit (Malware). Go.
IP

 The following are a few interesting techniques around IP addresses:
The following are a few interesting techniques around IP addresses:
- Your details. IP. This shows your browser details.
- IP address analyser. IP. This involves converting an IP address to the host and network part of the address.
- IP subnet analyser. IP subnets. This involves converting an IP address to the host and network part of the address.
- IP address analyser. IP. This involves analysing IP addresses.
- Max subnets. Max subnets. This involves converting an IP address to the host and network part of the address.
- Route summarization. Summarization. This involves converting an IP address to the host and network part of the address.
- Whois. Whois. This does a basic Whois on a domain.
- URL Obfuscation. Obfuscation. This outlines URL obfuscation.
- HTTP Responses. Test. HTTP.
- Capturing Network Packets (Python). WinPCap. HTTP.
Cisco related
- Routing table. Routing table. This involves viewing a routing table for a Cisco device.
- ACL Generator. ACL. This involves a simple calculator for ACLs on network ranges.
- EIGRP metrics. EIGRP. Learn the basics of EIGRP metrics.
- VoIP B/W. VoIP. Calculate bandwidth for VoIP.
- Wild Card. Wild Card. On a Cisco device a wildcard mask is used to identify the parts of an IP address that need to be matched. It thus uses a wildcard mask, where a 0 in the bit position identifies that the device should match that bit, else a 1 shows that it should ignore it.
Protocols
- HTTP. HTTP. Show the request and response for HTTP.
- Ping analyser. IP. This involves converting a ping of a site.
IP Challenges
-
IP Test 1. IP Test. IP Classification test. This is a simple test which generates a range of IP addresses, and you must determine the IP address classification.
IP Subnet Challenge 1 Demo
-
IP Test 2. IP Test. IP Classification test Part 2. This test provides an address classification, and the user must find the addresses which are of this classification.
IP Subnet Challenge 2 Demo
-
IP Test 3. IP Test. IP Classification test Part 3. This test provides an address classification, where the network part of the address is determined.
IP Subnet Challenge 3 Demo
Subnet Challenges
- Subnet Test 1. Subnet Test. Subnet Test.
-
Subnet Test 2. Subnet Test. Subnet bits.
- Subnet Test 3. Subnet Test. Find the nth usable subnet. This test involves finding the nth usable subnet.
- Subnet Test 4. Subnet Test. Maximum subnets. This is a test page to determine the maximum number of subnets and hosts/subnet for IP classed addressing.
- Subnet Test 5. Subnet Test. Maximum host/subnet. This is a test page to determine the maximum number of hosts per subnet.
- Subnet Test 6. Subnet Test. Determine the required subnet mask for a given number of subnets. This is a test page to determine the required subnet mask for a given number of subnets and a given IP address classification.
- Subnet Test 7. Subnet Test. Determine the required subnet mask for a given number of host/subnet. This is a test page to determine the required subnet mask for a given number of hosts per subnet and a given IP address classification.
- Subnet Test 8. Subnet Test. Route summarization. This involves a calculation on route summarization.
- Subnet Test 9. Subnet Test. Binary to IP.
- Subnet Test 10. Subnet Test. Hex to IP.
-
Subnet Test 13. Subnet Test. Wild card mask network bits. Find the number of bits in the network part of the wild card mask. IP Wildcard challenge
- Subnet Test 14. Subnet Test. Wild card mask host bits. Find the number of bits in the host part of the wild card mask. IP Wildcard challenge
- Subnet Test 15. Subnet Test. Wild card mask ... find the network address. Find the network for the wild card mask. IP Wildcard challenge 2
- Subnet Test 16. Subnet Test. Find a matching IP address for a network and wild card mask. Find the IP for a network and a wild card mask.
- Subnet Test 17. Subnet Test. Find an address which is on a given network. Find an IP address on a network, for a given network address and subnet mask.
- Subnet Test 18. Subnet Test. Find an IP address on the same network. Find an IP address on the same subnet.
- Subnet Test 19. Subnet Test. Find subnet. Convert subnet mask.
- Megatest. Subnet Test. Challenging test for subnets.
JavaScript

JavaScript code allows execution within the browser, rather than on the server. It is often faster than code that runs on a server. Along with this we can also use Node.js, and which runs JavaScript code on a server.
Symmetric key
- AES. AES. In this example, we will use either a pre-generated key or a random one, and use AES (Rijndael) encryption.
- ChaCha20 and Poly1305. ChaCha. This page outlines Poly1305 and ChaCha20. ChaCha20 is a symmetric key method and Poly1305 is a message authentication code (MAC). They were created by Daniel J. Bernstein, and are alternatives to AES and HMAC.
- CMS (Padding). CMS. This page uses PKIJS encrypting on CMS. With CMS we can This document describes the Cryptographic Message Syntax (CMS). With this we can encapsulate an message within an encrypted entity.

Hashing
- Hash. Hash. This page defines a JavaScript Hash calculator. This uses a client-side JavaScript code to determine the hash signatures of a text value.
Signatures
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
- Boneh–Lynn–Shacham (BLS) signature. BLS. Boneh–Lynn–Shacham (BLS) signature method produces short signatures. They use elliptic curve pairing (and which are also known as bilinear maps).
Key exchange
- ECDH. ECDH. Elliptic Curve Diffie Hellman (ECDH) is used to generate a shared key. This implementation uses Elliptic Curve Cryptography (ECC) with JavaScript.
CryptoJS
- CryptoJS. CryptoJS. This page uses client-side JavaScript code to hashing, encrypt and sign, including for symmetric key (AES), streaming ciphers, hashing methods, and HMAC.
Blockchain
- PATRICIA trie. PATRICIA. In the following, we have the Top 2,500 Web sites in the world, and implemented with a Radix Trie (aka PATRICIA trie) In the following we have the Top 2,000 web sites on the Internet, and which have been indexed using the PATRICIA trie.
Public key
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
- RSA. RSA. RSA is an asymmetric encryption algorithm, which uses two keys, one to encrypt and the other to decrypt. It was created in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman, and is still one of the most widely used encryption methods. A typical application is in authenticating a sender, where the senders private key is used to encrypt a message, and then is decrypted by the receiver with the senders public key (which is known to anyone who wants it). It is also typically used for encrypting disks/files, such as for EFS.
Digital Certificates
- X.509 certificates in JavaScript. RSA and ECDSA Signed certificates. This page will generate either RSA and ECC key pairs, and then generate X.509 certificates, using either a signature of SHA1withRSA or SHA256withECDSA. For RSA signing we use an RSA private key to sign the certificate, and with ECDSA signing we use an ECC private key to sign the certificate.
Tokens
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
Random
- Random number generator. Rand. In the past, encryption and decryption had to be done through native code libraries, such as with Bouncy Castle and OpenSSL. With the increasing processing power of Web browsers, it is now possible to use encryption using JavaScript, which thus provides client-side processing of data. This Web page uses Javascript encryption, and generates a random 256-bit text key or a hex version. The 256-bit key is generated by generating 60 random numbers (from 0-25), and converting these to an ASCII character.
Malware obfuscation
- Malware obfuscation. Obfuscation. A malware writer will often hide certain keywords from the browser/human by encoding them in another format. This is typically done for hex coding (\xZZ), 16-bit unicoding (\uZZZZ) and octal coding (\ZZZ). To test, enter a value, and then press the button and it will convert encoded string.
Message Authentication Codes
- Chaskey (MAC). Chaskey. Chaskey Cipher is light-weight cryptography method for signing messages (MAC) using a 128-bit key. The hardware implementation only requires 3,334.33 gate equivalent with an operating clock frequency of 1 MHz (whereas Keccak requires 4,658 GE). In the page we create the Mac signature and also encrypt for CBC.
Other
- Password generation/hashing. Hashing. Linux can use salted passwords where the username, hashing method and hashed password are stored in a password file [More details]. The main methods are
Hashing

At times we need to generate secrets, such as encryption keys, from passwords or nonce values. A Key Derivation Function (KDF) is a verifiable way of doing this.
Key Derivation Functions (KDFs)
The following are the tips related to hashing:
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Password strength. Test. This outlines the strength of various passwords types.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
HKDF
The following are the tips related to Key derivation hashing:
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Hazmat HKDF for different hashing methods. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
-
HKDF key derivation with OpenSSL [
here]
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
PBKDF2
The following are the tips related to Key derivation hashing:
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- AES GCM (Python) with PBKDF2. AES GCM (Python) with PBKDF2.
- Fernet with PBKDF2 . AES GCM (Python) with PBKDF2.
- PBKDF2 key derivation. AES GCM (Python) with PBKDF2.
- Key Rotation with Fernet. AES GCM (Python) with PBKDF2.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Bcrypt
The following are the tips related to Key derivation hashing:
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- BCrypt. BCrypt. BCrypt with Rust.
-
Hash to password with Go. Hashing to Argon2, Scrypt and BCrypt. Hash to password with Go, including Argon2, Scrypt and BCrypt.
scrypt
- scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Argon 2
The following are the tips related to Key derivation hashing:
- Argon 2. Go. Outline of Argon2.
- Argon 2 with NaCl. Go. Outline of Argon2 using NaCl.
- Argon 2. Argon 2. Argon 2 with Rust.
- Balloon. Go. Outline of Balloon.
Other
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
- Double ratchet. Go. Outline of double ratcheting.
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
Outline
HMAC Key Derivation function (HKDF) is used to derive an encryption key from a passphrase. Initially, HKDF creates a pseudorandom key (PRK) using a passphrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), and along with a salt value. Next, the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys [RFC 5869][article]. In this case, we will use SHA-256.
The following shows how an encryption key can be generated using HKDF, and where we need a secret and a salt value. Both Bob and Alice have the same secret and salt.

With PBKDF2 (Password Based Key Derivation Function 2), we hash for a given number of rounds:

Key exchange

Key exchange is a way for Bob and Alice to communicate and for them to agree on a shared secret. The original method defined uses discrete logarithms (Diffie-Hellman), but most modern methods use elliptic curve techniques (ECDH). As quantum computers can crack both discrete log and elliptic curve methods, there are post quantum cryptography methods proposed. This includes SIDH, CSIDH, SIKE, and NewHope.
Key interchange/generation (Diffie-Hellman)
The following relates to key interchange:
- Selecting \(g\) in Diffie Hellman. G in Diffie Hellman. Picking a safe value of the generator \(g\) in discrete logarithms.
- Diffie-Hellman. Diffie-Hellman Calculation. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Real example). Diffie-Hellman Real. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Python). Diffie-Hellman. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (pre-compute). Diffie-Hellman (pre-compute). Many sites use the same prime numbers, which can then be cracked with a pre-computing attack.
- Key generation. Key gen. This will generate keys for different methods based on a passphrase.
- Diffie-Hellman (Man-in-the-middle). DF. This outlines the man-in-the-middle method for Diffie-Hellman.
- An Alternative Diffie-Hellman method. Alterative DH. This outlines an alternative Diffie-Hellman method.
Authenticated Key Exchange
The following are the tips related to Key derivation hashing:
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- MTI/A0. MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{ax+by} \pmod p\). MTI (Matsumoto, Takashima, Imai).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0. MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{x+y} \pmod p\)
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). The resultant key is \(xyG \)
- MTI/C0. MTI/C0. This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{xy} \pmod p\)
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG\).
- MTI/C1. MTI/C1. This outlines MTI/C1, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{abxy} \pmod p\).
- MQV (Menezes–Qu–Vanstone). MQV. MQV was created Alfred Menezes, Minghua Qu and Scott Vanstone in 1995 and is an authenticated key exchange method. Alice holds a key pair \((A,a)\) and Bob has a key pair \((B,b)\). With this \(a\) is Alice's private key, and \(A=aG\) is her public key. For Bob, his public key will be \(B=aG\) and a private key of \(b\), and where \(G\) is the base point on the elliptic curve.
- HMQV (Menezes–Qu–Vanstone). HMQV. HMQV builds on MQV and adds the identity of Bob and Alice.
- ECDH with X25519 and Blake2b. ECDH with X25519 and Blake2b. This uses PyNaCl to create an authenticated key exchange and uses X25519 and Blake2b.
Elliptic Curve (ECDH) - Python
The following are the tips related to ECC:
- Elliptic Curve. Elliptic Curve. Elliptic Curve is a public key method which can also be used to generate a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with simple parameters. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
Elliptic Curve (ECDH) - Golang and Node.js
The following are the tips related to ECC:
- ECDH with Go. ECDH. ECDH with Go.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with node.js. ECDH. ECDH with node.js.
- ECDH with JavaScript. ECDH. Elliptic Curve Diffie Hellman.
Password Authenticated Key Exchange (PAKE)
The following are the tips related to Key derivation hashing:
- SPAKE2. Go. Outline of SPAKE2.
- OPAQUE. Go. Outline of OPAQUE.
- SPEKE. Go. Outline of SPEKE (Simple Password Exponential Key Exchange).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
- J-PAKE. J-PAKE. This example generates a shared key based on a shared password.
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses discrete logs.
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
PQC NIST Finalists (Key Exchange)
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Key interchange/generation (Other)

The following relates to key interchange:
- Curve25519. Curve25519. This outlines Curve25519, which is used in the Tor network.
- Authenticated Key Exchange (Discrete logs). YAK. Key exchange with public keys and uses discrete logs.
- Authenticated Key Exchange (ECC). YAK. Key exchange with public keys and uses elliptic curve methods.
- Shamir No-key protocol. Shamir No Key. In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated.
- Shamir No-key protocol (sepc256k1). Shamir No Key (EC). In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated using the sepc256k1 elliptic curve.
- Conference keying (Burmester-Desmedt method). Conference keying. In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it.
- Conference keying (Burmester-Desmedt method) - Elliptic Curve (sepc256k1). Conference keying Elliptic Curve (sepc256k1). In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it, and uses the sepc256k1 elliptic curve.
Key exchange (with pairing)
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Kryptology

We need to build a new Internet. One that is build on mathematics and certainty, rather than the patchy version we have now. For this we need a layer of cryptography at the lowest level, and build software interfaces on top of this. Along with this we now have cryptographic methods which can now provide a foundation of trust, and which preserve privacy. And so the old libraries of OpenSSL are being squeezed out in favour of the new ones which are built on a solid foundation. The latest of these new "privacy-aware" libraries is Kryptology, and created by Coinbase. This library provides the APIs that developers need, in order to apply to areas of blockchain development. This library include BLS (Boneh-Lynn-Shacham) signatures, Zero-knowledge Proofs (ZKPs) and Shamir Secret Shares (SSS). With BLS we can digitally sign for data, but also preserve its privacy. Applications of this include group signatures, where multiple entities can merge their signing keys together and provide a single signature for a transaction. With SSS, we can split encryption keys up into shares, and then distribute them across a network. When required, we can call these shares back to reconstruct the key.
The focus for Coinbase seems to be the application of privacy coins, and where no tracking can be applied to the usage of these digital coins. This should support full anonymity for transactions, as opposed to Bitcoin which only supports pseudo-anonymity.

ECC Basics
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining n.G for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Points (Base Point and Others). Elliptic Curve points. Two common curves used in ECC (Elliptic Curve Cryptography) are secp256k1 (as used in Bitcoin and Ethereum) and P256 (secp256r1). The "k1" refers to the Kolbitz curve 1 (named after the creator of ECC). With these we have a base point which are can operate on. This is typically defined as \(G\). We can then operate on this with add and multiply operation. For example, \(2G=G+G\) and \(P=n.G\). In this following we will show the base point for a number of common curves, such as secp256r1, P256, Pallas, Curve 25519, BLS12381G1, BLS12381G2, BLS12377G1 and BLS12377G2.
ECDH
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret. We will use Golang and the Krytology library.
Simple ECC on curves
- Public key points for curves. Simple. Display public key points for scalars.
BLS Curve
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
Accumulator and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
Pallas Curve
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
Pairing-based Crypto
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
ElGamal and ECC
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a numerical input.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
Shamir Secret Shares
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Homomorphic Encryption
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Zero knowledge proofs
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
Verifiable Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Hash to scalar and point
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
CP-ABE
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Lattice cryptography

Latice cryptography is proposed as a post-quantum robust method for public key encryption, especially focused on digital signatures and key exchange mechanisms (KEMs).
Principles
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
NTRU
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- Lattice Encryption: NTRU Key Generation Python). NTRU. Outlines how NTRU operates for key generation.
Homomorphic
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Digital Signatures
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
Public-Key Encryption/Key Exchange
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
Light-weight cryptography

While AES and SHA work well together within computer systems, they struggle in an IoT/embedded world as they take up: too much processing power; too much physical space; and consume too much battery power. So NIST outlines a number of methods which can be used for light-weight cryptography, and which could be useful in IoT and RFID devices [1]. They define the device spectrum as:
- Conventional cryptography. Servers and Desktops. Tablets and smart phones.
- Light-weight cryptography. Embedded Systems. RFID and Sensor Networks.
With embedded systems, we commonly see 8-bit, 16-bit and 32-bit microcontrollers, and which would struggle to cope with real-time demands for conventional cryptography methods. And in the 40+ years since the first 4-bit processor, there is even a strong market for 4-bit processors. RFID and sensor network devices, especially, have limited numbers of gates available for security, and are often highly constrained with the power drain on the device.
So AES is typically a non-starter for many embedded devices. In light-weight cryptography, we often see smaller block size (typically 64 bits or 80 bits), smaller keys (often less than 90 bits) and less complex rounds (and where the S-boxes often just have 4-bits).
For light-weight cryptography the main constraints that we have are typically related to ener requirements, gate equivalents (GEs), and timing. With passive RFID devices, we do not have an associated battery for the power supply, and where the chip must power itself from energy coupled from the radio wave. An RFID device is thus likely to be severely constrained in the power drain associated with any cryptography functions, along with being constrained for the timing requirements and for the number of gates used. Even if an RFID device has an associated battery (active RFID), it may be difficult to recharge the battery, so the drain on power must often be minimised.
There is thus often a compromise between the cryptography method used and the overall security of the method. Thus often light-weight cryptography methods balance performance (throughput) against power drain and GE, and do not perform as well as main-stream cryptography standards (such as AES and SHA-256). Along with this the method must also have a low requirement for RAM (where the method requires the usage of running memory to perform its operation) and ROM (where the method is stored on the device). In order to assess the strengths of various methods we often define the area that the cryptography function will use on the device – and which is defined in \(µm^2\). The NIST finalists are defined in this [article]
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- GIFT AEAD. GIFT. GIFT is a light-weight block cipher. It is a (NIST Finalist)
- Elephant. Elephant. Elephant is a light-weight stream cipher. It is a (NIST Finalist).
- TinyJambu. TinyJambu. TinyJambu is a light-weight block cipher. It is a (NIST Finalist)
- Isap AEAD. Isap. Isap is a light-weight block cipher. It is a (NIST Finalist)
- PHOTON-Beetle AEAD. PHOTON-Beetle. PHOTON-Beetle is a light-weight block cipher. It is a (NIST Finalist)
- Romulus AEAD. Romulus. Romulus is a light-weight block cipher. It is a (NIST Finalist)
- Sparkle AEAD. Sparkle. Sparkle is a light-weight block cipher. It is a (NIST Finalist)
- CLEFIA. CLEFIA. CLEFIA is a light-weight block cipher.
- LED. LED. LED is a light-weight block cipher.
- Piccolo. Piccolo. Piccolo is an ultra light-weight block cipher.
- PRESENT. PRESENT. Present is a light-weight block cipher.
- Pyjamask. Pyjamask. Pyjamask is a light-weight block cipher.
- SIMON. SIMON. SIMON is a light-weight block cipher.
- SKINNY. SKINNY. SKINNEY is a light-weight block cipher.
- SPECK. SPECK. SPECK is a light-weight block cipher.
- XTEA. XTEA. XTEA is a light-weight block cipher.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encryption/Decryption. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.
Light-weight crypto (Other)
- Chaskey (MAC). Chaskey. Chaskey is a light-weight MAC function.
- Chaskey (MAC). Chaskey (Python). Chaskey is a light-weight MAC function.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (ASCON)
ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRFF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
Discrete Logs (Solving)

A discrete log problem is in the form of \(g^x \pmod p\) and where we know \(g\) and \(p\) and must solve for \(x\).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Message Authentication Code (MAC)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
HMAC
The following are the tips related to Key-based hashing:
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authentication both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2), Blake2b, SM3 and SHA-3. This page outlines the HMAC-MD5 methods using the Hazmat cryptography layer.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- HMAC (COSE). Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT with HMMAC. Go. In this case we create a CWT token, and sign with an HMAC signature.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- HMAC with Rust. HMAC. HMAC with Rust.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HMAC with OpenSSL. MACs with OpenSSL. HMAC in OpenSSL for a given input value, password and hashing method.
Cipher MACs
The following are the tips related to Key-based hashing:
- MACs with OpenSSL. MACs with OpenSSL. MAC methods implemented in OpenSSL, including CMAC and GMAC.
Key-based hashing
The following are the tips related to Key-based hashing:
- SipHash. Siphash. Siphash is a fast key-based hashing method.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Meow. Meow. Meow is one of the fastest hashing methods.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
Magic Numbers

This pages contains information related to magic numbers in file formats.
Network and File Forensics
- Magic numbers. Magic. This provides information on magic number for file forensics.
Graphics formats
- JPEG Analysis. JPEGs. This provides an analysis of JPEG files.
- GIF Analysis. GIFs. This provides an analysis of GIF files.
- TIF Analysis. TIFs. This provides an analysis of TIF files.
- PNG Analysis. PNGs. This provides an analysis of PNG files.
- BMP Analysis. BMPs. This provides an analysis of BMP files.
- PSD Analysis. PSDs. This provides an analysis of PSD files.
- WMF Analysis. WMF. This provides an analysis of WMF files.
- Adobe Illustrator Analysis. AI. This provides an analysis of AI files.
- Adobe In Design Analysis. INDD. This provides an analysis of INDD files.
- MIDI file. MIDI. This provides an analysis of MID files.
- ICO file. ICO. This provides an analysis of ICO files.
- PS file. PS. This provides an analysis of PS files.
- EPS file. EPS. This provides an analysis of EPS files.
- VSD file. VSD. This provides an analysis of Microsft Visio (VSD) files.
Video and audio formats
- MP3 Analysis. MP3s. This provides an analysis of MP3 files.
- AVI Analysis. AVIs. This provides an analysis of AVI files.
- Flash SWF Analysis. SWFs. This provides an analysis of Flash files.
- Flash FLV Analysis. FLVs. This provides an analysis of FLV files.
- MP4 Analysis. MP4. This provides an analysis of MP4 files.
- MOV Analysis. MOV. This provides an analysis of MOV files.
- WMV Analysis. WMV. This provides an analysis of WMV files.
- WMA Analysis. WMA. This provides an analysis of WMA files.
- JPEG 2000 Analysis. JPEG 2. This provides an analysis of JPEG 2000 files.
- WAV Analysis. WAV. This provides an analysis of WAV files.
Zips, Archives and Library files
- ZIP/Archive Analysis. ZIPs. This provides an analysis of ZIP/Achive files.
- GZ Analysis. GZ. This provides an analysis of GZip files.
- Tar Analysis. Tar. This provides an analysis of TAR files.
- MSI Analysis. MSI. This provides an analysis of MSI files.
- OBJ Analysis. OBJ. This provides an analysis of OBJ files.
- DLL Analysis. DLL. This provides an analysis of DLL files.
- CAB Analysis. CAB. This provides an analysis of CAB files.
- EXE Analysis. EXE. This provides an analysis of EXE files.
- RAR Analysis. RAR. This provides an analysis of RAR files.
- SYS Analysis. SYS. This provides an analysis of SYS files.
- HLP Analysis. HLP. This provides an analysis of HLP files.
- VMDK Analysis. VMDK. This provides an analysis of VMDK files (VMWare Virtual Disks).
- PST Analysis. PST. This provides an analysis of PST files (Outlook Email File).
- JAR Analysis. JAR. This provides an analysis of JAR files.
- SLN Analysis. SLN. This provides an analysis of Microsoft SLN files.
- Class Analysis. Class. This provides an analysis of Java Class files.
- Zlib. Zlib. This provides an analysis of Zlib files.
Documents
- PDF Analysis. PDFs. This provides an analysis of PDF files.
- DOC Analysis. DOCs. This provides an analysis of DOC files.
- RTF Analysis. RTFs. This provides an analysis of RTF files.
- XLS Analysis. XLSs. This provides an analysis of XLS files.
- PPT Analysis. PPTs. This provides an analysis of PPT files.
- MMP File. MMP. This provides an analysis of MMP files.
- DOCX Analysis. DOCX. This provides an analysis of DOCX files.
- XLSX Analysis. XLSX. This provides an analysis of XLSX files.
- PPTX Analysis. PPTX. This provides an analysis of PPTX files.
- MDB Analysis. MDB. This provides an analysis of MDB files.
- Outlook Message Analysis. MSG. This provides an analysis of MSG files.
Disk Image
- Raw disk format. RAW. This provides an analysis of the RAW disk format.
Tests
- File Forensics Test. File Test File Forensics Test.
- File Forensics Test (Fun). File Test (Fun) File Forensics Test.
Presentations
MIRACL Core Library

MIRACL Core is an open source library, and includes a wide range of public key encryption methods. It is especially focused on elliptic curve and pairing-friendly methods, but also supports a wide range of encryption methods, including RSA, AES and hashing. Overall, it can be ported onto a wide range of systems and supports C, C++, Go, Rust, Python, Java, Javascript and Swift. Along with this it supports limited capability devices such as the Arduino infrastructure. The GitHub repository is [here].
BN254
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.

Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- CL Signatures. CL. CL Signatures in Go using MIRACL.
- CL Signatures (advanced pairing). CL. CL Signatures in Go using MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages using MIRACL.
- PS Signatures. PS. Signatures using PS for short signatures using MIRACL.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures using MIRACL.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.

Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
Rust examples
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
NaCl

PyNaCl is a Python port of LibSodium. It integrates the latest cryptography methods, such as AES, XChaCha20, Blake2b and X25519.
Symmetric Key
- Symmetric key. Symmetric key (XChaCha20 and Poly1305). With symmetric key, Bob and Alice have the same key. NaCl uses the XChaCha20 method, and which supports stream encryption (and which does not require padding as a block cipher does, and is also faster than block cipher modes). ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16 byte nonce. XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24 byte nonce. It has a lower propability of nonce misuse than ChaCha20.
- Encryption with a password. Symmetric Key with KDF. In symmetric key, we generate a secret key. This key is typically a random value or generated from a password and a salt value. If we use a password, we typically use a KDF (Key Derivation Function), and which uses a password and a salt value, in order to create a key of a given size. In this case we will use Argon2i, and which is memory resilent.
Hybrid Encryption
- Box. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Hashing
- Hashing and KDF (Argon2 and scrypt). Hashing and KDF. This case we will use PyNaCl (Networking and Cryptography) library, and which is a Python binding to libsodium. We will hash a password using SHA-256 and SHA-512, and also create a KDF (Key Derivation Function) using scrypt and Argon2.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
Ed25519
-
Ed25519. Ed25519. Using Ed25519 for digital signatures.
-
Finding Points on Ed25519. X25519 (Points).
In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 (Key Exchange)
- X25519 + BLAKE2b key-exchange. X25519. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
Curve 25519
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
Node.js

Node.js uses the JavaScript programming langauge as its base, and allows for code to be run on a server, rather than in the browser (such as with pure JavaScript). To run a node.js program, we run "node myfile.js", and use NPM to install libraries.
Symmetric key
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
RSA and public key
- RSA Opt imal Asymmetric Encryption Padding (OAEP) using Node.js. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
ECC Keys
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.

Hashing
- Hashing with node.js (All). Hashing. Hashing with node.js.
- Hashing with node.js (Selection). Hashing. Hashing with node.js.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- ECDSA with node.js. ECDSA. ECDSA with node.js.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
Key exchange
- Diffie-Hellman with node.js (random prime). DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method and uses a randomly generated prime number (press the button to generate a new prime).
- Diffie-Hellman with node.js. DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method. Each time the prime number will be fixed for the DH group selected.
- ECDH with node.js. ECDH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Elliptic Curve Diffie Hellman (ECDH) key exchange method.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
Key derivation
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
CryptoJS
- CryptoJS (in node.js). CryptoJS (Node.js). Various crypto methods in the browser.
Bulletproofs
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
Blockchain
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
Proxy encryption
- Proxy Encryption - Encrypting With Public Key, And Decrypt with Private Key. Proxy01. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This page just creates a key pair for Alice, and uses it to encrypt with the public key , and decrypt with the private key.
- Proxy Encryption. Proxy02. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This will go through the full use case of proxy re-encryption.
Tokens
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
Random
- Fortuna with node.js. Fortuna. Fortuna random numbers with node.js.
Other
- FPE with node.js. FPR. FPE with node.js.
- Puny with node.js. Puny. Puny character format with node.js.
Accumulators and Witnesses
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
PGP
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Password Entropy
- Password Entropy with Node.js. Password Entropy. Password entropy measures the strength of a password, and is measured as the number of bits which could represent all of the possibilities. An entropy score of less than 25 identifies a poor password, and between 25 and 50 is a weak password. For 50 to 75 we have a reasonable password, and between 75 and 100 is a very good password. Over 100 is an excellent password. The strength of the password relates to the number of characters used, and also the number of characters in the password.
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
- Homomorphic Encryption with Node.js and BGV. Homomorphic Encryption with Node.js and BFG. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BGV method.
Oblivious Transfer (OT)

Oblivious Transfer allows Bob to select data from Alice, but for Alice not to know which value has been selected.
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
OpenSSH

OpenSSH supports the usage of the SSH protocol. This allows for a remote login. One tool which is uses is ssh-keygen, and which allow for the generation of RSA, DSA and elliptic-curve keys that. These can be used for user and host authentication, such as for GitHub login and Cloud instance login.
OpenSSH
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here].
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
Outline

OpenSSL

OpenSSL is a standard library that implements cryptography.
Symmetric key (Command line)
-
Symmetric Key Encryption (OpenSSL 1.x) [here]. In this case we will create cipher text from OpenSSL 1.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 1.x) [here].In this case we will decrypt cipher text from OpenSSL 1.x using a key derived from a password
-
Symmetric Key Encryption (OpenSSL 3.x) [here]. In this case we will create cipher text from OpenSSL 3.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 3.x) [here].In this case we will decrypt cipher text from OpenSSL 3.x using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password.
Hashing
-
Hashing [here] OpenSSL supports a wide range of hashing methods including BLAKE2b, Gost, MD4, MD5, RMD-160, SHA-1, SHA-3, SHA-256 and SHA-512.
Libre OpenSSL
-
Symmetric Key Encryption using Libre OpenSSL [here]. In this case we will create cipher text from Libre OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption using Libre OpenSSL [here]. In this case we will decrypt ciphertext from Libre OpenSSL using a key derived from a password.
-
Hashing [here] Libre OpenSSL supports a wide range of hashing methods including Gost, MD4, MD5, RMD-160, SHA-1, SHA-256 and SHA-512.
Diffie-Hellman parameter generation
-
DH Parameters with OpenSSL [here]. The Diffie-Hellman (DH) method is perhaps one of the greatest inventions in Cybersecurity, and was created by Whitfield Diffie and Marty Hellman. With the DH method, Bob creates a random value (\(b\)) and Alice also creates a random value (\(a\)). Next Bob computes \(B=g^b \pmod p\) and sends it to Alice. Alice computes \(A=g^a \pmod p\) and sends this to Bob. Bob raises the value of \(A\) to the power of \(b\) and takes \(\pmod p\), and Alice raises \(B\) to the power of \(a\) and takes \(\pmod p\). In the end, they will have the same shared value: \(g^{ab} \pmod p\). This can then be used to derive an encryption key that they can use for a secure tunnel. Overall, \(p\) is the large prime number, and also known as the shared modulus between Bob and Alice.
Key derivation function
-
PBKDF2 key derivation with OpenSSL [here] PBKDF2 (Password Key Derivation Function 2) is a key derivation method. Overall it is relatively slow in its operation and where we take a password, a salt value, hashing method, and a number of iterations, in order to produce a given size of encryption key.
-
HKDF key derivation with OpenSSL [here] HKDF (HMAC Key Derivation function) is used to derive an encryption key from a pass phrase. Initially HKDF creates a pseudorandom key (PRK) using a pass phrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), andalong with a salt value. Next the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys.
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Passwords
-
Password example [here]. This page uses the OpenSSL library hash password generator, which is used in UNIX systems for the hashing of passwords which are contained in /etc/shadow and /etc/passwd. For newer passwords, the "-1" options is used to created the hashed value.
-
Hashed passwords with OpenSSL [here].
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
Public key
-
Generating an ECC key pair with OpenSSL [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)).
-
Generating an RSA key pair with OpenSSL [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2).
-
Generating an RSA key pair with OpenSSL with encryption [here]. This page implements RSA key pair generation with an encrypted key pair. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). In this case we will encrypt the key pair with either 3DES, 128-bit AES, 192-bit AES or 256-bit AES. The same password must be used to encrypt and decrypt.
-
Generate prime with OpenSSL [here]. Prime numbers are important in public key encrytion, and are used with RSA and ECC. For RSA, we generate two prime numbers (\(p\) and \(q\)) and which are multiplied together to create a modulus (\(N\)). If these prime numbers have 512 bit values, the modulus will be a 1,024 bit value. This defines the basic secure of RSA. With elliptic curve we use smaller prime numbers, such as 256-bit values for the secp256k1 curve.
ASN1 parsing
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). We will parse using asn1parse, and reveal the parameters.
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)) [RSA key pair]. We will parse using asn1parse, and reveal the parameters.
- DSA Parameters with asn1parse. DSA parameters with OpenSSL with asn1parse. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA (Digital Signature Algorithm)
- DSA Parameters. DSA parameters with OpenSSL. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
MAC (Message Authentication Code)
- HMAC with OpenSSL. MACs with OpenSSL. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authenticate both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2) and SHA-3. In this case we will use OpenSSL to generate the HMAC value.
- MACs with OpenSSL. MACs with OpenSSL. In the following we will generate MACs for HMAC, GMAC, CMAC, Blake2bmac, Blake2smac, KMAC128 and KMAC256. Overall, we will use an encryption key defined as a hex value for GMAC and CMAC, and a pass phrase for the others. The message is "hello".
Signing
- Digital signing a plaintext message with OpenSSL. Signing with OpenSSL. With digital signing, we can take a message, and create a signature. This normally involves signing with a private key and digital certificate. The signed message can be an a MIME format, and which can be integrated into an email message. In this can we have a 512-bit RSA key pair that will sign a plain text message.
Encrypting emails
- Encrypting an email message in OpenSSL. Encrypting messages with OpenSSL. With public key encryption, we can take a message, and encrypt it with the recipiant's public key. In this can we have a 512-bit RSA public key to encrypt a message.
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Random number generation with OpenSSL
-
Random number generator [here]. Random numbers are important in generating encryption keys and salt values. In this case OpenSSL generates a random number (in a Base64 format) for a given number of bytes.
Outline (C#/Python)
-
Symmetric Key Encryption (C#) [here]. This page uses the OpenSSL library through a C#/.NET wrapper. The DLLs it interfaces to are libeay32.dll and ssleay32.dll. OpenSSL supports a wide range of encryption methods, including 128-bit AES, 192-bit AES, 256-bit AES and Blowfish (bf). Different modes of ECB, CBC, and OFB are implemented. The examples use a default IV of "1234".
-
AES in Python with OpenSSL output [here]
-
Producing OpenSSL AES Encrypted String from C# [here]
Digital Certificates
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
Paillier - Partial Homomorphic Encryption

The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Fundamentals
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier).
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Using RSA
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
Applications
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
Go Format Preserving Encryption (FPE)
- FPE with Go. FPE. An implementation of Format Preserving Encryption (FPE) for FFX1 and FFX3.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
AWS Encryption
- AWS Symmetric Key Encryption. AWS (Symmetric key). Using symmetric key in AWS.
Go Oblivious Transfer
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Dragon Fly
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
Embedding data in an ECC point
- Embedding data in a point. Go. With Elliptic Curve Cryptography (ECC), we use points on an elliptic curve to represent our data. These are defined with (x,y) points. With this, it is possible to embedded a certain amount of data into the point - as long as it still gives us a valid point on the curve. This example will Curve 25519 to embed data, and is achieved by storing the length of the data in a single byte in the point, and then store the data as byte values in the point (followed by random data). To decode, we can then just read the first byte for the length of the message, and then reveal the data encoded into the point..
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Hashing (Cryptographic)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
Benchmarks and Password strength
The following are the tips related to hashing:
- Password strength. Test. This outlines the strength of various passwords types.
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
Theory
The following are the tips related to hashing:
- Balls in bins. BiBa. This implemented balls in bins.
- Birthday attack (with Big Integers). Calc. This provides a simple example of the birthday attack.
- Birthday attack. Calc. This provides a simple example of the birthday attack.
- Differential Cryptanalysis (Hashing). Cryptanalysis. This provides an implementation of differential cryptanalysis for hashing methods.
MD5, SHA-1
The following are the tips related to hashing:
- MD2 and MD4 MD2/4. The MD2 and MD4 hashing functions were developed by Prof Ronald Rivest in 1989 and 1990, respectively. They both produce a 128-bit hash, but have been shown be vulnerable to attack (see the Collision section in the page).
- MD5 and SHA-1 (to Base-64) with salt Salt. It is possible to add salt to the MD5 algorithm, to mix it up a little.
- MD5 and SHA-1 (to Base-64) Hash. MD5 and SHA-1 produces a hash signature, and the output is typically shown in a hex format or a Base-64. In this example the output is converted into a Base-64 format.
- MD5 and SHA-1. Hash. MD5 and SHA-1 methods produce a hash signature, and are the two of the most widely used methods. The MD5 algorithm has been shown to have weaknesses, and a collision of message hashes has been shown to occur in less than one day. An MD5 signature has 128 bits, an SHA-1 signature has 160 bits, and an SHA-256 signature has 256 bits.
- MD5 Cracking. Hash Cracker. MD5 has a 128-bit signature and can be cracked using rainbow tables. This page tries to crack the MD5 signature.
- Hashing with Go. Hashing. Hashes with Go.
- Detecting hash types. Hash type. This detects has values.
- OpenSSL hashing. Range of methods. Outlines the methods used in OpenSSL
- Hash. Hash. Hashing using JavaScript
- Hashing with node.js. Hashing. Hashing with node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Hashing methods
-
Hazmat Hashes. Hazmat Hashes. This includes the hashing methods in the Hazmat cryptography library. This includes Blake2p, Blake2s, MD5, SHA1, SHA224, SHA256, SGA384, SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHA512, SHA512-224, SHAKE128 and SHA256.
-
Hazmat Hashes. Hazmat Hashes. In this case we will implement Python code to determine SHA1, SHA2, SHA3, Blake2, MD5 and SM3 hashes.
OpenSSL Passwords
-
Password example [here]
-
Hashed passwords with OpenSSL [here]
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Blake 3 hashes
The following are the tips related to similarity hashing:
- Blake 3 in Python. Hashing. Blake 3 hashing.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
Other Hash functions
The following are the tips related to hashing:
- Bloom Filter Bloom filter. A Bloom filter goes a probabilistic method of determining if an element is in a data structure, using indexed hashing methods.
- Cuckoo Table Cuckoo filter. A Cockoo table uses two hash funtions.
- Chaffing. Chaffing. This produces a keyless system.
- GP Hashing with Go. GP Hashing. GP Hashes with Go.
- LDAP. LDAP. This produces a LDAP hash signature for a password.
- LM Hash. LM Hash. This is an LM Hash Calculator. LM Hash is used in many versions of Windows to store user passwords that are fewer than 15 characters long.
- Murmur and FNV Murmur and FNV. While hashing methods such as MD5 and SHA-1 use crypto methods, the Murmur and FNV hashes uses a non-cryptographic hash function. This can be used for general hash-based lookup and was designed by Austin Appleby. It has good performance compared with other hashing methods.
- Pearson. Pearson. This uses a non-crypto hash.
- phpass. phpass. This produces a phpass hash signature for a password.
- Tiger. Tiger. Tiger is a 192-bit hash function and was designed by Ross Anderson and Eli Biham in 1995. It is often used by clients within Gnutella file-sharing networks and does not suffer from known attacks on MD5 and SHA-0/SHA-1. Tiger2 is an addition, in which the message is padded with a byte of 0x80 (in a similar way to MD4, MD5, and SHA), whereas in Tiger it is 0x01. Otherwise, the two methods are the same in their operation.
- Whirlpool. Whirlpool. Whirlpool is a 512-bit cryptographic hash function and was created by Vincent Rijmen (one of the AES creators) and Paulo Barreto, in 2000.
- WPA-2 hash . WPA-2 hash. Implements SHA-2 hash.
- Reusable hash collisions. Reusable hash collisions. Reusable hash collisions.
- The Length Extension Attack. Length Extension Attack. The MD construct has many weaknesses, and one of the most serious is the length extension attack. With this an adversary (Eve) can take a hash for an unknown message, and then add additional data to produce a new valid hash. The hash methods which are at risk against the length extension attack are MD5, SHA-1 and SHA-256. Please follow the code link below to run an example.
- Consistent hashing. Consistent hash. This outlines the usage of Consistent hashes.
- ROR13 (Module and Function). ROR13. With ROR13 we take each 8-bit character and then convert to a unicode value (with 16 bits). Then for each character we rotate the bits right by thirteen places. The resultant hash is then just the accumuluation of the rotated values.
- ROR13 (Function). ROR13 (Function). With ROR13 we take each 8-bit character and then convert to a unicode value (with 16 bits). Then for each character we rotate the bits right by thirteen places. The resultant hash is then just the accumuluation of the rotated values.
- GOST, Streebog256 and Streebog512. GOST, Streebog256 and Streebog512. GOST94 is a hashing method developed with Euro-Asian Council for Standardization, Metrology and Certification (EASC). This has since been developed in the Streebog256 and Streebog512 hashing method. In this case, we will use Libre OpenSSL to convert data into a hashed value.
RIPEMD
- RIPEMD (RACE Integrity Primitives Evaluation Message Digest) and GOST. RIPEM160. RIPEMD is a 128-bit, 160-bit, 256-bit or 320-bit cryptographic hash function, and was created by Hans Dobbertin, Antoon Bosselaers, and Bart Preneel. It is used on TrueCrypt and is open source. The 160-bit version is seen as an alternative to SHA-1, and is part of ISO/IEC 10118
- RIPEMD160. RIPEM160. RIPEMD160 is a 160-bit cryptographic hash function, and was created by Hans Dobbertin, Antoon Bosselaers and Bart Preneel. RIPEMD160 is used in Bitcoin applications.
Chameleon hashes
The following are the tips related to Chameleon hashing:
- Chameleon hash in Golang Chameleon. With a Chameleon hash, we have a normal hash value which is resistant to collisions, but with a known secret we can easily create a collision. The concept was first defined by Krawcyk and Rabin.
Similarity hashes
The following are the tips related to similarity hashing:
- Similarity hash: SimHash (Charikar similarity) in Python Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash (Nilsimsa similarity) Nilsimsa. The Nilsimsa similarity is used to find similarities between spam emails.
- Minhash (Jaccard similarity) Jaccard similarity. The Minhash method is used to find similarities between strings, files and metadata.
- String enthropy String enthropy. Measurement of the entropy of strings.
- Counting identical elements (HyperLogLog) HyperLogLog. Counting the number of identical elements.
SHA-3 and SHA-3 contenders
The following are the tips related to Key derivation hashing:
- Blake and Blake 2. Blake. Implements Blake and Blake 2 (SHA-3 contender).
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
- Grøstl. Grøstl. Implements Grøstl (SHA-3 contender).
- KangarooTwelve. KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- SHA-3, Keccak and SHAKE . SHA-3. Implements SHA-3, Keccak and SHAKE (SHA-3 winner).
- SHA-3. SHA-3. SHA-3 was known as Keccak and is a hash function designed by Guido Bertoni, Joan Daemen, Michaël Peeters, and Gilles Van Assche. MD5 and SHA-0 have been shown to be susceptible to attacks, along with theoretical attacks on SHA-1. NIST thus defined there was a need for a new hashing method which did not use the existing methods for hashing, and setup a competition for competing algorithms. In October 2012, Keccak won the NIST hash function competition and is proposed as the SHA-3 standard. It should be noted that it is not replacement SHA-2, which is currently a secure method. Overall Keccak uses the sponge construction where the message blocks are XORed into the initial bits of the state, and then inevitably permuted.
- cSHAKE. cSHAKE. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS. With the SHA-3 hashing method, we have four different cryptographic hashing methods (SHA3-224, SHA3-256, SHA3-384, and SHA3-512) and two XOF functions (SHAKE128 and SHAKE256). With SHAKE128 and SHAKE256 we can integrate domain separation between different functions — and which are known as cSHAKE128 and cSHAKE256.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- Skein. Skein. Implements Skein (SHA-3 contender).
Key derivation hashing
The following are the tips related to Key derivation hashing:
- Argon2. Go. Outline of Argon2.
- Argon2 with NaCl. Go. Outline of Argon2 using NaCl.
- Balloon. Go. Outline of Balloon.
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- Double ratchet. Go. Outline of double ratcheting.
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- Scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat HKDF. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
Non-crypto/fast hashing
The following are the tips related to non-crypto hashing:
- A perfect hash Perfect hash. This is a non-crypto hash which optimizes the hash value.
- The universal hash Universal hash. This related to the concept of a universal hash.
- FNV. FNV. FNV is one of the fastest hashing methods.
- Murmur. Murmur. Murmur is one of the fastest hashing methods.
- Siphash. Siphash. Siphash is a fast hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- xxHash. xxHash. xxHash is one of the fastest hashing methods.
- Meow. Meow. Meow is one of the fastest hashing methods.
- o1Hash. o1Hash. o1Hash is one of the fastest hashing methods.
- CRC-32. CRC-32. CRC-32 is one of the fastest hashing methods.
- wyhash. wyhash. wyhash is one of the fastest hashing methods.
- CityHash. CityHash. CityHash is one of the fastest hashing methods, and is generally free of security problems.
- FarmHash. FarmHash. FarmHash is one of the fastest hashing methods, and is generally free of security problems.
- Non-crypto. Non-crypto. This includes a range of fast non-cryptography hashing methods.
- Non-crypto hashes (C++): Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro. Non-crypto hashes: Farm, City, xxHash, MUM, Spooky 2, Murmur, Metro and t1ha0. This includes a range of fast non-cryptography hashing methods for Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro using C++ methods.
- Pearson. Pearson. Pearson is one of the fastest hashing methods, and has been designed for 8-bit processors.
- C++: t1ha. t1ha. t1ha is one of the fastest hashing methods, and has been designed for 64-bit processors.
- C++: Spooky. Spooky. Spooky is one of the fastest hashing methods, and V2 has a 32-bit, 64-bit and 128-bit version.
- C++: xxHash. xxHash. xxHash is one of the fastest hashing methods, and has good performance for short data inputs.
- C++: MUM. MUM. MUM is one of the fastest hashing methods.
- C++: FNV 1/1a. FNV 1/1a. FNV 1/1a is one of the fastest hashing methods, and is particularily useful when there are small changes in strings, such as with IP addresses and URLs.
- C++: MetroHash. MetroHash. MetroHash is one of the fastest hashing methods.
- C++: CityHash. CityHash. CityHash was created by Google and is one of the fastest hashing methods. It was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Farm. FarmHash. FarmHash was created by Google and is one of the fastest hashing methods. It is an improvement to CityHash.
- C++: Murmur. Murmur. Murmur is one of the fastest hashing methods, but was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Halftime. Halftime. Halftime is one of the fastest hashing methods and was created by Jim Apple at Apache.
- C++: Highway. Highway. Highway is an ultra-fast keyed-hash, and is more than five times faster than SipHash. It was created by Jyrki Alakuijala, Bill Cox, Jan Wassenberg at Google.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
- C++: CLHash. CLHash. CLHash is an ultra-fast hashing method and focused on improving performance of the hashing of long strings.
- C++: FalkHash. FalkHash. FalkHash is an ultra-fast hashing method and beats most of the other non-cryptography methods for performance. It is focused on the x64 architecture and integrates with AES-NI.
- C++: wyHash. wyHash. wyHash is an ultra-fast hashing method.
- C++: Fibonacci. Fibonacci. Fibonacci is an ultra-fast hashing method.
- C++: Lookup3. Lookup3. Lookup3 is an ultra-fast hashing method.
Key-based hashing
The following are the tips related to Key-based hashing:
- SiphashSiphash. Siphash is a fast key-based hashing method.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
One Time Passwords/Time Stamps
The following are the tips related to hashing:
- One Time Passwords. One Time. This allows a new unique password to be created each instance, based on an initial seed.
- Timed One Time Password (TOTP). Timed One Time Password. This allows a new unique passcode to be created each instance, based on an initial seed for a given time window. We will use a five second window in this case, where a new passcode is generated every five seconds, based on an initial seed of a pass phrase.
- Hashed One Time Password (HOTP). Hashed One Time Password. This allows a new unique passcode to be created each instance, based on a counter value and an initial seed.
- Time Stamp Protocol. TSP. This creates a time stamp for data.
- HOTP and TOTP (Python). OTP. This creates hashed passwords.
eXtendable-Output Function (XOF)
- eXtendable-Output Function (XOF) usign CIRCL. XOF. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS.
SHAKE
The following are the tips related to hashing:
- SHAKE. SHAKE. Implements SHAKE and which is an Extendable Output Function (XOF).
- SHAKE with Go. SHAKE. This implements SHAKE in Go.
- libDisco with Go. libDisco. This implements libDisco.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify
the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods
such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC methods using the Python cryptography primitives for HMAC-MD5.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
Quantum-robust Public Key (Hash-based signature)
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
Hash to ECC point
- Hash to password with Go. Hash to password. Hash to password with Go.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve with libnum.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.

Password-hashing functions using Rust
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing (Non-cryptographic)

You might know those slow old hashing methods, such as MD5, SHA-1, and SHA-256. Well, they were designed to be fast, but also highly secure. But, if we just need a hashing method, such as for a hashtable or Bloom filter, we often don’t need all the security that comes with the main cryptography hashing methods. And so we have the non-cryptography hashing methods, and which are often ultra-fast and highly efficient. To show the difference, in a test, SHA-1 — one of the fastest cryptography hashing methods — managed a processing rate of 364.95 MiB/s, while t1ha was nearly a 100 times faster, at 34,636 MiB/s.
Non-crypto/fast hashing
The following are the tips related to non-crypto hashing:
- A perfect hash Perfect hash. This is a non-crypto hash which optimizes the hash value.
- The universal hash Universal hash. This related to the concept of a universal hash.
- FNV. FNV. FNV is one of the fastest hashing methods.
- Murmur. Murmur. Murmur is one of the fastest hashing methods.
- Siphash. Siphash. Siphash is a fast hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- xxHash. xxHash. xxHash is one of the fastest hashing methods.
- Meow. Meow. Meow is one of the fastest hashing methods.
- o1Hash. o1Hash. o1Hash is one of the fastest hashing methods.
- CRC-32. CRC-32. CRC-32 is one of the fastest hashing methods.
- wyhash. wyhash. wyhash is one of the fastest hashing methods.
- CityHash. CityHash. CityHash is one of the fastest hashing methods, and is generally free of security problems.
- FarmHash. FarmHash. FarmHash is one of the fastest hashing methods, and is generally free of security problems.
- Non-crypto. Non-crypto. This includes a range of fast non-cryptography hashing methods.
- Non-crypto hashes (C++): Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro. Non-crypto hashes: Farm, City, xxHash, MUM, Spooky 2, Murmur, Metro and t1ha0. This includes a range of fast non-cryptography hashing methods for Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro using C++ methods.
- Pearson. Pearson. Pearson is one of the fastest hashing methods, and has been designed for 8-bit processors.
- C++: t1ha. t1ha. t1ha is one of the fastest hashing methods, and has been designed for 64-bit processors.
- C++: Spooky. Spooky. Spooky is one of the fastest hashing methods, and V2 has a 32-bit, 64-bit and 128-bit version.
- C++: xxHash. xxHash. xxHash is one of the fastest hashing methods, and has good performance for short data inputs.
- C++: MUM. MUM. MUM is one of the fastest hashing methods.
- C++: FNV 1/1a. FNV 1/1a. FNV 1/1a is one of the fastest hashing methods, and is particularily useful when there are small changes in strings, such as with IP addresses and URLs.
- C++: MetroHash. MetroHash. MetroHash is one of the fastest hashing methods.
- C++: CityHash. CityHash. CityHash was created by Google and is one of the fastest hashing methods. It was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Farm. FarmHash. FarmHash was created by Google and is one of the fastest hashing methods. It is an improvement to CityHash.
- C++: Murmur. Murmur. Murmur is one of the fastest hashing methods, but was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Halftime. Halftime. Halftime is one of the fastest hashing methods and was created by Jim Apple at Apache.
- C++: Highway. Highway. Highway is an ultra-fast keyed-hash, and is more than five times faster than SipHash. It was created by Jyrki Alakuijala, Bill Cox, Jan Wassenberg at Google.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
- C++: CLHash. CLHash. CLHash is an ultra-fast hashing method and focused on improving performance of the hashing of long strings.
- C++: FalkHash. FalkHash. FalkHash is an ultra-fast hashing method and beats most of the other non-cryptography methods for performance. It is focused on the x64 architecture and integrates with AES-NI.
- C++: wyHash. wyHash. wyHash is an ultra-fast hashing method.
- C++: Fibonacci. Fibonacci. Fibonacci is an ultra-fast hashing method.
- C++: Lookup3. Lookup3. Lookup3 is an ultra-fast hashing method.
A fuller test with SMHasher gives [here]:
Hash function MiB/sec cycl./hash cycl./map Quality problems
------------------------------------------------------------------
o1hash 12439661.09 16.77 166.13 insecure, no seed, zeros, fails all tests
crc32_hw1 23208.73 46.74 179.70 insecure, 100% bias, collisions, distrib, BIC, machine-specific (x86 SSE4.2)
t1ha0_aes_noavx 22785.26 38.71 180.61 LongNeighbors, machine-specific (x86 AES-NI)
t1ha0_aes_avx1 22714.85 48.12 226.52 LongNeighbors, machine-specific (x64 AVX.txt)
t1ha0_aes_avx2 22345.33 44.38 556.47 LongNeighbors, machine-specific (x64 AVX2)
falkhash 20202.42 173.63 321.52 Sparse, LongNeighbors, machine-specific (x64 AES-NI)
MeowHash64low 17378.06 85.48 237.60 Sparse, invertible, machine-specific (x64 AES-NI)
MeowHash32low 17374.64 85.48 258.53 Sparse, invertible, machine-specific (x64 AES-NI)
MeowHash 17371.91 85.48 247.96 Sparse, invertible, machine-specific (x64 AES-NI)
FarmHash32 17112.05 47.7 214.71 machine-specific (x64 SSE4/AVX)
xxh3 16538.52 32.81 184.86 DiffDist bit 7 w. 36 bits, BIC
xxh3low 16462.36 32.77 199.79
farmhash32_c 16299.81 47.79 219.19 machine-specific (x64 SSE4/AVX)
xxh128low 15174.85 33.79 187.05
xxh128 15174.14 40.46 195.65
farsh32 14053.09 74.29 245.33 insecure: AppendedZeroes, collisions+bias, MomentChi2, LongNeighbors
metrohash64crc_2 14034.84 48.94 162.54 UB, Cyclic 8/8 byte, DiffDist, BIC, machine-specific (SSE4.2/NEON)
metrohash64crc_1 14000.5 49.08 150.54 UB, Cyclic 8/8 byte, DiffDist, BIC, MomentChi2, machine-specific (SSE4.2/NEON)
metrohash128crc_1 13948.67 65.2 168.08 UB, machine-specific (SSE4.2/NEON)
metrohash128crc_2 13920.19 65.12 176.70 UB, machine-specific (SSE4.2/NEON)
halftime_hash128 13478.23 97.79 252.14
wyhash32low 12911.09 29.59 205.43 2 bad seeds
wyhash 12879 30.35 196.77 2^33 bad seeds
CityCrc128 12343.43 74.5 209.75
fletcher2 12011.15 25.29 298.60 bad seed 0, UB, fails all tests
fletcher4 11928.55 25.27 293.49 bad seed 0, UB, fails all tests
halftime_hash256 11620.28 98.44 252.60
fibonacci 11339.87 26.33 705.64 UB, zeros, fails all tests
ahash64 9862.62 27.32 181.68 rust
Spooky128 9751.14 63.84 192.47 UB
Spooky64 9747.47 62.2 191.71 UB
Spooky32 9747.13 62.24 196.96 UB
t1ha1_64le 9723.86 34.39 176.91 Avalanche
cmetrohash64_1 9683.33 45.2 161.01 UB, LongNeighbors, BIC, MomentChi2
cmetrohash64_2 9669.95 44.75 149.67 LongNeighbors
metrohash64_2 9668.51 44.45 164.30 UB, LongNeighbors
metrohash64 9664.61 44.59 150.74 UB, LongNeighbors, BIC
metrohash64_1 9664.57 45.37 152.31 UB, LongNeighbors, BIC, MomentChi2
cmetrohash64_1o 9658.31 42.84 163.45 UB, LongNeighbors, BIC, MomentChi2
FNV1a_YT 9643.42 32.06 175.19 bad seed, UB, fails all tests
City128 9640.19 88.45 225.38
metrohash128_2 9584.94 59.1 167.43 UB, LongNeighbors
metrohash128 9569.16 58.68 167.53 UB, LongNeighbors
metrohash128_1 9558.17 59.04 175.94 UB, LongNeighbors
FarmHash128 9409.63 74.52 210.25
VHASH_32 9404.99 77.01 250.57 sanity, Seed, MomentChi2
VHASH_64 9392.39 74.72 227.92 sanity, Seed, MomentChi2
farmhash128_c 9244.13 79.08 209.44
t1ha2_atonce 9237.12 38.94 194.32 Zeroes low3
City64noSeed 9090.42 32.23 171.53 Avalanche, Sparse, TwoBytes, MomentChi2, Seed
City64low 9089.45 47.75 201.73
t1ha2_stream 9068.55 74.56 219.85 Sparse, Permutation, LongNeighbors
City64 9066.9 47.81 197.78 Sparse, TwoBytes
t1ha2_stream128 9065.5 93.19 236.50 Sparse, Permutation, LongNeighbors
xxHash64 8936.63 51.31 174.34
pengyhash 8744.48 85.31 222.45
farmhash64_c 8713.16 47.96 201.00
FarmHash64 8684.76 48.13 200.51
crc64_hw 8440.13 34.94 141.15 insecure, 100% bias, collisions, distrib, BIC, machine-specific (SSE4.2/NEON)
t1ha2_atonce128 8350.99 55.65 203.53 LongNeighbors
PMPML_64 8161.19 53.2 179.16 unseeded: Seed, MomentChi2, BIC
halftime_hash512 7681.62 125.81 274.01
tabulation 7621.75 42.19 179.93
t1ha1_64be 7481.37 38.16 193.22 Avalanche
MUMlow 7225.18 37.85 197.92 UB, 5 bad seeds
farsh64 7216.29 130.3 302.44 insecure: AppendedZeroes, collisions+bias, MomentChi2, LongNeighbors
MUM 7134.56 37.85 172.34 UB, too many bad seeds, machine-specific (32/64 differs)
nmhash32 7003.3 68.93 216.59
PMPML_32 6704.53 53.5 197.43 Avalanche >512, unseeded: Seed, BIC, MomentChi2, PerlinNoise
nmhash32x 6342.95 56.41 217.75
crc32_hw 6330.42 35.55 170.16 insecure, 100% bias, collisions, distrib, BIC, machine-specific (SSE4.2/NEON)
FNV2 6258.84 33.25 142.89 fails all tests
FNV1A_Pippip_Yurii 6258.46 28.19 184.41 UB, sanity, fails all tests
FNV1A_Totenschiff 6258.23 27.99 198.20 UB, zeros, fails all tests
HighwayHash64 6242.58 99.55 248.41
mx3 6146.02 52.48 173.09 UB
xxHash32 6040.87 51.77 177.91 LongNeighbors, collisions with 4bit diff, MomentChi2 220
prvhash64s_64 5481.48 170.05 325.39
mirhash 5413.73 39.68 154.47 UB, 2^36 bad seeds, LongNeighbors, machine-specific (32/64 differs)
mirhash32low 5412.76 39.79 182.13 UB, 4 bad seeds, Cyclic, LongNeighbors, machine-specific (32/64 differs)
Murmur3F 5226.4 52.18 175.85 UB
prvhash64s_128 5161.33 260.96 442.70
t1ha0_32le 5132.18 54.83 193.53 Sparse, LongNeighbors
halftime_hash64 4990.72 120.55 281.64
Murmur2B 4882.95 39.72 149.43 UB, 1.8% bias, collisions, 3.4% distrib, BIC
seahash32low 4801.33 58.54 227.31 PerlinNoise 32, !msvc
seahash 4796.97 58.55 201.58 PerlinNoise, !msvc
fasthash32 4737.61 45.32 181.86 UB, insecure
fasthash64 4737.21 42.79 164.87 UB, insecure, Moment Chi2 5159 !
umash32_hi 4662.92 54.22 214.20
umash64 4662.09 53.42 188.09
umash32 4633.19 53.42 216.33
t1ha0_32be 4585.59 55.98 183.45 Sparse, LongNeighbors
clhash 4472.31 82.72 229.73 PerlinNoise, machine-specific (x64 SSE4.2)
tabulation32 4317.34 35.45 197.20 collisions
Murmur2C 4092.99 51.84 164.65 UB, 2^32 bad seeds, 91% bias, collisions, distr, BIC, LongNeighbors
farsh128 3776.92 232.48 398.67
City32 3675.04 57.73 212.04
TSip 3228.14 57.96 211.71 !msvc
Murmur3C 3197.63 67.9 198.00 UB, LongNeighbors, Text, DiffDist
Crap8 3149.63 36.23 195.11 UB, 2.42% bias, collisions, 2% distrib
Murmur2 3146.91 41.87 187.89 UB, 1 bad seed, 1.7% bias, 81x coll, 1.7% distrib, BIC
Murmur2A 3146.79 46.87 191.96 UB, 1 bad seed, 12.7% bias, LongNeighbors
aesnihash 2963.39 71.24 217.73 fails many tests, machine-specific (x64 AES-NI)
BEBB4185 2951.62 222.03 343.63 UB, too many bad seeds, msvc-specific
jodyhash6 2848.42 29.99 164.36 bias, collisions, distr, BIC, LongNeighbors
wyhash32 2532.89 48.4 484.57 2 bad seeds, 32-bit
umash128 2427.46 70.6 197.29
Murmur3A 2413.88 53.36 182.37 UB, 1 bad seed, Moment Chi2 69
prvhash64_64m 2386.19 51.18 186.87
prvhash64_128 2383.57 103.44 246.45
prvhash64_64 2375.72 51.61 190.97
hasshe2 2372.52 68.64 216.74 Permutation,TwoBytes,Zeroes,Seed
PMurHash32 2344.78 58.48 196.43 1 bad seed, Moment Chi2 69
mirhashstrict32low 2218.87 65.48 190.59 1 bad seed, MomentChi2 9
mirhashstrict 2217.32 65.53 182.07
sha1ni 2019.96 135.84 564.40 insecure,sanity, Permutation, Zeroes, machine-specific
sha1ni_32 2019.94 136.82 589.46 machine-specific
superfast 1956.25 53.61 180.10 UB, bad seed 0, 91% bias, 5273.01x collisions, 37% distr, BIC
sha2ni-256_64 1910.34 146.06 595.16 Zeroes, machine-specific
sha2ni-256 1906.77 145.47 603.08 insecure,sanity, Permutation, Zeroes, machine-specific
farsh256 1895.77 459.86 575.95
SipHash13 1889.1 89 199.95 0.9% bias
Murmur1 1804.67 51.51 188.41 UB, 1 bad seed, 511x collisions, Diff, BIC
lookup3 1658.31 48.84 194.15 UB, 28% bias, collisions, 30% distr, BIC
pearsonbhash64 1486.34 104.32 185.03
poly_1_mersenne 1431.65 54.49 189.52 fails most tests
jodyhash32 1428.37 44.36 185.85 bias, collisions, distr, BIC LongNeighbors
pearsonbhash128 1347.03 121.75 214.84
poly_2_mersenne 1323.69 66.93 190.88
poly_3_mersenne 1323.59 74.86 206.77
poly_4_mersenne 1323.57 82.67 200.36
blake3_c 1285.91 340.01 552.63 no 32bit portability
GoodOAAT 1052 71.62 192.19
pearsonbhash256 998.9 167.05 261.29
SipHash 980.88 127.77 246.19
MicroOAAT 977.6 59.61 185.06 100% bias, distrib, BIC
FNV1a 791.84 69.69 177.84 bad seed, zeros, fails all tests
sdbm 791.84 67.69 177.06 bad seed 0, fails all tests
FNV64 791.82 70.24 159.29 fails all tests
bernstein 791.82 68.63 180.71 bad seed 0, fails all tests
beamsplitter 789.22 682.45 1150.3 UB, too many bad seeds
HalfSipHash 755.78 114.47 243.72 zeroes
chaskey 753.23 153.42 288.26 PerlinNoise
x17 527.9 98.78 184.09 99.98% bias, fails all tests
JenkinsOOAT_perl 452.49 118.78 194.78 bad seed 0, test FAIL
MurmurOAAT 452.49 113.07 197.83 bad seed 0, 1.5-11.5% bias, 7.2x collisions, BIC, LongNeighbors
JenkinsOOAT 452.48 142.85 213.93 bad seed 0, 1.5-11.5% bias, 7.2x collisions, BIC, LongNeighbors
crc32 392.1 131.62 204.58 insecure, 8590x collisions, distrib, PerlinNoise
sha1-160 364.95 1470.55 1794.1 Comb/Cyclic low32
rmd256 362.49 617.02 815.44 Bad seeds
blake2b-256_64 356.97 1222.76 1435.0
blake2b-224 356.59 1228.5 1425.87
blake2b-160 356.08 1236.84 1458.15
blake2b-256 355.97 1232.22 1443.31 Sparse high 32-bit
md5-128 353.76 638.29 803.39
md5_32a 353.64 629.85 799.56 Sparse high 32-bit
sha1_32a 353.03 1385.8 1759.9 Cyclic low32, 36.6% distrib
rmd128 334.36 659.03 838.32 Bad seeds
blake2s-128 295.3 698.09 1059.2
pearsonhash64 287.95 174.11 196.50 Avalanche, Seed, SSSE3 only. broken MSVC
pearsonhash128 287.95 171.72 194.61 Avalanche, Seed, SSSE3 only. broken MSVC
pearsonhash256 264.51 184.87 218.79 Avalanche, Seed, SSSE3 only. broken MSVC
blake2s-256 215.28 1014.88 1230.38
blake2s-160 215.01 1026.74 1239.54
blake2s-256_64 211.52 1044.22 1228.43
blake2s-224 207.06 1063.86 1236.50
rmd160 202.16 1045.79 1287.74 Bad seeds, Cyclic hi32
sha2-256_64 148.01 1376.34 1624.71 Bad seeds, Moment Chi2 7
sha2-256 147.8 1374.9 1606.06 Bad seeds, Moment Chi2 4
sha2-224_64 147.6 1360.1 1620.93 Bad seeds, Cyclic low32
sha2-224 147.13 1354.81 1589.92 Bad seeds, Comb low32
asconhashv12 144.98 885.02 1324.23
sha3-256 100.58 3877.18 4159.79 PerlinNoise
sha3-256_64 100.57 3909 4174.63 PerlinNoise
asconhashv12_64 86.73 684.02 606.93
floppsyhash 35.72 1868.92 1411.07
tifuhash_64 35.6 1679.52 1212.75 Cyclic low32
Problems include:
- Bad Seeds. A random seed is often used to initialise the hash. This problem relates to having a bad seed..
- Undefined behaviour (UB). This includes Misaligned, oob (Out of bounds), Signed integer overflow and Shift exponent overflow.
o1hash is the fastest, and a quick and dirty hashing method. It is generally not secure. t1h (Fast Positive Hash) requires AES-NI (Intel Advanced Encryption Standard Instructions) and is one of the fastest hashes at 22.785 Gbps. It has fairly good security levels. Meow comes in around 17.378 Gbps. We can see that SHA-1-160 runs as 364 Mbps, while Meow runs at 17.378 Gbps. Blake 3 is one of the fast cryptography hash and has a rate of 1.285 Gbps, and Blake 2 gives a rate around 215 Mbps. SHA-3 gives hashing rates of 100.58 Mbps.
Google recommend the following for 64-bit hashes without quality problems:
- xxh3low
-
wyhash
-
ahash64
-
t1ha2_atonce
-
FarmHash
-
halftime_hash128
-
Spooky32
-
pengyhash
-
nmhash32
-
mx3
-
MUM/mir
- fasthash32
Hash-based Signatures

With hash-based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature, unless we create a stateless method, such as SPHINCS+ [1]. Currently NIST have the final round for the Post Quantum Cryptography competition, and for digital signatures, SPHINCS+ is one of the alterative finalists (alongside Picnic).
Hash-based signature (theory)
- BiBa (Go). BiBa. An overview of BiBa One Time Signature [9]. Basically the method involves us taking a hash of a value using a standard hashing method, such as with SHA-256. There will then be \(2^{256}\) different hashing values. We aim to create a signature for a message, so Bob (the signer) selects a number of random values for his private key value and then publishes the hash of each of these (\(P_1\), \(P_2\), etc). He then sends these public keys to Alice. Now when Bob wants to sign a message, he will take one of his private key values, and then hashes it, and then determines the bin that it should be placed. In this case, we could use the \(\pmod N\) function on the hash, and where \(N\) is the number of bins. If we select \(2^{10}\) there will be 1,024 bins.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature [9].
Hash-based signature (stateful)
- BLISS - Post-quantum signing. BLISS. One of the alteratives to the usage of our existing public key methods is the usage of lattice cryptography, and especially in the usage of Ring Learning With Errors (RLWE). An important application is within digital signatures, and where Bob will sign something with his private key, and then Alice can prove that he signed it with his public key. One post-quantum signature method is BLISS (short for Bimodal Lattice Signature Scheme) [8]. It was created by Léo Ducas, Alain Durmus, Tancrède Lepoint and Vadim Lyubashevsky in 2013.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Hash to Obtain Random Subset (HORS) [3] is a quantum robust hashed-based one-time signature. With this we create a series of integers for our private keys and organise into an indexable form. Then we hash them to a sequence of public key values. Next we segment the hash of the message into a series of n-bit integer values. The signature is then achieved through a look-up of the value in the public key list.
- Lamport Signatures. Lamport. Outlines Lamport signatures [7]. When we sign a message we take its hash and then encrypt with our private key. The public key is then used to prove it, and will prove that we signed it with our private key. The Lamport signature uses 512 random hashes for the private key, and which are split into Set A and Set B. The public key is the hash of each of these values. The size of the private key is 16KB (2×256×256 bits) and the public key size is also 16 KB (512 hashes with each of 256 bits).
- Winternitz Signatures (W-OTS). Winternitz. Outlines Winternitz signatures [4, 5]. W-OTS uses relatively small key and signatures sizes, and is thought to be quantum robust. It generates 32x256 bit random private keys. We then hash these a number of times, and is defined by a parameter (w). If we use w=8, we hash the private keys by (2w). This creates 32x256 bits public keys. The signature is the created by taking eight bits at a time, and then the 8-bit binary int (n) is subtracted from 256 and the private key is the hashed 256-n times. The signature is then 32 hashes which are derived from random private keys. To verify the signature, the recipient parses the hash of the signature (using 8 bits at a time, and extracting the 8 bit int, n).
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method [6], and which is used within speeds-up of Hashing-based signature methods. Using methods such as SHA-1 and SHA-2 (aka SHA-256) will be inefficient as they tend to compress the data inputs through a number of stages. Haraka v2 [6] is different as focuses on inputs of just 256 bits (32 bytes) or 512 bits (64 bytes). This makes the method useful when we are dealing with key and hash values, and is especially useful for hash-based signatures. The output is 256 bits long, but where the input can be either be 256 bits (Haraka256) or 512 bits (Haraka512). These lengths are typically for the outputs of modern hashing applications. The Haraka method, too, has been optimized with AES instructions (AES-NI - Intel Advanced Encryption Standard New Instructions) and which are supported within the hardware of the processor. As Haraka is focused on short messages, the number of rounds within the hashing process has been reduced.
Hash-based signature (stateless)
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ digital signature. SPHINCS digital signature. Outline of the a SPHINCS stateless digital signature method [1].
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
Hash-based signature (Merkle-based)
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
Introduction
Many of the problems we see on the Internet relate to the lack of trust within transactions. The emails you receive and the Web sites that you visit often have very little trust built into them. For trust the email address of the sender, but anyone can fake that address. So increasingly we create a digital signature, and where we sign our messages. In this way, we can check for authentication, integrity and non-repudiation.
With the Alice creates a key-pair: a public key and a private key. She then takes a hash of the message, and then encrypts this hash with her private key, and passes the message and the signature to Bob. Bob then reads the message and takes a hash of it. He then decrypts Alice's signature with her public and checks the hashes. If they match, he knows that she signed and that it has not been changed along the way:
Currently, we often use RSA, DSA and ECDSA to sign our messages. These are based on the difficulty of finding out the factors of a number and on the processing of discrete logarithms. At the current time these methods are computationally hard problems, but with quantum computers, they become much easier. This was shown by Peter Shor who illustrated that it was possible to crack them in polynomial time.
Of all the methods that are being proposed, the hash-based methods look as if they have a good chance of success of creating quantum robust signatures. methods and code-based methods are being researched, but the usage of hashing methods is already well and could provide the best alternative to the existing methods. Hashing methods, too, often bring other advantages, such as forward secure, which means that a key which is cracked will not reveal all the previous keys.
Merkle trees
The root of hash-based methods isin Merkle trees, and which are a way of hashing is used in many applications, including with Bitcoin, Ethereum, Git distribution systems, No SQL, and in many P2P applications. With a Merkle tree we take our data elements, and then hash them, and take pairs of these hashes to create a new hash, and so we build a table. At the top of the tree is the root element (in this case Hash1234):

In this way, we can use the tree to see if we have matching data on systems.On a P2P network, we can transfer a file by splitting it into data segments and then distributing these segments across the network. A trusted source will have the complete Merkle tree for rebuilding the file, and a client can thus rebuild from the Merkle tree and determine the parts of the file which are still missing. Once transferred the root hash (and all the other hashes) will then match. In its core method, the Merkle Signature Scheme (MSS) has serious performance and memory issues, but enhanced methods such as XMSS create with much less of a performance hit.
One-time signatures (Lamport)
The core method used in hash-based signatures is that of the one-time signature, and where we create a new key pair for every method we need to create. If the keys were reused, an attacker could start to learn the private key, and thus spoof messages. One of the first methods was produced by Leslie Lamport and Whitfield Diffie, in 1979, and is defined as:
- We create two data sets with 256 random 256-bit numbers (Set A and Set B). These are the private key (512 values).
- we take the hash of each of the random numbers. This will give 512 hashes and will be the public key.
- We then hash the message using and then test each bit of the hash (0 ... 255). If it is a 0, we use the ith number in Set A, else we use the ith number from Set B.
- The signature is then 256 random numbers (taken from either Set A or Set B) and the public key is the 512 hashes (of Set A and Set B).
The public and private keys are then each 16KB in size. A demo of the method is here.

Figure 1: Lamport method
The major problem with the method is that a key pair for every message. also in 1979, found a solution with Merkle trees.
One-time signature (W-OTS)
To improve performance method (and which reduced key sizes), Merkle proposed Winternitz OTS (named after Robert Winternitz). With this method was possible to sign many bits at the same time. The method is:
- We create 32 256-bit random numbers. These 32 values will be our private key.
- We then hash each of these values 256 times. These 32 values will be our public key.
- We now take the message and hash it using SHA-256. This produces 32 8-bit values (N1, N2 ... N32).
- Next we take each 8-bit value in the hash of the message, and then hash 256-N times (where N is the value of the 8-bit value).
- To prove the signature, we take the message and hash it with SHA-256, and then take each 8-bit value. We then hash the 8-bit signature value by the number of times defined by the message hash value (N1, N2..). The result for each operation should equal the public key value.
This is illustrated below in Figure 2. A demo of the method is here.

Figure 2: W-OTS
Hash-based Signatures
The methods such as W-OTS and Lamport only provide for a one-time signature. In order to sign many messages, we can use the Merkel signature scheme (MSS). With this we take a hash of the keys and build these as the leaves of the tree. The root of the tree is then the public key - the verification key. We then just use the private key of the W-OTS method to create the signature. The sender also sends the authentication path, which is the neighbouring nodes within the path and which leads to the root of the tree. The recipient can then rebuild the tree using the verification key (which can be received a digital certificate) and the authentication path. For the next message we move onto another key pair and where the index of the key part is revealed.
In the following example we have our root as the public key, and then want to sign with Key3. We then show the authentication path which takes us to the root (as defined in the bold arrows):

Conclusions
Hashed-based methods look to be a strong contender for weaning us off RSA, DSA and ECDSA, but we will have to look at the stateful generation of keys. For this we will have to generate a bank of key pairs (2, 4, 8, 16, etc) and then create the public key from the root of the Merkle tree. We must then remember the keys we have used previously, and only use an unused one. Once we use our new key pair, we then show our working-out as to how the private key is integrated into our tree. It is a bit like a teacher marking a question correctly, and asking for the working out that go you to the answer.
References
[1] Bernstein, D. J., Hopwood, D., Hülsing, A., Lange, T., Niederhagen, R., Papachristodoulou, L., ... & Wilcox-O’Hearn, Z. (2015, April). SPHINCS: practical stateless hash-based signatures. In Annual international conference on the theory and applications of cryptographic techniques (pp. 368-397). Springer, Berlin, Heidelberg [paper].
[2] Bernstein, D. J., Hülsing, A., Kölbl, S., Niederhagen, R., Rijneveld, J., & Schwabe, P. (2019, November). The SPHINCS+ signature framework. In Proceedings of the 2019 ACM SIGSAC conference on computer and communications security (pp. 2129-2146) [paper].
[3] Reyzin, L., & Reyzin, N. (2002, July). Better than BiBa: Short one-time signatures with fast signing and verifying. In Australasian Conference on Information Security and Privacy (pp. 144-153). Springer, Berlin, Heidelberg [paper].
[4] Merkle, R. C. (1989, August). A certified digital signature. In Conference on the Theory and Application of Cryptology (pp. 218-238). Springer, New York, NY.
[5] Hülsing, A. (2013, June). W-OTS+–shorter signatures for hash-based signature schemes. In International Conference on Cryptology in Africa (pp. 173-188). Springer, Berlin, Heidelberg.
[6] Kölbl, S., Lauridsen, M. M., Mendel, F., & Rechberger, C. (2016). Haraka v2–efficient short-input hashing for post-quantum applications. IACR Transactions on Symmetric Cryptology, 1-29. [here]
[7] Lamport, L. (1979). Constructing digital signatures from a one-way function (Vol. 238). Technical Report CSL-98, SRI International. [paper]
[8] Ducas, L., Durmus, A., Lepoint, T., & Lyubashevsky, V. (2013, August). Lattice signatures and bimodal Gaussians. In Annual Cryptology Conference (pp. 40-56). Springer, Berlin, Heidelberg [paper].
[9] Perrig, A. (2001, November). The BiBa one-time signature and broadcast authentication protocol. In Proceedings of the 8th ACM Conference on Computer and Communications Security (pp. 28-37) [paper] .
Hashing (Simularity)

Similarity hashes allow for two data objects to be compared for their similarity.
Similarity assessment methods
The following relate to the basic methods used for string similarity:
- String similarity String similarity. This measures edit distance (including Levenshtein distance), Jaro (including Jaro-Winkler), and QGrams.
- String enthropy String enthropy. Measurement of the entropy of strings.
- Soundex Soundex. Soundex uses a phonetic algorithm to classify a sound as it is pronounced. It focuses on matching phrases which have minor spelling errors.
Similarity hashes
The following are the tips related to similarity hashing:
- Similarity hash: SimHash (Charikar similarity) in Python Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash (Nilsimsa similarity) Nilsimsa. The Nilsimsa similarity is used to find similarities between spam emails.
- Context Triggered Piecewise Hashes (CTPH): ssdeep CTPH similarity. Kornblum [6] created ssdeep and which computes fuzzy hashes. This aims to match similar byte sequences, no matter if there are differences between these sequences. For this we break a file up into fragments with a rolling hash function. We then produce a small hash for each of those fragments. These are then aggregated to produce the complete hash of a file. In comparing file signatures, we treat the resultant hash value as a string, and then uses an edit distance method to compare.
- TLSH (A Locality Sensitive Hash) TLSH similarity. In malware analysis and in text similarity, we often have to identify areas of data within files which are similar. One method is TLSH (A Locality Sensitive Hash), and which was defined by Oliver et al [7]. It is used - along with ssdeep - by VirusTotal to identify a hash value for malware.
- Minhash (Jaccard similarity) Jaccard similarity. The Minhash method is used to find similarities between strings, files and metadata.
- Counting identical elements (HyperLogLog) HyperLogLog. Counting the number of identical elements.
Hazmat cryptography

The Cryptography library in Python contains interfaces to common cryptographic algorithms, including symmetric key methods, hashing, public key, and key derivation functions. Many of these are contained with the Hazmat (Harzardous Material) primative setup.
Hashing, HMAC, CMAC, Poly1305 and HKDF
-
Hazmat Hashes. Hazmat Hashes. This includes the hashing methods in the Hazmat cryptography library. This includes Blake2p, Blake2s, MD5, SHA1, SHA224, SHA256, SGA384, SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHA512, SHA512-224, SHAKE128 and SHA256.
-
Hazmat Hashes. Hazmat Hashes. In this case we will implement Python code to determine SHA1, SHA2, SHA3, Blake2, MD5 and SM3 hashes.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
- Hazmat HKDF. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
- Hazmat CMAC. Hazmat CMAC. CMAC methods using the Python cryptography primitives.
- Hazmat Poly1305. Hazmat Poly1305. Poly1305 methods using the Python cryptography primitives.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
Symmetric key
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat. Implementation of ChaCha20/Poly1305 with a random key using Hazmat.
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat. Implementation of AES GCM with a random key using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hazmat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Hazmat Symmetric Key Padding. Symmetric key. This includes the coverage of padding with Hazmat.
- Hazmat Symmetric Key Padding. Symmetric key. This includes the coverage of padding with Hazmat.
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
- Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . With 3DES encryption, we use a 128-bit key and a 64-bit IV value. The two modes supported are ECB (without salt) and CBC (with salt). The DES algorithm has been around for a long time, and the 56-bit version is now easily crackable (in less than a day on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases, and splits the key into two. Overall the key size is typically 112 bits (with a combination of the three keys - of which two of the keys are the same). In this case we will use PKCS7 padding, and which fills the input data with a value that is equal to the number of padding bytes. Overall, DES has a 64-bit block size, and which equates to eight ASCII characters.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key . And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.
Asymmetric key
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- ECC key generaton with Hazmat. Elliptic Curve key gen. Creating ECC keys using Hazmat and Python.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- Hazmat RSA signing (with key values). RSA signing with Hazmat. RSA signing using Python and with Hazmat (with key values).
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here]
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Signatures. DSA Signatures. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. The ECDSA method is an extension of DSA, but implemented with elliptic curve (EC) methods. As with most public key signing methods, we take a hash of a message, and then apply a private key to create a signature (\(r,s\)). This is done by creating a random value (\(k\)) to produce the signature. The signature is then verified using the associated public key. This then verifies the creator of the signature and that the message has not been changed.
Digital Signature: ECDSA/EdDSA
- ECDSA with Hazmat. ECDSA wih Hazmat. This outlines ECDSA with Hazmat.
- Ed25519 for EdDSA signatures with Hazmat. EdDSA: Ed25519. This page uses the Hazmat primitives for the cryptography library.
- Ed448 for EdDSA signatures with Hazmat. EdDSA: Ed448. This page uses the Hazmat primitives for the cryptography library.
- Ed25519 using NaCl. Ed25519. This page uses the NaCl port from libsodium.
- ECDSA Signatures with Hazmat (SECP256R1, SECP384R1, SECP521R1, SECP224R1, SECP192R1, and SECP256K1). ECC Signatures. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and then creates an ECDSA signature for a given message.
Digital Signature: RSA
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
Key exchange: ECDH/X25519
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives and showing the byte values for the key.
Tokens
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
Homomorphic Encryption

Homomorphic encryption supports mathematical operations on encrypted values. Partial Homomorphic Encryption (PHE) supports a few arithmatic operations, while Full Homomorphic Encryption (FHE) supports add, subtract, multiply, and divide. Homomorphic encryption normally involves a public key to encrypt the data, and a private key to decrypt it. There have been four main generations of homomorphic encryption, and the most recent being the HEAAN method.
Simple
- Simple Homomorphic Cipher. Hom. This outlines a Simple Homomorphic cipher.
- Simple Homomorphic Cipher (Python). Hom. This outlines a Simple Homomorphic cipher with Python.
- Full Homomorphic Cipher with a Public Key. Public key. This outlines a Simple Homomorphic cipher using a public key
ElGamal
- ElGamal Homomorphic Cipher (Go). ElGamal. This outlines ElGamal Homomorphic cipher with Go.
- ElGamal Homomorphic Cipher (Go) - Divide. ElGamal. This outlines ElGamal Homomorphic cipher with Go with divide.
- ElGamal Homomorphic Cipher (Go) - Additive. ElGamal. This outlines ElGamal Homomorphic cipher with Go with addition.
- ElGamal Homomorphic Cipher for Multiplication (Python). ElGamal. This outlines ElGamal Homomorphic multiplication with Python.
- ElGamal Homomorphic Cipher for Division (Python). ElGamal. This outlines ElGamal Homomorphic division with Python.
- ElGamal Homomorphic Cipher for Addition (Python). ElGamal. This outlines ElGamal Homomorphic addition with Python.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (Python). ElGamal. This outlines ElGamal Homomorphic subtraction with Python.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
RSA
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
ZKP
- Full Homomorphic Cipher to determine if Bob is older. Older. This outlines a Simple Homomorphic cipher to determine if Bob is older than Alice.
- Full Homomorphic Cipher to determine matching password. Password. This outlines a Simple Homomorphic cipher to determine if a password matches
- Interactive ZKP With Probablistic Methods. ZKP. Interactive ZKP With Probablistic Methods using Python.
- Full Homomorphic Cipher for Millionaire's Problem. Millionaire. This outlines a Simple Homomorphic cipher for the Millionaire's Problem
Voting
- Trusted voting. Trusted. A trusted voting method.
Secret share
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Lattice
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
Full Homomorphic Cipher
- Full Homomorphic Cipher for 2-bit Adder. Adder. This outlines a Simple Homomorphic cipher for a 2-bit adder with DGHV.
- Full Homomorphic Cipher for Full Adder. Full Adder. This outlines a Simple Homomorphic cipher for a full adder with DGHV.
- Full Homomorphic Cipher for 4-bit Adder. Adder. This outlines a Simple Homomorphic cipher for a 4-bit adder with DGHV.
- Full Homomorphic Cipher for 4-bit Adder/Subtractor. Subtract. This outlines a Simple Homomorphic cipher for a 4-bit adder/subtractor with DGHV.
- Full Homomorphic Cipher to XOR two integers. X-OR. This outlines a Simple Homomorphic cipher to X-OR two integers
Paillier
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier) .
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Damgård-Jurik Homomorphic Encryption With Secret Shares. Damgård-Jurik Method. Two of the major areas of developments within cybersecurity will be the usage of homomorphic encryption, and in the usage of Shamir secret sharing. With homomorphic encryption, we can encrypt values, and then operate on them with arithmetic functions (such as add, subtract and multiply), and with Shamir secret sharing, we can split secrets into shares, and then distributed them over networks. These approaches will take privacy to new levels. So let’s look at the Damgård-Jurik method.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Learning with Errors (LWE)
- Learning With Errors . LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret key value (s) and another value (e). Next we select a number of values (t[]) and calculate g[] = t[] x s + e. The values of g[] and t[] become our public key.
- Public Key Encryption with Learning With Errors (LWE). LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret value (s) and which is our private key. We then create a public key which is based on random numbers (A), and then generate another set of numbers (B) which is based on A,s and random errors e. An example of encryption with multiple bits is given.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE)
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Others
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
- SIDH Go. SIDH. Post-quantum key exchange.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Anonymous crypto. Anon. Anonymous crypto.
- Rho factorization. Rho. Rho alogorithm.
- Post-quantum signing (BLISS). BLISS. BLISS method.
Homomorphic Encryption with Krytology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Homomorphic hashing
- Homomorphic Hashing with Golang. Homomorphic hashing. Normally with hashing methods, we need to take all the previous data and new data in order to create a new hash value for our data. In a homomorphic hashing method, we can basically take the previous hash, and then add on any new data values. We can also remove previous data values from our hash, too. This is more efficient in computing, as we do not have to process all of our data into a new hash, and can use simple homomorphic operations for the computation. The method we will use (LtHash) was initially defined by Bellare and Micciancio and updated Lewi et al at Facebook.
Identity Based Encryption (IBE)

This page outlines a few basic principles around the usage of IBE.
Identity Based Encryption (Pairing based)
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pair-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Identity Based Encryption (Others)
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Güther's implicitly certified identity-based public keys (IBE). Günther. This method allows Bob to generate Alices public key from her identity and publicly available parameters.
- Girault's self-certified public keys (IBE). Girault. This method allows Bob to generate Alices public key from her identity and publicly available parameters, and where we use an RSA key pair to self-certify Alice's public key.
Intrusion Detection Systems (IDS)
- Intrusion Detection Systems. Snort. This outlines some of the basics of IDS, including the requirement for Intrusion Detection Systems (IDSs), and where they are used.
- Advanced Network Forensics (Snort). Adv Network Forensics. This provides information on how to detect threats through network forensics with Snort
Snort

- Snort IDS. Snort. This is a Snort Analyser.
- Snort IDS 2 with rules editor. Snort. This provides information on how to detect threats through network forensics with Snort, and with an editing function for rules.
Presentation
IoT

The key objectives of this page are: Understand how a Pen Tester can generate vulnerabilities and test using the Metasploit framework; Define the options and payloads required to generate and use vulnerabilities; and Gaining remote access.
Devices
- Access the Wi-fi kettle. Go. This page outines how to access a wi-fi enabled kettle.
- Philips Hue Wireless Lighting. Go. This page shows how to use RESTful Web services to access to the Hue Led Lamps.
- Kali and R-PI. Go. This page shows the setup of a security testing infrastructure using a Raspberry Pi (R-PI) and a wifi access point.
- Kali, R-PI and RF electrical socket. Go. This page shows the control of an RF electical socket from a RPI.
- Capture from a Polar H10 heat rate sensor. Go. This page shows the capture of the Polar H10 heart sensor with an Ubertooth One.
- Trusted IoT: Linking IoT Devices to NFTs. Go. This page outlines a research paper which links a device to an NFT (Non-fungible Token).
Shodan Scanning
-
IoT Scan (Shodan). Go. This page includes a search of the Internet for key terms, such as for "apache", "mysql" and "cisco".
- IoT Banner Scan (Shodan). Go. This page includes a search of the Internet for key terms with the banner as a result (for the Top 10)
- Internet Services (Shodan). Go. This page includes a search of the Internet for key terms and display the IP address and port.
IoT Libraries
- libDisco with Go. libDisco. libdisco is a Golang library which can be used to create secure connections. It is based on the STROBE protocol framework. Symmetric cryptographic primitives rely on SHA-3 permutation, and asymmetric cryptographic primitives on X25519 and ed25519. STROBE defines a range of cryptographic protocols to integrate with IoT devices. In order to reduce processing, energy and memory requirements, it only uses Keccak (SHA-3) to encrypt and authenticate messages.
COSE/COBR
In computer security, we often have to represent binary data, in single values or groups of characters, bytes, words, long words, signed integers, floating-point values, double-precision floating-point values, and so on. This might be in the form of a data object, a signature or even encrypted content. For this, the ANS.1 DER format is often used, such as presenting digital certificates and signatures. An improvement on this for small messages with security is Concise Binary Object Representation (CBOR) — and which is defined in RFC8949 [1]. While JSON represents text-based data objects CBOR focuses on binary objects. It has been designed to create a lightweight encoder and decoder. This supports the use of CBOR within an IoT infrastructure. The data, also, does not require a data schema to be able to decode it, along with being extensible. CBOR defines the format of binary data with data objects and messages. We can then integrate security with CBOR Object Signing and Encryption (COSE), and which is defined in RFC8152 [2]. This includes signatures, message authentication codes (MACs), encryption and creating serialised objects.
- 128-bit AES GCM. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) can then build on this to include signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use a symmetric key to encrypt a message, and then decrypt it. In this case we will use AES GCM with a static 128-bit key ("0x000102030405060708090a0b0c0d0e0f").
- 256-bit AES GCM. Go. In this case we will use AES GCM using a random 256-bit key (32 bytes).
- EdDSA. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) [2] can then build on this to includes signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use EdDSA to create a signature for a message.
- ECDSA. Go. In this case we will use ECDSA to create a signature for a message.
- HMAC. Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT. Go. In this case we create a CWT token, and sign with an HMAC signature.
- ECDH. Go. In this case we create a symmetric key from ECDH. For this we will derive a shared key from the public key of Alice and Bob, and then define a single recipient which can derive the CEK (Content Encryption Key) using their private key. We will use the curves of P-256 (secp256r1), P-384 (secp384r1), P-521 (secp521r1) or SECP256K1 (as used with Bitcoin).
- RSA using COSE and CBOR. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\).
- RSA: dQ, dP and InvQ. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). The key pair also includes \(dQ\), \(dP\) and \(InvQ\), and these can be used with the Chinese remainder theory to optimize the decryption process.
Metasploit
- Armitage and Metasploit. Go.
- Exploiting Android with Metasploit. Go.
- Exploiting Android with Metasploit - Part 2. Go.
- Exploiting Windows/Mac OS X with Metasploit. Go.
- Remote Desktop Windows/Mac OS X with Metasploit. Go.
- Metasploit. Go.
- Internet of Things Security. Go.
- Metasploit (Enumeration and Scanning). Go.
- Metasploit (Malware). Go.
IP

 The following are a few interesting techniques around IP addresses:
The following are a few interesting techniques around IP addresses:
- Your details. IP. This shows your browser details.
- IP address analyser. IP. This involves converting an IP address to the host and network part of the address.
- IP subnet analyser. IP subnets. This involves converting an IP address to the host and network part of the address.
- IP address analyser. IP. This involves analysing IP addresses.
- Max subnets. Max subnets. This involves converting an IP address to the host and network part of the address.
- Route summarization. Summarization. This involves converting an IP address to the host and network part of the address.
- Whois. Whois. This does a basic Whois on a domain.
- URL Obfuscation. Obfuscation. This outlines URL obfuscation.
- HTTP Responses. Test. HTTP.
- Capturing Network Packets (Python). WinPCap. HTTP.
Cisco related
- Routing table. Routing table. This involves viewing a routing table for a Cisco device.
- ACL Generator. ACL. This involves a simple calculator for ACLs on network ranges.
- EIGRP metrics. EIGRP. Learn the basics of EIGRP metrics.
- VoIP B/W. VoIP. Calculate bandwidth for VoIP.
- Wild Card. Wild Card. On a Cisco device a wildcard mask is used to identify the parts of an IP address that need to be matched. It thus uses a wildcard mask, where a 0 in the bit position identifies that the device should match that bit, else a 1 shows that it should ignore it.
Protocols
- HTTP. HTTP. Show the request and response for HTTP.
- Ping analyser. IP. This involves converting a ping of a site.
IP Challenges
-
IP Test 1. IP Test. IP Classification test. This is a simple test which generates a range of IP addresses, and you must determine the IP address classification.
IP Subnet Challenge 1 Demo
-
IP Test 2. IP Test. IP Classification test Part 2. This test provides an address classification, and the user must find the addresses which are of this classification.
IP Subnet Challenge 2 Demo
-
IP Test 3. IP Test. IP Classification test Part 3. This test provides an address classification, where the network part of the address is determined.
IP Subnet Challenge 3 Demo
Subnet Challenges
- Subnet Test 1. Subnet Test. Subnet Test.
-
Subnet Test 2. Subnet Test. Subnet bits.
- Subnet Test 3. Subnet Test. Find the nth usable subnet. This test involves finding the nth usable subnet.
- Subnet Test 4. Subnet Test. Maximum subnets. This is a test page to determine the maximum number of subnets and hosts/subnet for IP classed addressing.
- Subnet Test 5. Subnet Test. Maximum host/subnet. This is a test page to determine the maximum number of hosts per subnet.
- Subnet Test 6. Subnet Test. Determine the required subnet mask for a given number of subnets. This is a test page to determine the required subnet mask for a given number of subnets and a given IP address classification.
- Subnet Test 7. Subnet Test. Determine the required subnet mask for a given number of host/subnet. This is a test page to determine the required subnet mask for a given number of hosts per subnet and a given IP address classification.
- Subnet Test 8. Subnet Test. Route summarization. This involves a calculation on route summarization.
- Subnet Test 9. Subnet Test. Binary to IP.
- Subnet Test 10. Subnet Test. Hex to IP.
-
Subnet Test 13. Subnet Test. Wild card mask network bits. Find the number of bits in the network part of the wild card mask. IP Wildcard challenge
- Subnet Test 14. Subnet Test. Wild card mask host bits. Find the number of bits in the host part of the wild card mask. IP Wildcard challenge
- Subnet Test 15. Subnet Test. Wild card mask ... find the network address. Find the network for the wild card mask. IP Wildcard challenge 2
- Subnet Test 16. Subnet Test. Find a matching IP address for a network and wild card mask. Find the IP for a network and a wild card mask.
- Subnet Test 17. Subnet Test. Find an address which is on a given network. Find an IP address on a network, for a given network address and subnet mask.
- Subnet Test 18. Subnet Test. Find an IP address on the same network. Find an IP address on the same subnet.
- Subnet Test 19. Subnet Test. Find subnet. Convert subnet mask.
- Megatest. Subnet Test. Challenging test for subnets.
JavaScript

JavaScript code allows execution within the browser, rather than on the server. It is often faster than code that runs on a server. Along with this we can also use Node.js, and which runs JavaScript code on a server.
Symmetric key
- AES. AES. In this example, we will use either a pre-generated key or a random one, and use AES (Rijndael) encryption.
- ChaCha20 and Poly1305. ChaCha. This page outlines Poly1305 and ChaCha20. ChaCha20 is a symmetric key method and Poly1305 is a message authentication code (MAC). They were created by Daniel J. Bernstein, and are alternatives to AES and HMAC.
- CMS (Padding). CMS. This page uses PKIJS encrypting on CMS. With CMS we can This document describes the Cryptographic Message Syntax (CMS). With this we can encapsulate an message within an encrypted entity.

Hashing
- Hash. Hash. This page defines a JavaScript Hash calculator. This uses a client-side JavaScript code to determine the hash signatures of a text value.
Signatures
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
- Boneh–Lynn–Shacham (BLS) signature. BLS. Boneh–Lynn–Shacham (BLS) signature method produces short signatures. They use elliptic curve pairing (and which are also known as bilinear maps).
Key exchange
- ECDH. ECDH. Elliptic Curve Diffie Hellman (ECDH) is used to generate a shared key. This implementation uses Elliptic Curve Cryptography (ECC) with JavaScript.
CryptoJS
- CryptoJS. CryptoJS. This page uses client-side JavaScript code to hashing, encrypt and sign, including for symmetric key (AES), streaming ciphers, hashing methods, and HMAC.
Blockchain
- PATRICIA trie. PATRICIA. In the following, we have the Top 2,500 Web sites in the world, and implemented with a Radix Trie (aka PATRICIA trie) In the following we have the Top 2,000 web sites on the Internet, and which have been indexed using the PATRICIA trie.
Public key
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
- RSA. RSA. RSA is an asymmetric encryption algorithm, which uses two keys, one to encrypt and the other to decrypt. It was created in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman, and is still one of the most widely used encryption methods. A typical application is in authenticating a sender, where the senders private key is used to encrypt a message, and then is decrypted by the receiver with the senders public key (which is known to anyone who wants it). It is also typically used for encrypting disks/files, such as for EFS.
Digital Certificates
- X.509 certificates in JavaScript. RSA and ECDSA Signed certificates. This page will generate either RSA and ECC key pairs, and then generate X.509 certificates, using either a signature of SHA1withRSA or SHA256withECDSA. For RSA signing we use an RSA private key to sign the certificate, and with ECDSA signing we use an ECC private key to sign the certificate.
Tokens
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
Random
- Random number generator. Rand. In the past, encryption and decryption had to be done through native code libraries, such as with Bouncy Castle and OpenSSL. With the increasing processing power of Web browsers, it is now possible to use encryption using JavaScript, which thus provides client-side processing of data. This Web page uses Javascript encryption, and generates a random 256-bit text key or a hex version. The 256-bit key is generated by generating 60 random numbers (from 0-25), and converting these to an ASCII character.
Malware obfuscation
- Malware obfuscation. Obfuscation. A malware writer will often hide certain keywords from the browser/human by encoding them in another format. This is typically done for hex coding (\xZZ), 16-bit unicoding (\uZZZZ) and octal coding (\ZZZ). To test, enter a value, and then press the button and it will convert encoded string.
Message Authentication Codes
- Chaskey (MAC). Chaskey. Chaskey Cipher is light-weight cryptography method for signing messages (MAC) using a 128-bit key. The hardware implementation only requires 3,334.33 gate equivalent with an operating clock frequency of 1 MHz (whereas Keccak requires 4,658 GE). In the page we create the Mac signature and also encrypt for CBC.
Other
- Password generation/hashing. Hashing. Linux can use salted passwords where the username, hashing method and hashed password are stored in a password file [More details]. The main methods are
Hashing

At times we need to generate secrets, such as encryption keys, from passwords or nonce values. A Key Derivation Function (KDF) is a verifiable way of doing this.
Key Derivation Functions (KDFs)
The following are the tips related to hashing:
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Password strength. Test. This outlines the strength of various passwords types.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
HKDF
The following are the tips related to Key derivation hashing:
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Hazmat HKDF for different hashing methods. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
-
HKDF key derivation with OpenSSL [
here]
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
PBKDF2
The following are the tips related to Key derivation hashing:
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- AES GCM (Python) with PBKDF2. AES GCM (Python) with PBKDF2.
- Fernet with PBKDF2 . AES GCM (Python) with PBKDF2.
- PBKDF2 key derivation. AES GCM (Python) with PBKDF2.
- Key Rotation with Fernet. AES GCM (Python) with PBKDF2.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Bcrypt
The following are the tips related to Key derivation hashing:
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- BCrypt. BCrypt. BCrypt with Rust.
-
Hash to password with Go. Hashing to Argon2, Scrypt and BCrypt. Hash to password with Go, including Argon2, Scrypt and BCrypt.
scrypt
- scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Argon 2
The following are the tips related to Key derivation hashing:
- Argon 2. Go. Outline of Argon2.
- Argon 2 with NaCl. Go. Outline of Argon2 using NaCl.
- Argon 2. Argon 2. Argon 2 with Rust.
- Balloon. Go. Outline of Balloon.
Other
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
- Double ratchet. Go. Outline of double ratcheting.
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
Outline
HMAC Key Derivation function (HKDF) is used to derive an encryption key from a passphrase. Initially, HKDF creates a pseudorandom key (PRK) using a passphrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), and along with a salt value. Next, the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys [RFC 5869][article]. In this case, we will use SHA-256.
The following shows how an encryption key can be generated using HKDF, and where we need a secret and a salt value. Both Bob and Alice have the same secret and salt.

With PBKDF2 (Password Based Key Derivation Function 2), we hash for a given number of rounds:

Key exchange

Key exchange is a way for Bob and Alice to communicate and for them to agree on a shared secret. The original method defined uses discrete logarithms (Diffie-Hellman), but most modern methods use elliptic curve techniques (ECDH). As quantum computers can crack both discrete log and elliptic curve methods, there are post quantum cryptography methods proposed. This includes SIDH, CSIDH, SIKE, and NewHope.
Key interchange/generation (Diffie-Hellman)
The following relates to key interchange:
- Selecting \(g\) in Diffie Hellman. G in Diffie Hellman. Picking a safe value of the generator \(g\) in discrete logarithms.
- Diffie-Hellman. Diffie-Hellman Calculation. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Real example). Diffie-Hellman Real. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Python). Diffie-Hellman. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (pre-compute). Diffie-Hellman (pre-compute). Many sites use the same prime numbers, which can then be cracked with a pre-computing attack.
- Key generation. Key gen. This will generate keys for different methods based on a passphrase.
- Diffie-Hellman (Man-in-the-middle). DF. This outlines the man-in-the-middle method for Diffie-Hellman.
- An Alternative Diffie-Hellman method. Alterative DH. This outlines an alternative Diffie-Hellman method.
Authenticated Key Exchange
The following are the tips related to Key derivation hashing:
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- MTI/A0. MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{ax+by} \pmod p\). MTI (Matsumoto, Takashima, Imai).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0. MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{x+y} \pmod p\)
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). The resultant key is \(xyG \)
- MTI/C0. MTI/C0. This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{xy} \pmod p\)
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG\).
- MTI/C1. MTI/C1. This outlines MTI/C1, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{abxy} \pmod p\).
- MQV (Menezes–Qu–Vanstone). MQV. MQV was created Alfred Menezes, Minghua Qu and Scott Vanstone in 1995 and is an authenticated key exchange method. Alice holds a key pair \((A,a)\) and Bob has a key pair \((B,b)\). With this \(a\) is Alice's private key, and \(A=aG\) is her public key. For Bob, his public key will be \(B=aG\) and a private key of \(b\), and where \(G\) is the base point on the elliptic curve.
- HMQV (Menezes–Qu–Vanstone). HMQV. HMQV builds on MQV and adds the identity of Bob and Alice.
- ECDH with X25519 and Blake2b. ECDH with X25519 and Blake2b. This uses PyNaCl to create an authenticated key exchange and uses X25519 and Blake2b.
Elliptic Curve (ECDH) - Python
The following are the tips related to ECC:
- Elliptic Curve. Elliptic Curve. Elliptic Curve is a public key method which can also be used to generate a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with simple parameters. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
Elliptic Curve (ECDH) - Golang and Node.js
The following are the tips related to ECC:
- ECDH with Go. ECDH. ECDH with Go.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with node.js. ECDH. ECDH with node.js.
- ECDH with JavaScript. ECDH. Elliptic Curve Diffie Hellman.
Password Authenticated Key Exchange (PAKE)
The following are the tips related to Key derivation hashing:
- SPAKE2. Go. Outline of SPAKE2.
- OPAQUE. Go. Outline of OPAQUE.
- SPEKE. Go. Outline of SPEKE (Simple Password Exponential Key Exchange).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
- J-PAKE. J-PAKE. This example generates a shared key based on a shared password.
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses discrete logs.
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
PQC NIST Finalists (Key Exchange)
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Key interchange/generation (Other)

The following relates to key interchange:
- Curve25519. Curve25519. This outlines Curve25519, which is used in the Tor network.
- Authenticated Key Exchange (Discrete logs). YAK. Key exchange with public keys and uses discrete logs.
- Authenticated Key Exchange (ECC). YAK. Key exchange with public keys and uses elliptic curve methods.
- Shamir No-key protocol. Shamir No Key. In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated.
- Shamir No-key protocol (sepc256k1). Shamir No Key (EC). In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated using the sepc256k1 elliptic curve.
- Conference keying (Burmester-Desmedt method). Conference keying. In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it.
- Conference keying (Burmester-Desmedt method) - Elliptic Curve (sepc256k1). Conference keying Elliptic Curve (sepc256k1). In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it, and uses the sepc256k1 elliptic curve.
Key exchange (with pairing)
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Kryptology

We need to build a new Internet. One that is build on mathematics and certainty, rather than the patchy version we have now. For this we need a layer of cryptography at the lowest level, and build software interfaces on top of this. Along with this we now have cryptographic methods which can now provide a foundation of trust, and which preserve privacy. And so the old libraries of OpenSSL are being squeezed out in favour of the new ones which are built on a solid foundation. The latest of these new "privacy-aware" libraries is Kryptology, and created by Coinbase. This library provides the APIs that developers need, in order to apply to areas of blockchain development. This library include BLS (Boneh-Lynn-Shacham) signatures, Zero-knowledge Proofs (ZKPs) and Shamir Secret Shares (SSS). With BLS we can digitally sign for data, but also preserve its privacy. Applications of this include group signatures, where multiple entities can merge their signing keys together and provide a single signature for a transaction. With SSS, we can split encryption keys up into shares, and then distribute them across a network. When required, we can call these shares back to reconstruct the key.
The focus for Coinbase seems to be the application of privacy coins, and where no tracking can be applied to the usage of these digital coins. This should support full anonymity for transactions, as opposed to Bitcoin which only supports pseudo-anonymity.

ECC Basics
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining n.G for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Points (Base Point and Others). Elliptic Curve points. Two common curves used in ECC (Elliptic Curve Cryptography) are secp256k1 (as used in Bitcoin and Ethereum) and P256 (secp256r1). The "k1" refers to the Kolbitz curve 1 (named after the creator of ECC). With these we have a base point which are can operate on. This is typically defined as \(G\). We can then operate on this with add and multiply operation. For example, \(2G=G+G\) and \(P=n.G\). In this following we will show the base point for a number of common curves, such as secp256r1, P256, Pallas, Curve 25519, BLS12381G1, BLS12381G2, BLS12377G1 and BLS12377G2.
ECDH
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret. We will use Golang and the Krytology library.
Simple ECC on curves
- Public key points for curves. Simple. Display public key points for scalars.
BLS Curve
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
Accumulator and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
Pallas Curve
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
Pairing-based Crypto
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
ElGamal and ECC
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a numerical input.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
Shamir Secret Shares
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Homomorphic Encryption
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Zero knowledge proofs
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
Verifiable Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Hash to scalar and point
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
CP-ABE
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Lattice cryptography

Latice cryptography is proposed as a post-quantum robust method for public key encryption, especially focused on digital signatures and key exchange mechanisms (KEMs).
Principles
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
NTRU
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- Lattice Encryption: NTRU Key Generation Python). NTRU. Outlines how NTRU operates for key generation.
Homomorphic
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Digital Signatures
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
Public-Key Encryption/Key Exchange
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
Light-weight cryptography

While AES and SHA work well together within computer systems, they struggle in an IoT/embedded world as they take up: too much processing power; too much physical space; and consume too much battery power. So NIST outlines a number of methods which can be used for light-weight cryptography, and which could be useful in IoT and RFID devices [1]. They define the device spectrum as:
- Conventional cryptography. Servers and Desktops. Tablets and smart phones.
- Light-weight cryptography. Embedded Systems. RFID and Sensor Networks.
With embedded systems, we commonly see 8-bit, 16-bit and 32-bit microcontrollers, and which would struggle to cope with real-time demands for conventional cryptography methods. And in the 40+ years since the first 4-bit processor, there is even a strong market for 4-bit processors. RFID and sensor network devices, especially, have limited numbers of gates available for security, and are often highly constrained with the power drain on the device.
So AES is typically a non-starter for many embedded devices. In light-weight cryptography, we often see smaller block size (typically 64 bits or 80 bits), smaller keys (often less than 90 bits) and less complex rounds (and where the S-boxes often just have 4-bits).
For light-weight cryptography the main constraints that we have are typically related to ener requirements, gate equivalents (GEs), and timing. With passive RFID devices, we do not have an associated battery for the power supply, and where the chip must power itself from energy coupled from the radio wave. An RFID device is thus likely to be severely constrained in the power drain associated with any cryptography functions, along with being constrained for the timing requirements and for the number of gates used. Even if an RFID device has an associated battery (active RFID), it may be difficult to recharge the battery, so the drain on power must often be minimised.
There is thus often a compromise between the cryptography method used and the overall security of the method. Thus often light-weight cryptography methods balance performance (throughput) against power drain and GE, and do not perform as well as main-stream cryptography standards (such as AES and SHA-256). Along with this the method must also have a low requirement for RAM (where the method requires the usage of running memory to perform its operation) and ROM (where the method is stored on the device). In order to assess the strengths of various methods we often define the area that the cryptography function will use on the device – and which is defined in \(µm^2\). The NIST finalists are defined in this [article]
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- GIFT AEAD. GIFT. GIFT is a light-weight block cipher. It is a (NIST Finalist)
- Elephant. Elephant. Elephant is a light-weight stream cipher. It is a (NIST Finalist).
- TinyJambu. TinyJambu. TinyJambu is a light-weight block cipher. It is a (NIST Finalist)
- Isap AEAD. Isap. Isap is a light-weight block cipher. It is a (NIST Finalist)
- PHOTON-Beetle AEAD. PHOTON-Beetle. PHOTON-Beetle is a light-weight block cipher. It is a (NIST Finalist)
- Romulus AEAD. Romulus. Romulus is a light-weight block cipher. It is a (NIST Finalist)
- Sparkle AEAD. Sparkle. Sparkle is a light-weight block cipher. It is a (NIST Finalist)
- CLEFIA. CLEFIA. CLEFIA is a light-weight block cipher.
- LED. LED. LED is a light-weight block cipher.
- Piccolo. Piccolo. Piccolo is an ultra light-weight block cipher.
- PRESENT. PRESENT. Present is a light-weight block cipher.
- Pyjamask. Pyjamask. Pyjamask is a light-weight block cipher.
- SIMON. SIMON. SIMON is a light-weight block cipher.
- SKINNY. SKINNY. SKINNEY is a light-weight block cipher.
- SPECK. SPECK. SPECK is a light-weight block cipher.
- XTEA. XTEA. XTEA is a light-weight block cipher.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encryption/Decryption. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.
Light-weight crypto (Other)
- Chaskey (MAC). Chaskey. Chaskey is a light-weight MAC function.
- Chaskey (MAC). Chaskey (Python). Chaskey is a light-weight MAC function.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (ASCON)
ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRFF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
Discrete Logs (Solving)

A discrete log problem is in the form of \(g^x \pmod p\) and where we know \(g\) and \(p\) and must solve for \(x\).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Message Authentication Code (MAC)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
HMAC
The following are the tips related to Key-based hashing:
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authentication both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2), Blake2b, SM3 and SHA-3. This page outlines the HMAC-MD5 methods using the Hazmat cryptography layer.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- HMAC (COSE). Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT with HMMAC. Go. In this case we create a CWT token, and sign with an HMAC signature.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- HMAC with Rust. HMAC. HMAC with Rust.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HMAC with OpenSSL. MACs with OpenSSL. HMAC in OpenSSL for a given input value, password and hashing method.
Cipher MACs
The following are the tips related to Key-based hashing:
- MACs with OpenSSL. MACs with OpenSSL. MAC methods implemented in OpenSSL, including CMAC and GMAC.
Key-based hashing
The following are the tips related to Key-based hashing:
- SipHash. Siphash. Siphash is a fast key-based hashing method.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Meow. Meow. Meow is one of the fastest hashing methods.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
Magic Numbers

This pages contains information related to magic numbers in file formats.
Network and File Forensics
- Magic numbers. Magic. This provides information on magic number for file forensics.
Graphics formats
- JPEG Analysis. JPEGs. This provides an analysis of JPEG files.
- GIF Analysis. GIFs. This provides an analysis of GIF files.
- TIF Analysis. TIFs. This provides an analysis of TIF files.
- PNG Analysis. PNGs. This provides an analysis of PNG files.
- BMP Analysis. BMPs. This provides an analysis of BMP files.
- PSD Analysis. PSDs. This provides an analysis of PSD files.
- WMF Analysis. WMF. This provides an analysis of WMF files.
- Adobe Illustrator Analysis. AI. This provides an analysis of AI files.
- Adobe In Design Analysis. INDD. This provides an analysis of INDD files.
- MIDI file. MIDI. This provides an analysis of MID files.
- ICO file. ICO. This provides an analysis of ICO files.
- PS file. PS. This provides an analysis of PS files.
- EPS file. EPS. This provides an analysis of EPS files.
- VSD file. VSD. This provides an analysis of Microsft Visio (VSD) files.
Video and audio formats
- MP3 Analysis. MP3s. This provides an analysis of MP3 files.
- AVI Analysis. AVIs. This provides an analysis of AVI files.
- Flash SWF Analysis. SWFs. This provides an analysis of Flash files.
- Flash FLV Analysis. FLVs. This provides an analysis of FLV files.
- MP4 Analysis. MP4. This provides an analysis of MP4 files.
- MOV Analysis. MOV. This provides an analysis of MOV files.
- WMV Analysis. WMV. This provides an analysis of WMV files.
- WMA Analysis. WMA. This provides an analysis of WMA files.
- JPEG 2000 Analysis. JPEG 2. This provides an analysis of JPEG 2000 files.
- WAV Analysis. WAV. This provides an analysis of WAV files.
Zips, Archives and Library files
- ZIP/Archive Analysis. ZIPs. This provides an analysis of ZIP/Achive files.
- GZ Analysis. GZ. This provides an analysis of GZip files.
- Tar Analysis. Tar. This provides an analysis of TAR files.
- MSI Analysis. MSI. This provides an analysis of MSI files.
- OBJ Analysis. OBJ. This provides an analysis of OBJ files.
- DLL Analysis. DLL. This provides an analysis of DLL files.
- CAB Analysis. CAB. This provides an analysis of CAB files.
- EXE Analysis. EXE. This provides an analysis of EXE files.
- RAR Analysis. RAR. This provides an analysis of RAR files.
- SYS Analysis. SYS. This provides an analysis of SYS files.
- HLP Analysis. HLP. This provides an analysis of HLP files.
- VMDK Analysis. VMDK. This provides an analysis of VMDK files (VMWare Virtual Disks).
- PST Analysis. PST. This provides an analysis of PST files (Outlook Email File).
- JAR Analysis. JAR. This provides an analysis of JAR files.
- SLN Analysis. SLN. This provides an analysis of Microsoft SLN files.
- Class Analysis. Class. This provides an analysis of Java Class files.
- Zlib. Zlib. This provides an analysis of Zlib files.
Documents
- PDF Analysis. PDFs. This provides an analysis of PDF files.
- DOC Analysis. DOCs. This provides an analysis of DOC files.
- RTF Analysis. RTFs. This provides an analysis of RTF files.
- XLS Analysis. XLSs. This provides an analysis of XLS files.
- PPT Analysis. PPTs. This provides an analysis of PPT files.
- MMP File. MMP. This provides an analysis of MMP files.
- DOCX Analysis. DOCX. This provides an analysis of DOCX files.
- XLSX Analysis. XLSX. This provides an analysis of XLSX files.
- PPTX Analysis. PPTX. This provides an analysis of PPTX files.
- MDB Analysis. MDB. This provides an analysis of MDB files.
- Outlook Message Analysis. MSG. This provides an analysis of MSG files.
Disk Image
- Raw disk format. RAW. This provides an analysis of the RAW disk format.
Tests
- File Forensics Test. File Test File Forensics Test.
- File Forensics Test (Fun). File Test (Fun) File Forensics Test.
Presentations
MIRACL Core Library

MIRACL Core is an open source library, and includes a wide range of public key encryption methods. It is especially focused on elliptic curve and pairing-friendly methods, but also supports a wide range of encryption methods, including RSA, AES and hashing. Overall, it can be ported onto a wide range of systems and supports C, C++, Go, Rust, Python, Java, Javascript and Swift. Along with this it supports limited capability devices such as the Arduino infrastructure. The GitHub repository is [here].
BN254
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.

Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- CL Signatures. CL. CL Signatures in Go using MIRACL.
- CL Signatures (advanced pairing). CL. CL Signatures in Go using MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages using MIRACL.
- PS Signatures. PS. Signatures using PS for short signatures using MIRACL.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures using MIRACL.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.

Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
Rust examples
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
NaCl

PyNaCl is a Python port of LibSodium. It integrates the latest cryptography methods, such as AES, XChaCha20, Blake2b and X25519.
Symmetric Key
- Symmetric key. Symmetric key (XChaCha20 and Poly1305). With symmetric key, Bob and Alice have the same key. NaCl uses the XChaCha20 method, and which supports stream encryption (and which does not require padding as a block cipher does, and is also faster than block cipher modes). ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16 byte nonce. XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24 byte nonce. It has a lower propability of nonce misuse than ChaCha20.
- Encryption with a password. Symmetric Key with KDF. In symmetric key, we generate a secret key. This key is typically a random value or generated from a password and a salt value. If we use a password, we typically use a KDF (Key Derivation Function), and which uses a password and a salt value, in order to create a key of a given size. In this case we will use Argon2i, and which is memory resilent.
Hybrid Encryption
- Box. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Hashing
- Hashing and KDF (Argon2 and scrypt). Hashing and KDF. This case we will use PyNaCl (Networking and Cryptography) library, and which is a Python binding to libsodium. We will hash a password using SHA-256 and SHA-512, and also create a KDF (Key Derivation Function) using scrypt and Argon2.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
Ed25519
-
Ed25519. Ed25519. Using Ed25519 for digital signatures.
-
Finding Points on Ed25519. X25519 (Points).
In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 (Key Exchange)
- X25519 + BLAKE2b key-exchange. X25519. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
Curve 25519
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
Node.js

Node.js uses the JavaScript programming langauge as its base, and allows for code to be run on a server, rather than in the browser (such as with pure JavaScript). To run a node.js program, we run "node myfile.js", and use NPM to install libraries.
Symmetric key
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
RSA and public key
- RSA Opt imal Asymmetric Encryption Padding (OAEP) using Node.js. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
ECC Keys
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.

Hashing
- Hashing with node.js (All). Hashing. Hashing with node.js.
- Hashing with node.js (Selection). Hashing. Hashing with node.js.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- ECDSA with node.js. ECDSA. ECDSA with node.js.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
Key exchange
- Diffie-Hellman with node.js (random prime). DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method and uses a randomly generated prime number (press the button to generate a new prime).
- Diffie-Hellman with node.js. DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method. Each time the prime number will be fixed for the DH group selected.
- ECDH with node.js. ECDH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Elliptic Curve Diffie Hellman (ECDH) key exchange method.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
Key derivation
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
CryptoJS
- CryptoJS (in node.js). CryptoJS (Node.js). Various crypto methods in the browser.
Bulletproofs
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
Blockchain
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
Proxy encryption
- Proxy Encryption - Encrypting With Public Key, And Decrypt with Private Key. Proxy01. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This page just creates a key pair for Alice, and uses it to encrypt with the public key , and decrypt with the private key.
- Proxy Encryption. Proxy02. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This will go through the full use case of proxy re-encryption.
Tokens
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
Random
- Fortuna with node.js. Fortuna. Fortuna random numbers with node.js.
Other
- FPE with node.js. FPR. FPE with node.js.
- Puny with node.js. Puny. Puny character format with node.js.
Accumulators and Witnesses
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
PGP
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Password Entropy
- Password Entropy with Node.js. Password Entropy. Password entropy measures the strength of a password, and is measured as the number of bits which could represent all of the possibilities. An entropy score of less than 25 identifies a poor password, and between 25 and 50 is a weak password. For 50 to 75 we have a reasonable password, and between 75 and 100 is a very good password. Over 100 is an excellent password. The strength of the password relates to the number of characters used, and also the number of characters in the password.
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
- Homomorphic Encryption with Node.js and BGV. Homomorphic Encryption with Node.js and BFG. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BGV method.
Oblivious Transfer (OT)

Oblivious Transfer allows Bob to select data from Alice, but for Alice not to know which value has been selected.
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
OpenSSH

OpenSSH supports the usage of the SSH protocol. This allows for a remote login. One tool which is uses is ssh-keygen, and which allow for the generation of RSA, DSA and elliptic-curve keys that. These can be used for user and host authentication, such as for GitHub login and Cloud instance login.
OpenSSH
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here].
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
Outline

OpenSSL

OpenSSL is a standard library that implements cryptography.
Symmetric key (Command line)
-
Symmetric Key Encryption (OpenSSL 1.x) [here]. In this case we will create cipher text from OpenSSL 1.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 1.x) [here].In this case we will decrypt cipher text from OpenSSL 1.x using a key derived from a password
-
Symmetric Key Encryption (OpenSSL 3.x) [here]. In this case we will create cipher text from OpenSSL 3.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 3.x) [here].In this case we will decrypt cipher text from OpenSSL 3.x using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password.
Hashing
-
Hashing [here] OpenSSL supports a wide range of hashing methods including BLAKE2b, Gost, MD4, MD5, RMD-160, SHA-1, SHA-3, SHA-256 and SHA-512.
Libre OpenSSL
-
Symmetric Key Encryption using Libre OpenSSL [here]. In this case we will create cipher text from Libre OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption using Libre OpenSSL [here]. In this case we will decrypt ciphertext from Libre OpenSSL using a key derived from a password.
-
Hashing [here] Libre OpenSSL supports a wide range of hashing methods including Gost, MD4, MD5, RMD-160, SHA-1, SHA-256 and SHA-512.
Diffie-Hellman parameter generation
-
DH Parameters with OpenSSL [here]. The Diffie-Hellman (DH) method is perhaps one of the greatest inventions in Cybersecurity, and was created by Whitfield Diffie and Marty Hellman. With the DH method, Bob creates a random value (\(b\)) and Alice also creates a random value (\(a\)). Next Bob computes \(B=g^b \pmod p\) and sends it to Alice. Alice computes \(A=g^a \pmod p\) and sends this to Bob. Bob raises the value of \(A\) to the power of \(b\) and takes \(\pmod p\), and Alice raises \(B\) to the power of \(a\) and takes \(\pmod p\). In the end, they will have the same shared value: \(g^{ab} \pmod p\). This can then be used to derive an encryption key that they can use for a secure tunnel. Overall, \(p\) is the large prime number, and also known as the shared modulus between Bob and Alice.
Key derivation function
-
PBKDF2 key derivation with OpenSSL [here] PBKDF2 (Password Key Derivation Function 2) is a key derivation method. Overall it is relatively slow in its operation and where we take a password, a salt value, hashing method, and a number of iterations, in order to produce a given size of encryption key.
-
HKDF key derivation with OpenSSL [here] HKDF (HMAC Key Derivation function) is used to derive an encryption key from a pass phrase. Initially HKDF creates a pseudorandom key (PRK) using a pass phrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), andalong with a salt value. Next the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys.
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Passwords
-
Password example [here]. This page uses the OpenSSL library hash password generator, which is used in UNIX systems for the hashing of passwords which are contained in /etc/shadow and /etc/passwd. For newer passwords, the "-1" options is used to created the hashed value.
-
Hashed passwords with OpenSSL [here].
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
Public key
-
Generating an ECC key pair with OpenSSL [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)).
-
Generating an RSA key pair with OpenSSL [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2).
-
Generating an RSA key pair with OpenSSL with encryption [here]. This page implements RSA key pair generation with an encrypted key pair. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). In this case we will encrypt the key pair with either 3DES, 128-bit AES, 192-bit AES or 256-bit AES. The same password must be used to encrypt and decrypt.
-
Generate prime with OpenSSL [here]. Prime numbers are important in public key encrytion, and are used with RSA and ECC. For RSA, we generate two prime numbers (\(p\) and \(q\)) and which are multiplied together to create a modulus (\(N\)). If these prime numbers have 512 bit values, the modulus will be a 1,024 bit value. This defines the basic secure of RSA. With elliptic curve we use smaller prime numbers, such as 256-bit values for the secp256k1 curve.
ASN1 parsing
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). We will parse using asn1parse, and reveal the parameters.
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)) [RSA key pair]. We will parse using asn1parse, and reveal the parameters.
- DSA Parameters with asn1parse. DSA parameters with OpenSSL with asn1parse. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA (Digital Signature Algorithm)
- DSA Parameters. DSA parameters with OpenSSL. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
MAC (Message Authentication Code)
- HMAC with OpenSSL. MACs with OpenSSL. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authenticate both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2) and SHA-3. In this case we will use OpenSSL to generate the HMAC value.
- MACs with OpenSSL. MACs with OpenSSL. In the following we will generate MACs for HMAC, GMAC, CMAC, Blake2bmac, Blake2smac, KMAC128 and KMAC256. Overall, we will use an encryption key defined as a hex value for GMAC and CMAC, and a pass phrase for the others. The message is "hello".
Signing
- Digital signing a plaintext message with OpenSSL. Signing with OpenSSL. With digital signing, we can take a message, and create a signature. This normally involves signing with a private key and digital certificate. The signed message can be an a MIME format, and which can be integrated into an email message. In this can we have a 512-bit RSA key pair that will sign a plain text message.
Encrypting emails
- Encrypting an email message in OpenSSL. Encrypting messages with OpenSSL. With public key encryption, we can take a message, and encrypt it with the recipiant's public key. In this can we have a 512-bit RSA public key to encrypt a message.
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Random number generation with OpenSSL
-
Random number generator [here]. Random numbers are important in generating encryption keys and salt values. In this case OpenSSL generates a random number (in a Base64 format) for a given number of bytes.
Outline (C#/Python)
-
Symmetric Key Encryption (C#) [here]. This page uses the OpenSSL library through a C#/.NET wrapper. The DLLs it interfaces to are libeay32.dll and ssleay32.dll. OpenSSL supports a wide range of encryption methods, including 128-bit AES, 192-bit AES, 256-bit AES and Blowfish (bf). Different modes of ECB, CBC, and OFB are implemented. The examples use a default IV of "1234".
-
AES in Python with OpenSSL output [here]
-
Producing OpenSSL AES Encrypted String from C# [here]
Digital Certificates
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
Paillier - Partial Homomorphic Encryption

The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Fundamentals
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier).
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Using RSA
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
Applications
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Dragon Fly
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
Embedding data in an ECC point
- Embedding data in a point. Go. With Elliptic Curve Cryptography (ECC), we use points on an elliptic curve to represent our data. These are defined with (x,y) points. With this, it is possible to embedded a certain amount of data into the point - as long as it still gives us a valid point on the curve. This example will Curve 25519 to embed data, and is achieved by storing the length of the data in a single byte in the point, and then store the data as byte values in the point (followed by random data). To decode, we can then just read the first byte for the length of the message, and then reveal the data encoded into the point..
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Hashing (Cryptographic)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
Benchmarks and Password strength
The following are the tips related to hashing:
- Password strength. Test. This outlines the strength of various passwords types.
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
Theory
The following are the tips related to hashing:
- Balls in bins. BiBa. This implemented balls in bins.
- Birthday attack (with Big Integers). Calc. This provides a simple example of the birthday attack.
- Birthday attack. Calc. This provides a simple example of the birthday attack.
- Differential Cryptanalysis (Hashing). Cryptanalysis. This provides an implementation of differential cryptanalysis for hashing methods.
MD5, SHA-1
The following are the tips related to hashing:
- MD2 and MD4 MD2/4. The MD2 and MD4 hashing functions were developed by Prof Ronald Rivest in 1989 and 1990, respectively. They both produce a 128-bit hash, but have been shown be vulnerable to attack (see the Collision section in the page).
- MD5 and SHA-1 (to Base-64) with salt Salt. It is possible to add salt to the MD5 algorithm, to mix it up a little.
- MD5 and SHA-1 (to Base-64) Hash. MD5 and SHA-1 produces a hash signature, and the output is typically shown in a hex format or a Base-64. In this example the output is converted into a Base-64 format.
- MD5 and SHA-1. Hash. MD5 and SHA-1 methods produce a hash signature, and are the two of the most widely used methods. The MD5 algorithm has been shown to have weaknesses, and a collision of message hashes has been shown to occur in less than one day. An MD5 signature has 128 bits, an SHA-1 signature has 160 bits, and an SHA-256 signature has 256 bits.
- MD5 Cracking. Hash Cracker. MD5 has a 128-bit signature and can be cracked using rainbow tables. This page tries to crack the MD5 signature.
- Hashing with Go. Hashing. Hashes with Go.
- Detecting hash types. Hash type. This detects has values.
- OpenSSL hashing. Range of methods. Outlines the methods used in OpenSSL
- Hash. Hash. Hashing using JavaScript
- Hashing with node.js. Hashing. Hashing with node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Hashing methods
-
Hazmat Hashes. Hazmat Hashes. This includes the hashing methods in the Hazmat cryptography library. This includes Blake2p, Blake2s, MD5, SHA1, SHA224, SHA256, SGA384, SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHA512, SHA512-224, SHAKE128 and SHA256.
-
Hazmat Hashes. Hazmat Hashes. In this case we will implement Python code to determine SHA1, SHA2, SHA3, Blake2, MD5 and SM3 hashes.
OpenSSL Passwords
-
Password example [here]
-
Hashed passwords with OpenSSL [here]
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Blake 3 hashes
The following are the tips related to similarity hashing:
- Blake 3 in Python. Hashing. Blake 3 hashing.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
Other Hash functions
The following are the tips related to hashing:
- Bloom Filter Bloom filter. A Bloom filter goes a probabilistic method of determining if an element is in a data structure, using indexed hashing methods.
- Cuckoo Table Cuckoo filter. A Cockoo table uses two hash funtions.
- Chaffing. Chaffing. This produces a keyless system.
- GP Hashing with Go. GP Hashing. GP Hashes with Go.
- LDAP. LDAP. This produces a LDAP hash signature for a password.
- LM Hash. LM Hash. This is an LM Hash Calculator. LM Hash is used in many versions of Windows to store user passwords that are fewer than 15 characters long.
- Murmur and FNV Murmur and FNV. While hashing methods such as MD5 and SHA-1 use crypto methods, the Murmur and FNV hashes uses a non-cryptographic hash function. This can be used for general hash-based lookup and was designed by Austin Appleby. It has good performance compared with other hashing methods.
- Pearson. Pearson. This uses a non-crypto hash.
- phpass. phpass. This produces a phpass hash signature for a password.
- Tiger. Tiger. Tiger is a 192-bit hash function and was designed by Ross Anderson and Eli Biham in 1995. It is often used by clients within Gnutella file-sharing networks and does not suffer from known attacks on MD5 and SHA-0/SHA-1. Tiger2 is an addition, in which the message is padded with a byte of 0x80 (in a similar way to MD4, MD5, and SHA), whereas in Tiger it is 0x01. Otherwise, the two methods are the same in their operation.
- Whirlpool. Whirlpool. Whirlpool is a 512-bit cryptographic hash function and was created by Vincent Rijmen (one of the AES creators) and Paulo Barreto, in 2000.
- WPA-2 hash . WPA-2 hash. Implements SHA-2 hash.
- Reusable hash collisions. Reusable hash collisions. Reusable hash collisions.
- The Length Extension Attack. Length Extension Attack. The MD construct has many weaknesses, and one of the most serious is the length extension attack. With this an adversary (Eve) can take a hash for an unknown message, and then add additional data to produce a new valid hash. The hash methods which are at risk against the length extension attack are MD5, SHA-1 and SHA-256. Please follow the code link below to run an example.
- Consistent hashing. Consistent hash. This outlines the usage of Consistent hashes.
- ROR13 (Module and Function). ROR13. With ROR13 we take each 8-bit character and then convert to a unicode value (with 16 bits). Then for each character we rotate the bits right by thirteen places. The resultant hash is then just the accumuluation of the rotated values.
- ROR13 (Function). ROR13 (Function). With ROR13 we take each 8-bit character and then convert to a unicode value (with 16 bits). Then for each character we rotate the bits right by thirteen places. The resultant hash is then just the accumuluation of the rotated values.
- GOST, Streebog256 and Streebog512. GOST, Streebog256 and Streebog512. GOST94 is a hashing method developed with Euro-Asian Council for Standardization, Metrology and Certification (EASC). This has since been developed in the Streebog256 and Streebog512 hashing method. In this case, we will use Libre OpenSSL to convert data into a hashed value.
RIPEMD
- RIPEMD (RACE Integrity Primitives Evaluation Message Digest) and GOST. RIPEM160. RIPEMD is a 128-bit, 160-bit, 256-bit or 320-bit cryptographic hash function, and was created by Hans Dobbertin, Antoon Bosselaers, and Bart Preneel. It is used on TrueCrypt and is open source. The 160-bit version is seen as an alternative to SHA-1, and is part of ISO/IEC 10118
- RIPEMD160. RIPEM160. RIPEMD160 is a 160-bit cryptographic hash function, and was created by Hans Dobbertin, Antoon Bosselaers and Bart Preneel. RIPEMD160 is used in Bitcoin applications.
Chameleon hashes
The following are the tips related to Chameleon hashing:
- Chameleon hash in Golang Chameleon. With a Chameleon hash, we have a normal hash value which is resistant to collisions, but with a known secret we can easily create a collision. The concept was first defined by Krawcyk and Rabin.
Similarity hashes
The following are the tips related to similarity hashing:
- Similarity hash: SimHash (Charikar similarity) in Python Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash (Nilsimsa similarity) Nilsimsa. The Nilsimsa similarity is used to find similarities between spam emails.
- Minhash (Jaccard similarity) Jaccard similarity. The Minhash method is used to find similarities between strings, files and metadata.
- String enthropy String enthropy. Measurement of the entropy of strings.
- Counting identical elements (HyperLogLog) HyperLogLog. Counting the number of identical elements.
SHA-3 and SHA-3 contenders
The following are the tips related to Key derivation hashing:
- Blake and Blake 2. Blake. Implements Blake and Blake 2 (SHA-3 contender).
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
- Grøstl. Grøstl. Implements Grøstl (SHA-3 contender).
- KangarooTwelve. KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- SHA-3, Keccak and SHAKE . SHA-3. Implements SHA-3, Keccak and SHAKE (SHA-3 winner).
- SHA-3. SHA-3. SHA-3 was known as Keccak and is a hash function designed by Guido Bertoni, Joan Daemen, Michaël Peeters, and Gilles Van Assche. MD5 and SHA-0 have been shown to be susceptible to attacks, along with theoretical attacks on SHA-1. NIST thus defined there was a need for a new hashing method which did not use the existing methods for hashing, and setup a competition for competing algorithms. In October 2012, Keccak won the NIST hash function competition and is proposed as the SHA-3 standard. It should be noted that it is not replacement SHA-2, which is currently a secure method. Overall Keccak uses the sponge construction where the message blocks are XORed into the initial bits of the state, and then inevitably permuted.
- cSHAKE. cSHAKE. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS. With the SHA-3 hashing method, we have four different cryptographic hashing methods (SHA3-224, SHA3-256, SHA3-384, and SHA3-512) and two XOF functions (SHAKE128 and SHAKE256). With SHAKE128 and SHAKE256 we can integrate domain separation between different functions — and which are known as cSHAKE128 and cSHAKE256.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- Skein. Skein. Implements Skein (SHA-3 contender).
Key derivation hashing
The following are the tips related to Key derivation hashing:
- Argon2. Go. Outline of Argon2.
- Argon2 with NaCl. Go. Outline of Argon2 using NaCl.
- Balloon. Go. Outline of Balloon.
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- Double ratchet. Go. Outline of double ratcheting.
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- Scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat HKDF. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
Non-crypto/fast hashing
The following are the tips related to non-crypto hashing:
- A perfect hash Perfect hash. This is a non-crypto hash which optimizes the hash value.
- The universal hash Universal hash. This related to the concept of a universal hash.
- FNV. FNV. FNV is one of the fastest hashing methods.
- Murmur. Murmur. Murmur is one of the fastest hashing methods.
- Siphash. Siphash. Siphash is a fast hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- xxHash. xxHash. xxHash is one of the fastest hashing methods.
- Meow. Meow. Meow is one of the fastest hashing methods.
- o1Hash. o1Hash. o1Hash is one of the fastest hashing methods.
- CRC-32. CRC-32. CRC-32 is one of the fastest hashing methods.
- wyhash. wyhash. wyhash is one of the fastest hashing methods.
- CityHash. CityHash. CityHash is one of the fastest hashing methods, and is generally free of security problems.
- FarmHash. FarmHash. FarmHash is one of the fastest hashing methods, and is generally free of security problems.
- Non-crypto. Non-crypto. This includes a range of fast non-cryptography hashing methods.
- Non-crypto hashes (C++): Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro. Non-crypto hashes: Farm, City, xxHash, MUM, Spooky 2, Murmur, Metro and t1ha0. This includes a range of fast non-cryptography hashing methods for Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro using C++ methods.
- Pearson. Pearson. Pearson is one of the fastest hashing methods, and has been designed for 8-bit processors.
- C++: t1ha. t1ha. t1ha is one of the fastest hashing methods, and has been designed for 64-bit processors.
- C++: Spooky. Spooky. Spooky is one of the fastest hashing methods, and V2 has a 32-bit, 64-bit and 128-bit version.
- C++: xxHash. xxHash. xxHash is one of the fastest hashing methods, and has good performance for short data inputs.
- C++: MUM. MUM. MUM is one of the fastest hashing methods.
- C++: FNV 1/1a. FNV 1/1a. FNV 1/1a is one of the fastest hashing methods, and is particularily useful when there are small changes in strings, such as with IP addresses and URLs.
- C++: MetroHash. MetroHash. MetroHash is one of the fastest hashing methods.
- C++: CityHash. CityHash. CityHash was created by Google and is one of the fastest hashing methods. It was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Farm. FarmHash. FarmHash was created by Google and is one of the fastest hashing methods. It is an improvement to CityHash.
- C++: Murmur. Murmur. Murmur is one of the fastest hashing methods, but was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Halftime. Halftime. Halftime is one of the fastest hashing methods and was created by Jim Apple at Apache.
- C++: Highway. Highway. Highway is an ultra-fast keyed-hash, and is more than five times faster than SipHash. It was created by Jyrki Alakuijala, Bill Cox, Jan Wassenberg at Google.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
- C++: CLHash. CLHash. CLHash is an ultra-fast hashing method and focused on improving performance of the hashing of long strings.
- C++: FalkHash. FalkHash. FalkHash is an ultra-fast hashing method and beats most of the other non-cryptography methods for performance. It is focused on the x64 architecture and integrates with AES-NI.
- C++: wyHash. wyHash. wyHash is an ultra-fast hashing method.
- C++: Fibonacci. Fibonacci. Fibonacci is an ultra-fast hashing method.
- C++: Lookup3. Lookup3. Lookup3 is an ultra-fast hashing method.
Key-based hashing
The following are the tips related to Key-based hashing:
- SiphashSiphash. Siphash is a fast key-based hashing method.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
One Time Passwords/Time Stamps
The following are the tips related to hashing:
- One Time Passwords. One Time. This allows a new unique password to be created each instance, based on an initial seed.
- Timed One Time Password (TOTP). Timed One Time Password. This allows a new unique passcode to be created each instance, based on an initial seed for a given time window. We will use a five second window in this case, where a new passcode is generated every five seconds, based on an initial seed of a pass phrase.
- Hashed One Time Password (HOTP). Hashed One Time Password. This allows a new unique passcode to be created each instance, based on a counter value and an initial seed.
- Time Stamp Protocol. TSP. This creates a time stamp for data.
- HOTP and TOTP (Python). OTP. This creates hashed passwords.
eXtendable-Output Function (XOF)
- eXtendable-Output Function (XOF) usign CIRCL. XOF. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS.
SHAKE
The following are the tips related to hashing:
- SHAKE. SHAKE. Implements SHAKE and which is an Extendable Output Function (XOF).
- SHAKE with Go. SHAKE. This implements SHAKE in Go.
- libDisco with Go. libDisco. This implements libDisco.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify
the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods
such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC methods using the Python cryptography primitives for HMAC-MD5.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
Quantum-robust Public Key (Hash-based signature)
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
Hash to ECC point
- Hash to password with Go. Hash to password. Hash to password with Go.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve with libnum.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.

Password-hashing functions using Rust
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing (Non-cryptographic)

You might know those slow old hashing methods, such as MD5, SHA-1, and SHA-256. Well, they were designed to be fast, but also highly secure. But, if we just need a hashing method, such as for a hashtable or Bloom filter, we often don’t need all the security that comes with the main cryptography hashing methods. And so we have the non-cryptography hashing methods, and which are often ultra-fast and highly efficient. To show the difference, in a test, SHA-1 — one of the fastest cryptography hashing methods — managed a processing rate of 364.95 MiB/s, while t1ha was nearly a 100 times faster, at 34,636 MiB/s.
Non-crypto/fast hashing
The following are the tips related to non-crypto hashing:
- A perfect hash Perfect hash. This is a non-crypto hash which optimizes the hash value.
- The universal hash Universal hash. This related to the concept of a universal hash.
- FNV. FNV. FNV is one of the fastest hashing methods.
- Murmur. Murmur. Murmur is one of the fastest hashing methods.
- Siphash. Siphash. Siphash is a fast hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- xxHash. xxHash. xxHash is one of the fastest hashing methods.
- Meow. Meow. Meow is one of the fastest hashing methods.
- o1Hash. o1Hash. o1Hash is one of the fastest hashing methods.
- CRC-32. CRC-32. CRC-32 is one of the fastest hashing methods.
- wyhash. wyhash. wyhash is one of the fastest hashing methods.
- CityHash. CityHash. CityHash is one of the fastest hashing methods, and is generally free of security problems.
- FarmHash. FarmHash. FarmHash is one of the fastest hashing methods, and is generally free of security problems.
- Non-crypto. Non-crypto. This includes a range of fast non-cryptography hashing methods.
- Non-crypto hashes (C++): Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro. Non-crypto hashes: Farm, City, xxHash, MUM, Spooky 2, Murmur, Metro and t1ha0. This includes a range of fast non-cryptography hashing methods for Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro using C++ methods.
- Pearson. Pearson. Pearson is one of the fastest hashing methods, and has been designed for 8-bit processors.
- C++: t1ha. t1ha. t1ha is one of the fastest hashing methods, and has been designed for 64-bit processors.
- C++: Spooky. Spooky. Spooky is one of the fastest hashing methods, and V2 has a 32-bit, 64-bit and 128-bit version.
- C++: xxHash. xxHash. xxHash is one of the fastest hashing methods, and has good performance for short data inputs.
- C++: MUM. MUM. MUM is one of the fastest hashing methods.
- C++: FNV 1/1a. FNV 1/1a. FNV 1/1a is one of the fastest hashing methods, and is particularily useful when there are small changes in strings, such as with IP addresses and URLs.
- C++: MetroHash. MetroHash. MetroHash is one of the fastest hashing methods.
- C++: CityHash. CityHash. CityHash was created by Google and is one of the fastest hashing methods. It was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Farm. FarmHash. FarmHash was created by Google and is one of the fastest hashing methods. It is an improvement to CityHash.
- C++: Murmur. Murmur. Murmur is one of the fastest hashing methods, but was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Halftime. Halftime. Halftime is one of the fastest hashing methods and was created by Jim Apple at Apache.
- C++: Highway. Highway. Highway is an ultra-fast keyed-hash, and is more than five times faster than SipHash. It was created by Jyrki Alakuijala, Bill Cox, Jan Wassenberg at Google.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
- C++: CLHash. CLHash. CLHash is an ultra-fast hashing method and focused on improving performance of the hashing of long strings.
- C++: FalkHash. FalkHash. FalkHash is an ultra-fast hashing method and beats most of the other non-cryptography methods for performance. It is focused on the x64 architecture and integrates with AES-NI.
- C++: wyHash. wyHash. wyHash is an ultra-fast hashing method.
- C++: Fibonacci. Fibonacci. Fibonacci is an ultra-fast hashing method.
- C++: Lookup3. Lookup3. Lookup3 is an ultra-fast hashing method.
A fuller test with SMHasher gives [here]:
Hash function MiB/sec cycl./hash cycl./map Quality problems
------------------------------------------------------------------
o1hash 12439661.09 16.77 166.13 insecure, no seed, zeros, fails all tests
crc32_hw1 23208.73 46.74 179.70 insecure, 100% bias, collisions, distrib, BIC, machine-specific (x86 SSE4.2)
t1ha0_aes_noavx 22785.26 38.71 180.61 LongNeighbors, machine-specific (x86 AES-NI)
t1ha0_aes_avx1 22714.85 48.12 226.52 LongNeighbors, machine-specific (x64 AVX.txt)
t1ha0_aes_avx2 22345.33 44.38 556.47 LongNeighbors, machine-specific (x64 AVX2)
falkhash 20202.42 173.63 321.52 Sparse, LongNeighbors, machine-specific (x64 AES-NI)
MeowHash64low 17378.06 85.48 237.60 Sparse, invertible, machine-specific (x64 AES-NI)
MeowHash32low 17374.64 85.48 258.53 Sparse, invertible, machine-specific (x64 AES-NI)
MeowHash 17371.91 85.48 247.96 Sparse, invertible, machine-specific (x64 AES-NI)
FarmHash32 17112.05 47.7 214.71 machine-specific (x64 SSE4/AVX)
xxh3 16538.52 32.81 184.86 DiffDist bit 7 w. 36 bits, BIC
xxh3low 16462.36 32.77 199.79
farmhash32_c 16299.81 47.79 219.19 machine-specific (x64 SSE4/AVX)
xxh128low 15174.85 33.79 187.05
xxh128 15174.14 40.46 195.65
farsh32 14053.09 74.29 245.33 insecure: AppendedZeroes, collisions+bias, MomentChi2, LongNeighbors
metrohash64crc_2 14034.84 48.94 162.54 UB, Cyclic 8/8 byte, DiffDist, BIC, machine-specific (SSE4.2/NEON)
metrohash64crc_1 14000.5 49.08 150.54 UB, Cyclic 8/8 byte, DiffDist, BIC, MomentChi2, machine-specific (SSE4.2/NEON)
metrohash128crc_1 13948.67 65.2 168.08 UB, machine-specific (SSE4.2/NEON)
metrohash128crc_2 13920.19 65.12 176.70 UB, machine-specific (SSE4.2/NEON)
halftime_hash128 13478.23 97.79 252.14
wyhash32low 12911.09 29.59 205.43 2 bad seeds
wyhash 12879 30.35 196.77 2^33 bad seeds
CityCrc128 12343.43 74.5 209.75
fletcher2 12011.15 25.29 298.60 bad seed 0, UB, fails all tests
fletcher4 11928.55 25.27 293.49 bad seed 0, UB, fails all tests
halftime_hash256 11620.28 98.44 252.60
fibonacci 11339.87 26.33 705.64 UB, zeros, fails all tests
ahash64 9862.62 27.32 181.68 rust
Spooky128 9751.14 63.84 192.47 UB
Spooky64 9747.47 62.2 191.71 UB
Spooky32 9747.13 62.24 196.96 UB
t1ha1_64le 9723.86 34.39 176.91 Avalanche
cmetrohash64_1 9683.33 45.2 161.01 UB, LongNeighbors, BIC, MomentChi2
cmetrohash64_2 9669.95 44.75 149.67 LongNeighbors
metrohash64_2 9668.51 44.45 164.30 UB, LongNeighbors
metrohash64 9664.61 44.59 150.74 UB, LongNeighbors, BIC
metrohash64_1 9664.57 45.37 152.31 UB, LongNeighbors, BIC, MomentChi2
cmetrohash64_1o 9658.31 42.84 163.45 UB, LongNeighbors, BIC, MomentChi2
FNV1a_YT 9643.42 32.06 175.19 bad seed, UB, fails all tests
City128 9640.19 88.45 225.38
metrohash128_2 9584.94 59.1 167.43 UB, LongNeighbors
metrohash128 9569.16 58.68 167.53 UB, LongNeighbors
metrohash128_1 9558.17 59.04 175.94 UB, LongNeighbors
FarmHash128 9409.63 74.52 210.25
VHASH_32 9404.99 77.01 250.57 sanity, Seed, MomentChi2
VHASH_64 9392.39 74.72 227.92 sanity, Seed, MomentChi2
farmhash128_c 9244.13 79.08 209.44
t1ha2_atonce 9237.12 38.94 194.32 Zeroes low3
City64noSeed 9090.42 32.23 171.53 Avalanche, Sparse, TwoBytes, MomentChi2, Seed
City64low 9089.45 47.75 201.73
t1ha2_stream 9068.55 74.56 219.85 Sparse, Permutation, LongNeighbors
City64 9066.9 47.81 197.78 Sparse, TwoBytes
t1ha2_stream128 9065.5 93.19 236.50 Sparse, Permutation, LongNeighbors
xxHash64 8936.63 51.31 174.34
pengyhash 8744.48 85.31 222.45
farmhash64_c 8713.16 47.96 201.00
FarmHash64 8684.76 48.13 200.51
crc64_hw 8440.13 34.94 141.15 insecure, 100% bias, collisions, distrib, BIC, machine-specific (SSE4.2/NEON)
t1ha2_atonce128 8350.99 55.65 203.53 LongNeighbors
PMPML_64 8161.19 53.2 179.16 unseeded: Seed, MomentChi2, BIC
halftime_hash512 7681.62 125.81 274.01
tabulation 7621.75 42.19 179.93
t1ha1_64be 7481.37 38.16 193.22 Avalanche
MUMlow 7225.18 37.85 197.92 UB, 5 bad seeds
farsh64 7216.29 130.3 302.44 insecure: AppendedZeroes, collisions+bias, MomentChi2, LongNeighbors
MUM 7134.56 37.85 172.34 UB, too many bad seeds, machine-specific (32/64 differs)
nmhash32 7003.3 68.93 216.59
PMPML_32 6704.53 53.5 197.43 Avalanche >512, unseeded: Seed, BIC, MomentChi2, PerlinNoise
nmhash32x 6342.95 56.41 217.75
crc32_hw 6330.42 35.55 170.16 insecure, 100% bias, collisions, distrib, BIC, machine-specific (SSE4.2/NEON)
FNV2 6258.84 33.25 142.89 fails all tests
FNV1A_Pippip_Yurii 6258.46 28.19 184.41 UB, sanity, fails all tests
FNV1A_Totenschiff 6258.23 27.99 198.20 UB, zeros, fails all tests
HighwayHash64 6242.58 99.55 248.41
mx3 6146.02 52.48 173.09 UB
xxHash32 6040.87 51.77 177.91 LongNeighbors, collisions with 4bit diff, MomentChi2 220
prvhash64s_64 5481.48 170.05 325.39
mirhash 5413.73 39.68 154.47 UB, 2^36 bad seeds, LongNeighbors, machine-specific (32/64 differs)
mirhash32low 5412.76 39.79 182.13 UB, 4 bad seeds, Cyclic, LongNeighbors, machine-specific (32/64 differs)
Murmur3F 5226.4 52.18 175.85 UB
prvhash64s_128 5161.33 260.96 442.70
t1ha0_32le 5132.18 54.83 193.53 Sparse, LongNeighbors
halftime_hash64 4990.72 120.55 281.64
Murmur2B 4882.95 39.72 149.43 UB, 1.8% bias, collisions, 3.4% distrib, BIC
seahash32low 4801.33 58.54 227.31 PerlinNoise 32, !msvc
seahash 4796.97 58.55 201.58 PerlinNoise, !msvc
fasthash32 4737.61 45.32 181.86 UB, insecure
fasthash64 4737.21 42.79 164.87 UB, insecure, Moment Chi2 5159 !
umash32_hi 4662.92 54.22 214.20
umash64 4662.09 53.42 188.09
umash32 4633.19 53.42 216.33
t1ha0_32be 4585.59 55.98 183.45 Sparse, LongNeighbors
clhash 4472.31 82.72 229.73 PerlinNoise, machine-specific (x64 SSE4.2)
tabulation32 4317.34 35.45 197.20 collisions
Murmur2C 4092.99 51.84 164.65 UB, 2^32 bad seeds, 91% bias, collisions, distr, BIC, LongNeighbors
farsh128 3776.92 232.48 398.67
City32 3675.04 57.73 212.04
TSip 3228.14 57.96 211.71 !msvc
Murmur3C 3197.63 67.9 198.00 UB, LongNeighbors, Text, DiffDist
Crap8 3149.63 36.23 195.11 UB, 2.42% bias, collisions, 2% distrib
Murmur2 3146.91 41.87 187.89 UB, 1 bad seed, 1.7% bias, 81x coll, 1.7% distrib, BIC
Murmur2A 3146.79 46.87 191.96 UB, 1 bad seed, 12.7% bias, LongNeighbors
aesnihash 2963.39 71.24 217.73 fails many tests, machine-specific (x64 AES-NI)
BEBB4185 2951.62 222.03 343.63 UB, too many bad seeds, msvc-specific
jodyhash6 2848.42 29.99 164.36 bias, collisions, distr, BIC, LongNeighbors
wyhash32 2532.89 48.4 484.57 2 bad seeds, 32-bit
umash128 2427.46 70.6 197.29
Murmur3A 2413.88 53.36 182.37 UB, 1 bad seed, Moment Chi2 69
prvhash64_64m 2386.19 51.18 186.87
prvhash64_128 2383.57 103.44 246.45
prvhash64_64 2375.72 51.61 190.97
hasshe2 2372.52 68.64 216.74 Permutation,TwoBytes,Zeroes,Seed
PMurHash32 2344.78 58.48 196.43 1 bad seed, Moment Chi2 69
mirhashstrict32low 2218.87 65.48 190.59 1 bad seed, MomentChi2 9
mirhashstrict 2217.32 65.53 182.07
sha1ni 2019.96 135.84 564.40 insecure,sanity, Permutation, Zeroes, machine-specific
sha1ni_32 2019.94 136.82 589.46 machine-specific
superfast 1956.25 53.61 180.10 UB, bad seed 0, 91% bias, 5273.01x collisions, 37% distr, BIC
sha2ni-256_64 1910.34 146.06 595.16 Zeroes, machine-specific
sha2ni-256 1906.77 145.47 603.08 insecure,sanity, Permutation, Zeroes, machine-specific
farsh256 1895.77 459.86 575.95
SipHash13 1889.1 89 199.95 0.9% bias
Murmur1 1804.67 51.51 188.41 UB, 1 bad seed, 511x collisions, Diff, BIC
lookup3 1658.31 48.84 194.15 UB, 28% bias, collisions, 30% distr, BIC
pearsonbhash64 1486.34 104.32 185.03
poly_1_mersenne 1431.65 54.49 189.52 fails most tests
jodyhash32 1428.37 44.36 185.85 bias, collisions, distr, BIC LongNeighbors
pearsonbhash128 1347.03 121.75 214.84
poly_2_mersenne 1323.69 66.93 190.88
poly_3_mersenne 1323.59 74.86 206.77
poly_4_mersenne 1323.57 82.67 200.36
blake3_c 1285.91 340.01 552.63 no 32bit portability
GoodOAAT 1052 71.62 192.19
pearsonbhash256 998.9 167.05 261.29
SipHash 980.88 127.77 246.19
MicroOAAT 977.6 59.61 185.06 100% bias, distrib, BIC
FNV1a 791.84 69.69 177.84 bad seed, zeros, fails all tests
sdbm 791.84 67.69 177.06 bad seed 0, fails all tests
FNV64 791.82 70.24 159.29 fails all tests
bernstein 791.82 68.63 180.71 bad seed 0, fails all tests
beamsplitter 789.22 682.45 1150.3 UB, too many bad seeds
HalfSipHash 755.78 114.47 243.72 zeroes
chaskey 753.23 153.42 288.26 PerlinNoise
x17 527.9 98.78 184.09 99.98% bias, fails all tests
JenkinsOOAT_perl 452.49 118.78 194.78 bad seed 0, test FAIL
MurmurOAAT 452.49 113.07 197.83 bad seed 0, 1.5-11.5% bias, 7.2x collisions, BIC, LongNeighbors
JenkinsOOAT 452.48 142.85 213.93 bad seed 0, 1.5-11.5% bias, 7.2x collisions, BIC, LongNeighbors
crc32 392.1 131.62 204.58 insecure, 8590x collisions, distrib, PerlinNoise
sha1-160 364.95 1470.55 1794.1 Comb/Cyclic low32
rmd256 362.49 617.02 815.44 Bad seeds
blake2b-256_64 356.97 1222.76 1435.0
blake2b-224 356.59 1228.5 1425.87
blake2b-160 356.08 1236.84 1458.15
blake2b-256 355.97 1232.22 1443.31 Sparse high 32-bit
md5-128 353.76 638.29 803.39
md5_32a 353.64 629.85 799.56 Sparse high 32-bit
sha1_32a 353.03 1385.8 1759.9 Cyclic low32, 36.6% distrib
rmd128 334.36 659.03 838.32 Bad seeds
blake2s-128 295.3 698.09 1059.2
pearsonhash64 287.95 174.11 196.50 Avalanche, Seed, SSSE3 only. broken MSVC
pearsonhash128 287.95 171.72 194.61 Avalanche, Seed, SSSE3 only. broken MSVC
pearsonhash256 264.51 184.87 218.79 Avalanche, Seed, SSSE3 only. broken MSVC
blake2s-256 215.28 1014.88 1230.38
blake2s-160 215.01 1026.74 1239.54
blake2s-256_64 211.52 1044.22 1228.43
blake2s-224 207.06 1063.86 1236.50
rmd160 202.16 1045.79 1287.74 Bad seeds, Cyclic hi32
sha2-256_64 148.01 1376.34 1624.71 Bad seeds, Moment Chi2 7
sha2-256 147.8 1374.9 1606.06 Bad seeds, Moment Chi2 4
sha2-224_64 147.6 1360.1 1620.93 Bad seeds, Cyclic low32
sha2-224 147.13 1354.81 1589.92 Bad seeds, Comb low32
asconhashv12 144.98 885.02 1324.23
sha3-256 100.58 3877.18 4159.79 PerlinNoise
sha3-256_64 100.57 3909 4174.63 PerlinNoise
asconhashv12_64 86.73 684.02 606.93
floppsyhash 35.72 1868.92 1411.07
tifuhash_64 35.6 1679.52 1212.75 Cyclic low32
Problems include:
- Bad Seeds. A random seed is often used to initialise the hash. This problem relates to having a bad seed..
- Undefined behaviour (UB). This includes Misaligned, oob (Out of bounds), Signed integer overflow and Shift exponent overflow.
o1hash is the fastest, and a quick and dirty hashing method. It is generally not secure. t1h (Fast Positive Hash) requires AES-NI (Intel Advanced Encryption Standard Instructions) and is one of the fastest hashes at 22.785 Gbps. It has fairly good security levels. Meow comes in around 17.378 Gbps. We can see that SHA-1-160 runs as 364 Mbps, while Meow runs at 17.378 Gbps. Blake 3 is one of the fast cryptography hash and has a rate of 1.285 Gbps, and Blake 2 gives a rate around 215 Mbps. SHA-3 gives hashing rates of 100.58 Mbps.
Google recommend the following for 64-bit hashes without quality problems:
- xxh3low
-
wyhash
-
ahash64
-
t1ha2_atonce
-
FarmHash
-
halftime_hash128
-
Spooky32
-
pengyhash
-
nmhash32
-
mx3
-
MUM/mir
- fasthash32
Hash-based Signatures

With hash-based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature, unless we create a stateless method, such as SPHINCS+ [1]. Currently NIST have the final round for the Post Quantum Cryptography competition, and for digital signatures, SPHINCS+ is one of the alterative finalists (alongside Picnic).
Hash-based signature (theory)
- BiBa (Go). BiBa. An overview of BiBa One Time Signature [9]. Basically the method involves us taking a hash of a value using a standard hashing method, such as with SHA-256. There will then be \(2^{256}\) different hashing values. We aim to create a signature for a message, so Bob (the signer) selects a number of random values for his private key value and then publishes the hash of each of these (\(P_1\), \(P_2\), etc). He then sends these public keys to Alice. Now when Bob wants to sign a message, he will take one of his private key values, and then hashes it, and then determines the bin that it should be placed. In this case, we could use the \(\pmod N\) function on the hash, and where \(N\) is the number of bins. If we select \(2^{10}\) there will be 1,024 bins.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature [9].
Hash-based signature (stateful)
- BLISS - Post-quantum signing. BLISS. One of the alteratives to the usage of our existing public key methods is the usage of lattice cryptography, and especially in the usage of Ring Learning With Errors (RLWE). An important application is within digital signatures, and where Bob will sign something with his private key, and then Alice can prove that he signed it with his public key. One post-quantum signature method is BLISS (short for Bimodal Lattice Signature Scheme) [8]. It was created by Léo Ducas, Alain Durmus, Tancrède Lepoint and Vadim Lyubashevsky in 2013.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Hash to Obtain Random Subset (HORS) [3] is a quantum robust hashed-based one-time signature. With this we create a series of integers for our private keys and organise into an indexable form. Then we hash them to a sequence of public key values. Next we segment the hash of the message into a series of n-bit integer values. The signature is then achieved through a look-up of the value in the public key list.
- Lamport Signatures. Lamport. Outlines Lamport signatures [7]. When we sign a message we take its hash and then encrypt with our private key. The public key is then used to prove it, and will prove that we signed it with our private key. The Lamport signature uses 512 random hashes for the private key, and which are split into Set A and Set B. The public key is the hash of each of these values. The size of the private key is 16KB (2×256×256 bits) and the public key size is also 16 KB (512 hashes with each of 256 bits).
- Winternitz Signatures (W-OTS). Winternitz. Outlines Winternitz signatures [4, 5]. W-OTS uses relatively small key and signatures sizes, and is thought to be quantum robust. It generates 32x256 bit random private keys. We then hash these a number of times, and is defined by a parameter (w). If we use w=8, we hash the private keys by (2w). This creates 32x256 bits public keys. The signature is the created by taking eight bits at a time, and then the 8-bit binary int (n) is subtracted from 256 and the private key is the hashed 256-n times. The signature is then 32 hashes which are derived from random private keys. To verify the signature, the recipient parses the hash of the signature (using 8 bits at a time, and extracting the 8 bit int, n).
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method [6], and which is used within speeds-up of Hashing-based signature methods. Using methods such as SHA-1 and SHA-2 (aka SHA-256) will be inefficient as they tend to compress the data inputs through a number of stages. Haraka v2 [6] is different as focuses on inputs of just 256 bits (32 bytes) or 512 bits (64 bytes). This makes the method useful when we are dealing with key and hash values, and is especially useful for hash-based signatures. The output is 256 bits long, but where the input can be either be 256 bits (Haraka256) or 512 bits (Haraka512). These lengths are typically for the outputs of modern hashing applications. The Haraka method, too, has been optimized with AES instructions (AES-NI - Intel Advanced Encryption Standard New Instructions) and which are supported within the hardware of the processor. As Haraka is focused on short messages, the number of rounds within the hashing process has been reduced.
Hash-based signature (stateless)
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ digital signature. SPHINCS digital signature. Outline of the a SPHINCS stateless digital signature method [1].
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
Hash-based signature (Merkle-based)
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
Introduction
Many of the problems we see on the Internet relate to the lack of trust within transactions. The emails you receive and the Web sites that you visit often have very little trust built into them. For trust the email address of the sender, but anyone can fake that address. So increasingly we create a digital signature, and where we sign our messages. In this way, we can check for authentication, integrity and non-repudiation.
With the Alice creates a key-pair: a public key and a private key. She then takes a hash of the message, and then encrypts this hash with her private key, and passes the message and the signature to Bob. Bob then reads the message and takes a hash of it. He then decrypts Alice's signature with her public and checks the hashes. If they match, he knows that she signed and that it has not been changed along the way:
Currently, we often use RSA, DSA and ECDSA to sign our messages. These are based on the difficulty of finding out the factors of a number and on the processing of discrete logarithms. At the current time these methods are computationally hard problems, but with quantum computers, they become much easier. This was shown by Peter Shor who illustrated that it was possible to crack them in polynomial time.
Of all the methods that are being proposed, the hash-based methods look as if they have a good chance of success of creating quantum robust signatures. methods and code-based methods are being researched, but the usage of hashing methods is already well and could provide the best alternative to the existing methods. Hashing methods, too, often bring other advantages, such as forward secure, which means that a key which is cracked will not reveal all the previous keys.
Merkle trees
The root of hash-based methods isin Merkle trees, and which are a way of hashing is used in many applications, including with Bitcoin, Ethereum, Git distribution systems, No SQL, and in many P2P applications. With a Merkle tree we take our data elements, and then hash them, and take pairs of these hashes to create a new hash, and so we build a table. At the top of the tree is the root element (in this case Hash1234):

In this way, we can use the tree to see if we have matching data on systems.On a P2P network, we can transfer a file by splitting it into data segments and then distributing these segments across the network. A trusted source will have the complete Merkle tree for rebuilding the file, and a client can thus rebuild from the Merkle tree and determine the parts of the file which are still missing. Once transferred the root hash (and all the other hashes) will then match. In its core method, the Merkle Signature Scheme (MSS) has serious performance and memory issues, but enhanced methods such as XMSS create with much less of a performance hit.
One-time signatures (Lamport)
The core method used in hash-based signatures is that of the one-time signature, and where we create a new key pair for every method we need to create. If the keys were reused, an attacker could start to learn the private key, and thus spoof messages. One of the first methods was produced by Leslie Lamport and Whitfield Diffie, in 1979, and is defined as:
- We create two data sets with 256 random 256-bit numbers (Set A and Set B). These are the private key (512 values).
- we take the hash of each of the random numbers. This will give 512 hashes and will be the public key.
- We then hash the message using and then test each bit of the hash (0 ... 255). If it is a 0, we use the ith number in Set A, else we use the ith number from Set B.
- The signature is then 256 random numbers (taken from either Set A or Set B) and the public key is the 512 hashes (of Set A and Set B).
The public and private keys are then each 16KB in size. A demo of the method is here.

Figure 1: Lamport method
The major problem with the method is that a key pair for every message. also in 1979, found a solution with Merkle trees.
One-time signature (W-OTS)
To improve performance method (and which reduced key sizes), Merkle proposed Winternitz OTS (named after Robert Winternitz). With this method was possible to sign many bits at the same time. The method is:
- We create 32 256-bit random numbers. These 32 values will be our private key.
- We then hash each of these values 256 times. These 32 values will be our public key.
- We now take the message and hash it using SHA-256. This produces 32 8-bit values (N1, N2 ... N32).
- Next we take each 8-bit value in the hash of the message, and then hash 256-N times (where N is the value of the 8-bit value).
- To prove the signature, we take the message and hash it with SHA-256, and then take each 8-bit value. We then hash the 8-bit signature value by the number of times defined by the message hash value (N1, N2..). The result for each operation should equal the public key value.
This is illustrated below in Figure 2. A demo of the method is here.

Figure 2: W-OTS
Hash-based Signatures
The methods such as W-OTS and Lamport only provide for a one-time signature. In order to sign many messages, we can use the Merkel signature scheme (MSS). With this we take a hash of the keys and build these as the leaves of the tree. The root of the tree is then the public key - the verification key. We then just use the private key of the W-OTS method to create the signature. The sender also sends the authentication path, which is the neighbouring nodes within the path and which leads to the root of the tree. The recipient can then rebuild the tree using the verification key (which can be received a digital certificate) and the authentication path. For the next message we move onto another key pair and where the index of the key part is revealed.
In the following example we have our root as the public key, and then want to sign with Key3. We then show the authentication path which takes us to the root (as defined in the bold arrows):

Conclusions
Hashed-based methods look to be a strong contender for weaning us off RSA, DSA and ECDSA, but we will have to look at the stateful generation of keys. For this we will have to generate a bank of key pairs (2, 4, 8, 16, etc) and then create the public key from the root of the Merkle tree. We must then remember the keys we have used previously, and only use an unused one. Once we use our new key pair, we then show our working-out as to how the private key is integrated into our tree. It is a bit like a teacher marking a question correctly, and asking for the working out that go you to the answer.
References
[1] Bernstein, D. J., Hopwood, D., Hülsing, A., Lange, T., Niederhagen, R., Papachristodoulou, L., ... & Wilcox-O’Hearn, Z. (2015, April). SPHINCS: practical stateless hash-based signatures. In Annual international conference on the theory and applications of cryptographic techniques (pp. 368-397). Springer, Berlin, Heidelberg [paper].
[2] Bernstein, D. J., Hülsing, A., Kölbl, S., Niederhagen, R., Rijneveld, J., & Schwabe, P. (2019, November). The SPHINCS+ signature framework. In Proceedings of the 2019 ACM SIGSAC conference on computer and communications security (pp. 2129-2146) [paper].
[3] Reyzin, L., & Reyzin, N. (2002, July). Better than BiBa: Short one-time signatures with fast signing and verifying. In Australasian Conference on Information Security and Privacy (pp. 144-153). Springer, Berlin, Heidelberg [paper].
[4] Merkle, R. C. (1989, August). A certified digital signature. In Conference on the Theory and Application of Cryptology (pp. 218-238). Springer, New York, NY.
[5] Hülsing, A. (2013, June). W-OTS+–shorter signatures for hash-based signature schemes. In International Conference on Cryptology in Africa (pp. 173-188). Springer, Berlin, Heidelberg.
[6] Kölbl, S., Lauridsen, M. M., Mendel, F., & Rechberger, C. (2016). Haraka v2–efficient short-input hashing for post-quantum applications. IACR Transactions on Symmetric Cryptology, 1-29. [here]
[7] Lamport, L. (1979). Constructing digital signatures from a one-way function (Vol. 238). Technical Report CSL-98, SRI International. [paper]
[8] Ducas, L., Durmus, A., Lepoint, T., & Lyubashevsky, V. (2013, August). Lattice signatures and bimodal Gaussians. In Annual Cryptology Conference (pp. 40-56). Springer, Berlin, Heidelberg [paper].
[9] Perrig, A. (2001, November). The BiBa one-time signature and broadcast authentication protocol. In Proceedings of the 8th ACM Conference on Computer and Communications Security (pp. 28-37) [paper] .
Hashing (Simularity)

Similarity hashes allow for two data objects to be compared for their similarity.
Similarity assessment methods
The following relate to the basic methods used for string similarity:
- String similarity String similarity. This measures edit distance (including Levenshtein distance), Jaro (including Jaro-Winkler), and QGrams.
- String enthropy String enthropy. Measurement of the entropy of strings.
- Soundex Soundex. Soundex uses a phonetic algorithm to classify a sound as it is pronounced. It focuses on matching phrases which have minor spelling errors.
Similarity hashes
The following are the tips related to similarity hashing:
- Similarity hash: SimHash (Charikar similarity) in Python Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash (Nilsimsa similarity) Nilsimsa. The Nilsimsa similarity is used to find similarities between spam emails.
- Context Triggered Piecewise Hashes (CTPH): ssdeep CTPH similarity. Kornblum [6] created ssdeep and which computes fuzzy hashes. This aims to match similar byte sequences, no matter if there are differences between these sequences. For this we break a file up into fragments with a rolling hash function. We then produce a small hash for each of those fragments. These are then aggregated to produce the complete hash of a file. In comparing file signatures, we treat the resultant hash value as a string, and then uses an edit distance method to compare.
- TLSH (A Locality Sensitive Hash) TLSH similarity. In malware analysis and in text similarity, we often have to identify areas of data within files which are similar. One method is TLSH (A Locality Sensitive Hash), and which was defined by Oliver et al [7]. It is used - along with ssdeep - by VirusTotal to identify a hash value for malware.
- Minhash (Jaccard similarity) Jaccard similarity. The Minhash method is used to find similarities between strings, files and metadata.
- Counting identical elements (HyperLogLog) HyperLogLog. Counting the number of identical elements.
Hazmat cryptography

The Cryptography library in Python contains interfaces to common cryptographic algorithms, including symmetric key methods, hashing, public key, and key derivation functions. Many of these are contained with the Hazmat (Harzardous Material) primative setup.
Hashing, HMAC, CMAC, Poly1305 and HKDF
-
Hazmat Hashes. Hazmat Hashes. This includes the hashing methods in the Hazmat cryptography library. This includes Blake2p, Blake2s, MD5, SHA1, SHA224, SHA256, SGA384, SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHA512, SHA512-224, SHAKE128 and SHA256.
-
Hazmat Hashes. Hazmat Hashes. In this case we will implement Python code to determine SHA1, SHA2, SHA3, Blake2, MD5 and SM3 hashes.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
- Hazmat HKDF. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
- Hazmat CMAC. Hazmat CMAC. CMAC methods using the Python cryptography primitives.
- Hazmat Poly1305. Hazmat Poly1305. Poly1305 methods using the Python cryptography primitives.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
Symmetric key
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat. Implementation of ChaCha20/Poly1305 with a random key using Hazmat.
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat. Implementation of AES GCM with a random key using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hazmat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Hazmat Symmetric Key Padding. Symmetric key. This includes the coverage of padding with Hazmat.
- Hazmat Symmetric Key Padding. Symmetric key. This includes the coverage of padding with Hazmat.
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
- Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . With 3DES encryption, we use a 128-bit key and a 64-bit IV value. The two modes supported are ECB (without salt) and CBC (with salt). The DES algorithm has been around for a long time, and the 56-bit version is now easily crackable (in less than a day on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases, and splits the key into two. Overall the key size is typically 112 bits (with a combination of the three keys - of which two of the keys are the same). In this case we will use PKCS7 padding, and which fills the input data with a value that is equal to the number of padding bytes. Overall, DES has a 64-bit block size, and which equates to eight ASCII characters.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key . And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.
Asymmetric key
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- ECC key generaton with Hazmat. Elliptic Curve key gen. Creating ECC keys using Hazmat and Python.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- Hazmat RSA signing (with key values). RSA signing with Hazmat. RSA signing using Python and with Hazmat (with key values).
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here]
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Signatures. DSA Signatures. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. The ECDSA method is an extension of DSA, but implemented with elliptic curve (EC) methods. As with most public key signing methods, we take a hash of a message, and then apply a private key to create a signature (\(r,s\)). This is done by creating a random value (\(k\)) to produce the signature. The signature is then verified using the associated public key. This then verifies the creator of the signature and that the message has not been changed.
Digital Signature: ECDSA/EdDSA
- ECDSA with Hazmat. ECDSA wih Hazmat. This outlines ECDSA with Hazmat.
- Ed25519 for EdDSA signatures with Hazmat. EdDSA: Ed25519. This page uses the Hazmat primitives for the cryptography library.
- Ed448 for EdDSA signatures with Hazmat. EdDSA: Ed448. This page uses the Hazmat primitives for the cryptography library.
- Ed25519 using NaCl. Ed25519. This page uses the NaCl port from libsodium.
- ECDSA Signatures with Hazmat (SECP256R1, SECP384R1, SECP521R1, SECP224R1, SECP192R1, and SECP256K1). ECC Signatures. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and then creates an ECDSA signature for a given message.
Digital Signature: RSA
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
Key exchange: ECDH/X25519
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives and showing the byte values for the key.
Tokens
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
Homomorphic Encryption

Homomorphic encryption supports mathematical operations on encrypted values. Partial Homomorphic Encryption (PHE) supports a few arithmatic operations, while Full Homomorphic Encryption (FHE) supports add, subtract, multiply, and divide. Homomorphic encryption normally involves a public key to encrypt the data, and a private key to decrypt it. There have been four main generations of homomorphic encryption, and the most recent being the HEAAN method.
Simple
- Simple Homomorphic Cipher. Hom. This outlines a Simple Homomorphic cipher.
- Simple Homomorphic Cipher (Python). Hom. This outlines a Simple Homomorphic cipher with Python.
- Full Homomorphic Cipher with a Public Key. Public key. This outlines a Simple Homomorphic cipher using a public key
ElGamal
- ElGamal Homomorphic Cipher (Go). ElGamal. This outlines ElGamal Homomorphic cipher with Go.
- ElGamal Homomorphic Cipher (Go) - Divide. ElGamal. This outlines ElGamal Homomorphic cipher with Go with divide.
- ElGamal Homomorphic Cipher (Go) - Additive. ElGamal. This outlines ElGamal Homomorphic cipher with Go with addition.
- ElGamal Homomorphic Cipher for Multiplication (Python). ElGamal. This outlines ElGamal Homomorphic multiplication with Python.
- ElGamal Homomorphic Cipher for Division (Python). ElGamal. This outlines ElGamal Homomorphic division with Python.
- ElGamal Homomorphic Cipher for Addition (Python). ElGamal. This outlines ElGamal Homomorphic addition with Python.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (Python). ElGamal. This outlines ElGamal Homomorphic subtraction with Python.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
RSA
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
ZKP
- Full Homomorphic Cipher to determine if Bob is older. Older. This outlines a Simple Homomorphic cipher to determine if Bob is older than Alice.
- Full Homomorphic Cipher to determine matching password. Password. This outlines a Simple Homomorphic cipher to determine if a password matches
- Interactive ZKP With Probablistic Methods. ZKP. Interactive ZKP With Probablistic Methods using Python.
- Full Homomorphic Cipher for Millionaire's Problem. Millionaire. This outlines a Simple Homomorphic cipher for the Millionaire's Problem
Voting
- Trusted voting. Trusted. A trusted voting method.
Secret share
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Lattice
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
Full Homomorphic Cipher
- Full Homomorphic Cipher for 2-bit Adder. Adder. This outlines a Simple Homomorphic cipher for a 2-bit adder with DGHV.
- Full Homomorphic Cipher for Full Adder. Full Adder. This outlines a Simple Homomorphic cipher for a full adder with DGHV.
- Full Homomorphic Cipher for 4-bit Adder. Adder. This outlines a Simple Homomorphic cipher for a 4-bit adder with DGHV.
- Full Homomorphic Cipher for 4-bit Adder/Subtractor. Subtract. This outlines a Simple Homomorphic cipher for a 4-bit adder/subtractor with DGHV.
- Full Homomorphic Cipher to XOR two integers. X-OR. This outlines a Simple Homomorphic cipher to X-OR two integers
Paillier
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier) .
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Damgård-Jurik Homomorphic Encryption With Secret Shares. Damgård-Jurik Method. Two of the major areas of developments within cybersecurity will be the usage of homomorphic encryption, and in the usage of Shamir secret sharing. With homomorphic encryption, we can encrypt values, and then operate on them with arithmetic functions (such as add, subtract and multiply), and with Shamir secret sharing, we can split secrets into shares, and then distributed them over networks. These approaches will take privacy to new levels. So let’s look at the Damgård-Jurik method.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Learning with Errors (LWE)
- Learning With Errors . LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret key value (s) and another value (e). Next we select a number of values (t[]) and calculate g[] = t[] x s + e. The values of g[] and t[] become our public key.
- Public Key Encryption with Learning With Errors (LWE). LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret value (s) and which is our private key. We then create a public key which is based on random numbers (A), and then generate another set of numbers (B) which is based on A,s and random errors e. An example of encryption with multiple bits is given.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE)
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Others
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
- SIDH Go. SIDH. Post-quantum key exchange.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Anonymous crypto. Anon. Anonymous crypto.
- Rho factorization. Rho. Rho alogorithm.
- Post-quantum signing (BLISS). BLISS. BLISS method.
Homomorphic Encryption with Krytology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Homomorphic hashing
- Homomorphic Hashing with Golang. Homomorphic hashing. Normally with hashing methods, we need to take all the previous data and new data in order to create a new hash value for our data. In a homomorphic hashing method, we can basically take the previous hash, and then add on any new data values. We can also remove previous data values from our hash, too. This is more efficient in computing, as we do not have to process all of our data into a new hash, and can use simple homomorphic operations for the computation. The method we will use (LtHash) was initially defined by Bellare and Micciancio and updated Lewi et al at Facebook.
Identity Based Encryption (IBE)

This page outlines a few basic principles around the usage of IBE.
Identity Based Encryption (Pairing based)
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pair-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Identity Based Encryption (Others)
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Güther's implicitly certified identity-based public keys (IBE). Günther. This method allows Bob to generate Alices public key from her identity and publicly available parameters.
- Girault's self-certified public keys (IBE). Girault. This method allows Bob to generate Alices public key from her identity and publicly available parameters, and where we use an RSA key pair to self-certify Alice's public key.
Intrusion Detection Systems (IDS)
- Intrusion Detection Systems. Snort. This outlines some of the basics of IDS, including the requirement for Intrusion Detection Systems (IDSs), and where they are used.
- Advanced Network Forensics (Snort). Adv Network Forensics. This provides information on how to detect threats through network forensics with Snort
Snort

- Snort IDS. Snort. This is a Snort Analyser.
- Snort IDS 2 with rules editor. Snort. This provides information on how to detect threats through network forensics with Snort, and with an editing function for rules.
Presentation
IoT

The key objectives of this page are: Understand how a Pen Tester can generate vulnerabilities and test using the Metasploit framework; Define the options and payloads required to generate and use vulnerabilities; and Gaining remote access.
Devices
- Access the Wi-fi kettle. Go. This page outines how to access a wi-fi enabled kettle.
- Philips Hue Wireless Lighting. Go. This page shows how to use RESTful Web services to access to the Hue Led Lamps.
- Kali and R-PI. Go. This page shows the setup of a security testing infrastructure using a Raspberry Pi (R-PI) and a wifi access point.
- Kali, R-PI and RF electrical socket. Go. This page shows the control of an RF electical socket from a RPI.
- Capture from a Polar H10 heat rate sensor. Go. This page shows the capture of the Polar H10 heart sensor with an Ubertooth One.
- Trusted IoT: Linking IoT Devices to NFTs. Go. This page outlines a research paper which links a device to an NFT (Non-fungible Token).
Shodan Scanning
-
IoT Scan (Shodan). Go. This page includes a search of the Internet for key terms, such as for "apache", "mysql" and "cisco".
- IoT Banner Scan (Shodan). Go. This page includes a search of the Internet for key terms with the banner as a result (for the Top 10)
- Internet Services (Shodan). Go. This page includes a search of the Internet for key terms and display the IP address and port.
IoT Libraries
- libDisco with Go. libDisco. libdisco is a Golang library which can be used to create secure connections. It is based on the STROBE protocol framework. Symmetric cryptographic primitives rely on SHA-3 permutation, and asymmetric cryptographic primitives on X25519 and ed25519. STROBE defines a range of cryptographic protocols to integrate with IoT devices. In order to reduce processing, energy and memory requirements, it only uses Keccak (SHA-3) to encrypt and authenticate messages.
COSE/COBR
In computer security, we often have to represent binary data, in single values or groups of characters, bytes, words, long words, signed integers, floating-point values, double-precision floating-point values, and so on. This might be in the form of a data object, a signature or even encrypted content. For this, the ANS.1 DER format is often used, such as presenting digital certificates and signatures. An improvement on this for small messages with security is Concise Binary Object Representation (CBOR) — and which is defined in RFC8949 [1]. While JSON represents text-based data objects CBOR focuses on binary objects. It has been designed to create a lightweight encoder and decoder. This supports the use of CBOR within an IoT infrastructure. The data, also, does not require a data schema to be able to decode it, along with being extensible. CBOR defines the format of binary data with data objects and messages. We can then integrate security with CBOR Object Signing and Encryption (COSE), and which is defined in RFC8152 [2]. This includes signatures, message authentication codes (MACs), encryption and creating serialised objects.
- 128-bit AES GCM. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) can then build on this to include signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use a symmetric key to encrypt a message, and then decrypt it. In this case we will use AES GCM with a static 128-bit key ("0x000102030405060708090a0b0c0d0e0f").
- 256-bit AES GCM. Go. In this case we will use AES GCM using a random 256-bit key (32 bytes).
- EdDSA. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) [2] can then build on this to includes signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use EdDSA to create a signature for a message.
- ECDSA. Go. In this case we will use ECDSA to create a signature for a message.
- HMAC. Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT. Go. In this case we create a CWT token, and sign with an HMAC signature.
- ECDH. Go. In this case we create a symmetric key from ECDH. For this we will derive a shared key from the public key of Alice and Bob, and then define a single recipient which can derive the CEK (Content Encryption Key) using their private key. We will use the curves of P-256 (secp256r1), P-384 (secp384r1), P-521 (secp521r1) or SECP256K1 (as used with Bitcoin).
- RSA using COSE and CBOR. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\).
- RSA: dQ, dP and InvQ. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). The key pair also includes \(dQ\), \(dP\) and \(InvQ\), and these can be used with the Chinese remainder theory to optimize the decryption process.
Metasploit
- Armitage and Metasploit. Go.
- Exploiting Android with Metasploit. Go.
- Exploiting Android with Metasploit - Part 2. Go.
- Exploiting Windows/Mac OS X with Metasploit. Go.
- Remote Desktop Windows/Mac OS X with Metasploit. Go.
- Metasploit. Go.
- Internet of Things Security. Go.
- Metasploit (Enumeration and Scanning). Go.
- Metasploit (Malware). Go.
IP

 The following are a few interesting techniques around IP addresses:
The following are a few interesting techniques around IP addresses:
- Your details. IP. This shows your browser details.
- IP address analyser. IP. This involves converting an IP address to the host and network part of the address.
- IP subnet analyser. IP subnets. This involves converting an IP address to the host and network part of the address.
- IP address analyser. IP. This involves analysing IP addresses.
- Max subnets. Max subnets. This involves converting an IP address to the host and network part of the address.
- Route summarization. Summarization. This involves converting an IP address to the host and network part of the address.
- Whois. Whois. This does a basic Whois on a domain.
- URL Obfuscation. Obfuscation. This outlines URL obfuscation.
- HTTP Responses. Test. HTTP.
- Capturing Network Packets (Python). WinPCap. HTTP.
Cisco related
- Routing table. Routing table. This involves viewing a routing table for a Cisco device.
- ACL Generator. ACL. This involves a simple calculator for ACLs on network ranges.
- EIGRP metrics. EIGRP. Learn the basics of EIGRP metrics.
- VoIP B/W. VoIP. Calculate bandwidth for VoIP.
- Wild Card. Wild Card. On a Cisco device a wildcard mask is used to identify the parts of an IP address that need to be matched. It thus uses a wildcard mask, where a 0 in the bit position identifies that the device should match that bit, else a 1 shows that it should ignore it.
Protocols
- HTTP. HTTP. Show the request and response for HTTP.
- Ping analyser. IP. This involves converting a ping of a site.
IP Challenges
-
IP Test 1. IP Test. IP Classification test. This is a simple test which generates a range of IP addresses, and you must determine the IP address classification.
IP Subnet Challenge 1 Demo
-
IP Test 2. IP Test. IP Classification test Part 2. This test provides an address classification, and the user must find the addresses which are of this classification.
IP Subnet Challenge 2 Demo
-
IP Test 3. IP Test. IP Classification test Part 3. This test provides an address classification, where the network part of the address is determined.
IP Subnet Challenge 3 Demo
Subnet Challenges
- Subnet Test 1. Subnet Test. Subnet Test.
-
Subnet Test 2. Subnet Test. Subnet bits.
- Subnet Test 3. Subnet Test. Find the nth usable subnet. This test involves finding the nth usable subnet.
- Subnet Test 4. Subnet Test. Maximum subnets. This is a test page to determine the maximum number of subnets and hosts/subnet for IP classed addressing.
- Subnet Test 5. Subnet Test. Maximum host/subnet. This is a test page to determine the maximum number of hosts per subnet.
- Subnet Test 6. Subnet Test. Determine the required subnet mask for a given number of subnets. This is a test page to determine the required subnet mask for a given number of subnets and a given IP address classification.
- Subnet Test 7. Subnet Test. Determine the required subnet mask for a given number of host/subnet. This is a test page to determine the required subnet mask for a given number of hosts per subnet and a given IP address classification.
- Subnet Test 8. Subnet Test. Route summarization. This involves a calculation on route summarization.
- Subnet Test 9. Subnet Test. Binary to IP.
- Subnet Test 10. Subnet Test. Hex to IP.
-
Subnet Test 13. Subnet Test. Wild card mask network bits. Find the number of bits in the network part of the wild card mask. IP Wildcard challenge
- Subnet Test 14. Subnet Test. Wild card mask host bits. Find the number of bits in the host part of the wild card mask. IP Wildcard challenge
- Subnet Test 15. Subnet Test. Wild card mask ... find the network address. Find the network for the wild card mask. IP Wildcard challenge 2
- Subnet Test 16. Subnet Test. Find a matching IP address for a network and wild card mask. Find the IP for a network and a wild card mask.
- Subnet Test 17. Subnet Test. Find an address which is on a given network. Find an IP address on a network, for a given network address and subnet mask.
- Subnet Test 18. Subnet Test. Find an IP address on the same network. Find an IP address on the same subnet.
- Subnet Test 19. Subnet Test. Find subnet. Convert subnet mask.
- Megatest. Subnet Test. Challenging test for subnets.
JavaScript

JavaScript code allows execution within the browser, rather than on the server. It is often faster than code that runs on a server. Along with this we can also use Node.js, and which runs JavaScript code on a server.
Symmetric key
- AES. AES. In this example, we will use either a pre-generated key or a random one, and use AES (Rijndael) encryption.
- ChaCha20 and Poly1305. ChaCha. This page outlines Poly1305 and ChaCha20. ChaCha20 is a symmetric key method and Poly1305 is a message authentication code (MAC). They were created by Daniel J. Bernstein, and are alternatives to AES and HMAC.
- CMS (Padding). CMS. This page uses PKIJS encrypting on CMS. With CMS we can This document describes the Cryptographic Message Syntax (CMS). With this we can encapsulate an message within an encrypted entity.

Hashing
- Hash. Hash. This page defines a JavaScript Hash calculator. This uses a client-side JavaScript code to determine the hash signatures of a text value.
Signatures
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
- Boneh–Lynn–Shacham (BLS) signature. BLS. Boneh–Lynn–Shacham (BLS) signature method produces short signatures. They use elliptic curve pairing (and which are also known as bilinear maps).
Key exchange
- ECDH. ECDH. Elliptic Curve Diffie Hellman (ECDH) is used to generate a shared key. This implementation uses Elliptic Curve Cryptography (ECC) with JavaScript.
CryptoJS
- CryptoJS. CryptoJS. This page uses client-side JavaScript code to hashing, encrypt and sign, including for symmetric key (AES), streaming ciphers, hashing methods, and HMAC.
Blockchain
- PATRICIA trie. PATRICIA. In the following, we have the Top 2,500 Web sites in the world, and implemented with a Radix Trie (aka PATRICIA trie) In the following we have the Top 2,000 web sites on the Internet, and which have been indexed using the PATRICIA trie.
Public key
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
- RSA. RSA. RSA is an asymmetric encryption algorithm, which uses two keys, one to encrypt and the other to decrypt. It was created in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman, and is still one of the most widely used encryption methods. A typical application is in authenticating a sender, where the senders private key is used to encrypt a message, and then is decrypted by the receiver with the senders public key (which is known to anyone who wants it). It is also typically used for encrypting disks/files, such as for EFS.
Digital Certificates
- X.509 certificates in JavaScript. RSA and ECDSA Signed certificates. This page will generate either RSA and ECC key pairs, and then generate X.509 certificates, using either a signature of SHA1withRSA or SHA256withECDSA. For RSA signing we use an RSA private key to sign the certificate, and with ECDSA signing we use an ECC private key to sign the certificate.
Tokens
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
Random
- Random number generator. Rand. In the past, encryption and decryption had to be done through native code libraries, such as with Bouncy Castle and OpenSSL. With the increasing processing power of Web browsers, it is now possible to use encryption using JavaScript, which thus provides client-side processing of data. This Web page uses Javascript encryption, and generates a random 256-bit text key or a hex version. The 256-bit key is generated by generating 60 random numbers (from 0-25), and converting these to an ASCII character.
Malware obfuscation
- Malware obfuscation. Obfuscation. A malware writer will often hide certain keywords from the browser/human by encoding them in another format. This is typically done for hex coding (\xZZ), 16-bit unicoding (\uZZZZ) and octal coding (\ZZZ). To test, enter a value, and then press the button and it will convert encoded string.
Message Authentication Codes
- Chaskey (MAC). Chaskey. Chaskey Cipher is light-weight cryptography method for signing messages (MAC) using a 128-bit key. The hardware implementation only requires 3,334.33 gate equivalent with an operating clock frequency of 1 MHz (whereas Keccak requires 4,658 GE). In the page we create the Mac signature and also encrypt for CBC.
Other
- Password generation/hashing. Hashing. Linux can use salted passwords where the username, hashing method and hashed password are stored in a password file [More details]. The main methods are
Hashing

At times we need to generate secrets, such as encryption keys, from passwords or nonce values. A Key Derivation Function (KDF) is a verifiable way of doing this.
Key Derivation Functions (KDFs)
The following are the tips related to hashing:
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Password strength. Test. This outlines the strength of various passwords types.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
HKDF
The following are the tips related to Key derivation hashing:
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Hazmat HKDF for different hashing methods. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
-
HKDF key derivation with OpenSSL [
here]
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
PBKDF2
The following are the tips related to Key derivation hashing:
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- AES GCM (Python) with PBKDF2. AES GCM (Python) with PBKDF2.
- Fernet with PBKDF2 . AES GCM (Python) with PBKDF2.
- PBKDF2 key derivation. AES GCM (Python) with PBKDF2.
- Key Rotation with Fernet. AES GCM (Python) with PBKDF2.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Bcrypt
The following are the tips related to Key derivation hashing:
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- BCrypt. BCrypt. BCrypt with Rust.
-
Hash to password with Go. Hashing to Argon2, Scrypt and BCrypt. Hash to password with Go, including Argon2, Scrypt and BCrypt.
scrypt
- scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Argon 2
The following are the tips related to Key derivation hashing:
- Argon 2. Go. Outline of Argon2.
- Argon 2 with NaCl. Go. Outline of Argon2 using NaCl.
- Argon 2. Argon 2. Argon 2 with Rust.
- Balloon. Go. Outline of Balloon.
Other
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
- Double ratchet. Go. Outline of double ratcheting.
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
Outline
HMAC Key Derivation function (HKDF) is used to derive an encryption key from a passphrase. Initially, HKDF creates a pseudorandom key (PRK) using a passphrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), and along with a salt value. Next, the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys [RFC 5869][article]. In this case, we will use SHA-256.
The following shows how an encryption key can be generated using HKDF, and where we need a secret and a salt value. Both Bob and Alice have the same secret and salt.

With PBKDF2 (Password Based Key Derivation Function 2), we hash for a given number of rounds:

Key exchange

Key exchange is a way for Bob and Alice to communicate and for them to agree on a shared secret. The original method defined uses discrete logarithms (Diffie-Hellman), but most modern methods use elliptic curve techniques (ECDH). As quantum computers can crack both discrete log and elliptic curve methods, there are post quantum cryptography methods proposed. This includes SIDH, CSIDH, SIKE, and NewHope.
Key interchange/generation (Diffie-Hellman)
The following relates to key interchange:
- Selecting \(g\) in Diffie Hellman. G in Diffie Hellman. Picking a safe value of the generator \(g\) in discrete logarithms.
- Diffie-Hellman. Diffie-Hellman Calculation. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Real example). Diffie-Hellman Real. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Python). Diffie-Hellman. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (pre-compute). Diffie-Hellman (pre-compute). Many sites use the same prime numbers, which can then be cracked with a pre-computing attack.
- Key generation. Key gen. This will generate keys for different methods based on a passphrase.
- Diffie-Hellman (Man-in-the-middle). DF. This outlines the man-in-the-middle method for Diffie-Hellman.
- An Alternative Diffie-Hellman method. Alterative DH. This outlines an alternative Diffie-Hellman method.
Authenticated Key Exchange
The following are the tips related to Key derivation hashing:
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- MTI/A0. MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{ax+by} \pmod p\). MTI (Matsumoto, Takashima, Imai).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0. MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{x+y} \pmod p\)
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). The resultant key is \(xyG \)
- MTI/C0. MTI/C0. This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{xy} \pmod p\)
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG\).
- MTI/C1. MTI/C1. This outlines MTI/C1, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{abxy} \pmod p\).
- MQV (Menezes–Qu–Vanstone). MQV. MQV was created Alfred Menezes, Minghua Qu and Scott Vanstone in 1995 and is an authenticated key exchange method. Alice holds a key pair \((A,a)\) and Bob has a key pair \((B,b)\). With this \(a\) is Alice's private key, and \(A=aG\) is her public key. For Bob, his public key will be \(B=aG\) and a private key of \(b\), and where \(G\) is the base point on the elliptic curve.
- HMQV (Menezes–Qu–Vanstone). HMQV. HMQV builds on MQV and adds the identity of Bob and Alice.
- ECDH with X25519 and Blake2b. ECDH with X25519 and Blake2b. This uses PyNaCl to create an authenticated key exchange and uses X25519 and Blake2b.
Elliptic Curve (ECDH) - Python
The following are the tips related to ECC:
- Elliptic Curve. Elliptic Curve. Elliptic Curve is a public key method which can also be used to generate a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with simple parameters. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
Elliptic Curve (ECDH) - Golang and Node.js
The following are the tips related to ECC:
- ECDH with Go. ECDH. ECDH with Go.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with node.js. ECDH. ECDH with node.js.
- ECDH with JavaScript. ECDH. Elliptic Curve Diffie Hellman.
Password Authenticated Key Exchange (PAKE)
The following are the tips related to Key derivation hashing:
- SPAKE2. Go. Outline of SPAKE2.
- OPAQUE. Go. Outline of OPAQUE.
- SPEKE. Go. Outline of SPEKE (Simple Password Exponential Key Exchange).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
- J-PAKE. J-PAKE. This example generates a shared key based on a shared password.
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses discrete logs.
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
PQC NIST Finalists (Key Exchange)
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Key interchange/generation (Other)

The following relates to key interchange:
- Curve25519. Curve25519. This outlines Curve25519, which is used in the Tor network.
- Authenticated Key Exchange (Discrete logs). YAK. Key exchange with public keys and uses discrete logs.
- Authenticated Key Exchange (ECC). YAK. Key exchange with public keys and uses elliptic curve methods.
- Shamir No-key protocol. Shamir No Key. In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated.
- Shamir No-key protocol (sepc256k1). Shamir No Key (EC). In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated using the sepc256k1 elliptic curve.
- Conference keying (Burmester-Desmedt method). Conference keying. In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it.
- Conference keying (Burmester-Desmedt method) - Elliptic Curve (sepc256k1). Conference keying Elliptic Curve (sepc256k1). In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it, and uses the sepc256k1 elliptic curve.
Key exchange (with pairing)
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Kryptology

We need to build a new Internet. One that is build on mathematics and certainty, rather than the patchy version we have now. For this we need a layer of cryptography at the lowest level, and build software interfaces on top of this. Along with this we now have cryptographic methods which can now provide a foundation of trust, and which preserve privacy. And so the old libraries of OpenSSL are being squeezed out in favour of the new ones which are built on a solid foundation. The latest of these new "privacy-aware" libraries is Kryptology, and created by Coinbase. This library provides the APIs that developers need, in order to apply to areas of blockchain development. This library include BLS (Boneh-Lynn-Shacham) signatures, Zero-knowledge Proofs (ZKPs) and Shamir Secret Shares (SSS). With BLS we can digitally sign for data, but also preserve its privacy. Applications of this include group signatures, where multiple entities can merge their signing keys together and provide a single signature for a transaction. With SSS, we can split encryption keys up into shares, and then distribute them across a network. When required, we can call these shares back to reconstruct the key.
The focus for Coinbase seems to be the application of privacy coins, and where no tracking can be applied to the usage of these digital coins. This should support full anonymity for transactions, as opposed to Bitcoin which only supports pseudo-anonymity.

ECC Basics
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining n.G for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Points (Base Point and Others). Elliptic Curve points. Two common curves used in ECC (Elliptic Curve Cryptography) are secp256k1 (as used in Bitcoin and Ethereum) and P256 (secp256r1). The "k1" refers to the Kolbitz curve 1 (named after the creator of ECC). With these we have a base point which are can operate on. This is typically defined as \(G\). We can then operate on this with add and multiply operation. For example, \(2G=G+G\) and \(P=n.G\). In this following we will show the base point for a number of common curves, such as secp256r1, P256, Pallas, Curve 25519, BLS12381G1, BLS12381G2, BLS12377G1 and BLS12377G2.
ECDH
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret. We will use Golang and the Krytology library.
Simple ECC on curves
- Public key points for curves. Simple. Display public key points for scalars.
BLS Curve
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
Accumulator and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
Pallas Curve
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
Pairing-based Crypto
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
ElGamal and ECC
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a numerical input.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
Shamir Secret Shares
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Homomorphic Encryption
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Zero knowledge proofs
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
Verifiable Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Hash to scalar and point
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
CP-ABE
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Lattice cryptography

Latice cryptography is proposed as a post-quantum robust method for public key encryption, especially focused on digital signatures and key exchange mechanisms (KEMs).
Principles
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
NTRU
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- Lattice Encryption: NTRU Key Generation Python). NTRU. Outlines how NTRU operates for key generation.
Homomorphic
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Digital Signatures
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
Public-Key Encryption/Key Exchange
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
Light-weight cryptography

While AES and SHA work well together within computer systems, they struggle in an IoT/embedded world as they take up: too much processing power; too much physical space; and consume too much battery power. So NIST outlines a number of methods which can be used for light-weight cryptography, and which could be useful in IoT and RFID devices [1]. They define the device spectrum as:
- Conventional cryptography. Servers and Desktops. Tablets and smart phones.
- Light-weight cryptography. Embedded Systems. RFID and Sensor Networks.
With embedded systems, we commonly see 8-bit, 16-bit and 32-bit microcontrollers, and which would struggle to cope with real-time demands for conventional cryptography methods. And in the 40+ years since the first 4-bit processor, there is even a strong market for 4-bit processors. RFID and sensor network devices, especially, have limited numbers of gates available for security, and are often highly constrained with the power drain on the device.
So AES is typically a non-starter for many embedded devices. In light-weight cryptography, we often see smaller block size (typically 64 bits or 80 bits), smaller keys (often less than 90 bits) and less complex rounds (and where the S-boxes often just have 4-bits).
For light-weight cryptography the main constraints that we have are typically related to ener requirements, gate equivalents (GEs), and timing. With passive RFID devices, we do not have an associated battery for the power supply, and where the chip must power itself from energy coupled from the radio wave. An RFID device is thus likely to be severely constrained in the power drain associated with any cryptography functions, along with being constrained for the timing requirements and for the number of gates used. Even if an RFID device has an associated battery (active RFID), it may be difficult to recharge the battery, so the drain on power must often be minimised.
There is thus often a compromise between the cryptography method used and the overall security of the method. Thus often light-weight cryptography methods balance performance (throughput) against power drain and GE, and do not perform as well as main-stream cryptography standards (such as AES and SHA-256). Along with this the method must also have a low requirement for RAM (where the method requires the usage of running memory to perform its operation) and ROM (where the method is stored on the device). In order to assess the strengths of various methods we often define the area that the cryptography function will use on the device – and which is defined in \(µm^2\). The NIST finalists are defined in this [article]
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- GIFT AEAD. GIFT. GIFT is a light-weight block cipher. It is a (NIST Finalist)
- Elephant. Elephant. Elephant is a light-weight stream cipher. It is a (NIST Finalist).
- TinyJambu. TinyJambu. TinyJambu is a light-weight block cipher. It is a (NIST Finalist)
- Isap AEAD. Isap. Isap is a light-weight block cipher. It is a (NIST Finalist)
- PHOTON-Beetle AEAD. PHOTON-Beetle. PHOTON-Beetle is a light-weight block cipher. It is a (NIST Finalist)
- Romulus AEAD. Romulus. Romulus is a light-weight block cipher. It is a (NIST Finalist)
- Sparkle AEAD. Sparkle. Sparkle is a light-weight block cipher. It is a (NIST Finalist)
- CLEFIA. CLEFIA. CLEFIA is a light-weight block cipher.
- LED. LED. LED is a light-weight block cipher.
- Piccolo. Piccolo. Piccolo is an ultra light-weight block cipher.
- PRESENT. PRESENT. Present is a light-weight block cipher.
- Pyjamask. Pyjamask. Pyjamask is a light-weight block cipher.
- SIMON. SIMON. SIMON is a light-weight block cipher.
- SKINNY. SKINNY. SKINNEY is a light-weight block cipher.
- SPECK. SPECK. SPECK is a light-weight block cipher.
- XTEA. XTEA. XTEA is a light-weight block cipher.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encryption/Decryption. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.
Light-weight crypto (Other)
- Chaskey (MAC). Chaskey. Chaskey is a light-weight MAC function.
- Chaskey (MAC). Chaskey (Python). Chaskey is a light-weight MAC function.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (ASCON)
ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRFF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
Discrete Logs (Solving)

A discrete log problem is in the form of \(g^x \pmod p\) and where we know \(g\) and \(p\) and must solve for \(x\).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Message Authentication Code (MAC)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
HMAC
The following are the tips related to Key-based hashing:
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authentication both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2), Blake2b, SM3 and SHA-3. This page outlines the HMAC-MD5 methods using the Hazmat cryptography layer.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- HMAC (COSE). Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT with HMMAC. Go. In this case we create a CWT token, and sign with an HMAC signature.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- HMAC with Rust. HMAC. HMAC with Rust.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HMAC with OpenSSL. MACs with OpenSSL. HMAC in OpenSSL for a given input value, password and hashing method.
Cipher MACs
The following are the tips related to Key-based hashing:
- MACs with OpenSSL. MACs with OpenSSL. MAC methods implemented in OpenSSL, including CMAC and GMAC.
Key-based hashing
The following are the tips related to Key-based hashing:
- SipHash. Siphash. Siphash is a fast key-based hashing method.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Meow. Meow. Meow is one of the fastest hashing methods.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
Magic Numbers

This pages contains information related to magic numbers in file formats.
Network and File Forensics
- Magic numbers. Magic. This provides information on magic number for file forensics.
Graphics formats
- JPEG Analysis. JPEGs. This provides an analysis of JPEG files.
- GIF Analysis. GIFs. This provides an analysis of GIF files.
- TIF Analysis. TIFs. This provides an analysis of TIF files.
- PNG Analysis. PNGs. This provides an analysis of PNG files.
- BMP Analysis. BMPs. This provides an analysis of BMP files.
- PSD Analysis. PSDs. This provides an analysis of PSD files.
- WMF Analysis. WMF. This provides an analysis of WMF files.
- Adobe Illustrator Analysis. AI. This provides an analysis of AI files.
- Adobe In Design Analysis. INDD. This provides an analysis of INDD files.
- MIDI file. MIDI. This provides an analysis of MID files.
- ICO file. ICO. This provides an analysis of ICO files.
- PS file. PS. This provides an analysis of PS files.
- EPS file. EPS. This provides an analysis of EPS files.
- VSD file. VSD. This provides an analysis of Microsft Visio (VSD) files.
Video and audio formats
- MP3 Analysis. MP3s. This provides an analysis of MP3 files.
- AVI Analysis. AVIs. This provides an analysis of AVI files.
- Flash SWF Analysis. SWFs. This provides an analysis of Flash files.
- Flash FLV Analysis. FLVs. This provides an analysis of FLV files.
- MP4 Analysis. MP4. This provides an analysis of MP4 files.
- MOV Analysis. MOV. This provides an analysis of MOV files.
- WMV Analysis. WMV. This provides an analysis of WMV files.
- WMA Analysis. WMA. This provides an analysis of WMA files.
- JPEG 2000 Analysis. JPEG 2. This provides an analysis of JPEG 2000 files.
- WAV Analysis. WAV. This provides an analysis of WAV files.
Zips, Archives and Library files
- ZIP/Archive Analysis. ZIPs. This provides an analysis of ZIP/Achive files.
- GZ Analysis. GZ. This provides an analysis of GZip files.
- Tar Analysis. Tar. This provides an analysis of TAR files.
- MSI Analysis. MSI. This provides an analysis of MSI files.
- OBJ Analysis. OBJ. This provides an analysis of OBJ files.
- DLL Analysis. DLL. This provides an analysis of DLL files.
- CAB Analysis. CAB. This provides an analysis of CAB files.
- EXE Analysis. EXE. This provides an analysis of EXE files.
- RAR Analysis. RAR. This provides an analysis of RAR files.
- SYS Analysis. SYS. This provides an analysis of SYS files.
- HLP Analysis. HLP. This provides an analysis of HLP files.
- VMDK Analysis. VMDK. This provides an analysis of VMDK files (VMWare Virtual Disks).
- PST Analysis. PST. This provides an analysis of PST files (Outlook Email File).
- JAR Analysis. JAR. This provides an analysis of JAR files.
- SLN Analysis. SLN. This provides an analysis of Microsoft SLN files.
- Class Analysis. Class. This provides an analysis of Java Class files.
- Zlib. Zlib. This provides an analysis of Zlib files.
Documents
- PDF Analysis. PDFs. This provides an analysis of PDF files.
- DOC Analysis. DOCs. This provides an analysis of DOC files.
- RTF Analysis. RTFs. This provides an analysis of RTF files.
- XLS Analysis. XLSs. This provides an analysis of XLS files.
- PPT Analysis. PPTs. This provides an analysis of PPT files.
- MMP File. MMP. This provides an analysis of MMP files.
- DOCX Analysis. DOCX. This provides an analysis of DOCX files.
- XLSX Analysis. XLSX. This provides an analysis of XLSX files.
- PPTX Analysis. PPTX. This provides an analysis of PPTX files.
- MDB Analysis. MDB. This provides an analysis of MDB files.
- Outlook Message Analysis. MSG. This provides an analysis of MSG files.
Disk Image
- Raw disk format. RAW. This provides an analysis of the RAW disk format.
Tests
- File Forensics Test. File Test File Forensics Test.
- File Forensics Test (Fun). File Test (Fun) File Forensics Test.
Presentations
MIRACL Core Library

MIRACL Core is an open source library, and includes a wide range of public key encryption methods. It is especially focused on elliptic curve and pairing-friendly methods, but also supports a wide range of encryption methods, including RSA, AES and hashing. Overall, it can be ported onto a wide range of systems and supports C, C++, Go, Rust, Python, Java, Javascript and Swift. Along with this it supports limited capability devices such as the Arduino infrastructure. The GitHub repository is [here].
BN254
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.

Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- CL Signatures. CL. CL Signatures in Go using MIRACL.
- CL Signatures (advanced pairing). CL. CL Signatures in Go using MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages using MIRACL.
- PS Signatures. PS. Signatures using PS for short signatures using MIRACL.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures using MIRACL.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.

Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
Rust examples
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
NaCl

PyNaCl is a Python port of LibSodium. It integrates the latest cryptography methods, such as AES, XChaCha20, Blake2b and X25519.
Symmetric Key
- Symmetric key. Symmetric key (XChaCha20 and Poly1305). With symmetric key, Bob and Alice have the same key. NaCl uses the XChaCha20 method, and which supports stream encryption (and which does not require padding as a block cipher does, and is also faster than block cipher modes). ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16 byte nonce. XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24 byte nonce. It has a lower propability of nonce misuse than ChaCha20.
- Encryption with a password. Symmetric Key with KDF. In symmetric key, we generate a secret key. This key is typically a random value or generated from a password and a salt value. If we use a password, we typically use a KDF (Key Derivation Function), and which uses a password and a salt value, in order to create a key of a given size. In this case we will use Argon2i, and which is memory resilent.
Hybrid Encryption
- Box. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Hashing
- Hashing and KDF (Argon2 and scrypt). Hashing and KDF. This case we will use PyNaCl (Networking and Cryptography) library, and which is a Python binding to libsodium. We will hash a password using SHA-256 and SHA-512, and also create a KDF (Key Derivation Function) using scrypt and Argon2.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
Ed25519
-
Ed25519. Ed25519. Using Ed25519 for digital signatures.
-
Finding Points on Ed25519. X25519 (Points).
In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 (Key Exchange)
- X25519 + BLAKE2b key-exchange. X25519. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
Curve 25519
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
Node.js

Node.js uses the JavaScript programming langauge as its base, and allows for code to be run on a server, rather than in the browser (such as with pure JavaScript). To run a node.js program, we run "node myfile.js", and use NPM to install libraries.
Symmetric key
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
RSA and public key
- RSA Opt imal Asymmetric Encryption Padding (OAEP) using Node.js. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
ECC Keys
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.

Hashing
- Hashing with node.js (All). Hashing. Hashing with node.js.
- Hashing with node.js (Selection). Hashing. Hashing with node.js.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- ECDSA with node.js. ECDSA. ECDSA with node.js.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
Key exchange
- Diffie-Hellman with node.js (random prime). DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method and uses a randomly generated prime number (press the button to generate a new prime).
- Diffie-Hellman with node.js. DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method. Each time the prime number will be fixed for the DH group selected.
- ECDH with node.js. ECDH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Elliptic Curve Diffie Hellman (ECDH) key exchange method.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
Key derivation
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
CryptoJS
- CryptoJS (in node.js). CryptoJS (Node.js). Various crypto methods in the browser.
Bulletproofs
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
Blockchain
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
Proxy encryption
- Proxy Encryption - Encrypting With Public Key, And Decrypt with Private Key. Proxy01. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This page just creates a key pair for Alice, and uses it to encrypt with the public key , and decrypt with the private key.
- Proxy Encryption. Proxy02. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This will go through the full use case of proxy re-encryption.
Tokens
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
Random
- Fortuna with node.js. Fortuna. Fortuna random numbers with node.js.
Other
- FPE with node.js. FPR. FPE with node.js.
- Puny with node.js. Puny. Puny character format with node.js.
Accumulators and Witnesses
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
PGP
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Password Entropy
- Password Entropy with Node.js. Password Entropy. Password entropy measures the strength of a password, and is measured as the number of bits which could represent all of the possibilities. An entropy score of less than 25 identifies a poor password, and between 25 and 50 is a weak password. For 50 to 75 we have a reasonable password, and between 75 and 100 is a very good password. Over 100 is an excellent password. The strength of the password relates to the number of characters used, and also the number of characters in the password.
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
- Homomorphic Encryption with Node.js and BGV. Homomorphic Encryption with Node.js and BFG. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BGV method.
Oblivious Transfer (OT)

Oblivious Transfer allows Bob to select data from Alice, but for Alice not to know which value has been selected.
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
OpenSSH

OpenSSH supports the usage of the SSH protocol. This allows for a remote login. One tool which is uses is ssh-keygen, and which allow for the generation of RSA, DSA and elliptic-curve keys that. These can be used for user and host authentication, such as for GitHub login and Cloud instance login.
OpenSSH
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here].
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
Outline

OpenSSL

OpenSSL is a standard library that implements cryptography.
Symmetric key (Command line)
-
Symmetric Key Encryption (OpenSSL 1.x) [here]. In this case we will create cipher text from OpenSSL 1.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 1.x) [here].In this case we will decrypt cipher text from OpenSSL 1.x using a key derived from a password
-
Symmetric Key Encryption (OpenSSL 3.x) [here]. In this case we will create cipher text from OpenSSL 3.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 3.x) [here].In this case we will decrypt cipher text from OpenSSL 3.x using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password.
Hashing
-
Hashing [here] OpenSSL supports a wide range of hashing methods including BLAKE2b, Gost, MD4, MD5, RMD-160, SHA-1, SHA-3, SHA-256 and SHA-512.
Libre OpenSSL
-
Symmetric Key Encryption using Libre OpenSSL [here]. In this case we will create cipher text from Libre OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption using Libre OpenSSL [here]. In this case we will decrypt ciphertext from Libre OpenSSL using a key derived from a password.
-
Hashing [here] Libre OpenSSL supports a wide range of hashing methods including Gost, MD4, MD5, RMD-160, SHA-1, SHA-256 and SHA-512.
Diffie-Hellman parameter generation
-
DH Parameters with OpenSSL [here]. The Diffie-Hellman (DH) method is perhaps one of the greatest inventions in Cybersecurity, and was created by Whitfield Diffie and Marty Hellman. With the DH method, Bob creates a random value (\(b\)) and Alice also creates a random value (\(a\)). Next Bob computes \(B=g^b \pmod p\) and sends it to Alice. Alice computes \(A=g^a \pmod p\) and sends this to Bob. Bob raises the value of \(A\) to the power of \(b\) and takes \(\pmod p\), and Alice raises \(B\) to the power of \(a\) and takes \(\pmod p\). In the end, they will have the same shared value: \(g^{ab} \pmod p\). This can then be used to derive an encryption key that they can use for a secure tunnel. Overall, \(p\) is the large prime number, and also known as the shared modulus between Bob and Alice.
Key derivation function
-
PBKDF2 key derivation with OpenSSL [here] PBKDF2 (Password Key Derivation Function 2) is a key derivation method. Overall it is relatively slow in its operation and where we take a password, a salt value, hashing method, and a number of iterations, in order to produce a given size of encryption key.
-
HKDF key derivation with OpenSSL [here] HKDF (HMAC Key Derivation function) is used to derive an encryption key from a pass phrase. Initially HKDF creates a pseudorandom key (PRK) using a pass phrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), andalong with a salt value. Next the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys.
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Passwords
-
Password example [here]. This page uses the OpenSSL library hash password generator, which is used in UNIX systems for the hashing of passwords which are contained in /etc/shadow and /etc/passwd. For newer passwords, the "-1" options is used to created the hashed value.
-
Hashed passwords with OpenSSL [here].
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
Public key
-
Generating an ECC key pair with OpenSSL [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)).
-
Generating an RSA key pair with OpenSSL [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2).
-
Generating an RSA key pair with OpenSSL with encryption [here]. This page implements RSA key pair generation with an encrypted key pair. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). In this case we will encrypt the key pair with either 3DES, 128-bit AES, 192-bit AES or 256-bit AES. The same password must be used to encrypt and decrypt.
-
Generate prime with OpenSSL [here]. Prime numbers are important in public key encrytion, and are used with RSA and ECC. For RSA, we generate two prime numbers (\(p\) and \(q\)) and which are multiplied together to create a modulus (\(N\)). If these prime numbers have 512 bit values, the modulus will be a 1,024 bit value. This defines the basic secure of RSA. With elliptic curve we use smaller prime numbers, such as 256-bit values for the secp256k1 curve.
ASN1 parsing
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). We will parse using asn1parse, and reveal the parameters.
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)) [RSA key pair]. We will parse using asn1parse, and reveal the parameters.
- DSA Parameters with asn1parse. DSA parameters with OpenSSL with asn1parse. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA (Digital Signature Algorithm)
- DSA Parameters. DSA parameters with OpenSSL. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
MAC (Message Authentication Code)
- HMAC with OpenSSL. MACs with OpenSSL. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authenticate both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2) and SHA-3. In this case we will use OpenSSL to generate the HMAC value.
- MACs with OpenSSL. MACs with OpenSSL. In the following we will generate MACs for HMAC, GMAC, CMAC, Blake2bmac, Blake2smac, KMAC128 and KMAC256. Overall, we will use an encryption key defined as a hex value for GMAC and CMAC, and a pass phrase for the others. The message is "hello".
Signing
- Digital signing a plaintext message with OpenSSL. Signing with OpenSSL. With digital signing, we can take a message, and create a signature. This normally involves signing with a private key and digital certificate. The signed message can be an a MIME format, and which can be integrated into an email message. In this can we have a 512-bit RSA key pair that will sign a plain text message.
Encrypting emails
- Encrypting an email message in OpenSSL. Encrypting messages with OpenSSL. With public key encryption, we can take a message, and encrypt it with the recipiant's public key. In this can we have a 512-bit RSA public key to encrypt a message.
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Random number generation with OpenSSL
-
Random number generator [here]. Random numbers are important in generating encryption keys and salt values. In this case OpenSSL generates a random number (in a Base64 format) for a given number of bytes.
Outline (C#/Python)
-
Symmetric Key Encryption (C#) [here]. This page uses the OpenSSL library through a C#/.NET wrapper. The DLLs it interfaces to are libeay32.dll and ssleay32.dll. OpenSSL supports a wide range of encryption methods, including 128-bit AES, 192-bit AES, 256-bit AES and Blowfish (bf). Different modes of ECB, CBC, and OFB are implemented. The examples use a default IV of "1234".
-
AES in Python with OpenSSL output [here]
-
Producing OpenSSL AES Encrypted String from C# [here]
Digital Certificates
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
Paillier - Partial Homomorphic Encryption

The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Fundamentals
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier).
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Using RSA
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
Applications
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
Embedding data in an ECC point
- Embedding data in a point. Go. With Elliptic Curve Cryptography (ECC), we use points on an elliptic curve to represent our data. These are defined with (x,y) points. With this, it is possible to embedded a certain amount of data into the point - as long as it still gives us a valid point on the curve. This example will Curve 25519 to embed data, and is achieved by storing the length of the data in a single byte in the point, and then store the data as byte values in the point (followed by random data). To decode, we can then just read the first byte for the length of the message, and then reveal the data encoded into the point..
JWT tokens
- Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
- Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Hashing (Cryptographic)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
Benchmarks and Password strength
The following are the tips related to hashing:
- Password strength. Test. This outlines the strength of various passwords types.
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
Theory
The following are the tips related to hashing:
- Balls in bins. BiBa. This implemented balls in bins.
- Birthday attack (with Big Integers). Calc. This provides a simple example of the birthday attack.
- Birthday attack. Calc. This provides a simple example of the birthday attack.
- Differential Cryptanalysis (Hashing). Cryptanalysis. This provides an implementation of differential cryptanalysis for hashing methods.
MD5, SHA-1
The following are the tips related to hashing:
- MD2 and MD4 MD2/4. The MD2 and MD4 hashing functions were developed by Prof Ronald Rivest in 1989 and 1990, respectively. They both produce a 128-bit hash, but have been shown be vulnerable to attack (see the Collision section in the page).
- MD5 and SHA-1 (to Base-64) with salt Salt. It is possible to add salt to the MD5 algorithm, to mix it up a little.
- MD5 and SHA-1 (to Base-64) Hash. MD5 and SHA-1 produces a hash signature, and the output is typically shown in a hex format or a Base-64. In this example the output is converted into a Base-64 format.
- MD5 and SHA-1. Hash. MD5 and SHA-1 methods produce a hash signature, and are the two of the most widely used methods. The MD5 algorithm has been shown to have weaknesses, and a collision of message hashes has been shown to occur in less than one day. An MD5 signature has 128 bits, an SHA-1 signature has 160 bits, and an SHA-256 signature has 256 bits.
- MD5 Cracking. Hash Cracker. MD5 has a 128-bit signature and can be cracked using rainbow tables. This page tries to crack the MD5 signature.
- Hashing with Go. Hashing. Hashes with Go.
- Detecting hash types. Hash type. This detects has values.
- OpenSSL hashing. Range of methods. Outlines the methods used in OpenSSL
- Hash. Hash. Hashing using JavaScript
- Hashing with node.js. Hashing. Hashing with node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Hashing methods
- Hazmat Hashes. Hazmat Hashes. This includes the hashing methods in the Hazmat cryptography library. This includes Blake2p, Blake2s, MD5, SHA1, SHA224, SHA256, SGA384, SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHA512, SHA512-224, SHAKE128 and SHA256.
- Hazmat Hashes. Hazmat Hashes. In this case we will implement Python code to determine SHA1, SHA2, SHA3, Blake2, MD5 and SM3 hashes.
OpenSSL Passwords
- Password example [here]
- Hashed passwords with OpenSSL [here]
- Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Blake 3 hashes
The following are the tips related to similarity hashing:
- Blake 3 in Python. Hashing. Blake 3 hashing.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
Other Hash functions
The following are the tips related to hashing:
- Bloom Filter Bloom filter. A Bloom filter goes a probabilistic method of determining if an element is in a data structure, using indexed hashing methods.
- Cuckoo Table Cuckoo filter. A Cockoo table uses two hash funtions.
- Chaffing. Chaffing. This produces a keyless system.
- GP Hashing with Go. GP Hashing. GP Hashes with Go.
- LDAP. LDAP. This produces a LDAP hash signature for a password.
- LM Hash. LM Hash. This is an LM Hash Calculator. LM Hash is used in many versions of Windows to store user passwords that are fewer than 15 characters long.
- Murmur and FNV Murmur and FNV. While hashing methods such as MD5 and SHA-1 use crypto methods, the Murmur and FNV hashes uses a non-cryptographic hash function. This can be used for general hash-based lookup and was designed by Austin Appleby. It has good performance compared with other hashing methods.
- Pearson. Pearson. This uses a non-crypto hash.
- phpass. phpass. This produces a phpass hash signature for a password.
- Tiger. Tiger. Tiger is a 192-bit hash function and was designed by Ross Anderson and Eli Biham in 1995. It is often used by clients within Gnutella file-sharing networks and does not suffer from known attacks on MD5 and SHA-0/SHA-1. Tiger2 is an addition, in which the message is padded with a byte of 0x80 (in a similar way to MD4, MD5, and SHA), whereas in Tiger it is 0x01. Otherwise, the two methods are the same in their operation.
- Whirlpool. Whirlpool. Whirlpool is a 512-bit cryptographic hash function and was created by Vincent Rijmen (one of the AES creators) and Paulo Barreto, in 2000.
- WPA-2 hash . WPA-2 hash. Implements SHA-2 hash.
- Reusable hash collisions. Reusable hash collisions. Reusable hash collisions.
- The Length Extension Attack. Length Extension Attack. The MD construct has many weaknesses, and one of the most serious is the length extension attack. With this an adversary (Eve) can take a hash for an unknown message, and then add additional data to produce a new valid hash. The hash methods which are at risk against the length extension attack are MD5, SHA-1 and SHA-256. Please follow the code link below to run an example.
- Consistent hashing. Consistent hash. This outlines the usage of Consistent hashes.
- ROR13 (Module and Function). ROR13. With ROR13 we take each 8-bit character and then convert to a unicode value (with 16 bits). Then for each character we rotate the bits right by thirteen places. The resultant hash is then just the accumuluation of the rotated values.
- ROR13 (Function). ROR13 (Function). With ROR13 we take each 8-bit character and then convert to a unicode value (with 16 bits). Then for each character we rotate the bits right by thirteen places. The resultant hash is then just the accumuluation of the rotated values.
- GOST, Streebog256 and Streebog512. GOST, Streebog256 and Streebog512. GOST94 is a hashing method developed with Euro-Asian Council for Standardization, Metrology and Certification (EASC). This has since been developed in the Streebog256 and Streebog512 hashing method. In this case, we will use Libre OpenSSL to convert data into a hashed value.
RIPEMD
- RIPEMD (RACE Integrity Primitives Evaluation Message Digest) and GOST. RIPEM160. RIPEMD is a 128-bit, 160-bit, 256-bit or 320-bit cryptographic hash function, and was created by Hans Dobbertin, Antoon Bosselaers, and Bart Preneel. It is used on TrueCrypt and is open source. The 160-bit version is seen as an alternative to SHA-1, and is part of ISO/IEC 10118
- RIPEMD160. RIPEM160. RIPEMD160 is a 160-bit cryptographic hash function, and was created by Hans Dobbertin, Antoon Bosselaers and Bart Preneel. RIPEMD160 is used in Bitcoin applications.
Chameleon hashes
The following are the tips related to Chameleon hashing:
- Chameleon hash in Golang Chameleon. With a Chameleon hash, we have a normal hash value which is resistant to collisions, but with a known secret we can easily create a collision. The concept was first defined by Krawcyk and Rabin.
Similarity hashes
The following are the tips related to similarity hashing:
- Similarity hash: SimHash (Charikar similarity) in Python Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash (Nilsimsa similarity) Nilsimsa. The Nilsimsa similarity is used to find similarities between spam emails.
- Minhash (Jaccard similarity) Jaccard similarity. The Minhash method is used to find similarities between strings, files and metadata.
- String enthropy String enthropy. Measurement of the entropy of strings.
- Counting identical elements (HyperLogLog) HyperLogLog. Counting the number of identical elements.
SHA-3 and SHA-3 contenders
The following are the tips related to Key derivation hashing:
- Blake and Blake 2. Blake. Implements Blake and Blake 2 (SHA-3 contender).
- Hashing with Rust. Hashing. Hashes with Rust (Blake 2 and Blake 3).
- Grøstl. Grøstl. Implements Grøstl (SHA-3 contender).
- KangarooTwelve. KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- SHA-3, Keccak and SHAKE . SHA-3. Implements SHA-3, Keccak and SHAKE (SHA-3 winner).
- SHA-3. SHA-3. SHA-3 was known as Keccak and is a hash function designed by Guido Bertoni, Joan Daemen, Michaël Peeters, and Gilles Van Assche. MD5 and SHA-0 have been shown to be susceptible to attacks, along with theoretical attacks on SHA-1. NIST thus defined there was a need for a new hashing method which did not use the existing methods for hashing, and setup a competition for competing algorithms. In October 2012, Keccak won the NIST hash function competition and is proposed as the SHA-3 standard. It should be noted that it is not replacement SHA-2, which is currently a secure method. Overall Keccak uses the sponge construction where the message blocks are XORed into the initial bits of the state, and then inevitably permuted.
- cSHAKE. cSHAKE. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS. With the SHA-3 hashing method, we have four different cryptographic hashing methods (SHA3-224, SHA3-256, SHA3-384, and SHA3-512) and two XOF functions (SHAKE128 and SHAKE256). With SHAKE128 and SHAKE256 we can integrate domain separation between different functions — and which are known as cSHAKE128 and cSHAKE256.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- Skein. Skein. Implements Skein (SHA-3 contender).
Key derivation hashing
The following are the tips related to Key derivation hashing:
- Argon2. Go. Outline of Argon2.
- Argon2 with NaCl. Go. Outline of Argon2 using NaCl.
- Balloon. Go. Outline of Balloon.
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- Double ratchet. Go. Outline of double ratcheting.
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- Scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat HKDF. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
Non-crypto/fast hashing
The following are the tips related to non-crypto hashing:
- A perfect hash Perfect hash. This is a non-crypto hash which optimizes the hash value.
- The universal hash Universal hash. This related to the concept of a universal hash.
- FNV. FNV. FNV is one of the fastest hashing methods.
- Murmur. Murmur. Murmur is one of the fastest hashing methods.
- Siphash. Siphash. Siphash is a fast hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- xxHash. xxHash. xxHash is one of the fastest hashing methods.
- Meow. Meow. Meow is one of the fastest hashing methods.
- o1Hash. o1Hash. o1Hash is one of the fastest hashing methods.
- CRC-32. CRC-32. CRC-32 is one of the fastest hashing methods.
- wyhash. wyhash. wyhash is one of the fastest hashing methods.
- CityHash. CityHash. CityHash is one of the fastest hashing methods, and is generally free of security problems.
- FarmHash. FarmHash. FarmHash is one of the fastest hashing methods, and is generally free of security problems.
- Non-crypto. Non-crypto. This includes a range of fast non-cryptography hashing methods.
- Non-crypto hashes (C++): Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro. Non-crypto hashes: Farm, City, xxHash, MUM, Spooky 2, Murmur, Metro and t1ha0. This includes a range of fast non-cryptography hashing methods for Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro using C++ methods.
- Pearson. Pearson. Pearson is one of the fastest hashing methods, and has been designed for 8-bit processors.
- C++: t1ha. t1ha. t1ha is one of the fastest hashing methods, and has been designed for 64-bit processors.
- C++: Spooky. Spooky. Spooky is one of the fastest hashing methods, and V2 has a 32-bit, 64-bit and 128-bit version.
- C++: xxHash. xxHash. xxHash is one of the fastest hashing methods, and has good performance for short data inputs.
- C++: MUM. MUM. MUM is one of the fastest hashing methods.
- C++: FNV 1/1a. FNV 1/1a. FNV 1/1a is one of the fastest hashing methods, and is particularily useful when there are small changes in strings, such as with IP addresses and URLs.
- C++: MetroHash. MetroHash. MetroHash is one of the fastest hashing methods.
- C++: CityHash. CityHash. CityHash was created by Google and is one of the fastest hashing methods. It was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Farm. FarmHash. FarmHash was created by Google and is one of the fastest hashing methods. It is an improvement to CityHash.
- C++: Murmur. Murmur. Murmur is one of the fastest hashing methods, but was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Halftime. Halftime. Halftime is one of the fastest hashing methods and was created by Jim Apple at Apache.
- C++: Highway. Highway. Highway is an ultra-fast keyed-hash, and is more than five times faster than SipHash. It was created by Jyrki Alakuijala, Bill Cox, Jan Wassenberg at Google.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
- C++: CLHash. CLHash. CLHash is an ultra-fast hashing method and focused on improving performance of the hashing of long strings.
- C++: FalkHash. FalkHash. FalkHash is an ultra-fast hashing method and beats most of the other non-cryptography methods for performance. It is focused on the x64 architecture and integrates with AES-NI.
- C++: wyHash. wyHash. wyHash is an ultra-fast hashing method.
- C++: Fibonacci. Fibonacci. Fibonacci is an ultra-fast hashing method.
- C++: Lookup3. Lookup3. Lookup3 is an ultra-fast hashing method.
Key-based hashing
The following are the tips related to Key-based hashing:
- SiphashSiphash. Siphash is a fast key-based hashing method.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
One Time Passwords/Time Stamps
The following are the tips related to hashing:
- One Time Passwords. One Time. This allows a new unique password to be created each instance, based on an initial seed.
- Timed One Time Password (TOTP). Timed One Time Password. This allows a new unique passcode to be created each instance, based on an initial seed for a given time window. We will use a five second window in this case, where a new passcode is generated every five seconds, based on an initial seed of a pass phrase.
- Hashed One Time Password (HOTP). Hashed One Time Password. This allows a new unique passcode to be created each instance, based on a counter value and an initial seed.
- Time Stamp Protocol. TSP. This creates a time stamp for data.
- HOTP and TOTP (Python). OTP. This creates hashed passwords.
eXtendable-Output Function (XOF)
- eXtendable-Output Function (XOF) usign CIRCL. XOF. An eXtendable-Output Function (XOF) produces a bit string that can be of any length. In fact, we can create an infinitely long bit string, if required. The main methods are SHAKE128, SHAKE256, BLAKE2XB and BLAKE2XS.
SHAKE
The following are the tips related to hashing:
- SHAKE. SHAKE. Implements SHAKE and which is an Extendable Output Function (XOF).
- SHAKE with Go. SHAKE. This implements SHAKE in Go.
- libDisco with Go. libDisco. This implements libDisco.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
- HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the strength depends on the quality of the hashing function, and the resulting number of code bits. Along with this the number of bits in the secret key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC methods using the Python cryptography primitives for HMAC-MD5.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
Quantum-robust Public Key (Hash-based signature)
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
Hash to ECC point
- Hash to password with Go. Hash to password. Hash to password with Go.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve.
- Hash to Elliptic Curve. Hash to ECC. In this we match a value to the nearest point on an elliptic curve with libnum.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
- KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.

Password-hashing functions using Rust
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing (Non-cryptographic)

You might know those slow old hashing methods, such as MD5, SHA-1, and SHA-256. Well, they were designed to be fast, but also highly secure. But, if we just need a hashing method, such as for a hashtable or Bloom filter, we often don’t need all the security that comes with the main cryptography hashing methods. And so we have the non-cryptography hashing methods, and which are often ultra-fast and highly efficient. To show the difference, in a test, SHA-1 — one of the fastest cryptography hashing methods — managed a processing rate of 364.95 MiB/s, while t1ha was nearly a 100 times faster, at 34,636 MiB/s.
Non-crypto/fast hashing
The following are the tips related to non-crypto hashing:
- A perfect hash Perfect hash. This is a non-crypto hash which optimizes the hash value.
- The universal hash Universal hash. This related to the concept of a universal hash.
- FNV. FNV. FNV is one of the fastest hashing methods.
- Murmur. Murmur. Murmur is one of the fastest hashing methods.
- Siphash. Siphash. Siphash is a fast hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- xxHash. xxHash. xxHash is one of the fastest hashing methods.
- Meow. Meow. Meow is one of the fastest hashing methods.
- o1Hash. o1Hash. o1Hash is one of the fastest hashing methods.
- CRC-32. CRC-32. CRC-32 is one of the fastest hashing methods.
- wyhash. wyhash. wyhash is one of the fastest hashing methods.
- CityHash. CityHash. CityHash is one of the fastest hashing methods, and is generally free of security problems.
- FarmHash. FarmHash. FarmHash is one of the fastest hashing methods, and is generally free of security problems.
- Non-crypto. Non-crypto. This includes a range of fast non-cryptography hashing methods.
- Non-crypto hashes (C++): Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro. Non-crypto hashes: Farm, City, xxHash, MUM, Spooky 2, Murmur, Metro and t1ha0. This includes a range of fast non-cryptography hashing methods for Farm, City, xxHash, MUM, Spooky 2, Murmur and Metro using C++ methods.
- Pearson. Pearson. Pearson is one of the fastest hashing methods, and has been designed for 8-bit processors.
- C++: t1ha. t1ha. t1ha is one of the fastest hashing methods, and has been designed for 64-bit processors.
- C++: Spooky. Spooky. Spooky is one of the fastest hashing methods, and V2 has a 32-bit, 64-bit and 128-bit version.
- C++: xxHash. xxHash. xxHash is one of the fastest hashing methods, and has good performance for short data inputs.
- C++: MUM. MUM. MUM is one of the fastest hashing methods.
- C++: FNV 1/1a. FNV 1/1a. FNV 1/1a is one of the fastest hashing methods, and is particularily useful when there are small changes in strings, such as with IP addresses and URLs.
- C++: MetroHash. MetroHash. MetroHash is one of the fastest hashing methods.
- C++: CityHash. CityHash. CityHash was created by Google and is one of the fastest hashing methods. It was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Farm. FarmHash. FarmHash was created by Google and is one of the fastest hashing methods. It is an improvement to CityHash.
- C++: Murmur. Murmur. Murmur is one of the fastest hashing methods, but was found to be vulnerable to DoS hashing vulnerabilities.
- C++: Halftime. Halftime. Halftime is one of the fastest hashing methods and was created by Jim Apple at Apache.
- C++: Highway. Highway. Highway is an ultra-fast keyed-hash, and is more than five times faster than SipHash. It was created by Jyrki Alakuijala, Bill Cox, Jan Wassenberg at Google.
- C++: SipHash. SipHash. SipHash is an ultra-fast keyed-hash and was created by Jean-Philippe Aumasson and Daniel J. Bernstein in 2012.
- C++: CLHash. CLHash. CLHash is an ultra-fast hashing method and focused on improving performance of the hashing of long strings.
- C++: FalkHash. FalkHash. FalkHash is an ultra-fast hashing method and beats most of the other non-cryptography methods for performance. It is focused on the x64 architecture and integrates with AES-NI.
- C++: wyHash. wyHash. wyHash is an ultra-fast hashing method.
- C++: Fibonacci. Fibonacci. Fibonacci is an ultra-fast hashing method.
- C++: Lookup3. Lookup3. Lookup3 is an ultra-fast hashing method.
A fuller test with SMHasher gives [here]:
Hash function MiB/sec cycl./hash cycl./map Quality problems ------------------------------------------------------------------ o1hash 12439661.09 16.77 166.13 insecure, no seed, zeros, fails all tests crc32_hw1 23208.73 46.74 179.70 insecure, 100% bias, collisions, distrib, BIC, machine-specific (x86 SSE4.2) t1ha0_aes_noavx 22785.26 38.71 180.61 LongNeighbors, machine-specific (x86 AES-NI) t1ha0_aes_avx1 22714.85 48.12 226.52 LongNeighbors, machine-specific (x64 AVX.txt) t1ha0_aes_avx2 22345.33 44.38 556.47 LongNeighbors, machine-specific (x64 AVX2) falkhash 20202.42 173.63 321.52 Sparse, LongNeighbors, machine-specific (x64 AES-NI) MeowHash64low 17378.06 85.48 237.60 Sparse, invertible, machine-specific (x64 AES-NI) MeowHash32low 17374.64 85.48 258.53 Sparse, invertible, machine-specific (x64 AES-NI) MeowHash 17371.91 85.48 247.96 Sparse, invertible, machine-specific (x64 AES-NI) FarmHash32 17112.05 47.7 214.71 machine-specific (x64 SSE4/AVX) xxh3 16538.52 32.81 184.86 DiffDist bit 7 w. 36 bits, BIC xxh3low 16462.36 32.77 199.79 farmhash32_c 16299.81 47.79 219.19 machine-specific (x64 SSE4/AVX) xxh128low 15174.85 33.79 187.05 xxh128 15174.14 40.46 195.65 farsh32 14053.09 74.29 245.33 insecure: AppendedZeroes, collisions+bias, MomentChi2, LongNeighbors metrohash64crc_2 14034.84 48.94 162.54 UB, Cyclic 8/8 byte, DiffDist, BIC, machine-specific (SSE4.2/NEON) metrohash64crc_1 14000.5 49.08 150.54 UB, Cyclic 8/8 byte, DiffDist, BIC, MomentChi2, machine-specific (SSE4.2/NEON) metrohash128crc_1 13948.67 65.2 168.08 UB, machine-specific (SSE4.2/NEON) metrohash128crc_2 13920.19 65.12 176.70 UB, machine-specific (SSE4.2/NEON) halftime_hash128 13478.23 97.79 252.14 wyhash32low 12911.09 29.59 205.43 2 bad seeds wyhash 12879 30.35 196.77 2^33 bad seeds CityCrc128 12343.43 74.5 209.75 fletcher2 12011.15 25.29 298.60 bad seed 0, UB, fails all tests fletcher4 11928.55 25.27 293.49 bad seed 0, UB, fails all tests halftime_hash256 11620.28 98.44 252.60 fibonacci 11339.87 26.33 705.64 UB, zeros, fails all tests ahash64 9862.62 27.32 181.68 rust Spooky128 9751.14 63.84 192.47 UB Spooky64 9747.47 62.2 191.71 UB Spooky32 9747.13 62.24 196.96 UB t1ha1_64le 9723.86 34.39 176.91 Avalanche cmetrohash64_1 9683.33 45.2 161.01 UB, LongNeighbors, BIC, MomentChi2 cmetrohash64_2 9669.95 44.75 149.67 LongNeighbors metrohash64_2 9668.51 44.45 164.30 UB, LongNeighbors metrohash64 9664.61 44.59 150.74 UB, LongNeighbors, BIC metrohash64_1 9664.57 45.37 152.31 UB, LongNeighbors, BIC, MomentChi2 cmetrohash64_1o 9658.31 42.84 163.45 UB, LongNeighbors, BIC, MomentChi2 FNV1a_YT 9643.42 32.06 175.19 bad seed, UB, fails all tests City128 9640.19 88.45 225.38 metrohash128_2 9584.94 59.1 167.43 UB, LongNeighbors metrohash128 9569.16 58.68 167.53 UB, LongNeighbors metrohash128_1 9558.17 59.04 175.94 UB, LongNeighbors FarmHash128 9409.63 74.52 210.25 VHASH_32 9404.99 77.01 250.57 sanity, Seed, MomentChi2 VHASH_64 9392.39 74.72 227.92 sanity, Seed, MomentChi2 farmhash128_c 9244.13 79.08 209.44 t1ha2_atonce 9237.12 38.94 194.32 Zeroes low3 City64noSeed 9090.42 32.23 171.53 Avalanche, Sparse, TwoBytes, MomentChi2, Seed City64low 9089.45 47.75 201.73 t1ha2_stream 9068.55 74.56 219.85 Sparse, Permutation, LongNeighbors City64 9066.9 47.81 197.78 Sparse, TwoBytes t1ha2_stream128 9065.5 93.19 236.50 Sparse, Permutation, LongNeighbors xxHash64 8936.63 51.31 174.34 pengyhash 8744.48 85.31 222.45 farmhash64_c 8713.16 47.96 201.00 FarmHash64 8684.76 48.13 200.51 crc64_hw 8440.13 34.94 141.15 insecure, 100% bias, collisions, distrib, BIC, machine-specific (SSE4.2/NEON) t1ha2_atonce128 8350.99 55.65 203.53 LongNeighbors PMPML_64 8161.19 53.2 179.16 unseeded: Seed, MomentChi2, BIC halftime_hash512 7681.62 125.81 274.01 tabulation 7621.75 42.19 179.93 t1ha1_64be 7481.37 38.16 193.22 Avalanche MUMlow 7225.18 37.85 197.92 UB, 5 bad seeds farsh64 7216.29 130.3 302.44 insecure: AppendedZeroes, collisions+bias, MomentChi2, LongNeighbors MUM 7134.56 37.85 172.34 UB, too many bad seeds, machine-specific (32/64 differs) nmhash32 7003.3 68.93 216.59 PMPML_32 6704.53 53.5 197.43 Avalanche >512, unseeded: Seed, BIC, MomentChi2, PerlinNoise nmhash32x 6342.95 56.41 217.75 crc32_hw 6330.42 35.55 170.16 insecure, 100% bias, collisions, distrib, BIC, machine-specific (SSE4.2/NEON) FNV2 6258.84 33.25 142.89 fails all tests FNV1A_Pippip_Yurii 6258.46 28.19 184.41 UB, sanity, fails all tests FNV1A_Totenschiff 6258.23 27.99 198.20 UB, zeros, fails all tests HighwayHash64 6242.58 99.55 248.41 mx3 6146.02 52.48 173.09 UB xxHash32 6040.87 51.77 177.91 LongNeighbors, collisions with 4bit diff, MomentChi2 220 prvhash64s_64 5481.48 170.05 325.39 mirhash 5413.73 39.68 154.47 UB, 2^36 bad seeds, LongNeighbors, machine-specific (32/64 differs) mirhash32low 5412.76 39.79 182.13 UB, 4 bad seeds, Cyclic, LongNeighbors, machine-specific (32/64 differs) Murmur3F 5226.4 52.18 175.85 UB prvhash64s_128 5161.33 260.96 442.70 t1ha0_32le 5132.18 54.83 193.53 Sparse, LongNeighbors halftime_hash64 4990.72 120.55 281.64 Murmur2B 4882.95 39.72 149.43 UB, 1.8% bias, collisions, 3.4% distrib, BIC seahash32low 4801.33 58.54 227.31 PerlinNoise 32, !msvc seahash 4796.97 58.55 201.58 PerlinNoise, !msvc fasthash32 4737.61 45.32 181.86 UB, insecure fasthash64 4737.21 42.79 164.87 UB, insecure, Moment Chi2 5159 ! umash32_hi 4662.92 54.22 214.20 umash64 4662.09 53.42 188.09 umash32 4633.19 53.42 216.33 t1ha0_32be 4585.59 55.98 183.45 Sparse, LongNeighbors clhash 4472.31 82.72 229.73 PerlinNoise, machine-specific (x64 SSE4.2) tabulation32 4317.34 35.45 197.20 collisions Murmur2C 4092.99 51.84 164.65 UB, 2^32 bad seeds, 91% bias, collisions, distr, BIC, LongNeighbors farsh128 3776.92 232.48 398.67 City32 3675.04 57.73 212.04 TSip 3228.14 57.96 211.71 !msvc Murmur3C 3197.63 67.9 198.00 UB, LongNeighbors, Text, DiffDist Crap8 3149.63 36.23 195.11 UB, 2.42% bias, collisions, 2% distrib Murmur2 3146.91 41.87 187.89 UB, 1 bad seed, 1.7% bias, 81x coll, 1.7% distrib, BIC Murmur2A 3146.79 46.87 191.96 UB, 1 bad seed, 12.7% bias, LongNeighbors aesnihash 2963.39 71.24 217.73 fails many tests, machine-specific (x64 AES-NI) BEBB4185 2951.62 222.03 343.63 UB, too many bad seeds, msvc-specific jodyhash6 2848.42 29.99 164.36 bias, collisions, distr, BIC, LongNeighbors wyhash32 2532.89 48.4 484.57 2 bad seeds, 32-bit umash128 2427.46 70.6 197.29 Murmur3A 2413.88 53.36 182.37 UB, 1 bad seed, Moment Chi2 69 prvhash64_64m 2386.19 51.18 186.87 prvhash64_128 2383.57 103.44 246.45 prvhash64_64 2375.72 51.61 190.97 hasshe2 2372.52 68.64 216.74 Permutation,TwoBytes,Zeroes,Seed PMurHash32 2344.78 58.48 196.43 1 bad seed, Moment Chi2 69 mirhashstrict32low 2218.87 65.48 190.59 1 bad seed, MomentChi2 9 mirhashstrict 2217.32 65.53 182.07 sha1ni 2019.96 135.84 564.40 insecure,sanity, Permutation, Zeroes, machine-specific sha1ni_32 2019.94 136.82 589.46 machine-specific superfast 1956.25 53.61 180.10 UB, bad seed 0, 91% bias, 5273.01x collisions, 37% distr, BIC sha2ni-256_64 1910.34 146.06 595.16 Zeroes, machine-specific sha2ni-256 1906.77 145.47 603.08 insecure,sanity, Permutation, Zeroes, machine-specific farsh256 1895.77 459.86 575.95 SipHash13 1889.1 89 199.95 0.9% bias Murmur1 1804.67 51.51 188.41 UB, 1 bad seed, 511x collisions, Diff, BIC lookup3 1658.31 48.84 194.15 UB, 28% bias, collisions, 30% distr, BIC pearsonbhash64 1486.34 104.32 185.03 poly_1_mersenne 1431.65 54.49 189.52 fails most tests jodyhash32 1428.37 44.36 185.85 bias, collisions, distr, BIC LongNeighbors pearsonbhash128 1347.03 121.75 214.84 poly_2_mersenne 1323.69 66.93 190.88 poly_3_mersenne 1323.59 74.86 206.77 poly_4_mersenne 1323.57 82.67 200.36 blake3_c 1285.91 340.01 552.63 no 32bit portability GoodOAAT 1052 71.62 192.19 pearsonbhash256 998.9 167.05 261.29 SipHash 980.88 127.77 246.19 MicroOAAT 977.6 59.61 185.06 100% bias, distrib, BIC FNV1a 791.84 69.69 177.84 bad seed, zeros, fails all tests sdbm 791.84 67.69 177.06 bad seed 0, fails all tests FNV64 791.82 70.24 159.29 fails all tests bernstein 791.82 68.63 180.71 bad seed 0, fails all tests beamsplitter 789.22 682.45 1150.3 UB, too many bad seeds HalfSipHash 755.78 114.47 243.72 zeroes chaskey 753.23 153.42 288.26 PerlinNoise x17 527.9 98.78 184.09 99.98% bias, fails all tests JenkinsOOAT_perl 452.49 118.78 194.78 bad seed 0, test FAIL MurmurOAAT 452.49 113.07 197.83 bad seed 0, 1.5-11.5% bias, 7.2x collisions, BIC, LongNeighbors JenkinsOOAT 452.48 142.85 213.93 bad seed 0, 1.5-11.5% bias, 7.2x collisions, BIC, LongNeighbors crc32 392.1 131.62 204.58 insecure, 8590x collisions, distrib, PerlinNoise sha1-160 364.95 1470.55 1794.1 Comb/Cyclic low32 rmd256 362.49 617.02 815.44 Bad seeds blake2b-256_64 356.97 1222.76 1435.0 blake2b-224 356.59 1228.5 1425.87 blake2b-160 356.08 1236.84 1458.15 blake2b-256 355.97 1232.22 1443.31 Sparse high 32-bit md5-128 353.76 638.29 803.39 md5_32a 353.64 629.85 799.56 Sparse high 32-bit sha1_32a 353.03 1385.8 1759.9 Cyclic low32, 36.6% distrib rmd128 334.36 659.03 838.32 Bad seeds blake2s-128 295.3 698.09 1059.2 pearsonhash64 287.95 174.11 196.50 Avalanche, Seed, SSSE3 only. broken MSVC pearsonhash128 287.95 171.72 194.61 Avalanche, Seed, SSSE3 only. broken MSVC pearsonhash256 264.51 184.87 218.79 Avalanche, Seed, SSSE3 only. broken MSVC blake2s-256 215.28 1014.88 1230.38 blake2s-160 215.01 1026.74 1239.54 blake2s-256_64 211.52 1044.22 1228.43 blake2s-224 207.06 1063.86 1236.50 rmd160 202.16 1045.79 1287.74 Bad seeds, Cyclic hi32 sha2-256_64 148.01 1376.34 1624.71 Bad seeds, Moment Chi2 7 sha2-256 147.8 1374.9 1606.06 Bad seeds, Moment Chi2 4 sha2-224_64 147.6 1360.1 1620.93 Bad seeds, Cyclic low32 sha2-224 147.13 1354.81 1589.92 Bad seeds, Comb low32 asconhashv12 144.98 885.02 1324.23 sha3-256 100.58 3877.18 4159.79 PerlinNoise sha3-256_64 100.57 3909 4174.63 PerlinNoise asconhashv12_64 86.73 684.02 606.93 floppsyhash 35.72 1868.92 1411.07 tifuhash_64 35.6 1679.52 1212.75 Cyclic low32
Problems include:
- Bad Seeds. A random seed is often used to initialise the hash. This problem relates to having a bad seed..
- Undefined behaviour (UB). This includes Misaligned, oob (Out of bounds), Signed integer overflow and Shift exponent overflow.
o1hash is the fastest, and a quick and dirty hashing method. It is generally not secure. t1h (Fast Positive Hash) requires AES-NI (Intel Advanced Encryption Standard Instructions) and is one of the fastest hashes at 22.785 Gbps. It has fairly good security levels. Meow comes in around 17.378 Gbps. We can see that SHA-1-160 runs as 364 Mbps, while Meow runs at 17.378 Gbps. Blake 3 is one of the fast cryptography hash and has a rate of 1.285 Gbps, and Blake 2 gives a rate around 215 Mbps. SHA-3 gives hashing rates of 100.58 Mbps.
Google recommend the following for 64-bit hashes without quality problems:
- xxh3low
- wyhash
- ahash64
- t1ha2_atonce
- FarmHash
- halftime_hash128
- Spooky32
- pengyhash
- nmhash32
- mx3
- MUM/mir
- fasthash32
Hash-based Signatures

With hash-based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature, unless we create a stateless method, such as SPHINCS+ [1]. Currently NIST have the final round for the Post Quantum Cryptography competition, and for digital signatures, SPHINCS+ is one of the alterative finalists (alongside Picnic).
Hash-based signature (theory)
- BiBa (Go). BiBa. An overview of BiBa One Time Signature [9]. Basically the method involves us taking a hash of a value using a standard hashing method, such as with SHA-256. There will then be \(2^{256}\) different hashing values. We aim to create a signature for a message, so Bob (the signer) selects a number of random values for his private key value and then publishes the hash of each of these (\(P_1\), \(P_2\), etc). He then sends these public keys to Alice. Now when Bob wants to sign a message, he will take one of his private key values, and then hashes it, and then determines the bin that it should be placed. In this case, we could use the \(\pmod N\) function on the hash, and where \(N\) is the number of bins. If we select \(2^{10}\) there will be 1,024 bins.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature [9].
Hash-based signature (stateful)
- BLISS - Post-quantum signing. BLISS. One of the alteratives to the usage of our existing public key methods is the usage of lattice cryptography, and especially in the usage of Ring Learning With Errors (RLWE). An important application is within digital signatures, and where Bob will sign something with his private key, and then Alice can prove that he signed it with his public key. One post-quantum signature method is BLISS (short for Bimodal Lattice Signature Scheme) [8]. It was created by Léo Ducas, Alain Durmus, Tancrède Lepoint and Vadim Lyubashevsky in 2013.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Hash to Obtain Random Subset (HORS) [3] is a quantum robust hashed-based one-time signature. With this we create a series of integers for our private keys and organise into an indexable form. Then we hash them to a sequence of public key values. Next we segment the hash of the message into a series of n-bit integer values. The signature is then achieved through a look-up of the value in the public key list.
- Lamport Signatures. Lamport. Outlines Lamport signatures [7]. When we sign a message we take its hash and then encrypt with our private key. The public key is then used to prove it, and will prove that we signed it with our private key. The Lamport signature uses 512 random hashes for the private key, and which are split into Set A and Set B. The public key is the hash of each of these values. The size of the private key is 16KB (2×256×256 bits) and the public key size is also 16 KB (512 hashes with each of 256 bits).
- Winternitz Signatures (W-OTS). Winternitz. Outlines Winternitz signatures [4, 5]. W-OTS uses relatively small key and signatures sizes, and is thought to be quantum robust. It generates 32x256 bit random private keys. We then hash these a number of times, and is defined by a parameter (w). If we use w=8, we hash the private keys by (2w). This creates 32x256 bits public keys. The signature is the created by taking eight bits at a time, and then the 8-bit binary int (n) is subtracted from 256 and the private key is the hashed 256-n times. The signature is then 32 hashes which are derived from random private keys. To verify the signature, the recipient parses the hash of the signature (using 8 bits at a time, and extracting the 8 bit int, n).
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method [6], and which is used within speeds-up of Hashing-based signature methods. Using methods such as SHA-1 and SHA-2 (aka SHA-256) will be inefficient as they tend to compress the data inputs through a number of stages. Haraka v2 [6] is different as focuses on inputs of just 256 bits (32 bytes) or 512 bits (64 bytes). This makes the method useful when we are dealing with key and hash values, and is especially useful for hash-based signatures. The output is 256 bits long, but where the input can be either be 256 bits (Haraka256) or 512 bits (Haraka512). These lengths are typically for the outputs of modern hashing applications. The Haraka method, too, has been optimized with AES instructions (AES-NI - Intel Advanced Encryption Standard New Instructions) and which are supported within the hardware of the processor. As Haraka is focused on short messages, the number of rounds within the hashing process has been reduced.
Hash-based signature (stateless)
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ digital signature. SPHINCS digital signature. Outline of the a SPHINCS stateless digital signature method [1].
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
Hash-based signature (Merkle-based)
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
Introduction
Many of the problems we see on the Internet relate to the lack of trust within transactions. The emails you receive and the Web sites that you visit often have very little trust built into them. For trust the email address of the sender, but anyone can fake that address. So increasingly we create a digital signature, and where we sign our messages. In this way, we can check for authentication, integrity and non-repudiation.
With the Alice creates a key-pair: a public key and a private key. She then takes a hash of the message, and then encrypts this hash with her private key, and passes the message and the signature to Bob. Bob then reads the message and takes a hash of it. He then decrypts Alice's signature with her public and checks the hashes. If they match, he knows that she signed and that it has not been changed along the way:
Currently, we often use RSA, DSA and ECDSA to sign our messages. These are based on the difficulty of finding out the factors of a number and on the processing of discrete logarithms. At the current time these methods are computationally hard problems, but with quantum computers, they become much easier. This was shown by Peter Shor who illustrated that it was possible to crack them in polynomial time.
Of all the methods that are being proposed, the hash-based methods look as if they have a good chance of success of creating quantum robust signatures. methods and code-based methods are being researched, but the usage of hashing methods is already well and could provide the best alternative to the existing methods. Hashing methods, too, often bring other advantages, such as forward secure, which means that a key which is cracked will not reveal all the previous keys.
Merkle trees
The root of hash-based methods isin Merkle trees, and which are a way of hashing is used in many applications, including with Bitcoin, Ethereum, Git distribution systems, No SQL, and in many P2P applications. With a Merkle tree we take our data elements, and then hash them, and take pairs of these hashes to create a new hash, and so we build a table. At the top of the tree is the root element (in this case Hash1234):

In this way, we can use the tree to see if we have matching data on systems.On a P2P network, we can transfer a file by splitting it into data segments and then distributing these segments across the network. A trusted source will have the complete Merkle tree for rebuilding the file, and a client can thus rebuild from the Merkle tree and determine the parts of the file which are still missing. Once transferred the root hash (and all the other hashes) will then match. In its core method, the Merkle Signature Scheme (MSS) has serious performance and memory issues, but enhanced methods such as XMSS create with much less of a performance hit.
One-time signatures (Lamport)
The core method used in hash-based signatures is that of the one-time signature, and where we create a new key pair for every method we need to create. If the keys were reused, an attacker could start to learn the private key, and thus spoof messages. One of the first methods was produced by Leslie Lamport and Whitfield Diffie, in 1979, and is defined as:
- We create two data sets with 256 random 256-bit numbers (Set A and Set B). These are the private key (512 values).
- we take the hash of each of the random numbers. This will give 512 hashes and will be the public key.
- We then hash the message using and then test each bit of the hash (0 ... 255). If it is a 0, we use the ith number in Set A, else we use the ith number from Set B.
- The signature is then 256 random numbers (taken from either Set A or Set B) and the public key is the 512 hashes (of Set A and Set B).
The public and private keys are then each 16KB in size. A demo of the method is here.

Figure 1: Lamport method
The major problem with the method is that a key pair for every message. also in 1979, found a solution with Merkle trees.
One-time signature (W-OTS)
To improve performance method (and which reduced key sizes), Merkle proposed Winternitz OTS (named after Robert Winternitz). With this method was possible to sign many bits at the same time. The method is:
- We create 32 256-bit random numbers. These 32 values will be our private key.
- We then hash each of these values 256 times. These 32 values will be our public key.
- We now take the message and hash it using SHA-256. This produces 32 8-bit values (N1, N2 ... N32).
- Next we take each 8-bit value in the hash of the message, and then hash 256-N times (where N is the value of the 8-bit value).
- To prove the signature, we take the message and hash it with SHA-256, and then take each 8-bit value. We then hash the 8-bit signature value by the number of times defined by the message hash value (N1, N2..). The result for each operation should equal the public key value.
This is illustrated below in Figure 2. A demo of the method is here.

Figure 2: W-OTS
Hash-based Signatures
The methods such as W-OTS and Lamport only provide for a one-time signature. In order to sign many messages, we can use the Merkel signature scheme (MSS). With this we take a hash of the keys and build these as the leaves of the tree. The root of the tree is then the public key - the verification key. We then just use the private key of the W-OTS method to create the signature. The sender also sends the authentication path, which is the neighbouring nodes within the path and which leads to the root of the tree. The recipient can then rebuild the tree using the verification key (which can be received a digital certificate) and the authentication path. For the next message we move onto another key pair and where the index of the key part is revealed.
In the following example we have our root as the public key, and then want to sign with Key3. We then show the authentication path which takes us to the root (as defined in the bold arrows):

Conclusions
Hashed-based methods look to be a strong contender for weaning us off RSA, DSA and ECDSA, but we will have to look at the stateful generation of keys. For this we will have to generate a bank of key pairs (2, 4, 8, 16, etc) and then create the public key from the root of the Merkle tree. We must then remember the keys we have used previously, and only use an unused one. Once we use our new key pair, we then show our working-out as to how the private key is integrated into our tree. It is a bit like a teacher marking a question correctly, and asking for the working out that go you to the answer.
References
[1] Bernstein, D. J., Hopwood, D., Hülsing, A., Lange, T., Niederhagen, R., Papachristodoulou, L., ... & Wilcox-O’Hearn, Z. (2015, April). SPHINCS: practical stateless hash-based signatures. In Annual international conference on the theory and applications of cryptographic techniques (pp. 368-397). Springer, Berlin, Heidelberg [paper].
[2] Bernstein, D. J., Hülsing, A., Kölbl, S., Niederhagen, R., Rijneveld, J., & Schwabe, P. (2019, November). The SPHINCS+ signature framework. In Proceedings of the 2019 ACM SIGSAC conference on computer and communications security (pp. 2129-2146) [paper].
[3] Reyzin, L., & Reyzin, N. (2002, July). Better than BiBa: Short one-time signatures with fast signing and verifying. In Australasian Conference on Information Security and Privacy (pp. 144-153). Springer, Berlin, Heidelberg [paper].
[4] Merkle, R. C. (1989, August). A certified digital signature. In Conference on the Theory and Application of Cryptology (pp. 218-238). Springer, New York, NY.
[5] Hülsing, A. (2013, June). W-OTS+–shorter signatures for hash-based signature schemes. In International Conference on Cryptology in Africa (pp. 173-188). Springer, Berlin, Heidelberg.
[6] Kölbl, S., Lauridsen, M. M., Mendel, F., & Rechberger, C. (2016). Haraka v2–efficient short-input hashing for post-quantum applications. IACR Transactions on Symmetric Cryptology, 1-29. [here]
[7] Lamport, L. (1979). Constructing digital signatures from a one-way function (Vol. 238). Technical Report CSL-98, SRI International. [paper]
[8] Ducas, L., Durmus, A., Lepoint, T., & Lyubashevsky, V. (2013, August). Lattice signatures and bimodal Gaussians. In Annual Cryptology Conference (pp. 40-56). Springer, Berlin, Heidelberg [paper].
[9] Perrig, A. (2001, November). The BiBa one-time signature and broadcast authentication protocol. In Proceedings of the 8th ACM Conference on Computer and Communications Security (pp. 28-37) [paper] .
Hashing (Simularity)

Similarity hashes allow for two data objects to be compared for their similarity.
Similarity assessment methods
The following relate to the basic methods used for string similarity:
- String similarity String similarity. This measures edit distance (including Levenshtein distance), Jaro (including Jaro-Winkler), and QGrams.
- String enthropy String enthropy. Measurement of the entropy of strings.
- Soundex Soundex. Soundex uses a phonetic algorithm to classify a sound as it is pronounced. It focuses on matching phrases which have minor spelling errors.
Similarity hashes
The following are the tips related to similarity hashing:
- Similarity hash: SimHash (Charikar similarity) in Python Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash: SimHash (Charikar similarity) in Golang Charikar similarity. The Charikar similarity is used to find similarities between strings, files and metadata.
- Similarity hash (Nilsimsa similarity) Nilsimsa. The Nilsimsa similarity is used to find similarities between spam emails.
- Context Triggered Piecewise Hashes (CTPH): ssdeep CTPH similarity. Kornblum [6] created ssdeep and which computes fuzzy hashes. This aims to match similar byte sequences, no matter if there are differences between these sequences. For this we break a file up into fragments with a rolling hash function. We then produce a small hash for each of those fragments. These are then aggregated to produce the complete hash of a file. In comparing file signatures, we treat the resultant hash value as a string, and then uses an edit distance method to compare.
- TLSH (A Locality Sensitive Hash) TLSH similarity. In malware analysis and in text similarity, we often have to identify areas of data within files which are similar. One method is TLSH (A Locality Sensitive Hash), and which was defined by Oliver et al [7]. It is used - along with ssdeep - by VirusTotal to identify a hash value for malware.
- Minhash (Jaccard similarity) Jaccard similarity. The Minhash method is used to find similarities between strings, files and metadata.
- Counting identical elements (HyperLogLog) HyperLogLog. Counting the number of identical elements.
Hazmat cryptography

The Cryptography library in Python contains interfaces to common cryptographic algorithms, including symmetric key methods, hashing, public key, and key derivation functions. Many of these are contained with the Hazmat (Harzardous Material) primative setup.
Hashing, HMAC, CMAC, Poly1305 and HKDF
- Hazmat Hashes. Hazmat Hashes. This includes the hashing methods in the Hazmat cryptography library. This includes Blake2p, Blake2s, MD5, SHA1, SHA224, SHA256, SGA384, SHA3-224, SHA3-256, SHA3-384, SHA3-512, SHA512, SHA512-224, SHAKE128 and SHA256.
- Hazmat Hashes. Hazmat Hashes. In this case we will implement Python code to determine SHA1, SHA2, SHA3, Blake2, MD5 and SM3 hashes.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
- Hazmat HKDF. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
- Hazmat CMAC. Hazmat CMAC. CMAC methods using the Python cryptography primitives.
- Hazmat Poly1305. Hazmat Poly1305. Poly1305 methods using the Python cryptography primitives.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
Symmetric key
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat. Implementation of ChaCha20/Poly1305 with a random key using Hazmat.
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat. Implementation of AES GCM with a random key using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hazmat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Hazmat Symmetric Key Padding. Symmetric key. This includes the coverage of padding with Hazmat.
- Hazmat Symmetric Key Padding. Symmetric key. This includes the coverage of padding with Hazmat.
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
- Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat 3DES Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . With 3DES encryption, we use a 128-bit key and a 64-bit IV value. The two modes supported are ECB (without salt) and CBC (with salt). The DES algorithm has been around for a long time, and the 56-bit version is now easily crackable (in less than a day on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases, and splits the key into two. Overall the key size is typically 112 bits (with a combination of the three keys - of which two of the keys are the same). In this case we will use PKCS7 padding, and which fills the input data with a value that is equal to the number of padding bytes. Overall, DES has a 64-bit block size, and which equates to eight ASCII characters.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key . And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.
Asymmetric key
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- ECC key generaton with Hazmat. Elliptic Curve key gen. Creating ECC keys using Hazmat and Python.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- Hazmat RSA signing (with key values). RSA signing with Hazmat. RSA signing using Python and with Hazmat (with key values).
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used. .
- Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
- Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
- ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
- Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [ here]
- DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
- RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
- DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
- DSA Signatures. DSA Signatures. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. The ECDSA method is an extension of DSA, but implemented with elliptic curve (EC) methods. As with most public key signing methods, we take a hash of a message, and then apply a private key to create a signature (\(r,s\)). This is done by creating a random value (\(k\)) to produce the signature. The signature is then verified using the associated public key. This then verifies the creator of the signature and that the message has not been changed.
Digital Signature: ECDSA/EdDSA
- ECDSA with Hazmat. ECDSA wih Hazmat. This outlines ECDSA with Hazmat.
- Ed25519 for EdDSA signatures with Hazmat. EdDSA: Ed25519. This page uses the Hazmat primitives for the cryptography library.
- Ed448 for EdDSA signatures with Hazmat. EdDSA: Ed448. This page uses the Hazmat primitives for the cryptography library.
- Ed25519 using NaCl. Ed25519. This page uses the NaCl port from libsodium.
- ECDSA Signatures with Hazmat (SECP256R1, SECP384R1, SECP521R1, SECP224R1, SECP192R1, and SECP256K1). ECC Signatures. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and then creates an ECDSA signature for a given message.
Digital Signature: RSA
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
Key exchange: ECDH/X25519
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives and showing the byte values for the key.
Tokens
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
Homomorphic Encryption

Homomorphic encryption supports mathematical operations on encrypted values. Partial Homomorphic Encryption (PHE) supports a few arithmatic operations, while Full Homomorphic Encryption (FHE) supports add, subtract, multiply, and divide. Homomorphic encryption normally involves a public key to encrypt the data, and a private key to decrypt it. There have been four main generations of homomorphic encryption, and the most recent being the HEAAN method.
Simple
- Simple Homomorphic Cipher. Hom. This outlines a Simple Homomorphic cipher.
- Simple Homomorphic Cipher (Python). Hom. This outlines a Simple Homomorphic cipher with Python.
- Full Homomorphic Cipher with a Public Key. Public key. This outlines a Simple Homomorphic cipher using a public key
ElGamal
- ElGamal Homomorphic Cipher (Go). ElGamal. This outlines ElGamal Homomorphic cipher with Go.
- ElGamal Homomorphic Cipher (Go) - Divide. ElGamal. This outlines ElGamal Homomorphic cipher with Go with divide.
- ElGamal Homomorphic Cipher (Go) - Additive. ElGamal. This outlines ElGamal Homomorphic cipher with Go with addition.
- ElGamal Homomorphic Cipher for Multiplication (Python). ElGamal. This outlines ElGamal Homomorphic multiplication with Python.
- ElGamal Homomorphic Cipher for Division (Python). ElGamal. This outlines ElGamal Homomorphic division with Python.
- ElGamal Homomorphic Cipher for Addition (Python). ElGamal. This outlines ElGamal Homomorphic addition with Python.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (Python). ElGamal. This outlines ElGamal Homomorphic subtraction with Python.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
RSA
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
ZKP
- Full Homomorphic Cipher to determine if Bob is older. Older. This outlines a Simple Homomorphic cipher to determine if Bob is older than Alice.
- Full Homomorphic Cipher to determine matching password. Password. This outlines a Simple Homomorphic cipher to determine if a password matches
- Interactive ZKP With Probablistic Methods. ZKP. Interactive ZKP With Probablistic Methods using Python.
- Full Homomorphic Cipher for Millionaire's Problem. Millionaire. This outlines a Simple Homomorphic cipher for the Millionaire's Problem
Voting
- Trusted voting. Trusted. A trusted voting method.
Secret share
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Lattice
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
Full Homomorphic Cipher
- Full Homomorphic Cipher for 2-bit Adder. Adder. This outlines a Simple Homomorphic cipher for a 2-bit adder with DGHV.
- Full Homomorphic Cipher for Full Adder. Full Adder. This outlines a Simple Homomorphic cipher for a full adder with DGHV.
- Full Homomorphic Cipher for 4-bit Adder. Adder. This outlines a Simple Homomorphic cipher for a 4-bit adder with DGHV.
- Full Homomorphic Cipher for 4-bit Adder/Subtractor. Subtract. This outlines a Simple Homomorphic cipher for a 4-bit adder/subtractor with DGHV.
- Full Homomorphic Cipher to XOR two integers. X-OR. This outlines a Simple Homomorphic cipher to X-OR two integers
Paillier
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier) .
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Damgård-Jurik Homomorphic Encryption With Secret Shares. Damgård-Jurik Method. Two of the major areas of developments within cybersecurity will be the usage of homomorphic encryption, and in the usage of Shamir secret sharing. With homomorphic encryption, we can encrypt values, and then operate on them with arithmetic functions (such as add, subtract and multiply), and with Shamir secret sharing, we can split secrets into shares, and then distributed them over networks. These approaches will take privacy to new levels. So let’s look at the Damgård-Jurik method.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Learning with Errors (LWE)
- Learning With Errors . LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret key value (s) and another value (e). Next we select a number of values (t[]) and calculate g[] = t[] x s + e. The values of g[] and t[] become our public key.
- Public Key Encryption with Learning With Errors (LWE). LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret value (s) and which is our private key. We then create a public key which is based on random numbers (A), and then generate another set of numbers (B) which is based on A,s and random errors e. An example of encryption with multiple bits is given.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE)
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Others
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
- SIDH Go. SIDH. Post-quantum key exchange.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Anonymous crypto. Anon. Anonymous crypto.
- Rho factorization. Rho. Rho alogorithm.
- Post-quantum signing (BLISS). BLISS. BLISS method.
Homomorphic Encryption with Krytology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Homomorphic hashing
- Homomorphic Hashing with Golang. Homomorphic hashing. Normally with hashing methods, we need to take all the previous data and new data in order to create a new hash value for our data. In a homomorphic hashing method, we can basically take the previous hash, and then add on any new data values. We can also remove previous data values from our hash, too. This is more efficient in computing, as we do not have to process all of our data into a new hash, and can use simple homomorphic operations for the computation. The method we will use (LtHash) was initially defined by Bellare and Micciancio and updated Lewi et al at Facebook.
Identity Based Encryption (IBE)

This page outlines a few basic principles around the usage of IBE.
Identity Based Encryption (Pairing based)
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pair-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Identity Based Encryption (Others)
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Güther's implicitly certified identity-based public keys (IBE). Günther. This method allows Bob to generate Alices public key from her identity and publicly available parameters.
- Girault's self-certified public keys (IBE). Girault. This method allows Bob to generate Alices public key from her identity and publicly available parameters, and where we use an RSA key pair to self-certify Alice's public key.
Intrusion Detection Systems (IDS)
- Intrusion Detection Systems. Snort. This outlines some of the basics of IDS, including the requirement for Intrusion Detection Systems (IDSs), and where they are used.
- Advanced Network Forensics (Snort). Adv Network Forensics. This provides information on how to detect threats through network forensics with Snort
Snort

- Snort IDS. Snort. This is a Snort Analyser.
- Snort IDS 2 with rules editor. Snort. This provides information on how to detect threats through network forensics with Snort, and with an editing function for rules.
Presentation
IoT

The key objectives of this page are: Understand how a Pen Tester can generate vulnerabilities and test using the Metasploit framework; Define the options and payloads required to generate and use vulnerabilities; and Gaining remote access.
Devices
- Access the Wi-fi kettle. Go. This page outines how to access a wi-fi enabled kettle.
- Philips Hue Wireless Lighting. Go. This page shows how to use RESTful Web services to access to the Hue Led Lamps.
- Kali and R-PI. Go. This page shows the setup of a security testing infrastructure using a Raspberry Pi (R-PI) and a wifi access point.
- Kali, R-PI and RF electrical socket. Go. This page shows the control of an RF electical socket from a RPI.
- Capture from a Polar H10 heat rate sensor. Go. This page shows the capture of the Polar H10 heart sensor with an Ubertooth One.
- Trusted IoT: Linking IoT Devices to NFTs. Go. This page outlines a research paper which links a device to an NFT (Non-fungible Token).
Shodan Scanning
-
IoT Scan (Shodan). Go. This page includes a search of the Internet for key terms, such as for "apache", "mysql" and "cisco".
- IoT Banner Scan (Shodan). Go. This page includes a search of the Internet for key terms with the banner as a result (for the Top 10)
- Internet Services (Shodan). Go. This page includes a search of the Internet for key terms and display the IP address and port.
IoT Libraries
- libDisco with Go. libDisco. libdisco is a Golang library which can be used to create secure connections. It is based on the STROBE protocol framework. Symmetric cryptographic primitives rely on SHA-3 permutation, and asymmetric cryptographic primitives on X25519 and ed25519. STROBE defines a range of cryptographic protocols to integrate with IoT devices. In order to reduce processing, energy and memory requirements, it only uses Keccak (SHA-3) to encrypt and authenticate messages.
COSE/COBR
In computer security, we often have to represent binary data, in single values or groups of characters, bytes, words, long words, signed integers, floating-point values, double-precision floating-point values, and so on. This might be in the form of a data object, a signature or even encrypted content. For this, the ANS.1 DER format is often used, such as presenting digital certificates and signatures. An improvement on this for small messages with security is Concise Binary Object Representation (CBOR) — and which is defined in RFC8949 [1]. While JSON represents text-based data objects CBOR focuses on binary objects. It has been designed to create a lightweight encoder and decoder. This supports the use of CBOR within an IoT infrastructure. The data, also, does not require a data schema to be able to decode it, along with being extensible. CBOR defines the format of binary data with data objects and messages. We can then integrate security with CBOR Object Signing and Encryption (COSE), and which is defined in RFC8152 [2]. This includes signatures, message authentication codes (MACs), encryption and creating serialised objects.
- 128-bit AES GCM. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) can then build on this to include signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use a symmetric key to encrypt a message, and then decrypt it. In this case we will use AES GCM with a static 128-bit key ("0x000102030405060708090a0b0c0d0e0f").
- 256-bit AES GCM. Go. In this case we will use AES GCM using a random 256-bit key (32 bytes).
- EdDSA. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) [2] can then build on this to includes signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use EdDSA to create a signature for a message.
- ECDSA. Go. In this case we will use ECDSA to create a signature for a message.
- HMAC. Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT. Go. In this case we create a CWT token, and sign with an HMAC signature.
- ECDH. Go. In this case we create a symmetric key from ECDH. For this we will derive a shared key from the public key of Alice and Bob, and then define a single recipient which can derive the CEK (Content Encryption Key) using their private key. We will use the curves of P-256 (secp256r1), P-384 (secp384r1), P-521 (secp521r1) or SECP256K1 (as used with Bitcoin).
- RSA using COSE and CBOR. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\).
- RSA: dQ, dP and InvQ. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). The key pair also includes \(dQ\), \(dP\) and \(InvQ\), and these can be used with the Chinese remainder theory to optimize the decryption process.
Metasploit
- Armitage and Metasploit. Go.
- Exploiting Android with Metasploit. Go.
- Exploiting Android with Metasploit - Part 2. Go.
- Exploiting Windows/Mac OS X with Metasploit. Go.
- Remote Desktop Windows/Mac OS X with Metasploit. Go.
- Metasploit. Go.
- Internet of Things Security. Go.
- Metasploit (Enumeration and Scanning). Go.
- Metasploit (Malware). Go.
IP

 The following are a few interesting techniques around IP addresses:
The following are a few interesting techniques around IP addresses:
- Your details. IP. This shows your browser details.
- IP address analyser. IP. This involves converting an IP address to the host and network part of the address.
- IP subnet analyser. IP subnets. This involves converting an IP address to the host and network part of the address.
- IP address analyser. IP. This involves analysing IP addresses.
- Max subnets. Max subnets. This involves converting an IP address to the host and network part of the address.
- Route summarization. Summarization. This involves converting an IP address to the host and network part of the address.
- Whois. Whois. This does a basic Whois on a domain.
- URL Obfuscation. Obfuscation. This outlines URL obfuscation.
- HTTP Responses. Test. HTTP.
- Capturing Network Packets (Python). WinPCap. HTTP.
Cisco related
- Routing table. Routing table. This involves viewing a routing table for a Cisco device.
- ACL Generator. ACL. This involves a simple calculator for ACLs on network ranges.
- EIGRP metrics. EIGRP. Learn the basics of EIGRP metrics.
- VoIP B/W. VoIP. Calculate bandwidth for VoIP.
- Wild Card. Wild Card. On a Cisco device a wildcard mask is used to identify the parts of an IP address that need to be matched. It thus uses a wildcard mask, where a 0 in the bit position identifies that the device should match that bit, else a 1 shows that it should ignore it.
Protocols
- HTTP. HTTP. Show the request and response for HTTP.
- Ping analyser. IP. This involves converting a ping of a site.
IP Challenges
-
IP Test 1. IP Test. IP Classification test. This is a simple test which generates a range of IP addresses, and you must determine the IP address classification.
IP Subnet Challenge 1 Demo
-
IP Test 2. IP Test. IP Classification test Part 2. This test provides an address classification, and the user must find the addresses which are of this classification.
IP Subnet Challenge 2 Demo
-
IP Test 3. IP Test. IP Classification test Part 3. This test provides an address classification, where the network part of the address is determined.
IP Subnet Challenge 3 Demo
Subnet Challenges
- Subnet Test 1. Subnet Test. Subnet Test.
-
Subnet Test 2. Subnet Test. Subnet bits.
- Subnet Test 3. Subnet Test. Find the nth usable subnet. This test involves finding the nth usable subnet.
- Subnet Test 4. Subnet Test. Maximum subnets. This is a test page to determine the maximum number of subnets and hosts/subnet for IP classed addressing.
- Subnet Test 5. Subnet Test. Maximum host/subnet. This is a test page to determine the maximum number of hosts per subnet.
- Subnet Test 6. Subnet Test. Determine the required subnet mask for a given number of subnets. This is a test page to determine the required subnet mask for a given number of subnets and a given IP address classification.
- Subnet Test 7. Subnet Test. Determine the required subnet mask for a given number of host/subnet. This is a test page to determine the required subnet mask for a given number of hosts per subnet and a given IP address classification.
- Subnet Test 8. Subnet Test. Route summarization. This involves a calculation on route summarization.
- Subnet Test 9. Subnet Test. Binary to IP.
- Subnet Test 10. Subnet Test. Hex to IP.
-
Subnet Test 13. Subnet Test. Wild card mask network bits. Find the number of bits in the network part of the wild card mask. IP Wildcard challenge
- Subnet Test 14. Subnet Test. Wild card mask host bits. Find the number of bits in the host part of the wild card mask. IP Wildcard challenge
- Subnet Test 15. Subnet Test. Wild card mask ... find the network address. Find the network for the wild card mask. IP Wildcard challenge 2
- Subnet Test 16. Subnet Test. Find a matching IP address for a network and wild card mask. Find the IP for a network and a wild card mask.
- Subnet Test 17. Subnet Test. Find an address which is on a given network. Find an IP address on a network, for a given network address and subnet mask.
- Subnet Test 18. Subnet Test. Find an IP address on the same network. Find an IP address on the same subnet.
- Subnet Test 19. Subnet Test. Find subnet. Convert subnet mask.
- Megatest. Subnet Test. Challenging test for subnets.
JavaScript

JavaScript code allows execution within the browser, rather than on the server. It is often faster than code that runs on a server. Along with this we can also use Node.js, and which runs JavaScript code on a server.
Symmetric key
- AES. AES. In this example, we will use either a pre-generated key or a random one, and use AES (Rijndael) encryption.
- ChaCha20 and Poly1305. ChaCha. This page outlines Poly1305 and ChaCha20. ChaCha20 is a symmetric key method and Poly1305 is a message authentication code (MAC). They were created by Daniel J. Bernstein, and are alternatives to AES and HMAC.
- CMS (Padding). CMS. This page uses PKIJS encrypting on CMS. With CMS we can This document describes the Cryptographic Message Syntax (CMS). With this we can encapsulate an message within an encrypted entity.

Hashing
- Hash. Hash. This page defines a JavaScript Hash calculator. This uses a client-side JavaScript code to determine the hash signatures of a text value.
Signatures
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
- Boneh–Lynn–Shacham (BLS) signature. BLS. Boneh–Lynn–Shacham (BLS) signature method produces short signatures. They use elliptic curve pairing (and which are also known as bilinear maps).
Key exchange
- ECDH. ECDH. Elliptic Curve Diffie Hellman (ECDH) is used to generate a shared key. This implementation uses Elliptic Curve Cryptography (ECC) with JavaScript.
CryptoJS
- CryptoJS. CryptoJS. This page uses client-side JavaScript code to hashing, encrypt and sign, including for symmetric key (AES), streaming ciphers, hashing methods, and HMAC.
Blockchain
- PATRICIA trie. PATRICIA. In the following, we have the Top 2,500 Web sites in the world, and implemented with a Radix Trie (aka PATRICIA trie) In the following we have the Top 2,000 web sites on the Internet, and which have been indexed using the PATRICIA trie.
Public key
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
- RSA. RSA. RSA is an asymmetric encryption algorithm, which uses two keys, one to encrypt and the other to decrypt. It was created in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman, and is still one of the most widely used encryption methods. A typical application is in authenticating a sender, where the senders private key is used to encrypt a message, and then is decrypted by the receiver with the senders public key (which is known to anyone who wants it). It is also typically used for encrypting disks/files, such as for EFS.
Digital Certificates
- X.509 certificates in JavaScript. RSA and ECDSA Signed certificates. This page will generate either RSA and ECC key pairs, and then generate X.509 certificates, using either a signature of SHA1withRSA or SHA256withECDSA. For RSA signing we use an RSA private key to sign the certificate, and with ECDSA signing we use an ECC private key to sign the certificate.
Tokens
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
Random
- Random number generator. Rand. In the past, encryption and decryption had to be done through native code libraries, such as with Bouncy Castle and OpenSSL. With the increasing processing power of Web browsers, it is now possible to use encryption using JavaScript, which thus provides client-side processing of data. This Web page uses Javascript encryption, and generates a random 256-bit text key or a hex version. The 256-bit key is generated by generating 60 random numbers (from 0-25), and converting these to an ASCII character.
Malware obfuscation
- Malware obfuscation. Obfuscation. A malware writer will often hide certain keywords from the browser/human by encoding them in another format. This is typically done for hex coding (\xZZ), 16-bit unicoding (\uZZZZ) and octal coding (\ZZZ). To test, enter a value, and then press the button and it will convert encoded string.
Message Authentication Codes
- Chaskey (MAC). Chaskey. Chaskey Cipher is light-weight cryptography method for signing messages (MAC) using a 128-bit key. The hardware implementation only requires 3,334.33 gate equivalent with an operating clock frequency of 1 MHz (whereas Keccak requires 4,658 GE). In the page we create the Mac signature and also encrypt for CBC.
Other
- Password generation/hashing. Hashing. Linux can use salted passwords where the username, hashing method and hashed password are stored in a password file [More details]. The main methods are
Hashing

At times we need to generate secrets, such as encryption keys, from passwords or nonce values. A Key Derivation Function (KDF) is a verifiable way of doing this.
Key Derivation Functions (KDFs)
The following are the tips related to hashing:
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Password strength. Test. This outlines the strength of various passwords types.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
HKDF
The following are the tips related to Key derivation hashing:
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Hazmat HKDF for different hashing methods. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
-
HKDF key derivation with OpenSSL [
here]
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
PBKDF2
The following are the tips related to Key derivation hashing:
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- AES GCM (Python) with PBKDF2. AES GCM (Python) with PBKDF2.
- Fernet with PBKDF2 . AES GCM (Python) with PBKDF2.
- PBKDF2 key derivation. AES GCM (Python) with PBKDF2.
- Key Rotation with Fernet. AES GCM (Python) with PBKDF2.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Bcrypt
The following are the tips related to Key derivation hashing:
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- BCrypt. BCrypt. BCrypt with Rust.
-
Hash to password with Go. Hashing to Argon2, Scrypt and BCrypt. Hash to password with Go, including Argon2, Scrypt and BCrypt.
scrypt
- scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Argon 2
The following are the tips related to Key derivation hashing:
- Argon 2. Go. Outline of Argon2.
- Argon 2 with NaCl. Go. Outline of Argon2 using NaCl.
- Argon 2. Argon 2. Argon 2 with Rust.
- Balloon. Go. Outline of Balloon.
Other
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
- Double ratchet. Go. Outline of double ratcheting.
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
Outline
HMAC Key Derivation function (HKDF) is used to derive an encryption key from a passphrase. Initially, HKDF creates a pseudorandom key (PRK) using a passphrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), and along with a salt value. Next, the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys [RFC 5869][article]. In this case, we will use SHA-256.
The following shows how an encryption key can be generated using HKDF, and where we need a secret and a salt value. Both Bob and Alice have the same secret and salt.

With PBKDF2 (Password Based Key Derivation Function 2), we hash for a given number of rounds:

Key exchange

Key exchange is a way for Bob and Alice to communicate and for them to agree on a shared secret. The original method defined uses discrete logarithms (Diffie-Hellman), but most modern methods use elliptic curve techniques (ECDH). As quantum computers can crack both discrete log and elliptic curve methods, there are post quantum cryptography methods proposed. This includes SIDH, CSIDH, SIKE, and NewHope.
Key interchange/generation (Diffie-Hellman)
The following relates to key interchange:
- Selecting \(g\) in Diffie Hellman. G in Diffie Hellman. Picking a safe value of the generator \(g\) in discrete logarithms.
- Diffie-Hellman. Diffie-Hellman Calculation. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Real example). Diffie-Hellman Real. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Python). Diffie-Hellman. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (pre-compute). Diffie-Hellman (pre-compute). Many sites use the same prime numbers, which can then be cracked with a pre-computing attack.
- Key generation. Key gen. This will generate keys for different methods based on a passphrase.
- Diffie-Hellman (Man-in-the-middle). DF. This outlines the man-in-the-middle method for Diffie-Hellman.
- An Alternative Diffie-Hellman method. Alterative DH. This outlines an alternative Diffie-Hellman method.
Authenticated Key Exchange
The following are the tips related to Key derivation hashing:
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- MTI/A0. MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{ax+by} \pmod p\). MTI (Matsumoto, Takashima, Imai).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0. MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{x+y} \pmod p\)
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). The resultant key is \(xyG \)
- MTI/C0. MTI/C0. This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{xy} \pmod p\)
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG\).
- MTI/C1. MTI/C1. This outlines MTI/C1, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{abxy} \pmod p\).
- MQV (Menezes–Qu–Vanstone). MQV. MQV was created Alfred Menezes, Minghua Qu and Scott Vanstone in 1995 and is an authenticated key exchange method. Alice holds a key pair \((A,a)\) and Bob has a key pair \((B,b)\). With this \(a\) is Alice's private key, and \(A=aG\) is her public key. For Bob, his public key will be \(B=aG\) and a private key of \(b\), and where \(G\) is the base point on the elliptic curve.
- HMQV (Menezes–Qu–Vanstone). HMQV. HMQV builds on MQV and adds the identity of Bob and Alice.
- ECDH with X25519 and Blake2b. ECDH with X25519 and Blake2b. This uses PyNaCl to create an authenticated key exchange and uses X25519 and Blake2b.
Elliptic Curve (ECDH) - Python
The following are the tips related to ECC:
- Elliptic Curve. Elliptic Curve. Elliptic Curve is a public key method which can also be used to generate a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with simple parameters. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
Elliptic Curve (ECDH) - Golang and Node.js
The following are the tips related to ECC:
- ECDH with Go. ECDH. ECDH with Go.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with node.js. ECDH. ECDH with node.js.
- ECDH with JavaScript. ECDH. Elliptic Curve Diffie Hellman.
Password Authenticated Key Exchange (PAKE)
The following are the tips related to Key derivation hashing:
- SPAKE2. Go. Outline of SPAKE2.
- OPAQUE. Go. Outline of OPAQUE.
- SPEKE. Go. Outline of SPEKE (Simple Password Exponential Key Exchange).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
- J-PAKE. J-PAKE. This example generates a shared key based on a shared password.
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses discrete logs.
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
PQC NIST Finalists (Key Exchange)
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Key interchange/generation (Other)

The following relates to key interchange:
- Curve25519. Curve25519. This outlines Curve25519, which is used in the Tor network.
- Authenticated Key Exchange (Discrete logs). YAK. Key exchange with public keys and uses discrete logs.
- Authenticated Key Exchange (ECC). YAK. Key exchange with public keys and uses elliptic curve methods.
- Shamir No-key protocol. Shamir No Key. In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated.
- Shamir No-key protocol (sepc256k1). Shamir No Key (EC). In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated using the sepc256k1 elliptic curve.
- Conference keying (Burmester-Desmedt method). Conference keying. In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it.
- Conference keying (Burmester-Desmedt method) - Elliptic Curve (sepc256k1). Conference keying Elliptic Curve (sepc256k1). In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it, and uses the sepc256k1 elliptic curve.
Key exchange (with pairing)
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Kryptology

We need to build a new Internet. One that is build on mathematics and certainty, rather than the patchy version we have now. For this we need a layer of cryptography at the lowest level, and build software interfaces on top of this. Along with this we now have cryptographic methods which can now provide a foundation of trust, and which preserve privacy. And so the old libraries of OpenSSL are being squeezed out in favour of the new ones which are built on a solid foundation. The latest of these new "privacy-aware" libraries is Kryptology, and created by Coinbase. This library provides the APIs that developers need, in order to apply to areas of blockchain development. This library include BLS (Boneh-Lynn-Shacham) signatures, Zero-knowledge Proofs (ZKPs) and Shamir Secret Shares (SSS). With BLS we can digitally sign for data, but also preserve its privacy. Applications of this include group signatures, where multiple entities can merge their signing keys together and provide a single signature for a transaction. With SSS, we can split encryption keys up into shares, and then distribute them across a network. When required, we can call these shares back to reconstruct the key.
The focus for Coinbase seems to be the application of privacy coins, and where no tracking can be applied to the usage of these digital coins. This should support full anonymity for transactions, as opposed to Bitcoin which only supports pseudo-anonymity.

ECC Basics
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining n.G for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Points (Base Point and Others). Elliptic Curve points. Two common curves used in ECC (Elliptic Curve Cryptography) are secp256k1 (as used in Bitcoin and Ethereum) and P256 (secp256r1). The "k1" refers to the Kolbitz curve 1 (named after the creator of ECC). With these we have a base point which are can operate on. This is typically defined as \(G\). We can then operate on this with add and multiply operation. For example, \(2G=G+G\) and \(P=n.G\). In this following we will show the base point for a number of common curves, such as secp256r1, P256, Pallas, Curve 25519, BLS12381G1, BLS12381G2, BLS12377G1 and BLS12377G2.
ECDH
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret. We will use Golang and the Krytology library.
Simple ECC on curves
- Public key points for curves. Simple. Display public key points for scalars.
BLS Curve
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
Accumulator and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
Pallas Curve
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
Pairing-based Crypto
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
ElGamal and ECC
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a numerical input.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
Shamir Secret Shares
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Homomorphic Encryption
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Zero knowledge proofs
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
Verifiable Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Hash to scalar and point
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
CP-ABE
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Lattice cryptography

Latice cryptography is proposed as a post-quantum robust method for public key encryption, especially focused on digital signatures and key exchange mechanisms (KEMs).
Principles
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
NTRU
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- Lattice Encryption: NTRU Key Generation Python). NTRU. Outlines how NTRU operates for key generation.
Homomorphic
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Digital Signatures
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
Public-Key Encryption/Key Exchange
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
Light-weight cryptography

While AES and SHA work well together within computer systems, they struggle in an IoT/embedded world as they take up: too much processing power; too much physical space; and consume too much battery power. So NIST outlines a number of methods which can be used for light-weight cryptography, and which could be useful in IoT and RFID devices [1]. They define the device spectrum as:
- Conventional cryptography. Servers and Desktops. Tablets and smart phones.
- Light-weight cryptography. Embedded Systems. RFID and Sensor Networks.
With embedded systems, we commonly see 8-bit, 16-bit and 32-bit microcontrollers, and which would struggle to cope with real-time demands for conventional cryptography methods. And in the 40+ years since the first 4-bit processor, there is even a strong market for 4-bit processors. RFID and sensor network devices, especially, have limited numbers of gates available for security, and are often highly constrained with the power drain on the device.
So AES is typically a non-starter for many embedded devices. In light-weight cryptography, we often see smaller block size (typically 64 bits or 80 bits), smaller keys (often less than 90 bits) and less complex rounds (and where the S-boxes often just have 4-bits).
For light-weight cryptography the main constraints that we have are typically related to ener requirements, gate equivalents (GEs), and timing. With passive RFID devices, we do not have an associated battery for the power supply, and where the chip must power itself from energy coupled from the radio wave. An RFID device is thus likely to be severely constrained in the power drain associated with any cryptography functions, along with being constrained for the timing requirements and for the number of gates used. Even if an RFID device has an associated battery (active RFID), it may be difficult to recharge the battery, so the drain on power must often be minimised.
There is thus often a compromise between the cryptography method used and the overall security of the method. Thus often light-weight cryptography methods balance performance (throughput) against power drain and GE, and do not perform as well as main-stream cryptography standards (such as AES and SHA-256). Along with this the method must also have a low requirement for RAM (where the method requires the usage of running memory to perform its operation) and ROM (where the method is stored on the device). In order to assess the strengths of various methods we often define the area that the cryptography function will use on the device – and which is defined in \(µm^2\). The NIST finalists are defined in this [article]
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- GIFT AEAD. GIFT. GIFT is a light-weight block cipher. It is a (NIST Finalist)
- Elephant. Elephant. Elephant is a light-weight stream cipher. It is a (NIST Finalist).
- TinyJambu. TinyJambu. TinyJambu is a light-weight block cipher. It is a (NIST Finalist)
- Isap AEAD. Isap. Isap is a light-weight block cipher. It is a (NIST Finalist)
- PHOTON-Beetle AEAD. PHOTON-Beetle. PHOTON-Beetle is a light-weight block cipher. It is a (NIST Finalist)
- Romulus AEAD. Romulus. Romulus is a light-weight block cipher. It is a (NIST Finalist)
- Sparkle AEAD. Sparkle. Sparkle is a light-weight block cipher. It is a (NIST Finalist)
- CLEFIA. CLEFIA. CLEFIA is a light-weight block cipher.
- LED. LED. LED is a light-weight block cipher.
- Piccolo. Piccolo. Piccolo is an ultra light-weight block cipher.
- PRESENT. PRESENT. Present is a light-weight block cipher.
- Pyjamask. Pyjamask. Pyjamask is a light-weight block cipher.
- SIMON. SIMON. SIMON is a light-weight block cipher.
- SKINNY. SKINNY. SKINNEY is a light-weight block cipher.
- SPECK. SPECK. SPECK is a light-weight block cipher.
- XTEA. XTEA. XTEA is a light-weight block cipher.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encryption/Decryption. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.
Light-weight crypto (Other)
- Chaskey (MAC). Chaskey. Chaskey is a light-weight MAC function.
- Chaskey (MAC). Chaskey (Python). Chaskey is a light-weight MAC function.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (ASCON)
ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRFF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
Discrete Logs (Solving)

A discrete log problem is in the form of \(g^x \pmod p\) and where we know \(g\) and \(p\) and must solve for \(x\).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Message Authentication Code (MAC)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
HMAC
The following are the tips related to Key-based hashing:
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authentication both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2), Blake2b, SM3 and SHA-3. This page outlines the HMAC-MD5 methods using the Hazmat cryptography layer.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- HMAC (COSE). Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT with HMMAC. Go. In this case we create a CWT token, and sign with an HMAC signature.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- HMAC with Rust. HMAC. HMAC with Rust.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HMAC with OpenSSL. MACs with OpenSSL. HMAC in OpenSSL for a given input value, password and hashing method.
Cipher MACs
The following are the tips related to Key-based hashing:
- MACs with OpenSSL. MACs with OpenSSL. MAC methods implemented in OpenSSL, including CMAC and GMAC.
Key-based hashing
The following are the tips related to Key-based hashing:
- SipHash. Siphash. Siphash is a fast key-based hashing method.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Meow. Meow. Meow is one of the fastest hashing methods.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
Magic Numbers

This pages contains information related to magic numbers in file formats.
Network and File Forensics
- Magic numbers. Magic. This provides information on magic number for file forensics.
Graphics formats
- JPEG Analysis. JPEGs. This provides an analysis of JPEG files.
- GIF Analysis. GIFs. This provides an analysis of GIF files.
- TIF Analysis. TIFs. This provides an analysis of TIF files.
- PNG Analysis. PNGs. This provides an analysis of PNG files.
- BMP Analysis. BMPs. This provides an analysis of BMP files.
- PSD Analysis. PSDs. This provides an analysis of PSD files.
- WMF Analysis. WMF. This provides an analysis of WMF files.
- Adobe Illustrator Analysis. AI. This provides an analysis of AI files.
- Adobe In Design Analysis. INDD. This provides an analysis of INDD files.
- MIDI file. MIDI. This provides an analysis of MID files.
- ICO file. ICO. This provides an analysis of ICO files.
- PS file. PS. This provides an analysis of PS files.
- EPS file. EPS. This provides an analysis of EPS files.
- VSD file. VSD. This provides an analysis of Microsft Visio (VSD) files.
Video and audio formats
- MP3 Analysis. MP3s. This provides an analysis of MP3 files.
- AVI Analysis. AVIs. This provides an analysis of AVI files.
- Flash SWF Analysis. SWFs. This provides an analysis of Flash files.
- Flash FLV Analysis. FLVs. This provides an analysis of FLV files.
- MP4 Analysis. MP4. This provides an analysis of MP4 files.
- MOV Analysis. MOV. This provides an analysis of MOV files.
- WMV Analysis. WMV. This provides an analysis of WMV files.
- WMA Analysis. WMA. This provides an analysis of WMA files.
- JPEG 2000 Analysis. JPEG 2. This provides an analysis of JPEG 2000 files.
- WAV Analysis. WAV. This provides an analysis of WAV files.
Zips, Archives and Library files
- ZIP/Archive Analysis. ZIPs. This provides an analysis of ZIP/Achive files.
- GZ Analysis. GZ. This provides an analysis of GZip files.
- Tar Analysis. Tar. This provides an analysis of TAR files.
- MSI Analysis. MSI. This provides an analysis of MSI files.
- OBJ Analysis. OBJ. This provides an analysis of OBJ files.
- DLL Analysis. DLL. This provides an analysis of DLL files.
- CAB Analysis. CAB. This provides an analysis of CAB files.
- EXE Analysis. EXE. This provides an analysis of EXE files.
- RAR Analysis. RAR. This provides an analysis of RAR files.
- SYS Analysis. SYS. This provides an analysis of SYS files.
- HLP Analysis. HLP. This provides an analysis of HLP files.
- VMDK Analysis. VMDK. This provides an analysis of VMDK files (VMWare Virtual Disks).
- PST Analysis. PST. This provides an analysis of PST files (Outlook Email File).
- JAR Analysis. JAR. This provides an analysis of JAR files.
- SLN Analysis. SLN. This provides an analysis of Microsoft SLN files.
- Class Analysis. Class. This provides an analysis of Java Class files.
- Zlib. Zlib. This provides an analysis of Zlib files.
Documents
- PDF Analysis. PDFs. This provides an analysis of PDF files.
- DOC Analysis. DOCs. This provides an analysis of DOC files.
- RTF Analysis. RTFs. This provides an analysis of RTF files.
- XLS Analysis. XLSs. This provides an analysis of XLS files.
- PPT Analysis. PPTs. This provides an analysis of PPT files.
- MMP File. MMP. This provides an analysis of MMP files.
- DOCX Analysis. DOCX. This provides an analysis of DOCX files.
- XLSX Analysis. XLSX. This provides an analysis of XLSX files.
- PPTX Analysis. PPTX. This provides an analysis of PPTX files.
- MDB Analysis. MDB. This provides an analysis of MDB files.
- Outlook Message Analysis. MSG. This provides an analysis of MSG files.
Disk Image
- Raw disk format. RAW. This provides an analysis of the RAW disk format.
Tests
- File Forensics Test. File Test File Forensics Test.
- File Forensics Test (Fun). File Test (Fun) File Forensics Test.
Presentations
MIRACL Core Library

MIRACL Core is an open source library, and includes a wide range of public key encryption methods. It is especially focused on elliptic curve and pairing-friendly methods, but also supports a wide range of encryption methods, including RSA, AES and hashing. Overall, it can be ported onto a wide range of systems and supports C, C++, Go, Rust, Python, Java, Javascript and Swift. Along with this it supports limited capability devices such as the Arduino infrastructure. The GitHub repository is [here].
BN254
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.

Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- CL Signatures. CL. CL Signatures in Go using MIRACL.
- CL Signatures (advanced pairing). CL. CL Signatures in Go using MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages using MIRACL.
- PS Signatures. PS. Signatures using PS for short signatures using MIRACL.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures using MIRACL.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.

Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
Rust examples
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
NaCl

PyNaCl is a Python port of LibSodium. It integrates the latest cryptography methods, such as AES, XChaCha20, Blake2b and X25519.
Symmetric Key
- Symmetric key. Symmetric key (XChaCha20 and Poly1305). With symmetric key, Bob and Alice have the same key. NaCl uses the XChaCha20 method, and which supports stream encryption (and which does not require padding as a block cipher does, and is also faster than block cipher modes). ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16 byte nonce. XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24 byte nonce. It has a lower propability of nonce misuse than ChaCha20.
- Encryption with a password. Symmetric Key with KDF. In symmetric key, we generate a secret key. This key is typically a random value or generated from a password and a salt value. If we use a password, we typically use a KDF (Key Derivation Function), and which uses a password and a salt value, in order to create a key of a given size. In this case we will use Argon2i, and which is memory resilent.
Hybrid Encryption
- Box. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Hashing
- Hashing and KDF (Argon2 and scrypt). Hashing and KDF. This case we will use PyNaCl (Networking and Cryptography) library, and which is a Python binding to libsodium. We will hash a password using SHA-256 and SHA-512, and also create a KDF (Key Derivation Function) using scrypt and Argon2.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
Ed25519
-
Ed25519. Ed25519. Using Ed25519 for digital signatures.
-
Finding Points on Ed25519. X25519 (Points).
In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 (Key Exchange)
- X25519 + BLAKE2b key-exchange. X25519. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
Curve 25519
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
Node.js

Node.js uses the JavaScript programming langauge as its base, and allows for code to be run on a server, rather than in the browser (such as with pure JavaScript). To run a node.js program, we run "node myfile.js", and use NPM to install libraries.
Symmetric key
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
RSA and public key
- RSA Opt imal Asymmetric Encryption Padding (OAEP) using Node.js. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
ECC Keys
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.

Hashing
- Hashing with node.js (All). Hashing. Hashing with node.js.
- Hashing with node.js (Selection). Hashing. Hashing with node.js.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- ECDSA with node.js. ECDSA. ECDSA with node.js.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
Key exchange
- Diffie-Hellman with node.js (random prime). DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method and uses a randomly generated prime number (press the button to generate a new prime).
- Diffie-Hellman with node.js. DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method. Each time the prime number will be fixed for the DH group selected.
- ECDH with node.js. ECDH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Elliptic Curve Diffie Hellman (ECDH) key exchange method.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
Key derivation
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
CryptoJS
- CryptoJS (in node.js). CryptoJS (Node.js). Various crypto methods in the browser.
Bulletproofs
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
Blockchain
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
Proxy encryption
- Proxy Encryption - Encrypting With Public Key, And Decrypt with Private Key. Proxy01. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This page just creates a key pair for Alice, and uses it to encrypt with the public key , and decrypt with the private key.
- Proxy Encryption. Proxy02. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This will go through the full use case of proxy re-encryption.
Tokens
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
Random
- Fortuna with node.js. Fortuna. Fortuna random numbers with node.js.
Other
- FPE with node.js. FPR. FPE with node.js.
- Puny with node.js. Puny. Puny character format with node.js.
Accumulators and Witnesses
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
PGP
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Password Entropy
- Password Entropy with Node.js. Password Entropy. Password entropy measures the strength of a password, and is measured as the number of bits which could represent all of the possibilities. An entropy score of less than 25 identifies a poor password, and between 25 and 50 is a weak password. For 50 to 75 we have a reasonable password, and between 75 and 100 is a very good password. Over 100 is an excellent password. The strength of the password relates to the number of characters used, and also the number of characters in the password.
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
- Homomorphic Encryption with Node.js and BGV. Homomorphic Encryption with Node.js and BFG. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BGV method.
Oblivious Transfer (OT)

Oblivious Transfer allows Bob to select data from Alice, but for Alice not to know which value has been selected.
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
OpenSSH

OpenSSH supports the usage of the SSH protocol. This allows for a remote login. One tool which is uses is ssh-keygen, and which allow for the generation of RSA, DSA and elliptic-curve keys that. These can be used for user and host authentication, such as for GitHub login and Cloud instance login.
OpenSSH
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here].
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
Outline

OpenSSL

OpenSSL is a standard library that implements cryptography.
Symmetric key (Command line)
-
Symmetric Key Encryption (OpenSSL 1.x) [here]. In this case we will create cipher text from OpenSSL 1.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 1.x) [here].In this case we will decrypt cipher text from OpenSSL 1.x using a key derived from a password
-
Symmetric Key Encryption (OpenSSL 3.x) [here]. In this case we will create cipher text from OpenSSL 3.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 3.x) [here].In this case we will decrypt cipher text from OpenSSL 3.x using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password.
Hashing
-
Hashing [here] OpenSSL supports a wide range of hashing methods including BLAKE2b, Gost, MD4, MD5, RMD-160, SHA-1, SHA-3, SHA-256 and SHA-512.
Libre OpenSSL
-
Symmetric Key Encryption using Libre OpenSSL [here]. In this case we will create cipher text from Libre OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption using Libre OpenSSL [here]. In this case we will decrypt ciphertext from Libre OpenSSL using a key derived from a password.
-
Hashing [here] Libre OpenSSL supports a wide range of hashing methods including Gost, MD4, MD5, RMD-160, SHA-1, SHA-256 and SHA-512.
Diffie-Hellman parameter generation
-
DH Parameters with OpenSSL [here]. The Diffie-Hellman (DH) method is perhaps one of the greatest inventions in Cybersecurity, and was created by Whitfield Diffie and Marty Hellman. With the DH method, Bob creates a random value (\(b\)) and Alice also creates a random value (\(a\)). Next Bob computes \(B=g^b \pmod p\) and sends it to Alice. Alice computes \(A=g^a \pmod p\) and sends this to Bob. Bob raises the value of \(A\) to the power of \(b\) and takes \(\pmod p\), and Alice raises \(B\) to the power of \(a\) and takes \(\pmod p\). In the end, they will have the same shared value: \(g^{ab} \pmod p\). This can then be used to derive an encryption key that they can use for a secure tunnel. Overall, \(p\) is the large prime number, and also known as the shared modulus between Bob and Alice.
Key derivation function
-
PBKDF2 key derivation with OpenSSL [here] PBKDF2 (Password Key Derivation Function 2) is a key derivation method. Overall it is relatively slow in its operation and where we take a password, a salt value, hashing method, and a number of iterations, in order to produce a given size of encryption key.
-
HKDF key derivation with OpenSSL [here] HKDF (HMAC Key Derivation function) is used to derive an encryption key from a pass phrase. Initially HKDF creates a pseudorandom key (PRK) using a pass phrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), andalong with a salt value. Next the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys.
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Passwords
-
Password example [here]. This page uses the OpenSSL library hash password generator, which is used in UNIX systems for the hashing of passwords which are contained in /etc/shadow and /etc/passwd. For newer passwords, the "-1" options is used to created the hashed value.
-
Hashed passwords with OpenSSL [here].
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
Public key
-
Generating an ECC key pair with OpenSSL [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)).
-
Generating an RSA key pair with OpenSSL [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2).
-
Generating an RSA key pair with OpenSSL with encryption [here]. This page implements RSA key pair generation with an encrypted key pair. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). In this case we will encrypt the key pair with either 3DES, 128-bit AES, 192-bit AES or 256-bit AES. The same password must be used to encrypt and decrypt.
-
Generate prime with OpenSSL [here]. Prime numbers are important in public key encrytion, and are used with RSA and ECC. For RSA, we generate two prime numbers (\(p\) and \(q\)) and which are multiplied together to create a modulus (\(N\)). If these prime numbers have 512 bit values, the modulus will be a 1,024 bit value. This defines the basic secure of RSA. With elliptic curve we use smaller prime numbers, such as 256-bit values for the secp256k1 curve.
ASN1 parsing
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). We will parse using asn1parse, and reveal the parameters.
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)) [RSA key pair]. We will parse using asn1parse, and reveal the parameters.
- DSA Parameters with asn1parse. DSA parameters with OpenSSL with asn1parse. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA (Digital Signature Algorithm)
- DSA Parameters. DSA parameters with OpenSSL. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
MAC (Message Authentication Code)
- HMAC with OpenSSL. MACs with OpenSSL. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authenticate both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2) and SHA-3. In this case we will use OpenSSL to generate the HMAC value.
- MACs with OpenSSL. MACs with OpenSSL. In the following we will generate MACs for HMAC, GMAC, CMAC, Blake2bmac, Blake2smac, KMAC128 and KMAC256. Overall, we will use an encryption key defined as a hex value for GMAC and CMAC, and a pass phrase for the others. The message is "hello".
Signing
- Digital signing a plaintext message with OpenSSL. Signing with OpenSSL. With digital signing, we can take a message, and create a signature. This normally involves signing with a private key and digital certificate. The signed message can be an a MIME format, and which can be integrated into an email message. In this can we have a 512-bit RSA key pair that will sign a plain text message.
Encrypting emails
- Encrypting an email message in OpenSSL. Encrypting messages with OpenSSL. With public key encryption, we can take a message, and encrypt it with the recipiant's public key. In this can we have a 512-bit RSA public key to encrypt a message.
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Random number generation with OpenSSL
-
Random number generator [here]. Random numbers are important in generating encryption keys and salt values. In this case OpenSSL generates a random number (in a Base64 format) for a given number of bytes.
Outline (C#/Python)
-
Symmetric Key Encryption (C#) [here]. This page uses the OpenSSL library through a C#/.NET wrapper. The DLLs it interfaces to are libeay32.dll and ssleay32.dll. OpenSSL supports a wide range of encryption methods, including 128-bit AES, 192-bit AES, 256-bit AES and Blowfish (bf). Different modes of ECB, CBC, and OFB are implemented. The examples use a default IV of "1234".
-
AES in Python with OpenSSL output [here]
-
Producing OpenSSL AES Encrypted String from C# [here]
Digital Certificates
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
Paillier - Partial Homomorphic Encryption

The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Fundamentals
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier).
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Using RSA
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
Applications
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Learning with Errors (LWE)
- Learning With Errors . LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret key value (s) and another value (e). Next we select a number of values (t[]) and calculate g[] = t[] x s + e. The values of g[] and t[] become our public key.
- Public Key Encryption with Learning With Errors (LWE). LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret value (s) and which is our private key. We then create a public key which is based on random numbers (A), and then generate another set of numbers (B) which is based on A,s and random errors e. An example of encryption with multiple bits is given.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE)
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Others
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
- SIDH Go. SIDH. Post-quantum key exchange.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Anonymous crypto. Anon. Anonymous crypto.
- Rho factorization. Rho. Rho alogorithm.
- Post-quantum signing (BLISS). BLISS. BLISS method.
Homomorphic Encryption with Krytology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Homomorphic hashing
- Homomorphic Hashing with Golang. Homomorphic hashing. Normally with hashing methods, we need to take all the previous data and new data in order to create a new hash value for our data. In a homomorphic hashing method, we can basically take the previous hash, and then add on any new data values. We can also remove previous data values from our hash, too. This is more efficient in computing, as we do not have to process all of our data into a new hash, and can use simple homomorphic operations for the computation. The method we will use (LtHash) was initially defined by Bellare and Micciancio and updated Lewi et al at Facebook.
Identity Based Encryption (IBE)

This page outlines a few basic principles around the usage of IBE.
Identity Based Encryption (Pairing based)
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pair-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Identity Based Encryption (Others)
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Güther's implicitly certified identity-based public keys (IBE). Günther. This method allows Bob to generate Alices public key from her identity and publicly available parameters.
- Girault's self-certified public keys (IBE). Girault. This method allows Bob to generate Alices public key from her identity and publicly available parameters, and where we use an RSA key pair to self-certify Alice's public key.
Intrusion Detection Systems (IDS)
- Intrusion Detection Systems. Snort. This outlines some of the basics of IDS, including the requirement for Intrusion Detection Systems (IDSs), and where they are used.
- Advanced Network Forensics (Snort). Adv Network Forensics. This provides information on how to detect threats through network forensics with Snort
Snort

- Snort IDS. Snort. This is a Snort Analyser.
- Snort IDS 2 with rules editor. Snort. This provides information on how to detect threats through network forensics with Snort, and with an editing function for rules.
Presentation
IoT

The key objectives of this page are: Understand how a Pen Tester can generate vulnerabilities and test using the Metasploit framework; Define the options and payloads required to generate and use vulnerabilities; and Gaining remote access.
Devices
- Access the Wi-fi kettle. Go. This page outines how to access a wi-fi enabled kettle.
- Philips Hue Wireless Lighting. Go. This page shows how to use RESTful Web services to access to the Hue Led Lamps.
- Kali and R-PI. Go. This page shows the setup of a security testing infrastructure using a Raspberry Pi (R-PI) and a wifi access point.
- Kali, R-PI and RF electrical socket. Go. This page shows the control of an RF electical socket from a RPI.
- Capture from a Polar H10 heat rate sensor. Go. This page shows the capture of the Polar H10 heart sensor with an Ubertooth One.
- Trusted IoT: Linking IoT Devices to NFTs. Go. This page outlines a research paper which links a device to an NFT (Non-fungible Token).
Shodan Scanning
-
IoT Scan (Shodan). Go. This page includes a search of the Internet for key terms, such as for "apache", "mysql" and "cisco".
- IoT Banner Scan (Shodan). Go. This page includes a search of the Internet for key terms with the banner as a result (for the Top 10)
- Internet Services (Shodan). Go. This page includes a search of the Internet for key terms and display the IP address and port.
IoT Libraries
- libDisco with Go. libDisco. libdisco is a Golang library which can be used to create secure connections. It is based on the STROBE protocol framework. Symmetric cryptographic primitives rely on SHA-3 permutation, and asymmetric cryptographic primitives on X25519 and ed25519. STROBE defines a range of cryptographic protocols to integrate with IoT devices. In order to reduce processing, energy and memory requirements, it only uses Keccak (SHA-3) to encrypt and authenticate messages.
COSE/COBR
In computer security, we often have to represent binary data, in single values or groups of characters, bytes, words, long words, signed integers, floating-point values, double-precision floating-point values, and so on. This might be in the form of a data object, a signature or even encrypted content. For this, the ANS.1 DER format is often used, such as presenting digital certificates and signatures. An improvement on this for small messages with security is Concise Binary Object Representation (CBOR) — and which is defined in RFC8949 [1]. While JSON represents text-based data objects CBOR focuses on binary objects. It has been designed to create a lightweight encoder and decoder. This supports the use of CBOR within an IoT infrastructure. The data, also, does not require a data schema to be able to decode it, along with being extensible. CBOR defines the format of binary data with data objects and messages. We can then integrate security with CBOR Object Signing and Encryption (COSE), and which is defined in RFC8152 [2]. This includes signatures, message authentication codes (MACs), encryption and creating serialised objects.
- 128-bit AES GCM. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) can then build on this to include signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use a symmetric key to encrypt a message, and then decrypt it. In this case we will use AES GCM with a static 128-bit key ("0x000102030405060708090a0b0c0d0e0f").
- 256-bit AES GCM. Go. In this case we will use AES GCM using a random 256-bit key (32 bytes).
- EdDSA. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) [2] can then build on this to includes signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use EdDSA to create a signature for a message.
- ECDSA. Go. In this case we will use ECDSA to create a signature for a message.
- HMAC. Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT. Go. In this case we create a CWT token, and sign with an HMAC signature.
- ECDH. Go. In this case we create a symmetric key from ECDH. For this we will derive a shared key from the public key of Alice and Bob, and then define a single recipient which can derive the CEK (Content Encryption Key) using their private key. We will use the curves of P-256 (secp256r1), P-384 (secp384r1), P-521 (secp521r1) or SECP256K1 (as used with Bitcoin).
- RSA using COSE and CBOR. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\).
- RSA: dQ, dP and InvQ. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). The key pair also includes \(dQ\), \(dP\) and \(InvQ\), and these can be used with the Chinese remainder theory to optimize the decryption process.
Metasploit
- Armitage and Metasploit. Go.
- Exploiting Android with Metasploit. Go.
- Exploiting Android with Metasploit - Part 2. Go.
- Exploiting Windows/Mac OS X with Metasploit. Go.
- Remote Desktop Windows/Mac OS X with Metasploit. Go.
- Metasploit. Go.
- Internet of Things Security. Go.
- Metasploit (Enumeration and Scanning). Go.
- Metasploit (Malware). Go.
IP

 The following are a few interesting techniques around IP addresses:
The following are a few interesting techniques around IP addresses:
- Your details. IP. This shows your browser details.
- IP address analyser. IP. This involves converting an IP address to the host and network part of the address.
- IP subnet analyser. IP subnets. This involves converting an IP address to the host and network part of the address.
- IP address analyser. IP. This involves analysing IP addresses.
- Max subnets. Max subnets. This involves converting an IP address to the host and network part of the address.
- Route summarization. Summarization. This involves converting an IP address to the host and network part of the address.
- Whois. Whois. This does a basic Whois on a domain.
- URL Obfuscation. Obfuscation. This outlines URL obfuscation.
- HTTP Responses. Test. HTTP.
- Capturing Network Packets (Python). WinPCap. HTTP.
Cisco related
- Routing table. Routing table. This involves viewing a routing table for a Cisco device.
- ACL Generator. ACL. This involves a simple calculator for ACLs on network ranges.
- EIGRP metrics. EIGRP. Learn the basics of EIGRP metrics.
- VoIP B/W. VoIP. Calculate bandwidth for VoIP.
- Wild Card. Wild Card. On a Cisco device a wildcard mask is used to identify the parts of an IP address that need to be matched. It thus uses a wildcard mask, where a 0 in the bit position identifies that the device should match that bit, else a 1 shows that it should ignore it.
Protocols
- HTTP. HTTP. Show the request and response for HTTP.
- Ping analyser. IP. This involves converting a ping of a site.
IP Challenges
-
IP Test 1. IP Test. IP Classification test. This is a simple test which generates a range of IP addresses, and you must determine the IP address classification.
IP Subnet Challenge 1 Demo
-
IP Test 2. IP Test. IP Classification test Part 2. This test provides an address classification, and the user must find the addresses which are of this classification.
IP Subnet Challenge 2 Demo
-
IP Test 3. IP Test. IP Classification test Part 3. This test provides an address classification, where the network part of the address is determined.
IP Subnet Challenge 3 Demo
Subnet Challenges
- Subnet Test 1. Subnet Test. Subnet Test.
-
Subnet Test 2. Subnet Test. Subnet bits.
- Subnet Test 3. Subnet Test. Find the nth usable subnet. This test involves finding the nth usable subnet.
- Subnet Test 4. Subnet Test. Maximum subnets. This is a test page to determine the maximum number of subnets and hosts/subnet for IP classed addressing.
- Subnet Test 5. Subnet Test. Maximum host/subnet. This is a test page to determine the maximum number of hosts per subnet.
- Subnet Test 6. Subnet Test. Determine the required subnet mask for a given number of subnets. This is a test page to determine the required subnet mask for a given number of subnets and a given IP address classification.
- Subnet Test 7. Subnet Test. Determine the required subnet mask for a given number of host/subnet. This is a test page to determine the required subnet mask for a given number of hosts per subnet and a given IP address classification.
- Subnet Test 8. Subnet Test. Route summarization. This involves a calculation on route summarization.
- Subnet Test 9. Subnet Test. Binary to IP.
- Subnet Test 10. Subnet Test. Hex to IP.
-
Subnet Test 13. Subnet Test. Wild card mask network bits. Find the number of bits in the network part of the wild card mask. IP Wildcard challenge
- Subnet Test 14. Subnet Test. Wild card mask host bits. Find the number of bits in the host part of the wild card mask. IP Wildcard challenge
- Subnet Test 15. Subnet Test. Wild card mask ... find the network address. Find the network for the wild card mask. IP Wildcard challenge 2
- Subnet Test 16. Subnet Test. Find a matching IP address for a network and wild card mask. Find the IP for a network and a wild card mask.
- Subnet Test 17. Subnet Test. Find an address which is on a given network. Find an IP address on a network, for a given network address and subnet mask.
- Subnet Test 18. Subnet Test. Find an IP address on the same network. Find an IP address on the same subnet.
- Subnet Test 19. Subnet Test. Find subnet. Convert subnet mask.
- Megatest. Subnet Test. Challenging test for subnets.
JavaScript

JavaScript code allows execution within the browser, rather than on the server. It is often faster than code that runs on a server. Along with this we can also use Node.js, and which runs JavaScript code on a server.
Symmetric key
- AES. AES. In this example, we will use either a pre-generated key or a random one, and use AES (Rijndael) encryption.
- ChaCha20 and Poly1305. ChaCha. This page outlines Poly1305 and ChaCha20. ChaCha20 is a symmetric key method and Poly1305 is a message authentication code (MAC). They were created by Daniel J. Bernstein, and are alternatives to AES and HMAC.
- CMS (Padding). CMS. This page uses PKIJS encrypting on CMS. With CMS we can This document describes the Cryptographic Message Syntax (CMS). With this we can encapsulate an message within an encrypted entity.

Hashing
- Hash. Hash. This page defines a JavaScript Hash calculator. This uses a client-side JavaScript code to determine the hash signatures of a text value.
Signatures
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
- Boneh–Lynn–Shacham (BLS) signature. BLS. Boneh–Lynn–Shacham (BLS) signature method produces short signatures. They use elliptic curve pairing (and which are also known as bilinear maps).
Key exchange
- ECDH. ECDH. Elliptic Curve Diffie Hellman (ECDH) is used to generate a shared key. This implementation uses Elliptic Curve Cryptography (ECC) with JavaScript.
CryptoJS
- CryptoJS. CryptoJS. This page uses client-side JavaScript code to hashing, encrypt and sign, including for symmetric key (AES), streaming ciphers, hashing methods, and HMAC.
Blockchain
- PATRICIA trie. PATRICIA. In the following, we have the Top 2,500 Web sites in the world, and implemented with a Radix Trie (aka PATRICIA trie) In the following we have the Top 2,000 web sites on the Internet, and which have been indexed using the PATRICIA trie.
Public key
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
- RSA. RSA. RSA is an asymmetric encryption algorithm, which uses two keys, one to encrypt and the other to decrypt. It was created in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman, and is still one of the most widely used encryption methods. A typical application is in authenticating a sender, where the senders private key is used to encrypt a message, and then is decrypted by the receiver with the senders public key (which is known to anyone who wants it). It is also typically used for encrypting disks/files, such as for EFS.
Digital Certificates
- X.509 certificates in JavaScript. RSA and ECDSA Signed certificates. This page will generate either RSA and ECC key pairs, and then generate X.509 certificates, using either a signature of SHA1withRSA or SHA256withECDSA. For RSA signing we use an RSA private key to sign the certificate, and with ECDSA signing we use an ECC private key to sign the certificate.
Tokens
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
Random
- Random number generator. Rand. In the past, encryption and decryption had to be done through native code libraries, such as with Bouncy Castle and OpenSSL. With the increasing processing power of Web browsers, it is now possible to use encryption using JavaScript, which thus provides client-side processing of data. This Web page uses Javascript encryption, and generates a random 256-bit text key or a hex version. The 256-bit key is generated by generating 60 random numbers (from 0-25), and converting these to an ASCII character.
Malware obfuscation
- Malware obfuscation. Obfuscation. A malware writer will often hide certain keywords from the browser/human by encoding them in another format. This is typically done for hex coding (\xZZ), 16-bit unicoding (\uZZZZ) and octal coding (\ZZZ). To test, enter a value, and then press the button and it will convert encoded string.
Message Authentication Codes
- Chaskey (MAC). Chaskey. Chaskey Cipher is light-weight cryptography method for signing messages (MAC) using a 128-bit key. The hardware implementation only requires 3,334.33 gate equivalent with an operating clock frequency of 1 MHz (whereas Keccak requires 4,658 GE). In the page we create the Mac signature and also encrypt for CBC.
Other
- Password generation/hashing. Hashing. Linux can use salted passwords where the username, hashing method and hashed password are stored in a password file [More details]. The main methods are
Hashing

At times we need to generate secrets, such as encryption keys, from passwords or nonce values. A Key Derivation Function (KDF) is a verifiable way of doing this.
Key Derivation Functions (KDFs)
The following are the tips related to hashing:
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Password strength. Test. This outlines the strength of various passwords types.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
HKDF
The following are the tips related to Key derivation hashing:
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Hazmat HKDF for different hashing methods. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
-
HKDF key derivation with OpenSSL [
here]
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
PBKDF2
The following are the tips related to Key derivation hashing:
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- AES GCM (Python) with PBKDF2. AES GCM (Python) with PBKDF2.
- Fernet with PBKDF2 . AES GCM (Python) with PBKDF2.
- PBKDF2 key derivation. AES GCM (Python) with PBKDF2.
- Key Rotation with Fernet. AES GCM (Python) with PBKDF2.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Bcrypt
The following are the tips related to Key derivation hashing:
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- BCrypt. BCrypt. BCrypt with Rust.
-
Hash to password with Go. Hashing to Argon2, Scrypt and BCrypt. Hash to password with Go, including Argon2, Scrypt and BCrypt.
scrypt
- scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Argon 2
The following are the tips related to Key derivation hashing:
- Argon 2. Go. Outline of Argon2.
- Argon 2 with NaCl. Go. Outline of Argon2 using NaCl.
- Argon 2. Argon 2. Argon 2 with Rust.
- Balloon. Go. Outline of Balloon.
Other
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
- Double ratchet. Go. Outline of double ratcheting.
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
Outline
HMAC Key Derivation function (HKDF) is used to derive an encryption key from a passphrase. Initially, HKDF creates a pseudorandom key (PRK) using a passphrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), and along with a salt value. Next, the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys [RFC 5869][article]. In this case, we will use SHA-256.
The following shows how an encryption key can be generated using HKDF, and where we need a secret and a salt value. Both Bob and Alice have the same secret and salt.

With PBKDF2 (Password Based Key Derivation Function 2), we hash for a given number of rounds:

Key exchange

Key exchange is a way for Bob and Alice to communicate and for them to agree on a shared secret. The original method defined uses discrete logarithms (Diffie-Hellman), but most modern methods use elliptic curve techniques (ECDH). As quantum computers can crack both discrete log and elliptic curve methods, there are post quantum cryptography methods proposed. This includes SIDH, CSIDH, SIKE, and NewHope.
Key interchange/generation (Diffie-Hellman)
The following relates to key interchange:
- Selecting \(g\) in Diffie Hellman. G in Diffie Hellman. Picking a safe value of the generator \(g\) in discrete logarithms.
- Diffie-Hellman. Diffie-Hellman Calculation. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Real example). Diffie-Hellman Real. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Python). Diffie-Hellman. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (pre-compute). Diffie-Hellman (pre-compute). Many sites use the same prime numbers, which can then be cracked with a pre-computing attack.
- Key generation. Key gen. This will generate keys for different methods based on a passphrase.
- Diffie-Hellman (Man-in-the-middle). DF. This outlines the man-in-the-middle method for Diffie-Hellman.
- An Alternative Diffie-Hellman method. Alterative DH. This outlines an alternative Diffie-Hellman method.
Authenticated Key Exchange
The following are the tips related to Key derivation hashing:
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- MTI/A0. MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{ax+by} \pmod p\). MTI (Matsumoto, Takashima, Imai).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0. MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{x+y} \pmod p\)
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). The resultant key is \(xyG \)
- MTI/C0. MTI/C0. This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{xy} \pmod p\)
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG\).
- MTI/C1. MTI/C1. This outlines MTI/C1, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{abxy} \pmod p\).
- MQV (Menezes–Qu–Vanstone). MQV. MQV was created Alfred Menezes, Minghua Qu and Scott Vanstone in 1995 and is an authenticated key exchange method. Alice holds a key pair \((A,a)\) and Bob has a key pair \((B,b)\). With this \(a\) is Alice's private key, and \(A=aG\) is her public key. For Bob, his public key will be \(B=aG\) and a private key of \(b\), and where \(G\) is the base point on the elliptic curve.
- HMQV (Menezes–Qu–Vanstone). HMQV. HMQV builds on MQV and adds the identity of Bob and Alice.
- ECDH with X25519 and Blake2b. ECDH with X25519 and Blake2b. This uses PyNaCl to create an authenticated key exchange and uses X25519 and Blake2b.
Elliptic Curve (ECDH) - Python
The following are the tips related to ECC:
- Elliptic Curve. Elliptic Curve. Elliptic Curve is a public key method which can also be used to generate a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with simple parameters. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
Elliptic Curve (ECDH) - Golang and Node.js
The following are the tips related to ECC:
- ECDH with Go. ECDH. ECDH with Go.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with node.js. ECDH. ECDH with node.js.
- ECDH with JavaScript. ECDH. Elliptic Curve Diffie Hellman.
Password Authenticated Key Exchange (PAKE)
The following are the tips related to Key derivation hashing:
- SPAKE2. Go. Outline of SPAKE2.
- OPAQUE. Go. Outline of OPAQUE.
- SPEKE. Go. Outline of SPEKE (Simple Password Exponential Key Exchange).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
- J-PAKE. J-PAKE. This example generates a shared key based on a shared password.
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses discrete logs.
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
PQC NIST Finalists (Key Exchange)
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Key interchange/generation (Other)

The following relates to key interchange:
- Curve25519. Curve25519. This outlines Curve25519, which is used in the Tor network.
- Authenticated Key Exchange (Discrete logs). YAK. Key exchange with public keys and uses discrete logs.
- Authenticated Key Exchange (ECC). YAK. Key exchange with public keys and uses elliptic curve methods.
- Shamir No-key protocol. Shamir No Key. In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated.
- Shamir No-key protocol (sepc256k1). Shamir No Key (EC). In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated using the sepc256k1 elliptic curve.
- Conference keying (Burmester-Desmedt method). Conference keying. In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it.
- Conference keying (Burmester-Desmedt method) - Elliptic Curve (sepc256k1). Conference keying Elliptic Curve (sepc256k1). In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it, and uses the sepc256k1 elliptic curve.
Key exchange (with pairing)
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Kryptology

We need to build a new Internet. One that is build on mathematics and certainty, rather than the patchy version we have now. For this we need a layer of cryptography at the lowest level, and build software interfaces on top of this. Along with this we now have cryptographic methods which can now provide a foundation of trust, and which preserve privacy. And so the old libraries of OpenSSL are being squeezed out in favour of the new ones which are built on a solid foundation. The latest of these new "privacy-aware" libraries is Kryptology, and created by Coinbase. This library provides the APIs that developers need, in order to apply to areas of blockchain development. This library include BLS (Boneh-Lynn-Shacham) signatures, Zero-knowledge Proofs (ZKPs) and Shamir Secret Shares (SSS). With BLS we can digitally sign for data, but also preserve its privacy. Applications of this include group signatures, where multiple entities can merge their signing keys together and provide a single signature for a transaction. With SSS, we can split encryption keys up into shares, and then distribute them across a network. When required, we can call these shares back to reconstruct the key.
The focus for Coinbase seems to be the application of privacy coins, and where no tracking can be applied to the usage of these digital coins. This should support full anonymity for transactions, as opposed to Bitcoin which only supports pseudo-anonymity.

ECC Basics
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining n.G for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Points (Base Point and Others). Elliptic Curve points. Two common curves used in ECC (Elliptic Curve Cryptography) are secp256k1 (as used in Bitcoin and Ethereum) and P256 (secp256r1). The "k1" refers to the Kolbitz curve 1 (named after the creator of ECC). With these we have a base point which are can operate on. This is typically defined as \(G\). We can then operate on this with add and multiply operation. For example, \(2G=G+G\) and \(P=n.G\). In this following we will show the base point for a number of common curves, such as secp256r1, P256, Pallas, Curve 25519, BLS12381G1, BLS12381G2, BLS12377G1 and BLS12377G2.
ECDH
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret. We will use Golang and the Krytology library.
Simple ECC on curves
- Public key points for curves. Simple. Display public key points for scalars.
BLS Curve
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
Accumulator and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
Pallas Curve
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
Pairing-based Crypto
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
ElGamal and ECC
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a numerical input.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
Shamir Secret Shares
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Homomorphic Encryption
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Zero knowledge proofs
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
Verifiable Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Hash to scalar and point
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
CP-ABE
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Lattice cryptography

Latice cryptography is proposed as a post-quantum robust method for public key encryption, especially focused on digital signatures and key exchange mechanisms (KEMs).
Principles
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
NTRU
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- Lattice Encryption: NTRU Key Generation Python). NTRU. Outlines how NTRU operates for key generation.
Homomorphic
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Digital Signatures
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
Public-Key Encryption/Key Exchange
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
Light-weight cryptography

While AES and SHA work well together within computer systems, they struggle in an IoT/embedded world as they take up: too much processing power; too much physical space; and consume too much battery power. So NIST outlines a number of methods which can be used for light-weight cryptography, and which could be useful in IoT and RFID devices [1]. They define the device spectrum as:
- Conventional cryptography. Servers and Desktops. Tablets and smart phones.
- Light-weight cryptography. Embedded Systems. RFID and Sensor Networks.
With embedded systems, we commonly see 8-bit, 16-bit and 32-bit microcontrollers, and which would struggle to cope with real-time demands for conventional cryptography methods. And in the 40+ years since the first 4-bit processor, there is even a strong market for 4-bit processors. RFID and sensor network devices, especially, have limited numbers of gates available for security, and are often highly constrained with the power drain on the device.
So AES is typically a non-starter for many embedded devices. In light-weight cryptography, we often see smaller block size (typically 64 bits or 80 bits), smaller keys (often less than 90 bits) and less complex rounds (and where the S-boxes often just have 4-bits).
For light-weight cryptography the main constraints that we have are typically related to ener requirements, gate equivalents (GEs), and timing. With passive RFID devices, we do not have an associated battery for the power supply, and where the chip must power itself from energy coupled from the radio wave. An RFID device is thus likely to be severely constrained in the power drain associated with any cryptography functions, along with being constrained for the timing requirements and for the number of gates used. Even if an RFID device has an associated battery (active RFID), it may be difficult to recharge the battery, so the drain on power must often be minimised.
There is thus often a compromise between the cryptography method used and the overall security of the method. Thus often light-weight cryptography methods balance performance (throughput) against power drain and GE, and do not perform as well as main-stream cryptography standards (such as AES and SHA-256). Along with this the method must also have a low requirement for RAM (where the method requires the usage of running memory to perform its operation) and ROM (where the method is stored on the device). In order to assess the strengths of various methods we often define the area that the cryptography function will use on the device – and which is defined in \(µm^2\). The NIST finalists are defined in this [article]
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- GIFT AEAD. GIFT. GIFT is a light-weight block cipher. It is a (NIST Finalist)
- Elephant. Elephant. Elephant is a light-weight stream cipher. It is a (NIST Finalist).
- TinyJambu. TinyJambu. TinyJambu is a light-weight block cipher. It is a (NIST Finalist)
- Isap AEAD. Isap. Isap is a light-weight block cipher. It is a (NIST Finalist)
- PHOTON-Beetle AEAD. PHOTON-Beetle. PHOTON-Beetle is a light-weight block cipher. It is a (NIST Finalist)
- Romulus AEAD. Romulus. Romulus is a light-weight block cipher. It is a (NIST Finalist)
- Sparkle AEAD. Sparkle. Sparkle is a light-weight block cipher. It is a (NIST Finalist)
- CLEFIA. CLEFIA. CLEFIA is a light-weight block cipher.
- LED. LED. LED is a light-weight block cipher.
- Piccolo. Piccolo. Piccolo is an ultra light-weight block cipher.
- PRESENT. PRESENT. Present is a light-weight block cipher.
- Pyjamask. Pyjamask. Pyjamask is a light-weight block cipher.
- SIMON. SIMON. SIMON is a light-weight block cipher.
- SKINNY. SKINNY. SKINNEY is a light-weight block cipher.
- SPECK. SPECK. SPECK is a light-weight block cipher.
- XTEA. XTEA. XTEA is a light-weight block cipher.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encryption/Decryption. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.
Light-weight crypto (Other)
- Chaskey (MAC). Chaskey. Chaskey is a light-weight MAC function.
- Chaskey (MAC). Chaskey (Python). Chaskey is a light-weight MAC function.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (ASCON)
ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRFF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
Discrete Logs (Solving)

A discrete log problem is in the form of \(g^x \pmod p\) and where we know \(g\) and \(p\) and must solve for \(x\).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Message Authentication Code (MAC)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
HMAC
The following are the tips related to Key-based hashing:
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authentication both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2), Blake2b, SM3 and SHA-3. This page outlines the HMAC-MD5 methods using the Hazmat cryptography layer.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- HMAC (COSE). Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT with HMMAC. Go. In this case we create a CWT token, and sign with an HMAC signature.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- HMAC with Rust. HMAC. HMAC with Rust.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HMAC with OpenSSL. MACs with OpenSSL. HMAC in OpenSSL for a given input value, password and hashing method.
Cipher MACs
The following are the tips related to Key-based hashing:
- MACs with OpenSSL. MACs with OpenSSL. MAC methods implemented in OpenSSL, including CMAC and GMAC.
Key-based hashing
The following are the tips related to Key-based hashing:
- SipHash. Siphash. Siphash is a fast key-based hashing method.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Meow. Meow. Meow is one of the fastest hashing methods.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
Magic Numbers

This pages contains information related to magic numbers in file formats.
Network and File Forensics
- Magic numbers. Magic. This provides information on magic number for file forensics.
Graphics formats
- JPEG Analysis. JPEGs. This provides an analysis of JPEG files.
- GIF Analysis. GIFs. This provides an analysis of GIF files.
- TIF Analysis. TIFs. This provides an analysis of TIF files.
- PNG Analysis. PNGs. This provides an analysis of PNG files.
- BMP Analysis. BMPs. This provides an analysis of BMP files.
- PSD Analysis. PSDs. This provides an analysis of PSD files.
- WMF Analysis. WMF. This provides an analysis of WMF files.
- Adobe Illustrator Analysis. AI. This provides an analysis of AI files.
- Adobe In Design Analysis. INDD. This provides an analysis of INDD files.
- MIDI file. MIDI. This provides an analysis of MID files.
- ICO file. ICO. This provides an analysis of ICO files.
- PS file. PS. This provides an analysis of PS files.
- EPS file. EPS. This provides an analysis of EPS files.
- VSD file. VSD. This provides an analysis of Microsft Visio (VSD) files.
Video and audio formats
- MP3 Analysis. MP3s. This provides an analysis of MP3 files.
- AVI Analysis. AVIs. This provides an analysis of AVI files.
- Flash SWF Analysis. SWFs. This provides an analysis of Flash files.
- Flash FLV Analysis. FLVs. This provides an analysis of FLV files.
- MP4 Analysis. MP4. This provides an analysis of MP4 files.
- MOV Analysis. MOV. This provides an analysis of MOV files.
- WMV Analysis. WMV. This provides an analysis of WMV files.
- WMA Analysis. WMA. This provides an analysis of WMA files.
- JPEG 2000 Analysis. JPEG 2. This provides an analysis of JPEG 2000 files.
- WAV Analysis. WAV. This provides an analysis of WAV files.
Zips, Archives and Library files
- ZIP/Archive Analysis. ZIPs. This provides an analysis of ZIP/Achive files.
- GZ Analysis. GZ. This provides an analysis of GZip files.
- Tar Analysis. Tar. This provides an analysis of TAR files.
- MSI Analysis. MSI. This provides an analysis of MSI files.
- OBJ Analysis. OBJ. This provides an analysis of OBJ files.
- DLL Analysis. DLL. This provides an analysis of DLL files.
- CAB Analysis. CAB. This provides an analysis of CAB files.
- EXE Analysis. EXE. This provides an analysis of EXE files.
- RAR Analysis. RAR. This provides an analysis of RAR files.
- SYS Analysis. SYS. This provides an analysis of SYS files.
- HLP Analysis. HLP. This provides an analysis of HLP files.
- VMDK Analysis. VMDK. This provides an analysis of VMDK files (VMWare Virtual Disks).
- PST Analysis. PST. This provides an analysis of PST files (Outlook Email File).
- JAR Analysis. JAR. This provides an analysis of JAR files.
- SLN Analysis. SLN. This provides an analysis of Microsoft SLN files.
- Class Analysis. Class. This provides an analysis of Java Class files.
- Zlib. Zlib. This provides an analysis of Zlib files.
Documents
- PDF Analysis. PDFs. This provides an analysis of PDF files.
- DOC Analysis. DOCs. This provides an analysis of DOC files.
- RTF Analysis. RTFs. This provides an analysis of RTF files.
- XLS Analysis. XLSs. This provides an analysis of XLS files.
- PPT Analysis. PPTs. This provides an analysis of PPT files.
- MMP File. MMP. This provides an analysis of MMP files.
- DOCX Analysis. DOCX. This provides an analysis of DOCX files.
- XLSX Analysis. XLSX. This provides an analysis of XLSX files.
- PPTX Analysis. PPTX. This provides an analysis of PPTX files.
- MDB Analysis. MDB. This provides an analysis of MDB files.
- Outlook Message Analysis. MSG. This provides an analysis of MSG files.
Disk Image
- Raw disk format. RAW. This provides an analysis of the RAW disk format.
Tests
- File Forensics Test. File Test File Forensics Test.
- File Forensics Test (Fun). File Test (Fun) File Forensics Test.
Presentations
MIRACL Core Library

MIRACL Core is an open source library, and includes a wide range of public key encryption methods. It is especially focused on elliptic curve and pairing-friendly methods, but also supports a wide range of encryption methods, including RSA, AES and hashing. Overall, it can be ported onto a wide range of systems and supports C, C++, Go, Rust, Python, Java, Javascript and Swift. Along with this it supports limited capability devices such as the Arduino infrastructure. The GitHub repository is [here].
BN254
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.

Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- CL Signatures. CL. CL Signatures in Go using MIRACL.
- CL Signatures (advanced pairing). CL. CL Signatures in Go using MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages using MIRACL.
- PS Signatures. PS. Signatures using PS for short signatures using MIRACL.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures using MIRACL.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.

Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
Rust examples
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
NaCl

PyNaCl is a Python port of LibSodium. It integrates the latest cryptography methods, such as AES, XChaCha20, Blake2b and X25519.
Symmetric Key
- Symmetric key. Symmetric key (XChaCha20 and Poly1305). With symmetric key, Bob and Alice have the same key. NaCl uses the XChaCha20 method, and which supports stream encryption (and which does not require padding as a block cipher does, and is also faster than block cipher modes). ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16 byte nonce. XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24 byte nonce. It has a lower propability of nonce misuse than ChaCha20.
- Encryption with a password. Symmetric Key with KDF. In symmetric key, we generate a secret key. This key is typically a random value or generated from a password and a salt value. If we use a password, we typically use a KDF (Key Derivation Function), and which uses a password and a salt value, in order to create a key of a given size. In this case we will use Argon2i, and which is memory resilent.
Hybrid Encryption
- Box. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Hashing
- Hashing and KDF (Argon2 and scrypt). Hashing and KDF. This case we will use PyNaCl (Networking and Cryptography) library, and which is a Python binding to libsodium. We will hash a password using SHA-256 and SHA-512, and also create a KDF (Key Derivation Function) using scrypt and Argon2.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
Ed25519
-
Ed25519. Ed25519. Using Ed25519 for digital signatures.
-
Finding Points on Ed25519. X25519 (Points).
In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 (Key Exchange)
- X25519 + BLAKE2b key-exchange. X25519. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
Curve 25519
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
Node.js

Node.js uses the JavaScript programming langauge as its base, and allows for code to be run on a server, rather than in the browser (such as with pure JavaScript). To run a node.js program, we run "node myfile.js", and use NPM to install libraries.
Symmetric key
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
RSA and public key
- RSA Opt imal Asymmetric Encryption Padding (OAEP) using Node.js. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
ECC Keys
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.

Hashing
- Hashing with node.js (All). Hashing. Hashing with node.js.
- Hashing with node.js (Selection). Hashing. Hashing with node.js.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- ECDSA with node.js. ECDSA. ECDSA with node.js.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
Key exchange
- Diffie-Hellman with node.js (random prime). DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method and uses a randomly generated prime number (press the button to generate a new prime).
- Diffie-Hellman with node.js. DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method. Each time the prime number will be fixed for the DH group selected.
- ECDH with node.js. ECDH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Elliptic Curve Diffie Hellman (ECDH) key exchange method.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
Key derivation
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
CryptoJS
- CryptoJS (in node.js). CryptoJS (Node.js). Various crypto methods in the browser.
Bulletproofs
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
Blockchain
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
Proxy encryption
- Proxy Encryption - Encrypting With Public Key, And Decrypt with Private Key. Proxy01. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This page just creates a key pair for Alice, and uses it to encrypt with the public key , and decrypt with the private key.
- Proxy Encryption. Proxy02. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This will go through the full use case of proxy re-encryption.
Tokens
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
Random
- Fortuna with node.js. Fortuna. Fortuna random numbers with node.js.
Other
- FPE with node.js. FPR. FPE with node.js.
- Puny with node.js. Puny. Puny character format with node.js.
Accumulators and Witnesses
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
PGP
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Password Entropy
- Password Entropy with Node.js. Password Entropy. Password entropy measures the strength of a password, and is measured as the number of bits which could represent all of the possibilities. An entropy score of less than 25 identifies a poor password, and between 25 and 50 is a weak password. For 50 to 75 we have a reasonable password, and between 75 and 100 is a very good password. Over 100 is an excellent password. The strength of the password relates to the number of characters used, and also the number of characters in the password.
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
- Homomorphic Encryption with Node.js and BGV. Homomorphic Encryption with Node.js and BFG. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BGV method.
Oblivious Transfer (OT)

Oblivious Transfer allows Bob to select data from Alice, but for Alice not to know which value has been selected.
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
OpenSSH

OpenSSH supports the usage of the SSH protocol. This allows for a remote login. One tool which is uses is ssh-keygen, and which allow for the generation of RSA, DSA and elliptic-curve keys that. These can be used for user and host authentication, such as for GitHub login and Cloud instance login.
OpenSSH
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here].
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
Outline

OpenSSL

OpenSSL is a standard library that implements cryptography.
Symmetric key (Command line)
-
Symmetric Key Encryption (OpenSSL 1.x) [here]. In this case we will create cipher text from OpenSSL 1.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 1.x) [here].In this case we will decrypt cipher text from OpenSSL 1.x using a key derived from a password
-
Symmetric Key Encryption (OpenSSL 3.x) [here]. In this case we will create cipher text from OpenSSL 3.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 3.x) [here].In this case we will decrypt cipher text from OpenSSL 3.x using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password.
Hashing
-
Hashing [here] OpenSSL supports a wide range of hashing methods including BLAKE2b, Gost, MD4, MD5, RMD-160, SHA-1, SHA-3, SHA-256 and SHA-512.
Libre OpenSSL
-
Symmetric Key Encryption using Libre OpenSSL [here]. In this case we will create cipher text from Libre OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption using Libre OpenSSL [here]. In this case we will decrypt ciphertext from Libre OpenSSL using a key derived from a password.
-
Hashing [here] Libre OpenSSL supports a wide range of hashing methods including Gost, MD4, MD5, RMD-160, SHA-1, SHA-256 and SHA-512.
Diffie-Hellman parameter generation
-
DH Parameters with OpenSSL [here]. The Diffie-Hellman (DH) method is perhaps one of the greatest inventions in Cybersecurity, and was created by Whitfield Diffie and Marty Hellman. With the DH method, Bob creates a random value (\(b\)) and Alice also creates a random value (\(a\)). Next Bob computes \(B=g^b \pmod p\) and sends it to Alice. Alice computes \(A=g^a \pmod p\) and sends this to Bob. Bob raises the value of \(A\) to the power of \(b\) and takes \(\pmod p\), and Alice raises \(B\) to the power of \(a\) and takes \(\pmod p\). In the end, they will have the same shared value: \(g^{ab} \pmod p\). This can then be used to derive an encryption key that they can use for a secure tunnel. Overall, \(p\) is the large prime number, and also known as the shared modulus between Bob and Alice.
Key derivation function
-
PBKDF2 key derivation with OpenSSL [here] PBKDF2 (Password Key Derivation Function 2) is a key derivation method. Overall it is relatively slow in its operation and where we take a password, a salt value, hashing method, and a number of iterations, in order to produce a given size of encryption key.
-
HKDF key derivation with OpenSSL [here] HKDF (HMAC Key Derivation function) is used to derive an encryption key from a pass phrase. Initially HKDF creates a pseudorandom key (PRK) using a pass phrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), andalong with a salt value. Next the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys.
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Passwords
-
Password example [here]. This page uses the OpenSSL library hash password generator, which is used in UNIX systems for the hashing of passwords which are contained in /etc/shadow and /etc/passwd. For newer passwords, the "-1" options is used to created the hashed value.
-
Hashed passwords with OpenSSL [here].
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
Public key
-
Generating an ECC key pair with OpenSSL [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)).
-
Generating an RSA key pair with OpenSSL [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2).
-
Generating an RSA key pair with OpenSSL with encryption [here]. This page implements RSA key pair generation with an encrypted key pair. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). In this case we will encrypt the key pair with either 3DES, 128-bit AES, 192-bit AES or 256-bit AES. The same password must be used to encrypt and decrypt.
-
Generate prime with OpenSSL [here]. Prime numbers are important in public key encrytion, and are used with RSA and ECC. For RSA, we generate two prime numbers (\(p\) and \(q\)) and which are multiplied together to create a modulus (\(N\)). If these prime numbers have 512 bit values, the modulus will be a 1,024 bit value. This defines the basic secure of RSA. With elliptic curve we use smaller prime numbers, such as 256-bit values for the secp256k1 curve.
ASN1 parsing
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). We will parse using asn1parse, and reveal the parameters.
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)) [RSA key pair]. We will parse using asn1parse, and reveal the parameters.
- DSA Parameters with asn1parse. DSA parameters with OpenSSL with asn1parse. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA (Digital Signature Algorithm)
- DSA Parameters. DSA parameters with OpenSSL. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
MAC (Message Authentication Code)
- HMAC with OpenSSL. MACs with OpenSSL. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authenticate both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2) and SHA-3. In this case we will use OpenSSL to generate the HMAC value.
- MACs with OpenSSL. MACs with OpenSSL. In the following we will generate MACs for HMAC, GMAC, CMAC, Blake2bmac, Blake2smac, KMAC128 and KMAC256. Overall, we will use an encryption key defined as a hex value for GMAC and CMAC, and a pass phrase for the others. The message is "hello".
Signing
- Digital signing a plaintext message with OpenSSL. Signing with OpenSSL. With digital signing, we can take a message, and create a signature. This normally involves signing with a private key and digital certificate. The signed message can be an a MIME format, and which can be integrated into an email message. In this can we have a 512-bit RSA key pair that will sign a plain text message.
Encrypting emails
- Encrypting an email message in OpenSSL. Encrypting messages with OpenSSL. With public key encryption, we can take a message, and encrypt it with the recipiant's public key. In this can we have a 512-bit RSA public key to encrypt a message.
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Random number generation with OpenSSL
-
Random number generator [here]. Random numbers are important in generating encryption keys and salt values. In this case OpenSSL generates a random number (in a Base64 format) for a given number of bytes.
Outline (C#/Python)
-
Symmetric Key Encryption (C#) [here]. This page uses the OpenSSL library through a C#/.NET wrapper. The DLLs it interfaces to are libeay32.dll and ssleay32.dll. OpenSSL supports a wide range of encryption methods, including 128-bit AES, 192-bit AES, 256-bit AES and Blowfish (bf). Different modes of ECB, CBC, and OFB are implemented. The examples use a default IV of "1234".
-
AES in Python with OpenSSL output [here]
-
Producing OpenSSL AES Encrypted String from C# [here]
Digital Certificates
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
Paillier - Partial Homomorphic Encryption

The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Fundamentals
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier).
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Using RSA
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
Applications
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Learning with Errors (LWE)
- Learning With Errors . LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret key value (s) and another value (e). Next we select a number of values (t[]) and calculate g[] = t[] x s + e. The values of g[] and t[] become our public key.
- Public Key Encryption with Learning With Errors (LWE). LWE. Learning With Errors (LWE) is a quantum robust method of cryptography. Initially we create a secret value (s) and which is our private key. We then create a public key which is based on random numbers (A), and then generate another set of numbers (B) which is based on A,s and random errors e. An example of encryption with multiple bits is given.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE)
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Others
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
- SIDH Go. SIDH. Post-quantum key exchange.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Anonymous crypto. Anon. Anonymous crypto.
- Rho factorization. Rho. Rho alogorithm.
- Post-quantum signing (BLISS). BLISS. BLISS method.
Homomorphic Encryption with Krytology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Homomorphic hashing
- Homomorphic Hashing with Golang. Homomorphic hashing. Normally with hashing methods, we need to take all the previous data and new data in order to create a new hash value for our data. In a homomorphic hashing method, we can basically take the previous hash, and then add on any new data values. We can also remove previous data values from our hash, too. This is more efficient in computing, as we do not have to process all of our data into a new hash, and can use simple homomorphic operations for the computation. The method we will use (LtHash) was initially defined by Bellare and Micciancio and updated Lewi et al at Facebook.
Identity Based Encryption (IBE)

This page outlines a few basic principles around the usage of IBE.
Identity Based Encryption (Pairing based)
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pair-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Identity Based Encryption (Others)
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Güther's implicitly certified identity-based public keys (IBE). Günther. This method allows Bob to generate Alices public key from her identity and publicly available parameters.
- Girault's self-certified public keys (IBE). Girault. This method allows Bob to generate Alices public key from her identity and publicly available parameters, and where we use an RSA key pair to self-certify Alice's public key.
Intrusion Detection Systems (IDS)
- Intrusion Detection Systems. Snort. This outlines some of the basics of IDS, including the requirement for Intrusion Detection Systems (IDSs), and where they are used.
- Advanced Network Forensics (Snort). Adv Network Forensics. This provides information on how to detect threats through network forensics with Snort
Snort

- Snort IDS. Snort. This is a Snort Analyser.
- Snort IDS 2 with rules editor. Snort. This provides information on how to detect threats through network forensics with Snort, and with an editing function for rules.
Presentation
IoT

The key objectives of this page are: Understand how a Pen Tester can generate vulnerabilities and test using the Metasploit framework; Define the options and payloads required to generate and use vulnerabilities; and Gaining remote access.
Devices
- Access the Wi-fi kettle. Go. This page outines how to access a wi-fi enabled kettle.
- Philips Hue Wireless Lighting. Go. This page shows how to use RESTful Web services to access to the Hue Led Lamps.
- Kali and R-PI. Go. This page shows the setup of a security testing infrastructure using a Raspberry Pi (R-PI) and a wifi access point.
- Kali, R-PI and RF electrical socket. Go. This page shows the control of an RF electical socket from a RPI.
- Capture from a Polar H10 heat rate sensor. Go. This page shows the capture of the Polar H10 heart sensor with an Ubertooth One.
- Trusted IoT: Linking IoT Devices to NFTs. Go. This page outlines a research paper which links a device to an NFT (Non-fungible Token).
Shodan Scanning
-
IoT Scan (Shodan). Go. This page includes a search of the Internet for key terms, such as for "apache", "mysql" and "cisco".
- IoT Banner Scan (Shodan). Go. This page includes a search of the Internet for key terms with the banner as a result (for the Top 10)
- Internet Services (Shodan). Go. This page includes a search of the Internet for key terms and display the IP address and port.
IoT Libraries
- libDisco with Go. libDisco. libdisco is a Golang library which can be used to create secure connections. It is based on the STROBE protocol framework. Symmetric cryptographic primitives rely on SHA-3 permutation, and asymmetric cryptographic primitives on X25519 and ed25519. STROBE defines a range of cryptographic protocols to integrate with IoT devices. In order to reduce processing, energy and memory requirements, it only uses Keccak (SHA-3) to encrypt and authenticate messages.
COSE/COBR
In computer security, we often have to represent binary data, in single values or groups of characters, bytes, words, long words, signed integers, floating-point values, double-precision floating-point values, and so on. This might be in the form of a data object, a signature or even encrypted content. For this, the ANS.1 DER format is often used, such as presenting digital certificates and signatures. An improvement on this for small messages with security is Concise Binary Object Representation (CBOR) — and which is defined in RFC8949 [1]. While JSON represents text-based data objects CBOR focuses on binary objects. It has been designed to create a lightweight encoder and decoder. This supports the use of CBOR within an IoT infrastructure. The data, also, does not require a data schema to be able to decode it, along with being extensible. CBOR defines the format of binary data with data objects and messages. We can then integrate security with CBOR Object Signing and Encryption (COSE), and which is defined in RFC8152 [2]. This includes signatures, message authentication codes (MACs), encryption and creating serialised objects.
- 128-bit AES GCM. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) can then build on this to include signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use a symmetric key to encrypt a message, and then decrypt it. In this case we will use AES GCM with a static 128-bit key ("0x000102030405060708090a0b0c0d0e0f").
- 256-bit AES GCM. Go. In this case we will use AES GCM using a random 256-bit key (32 bytes).
- EdDSA. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) [2] can then build on this to includes signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use EdDSA to create a signature for a message.
- ECDSA. Go. In this case we will use ECDSA to create a signature for a message.
- HMAC. Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT. Go. In this case we create a CWT token, and sign with an HMAC signature.
- ECDH. Go. In this case we create a symmetric key from ECDH. For this we will derive a shared key from the public key of Alice and Bob, and then define a single recipient which can derive the CEK (Content Encryption Key) using their private key. We will use the curves of P-256 (secp256r1), P-384 (secp384r1), P-521 (secp521r1) or SECP256K1 (as used with Bitcoin).
- RSA using COSE and CBOR. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\).
- RSA: dQ, dP and InvQ. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). The key pair also includes \(dQ\), \(dP\) and \(InvQ\), and these can be used with the Chinese remainder theory to optimize the decryption process.
Metasploit
- Armitage and Metasploit. Go.
- Exploiting Android with Metasploit. Go.
- Exploiting Android with Metasploit - Part 2. Go.
- Exploiting Windows/Mac OS X with Metasploit. Go.
- Remote Desktop Windows/Mac OS X with Metasploit. Go.
- Metasploit. Go.
- Internet of Things Security. Go.
- Metasploit (Enumeration and Scanning). Go.
- Metasploit (Malware). Go.
IP

 The following are a few interesting techniques around IP addresses:
The following are a few interesting techniques around IP addresses:
- Your details. IP. This shows your browser details.
- IP address analyser. IP. This involves converting an IP address to the host and network part of the address.
- IP subnet analyser. IP subnets. This involves converting an IP address to the host and network part of the address.
- IP address analyser. IP. This involves analysing IP addresses.
- Max subnets. Max subnets. This involves converting an IP address to the host and network part of the address.
- Route summarization. Summarization. This involves converting an IP address to the host and network part of the address.
- Whois. Whois. This does a basic Whois on a domain.
- URL Obfuscation. Obfuscation. This outlines URL obfuscation.
- HTTP Responses. Test. HTTP.
- Capturing Network Packets (Python). WinPCap. HTTP.
Cisco related
- Routing table. Routing table. This involves viewing a routing table for a Cisco device.
- ACL Generator. ACL. This involves a simple calculator for ACLs on network ranges.
- EIGRP metrics. EIGRP. Learn the basics of EIGRP metrics.
- VoIP B/W. VoIP. Calculate bandwidth for VoIP.
- Wild Card. Wild Card. On a Cisco device a wildcard mask is used to identify the parts of an IP address that need to be matched. It thus uses a wildcard mask, where a 0 in the bit position identifies that the device should match that bit, else a 1 shows that it should ignore it.
Protocols
- HTTP. HTTP. Show the request and response for HTTP.
- Ping analyser. IP. This involves converting a ping of a site.
IP Challenges
-
IP Test 1. IP Test. IP Classification test. This is a simple test which generates a range of IP addresses, and you must determine the IP address classification.
IP Subnet Challenge 1 Demo
-
IP Test 2. IP Test. IP Classification test Part 2. This test provides an address classification, and the user must find the addresses which are of this classification.
IP Subnet Challenge 2 Demo
-
IP Test 3. IP Test. IP Classification test Part 3. This test provides an address classification, where the network part of the address is determined.
IP Subnet Challenge 3 Demo
Subnet Challenges
- Subnet Test 1. Subnet Test. Subnet Test.
-
Subnet Test 2. Subnet Test. Subnet bits.
- Subnet Test 3. Subnet Test. Find the nth usable subnet. This test involves finding the nth usable subnet.
- Subnet Test 4. Subnet Test. Maximum subnets. This is a test page to determine the maximum number of subnets and hosts/subnet for IP classed addressing.
- Subnet Test 5. Subnet Test. Maximum host/subnet. This is a test page to determine the maximum number of hosts per subnet.
- Subnet Test 6. Subnet Test. Determine the required subnet mask for a given number of subnets. This is a test page to determine the required subnet mask for a given number of subnets and a given IP address classification.
- Subnet Test 7. Subnet Test. Determine the required subnet mask for a given number of host/subnet. This is a test page to determine the required subnet mask for a given number of hosts per subnet and a given IP address classification.
- Subnet Test 8. Subnet Test. Route summarization. This involves a calculation on route summarization.
- Subnet Test 9. Subnet Test. Binary to IP.
- Subnet Test 10. Subnet Test. Hex to IP.
-
Subnet Test 13. Subnet Test. Wild card mask network bits. Find the number of bits in the network part of the wild card mask. IP Wildcard challenge
- Subnet Test 14. Subnet Test. Wild card mask host bits. Find the number of bits in the host part of the wild card mask. IP Wildcard challenge
- Subnet Test 15. Subnet Test. Wild card mask ... find the network address. Find the network for the wild card mask. IP Wildcard challenge 2
- Subnet Test 16. Subnet Test. Find a matching IP address for a network and wild card mask. Find the IP for a network and a wild card mask.
- Subnet Test 17. Subnet Test. Find an address which is on a given network. Find an IP address on a network, for a given network address and subnet mask.
- Subnet Test 18. Subnet Test. Find an IP address on the same network. Find an IP address on the same subnet.
- Subnet Test 19. Subnet Test. Find subnet. Convert subnet mask.
- Megatest. Subnet Test. Challenging test for subnets.
JavaScript

JavaScript code allows execution within the browser, rather than on the server. It is often faster than code that runs on a server. Along with this we can also use Node.js, and which runs JavaScript code on a server.
Symmetric key
- AES. AES. In this example, we will use either a pre-generated key or a random one, and use AES (Rijndael) encryption.
- ChaCha20 and Poly1305. ChaCha. This page outlines Poly1305 and ChaCha20. ChaCha20 is a symmetric key method and Poly1305 is a message authentication code (MAC). They were created by Daniel J. Bernstein, and are alternatives to AES and HMAC.
- CMS (Padding). CMS. This page uses PKIJS encrypting on CMS. With CMS we can This document describes the Cryptographic Message Syntax (CMS). With this we can encapsulate an message within an encrypted entity.

Hashing
- Hash. Hash. This page defines a JavaScript Hash calculator. This uses a client-side JavaScript code to determine the hash signatures of a text value.
Signatures
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
- Boneh–Lynn–Shacham (BLS) signature. BLS. Boneh–Lynn–Shacham (BLS) signature method produces short signatures. They use elliptic curve pairing (and which are also known as bilinear maps).
Key exchange
- ECDH. ECDH. Elliptic Curve Diffie Hellman (ECDH) is used to generate a shared key. This implementation uses Elliptic Curve Cryptography (ECC) with JavaScript.
CryptoJS
- CryptoJS. CryptoJS. This page uses client-side JavaScript code to hashing, encrypt and sign, including for symmetric key (AES), streaming ciphers, hashing methods, and HMAC.
Blockchain
- PATRICIA trie. PATRICIA. In the following, we have the Top 2,500 Web sites in the world, and implemented with a Radix Trie (aka PATRICIA trie) In the following we have the Top 2,000 web sites on the Internet, and which have been indexed using the PATRICIA trie.
Public key
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
- RSA. RSA. RSA is an asymmetric encryption algorithm, which uses two keys, one to encrypt and the other to decrypt. It was created in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman, and is still one of the most widely used encryption methods. A typical application is in authenticating a sender, where the senders private key is used to encrypt a message, and then is decrypted by the receiver with the senders public key (which is known to anyone who wants it). It is also typically used for encrypting disks/files, such as for EFS.
Digital Certificates
- X.509 certificates in JavaScript. RSA and ECDSA Signed certificates. This page will generate either RSA and ECC key pairs, and then generate X.509 certificates, using either a signature of SHA1withRSA or SHA256withECDSA. For RSA signing we use an RSA private key to sign the certificate, and with ECDSA signing we use an ECC private key to sign the certificate.
Tokens
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
Random
- Random number generator. Rand. In the past, encryption and decryption had to be done through native code libraries, such as with Bouncy Castle and OpenSSL. With the increasing processing power of Web browsers, it is now possible to use encryption using JavaScript, which thus provides client-side processing of data. This Web page uses Javascript encryption, and generates a random 256-bit text key or a hex version. The 256-bit key is generated by generating 60 random numbers (from 0-25), and converting these to an ASCII character.
Malware obfuscation
- Malware obfuscation. Obfuscation. A malware writer will often hide certain keywords from the browser/human by encoding them in another format. This is typically done for hex coding (\xZZ), 16-bit unicoding (\uZZZZ) and octal coding (\ZZZ). To test, enter a value, and then press the button and it will convert encoded string.
Message Authentication Codes
- Chaskey (MAC). Chaskey. Chaskey Cipher is light-weight cryptography method for signing messages (MAC) using a 128-bit key. The hardware implementation only requires 3,334.33 gate equivalent with an operating clock frequency of 1 MHz (whereas Keccak requires 4,658 GE). In the page we create the Mac signature and also encrypt for CBC.
Other
- Password generation/hashing. Hashing. Linux can use salted passwords where the username, hashing method and hashed password are stored in a password file [More details]. The main methods are
Hashing

At times we need to generate secrets, such as encryption keys, from passwords or nonce values. A Key Derivation Function (KDF) is a verifiable way of doing this.
Key Derivation Functions (KDFs)
The following are the tips related to hashing:
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Password strength. Test. This outlines the strength of various passwords types.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
HKDF
The following are the tips related to Key derivation hashing:
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Hazmat HKDF for different hashing methods. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
-
HKDF key derivation with OpenSSL [
here]
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
PBKDF2
The following are the tips related to Key derivation hashing:
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- AES GCM (Python) with PBKDF2. AES GCM (Python) with PBKDF2.
- Fernet with PBKDF2 . AES GCM (Python) with PBKDF2.
- PBKDF2 key derivation. AES GCM (Python) with PBKDF2.
- Key Rotation with Fernet. AES GCM (Python) with PBKDF2.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Bcrypt
The following are the tips related to Key derivation hashing:
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- BCrypt. BCrypt. BCrypt with Rust.
-
Hash to password with Go. Hashing to Argon2, Scrypt and BCrypt. Hash to password with Go, including Argon2, Scrypt and BCrypt.
scrypt
- scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Argon 2
The following are the tips related to Key derivation hashing:
- Argon 2. Go. Outline of Argon2.
- Argon 2 with NaCl. Go. Outline of Argon2 using NaCl.
- Argon 2. Argon 2. Argon 2 with Rust.
- Balloon. Go. Outline of Balloon.
Other
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
- Double ratchet. Go. Outline of double ratcheting.
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
Outline
HMAC Key Derivation function (HKDF) is used to derive an encryption key from a passphrase. Initially, HKDF creates a pseudorandom key (PRK) using a passphrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), and along with a salt value. Next, the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys [RFC 5869][article]. In this case, we will use SHA-256.
The following shows how an encryption key can be generated using HKDF, and where we need a secret and a salt value. Both Bob and Alice have the same secret and salt.

With PBKDF2 (Password Based Key Derivation Function 2), we hash for a given number of rounds:

Key exchange

Key exchange is a way for Bob and Alice to communicate and for them to agree on a shared secret. The original method defined uses discrete logarithms (Diffie-Hellman), but most modern methods use elliptic curve techniques (ECDH). As quantum computers can crack both discrete log and elliptic curve methods, there are post quantum cryptography methods proposed. This includes SIDH, CSIDH, SIKE, and NewHope.
Key interchange/generation (Diffie-Hellman)
The following relates to key interchange:
- Selecting \(g\) in Diffie Hellman. G in Diffie Hellman. Picking a safe value of the generator \(g\) in discrete logarithms.
- Diffie-Hellman. Diffie-Hellman Calculation. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Real example). Diffie-Hellman Real. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Python). Diffie-Hellman. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (pre-compute). Diffie-Hellman (pre-compute). Many sites use the same prime numbers, which can then be cracked with a pre-computing attack.
- Key generation. Key gen. This will generate keys for different methods based on a passphrase.
- Diffie-Hellman (Man-in-the-middle). DF. This outlines the man-in-the-middle method for Diffie-Hellman.
- An Alternative Diffie-Hellman method. Alterative DH. This outlines an alternative Diffie-Hellman method.
Authenticated Key Exchange
The following are the tips related to Key derivation hashing:
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- MTI/A0. MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{ax+by} \pmod p\). MTI (Matsumoto, Takashima, Imai).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0. MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{x+y} \pmod p\)
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). The resultant key is \(xyG \)
- MTI/C0. MTI/C0. This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{xy} \pmod p\)
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG\).
- MTI/C1. MTI/C1. This outlines MTI/C1, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{abxy} \pmod p\).
- MQV (Menezes–Qu–Vanstone). MQV. MQV was created Alfred Menezes, Minghua Qu and Scott Vanstone in 1995 and is an authenticated key exchange method. Alice holds a key pair \((A,a)\) and Bob has a key pair \((B,b)\). With this \(a\) is Alice's private key, and \(A=aG\) is her public key. For Bob, his public key will be \(B=aG\) and a private key of \(b\), and where \(G\) is the base point on the elliptic curve.
- HMQV (Menezes–Qu–Vanstone). HMQV. HMQV builds on MQV and adds the identity of Bob and Alice.
- ECDH with X25519 and Blake2b. ECDH with X25519 and Blake2b. This uses PyNaCl to create an authenticated key exchange and uses X25519 and Blake2b.
Elliptic Curve (ECDH) - Python
The following are the tips related to ECC:
- Elliptic Curve. Elliptic Curve. Elliptic Curve is a public key method which can also be used to generate a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with simple parameters. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
Elliptic Curve (ECDH) - Golang and Node.js
The following are the tips related to ECC:
- ECDH with Go. ECDH. ECDH with Go.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with node.js. ECDH. ECDH with node.js.
- ECDH with JavaScript. ECDH. Elliptic Curve Diffie Hellman.
Password Authenticated Key Exchange (PAKE)
The following are the tips related to Key derivation hashing:
- SPAKE2. Go. Outline of SPAKE2.
- OPAQUE. Go. Outline of OPAQUE.
- SPEKE. Go. Outline of SPEKE (Simple Password Exponential Key Exchange).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
- J-PAKE. J-PAKE. This example generates a shared key based on a shared password.
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses discrete logs.
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
PQC NIST Finalists (Key Exchange)
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Key interchange/generation (Other)

The following relates to key interchange:
- Curve25519. Curve25519. This outlines Curve25519, which is used in the Tor network.
- Authenticated Key Exchange (Discrete logs). YAK. Key exchange with public keys and uses discrete logs.
- Authenticated Key Exchange (ECC). YAK. Key exchange with public keys and uses elliptic curve methods.
- Shamir No-key protocol. Shamir No Key. In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated.
- Shamir No-key protocol (sepc256k1). Shamir No Key (EC). In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated using the sepc256k1 elliptic curve.
- Conference keying (Burmester-Desmedt method). Conference keying. In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it.
- Conference keying (Burmester-Desmedt method) - Elliptic Curve (sepc256k1). Conference keying Elliptic Curve (sepc256k1). In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it, and uses the sepc256k1 elliptic curve.
Key exchange (with pairing)
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Kryptology

We need to build a new Internet. One that is build on mathematics and certainty, rather than the patchy version we have now. For this we need a layer of cryptography at the lowest level, and build software interfaces on top of this. Along with this we now have cryptographic methods which can now provide a foundation of trust, and which preserve privacy. And so the old libraries of OpenSSL are being squeezed out in favour of the new ones which are built on a solid foundation. The latest of these new "privacy-aware" libraries is Kryptology, and created by Coinbase. This library provides the APIs that developers need, in order to apply to areas of blockchain development. This library include BLS (Boneh-Lynn-Shacham) signatures, Zero-knowledge Proofs (ZKPs) and Shamir Secret Shares (SSS). With BLS we can digitally sign for data, but also preserve its privacy. Applications of this include group signatures, where multiple entities can merge their signing keys together and provide a single signature for a transaction. With SSS, we can split encryption keys up into shares, and then distribute them across a network. When required, we can call these shares back to reconstruct the key.
The focus for Coinbase seems to be the application of privacy coins, and where no tracking can be applied to the usage of these digital coins. This should support full anonymity for transactions, as opposed to Bitcoin which only supports pseudo-anonymity.

ECC Basics
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining n.G for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Points (Base Point and Others). Elliptic Curve points. Two common curves used in ECC (Elliptic Curve Cryptography) are secp256k1 (as used in Bitcoin and Ethereum) and P256 (secp256r1). The "k1" refers to the Kolbitz curve 1 (named after the creator of ECC). With these we have a base point which are can operate on. This is typically defined as \(G\). We can then operate on this with add and multiply operation. For example, \(2G=G+G\) and \(P=n.G\). In this following we will show the base point for a number of common curves, such as secp256r1, P256, Pallas, Curve 25519, BLS12381G1, BLS12381G2, BLS12377G1 and BLS12377G2.
ECDH
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret. We will use Golang and the Krytology library.
Simple ECC on curves
- Public key points for curves. Simple. Display public key points for scalars.
BLS Curve
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
Accumulator and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
Pallas Curve
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
Pairing-based Crypto
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
ElGamal and ECC
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a numerical input.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
Shamir Secret Shares
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Homomorphic Encryption
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Zero knowledge proofs
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
Verifiable Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Hash to scalar and point
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
CP-ABE
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Lattice cryptography

Latice cryptography is proposed as a post-quantum robust method for public key encryption, especially focused on digital signatures and key exchange mechanisms (KEMs).
Principles
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
NTRU
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- Lattice Encryption: NTRU Key Generation Python). NTRU. Outlines how NTRU operates for key generation.
Homomorphic
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Digital Signatures
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
Public-Key Encryption/Key Exchange
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
Light-weight cryptography

While AES and SHA work well together within computer systems, they struggle in an IoT/embedded world as they take up: too much processing power; too much physical space; and consume too much battery power. So NIST outlines a number of methods which can be used for light-weight cryptography, and which could be useful in IoT and RFID devices [1]. They define the device spectrum as:
- Conventional cryptography. Servers and Desktops. Tablets and smart phones.
- Light-weight cryptography. Embedded Systems. RFID and Sensor Networks.
With embedded systems, we commonly see 8-bit, 16-bit and 32-bit microcontrollers, and which would struggle to cope with real-time demands for conventional cryptography methods. And in the 40+ years since the first 4-bit processor, there is even a strong market for 4-bit processors. RFID and sensor network devices, especially, have limited numbers of gates available for security, and are often highly constrained with the power drain on the device.
So AES is typically a non-starter for many embedded devices. In light-weight cryptography, we often see smaller block size (typically 64 bits or 80 bits), smaller keys (often less than 90 bits) and less complex rounds (and where the S-boxes often just have 4-bits).
For light-weight cryptography the main constraints that we have are typically related to ener requirements, gate equivalents (GEs), and timing. With passive RFID devices, we do not have an associated battery for the power supply, and where the chip must power itself from energy coupled from the radio wave. An RFID device is thus likely to be severely constrained in the power drain associated with any cryptography functions, along with being constrained for the timing requirements and for the number of gates used. Even if an RFID device has an associated battery (active RFID), it may be difficult to recharge the battery, so the drain on power must often be minimised.
There is thus often a compromise between the cryptography method used and the overall security of the method. Thus often light-weight cryptography methods balance performance (throughput) against power drain and GE, and do not perform as well as main-stream cryptography standards (such as AES and SHA-256). Along with this the method must also have a low requirement for RAM (where the method requires the usage of running memory to perform its operation) and ROM (where the method is stored on the device). In order to assess the strengths of various methods we often define the area that the cryptography function will use on the device – and which is defined in \(µm^2\). The NIST finalists are defined in this [article]
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- GIFT AEAD. GIFT. GIFT is a light-weight block cipher. It is a (NIST Finalist)
- Elephant. Elephant. Elephant is a light-weight stream cipher. It is a (NIST Finalist).
- TinyJambu. TinyJambu. TinyJambu is a light-weight block cipher. It is a (NIST Finalist)
- Isap AEAD. Isap. Isap is a light-weight block cipher. It is a (NIST Finalist)
- PHOTON-Beetle AEAD. PHOTON-Beetle. PHOTON-Beetle is a light-weight block cipher. It is a (NIST Finalist)
- Romulus AEAD. Romulus. Romulus is a light-weight block cipher. It is a (NIST Finalist)
- Sparkle AEAD. Sparkle. Sparkle is a light-weight block cipher. It is a (NIST Finalist)
- CLEFIA. CLEFIA. CLEFIA is a light-weight block cipher.
- LED. LED. LED is a light-weight block cipher.
- Piccolo. Piccolo. Piccolo is an ultra light-weight block cipher.
- PRESENT. PRESENT. Present is a light-weight block cipher.
- Pyjamask. Pyjamask. Pyjamask is a light-weight block cipher.
- SIMON. SIMON. SIMON is a light-weight block cipher.
- SKINNY. SKINNY. SKINNEY is a light-weight block cipher.
- SPECK. SPECK. SPECK is a light-weight block cipher.
- XTEA. XTEA. XTEA is a light-weight block cipher.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encryption/Decryption. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.
Light-weight crypto (Other)
- Chaskey (MAC). Chaskey. Chaskey is a light-weight MAC function.
- Chaskey (MAC). Chaskey (Python). Chaskey is a light-weight MAC function.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (ASCON)
ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRFF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
Discrete Logs (Solving)

A discrete log problem is in the form of \(g^x \pmod p\) and where we know \(g\) and \(p\) and must solve for \(x\).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Message Authentication Code (MAC)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
HMAC
The following are the tips related to Key-based hashing:
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authentication both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2), Blake2b, SM3 and SHA-3. This page outlines the HMAC-MD5 methods using the Hazmat cryptography layer.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- HMAC (COSE). Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT with HMMAC. Go. In this case we create a CWT token, and sign with an HMAC signature.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- HMAC with Rust. HMAC. HMAC with Rust.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HMAC with OpenSSL. MACs with OpenSSL. HMAC in OpenSSL for a given input value, password and hashing method.
Cipher MACs
The following are the tips related to Key-based hashing:
- MACs with OpenSSL. MACs with OpenSSL. MAC methods implemented in OpenSSL, including CMAC and GMAC.
Key-based hashing
The following are the tips related to Key-based hashing:
- SipHash. Siphash. Siphash is a fast key-based hashing method.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Meow. Meow. Meow is one of the fastest hashing methods.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
Magic Numbers

This pages contains information related to magic numbers in file formats.
Network and File Forensics
- Magic numbers. Magic. This provides information on magic number for file forensics.
Graphics formats
- JPEG Analysis. JPEGs. This provides an analysis of JPEG files.
- GIF Analysis. GIFs. This provides an analysis of GIF files.
- TIF Analysis. TIFs. This provides an analysis of TIF files.
- PNG Analysis. PNGs. This provides an analysis of PNG files.
- BMP Analysis. BMPs. This provides an analysis of BMP files.
- PSD Analysis. PSDs. This provides an analysis of PSD files.
- WMF Analysis. WMF. This provides an analysis of WMF files.
- Adobe Illustrator Analysis. AI. This provides an analysis of AI files.
- Adobe In Design Analysis. INDD. This provides an analysis of INDD files.
- MIDI file. MIDI. This provides an analysis of MID files.
- ICO file. ICO. This provides an analysis of ICO files.
- PS file. PS. This provides an analysis of PS files.
- EPS file. EPS. This provides an analysis of EPS files.
- VSD file. VSD. This provides an analysis of Microsft Visio (VSD) files.
Video and audio formats
- MP3 Analysis. MP3s. This provides an analysis of MP3 files.
- AVI Analysis. AVIs. This provides an analysis of AVI files.
- Flash SWF Analysis. SWFs. This provides an analysis of Flash files.
- Flash FLV Analysis. FLVs. This provides an analysis of FLV files.
- MP4 Analysis. MP4. This provides an analysis of MP4 files.
- MOV Analysis. MOV. This provides an analysis of MOV files.
- WMV Analysis. WMV. This provides an analysis of WMV files.
- WMA Analysis. WMA. This provides an analysis of WMA files.
- JPEG 2000 Analysis. JPEG 2. This provides an analysis of JPEG 2000 files.
- WAV Analysis. WAV. This provides an analysis of WAV files.
Zips, Archives and Library files
- ZIP/Archive Analysis. ZIPs. This provides an analysis of ZIP/Achive files.
- GZ Analysis. GZ. This provides an analysis of GZip files.
- Tar Analysis. Tar. This provides an analysis of TAR files.
- MSI Analysis. MSI. This provides an analysis of MSI files.
- OBJ Analysis. OBJ. This provides an analysis of OBJ files.
- DLL Analysis. DLL. This provides an analysis of DLL files.
- CAB Analysis. CAB. This provides an analysis of CAB files.
- EXE Analysis. EXE. This provides an analysis of EXE files.
- RAR Analysis. RAR. This provides an analysis of RAR files.
- SYS Analysis. SYS. This provides an analysis of SYS files.
- HLP Analysis. HLP. This provides an analysis of HLP files.
- VMDK Analysis. VMDK. This provides an analysis of VMDK files (VMWare Virtual Disks).
- PST Analysis. PST. This provides an analysis of PST files (Outlook Email File).
- JAR Analysis. JAR. This provides an analysis of JAR files.
- SLN Analysis. SLN. This provides an analysis of Microsoft SLN files.
- Class Analysis. Class. This provides an analysis of Java Class files.
- Zlib. Zlib. This provides an analysis of Zlib files.
Documents
- PDF Analysis. PDFs. This provides an analysis of PDF files.
- DOC Analysis. DOCs. This provides an analysis of DOC files.
- RTF Analysis. RTFs. This provides an analysis of RTF files.
- XLS Analysis. XLSs. This provides an analysis of XLS files.
- PPT Analysis. PPTs. This provides an analysis of PPT files.
- MMP File. MMP. This provides an analysis of MMP files.
- DOCX Analysis. DOCX. This provides an analysis of DOCX files.
- XLSX Analysis. XLSX. This provides an analysis of XLSX files.
- PPTX Analysis. PPTX. This provides an analysis of PPTX files.
- MDB Analysis. MDB. This provides an analysis of MDB files.
- Outlook Message Analysis. MSG. This provides an analysis of MSG files.
Disk Image
- Raw disk format. RAW. This provides an analysis of the RAW disk format.
Tests
- File Forensics Test. File Test File Forensics Test.
- File Forensics Test (Fun). File Test (Fun) File Forensics Test.
Presentations
MIRACL Core Library

MIRACL Core is an open source library, and includes a wide range of public key encryption methods. It is especially focused on elliptic curve and pairing-friendly methods, but also supports a wide range of encryption methods, including RSA, AES and hashing. Overall, it can be ported onto a wide range of systems and supports C, C++, Go, Rust, Python, Java, Javascript and Swift. Along with this it supports limited capability devices such as the Arduino infrastructure. The GitHub repository is [here].
BN254
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.

Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- CL Signatures. CL. CL Signatures in Go using MIRACL.
- CL Signatures (advanced pairing). CL. CL Signatures in Go using MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages using MIRACL.
- PS Signatures. PS. Signatures using PS for short signatures using MIRACL.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures using MIRACL.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.

Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
Rust examples
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
NaCl

PyNaCl is a Python port of LibSodium. It integrates the latest cryptography methods, such as AES, XChaCha20, Blake2b and X25519.
Symmetric Key
- Symmetric key. Symmetric key (XChaCha20 and Poly1305). With symmetric key, Bob and Alice have the same key. NaCl uses the XChaCha20 method, and which supports stream encryption (and which does not require padding as a block cipher does, and is also faster than block cipher modes). ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16 byte nonce. XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24 byte nonce. It has a lower propability of nonce misuse than ChaCha20.
- Encryption with a password. Symmetric Key with KDF. In symmetric key, we generate a secret key. This key is typically a random value or generated from a password and a salt value. If we use a password, we typically use a KDF (Key Derivation Function), and which uses a password and a salt value, in order to create a key of a given size. In this case we will use Argon2i, and which is memory resilent.
Hybrid Encryption
- Box. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Hashing
- Hashing and KDF (Argon2 and scrypt). Hashing and KDF. This case we will use PyNaCl (Networking and Cryptography) library, and which is a Python binding to libsodium. We will hash a password using SHA-256 and SHA-512, and also create a KDF (Key Derivation Function) using scrypt and Argon2.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
Ed25519
-
Ed25519. Ed25519. Using Ed25519 for digital signatures.
-
Finding Points on Ed25519. X25519 (Points).
In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 (Key Exchange)
- X25519 + BLAKE2b key-exchange. X25519. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
Curve 25519
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
Node.js

Node.js uses the JavaScript programming langauge as its base, and allows for code to be run on a server, rather than in the browser (such as with pure JavaScript). To run a node.js program, we run "node myfile.js", and use NPM to install libraries.
Symmetric key
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
RSA and public key
- RSA Opt imal Asymmetric Encryption Padding (OAEP) using Node.js. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
ECC Keys
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.

Hashing
- Hashing with node.js (All). Hashing. Hashing with node.js.
- Hashing with node.js (Selection). Hashing. Hashing with node.js.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- ECDSA with node.js. ECDSA. ECDSA with node.js.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
Key exchange
- Diffie-Hellman with node.js (random prime). DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method and uses a randomly generated prime number (press the button to generate a new prime).
- Diffie-Hellman with node.js. DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method. Each time the prime number will be fixed for the DH group selected.
- ECDH with node.js. ECDH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Elliptic Curve Diffie Hellman (ECDH) key exchange method.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
Key derivation
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
CryptoJS
- CryptoJS (in node.js). CryptoJS (Node.js). Various crypto methods in the browser.
Bulletproofs
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
Blockchain
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
Proxy encryption
- Proxy Encryption - Encrypting With Public Key, And Decrypt with Private Key. Proxy01. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This page just creates a key pair for Alice, and uses it to encrypt with the public key , and decrypt with the private key.
- Proxy Encryption. Proxy02. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This will go through the full use case of proxy re-encryption.
Tokens
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
Random
- Fortuna with node.js. Fortuna. Fortuna random numbers with node.js.
Other
- FPE with node.js. FPR. FPE with node.js.
- Puny with node.js. Puny. Puny character format with node.js.
Accumulators and Witnesses
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
PGP
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Password Entropy
- Password Entropy with Node.js. Password Entropy. Password entropy measures the strength of a password, and is measured as the number of bits which could represent all of the possibilities. An entropy score of less than 25 identifies a poor password, and between 25 and 50 is a weak password. For 50 to 75 we have a reasonable password, and between 75 and 100 is a very good password. Over 100 is an excellent password. The strength of the password relates to the number of characters used, and also the number of characters in the password.
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
- Homomorphic Encryption with Node.js and BGV. Homomorphic Encryption with Node.js and BFG. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BGV method.
Oblivious Transfer (OT)

Oblivious Transfer allows Bob to select data from Alice, but for Alice not to know which value has been selected.
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
OpenSSH

OpenSSH supports the usage of the SSH protocol. This allows for a remote login. One tool which is uses is ssh-keygen, and which allow for the generation of RSA, DSA and elliptic-curve keys that. These can be used for user and host authentication, such as for GitHub login and Cloud instance login.
OpenSSH
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here].
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
Outline

OpenSSL

OpenSSL is a standard library that implements cryptography.
Symmetric key (Command line)
-
Symmetric Key Encryption (OpenSSL 1.x) [here]. In this case we will create cipher text from OpenSSL 1.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 1.x) [here].In this case we will decrypt cipher text from OpenSSL 1.x using a key derived from a password
-
Symmetric Key Encryption (OpenSSL 3.x) [here]. In this case we will create cipher text from OpenSSL 3.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 3.x) [here].In this case we will decrypt cipher text from OpenSSL 3.x using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password.
Hashing
-
Hashing [here] OpenSSL supports a wide range of hashing methods including BLAKE2b, Gost, MD4, MD5, RMD-160, SHA-1, SHA-3, SHA-256 and SHA-512.
Libre OpenSSL
-
Symmetric Key Encryption using Libre OpenSSL [here]. In this case we will create cipher text from Libre OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption using Libre OpenSSL [here]. In this case we will decrypt ciphertext from Libre OpenSSL using a key derived from a password.
-
Hashing [here] Libre OpenSSL supports a wide range of hashing methods including Gost, MD4, MD5, RMD-160, SHA-1, SHA-256 and SHA-512.
Diffie-Hellman parameter generation
-
DH Parameters with OpenSSL [here]. The Diffie-Hellman (DH) method is perhaps one of the greatest inventions in Cybersecurity, and was created by Whitfield Diffie and Marty Hellman. With the DH method, Bob creates a random value (\(b\)) and Alice also creates a random value (\(a\)). Next Bob computes \(B=g^b \pmod p\) and sends it to Alice. Alice computes \(A=g^a \pmod p\) and sends this to Bob. Bob raises the value of \(A\) to the power of \(b\) and takes \(\pmod p\), and Alice raises \(B\) to the power of \(a\) and takes \(\pmod p\). In the end, they will have the same shared value: \(g^{ab} \pmod p\). This can then be used to derive an encryption key that they can use for a secure tunnel. Overall, \(p\) is the large prime number, and also known as the shared modulus between Bob and Alice.
Key derivation function
-
PBKDF2 key derivation with OpenSSL [here] PBKDF2 (Password Key Derivation Function 2) is a key derivation method. Overall it is relatively slow in its operation and where we take a password, a salt value, hashing method, and a number of iterations, in order to produce a given size of encryption key.
-
HKDF key derivation with OpenSSL [here] HKDF (HMAC Key Derivation function) is used to derive an encryption key from a pass phrase. Initially HKDF creates a pseudorandom key (PRK) using a pass phrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), andalong with a salt value. Next the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys.
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Passwords
-
Password example [here]. This page uses the OpenSSL library hash password generator, which is used in UNIX systems for the hashing of passwords which are contained in /etc/shadow and /etc/passwd. For newer passwords, the "-1" options is used to created the hashed value.
-
Hashed passwords with OpenSSL [here].
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
Public key
-
Generating an ECC key pair with OpenSSL [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)).
-
Generating an RSA key pair with OpenSSL [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2).
-
Generating an RSA key pair with OpenSSL with encryption [here]. This page implements RSA key pair generation with an encrypted key pair. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). In this case we will encrypt the key pair with either 3DES, 128-bit AES, 192-bit AES or 256-bit AES. The same password must be used to encrypt and decrypt.
-
Generate prime with OpenSSL [here]. Prime numbers are important in public key encrytion, and are used with RSA and ECC. For RSA, we generate two prime numbers (\(p\) and \(q\)) and which are multiplied together to create a modulus (\(N\)). If these prime numbers have 512 bit values, the modulus will be a 1,024 bit value. This defines the basic secure of RSA. With elliptic curve we use smaller prime numbers, such as 256-bit values for the secp256k1 curve.
ASN1 parsing
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). We will parse using asn1parse, and reveal the parameters.
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)) [RSA key pair]. We will parse using asn1parse, and reveal the parameters.
- DSA Parameters with asn1parse. DSA parameters with OpenSSL with asn1parse. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA (Digital Signature Algorithm)
- DSA Parameters. DSA parameters with OpenSSL. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
MAC (Message Authentication Code)
- HMAC with OpenSSL. MACs with OpenSSL. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authenticate both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2) and SHA-3. In this case we will use OpenSSL to generate the HMAC value.
- MACs with OpenSSL. MACs with OpenSSL. In the following we will generate MACs for HMAC, GMAC, CMAC, Blake2bmac, Blake2smac, KMAC128 and KMAC256. Overall, we will use an encryption key defined as a hex value for GMAC and CMAC, and a pass phrase for the others. The message is "hello".
Signing
- Digital signing a plaintext message with OpenSSL. Signing with OpenSSL. With digital signing, we can take a message, and create a signature. This normally involves signing with a private key and digital certificate. The signed message can be an a MIME format, and which can be integrated into an email message. In this can we have a 512-bit RSA key pair that will sign a plain text message.
Encrypting emails
- Encrypting an email message in OpenSSL. Encrypting messages with OpenSSL. With public key encryption, we can take a message, and encrypt it with the recipiant's public key. In this can we have a 512-bit RSA public key to encrypt a message.
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Random number generation with OpenSSL
-
Random number generator [here]. Random numbers are important in generating encryption keys and salt values. In this case OpenSSL generates a random number (in a Base64 format) for a given number of bytes.
Outline (C#/Python)
-
Symmetric Key Encryption (C#) [here]. This page uses the OpenSSL library through a C#/.NET wrapper. The DLLs it interfaces to are libeay32.dll and ssleay32.dll. OpenSSL supports a wide range of encryption methods, including 128-bit AES, 192-bit AES, 256-bit AES and Blowfish (bf). Different modes of ECB, CBC, and OFB are implemented. The examples use a default IV of "1234".
-
AES in Python with OpenSSL output [here]
-
Producing OpenSSL AES Encrypted String from C# [here]
Digital Certificates
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
Paillier - Partial Homomorphic Encryption

The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Fundamentals
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier).
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Using RSA
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
Applications
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Homomorphic hashing
- Homomorphic Hashing with Golang. Homomorphic hashing. Normally with hashing methods, we need to take all the previous data and new data in order to create a new hash value for our data. In a homomorphic hashing method, we can basically take the previous hash, and then add on any new data values. We can also remove previous data values from our hash, too. This is more efficient in computing, as we do not have to process all of our data into a new hash, and can use simple homomorphic operations for the computation. The method we will use (LtHash) was initially defined by Bellare and Micciancio and updated Lewi et al at Facebook.
Identity Based Encryption (IBE)

This page outlines a few basic principles around the usage of IBE.
Identity Based Encryption (Pairing based)
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pair-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Identity Based Encryption (Others)
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Güther's implicitly certified identity-based public keys (IBE). Günther. This method allows Bob to generate Alices public key from her identity and publicly available parameters.
- Girault's self-certified public keys (IBE). Girault. This method allows Bob to generate Alices public key from her identity and publicly available parameters, and where we use an RSA key pair to self-certify Alice's public key.
Intrusion Detection Systems (IDS)
- Intrusion Detection Systems. Snort. This outlines some of the basics of IDS, including the requirement for Intrusion Detection Systems (IDSs), and where they are used.
- Advanced Network Forensics (Snort). Adv Network Forensics. This provides information on how to detect threats through network forensics with Snort
Snort

- Snort IDS. Snort. This is a Snort Analyser.
- Snort IDS 2 with rules editor. Snort. This provides information on how to detect threats through network forensics with Snort, and with an editing function for rules.
Presentation
IoT

The key objectives of this page are: Understand how a Pen Tester can generate vulnerabilities and test using the Metasploit framework; Define the options and payloads required to generate and use vulnerabilities; and Gaining remote access.
Devices
- Access the Wi-fi kettle. Go. This page outines how to access a wi-fi enabled kettle.
- Philips Hue Wireless Lighting. Go. This page shows how to use RESTful Web services to access to the Hue Led Lamps.
- Kali and R-PI. Go. This page shows the setup of a security testing infrastructure using a Raspberry Pi (R-PI) and a wifi access point.
- Kali, R-PI and RF electrical socket. Go. This page shows the control of an RF electical socket from a RPI.
- Capture from a Polar H10 heat rate sensor. Go. This page shows the capture of the Polar H10 heart sensor with an Ubertooth One.
- Trusted IoT: Linking IoT Devices to NFTs. Go. This page outlines a research paper which links a device to an NFT (Non-fungible Token).
Shodan Scanning
-
IoT Scan (Shodan). Go. This page includes a search of the Internet for key terms, such as for "apache", "mysql" and "cisco".
- IoT Banner Scan (Shodan). Go. This page includes a search of the Internet for key terms with the banner as a result (for the Top 10)
- Internet Services (Shodan). Go. This page includes a search of the Internet for key terms and display the IP address and port.
IoT Libraries
- libDisco with Go. libDisco. libdisco is a Golang library which can be used to create secure connections. It is based on the STROBE protocol framework. Symmetric cryptographic primitives rely on SHA-3 permutation, and asymmetric cryptographic primitives on X25519 and ed25519. STROBE defines a range of cryptographic protocols to integrate with IoT devices. In order to reduce processing, energy and memory requirements, it only uses Keccak (SHA-3) to encrypt and authenticate messages.
COSE/COBR
In computer security, we often have to represent binary data, in single values or groups of characters, bytes, words, long words, signed integers, floating-point values, double-precision floating-point values, and so on. This might be in the form of a data object, a signature or even encrypted content. For this, the ANS.1 DER format is often used, such as presenting digital certificates and signatures. An improvement on this for small messages with security is Concise Binary Object Representation (CBOR) — and which is defined in RFC8949 [1]. While JSON represents text-based data objects CBOR focuses on binary objects. It has been designed to create a lightweight encoder and decoder. This supports the use of CBOR within an IoT infrastructure. The data, also, does not require a data schema to be able to decode it, along with being extensible. CBOR defines the format of binary data with data objects and messages. We can then integrate security with CBOR Object Signing and Encryption (COSE), and which is defined in RFC8152 [2]. This includes signatures, message authentication codes (MACs), encryption and creating serialised objects.
- 128-bit AES GCM. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) can then build on this to include signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use a symmetric key to encrypt a message, and then decrypt it. In this case we will use AES GCM with a static 128-bit key ("0x000102030405060708090a0b0c0d0e0f").
- 256-bit AES GCM. Go. In this case we will use AES GCM using a random 256-bit key (32 bytes).
- EdDSA. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) [2] can then build on this to includes signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use EdDSA to create a signature for a message.
- ECDSA. Go. In this case we will use ECDSA to create a signature for a message.
- HMAC. Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT. Go. In this case we create a CWT token, and sign with an HMAC signature.
- ECDH. Go. In this case we create a symmetric key from ECDH. For this we will derive a shared key from the public key of Alice and Bob, and then define a single recipient which can derive the CEK (Content Encryption Key) using their private key. We will use the curves of P-256 (secp256r1), P-384 (secp384r1), P-521 (secp521r1) or SECP256K1 (as used with Bitcoin).
- RSA using COSE and CBOR. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\).
- RSA: dQ, dP and InvQ. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). The key pair also includes \(dQ\), \(dP\) and \(InvQ\), and these can be used with the Chinese remainder theory to optimize the decryption process.
Metasploit
- Armitage and Metasploit. Go.
- Exploiting Android with Metasploit. Go.
- Exploiting Android with Metasploit - Part 2. Go.
- Exploiting Windows/Mac OS X with Metasploit. Go.
- Remote Desktop Windows/Mac OS X with Metasploit. Go.
- Metasploit. Go.
- Internet of Things Security. Go.
- Metasploit (Enumeration and Scanning). Go.
- Metasploit (Malware). Go.
IP

 The following are a few interesting techniques around IP addresses:
The following are a few interesting techniques around IP addresses:
- Your details. IP. This shows your browser details.
- IP address analyser. IP. This involves converting an IP address to the host and network part of the address.
- IP subnet analyser. IP subnets. This involves converting an IP address to the host and network part of the address.
- IP address analyser. IP. This involves analysing IP addresses.
- Max subnets. Max subnets. This involves converting an IP address to the host and network part of the address.
- Route summarization. Summarization. This involves converting an IP address to the host and network part of the address.
- Whois. Whois. This does a basic Whois on a domain.
- URL Obfuscation. Obfuscation. This outlines URL obfuscation.
- HTTP Responses. Test. HTTP.
- Capturing Network Packets (Python). WinPCap. HTTP.
Cisco related
- Routing table. Routing table. This involves viewing a routing table for a Cisco device.
- ACL Generator. ACL. This involves a simple calculator for ACLs on network ranges.
- EIGRP metrics. EIGRP. Learn the basics of EIGRP metrics.
- VoIP B/W. VoIP. Calculate bandwidth for VoIP.
- Wild Card. Wild Card. On a Cisco device a wildcard mask is used to identify the parts of an IP address that need to be matched. It thus uses a wildcard mask, where a 0 in the bit position identifies that the device should match that bit, else a 1 shows that it should ignore it.
Protocols
- HTTP. HTTP. Show the request and response for HTTP.
- Ping analyser. IP. This involves converting a ping of a site.
IP Challenges
-
IP Test 1. IP Test. IP Classification test. This is a simple test which generates a range of IP addresses, and you must determine the IP address classification.
IP Subnet Challenge 1 Demo
-
IP Test 2. IP Test. IP Classification test Part 2. This test provides an address classification, and the user must find the addresses which are of this classification.
IP Subnet Challenge 2 Demo
-
IP Test 3. IP Test. IP Classification test Part 3. This test provides an address classification, where the network part of the address is determined.
IP Subnet Challenge 3 Demo
Subnet Challenges
- Subnet Test 1. Subnet Test. Subnet Test.
-
Subnet Test 2. Subnet Test. Subnet bits.
- Subnet Test 3. Subnet Test. Find the nth usable subnet. This test involves finding the nth usable subnet.
- Subnet Test 4. Subnet Test. Maximum subnets. This is a test page to determine the maximum number of subnets and hosts/subnet for IP classed addressing.
- Subnet Test 5. Subnet Test. Maximum host/subnet. This is a test page to determine the maximum number of hosts per subnet.
- Subnet Test 6. Subnet Test. Determine the required subnet mask for a given number of subnets. This is a test page to determine the required subnet mask for a given number of subnets and a given IP address classification.
- Subnet Test 7. Subnet Test. Determine the required subnet mask for a given number of host/subnet. This is a test page to determine the required subnet mask for a given number of hosts per subnet and a given IP address classification.
- Subnet Test 8. Subnet Test. Route summarization. This involves a calculation on route summarization.
- Subnet Test 9. Subnet Test. Binary to IP.
- Subnet Test 10. Subnet Test. Hex to IP.
-
Subnet Test 13. Subnet Test. Wild card mask network bits. Find the number of bits in the network part of the wild card mask. IP Wildcard challenge
- Subnet Test 14. Subnet Test. Wild card mask host bits. Find the number of bits in the host part of the wild card mask. IP Wildcard challenge
- Subnet Test 15. Subnet Test. Wild card mask ... find the network address. Find the network for the wild card mask. IP Wildcard challenge 2
- Subnet Test 16. Subnet Test. Find a matching IP address for a network and wild card mask. Find the IP for a network and a wild card mask.
- Subnet Test 17. Subnet Test. Find an address which is on a given network. Find an IP address on a network, for a given network address and subnet mask.
- Subnet Test 18. Subnet Test. Find an IP address on the same network. Find an IP address on the same subnet.
- Subnet Test 19. Subnet Test. Find subnet. Convert subnet mask.
- Megatest. Subnet Test. Challenging test for subnets.
JavaScript

JavaScript code allows execution within the browser, rather than on the server. It is often faster than code that runs on a server. Along with this we can also use Node.js, and which runs JavaScript code on a server.
Symmetric key
- AES. AES. In this example, we will use either a pre-generated key or a random one, and use AES (Rijndael) encryption.
- ChaCha20 and Poly1305. ChaCha. This page outlines Poly1305 and ChaCha20. ChaCha20 is a symmetric key method and Poly1305 is a message authentication code (MAC). They were created by Daniel J. Bernstein, and are alternatives to AES and HMAC.
- CMS (Padding). CMS. This page uses PKIJS encrypting on CMS. With CMS we can This document describes the Cryptographic Message Syntax (CMS). With this we can encapsulate an message within an encrypted entity.

Hashing
- Hash. Hash. This page defines a JavaScript Hash calculator. This uses a client-side JavaScript code to determine the hash signatures of a text value.
Signatures
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
- Boneh–Lynn–Shacham (BLS) signature. BLS. Boneh–Lynn–Shacham (BLS) signature method produces short signatures. They use elliptic curve pairing (and which are also known as bilinear maps).
Key exchange
- ECDH. ECDH. Elliptic Curve Diffie Hellman (ECDH) is used to generate a shared key. This implementation uses Elliptic Curve Cryptography (ECC) with JavaScript.
CryptoJS
- CryptoJS. CryptoJS. This page uses client-side JavaScript code to hashing, encrypt and sign, including for symmetric key (AES), streaming ciphers, hashing methods, and HMAC.
Blockchain
- PATRICIA trie. PATRICIA. In the following, we have the Top 2,500 Web sites in the world, and implemented with a Radix Trie (aka PATRICIA trie) In the following we have the Top 2,000 web sites on the Internet, and which have been indexed using the PATRICIA trie.
Public key
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
- RSA. RSA. RSA is an asymmetric encryption algorithm, which uses two keys, one to encrypt and the other to decrypt. It was created in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman, and is still one of the most widely used encryption methods. A typical application is in authenticating a sender, where the senders private key is used to encrypt a message, and then is decrypted by the receiver with the senders public key (which is known to anyone who wants it). It is also typically used for encrypting disks/files, such as for EFS.
Digital Certificates
- X.509 certificates in JavaScript. RSA and ECDSA Signed certificates. This page will generate either RSA and ECC key pairs, and then generate X.509 certificates, using either a signature of SHA1withRSA or SHA256withECDSA. For RSA signing we use an RSA private key to sign the certificate, and with ECDSA signing we use an ECC private key to sign the certificate.
Tokens
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
Random
- Random number generator. Rand. In the past, encryption and decryption had to be done through native code libraries, such as with Bouncy Castle and OpenSSL. With the increasing processing power of Web browsers, it is now possible to use encryption using JavaScript, which thus provides client-side processing of data. This Web page uses Javascript encryption, and generates a random 256-bit text key or a hex version. The 256-bit key is generated by generating 60 random numbers (from 0-25), and converting these to an ASCII character.
Malware obfuscation
- Malware obfuscation. Obfuscation. A malware writer will often hide certain keywords from the browser/human by encoding them in another format. This is typically done for hex coding (\xZZ), 16-bit unicoding (\uZZZZ) and octal coding (\ZZZ). To test, enter a value, and then press the button and it will convert encoded string.
Message Authentication Codes
- Chaskey (MAC). Chaskey. Chaskey Cipher is light-weight cryptography method for signing messages (MAC) using a 128-bit key. The hardware implementation only requires 3,334.33 gate equivalent with an operating clock frequency of 1 MHz (whereas Keccak requires 4,658 GE). In the page we create the Mac signature and also encrypt for CBC.
Other
- Password generation/hashing. Hashing. Linux can use salted passwords where the username, hashing method and hashed password are stored in a password file [More details]. The main methods are
Hashing

At times we need to generate secrets, such as encryption keys, from passwords or nonce values. A Key Derivation Function (KDF) is a verifiable way of doing this.
Key Derivation Functions (KDFs)
The following are the tips related to hashing:
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Password strength. Test. This outlines the strength of various passwords types.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
HKDF
The following are the tips related to Key derivation hashing:
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Hazmat HKDF for different hashing methods. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
-
HKDF key derivation with OpenSSL [
here]
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
PBKDF2
The following are the tips related to Key derivation hashing:
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- AES GCM (Python) with PBKDF2. AES GCM (Python) with PBKDF2.
- Fernet with PBKDF2 . AES GCM (Python) with PBKDF2.
- PBKDF2 key derivation. AES GCM (Python) with PBKDF2.
- Key Rotation with Fernet. AES GCM (Python) with PBKDF2.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Bcrypt
The following are the tips related to Key derivation hashing:
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- BCrypt. BCrypt. BCrypt with Rust.
-
Hash to password with Go. Hashing to Argon2, Scrypt and BCrypt. Hash to password with Go, including Argon2, Scrypt and BCrypt.
scrypt
- scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Argon 2
The following are the tips related to Key derivation hashing:
- Argon 2. Go. Outline of Argon2.
- Argon 2 with NaCl. Go. Outline of Argon2 using NaCl.
- Argon 2. Argon 2. Argon 2 with Rust.
- Balloon. Go. Outline of Balloon.
Other
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
- Double ratchet. Go. Outline of double ratcheting.
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
Outline
HMAC Key Derivation function (HKDF) is used to derive an encryption key from a passphrase. Initially, HKDF creates a pseudorandom key (PRK) using a passphrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), and along with a salt value. Next, the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys [RFC 5869][article]. In this case, we will use SHA-256.
The following shows how an encryption key can be generated using HKDF, and where we need a secret and a salt value. Both Bob and Alice have the same secret and salt.

With PBKDF2 (Password Based Key Derivation Function 2), we hash for a given number of rounds:

Key exchange

Key exchange is a way for Bob and Alice to communicate and for them to agree on a shared secret. The original method defined uses discrete logarithms (Diffie-Hellman), but most modern methods use elliptic curve techniques (ECDH). As quantum computers can crack both discrete log and elliptic curve methods, there are post quantum cryptography methods proposed. This includes SIDH, CSIDH, SIKE, and NewHope.
Key interchange/generation (Diffie-Hellman)
The following relates to key interchange:
- Selecting \(g\) in Diffie Hellman. G in Diffie Hellman. Picking a safe value of the generator \(g\) in discrete logarithms.
- Diffie-Hellman. Diffie-Hellman Calculation. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Real example). Diffie-Hellman Real. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Python). Diffie-Hellman. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (pre-compute). Diffie-Hellman (pre-compute). Many sites use the same prime numbers, which can then be cracked with a pre-computing attack.
- Key generation. Key gen. This will generate keys for different methods based on a passphrase.
- Diffie-Hellman (Man-in-the-middle). DF. This outlines the man-in-the-middle method for Diffie-Hellman.
- An Alternative Diffie-Hellman method. Alterative DH. This outlines an alternative Diffie-Hellman method.
Authenticated Key Exchange
The following are the tips related to Key derivation hashing:
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- MTI/A0. MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{ax+by} \pmod p\). MTI (Matsumoto, Takashima, Imai).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0. MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{x+y} \pmod p\)
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). The resultant key is \(xyG \)
- MTI/C0. MTI/C0. This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{xy} \pmod p\)
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG\).
- MTI/C1. MTI/C1. This outlines MTI/C1, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{abxy} \pmod p\).
- MQV (Menezes–Qu–Vanstone). MQV. MQV was created Alfred Menezes, Minghua Qu and Scott Vanstone in 1995 and is an authenticated key exchange method. Alice holds a key pair \((A,a)\) and Bob has a key pair \((B,b)\). With this \(a\) is Alice's private key, and \(A=aG\) is her public key. For Bob, his public key will be \(B=aG\) and a private key of \(b\), and where \(G\) is the base point on the elliptic curve.
- HMQV (Menezes–Qu–Vanstone). HMQV. HMQV builds on MQV and adds the identity of Bob and Alice.
- ECDH with X25519 and Blake2b. ECDH with X25519 and Blake2b. This uses PyNaCl to create an authenticated key exchange and uses X25519 and Blake2b.
Elliptic Curve (ECDH) - Python
The following are the tips related to ECC:
- Elliptic Curve. Elliptic Curve. Elliptic Curve is a public key method which can also be used to generate a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with simple parameters. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
Elliptic Curve (ECDH) - Golang and Node.js
The following are the tips related to ECC:
- ECDH with Go. ECDH. ECDH with Go.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with node.js. ECDH. ECDH with node.js.
- ECDH with JavaScript. ECDH. Elliptic Curve Diffie Hellman.
Password Authenticated Key Exchange (PAKE)
The following are the tips related to Key derivation hashing:
- SPAKE2. Go. Outline of SPAKE2.
- OPAQUE. Go. Outline of OPAQUE.
- SPEKE. Go. Outline of SPEKE (Simple Password Exponential Key Exchange).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
- J-PAKE. J-PAKE. This example generates a shared key based on a shared password.
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses discrete logs.
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
PQC NIST Finalists (Key Exchange)
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Key interchange/generation (Other)

The following relates to key interchange:
- Curve25519. Curve25519. This outlines Curve25519, which is used in the Tor network.
- Authenticated Key Exchange (Discrete logs). YAK. Key exchange with public keys and uses discrete logs.
- Authenticated Key Exchange (ECC). YAK. Key exchange with public keys and uses elliptic curve methods.
- Shamir No-key protocol. Shamir No Key. In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated.
- Shamir No-key protocol (sepc256k1). Shamir No Key (EC). In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated using the sepc256k1 elliptic curve.
- Conference keying (Burmester-Desmedt method). Conference keying. In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it.
- Conference keying (Burmester-Desmedt method) - Elliptic Curve (sepc256k1). Conference keying Elliptic Curve (sepc256k1). In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it, and uses the sepc256k1 elliptic curve.
Key exchange (with pairing)
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Kryptology

We need to build a new Internet. One that is build on mathematics and certainty, rather than the patchy version we have now. For this we need a layer of cryptography at the lowest level, and build software interfaces on top of this. Along with this we now have cryptographic methods which can now provide a foundation of trust, and which preserve privacy. And so the old libraries of OpenSSL are being squeezed out in favour of the new ones which are built on a solid foundation. The latest of these new "privacy-aware" libraries is Kryptology, and created by Coinbase. This library provides the APIs that developers need, in order to apply to areas of blockchain development. This library include BLS (Boneh-Lynn-Shacham) signatures, Zero-knowledge Proofs (ZKPs) and Shamir Secret Shares (SSS). With BLS we can digitally sign for data, but also preserve its privacy. Applications of this include group signatures, where multiple entities can merge their signing keys together and provide a single signature for a transaction. With SSS, we can split encryption keys up into shares, and then distribute them across a network. When required, we can call these shares back to reconstruct the key.
The focus for Coinbase seems to be the application of privacy coins, and where no tracking can be applied to the usage of these digital coins. This should support full anonymity for transactions, as opposed to Bitcoin which only supports pseudo-anonymity.

ECC Basics
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining n.G for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Points (Base Point and Others). Elliptic Curve points. Two common curves used in ECC (Elliptic Curve Cryptography) are secp256k1 (as used in Bitcoin and Ethereum) and P256 (secp256r1). The "k1" refers to the Kolbitz curve 1 (named after the creator of ECC). With these we have a base point which are can operate on. This is typically defined as \(G\). We can then operate on this with add and multiply operation. For example, \(2G=G+G\) and \(P=n.G\). In this following we will show the base point for a number of common curves, such as secp256r1, P256, Pallas, Curve 25519, BLS12381G1, BLS12381G2, BLS12377G1 and BLS12377G2.
ECDH
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret. We will use Golang and the Krytology library.
Simple ECC on curves
- Public key points for curves. Simple. Display public key points for scalars.
BLS Curve
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
Accumulator and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
Pallas Curve
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
Pairing-based Crypto
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
ElGamal and ECC
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a numerical input.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
Shamir Secret Shares
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Homomorphic Encryption
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Zero knowledge proofs
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
Verifiable Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Hash to scalar and point
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
CP-ABE
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Lattice cryptography

Latice cryptography is proposed as a post-quantum robust method for public key encryption, especially focused on digital signatures and key exchange mechanisms (KEMs).
Principles
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
NTRU
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- Lattice Encryption: NTRU Key Generation Python). NTRU. Outlines how NTRU operates for key generation.
Homomorphic
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Digital Signatures
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
Public-Key Encryption/Key Exchange
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
Light-weight cryptography

While AES and SHA work well together within computer systems, they struggle in an IoT/embedded world as they take up: too much processing power; too much physical space; and consume too much battery power. So NIST outlines a number of methods which can be used for light-weight cryptography, and which could be useful in IoT and RFID devices [1]. They define the device spectrum as:
- Conventional cryptography. Servers and Desktops. Tablets and smart phones.
- Light-weight cryptography. Embedded Systems. RFID and Sensor Networks.
With embedded systems, we commonly see 8-bit, 16-bit and 32-bit microcontrollers, and which would struggle to cope with real-time demands for conventional cryptography methods. And in the 40+ years since the first 4-bit processor, there is even a strong market for 4-bit processors. RFID and sensor network devices, especially, have limited numbers of gates available for security, and are often highly constrained with the power drain on the device.
So AES is typically a non-starter for many embedded devices. In light-weight cryptography, we often see smaller block size (typically 64 bits or 80 bits), smaller keys (often less than 90 bits) and less complex rounds (and where the S-boxes often just have 4-bits).
For light-weight cryptography the main constraints that we have are typically related to ener requirements, gate equivalents (GEs), and timing. With passive RFID devices, we do not have an associated battery for the power supply, and where the chip must power itself from energy coupled from the radio wave. An RFID device is thus likely to be severely constrained in the power drain associated with any cryptography functions, along with being constrained for the timing requirements and for the number of gates used. Even if an RFID device has an associated battery (active RFID), it may be difficult to recharge the battery, so the drain on power must often be minimised.
There is thus often a compromise between the cryptography method used and the overall security of the method. Thus often light-weight cryptography methods balance performance (throughput) against power drain and GE, and do not perform as well as main-stream cryptography standards (such as AES and SHA-256). Along with this the method must also have a low requirement for RAM (where the method requires the usage of running memory to perform its operation) and ROM (where the method is stored on the device). In order to assess the strengths of various methods we often define the area that the cryptography function will use on the device – and which is defined in \(µm^2\). The NIST finalists are defined in this [article]
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- GIFT AEAD. GIFT. GIFT is a light-weight block cipher. It is a (NIST Finalist)
- Elephant. Elephant. Elephant is a light-weight stream cipher. It is a (NIST Finalist).
- TinyJambu. TinyJambu. TinyJambu is a light-weight block cipher. It is a (NIST Finalist)
- Isap AEAD. Isap. Isap is a light-weight block cipher. It is a (NIST Finalist)
- PHOTON-Beetle AEAD. PHOTON-Beetle. PHOTON-Beetle is a light-weight block cipher. It is a (NIST Finalist)
- Romulus AEAD. Romulus. Romulus is a light-weight block cipher. It is a (NIST Finalist)
- Sparkle AEAD. Sparkle. Sparkle is a light-weight block cipher. It is a (NIST Finalist)
- CLEFIA. CLEFIA. CLEFIA is a light-weight block cipher.
- LED. LED. LED is a light-weight block cipher.
- Piccolo. Piccolo. Piccolo is an ultra light-weight block cipher.
- PRESENT. PRESENT. Present is a light-weight block cipher.
- Pyjamask. Pyjamask. Pyjamask is a light-weight block cipher.
- SIMON. SIMON. SIMON is a light-weight block cipher.
- SKINNY. SKINNY. SKINNEY is a light-weight block cipher.
- SPECK. SPECK. SPECK is a light-weight block cipher.
- XTEA. XTEA. XTEA is a light-weight block cipher.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encryption/Decryption. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.
Light-weight crypto (Other)
- Chaskey (MAC). Chaskey. Chaskey is a light-weight MAC function.
- Chaskey (MAC). Chaskey (Python). Chaskey is a light-weight MAC function.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (ASCON)
ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRFF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
Discrete Logs (Solving)

A discrete log problem is in the form of \(g^x \pmod p\) and where we know \(g\) and \(p\) and must solve for \(x\).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Message Authentication Code (MAC)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
HMAC
The following are the tips related to Key-based hashing:
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authentication both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2), Blake2b, SM3 and SHA-3. This page outlines the HMAC-MD5 methods using the Hazmat cryptography layer.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- HMAC (COSE). Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT with HMMAC. Go. In this case we create a CWT token, and sign with an HMAC signature.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- HMAC with Rust. HMAC. HMAC with Rust.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HMAC with OpenSSL. MACs with OpenSSL. HMAC in OpenSSL for a given input value, password and hashing method.
Cipher MACs
The following are the tips related to Key-based hashing:
- MACs with OpenSSL. MACs with OpenSSL. MAC methods implemented in OpenSSL, including CMAC and GMAC.
Key-based hashing
The following are the tips related to Key-based hashing:
- SipHash. Siphash. Siphash is a fast key-based hashing method.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Meow. Meow. Meow is one of the fastest hashing methods.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
Magic Numbers

This pages contains information related to magic numbers in file formats.
Network and File Forensics
- Magic numbers. Magic. This provides information on magic number for file forensics.
Graphics formats
- JPEG Analysis. JPEGs. This provides an analysis of JPEG files.
- GIF Analysis. GIFs. This provides an analysis of GIF files.
- TIF Analysis. TIFs. This provides an analysis of TIF files.
- PNG Analysis. PNGs. This provides an analysis of PNG files.
- BMP Analysis. BMPs. This provides an analysis of BMP files.
- PSD Analysis. PSDs. This provides an analysis of PSD files.
- WMF Analysis. WMF. This provides an analysis of WMF files.
- Adobe Illustrator Analysis. AI. This provides an analysis of AI files.
- Adobe In Design Analysis. INDD. This provides an analysis of INDD files.
- MIDI file. MIDI. This provides an analysis of MID files.
- ICO file. ICO. This provides an analysis of ICO files.
- PS file. PS. This provides an analysis of PS files.
- EPS file. EPS. This provides an analysis of EPS files.
- VSD file. VSD. This provides an analysis of Microsft Visio (VSD) files.
Video and audio formats
- MP3 Analysis. MP3s. This provides an analysis of MP3 files.
- AVI Analysis. AVIs. This provides an analysis of AVI files.
- Flash SWF Analysis. SWFs. This provides an analysis of Flash files.
- Flash FLV Analysis. FLVs. This provides an analysis of FLV files.
- MP4 Analysis. MP4. This provides an analysis of MP4 files.
- MOV Analysis. MOV. This provides an analysis of MOV files.
- WMV Analysis. WMV. This provides an analysis of WMV files.
- WMA Analysis. WMA. This provides an analysis of WMA files.
- JPEG 2000 Analysis. JPEG 2. This provides an analysis of JPEG 2000 files.
- WAV Analysis. WAV. This provides an analysis of WAV files.
Zips, Archives and Library files
- ZIP/Archive Analysis. ZIPs. This provides an analysis of ZIP/Achive files.
- GZ Analysis. GZ. This provides an analysis of GZip files.
- Tar Analysis. Tar. This provides an analysis of TAR files.
- MSI Analysis. MSI. This provides an analysis of MSI files.
- OBJ Analysis. OBJ. This provides an analysis of OBJ files.
- DLL Analysis. DLL. This provides an analysis of DLL files.
- CAB Analysis. CAB. This provides an analysis of CAB files.
- EXE Analysis. EXE. This provides an analysis of EXE files.
- RAR Analysis. RAR. This provides an analysis of RAR files.
- SYS Analysis. SYS. This provides an analysis of SYS files.
- HLP Analysis. HLP. This provides an analysis of HLP files.
- VMDK Analysis. VMDK. This provides an analysis of VMDK files (VMWare Virtual Disks).
- PST Analysis. PST. This provides an analysis of PST files (Outlook Email File).
- JAR Analysis. JAR. This provides an analysis of JAR files.
- SLN Analysis. SLN. This provides an analysis of Microsoft SLN files.
- Class Analysis. Class. This provides an analysis of Java Class files.
- Zlib. Zlib. This provides an analysis of Zlib files.
Documents
- PDF Analysis. PDFs. This provides an analysis of PDF files.
- DOC Analysis. DOCs. This provides an analysis of DOC files.
- RTF Analysis. RTFs. This provides an analysis of RTF files.
- XLS Analysis. XLSs. This provides an analysis of XLS files.
- PPT Analysis. PPTs. This provides an analysis of PPT files.
- MMP File. MMP. This provides an analysis of MMP files.
- DOCX Analysis. DOCX. This provides an analysis of DOCX files.
- XLSX Analysis. XLSX. This provides an analysis of XLSX files.
- PPTX Analysis. PPTX. This provides an analysis of PPTX files.
- MDB Analysis. MDB. This provides an analysis of MDB files.
- Outlook Message Analysis. MSG. This provides an analysis of MSG files.
Disk Image
- Raw disk format. RAW. This provides an analysis of the RAW disk format.
Tests
- File Forensics Test. File Test File Forensics Test.
- File Forensics Test (Fun). File Test (Fun) File Forensics Test.
Presentations
MIRACL Core Library

MIRACL Core is an open source library, and includes a wide range of public key encryption methods. It is especially focused on elliptic curve and pairing-friendly methods, but also supports a wide range of encryption methods, including RSA, AES and hashing. Overall, it can be ported onto a wide range of systems and supports C, C++, Go, Rust, Python, Java, Javascript and Swift. Along with this it supports limited capability devices such as the Arduino infrastructure. The GitHub repository is [here].
BN254
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.

Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- CL Signatures. CL. CL Signatures in Go using MIRACL.
- CL Signatures (advanced pairing). CL. CL Signatures in Go using MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages using MIRACL.
- PS Signatures. PS. Signatures using PS for short signatures using MIRACL.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures using MIRACL.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.

Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
Rust examples
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
NaCl

PyNaCl is a Python port of LibSodium. It integrates the latest cryptography methods, such as AES, XChaCha20, Blake2b and X25519.
Symmetric Key
- Symmetric key. Symmetric key (XChaCha20 and Poly1305). With symmetric key, Bob and Alice have the same key. NaCl uses the XChaCha20 method, and which supports stream encryption (and which does not require padding as a block cipher does, and is also faster than block cipher modes). ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16 byte nonce. XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24 byte nonce. It has a lower propability of nonce misuse than ChaCha20.
- Encryption with a password. Symmetric Key with KDF. In symmetric key, we generate a secret key. This key is typically a random value or generated from a password and a salt value. If we use a password, we typically use a KDF (Key Derivation Function), and which uses a password and a salt value, in order to create a key of a given size. In this case we will use Argon2i, and which is memory resilent.
Hybrid Encryption
- Box. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Hashing
- Hashing and KDF (Argon2 and scrypt). Hashing and KDF. This case we will use PyNaCl (Networking and Cryptography) library, and which is a Python binding to libsodium. We will hash a password using SHA-256 and SHA-512, and also create a KDF (Key Derivation Function) using scrypt and Argon2.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
Ed25519
-
Ed25519. Ed25519. Using Ed25519 for digital signatures.
-
Finding Points on Ed25519. X25519 (Points).
In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 (Key Exchange)
- X25519 + BLAKE2b key-exchange. X25519. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
Curve 25519
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
Node.js

Node.js uses the JavaScript programming langauge as its base, and allows for code to be run on a server, rather than in the browser (such as with pure JavaScript). To run a node.js program, we run "node myfile.js", and use NPM to install libraries.
Symmetric key
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
RSA and public key
- RSA Opt imal Asymmetric Encryption Padding (OAEP) using Node.js. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
ECC Keys
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.

Hashing
- Hashing with node.js (All). Hashing. Hashing with node.js.
- Hashing with node.js (Selection). Hashing. Hashing with node.js.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- ECDSA with node.js. ECDSA. ECDSA with node.js.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
Key exchange
- Diffie-Hellman with node.js (random prime). DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method and uses a randomly generated prime number (press the button to generate a new prime).
- Diffie-Hellman with node.js. DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method. Each time the prime number will be fixed for the DH group selected.
- ECDH with node.js. ECDH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Elliptic Curve Diffie Hellman (ECDH) key exchange method.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
Key derivation
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
CryptoJS
- CryptoJS (in node.js). CryptoJS (Node.js). Various crypto methods in the browser.
Bulletproofs
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
Blockchain
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
Proxy encryption
- Proxy Encryption - Encrypting With Public Key, And Decrypt with Private Key. Proxy01. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This page just creates a key pair for Alice, and uses it to encrypt with the public key , and decrypt with the private key.
- Proxy Encryption. Proxy02. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This will go through the full use case of proxy re-encryption.
Tokens
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
Random
- Fortuna with node.js. Fortuna. Fortuna random numbers with node.js.
Other
- FPE with node.js. FPR. FPE with node.js.
- Puny with node.js. Puny. Puny character format with node.js.
Accumulators and Witnesses
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
PGP
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Password Entropy
- Password Entropy with Node.js. Password Entropy. Password entropy measures the strength of a password, and is measured as the number of bits which could represent all of the possibilities. An entropy score of less than 25 identifies a poor password, and between 25 and 50 is a weak password. For 50 to 75 we have a reasonable password, and between 75 and 100 is a very good password. Over 100 is an excellent password. The strength of the password relates to the number of characters used, and also the number of characters in the password.
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
- Homomorphic Encryption with Node.js and BGV. Homomorphic Encryption with Node.js and BFG. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BGV method.
Oblivious Transfer (OT)

Oblivious Transfer allows Bob to select data from Alice, but for Alice not to know which value has been selected.
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
OpenSSH

OpenSSH supports the usage of the SSH protocol. This allows for a remote login. One tool which is uses is ssh-keygen, and which allow for the generation of RSA, DSA and elliptic-curve keys that. These can be used for user and host authentication, such as for GitHub login and Cloud instance login.
OpenSSH
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here].
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
Outline

OpenSSL

OpenSSL is a standard library that implements cryptography.
Symmetric key (Command line)
-
Symmetric Key Encryption (OpenSSL 1.x) [here]. In this case we will create cipher text from OpenSSL 1.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 1.x) [here].In this case we will decrypt cipher text from OpenSSL 1.x using a key derived from a password
-
Symmetric Key Encryption (OpenSSL 3.x) [here]. In this case we will create cipher text from OpenSSL 3.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 3.x) [here].In this case we will decrypt cipher text from OpenSSL 3.x using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password.
Hashing
-
Hashing [here] OpenSSL supports a wide range of hashing methods including BLAKE2b, Gost, MD4, MD5, RMD-160, SHA-1, SHA-3, SHA-256 and SHA-512.
Libre OpenSSL
-
Symmetric Key Encryption using Libre OpenSSL [here]. In this case we will create cipher text from Libre OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption using Libre OpenSSL [here]. In this case we will decrypt ciphertext from Libre OpenSSL using a key derived from a password.
-
Hashing [here] Libre OpenSSL supports a wide range of hashing methods including Gost, MD4, MD5, RMD-160, SHA-1, SHA-256 and SHA-512.
Diffie-Hellman parameter generation
-
DH Parameters with OpenSSL [here]. The Diffie-Hellman (DH) method is perhaps one of the greatest inventions in Cybersecurity, and was created by Whitfield Diffie and Marty Hellman. With the DH method, Bob creates a random value (\(b\)) and Alice also creates a random value (\(a\)). Next Bob computes \(B=g^b \pmod p\) and sends it to Alice. Alice computes \(A=g^a \pmod p\) and sends this to Bob. Bob raises the value of \(A\) to the power of \(b\) and takes \(\pmod p\), and Alice raises \(B\) to the power of \(a\) and takes \(\pmod p\). In the end, they will have the same shared value: \(g^{ab} \pmod p\). This can then be used to derive an encryption key that they can use for a secure tunnel. Overall, \(p\) is the large prime number, and also known as the shared modulus between Bob and Alice.
Key derivation function
-
PBKDF2 key derivation with OpenSSL [here] PBKDF2 (Password Key Derivation Function 2) is a key derivation method. Overall it is relatively slow in its operation and where we take a password, a salt value, hashing method, and a number of iterations, in order to produce a given size of encryption key.
-
HKDF key derivation with OpenSSL [here] HKDF (HMAC Key Derivation function) is used to derive an encryption key from a pass phrase. Initially HKDF creates a pseudorandom key (PRK) using a pass phrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), andalong with a salt value. Next the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys.
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Passwords
-
Password example [here]. This page uses the OpenSSL library hash password generator, which is used in UNIX systems for the hashing of passwords which are contained in /etc/shadow and /etc/passwd. For newer passwords, the "-1" options is used to created the hashed value.
-
Hashed passwords with OpenSSL [here].
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
Public key
-
Generating an ECC key pair with OpenSSL [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)).
-
Generating an RSA key pair with OpenSSL [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2).
-
Generating an RSA key pair with OpenSSL with encryption [here]. This page implements RSA key pair generation with an encrypted key pair. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). In this case we will encrypt the key pair with either 3DES, 128-bit AES, 192-bit AES or 256-bit AES. The same password must be used to encrypt and decrypt.
-
Generate prime with OpenSSL [here]. Prime numbers are important in public key encrytion, and are used with RSA and ECC. For RSA, we generate two prime numbers (\(p\) and \(q\)) and which are multiplied together to create a modulus (\(N\)). If these prime numbers have 512 bit values, the modulus will be a 1,024 bit value. This defines the basic secure of RSA. With elliptic curve we use smaller prime numbers, such as 256-bit values for the secp256k1 curve.
ASN1 parsing
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). We will parse using asn1parse, and reveal the parameters.
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)) [RSA key pair]. We will parse using asn1parse, and reveal the parameters.
- DSA Parameters with asn1parse. DSA parameters with OpenSSL with asn1parse. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA (Digital Signature Algorithm)
- DSA Parameters. DSA parameters with OpenSSL. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
MAC (Message Authentication Code)
- HMAC with OpenSSL. MACs with OpenSSL. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authenticate both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2) and SHA-3. In this case we will use OpenSSL to generate the HMAC value.
- MACs with OpenSSL. MACs with OpenSSL. In the following we will generate MACs for HMAC, GMAC, CMAC, Blake2bmac, Blake2smac, KMAC128 and KMAC256. Overall, we will use an encryption key defined as a hex value for GMAC and CMAC, and a pass phrase for the others. The message is "hello".
Signing
- Digital signing a plaintext message with OpenSSL. Signing with OpenSSL. With digital signing, we can take a message, and create a signature. This normally involves signing with a private key and digital certificate. The signed message can be an a MIME format, and which can be integrated into an email message. In this can we have a 512-bit RSA key pair that will sign a plain text message.
Encrypting emails
- Encrypting an email message in OpenSSL. Encrypting messages with OpenSSL. With public key encryption, we can take a message, and encrypt it with the recipiant's public key. In this can we have a 512-bit RSA public key to encrypt a message.
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Random number generation with OpenSSL
-
Random number generator [here]. Random numbers are important in generating encryption keys and salt values. In this case OpenSSL generates a random number (in a Base64 format) for a given number of bytes.
Outline (C#/Python)
-
Symmetric Key Encryption (C#) [here]. This page uses the OpenSSL library through a C#/.NET wrapper. The DLLs it interfaces to are libeay32.dll and ssleay32.dll. OpenSSL supports a wide range of encryption methods, including 128-bit AES, 192-bit AES, 256-bit AES and Blowfish (bf). Different modes of ECB, CBC, and OFB are implemented. The examples use a default IV of "1234".
-
AES in Python with OpenSSL output [here]
-
Producing OpenSSL AES Encrypted String from C# [here]
Digital Certificates
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
Paillier - Partial Homomorphic Encryption

The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Fundamentals
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier).
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Using RSA
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
Applications
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Homomorphic Hashing with Golang. Homomorphic hashing. Normally with hashing methods, we need to take all the previous data and new data in order to create a new hash value for our data. In a homomorphic hashing method, we can basically take the previous hash, and then add on any new data values. We can also remove previous data values from our hash, too. This is more efficient in computing, as we do not have to process all of our data into a new hash, and can use simple homomorphic operations for the computation. The method we will use (LtHash) was initially defined by Bellare and Micciancio and updated Lewi et al at Facebook.
Identity Based Encryption (IBE)

This page outlines a few basic principles around the usage of IBE.
Identity Based Encryption (Pairing based)
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pair-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Identity Based Encryption (Others)
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Güther's implicitly certified identity-based public keys (IBE). Günther. This method allows Bob to generate Alices public key from her identity and publicly available parameters.
- Girault's self-certified public keys (IBE). Girault. This method allows Bob to generate Alices public key from her identity and publicly available parameters, and where we use an RSA key pair to self-certify Alice's public key.
Intrusion Detection Systems (IDS)
- Intrusion Detection Systems. Snort. This outlines some of the basics of IDS, including the requirement for Intrusion Detection Systems (IDSs), and where they are used.
- Advanced Network Forensics (Snort). Adv Network Forensics. This provides information on how to detect threats through network forensics with Snort
Snort

- Snort IDS. Snort. This is a Snort Analyser.
- Snort IDS 2 with rules editor. Snort. This provides information on how to detect threats through network forensics with Snort, and with an editing function for rules.
Presentation
IoT

The key objectives of this page are: Understand how a Pen Tester can generate vulnerabilities and test using the Metasploit framework; Define the options and payloads required to generate and use vulnerabilities; and Gaining remote access.
Devices
- Access the Wi-fi kettle. Go. This page outines how to access a wi-fi enabled kettle.
- Philips Hue Wireless Lighting. Go. This page shows how to use RESTful Web services to access to the Hue Led Lamps.
- Kali and R-PI. Go. This page shows the setup of a security testing infrastructure using a Raspberry Pi (R-PI) and a wifi access point.
- Kali, R-PI and RF electrical socket. Go. This page shows the control of an RF electical socket from a RPI.
- Capture from a Polar H10 heat rate sensor. Go. This page shows the capture of the Polar H10 heart sensor with an Ubertooth One.
- Trusted IoT: Linking IoT Devices to NFTs. Go. This page outlines a research paper which links a device to an NFT (Non-fungible Token).
Shodan Scanning
- IoT Scan (Shodan). Go. This page includes a search of the Internet for key terms, such as for "apache", "mysql" and "cisco".
- IoT Banner Scan (Shodan). Go. This page includes a search of the Internet for key terms with the banner as a result (for the Top 10)
- Internet Services (Shodan). Go. This page includes a search of the Internet for key terms and display the IP address and port.
IoT Libraries
- libDisco with Go. libDisco. libdisco is a Golang library which can be used to create secure connections. It is based on the STROBE protocol framework. Symmetric cryptographic primitives rely on SHA-3 permutation, and asymmetric cryptographic primitives on X25519 and ed25519. STROBE defines a range of cryptographic protocols to integrate with IoT devices. In order to reduce processing, energy and memory requirements, it only uses Keccak (SHA-3) to encrypt and authenticate messages.
COSE/COBR
In computer security, we often have to represent binary data, in single values or groups of characters, bytes, words, long words, signed integers, floating-point values, double-precision floating-point values, and so on. This might be in the form of a data object, a signature or even encrypted content. For this, the ANS.1 DER format is often used, such as presenting digital certificates and signatures. An improvement on this for small messages with security is Concise Binary Object Representation (CBOR) — and which is defined in RFC8949 [1]. While JSON represents text-based data objects CBOR focuses on binary objects. It has been designed to create a lightweight encoder and decoder. This supports the use of CBOR within an IoT infrastructure. The data, also, does not require a data schema to be able to decode it, along with being extensible. CBOR defines the format of binary data with data objects and messages. We can then integrate security with CBOR Object Signing and Encryption (COSE), and which is defined in RFC8152 [2]. This includes signatures, message authentication codes (MACs), encryption and creating serialised objects.
- 128-bit AES GCM. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) can then build on this to include signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use a symmetric key to encrypt a message, and then decrypt it. In this case we will use AES GCM with a static 128-bit key ("0x000102030405060708090a0b0c0d0e0f").
- 256-bit AES GCM. Go. In this case we will use AES GCM using a random 256-bit key (32 bytes).
- EdDSA. Go. Concise Binary Object Representation (CBOR) [1] integrates security into small data objects and small message sizes. COSE (CBOR Object Signing and Encryption) [2] can then build on this to includes signatures, message authentication codes (MACs) and encryption and creating serialised objects. In this case we will use EdDSA to create a signature for a message.
- ECDSA. Go. In this case we will use ECDSA to create a signature for a message.
- HMAC. Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT. Go. In this case we create a CWT token, and sign with an HMAC signature.
- ECDH. Go. In this case we create a symmetric key from ECDH. For this we will derive a shared key from the public key of Alice and Bob, and then define a single recipient which can derive the CEK (Content Encryption Key) using their private key. We will use the curves of P-256 (secp256r1), P-384 (secp384r1), P-521 (secp521r1) or SECP256K1 (as used with Bitcoin).
- RSA using COSE and CBOR. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\).
- RSA: dQ, dP and InvQ. Go. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). The key pair also includes \(dQ\), \(dP\) and \(InvQ\), and these can be used with the Chinese remainder theory to optimize the decryption process.
Metasploit
- Armitage and Metasploit. Go.
- Exploiting Android with Metasploit. Go.
- Exploiting Android with Metasploit - Part 2. Go.
- Exploiting Windows/Mac OS X with Metasploit. Go.
- Remote Desktop Windows/Mac OS X with Metasploit. Go.
- Metasploit. Go.
- Internet of Things Security. Go.
- Metasploit (Enumeration and Scanning). Go.
- Metasploit (Malware). Go.
IP

 The following are a few interesting techniques around IP addresses:
The following are a few interesting techniques around IP addresses:
- Your details. IP. This shows your browser details.
- IP address analyser. IP. This involves converting an IP address to the host and network part of the address.
- IP subnet analyser. IP subnets. This involves converting an IP address to the host and network part of the address.
- IP address analyser. IP. This involves analysing IP addresses.
- Max subnets. Max subnets. This involves converting an IP address to the host and network part of the address.
- Route summarization. Summarization. This involves converting an IP address to the host and network part of the address.
- Whois. Whois. This does a basic Whois on a domain.
- URL Obfuscation. Obfuscation. This outlines URL obfuscation.
- HTTP Responses. Test. HTTP.
- Capturing Network Packets (Python). WinPCap. HTTP.
Cisco related
- Routing table. Routing table. This involves viewing a routing table for a Cisco device.
- ACL Generator. ACL. This involves a simple calculator for ACLs on network ranges.
- EIGRP metrics. EIGRP. Learn the basics of EIGRP metrics.
- VoIP B/W. VoIP. Calculate bandwidth for VoIP.
- Wild Card. Wild Card. On a Cisco device a wildcard mask is used to identify the parts of an IP address that need to be matched. It thus uses a wildcard mask, where a 0 in the bit position identifies that the device should match that bit, else a 1 shows that it should ignore it.
Protocols
- HTTP. HTTP. Show the request and response for HTTP.
- Ping analyser. IP. This involves converting a ping of a site.
IP Challenges
- IP Test 1. IP Test. IP Classification test. This is a simple test which generates a range of IP addresses, and you must determine the IP address classification. IP Subnet Challenge 1 Demo
- IP Test 2. IP Test. IP Classification test Part 2. This test provides an address classification, and the user must find the addresses which are of this classification. IP Subnet Challenge 2 Demo
- IP Test 3. IP Test. IP Classification test Part 3. This test provides an address classification, where the network part of the address is determined. IP Subnet Challenge 3 Demo
Subnet Challenges
- Subnet Test 1. Subnet Test. Subnet Test.
- Subnet Test 2. Subnet Test. Subnet bits.
- Subnet Test 3. Subnet Test. Find the nth usable subnet. This test involves finding the nth usable subnet.
- Subnet Test 4. Subnet Test. Maximum subnets. This is a test page to determine the maximum number of subnets and hosts/subnet for IP classed addressing.
- Subnet Test 5. Subnet Test. Maximum host/subnet. This is a test page to determine the maximum number of hosts per subnet.
- Subnet Test 6. Subnet Test. Determine the required subnet mask for a given number of subnets. This is a test page to determine the required subnet mask for a given number of subnets and a given IP address classification.
- Subnet Test 7. Subnet Test. Determine the required subnet mask for a given number of host/subnet. This is a test page to determine the required subnet mask for a given number of hosts per subnet and a given IP address classification.
- Subnet Test 8. Subnet Test. Route summarization. This involves a calculation on route summarization.
- Subnet Test 9. Subnet Test. Binary to IP.
- Subnet Test 10. Subnet Test. Hex to IP.
- Subnet Test 13. Subnet Test. Wild card mask network bits. Find the number of bits in the network part of the wild card mask. IP Wildcard challenge
- Subnet Test 14. Subnet Test. Wild card mask host bits. Find the number of bits in the host part of the wild card mask. IP Wildcard challenge
- Subnet Test 15. Subnet Test. Wild card mask ... find the network address. Find the network for the wild card mask. IP Wildcard challenge 2
- Subnet Test 16. Subnet Test. Find a matching IP address for a network and wild card mask. Find the IP for a network and a wild card mask.
- Subnet Test 17. Subnet Test. Find an address which is on a given network. Find an IP address on a network, for a given network address and subnet mask.
- Subnet Test 18. Subnet Test. Find an IP address on the same network. Find an IP address on the same subnet.
- Subnet Test 19. Subnet Test. Find subnet. Convert subnet mask.
- Megatest. Subnet Test. Challenging test for subnets.
JavaScript

JavaScript code allows execution within the browser, rather than on the server. It is often faster than code that runs on a server. Along with this we can also use Node.js, and which runs JavaScript code on a server.
Symmetric key
- AES. AES. In this example, we will use either a pre-generated key or a random one, and use AES (Rijndael) encryption.
- ChaCha20 and Poly1305. ChaCha. This page outlines Poly1305 and ChaCha20. ChaCha20 is a symmetric key method and Poly1305 is a message authentication code (MAC). They were created by Daniel J. Bernstein, and are alternatives to AES and HMAC.
- CMS (Padding). CMS. This page uses PKIJS encrypting on CMS. With CMS we can This document describes the Cryptographic Message Syntax (CMS). With this we can encapsulate an message within an encrypted entity.

Hashing
- Hash. Hash. This page defines a JavaScript Hash calculator. This uses a client-side JavaScript code to determine the hash signatures of a text value.
Signatures
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
- Boneh–Lynn–Shacham (BLS) signature. BLS. Boneh–Lynn–Shacham (BLS) signature method produces short signatures. They use elliptic curve pairing (and which are also known as bilinear maps).
Key exchange
- ECDH. ECDH. Elliptic Curve Diffie Hellman (ECDH) is used to generate a shared key. This implementation uses Elliptic Curve Cryptography (ECC) with JavaScript.
CryptoJS
- CryptoJS. CryptoJS. This page uses client-side JavaScript code to hashing, encrypt and sign, including for symmetric key (AES), streaming ciphers, hashing methods, and HMAC.
Blockchain
- PATRICIA trie. PATRICIA. In the following, we have the Top 2,500 Web sites in the world, and implemented with a Radix Trie (aka PATRICIA trie) In the following we have the Top 2,000 web sites on the Internet, and which have been indexed using the PATRICIA trie.
Public key
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
- RSA. RSA. RSA is an asymmetric encryption algorithm, which uses two keys, one to encrypt and the other to decrypt. It was created in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman, and is still one of the most widely used encryption methods. A typical application is in authenticating a sender, where the senders private key is used to encrypt a message, and then is decrypted by the receiver with the senders public key (which is known to anyone who wants it). It is also typically used for encrypting disks/files, such as for EFS.
Digital Certificates
- X.509 certificates in JavaScript. RSA and ECDSA Signed certificates. This page will generate either RSA and ECC key pairs, and then generate X.509 certificates, using either a signature of SHA1withRSA or SHA256withECDSA. For RSA signing we use an RSA private key to sign the certificate, and with ECDSA signing we use an ECC private key to sign the certificate.
Tokens
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
Random
- Random number generator. Rand. In the past, encryption and decryption had to be done through native code libraries, such as with Bouncy Castle and OpenSSL. With the increasing processing power of Web browsers, it is now possible to use encryption using JavaScript, which thus provides client-side processing of data. This Web page uses Javascript encryption, and generates a random 256-bit text key or a hex version. The 256-bit key is generated by generating 60 random numbers (from 0-25), and converting these to an ASCII character.
Malware obfuscation
- Malware obfuscation. Obfuscation. A malware writer will often hide certain keywords from the browser/human by encoding them in another format. This is typically done for hex coding (\xZZ), 16-bit unicoding (\uZZZZ) and octal coding (\ZZZ). To test, enter a value, and then press the button and it will convert encoded string.
Message Authentication Codes
- Chaskey (MAC). Chaskey. Chaskey Cipher is light-weight cryptography method for signing messages (MAC) using a 128-bit key. The hardware implementation only requires 3,334.33 gate equivalent with an operating clock frequency of 1 MHz (whereas Keccak requires 4,658 GE). In the page we create the Mac signature and also encrypt for CBC.
Other
- Password generation/hashing. Hashing. Linux can use salted passwords where the username, hashing method and hashed password are stored in a password file [More details]. The main methods are
Hashing

At times we need to generate secrets, such as encryption keys, from passwords or nonce values. A Key Derivation Function (KDF) is a verifiable way of doing this.
Key Derivation Functions (KDFs)
The following are the tips related to hashing:
- Hash benchmark. Benchmark. Benchmarks some hashing methods.
- Hash values. Hashes. Outlines hash method.
- Open SSL Hash passwords. Open SSL Passwords. This creates a hash value which has salt using a range of methods.
- Password strength. Test. This outlines the strength of various passwords types.
- Key entropy for different character sets and characters. Key entropy. This outlines key entropy for different character sets and characters.
- Password generation/hashing. Hashing. Password generation/hashing using JavaScript
- Splunk hashed passwords (SHA512crypt). Splunk. This implemented SHA512crypt, as used in Splunk.
HKDF
The following are the tips related to Key derivation hashing:
- HKDF (Python). Go. Outline of HKDF (HMAC Key Derivation Function) in Python and tested against RFC 5869
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- Hazmat HKDF for different hashing methods. Hazmat HKDF. HKDF methods using the Python cryptography primitives.
- HKDF key derivation with OpenSSL [ here]
- ChaCha20/Poly1305 with Hazmat. ChaCha20/Poly1305 with Hazmat using HKDF. Implementation of ChaCha20/Poly1305 with a key generated from HKDF using Hazmat.
- AES GCM with Hazmat. AES GCM with Hazmat using HKDF. Implementation of AES GCM with a key generated from HKDF using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
PBKDF2
The following are the tips related to Key derivation hashing:
- PBKDF2 (Part 2). PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2. PBKDF2. The PBKDF2 method created a salted hashed value, and which is used to generate the main key for TrueCrypt.
- PBKDF2 (Python). PBKDF2. The PBKDF2 method created a salted hashed value.
- PBKDF2, bcrypt, scrypt and HKDF. PBKDF2, bcrypt, scrypt and HKDF. The implement a hash password with salting.
- AES GCM (Python) with PBKDF2. AES GCM (Python) with PBKDF2.
- Fernet with PBKDF2 . AES GCM (Python) with PBKDF2.
- PBKDF2 key derivation. AES GCM (Python) with PBKDF2.
- Key Rotation with Fernet. AES GCM (Python) with PBKDF2.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
- Hazmat PBKDF2. Hazmat PBKDF2. PBKDF2 (Password-Based Key Derivation Function 2) is defined in RFC 2898 and generates a salted hash. Often this is used to create an encryption key from a defined password, and where it is not possible to reverse the password from the hashed value. It is used in TrueCrypt to generate the key required to read the header information of the encrypted drive, and which stores the encryption keys. Also, it is used in WPA-2 in order to create a hashed version of the password. With this, WPA-2 uses 4,096 interations.
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT
- HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Bcrypt
The following are the tips related to Key derivation hashing:
- Bcrypt. Bcrypt. This creates a hash value which has salt.
- BCrypt. BCrypt. BCrypt with Rust.
- Hash to password with Go. Hashing to Argon2, Scrypt and BCrypt. Hash to password with Go, including Argon2, Scrypt and BCrypt.
scrypt
- scrypt. Scrypt. The Scrypt method created a salted hashed value using iterations and salting.
- Hazmat scrypt. Hazmat scrypt. scrypt is a password-based key derivation function which produces a hash with a salt and iterations. The iteration count slows down the cracking and the salt makes pre-computation difficult. The main parameters are: passphrase (P); salt (S); Blocksize (r) and CPU/Memory cost parameter (N - a power of 2).
APR1
- APR1. APR1. This produces an APR1 hash signature for a password.
Argon 2
The following are the tips related to Key derivation hashing:
- Argon 2. Go. Outline of Argon2.
- Argon 2 with NaCl. Go. Outline of Argon2 using NaCl.
- Argon 2. Argon 2. Argon 2 with Rust.
- Balloon. Go. Outline of Balloon.
Other
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
- Double ratchet. Go. Outline of double ratcheting.
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
Outline
HMAC Key Derivation function (HKDF) is used to derive an encryption key from a passphrase. Initially, HKDF creates a pseudorandom key (PRK) using a passphrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), and along with a salt value. Next, the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys [RFC 5869][article]. In this case, we will use SHA-256.
The following shows how an encryption key can be generated using HKDF, and where we need a secret and a salt value. Both Bob and Alice have the same secret and salt.

With PBKDF2 (Password Based Key Derivation Function 2), we hash for a given number of rounds:

Key exchange

Key exchange is a way for Bob and Alice to communicate and for them to agree on a shared secret. The original method defined uses discrete logarithms (Diffie-Hellman), but most modern methods use elliptic curve techniques (ECDH). As quantum computers can crack both discrete log and elliptic curve methods, there are post quantum cryptography methods proposed. This includes SIDH, CSIDH, SIKE, and NewHope.
Key interchange/generation (Diffie-Hellman)
The following relates to key interchange:
- Selecting \(g\) in Diffie Hellman. G in Diffie Hellman. Picking a safe value of the generator \(g\) in discrete logarithms.
- Diffie-Hellman. Diffie-Hellman Calculation. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Real example). Diffie-Hellman Real. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (Python). Diffie-Hellman. Diffie-Hellman is a standard method of Alice and Bob being able to communicate, and end up with the same secret encryption key. It is used in many applications.
- Diffie-Hellman (pre-compute). Diffie-Hellman (pre-compute). Many sites use the same prime numbers, which can then be cracked with a pre-computing attack.
- Key generation. Key gen. This will generate keys for different methods based on a passphrase.
- Diffie-Hellman (Man-in-the-middle). DF. This outlines the man-in-the-middle method for Diffie-Hellman.
- An Alternative Diffie-Hellman method. Alterative DH. This outlines an alternative Diffie-Hellman method.
Authenticated Key Exchange
The following are the tips related to Key derivation hashing:
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- MTI/A0. MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{ax+by} \pmod p\). MTI (Matsumoto, Takashima, Imai).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0. This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0. MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{x+y} \pmod p\)
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0. This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). The resultant key is \(xyG \)
- MTI/C0. MTI/C0. This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{xy} \pmod p\)
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG\).
- MTI/C1. MTI/C1. This outlines MTI/C1, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. The resultant key is \(g^{abxy} \pmod p\).
- MQV (Menezes–Qu–Vanstone). MQV. MQV was created Alfred Menezes, Minghua Qu and Scott Vanstone in 1995 and is an authenticated key exchange method. Alice holds a key pair \((A,a)\) and Bob has a key pair \((B,b)\). With this \(a\) is Alice's private key, and \(A=aG\) is her public key. For Bob, his public key will be \(B=aG\) and a private key of \(b\), and where \(G\) is the base point on the elliptic curve.
- HMQV (Menezes–Qu–Vanstone). HMQV. HMQV builds on MQV and adds the identity of Bob and Alice.
- ECDH with X25519 and Blake2b. ECDH with X25519 and Blake2b. This uses PyNaCl to create an authenticated key exchange and uses X25519 and Blake2b.
Elliptic Curve (ECDH) - Python
The following are the tips related to ECC:
- Elliptic Curve. Elliptic Curve. Elliptic Curve is a public key method which can also be used to generate a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with simple parameters. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1. ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- ECDH with Hazmat. ECDH with Hazmat. Generate a shared key with ECDH and using the Hazmat primitives.
Elliptic Curve (ECDH) - Golang and Node.js
The following are the tips related to ECC:
- ECDH with Go. ECDH. ECDH with Go.
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
- ECDH with node.js. ECDH. ECDH with node.js.
- ECDH with JavaScript. ECDH. Elliptic Curve Diffie Hellman.
Password Authenticated Key Exchange (PAKE)
The following are the tips related to Key derivation hashing:
- SPAKE2. Go. Outline of SPAKE2.
- OPAQUE. Go. Outline of OPAQUE.
- SPEKE. Go. Outline of SPEKE (Simple Password Exponential Key Exchange).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
- J-PAKE. J-PAKE. This example generates a shared key based on a shared password.
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses discrete logs.
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
PQC NIST Finalists (Key Exchange)
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Key interchange/generation (Other)
The following relates to key interchange:
- Curve25519. Curve25519. This outlines Curve25519, which is used in the Tor network.
- Authenticated Key Exchange (Discrete logs). YAK. Key exchange with public keys and uses discrete logs.
- Authenticated Key Exchange (ECC). YAK. Key exchange with public keys and uses elliptic curve methods.
- Shamir No-key protocol. Shamir No Key. In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated.
- Shamir No-key protocol (sepc256k1). Shamir No Key (EC). In this method Bob and Alice exchange three open messages, and end up with the same shared secret that Alice generated using the sepc256k1 elliptic curve.
- Conference keying (Burmester-Desmedt method). Conference keying. In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it.
- Conference keying (Burmester-Desmedt method) - Elliptic Curve (sepc256k1). Conference keying Elliptic Curve (sepc256k1). In this method Bob, Alice, Carol, Dave and Faith can create a shared conference key, without Eve finding it, and uses the sepc256k1 elliptic curve.
Key exchange (with pairing)
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Kryptology

We need to build a new Internet. One that is build on mathematics and certainty, rather than the patchy version we have now. For this we need a layer of cryptography at the lowest level, and build software interfaces on top of this. Along with this we now have cryptographic methods which can now provide a foundation of trust, and which preserve privacy. And so the old libraries of OpenSSL are being squeezed out in favour of the new ones which are built on a solid foundation. The latest of these new "privacy-aware" libraries is Kryptology, and created by Coinbase. This library provides the APIs that developers need, in order to apply to areas of blockchain development. This library include BLS (Boneh-Lynn-Shacham) signatures, Zero-knowledge Proofs (ZKPs) and Shamir Secret Shares (SSS). With BLS we can digitally sign for data, but also preserve its privacy. Applications of this include group signatures, where multiple entities can merge their signing keys together and provide a single signature for a transaction. With SSS, we can split encryption keys up into shares, and then distribute them across a network. When required, we can call these shares back to reconstruct the key. The focus for Coinbase seems to be the application of privacy coins, and where no tracking can be applied to the usage of these digital coins. This should support full anonymity for transactions, as opposed to Bitcoin which only supports pseudo-anonymity.

ECC Basics
- Elliptic Curves and nG (Kryptology). Elliptic Curve and nG with Kryptology and Golang. Determining n.G for a range of curves in Golang and Kryptology.
- ECC Double-and-add for point multiplication (Kryptology and Golang). Montgomery’s Ladder. Determining n.G for a range of curves in Golang and Kryptology using the Montgomery’s Ladder.
- Elliptic Curve Points (Base Point and Others). Elliptic Curve points. Two common curves used in ECC (Elliptic Curve Cryptography) are secp256k1 (as used in Bitcoin and Ethereum) and P256 (secp256r1). The "k1" refers to the Kolbitz curve 1 (named after the creator of ECC). With these we have a base point which are can operate on. This is typically defined as \(G\). We can then operate on this with add and multiply operation. For example, \(2G=G+G\) and \(P=n.G\). In this following we will show the base point for a number of common curves, such as secp256r1, P256, Pallas, Curve 25519, BLS12381G1, BLS12381G2, BLS12377G1 and BLS12377G2.
ECDH
- Elliptic Curve Diffie Hellman (ECDH). ECDH. With ECDH, Bob and Alice generate a secret value and then pass a public key value related to this. They can then generate a shared secret. We will use Golang and the Krytology library.
Simple ECC on curves
- Public key points for curves. Simple. Display public key points for scalars.
BLS Curve
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
Accumulator and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
Pallas Curve
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
Pairing-based Crypto
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
ElGamal and ECC
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a numerical input.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
Shamir Secret Shares
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Homomorphic Encryption
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Zero knowledge proofs
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
Verifiable Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Hash to scalar and point
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
CP-ABE
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Lattice cryptography

Latice cryptography is proposed as a post-quantum robust method for public key encryption, especially focused on digital signatures and key exchange mechanisms (KEMs).
Principles
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
NTRU
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- Lattice Encryption: NTRU Key Generation Python). NTRU. Outlines how NTRU operates for key generation.
Homomorphic
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Digital Signatures
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
Public-Key Encryption/Key Exchange
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
Light-weight cryptography

While AES and SHA work well together within computer systems, they struggle in an IoT/embedded world as they take up: too much processing power; too much physical space; and consume too much battery power. So NIST outlines a number of methods which can be used for light-weight cryptography, and which could be useful in IoT and RFID devices [1]. They define the device spectrum as:
- Conventional cryptography. Servers and Desktops. Tablets and smart phones.
- Light-weight cryptography. Embedded Systems. RFID and Sensor Networks.
With embedded systems, we commonly see 8-bit, 16-bit and 32-bit microcontrollers, and which would struggle to cope with real-time demands for conventional cryptography methods. And in the 40+ years since the first 4-bit processor, there is even a strong market for 4-bit processors. RFID and sensor network devices, especially, have limited numbers of gates available for security, and are often highly constrained with the power drain on the device.
So AES is typically a non-starter for many embedded devices. In light-weight cryptography, we often see smaller block size (typically 64 bits or 80 bits), smaller keys (often less than 90 bits) and less complex rounds (and where the S-boxes often just have 4-bits).
For light-weight cryptography the main constraints that we have are typically related to ener requirements, gate equivalents (GEs), and timing. With passive RFID devices, we do not have an associated battery for the power supply, and where the chip must power itself from energy coupled from the radio wave. An RFID device is thus likely to be severely constrained in the power drain associated with any cryptography functions, along with being constrained for the timing requirements and for the number of gates used. Even if an RFID device has an associated battery (active RFID), it may be difficult to recharge the battery, so the drain on power must often be minimised.
There is thus often a compromise between the cryptography method used and the overall security of the method. Thus often light-weight cryptography methods balance performance (throughput) against power drain and GE, and do not perform as well as main-stream cryptography standards (such as AES and SHA-256). Along with this the method must also have a low requirement for RAM (where the method requires the usage of running memory to perform its operation) and ROM (where the method is stored on the device). In order to assess the strengths of various methods we often define the area that the cryptography function will use on the device – and which is defined in \(µm^2\). The NIST finalists are defined in this [article]
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- GIFT AEAD. GIFT. GIFT is a light-weight block cipher. It is a (NIST Finalist)
- Elephant. Elephant. Elephant is a light-weight stream cipher. It is a (NIST Finalist).
- TinyJambu. TinyJambu. TinyJambu is a light-weight block cipher. It is a (NIST Finalist)
- Isap AEAD. Isap. Isap is a light-weight block cipher. It is a (NIST Finalist)
- PHOTON-Beetle AEAD. PHOTON-Beetle. PHOTON-Beetle is a light-weight block cipher. It is a (NIST Finalist)
- Romulus AEAD. Romulus. Romulus is a light-weight block cipher. It is a (NIST Finalist)
- Sparkle AEAD. Sparkle. Sparkle is a light-weight block cipher. It is a (NIST Finalist)
- CLEFIA. CLEFIA. CLEFIA is a light-weight block cipher.
- LED. LED. LED is a light-weight block cipher.
- Piccolo. Piccolo. Piccolo is an ultra light-weight block cipher.
- PRESENT. PRESENT. Present is a light-weight block cipher.
- Pyjamask. Pyjamask. Pyjamask is a light-weight block cipher.
- SIMON. SIMON. SIMON is a light-weight block cipher.
- SKINNY. SKINNY. SKINNEY is a light-weight block cipher.
- SPECK. SPECK. SPECK is a light-weight block cipher.
- XTEA. XTEA. XTEA is a light-weight block cipher.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encryption/Decryption. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.
Light-weight crypto (Other)
- Chaskey (MAC). Chaskey. Chaskey is a light-weight MAC function.
- Chaskey (MAC). Chaskey (Python). Chaskey is a light-weight MAC function.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (ASCON)
ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRFF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
Discrete Logs (Solving)

A discrete log problem is in the form of \(g^x \pmod p\) and where we know \(g\) and \(p\) and must solve for \(x\).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Message Authentication Code (MAC)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
HMAC
The following are the tips related to Key-based hashing:
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authentication both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2), Blake2b, SM3 and SHA-3. This page outlines the HMAC-MD5 methods using the Hazmat cryptography layer.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- HMAC (COSE). Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT with HMMAC. Go. In this case we create a CWT token, and sign with an HMAC signature.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- HMAC with Rust. HMAC. HMAC with Rust.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HMAC with OpenSSL. MACs with OpenSSL. HMAC in OpenSSL for a given input value, password and hashing method.
Cipher MACs
The following are the tips related to Key-based hashing:
- MACs with OpenSSL. MACs with OpenSSL. MAC methods implemented in OpenSSL, including CMAC and GMAC.
Key-based hashing
The following are the tips related to Key-based hashing:
- SipHash. Siphash. Siphash is a fast key-based hashing method.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Meow. Meow. Meow is one of the fastest hashing methods.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
Magic Numbers

This pages contains information related to magic numbers in file formats.
Network and File Forensics
- Magic numbers. Magic. This provides information on magic number for file forensics.
Graphics formats
- JPEG Analysis. JPEGs. This provides an analysis of JPEG files.
- GIF Analysis. GIFs. This provides an analysis of GIF files.
- TIF Analysis. TIFs. This provides an analysis of TIF files.
- PNG Analysis. PNGs. This provides an analysis of PNG files.
- BMP Analysis. BMPs. This provides an analysis of BMP files.
- PSD Analysis. PSDs. This provides an analysis of PSD files.
- WMF Analysis. WMF. This provides an analysis of WMF files.
- Adobe Illustrator Analysis. AI. This provides an analysis of AI files.
- Adobe In Design Analysis. INDD. This provides an analysis of INDD files.
- MIDI file. MIDI. This provides an analysis of MID files.
- ICO file. ICO. This provides an analysis of ICO files.
- PS file. PS. This provides an analysis of PS files.
- EPS file. EPS. This provides an analysis of EPS files.
- VSD file. VSD. This provides an analysis of Microsft Visio (VSD) files.
Video and audio formats
- MP3 Analysis. MP3s. This provides an analysis of MP3 files.
- AVI Analysis. AVIs. This provides an analysis of AVI files.
- Flash SWF Analysis. SWFs. This provides an analysis of Flash files.
- Flash FLV Analysis. FLVs. This provides an analysis of FLV files.
- MP4 Analysis. MP4. This provides an analysis of MP4 files.
- MOV Analysis. MOV. This provides an analysis of MOV files.
- WMV Analysis. WMV. This provides an analysis of WMV files.
- WMA Analysis. WMA. This provides an analysis of WMA files.
- JPEG 2000 Analysis. JPEG 2. This provides an analysis of JPEG 2000 files.
- WAV Analysis. WAV. This provides an analysis of WAV files.
Zips, Archives and Library files
- ZIP/Archive Analysis. ZIPs. This provides an analysis of ZIP/Achive files.
- GZ Analysis. GZ. This provides an analysis of GZip files.
- Tar Analysis. Tar. This provides an analysis of TAR files.
- MSI Analysis. MSI. This provides an analysis of MSI files.
- OBJ Analysis. OBJ. This provides an analysis of OBJ files.
- DLL Analysis. DLL. This provides an analysis of DLL files.
- CAB Analysis. CAB. This provides an analysis of CAB files.
- EXE Analysis. EXE. This provides an analysis of EXE files.
- RAR Analysis. RAR. This provides an analysis of RAR files.
- SYS Analysis. SYS. This provides an analysis of SYS files.
- HLP Analysis. HLP. This provides an analysis of HLP files.
- VMDK Analysis. VMDK. This provides an analysis of VMDK files (VMWare Virtual Disks).
- PST Analysis. PST. This provides an analysis of PST files (Outlook Email File).
- JAR Analysis. JAR. This provides an analysis of JAR files.
- SLN Analysis. SLN. This provides an analysis of Microsoft SLN files.
- Class Analysis. Class. This provides an analysis of Java Class files.
- Zlib. Zlib. This provides an analysis of Zlib files.
Documents
- PDF Analysis. PDFs. This provides an analysis of PDF files.
- DOC Analysis. DOCs. This provides an analysis of DOC files.
- RTF Analysis. RTFs. This provides an analysis of RTF files.
- XLS Analysis. XLSs. This provides an analysis of XLS files.
- PPT Analysis. PPTs. This provides an analysis of PPT files.
- MMP File. MMP. This provides an analysis of MMP files.
- DOCX Analysis. DOCX. This provides an analysis of DOCX files.
- XLSX Analysis. XLSX. This provides an analysis of XLSX files.
- PPTX Analysis. PPTX. This provides an analysis of PPTX files.
- MDB Analysis. MDB. This provides an analysis of MDB files.
- Outlook Message Analysis. MSG. This provides an analysis of MSG files.
Disk Image
- Raw disk format. RAW. This provides an analysis of the RAW disk format.
Tests
- File Forensics Test. File Test File Forensics Test.
- File Forensics Test (Fun). File Test (Fun) File Forensics Test.
Presentations
MIRACL Core Library

MIRACL Core is an open source library, and includes a wide range of public key encryption methods. It is especially focused on elliptic curve and pairing-friendly methods, but also supports a wide range of encryption methods, including RSA, AES and hashing. Overall, it can be ported onto a wide range of systems and supports C, C++, Go, Rust, Python, Java, Javascript and Swift. Along with this it supports limited capability devices such as the Arduino infrastructure. The GitHub repository is [here].
BN254
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.

Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- CL Signatures. CL. CL Signatures in Go using MIRACL.
- CL Signatures (advanced pairing). CL. CL Signatures in Go using MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages using MIRACL.
- PS Signatures. PS. Signatures using PS for short signatures using MIRACL.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures using MIRACL.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.

Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
Rust examples
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
NaCl

PyNaCl is a Python port of LibSodium. It integrates the latest cryptography methods, such as AES, XChaCha20, Blake2b and X25519.
Symmetric Key
- Symmetric key. Symmetric key (XChaCha20 and Poly1305). With symmetric key, Bob and Alice have the same key. NaCl uses the XChaCha20 method, and which supports stream encryption (and which does not require padding as a block cipher does, and is also faster than block cipher modes). ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16 byte nonce. XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24 byte nonce. It has a lower propability of nonce misuse than ChaCha20.
- Encryption with a password. Symmetric Key with KDF. In symmetric key, we generate a secret key. This key is typically a random value or generated from a password and a salt value. If we use a password, we typically use a KDF (Key Derivation Function), and which uses a password and a salt value, in order to create a key of a given size. In this case we will use Argon2i, and which is memory resilent.
Hybrid Encryption
- Box. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Hashing
- Hashing and KDF (Argon2 and scrypt). Hashing and KDF. This case we will use PyNaCl (Networking and Cryptography) library, and which is a Python binding to libsodium. We will hash a password using SHA-256 and SHA-512, and also create a KDF (Key Derivation Function) using scrypt and Argon2.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
Ed25519
-
Ed25519. Ed25519. Using Ed25519 for digital signatures.
-
Finding Points on Ed25519. X25519 (Points).
In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 (Key Exchange)
- X25519 + BLAKE2b key-exchange. X25519. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
Curve 25519
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
Node.js

Node.js uses the JavaScript programming langauge as its base, and allows for code to be run on a server, rather than in the browser (such as with pure JavaScript). To run a node.js program, we run "node myfile.js", and use NPM to install libraries.
Symmetric key
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
RSA and public key
- RSA Opt imal Asymmetric Encryption Padding (OAEP) using Node.js. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
ECC Keys
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.

Hashing
- Hashing with node.js (All). Hashing. Hashing with node.js.
- Hashing with node.js (Selection). Hashing. Hashing with node.js.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- ECDSA with node.js. ECDSA. ECDSA with node.js.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
Key exchange
- Diffie-Hellman with node.js (random prime). DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method and uses a randomly generated prime number (press the button to generate a new prime).
- Diffie-Hellman with node.js. DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method. Each time the prime number will be fixed for the DH group selected.
- ECDH with node.js. ECDH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Elliptic Curve Diffie Hellman (ECDH) key exchange method.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
Key derivation
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
CryptoJS
- CryptoJS (in node.js). CryptoJS (Node.js). Various crypto methods in the browser.
Bulletproofs
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
Blockchain
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
Proxy encryption
- Proxy Encryption - Encrypting With Public Key, And Decrypt with Private Key. Proxy01. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This page just creates a key pair for Alice, and uses it to encrypt with the public key , and decrypt with the private key.
- Proxy Encryption. Proxy02. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This will go through the full use case of proxy re-encryption.
Tokens
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
Random
- Fortuna with node.js. Fortuna. Fortuna random numbers with node.js.
Other
- FPE with node.js. FPR. FPE with node.js.
- Puny with node.js. Puny. Puny character format with node.js.
Accumulators and Witnesses
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
PGP
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Password Entropy
- Password Entropy with Node.js. Password Entropy. Password entropy measures the strength of a password, and is measured as the number of bits which could represent all of the possibilities. An entropy score of less than 25 identifies a poor password, and between 25 and 50 is a weak password. For 50 to 75 we have a reasonable password, and between 75 and 100 is a very good password. Over 100 is an excellent password. The strength of the password relates to the number of characters used, and also the number of characters in the password.
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
- Homomorphic Encryption with Node.js and BGV. Homomorphic Encryption with Node.js and BFG. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BGV method.
Oblivious Transfer (OT)

Oblivious Transfer allows Bob to select data from Alice, but for Alice not to know which value has been selected.
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
OpenSSH

OpenSSH supports the usage of the SSH protocol. This allows for a remote login. One tool which is uses is ssh-keygen, and which allow for the generation of RSA, DSA and elliptic-curve keys that. These can be used for user and host authentication, such as for GitHub login and Cloud instance login.
OpenSSH
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here].
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
Outline

OpenSSL

OpenSSL is a standard library that implements cryptography.
Symmetric key (Command line)
-
Symmetric Key Encryption (OpenSSL 1.x) [here]. In this case we will create cipher text from OpenSSL 1.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 1.x) [here].In this case we will decrypt cipher text from OpenSSL 1.x using a key derived from a password
-
Symmetric Key Encryption (OpenSSL 3.x) [here]. In this case we will create cipher text from OpenSSL 3.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 3.x) [here].In this case we will decrypt cipher text from OpenSSL 3.x using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password.
Hashing
-
Hashing [here] OpenSSL supports a wide range of hashing methods including BLAKE2b, Gost, MD4, MD5, RMD-160, SHA-1, SHA-3, SHA-256 and SHA-512.
Libre OpenSSL
-
Symmetric Key Encryption using Libre OpenSSL [here]. In this case we will create cipher text from Libre OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption using Libre OpenSSL [here]. In this case we will decrypt ciphertext from Libre OpenSSL using a key derived from a password.
-
Hashing [here] Libre OpenSSL supports a wide range of hashing methods including Gost, MD4, MD5, RMD-160, SHA-1, SHA-256 and SHA-512.
Diffie-Hellman parameter generation
-
DH Parameters with OpenSSL [here]. The Diffie-Hellman (DH) method is perhaps one of the greatest inventions in Cybersecurity, and was created by Whitfield Diffie and Marty Hellman. With the DH method, Bob creates a random value (\(b\)) and Alice also creates a random value (\(a\)). Next Bob computes \(B=g^b \pmod p\) and sends it to Alice. Alice computes \(A=g^a \pmod p\) and sends this to Bob. Bob raises the value of \(A\) to the power of \(b\) and takes \(\pmod p\), and Alice raises \(B\) to the power of \(a\) and takes \(\pmod p\). In the end, they will have the same shared value: \(g^{ab} \pmod p\). This can then be used to derive an encryption key that they can use for a secure tunnel. Overall, \(p\) is the large prime number, and also known as the shared modulus between Bob and Alice.
Key derivation function
-
PBKDF2 key derivation with OpenSSL [here] PBKDF2 (Password Key Derivation Function 2) is a key derivation method. Overall it is relatively slow in its operation and where we take a password, a salt value, hashing method, and a number of iterations, in order to produce a given size of encryption key.
-
HKDF key derivation with OpenSSL [here] HKDF (HMAC Key Derivation function) is used to derive an encryption key from a pass phrase. Initially HKDF creates a pseudorandom key (PRK) using a pass phrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), andalong with a salt value. Next the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys.
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Passwords
-
Password example [here]. This page uses the OpenSSL library hash password generator, which is used in UNIX systems for the hashing of passwords which are contained in /etc/shadow and /etc/passwd. For newer passwords, the "-1" options is used to created the hashed value.
-
Hashed passwords with OpenSSL [here].
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
Public key
-
Generating an ECC key pair with OpenSSL [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)).
-
Generating an RSA key pair with OpenSSL [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2).
-
Generating an RSA key pair with OpenSSL with encryption [here]. This page implements RSA key pair generation with an encrypted key pair. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). In this case we will encrypt the key pair with either 3DES, 128-bit AES, 192-bit AES or 256-bit AES. The same password must be used to encrypt and decrypt.
-
Generate prime with OpenSSL [here]. Prime numbers are important in public key encrytion, and are used with RSA and ECC. For RSA, we generate two prime numbers (\(p\) and \(q\)) and which are multiplied together to create a modulus (\(N\)). If these prime numbers have 512 bit values, the modulus will be a 1,024 bit value. This defines the basic secure of RSA. With elliptic curve we use smaller prime numbers, such as 256-bit values for the secp256k1 curve.
ASN1 parsing
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). We will parse using asn1parse, and reveal the parameters.
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)) [RSA key pair]. We will parse using asn1parse, and reveal the parameters.
- DSA Parameters with asn1parse. DSA parameters with OpenSSL with asn1parse. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA (Digital Signature Algorithm)
- DSA Parameters. DSA parameters with OpenSSL. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
MAC (Message Authentication Code)
- HMAC with OpenSSL. MACs with OpenSSL. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authenticate both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2) and SHA-3. In this case we will use OpenSSL to generate the HMAC value.
- MACs with OpenSSL. MACs with OpenSSL. In the following we will generate MACs for HMAC, GMAC, CMAC, Blake2bmac, Blake2smac, KMAC128 and KMAC256. Overall, we will use an encryption key defined as a hex value for GMAC and CMAC, and a pass phrase for the others. The message is "hello".
Signing
- Digital signing a plaintext message with OpenSSL. Signing with OpenSSL. With digital signing, we can take a message, and create a signature. This normally involves signing with a private key and digital certificate. The signed message can be an a MIME format, and which can be integrated into an email message. In this can we have a 512-bit RSA key pair that will sign a plain text message.
Encrypting emails
- Encrypting an email message in OpenSSL. Encrypting messages with OpenSSL. With public key encryption, we can take a message, and encrypt it with the recipiant's public key. In this can we have a 512-bit RSA public key to encrypt a message.
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Random number generation with OpenSSL
-
Random number generator [here]. Random numbers are important in generating encryption keys and salt values. In this case OpenSSL generates a random number (in a Base64 format) for a given number of bytes.
Outline (C#/Python)
-
Symmetric Key Encryption (C#) [here]. This page uses the OpenSSL library through a C#/.NET wrapper. The DLLs it interfaces to are libeay32.dll and ssleay32.dll. OpenSSL supports a wide range of encryption methods, including 128-bit AES, 192-bit AES, 256-bit AES and Blowfish (bf). Different modes of ECB, CBC, and OFB are implemented. The examples use a default IV of "1234".
-
AES in Python with OpenSSL output [here]
-
Producing OpenSSL AES Encrypted String from C# [here]
Digital Certificates
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
Paillier - Partial Homomorphic Encryption

The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Fundamentals
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier).
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Using RSA
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
Applications
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Public key points for curves. Simple. Display public key points for scalars.
BLS Curve
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
Accumulator and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
Pallas Curve
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
Pairing-based Crypto
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
ElGamal and ECC
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a numerical input.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
Shamir Secret Shares
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Homomorphic Encryption
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Zero knowledge proofs
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
Verifiable Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Hash to scalar and point
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
CP-ABE
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Lattice cryptography

Latice cryptography is proposed as a post-quantum robust method for public key encryption, especially focused on digital signatures and key exchange mechanisms (KEMs).
Principles
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
NTRU
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- Lattice Encryption: NTRU Key Generation Python). NTRU. Outlines how NTRU operates for key generation.
Homomorphic
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Digital Signatures
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
Public-Key Encryption/Key Exchange
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
Light-weight cryptography

While AES and SHA work well together within computer systems, they struggle in an IoT/embedded world as they take up: too much processing power; too much physical space; and consume too much battery power. So NIST outlines a number of methods which can be used for light-weight cryptography, and which could be useful in IoT and RFID devices [1]. They define the device spectrum as:
- Conventional cryptography. Servers and Desktops. Tablets and smart phones.
- Light-weight cryptography. Embedded Systems. RFID and Sensor Networks.
With embedded systems, we commonly see 8-bit, 16-bit and 32-bit microcontrollers, and which would struggle to cope with real-time demands for conventional cryptography methods. And in the 40+ years since the first 4-bit processor, there is even a strong market for 4-bit processors. RFID and sensor network devices, especially, have limited numbers of gates available for security, and are often highly constrained with the power drain on the device.
So AES is typically a non-starter for many embedded devices. In light-weight cryptography, we often see smaller block size (typically 64 bits or 80 bits), smaller keys (often less than 90 bits) and less complex rounds (and where the S-boxes often just have 4-bits).
For light-weight cryptography the main constraints that we have are typically related to ener requirements, gate equivalents (GEs), and timing. With passive RFID devices, we do not have an associated battery for the power supply, and where the chip must power itself from energy coupled from the radio wave. An RFID device is thus likely to be severely constrained in the power drain associated with any cryptography functions, along with being constrained for the timing requirements and for the number of gates used. Even if an RFID device has an associated battery (active RFID), it may be difficult to recharge the battery, so the drain on power must often be minimised.
There is thus often a compromise between the cryptography method used and the overall security of the method. Thus often light-weight cryptography methods balance performance (throughput) against power drain and GE, and do not perform as well as main-stream cryptography standards (such as AES and SHA-256). Along with this the method must also have a low requirement for RAM (where the method requires the usage of running memory to perform its operation) and ROM (where the method is stored on the device). In order to assess the strengths of various methods we often define the area that the cryptography function will use on the device – and which is defined in \(µm^2\). The NIST finalists are defined in this [article]
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- GIFT AEAD. GIFT. GIFT is a light-weight block cipher. It is a (NIST Finalist)
- Elephant. Elephant. Elephant is a light-weight stream cipher. It is a (NIST Finalist).
- TinyJambu. TinyJambu. TinyJambu is a light-weight block cipher. It is a (NIST Finalist)
- Isap AEAD. Isap. Isap is a light-weight block cipher. It is a (NIST Finalist)
- PHOTON-Beetle AEAD. PHOTON-Beetle. PHOTON-Beetle is a light-weight block cipher. It is a (NIST Finalist)
- Romulus AEAD. Romulus. Romulus is a light-weight block cipher. It is a (NIST Finalist)
- Sparkle AEAD. Sparkle. Sparkle is a light-weight block cipher. It is a (NIST Finalist)
- CLEFIA. CLEFIA. CLEFIA is a light-weight block cipher.
- LED. LED. LED is a light-weight block cipher.
- Piccolo. Piccolo. Piccolo is an ultra light-weight block cipher.
- PRESENT. PRESENT. Present is a light-weight block cipher.
- Pyjamask. Pyjamask. Pyjamask is a light-weight block cipher.
- SIMON. SIMON. SIMON is a light-weight block cipher.
- SKINNY. SKINNY. SKINNEY is a light-weight block cipher.
- SPECK. SPECK. SPECK is a light-weight block cipher.
- XTEA. XTEA. XTEA is a light-weight block cipher.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encryption/Decryption. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.
Light-weight crypto (Other)
- Chaskey (MAC). Chaskey. Chaskey is a light-weight MAC function.
- Chaskey (MAC). Chaskey (Python). Chaskey is a light-weight MAC function.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (ASCON)
ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRFF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
Discrete Logs (Solving)

A discrete log problem is in the form of \(g^x \pmod p\) and where we know \(g\) and \(p\) and must solve for \(x\).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Message Authentication Code (MAC)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
HMAC
The following are the tips related to Key-based hashing:
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authentication both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2), Blake2b, SM3 and SHA-3. This page outlines the HMAC-MD5 methods using the Hazmat cryptography layer.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- HMAC (COSE). Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT with HMMAC. Go. In this case we create a CWT token, and sign with an HMAC signature.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- HMAC with Rust. HMAC. HMAC with Rust.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HMAC with OpenSSL. MACs with OpenSSL. HMAC in OpenSSL for a given input value, password and hashing method.
Cipher MACs
The following are the tips related to Key-based hashing:
- MACs with OpenSSL. MACs with OpenSSL. MAC methods implemented in OpenSSL, including CMAC and GMAC.
Key-based hashing
The following are the tips related to Key-based hashing:
- SipHash. Siphash. Siphash is a fast key-based hashing method.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Meow. Meow. Meow is one of the fastest hashing methods.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
Magic Numbers

This pages contains information related to magic numbers in file formats.
Network and File Forensics
- Magic numbers. Magic. This provides information on magic number for file forensics.
Graphics formats
- JPEG Analysis. JPEGs. This provides an analysis of JPEG files.
- GIF Analysis. GIFs. This provides an analysis of GIF files.
- TIF Analysis. TIFs. This provides an analysis of TIF files.
- PNG Analysis. PNGs. This provides an analysis of PNG files.
- BMP Analysis. BMPs. This provides an analysis of BMP files.
- PSD Analysis. PSDs. This provides an analysis of PSD files.
- WMF Analysis. WMF. This provides an analysis of WMF files.
- Adobe Illustrator Analysis. AI. This provides an analysis of AI files.
- Adobe In Design Analysis. INDD. This provides an analysis of INDD files.
- MIDI file. MIDI. This provides an analysis of MID files.
- ICO file. ICO. This provides an analysis of ICO files.
- PS file. PS. This provides an analysis of PS files.
- EPS file. EPS. This provides an analysis of EPS files.
- VSD file. VSD. This provides an analysis of Microsft Visio (VSD) files.
Video and audio formats
- MP3 Analysis. MP3s. This provides an analysis of MP3 files.
- AVI Analysis. AVIs. This provides an analysis of AVI files.
- Flash SWF Analysis. SWFs. This provides an analysis of Flash files.
- Flash FLV Analysis. FLVs. This provides an analysis of FLV files.
- MP4 Analysis. MP4. This provides an analysis of MP4 files.
- MOV Analysis. MOV. This provides an analysis of MOV files.
- WMV Analysis. WMV. This provides an analysis of WMV files.
- WMA Analysis. WMA. This provides an analysis of WMA files.
- JPEG 2000 Analysis. JPEG 2. This provides an analysis of JPEG 2000 files.
- WAV Analysis. WAV. This provides an analysis of WAV files.
Zips, Archives and Library files
- ZIP/Archive Analysis. ZIPs. This provides an analysis of ZIP/Achive files.
- GZ Analysis. GZ. This provides an analysis of GZip files.
- Tar Analysis. Tar. This provides an analysis of TAR files.
- MSI Analysis. MSI. This provides an analysis of MSI files.
- OBJ Analysis. OBJ. This provides an analysis of OBJ files.
- DLL Analysis. DLL. This provides an analysis of DLL files.
- CAB Analysis. CAB. This provides an analysis of CAB files.
- EXE Analysis. EXE. This provides an analysis of EXE files.
- RAR Analysis. RAR. This provides an analysis of RAR files.
- SYS Analysis. SYS. This provides an analysis of SYS files.
- HLP Analysis. HLP. This provides an analysis of HLP files.
- VMDK Analysis. VMDK. This provides an analysis of VMDK files (VMWare Virtual Disks).
- PST Analysis. PST. This provides an analysis of PST files (Outlook Email File).
- JAR Analysis. JAR. This provides an analysis of JAR files.
- SLN Analysis. SLN. This provides an analysis of Microsoft SLN files.
- Class Analysis. Class. This provides an analysis of Java Class files.
- Zlib. Zlib. This provides an analysis of Zlib files.
Documents
- PDF Analysis. PDFs. This provides an analysis of PDF files.
- DOC Analysis. DOCs. This provides an analysis of DOC files.
- RTF Analysis. RTFs. This provides an analysis of RTF files.
- XLS Analysis. XLSs. This provides an analysis of XLS files.
- PPT Analysis. PPTs. This provides an analysis of PPT files.
- MMP File. MMP. This provides an analysis of MMP files.
- DOCX Analysis. DOCX. This provides an analysis of DOCX files.
- XLSX Analysis. XLSX. This provides an analysis of XLSX files.
- PPTX Analysis. PPTX. This provides an analysis of PPTX files.
- MDB Analysis. MDB. This provides an analysis of MDB files.
- Outlook Message Analysis. MSG. This provides an analysis of MSG files.
Disk Image
- Raw disk format. RAW. This provides an analysis of the RAW disk format.
Tests
- File Forensics Test. File Test File Forensics Test.
- File Forensics Test (Fun). File Test (Fun) File Forensics Test.
Presentations
MIRACL Core Library

MIRACL Core is an open source library, and includes a wide range of public key encryption methods. It is especially focused on elliptic curve and pairing-friendly methods, but also supports a wide range of encryption methods, including RSA, AES and hashing. Overall, it can be ported onto a wide range of systems and supports C, C++, Go, Rust, Python, Java, Javascript and Swift. Along with this it supports limited capability devices such as the Arduino infrastructure. The GitHub repository is [here].
BN254
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.

Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- CL Signatures. CL. CL Signatures in Go using MIRACL.
- CL Signatures (advanced pairing). CL. CL Signatures in Go using MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages using MIRACL.
- PS Signatures. PS. Signatures using PS for short signatures using MIRACL.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures using MIRACL.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.

Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
Rust examples
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
NaCl

PyNaCl is a Python port of LibSodium. It integrates the latest cryptography methods, such as AES, XChaCha20, Blake2b and X25519.
Symmetric Key
- Symmetric key. Symmetric key (XChaCha20 and Poly1305). With symmetric key, Bob and Alice have the same key. NaCl uses the XChaCha20 method, and which supports stream encryption (and which does not require padding as a block cipher does, and is also faster than block cipher modes). ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16 byte nonce. XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24 byte nonce. It has a lower propability of nonce misuse than ChaCha20.
- Encryption with a password. Symmetric Key with KDF. In symmetric key, we generate a secret key. This key is typically a random value or generated from a password and a salt value. If we use a password, we typically use a KDF (Key Derivation Function), and which uses a password and a salt value, in order to create a key of a given size. In this case we will use Argon2i, and which is memory resilent.
Hybrid Encryption
- Box. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Hashing
- Hashing and KDF (Argon2 and scrypt). Hashing and KDF. This case we will use PyNaCl (Networking and Cryptography) library, and which is a Python binding to libsodium. We will hash a password using SHA-256 and SHA-512, and also create a KDF (Key Derivation Function) using scrypt and Argon2.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
Ed25519
-
Ed25519. Ed25519. Using Ed25519 for digital signatures.
-
Finding Points on Ed25519. X25519 (Points).
In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 (Key Exchange)
- X25519 + BLAKE2b key-exchange. X25519. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
Curve 25519
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
Node.js

Node.js uses the JavaScript programming langauge as its base, and allows for code to be run on a server, rather than in the browser (such as with pure JavaScript). To run a node.js program, we run "node myfile.js", and use NPM to install libraries.
Symmetric key
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
RSA and public key
- RSA Opt imal Asymmetric Encryption Padding (OAEP) using Node.js. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
ECC Keys
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.

Hashing
- Hashing with node.js (All). Hashing. Hashing with node.js.
- Hashing with node.js (Selection). Hashing. Hashing with node.js.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- ECDSA with node.js. ECDSA. ECDSA with node.js.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
Key exchange
- Diffie-Hellman with node.js (random prime). DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method and uses a randomly generated prime number (press the button to generate a new prime).
- Diffie-Hellman with node.js. DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method. Each time the prime number will be fixed for the DH group selected.
- ECDH with node.js. ECDH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Elliptic Curve Diffie Hellman (ECDH) key exchange method.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
Key derivation
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
CryptoJS
- CryptoJS (in node.js). CryptoJS (Node.js). Various crypto methods in the browser.
Bulletproofs
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
Blockchain
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
Proxy encryption
- Proxy Encryption - Encrypting With Public Key, And Decrypt with Private Key. Proxy01. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This page just creates a key pair for Alice, and uses it to encrypt with the public key , and decrypt with the private key.
- Proxy Encryption. Proxy02. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This will go through the full use case of proxy re-encryption.
Tokens
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
Random
- Fortuna with node.js. Fortuna. Fortuna random numbers with node.js.
Other
- FPE with node.js. FPR. FPE with node.js.
- Puny with node.js. Puny. Puny character format with node.js.
Accumulators and Witnesses
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
PGP
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Password Entropy
- Password Entropy with Node.js. Password Entropy. Password entropy measures the strength of a password, and is measured as the number of bits which could represent all of the possibilities. An entropy score of less than 25 identifies a poor password, and between 25 and 50 is a weak password. For 50 to 75 we have a reasonable password, and between 75 and 100 is a very good password. Over 100 is an excellent password. The strength of the password relates to the number of characters used, and also the number of characters in the password.
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
- Homomorphic Encryption with Node.js and BGV. Homomorphic Encryption with Node.js and BFG. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BGV method.
Oblivious Transfer (OT)

Oblivious Transfer allows Bob to select data from Alice, but for Alice not to know which value has been selected.
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
OpenSSH

OpenSSH supports the usage of the SSH protocol. This allows for a remote login. One tool which is uses is ssh-keygen, and which allow for the generation of RSA, DSA and elliptic-curve keys that. These can be used for user and host authentication, such as for GitHub login and Cloud instance login.
OpenSSH
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here].
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
Outline

OpenSSL

OpenSSL is a standard library that implements cryptography.
Symmetric key (Command line)
-
Symmetric Key Encryption (OpenSSL 1.x) [here]. In this case we will create cipher text from OpenSSL 1.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 1.x) [here].In this case we will decrypt cipher text from OpenSSL 1.x using a key derived from a password
-
Symmetric Key Encryption (OpenSSL 3.x) [here]. In this case we will create cipher text from OpenSSL 3.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 3.x) [here].In this case we will decrypt cipher text from OpenSSL 3.x using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password.
Hashing
-
Hashing [here] OpenSSL supports a wide range of hashing methods including BLAKE2b, Gost, MD4, MD5, RMD-160, SHA-1, SHA-3, SHA-256 and SHA-512.
Libre OpenSSL
-
Symmetric Key Encryption using Libre OpenSSL [here]. In this case we will create cipher text from Libre OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption using Libre OpenSSL [here]. In this case we will decrypt ciphertext from Libre OpenSSL using a key derived from a password.
-
Hashing [here] Libre OpenSSL supports a wide range of hashing methods including Gost, MD4, MD5, RMD-160, SHA-1, SHA-256 and SHA-512.
Diffie-Hellman parameter generation
-
DH Parameters with OpenSSL [here]. The Diffie-Hellman (DH) method is perhaps one of the greatest inventions in Cybersecurity, and was created by Whitfield Diffie and Marty Hellman. With the DH method, Bob creates a random value (\(b\)) and Alice also creates a random value (\(a\)). Next Bob computes \(B=g^b \pmod p\) and sends it to Alice. Alice computes \(A=g^a \pmod p\) and sends this to Bob. Bob raises the value of \(A\) to the power of \(b\) and takes \(\pmod p\), and Alice raises \(B\) to the power of \(a\) and takes \(\pmod p\). In the end, they will have the same shared value: \(g^{ab} \pmod p\). This can then be used to derive an encryption key that they can use for a secure tunnel. Overall, \(p\) is the large prime number, and also known as the shared modulus between Bob and Alice.
Key derivation function
-
PBKDF2 key derivation with OpenSSL [here] PBKDF2 (Password Key Derivation Function 2) is a key derivation method. Overall it is relatively slow in its operation and where we take a password, a salt value, hashing method, and a number of iterations, in order to produce a given size of encryption key.
-
HKDF key derivation with OpenSSL [here] HKDF (HMAC Key Derivation function) is used to derive an encryption key from a pass phrase. Initially HKDF creates a pseudorandom key (PRK) using a pass phrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), andalong with a salt value. Next the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys.
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Passwords
-
Password example [here]. This page uses the OpenSSL library hash password generator, which is used in UNIX systems for the hashing of passwords which are contained in /etc/shadow and /etc/passwd. For newer passwords, the "-1" options is used to created the hashed value.
-
Hashed passwords with OpenSSL [here].
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
Public key
-
Generating an ECC key pair with OpenSSL [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)).
-
Generating an RSA key pair with OpenSSL [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2).
-
Generating an RSA key pair with OpenSSL with encryption [here]. This page implements RSA key pair generation with an encrypted key pair. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). In this case we will encrypt the key pair with either 3DES, 128-bit AES, 192-bit AES or 256-bit AES. The same password must be used to encrypt and decrypt.
-
Generate prime with OpenSSL [here]. Prime numbers are important in public key encrytion, and are used with RSA and ECC. For RSA, we generate two prime numbers (\(p\) and \(q\)) and which are multiplied together to create a modulus (\(N\)). If these prime numbers have 512 bit values, the modulus will be a 1,024 bit value. This defines the basic secure of RSA. With elliptic curve we use smaller prime numbers, such as 256-bit values for the secp256k1 curve.
ASN1 parsing
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). We will parse using asn1parse, and reveal the parameters.
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)) [RSA key pair]. We will parse using asn1parse, and reveal the parameters.
- DSA Parameters with asn1parse. DSA parameters with OpenSSL with asn1parse. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA (Digital Signature Algorithm)
- DSA Parameters. DSA parameters with OpenSSL. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
MAC (Message Authentication Code)
- HMAC with OpenSSL. MACs with OpenSSL. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authenticate both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2) and SHA-3. In this case we will use OpenSSL to generate the HMAC value.
- MACs with OpenSSL. MACs with OpenSSL. In the following we will generate MACs for HMAC, GMAC, CMAC, Blake2bmac, Blake2smac, KMAC128 and KMAC256. Overall, we will use an encryption key defined as a hex value for GMAC and CMAC, and a pass phrase for the others. The message is "hello".
Signing
- Digital signing a plaintext message with OpenSSL. Signing with OpenSSL. With digital signing, we can take a message, and create a signature. This normally involves signing with a private key and digital certificate. The signed message can be an a MIME format, and which can be integrated into an email message. In this can we have a 512-bit RSA key pair that will sign a plain text message.
Encrypting emails
- Encrypting an email message in OpenSSL. Encrypting messages with OpenSSL. With public key encryption, we can take a message, and encrypt it with the recipiant's public key. In this can we have a 512-bit RSA public key to encrypt a message.
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Random number generation with OpenSSL
-
Random number generator [here]. Random numbers are important in generating encryption keys and salt values. In this case OpenSSL generates a random number (in a Base64 format) for a given number of bytes.
Outline (C#/Python)
-
Symmetric Key Encryption (C#) [here]. This page uses the OpenSSL library through a C#/.NET wrapper. The DLLs it interfaces to are libeay32.dll and ssleay32.dll. OpenSSL supports a wide range of encryption methods, including 128-bit AES, 192-bit AES, 256-bit AES and Blowfish (bf). Different modes of ECB, CBC, and OFB are implemented. The examples use a default IV of "1234".
-
AES in Python with OpenSSL output [here]
-
Producing OpenSSL AES Encrypted String from C# [here]
Digital Certificates
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
Paillier - Partial Homomorphic Encryption

The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Fundamentals
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier).
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Using RSA
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
Applications
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- BLS12 curves. BLS12-337/381. Finding the base point and public key value for BLS12 curves.
- BLS signing messages. Signing. Signing messages with BLS.
- BBS signing messages. Signing. Signing multiple messages with BBS.
Accumulator and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
Pallas Curve
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
Pairing-based Crypto
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
ElGamal and ECC
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a numerical input.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
Shamir Secret Shares
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Homomorphic Encryption
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Zero knowledge proofs
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
Verifiable Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Hash to scalar and point
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
CP-ABE
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Lattice cryptography

Latice cryptography is proposed as a post-quantum robust method for public key encryption, especially focused on digital signatures and key exchange mechanisms (KEMs).
Principles
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
NTRU
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- Lattice Encryption: NTRU Key Generation Python). NTRU. Outlines how NTRU operates for key generation.
Homomorphic
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Digital Signatures
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
Public-Key Encryption/Key Exchange
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
Light-weight cryptography

While AES and SHA work well together within computer systems, they struggle in an IoT/embedded world as they take up: too much processing power; too much physical space; and consume too much battery power. So NIST outlines a number of methods which can be used for light-weight cryptography, and which could be useful in IoT and RFID devices [1]. They define the device spectrum as:
- Conventional cryptography. Servers and Desktops. Tablets and smart phones.
- Light-weight cryptography. Embedded Systems. RFID and Sensor Networks.
With embedded systems, we commonly see 8-bit, 16-bit and 32-bit microcontrollers, and which would struggle to cope with real-time demands for conventional cryptography methods. And in the 40+ years since the first 4-bit processor, there is even a strong market for 4-bit processors. RFID and sensor network devices, especially, have limited numbers of gates available for security, and are often highly constrained with the power drain on the device.
So AES is typically a non-starter for many embedded devices. In light-weight cryptography, we often see smaller block size (typically 64 bits or 80 bits), smaller keys (often less than 90 bits) and less complex rounds (and where the S-boxes often just have 4-bits).
For light-weight cryptography the main constraints that we have are typically related to ener requirements, gate equivalents (GEs), and timing. With passive RFID devices, we do not have an associated battery for the power supply, and where the chip must power itself from energy coupled from the radio wave. An RFID device is thus likely to be severely constrained in the power drain associated with any cryptography functions, along with being constrained for the timing requirements and for the number of gates used. Even if an RFID device has an associated battery (active RFID), it may be difficult to recharge the battery, so the drain on power must often be minimised.
There is thus often a compromise between the cryptography method used and the overall security of the method. Thus often light-weight cryptography methods balance performance (throughput) against power drain and GE, and do not perform as well as main-stream cryptography standards (such as AES and SHA-256). Along with this the method must also have a low requirement for RAM (where the method requires the usage of running memory to perform its operation) and ROM (where the method is stored on the device). In order to assess the strengths of various methods we often define the area that the cryptography function will use on the device – and which is defined in \(µm^2\). The NIST finalists are defined in this [article]
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- GIFT AEAD. GIFT. GIFT is a light-weight block cipher. It is a (NIST Finalist)
- Elephant. Elephant. Elephant is a light-weight stream cipher. It is a (NIST Finalist).
- TinyJambu. TinyJambu. TinyJambu is a light-weight block cipher. It is a (NIST Finalist)
- Isap AEAD. Isap. Isap is a light-weight block cipher. It is a (NIST Finalist)
- PHOTON-Beetle AEAD. PHOTON-Beetle. PHOTON-Beetle is a light-weight block cipher. It is a (NIST Finalist)
- Romulus AEAD. Romulus. Romulus is a light-weight block cipher. It is a (NIST Finalist)
- Sparkle AEAD. Sparkle. Sparkle is a light-weight block cipher. It is a (NIST Finalist)
- CLEFIA. CLEFIA. CLEFIA is a light-weight block cipher.
- LED. LED. LED is a light-weight block cipher.
- Piccolo. Piccolo. Piccolo is an ultra light-weight block cipher.
- PRESENT. PRESENT. Present is a light-weight block cipher.
- Pyjamask. Pyjamask. Pyjamask is a light-weight block cipher.
- SIMON. SIMON. SIMON is a light-weight block cipher.
- SKINNY. SKINNY. SKINNEY is a light-weight block cipher.
- SPECK. SPECK. SPECK is a light-weight block cipher.
- XTEA. XTEA. XTEA is a light-weight block cipher.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encryption/Decryption. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.
Light-weight crypto (Other)
- Chaskey (MAC). Chaskey. Chaskey is a light-weight MAC function.
- Chaskey (MAC). Chaskey (Python). Chaskey is a light-weight MAC function.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (ASCON)
ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRFF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
Discrete Logs (Solving)

A discrete log problem is in the form of \(g^x \pmod p\) and where we know \(g\) and \(p\) and must solve for \(x\).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Message Authentication Code (MAC)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
HMAC
The following are the tips related to Key-based hashing:
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authentication both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2), Blake2b, SM3 and SHA-3. This page outlines the HMAC-MD5 methods using the Hazmat cryptography layer.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- HMAC (COSE). Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT with HMMAC. Go. In this case we create a CWT token, and sign with an HMAC signature.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- HMAC with Rust. HMAC. HMAC with Rust.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HMAC with OpenSSL. MACs with OpenSSL. HMAC in OpenSSL for a given input value, password and hashing method.
Cipher MACs
The following are the tips related to Key-based hashing:
- MACs with OpenSSL. MACs with OpenSSL. MAC methods implemented in OpenSSL, including CMAC and GMAC.
Key-based hashing
The following are the tips related to Key-based hashing:
- SipHash. Siphash. Siphash is a fast key-based hashing method.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Meow. Meow. Meow is one of the fastest hashing methods.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
Magic Numbers

This pages contains information related to magic numbers in file formats.
Network and File Forensics
- Magic numbers. Magic. This provides information on magic number for file forensics.
Graphics formats
- JPEG Analysis. JPEGs. This provides an analysis of JPEG files.
- GIF Analysis. GIFs. This provides an analysis of GIF files.
- TIF Analysis. TIFs. This provides an analysis of TIF files.
- PNG Analysis. PNGs. This provides an analysis of PNG files.
- BMP Analysis. BMPs. This provides an analysis of BMP files.
- PSD Analysis. PSDs. This provides an analysis of PSD files.
- WMF Analysis. WMF. This provides an analysis of WMF files.
- Adobe Illustrator Analysis. AI. This provides an analysis of AI files.
- Adobe In Design Analysis. INDD. This provides an analysis of INDD files.
- MIDI file. MIDI. This provides an analysis of MID files.
- ICO file. ICO. This provides an analysis of ICO files.
- PS file. PS. This provides an analysis of PS files.
- EPS file. EPS. This provides an analysis of EPS files.
- VSD file. VSD. This provides an analysis of Microsft Visio (VSD) files.
Video and audio formats
- MP3 Analysis. MP3s. This provides an analysis of MP3 files.
- AVI Analysis. AVIs. This provides an analysis of AVI files.
- Flash SWF Analysis. SWFs. This provides an analysis of Flash files.
- Flash FLV Analysis. FLVs. This provides an analysis of FLV files.
- MP4 Analysis. MP4. This provides an analysis of MP4 files.
- MOV Analysis. MOV. This provides an analysis of MOV files.
- WMV Analysis. WMV. This provides an analysis of WMV files.
- WMA Analysis. WMA. This provides an analysis of WMA files.
- JPEG 2000 Analysis. JPEG 2. This provides an analysis of JPEG 2000 files.
- WAV Analysis. WAV. This provides an analysis of WAV files.
Zips, Archives and Library files
- ZIP/Archive Analysis. ZIPs. This provides an analysis of ZIP/Achive files.
- GZ Analysis. GZ. This provides an analysis of GZip files.
- Tar Analysis. Tar. This provides an analysis of TAR files.
- MSI Analysis. MSI. This provides an analysis of MSI files.
- OBJ Analysis. OBJ. This provides an analysis of OBJ files.
- DLL Analysis. DLL. This provides an analysis of DLL files.
- CAB Analysis. CAB. This provides an analysis of CAB files.
- EXE Analysis. EXE. This provides an analysis of EXE files.
- RAR Analysis. RAR. This provides an analysis of RAR files.
- SYS Analysis. SYS. This provides an analysis of SYS files.
- HLP Analysis. HLP. This provides an analysis of HLP files.
- VMDK Analysis. VMDK. This provides an analysis of VMDK files (VMWare Virtual Disks).
- PST Analysis. PST. This provides an analysis of PST files (Outlook Email File).
- JAR Analysis. JAR. This provides an analysis of JAR files.
- SLN Analysis. SLN. This provides an analysis of Microsoft SLN files.
- Class Analysis. Class. This provides an analysis of Java Class files.
- Zlib. Zlib. This provides an analysis of Zlib files.
Documents
- PDF Analysis. PDFs. This provides an analysis of PDF files.
- DOC Analysis. DOCs. This provides an analysis of DOC files.
- RTF Analysis. RTFs. This provides an analysis of RTF files.
- XLS Analysis. XLSs. This provides an analysis of XLS files.
- PPT Analysis. PPTs. This provides an analysis of PPT files.
- MMP File. MMP. This provides an analysis of MMP files.
- DOCX Analysis. DOCX. This provides an analysis of DOCX files.
- XLSX Analysis. XLSX. This provides an analysis of XLSX files.
- PPTX Analysis. PPTX. This provides an analysis of PPTX files.
- MDB Analysis. MDB. This provides an analysis of MDB files.
- Outlook Message Analysis. MSG. This provides an analysis of MSG files.
Disk Image
- Raw disk format. RAW. This provides an analysis of the RAW disk format.
Tests
- File Forensics Test. File Test File Forensics Test.
- File Forensics Test (Fun). File Test (Fun) File Forensics Test.
Presentations
MIRACL Core Library

MIRACL Core is an open source library, and includes a wide range of public key encryption methods. It is especially focused on elliptic curve and pairing-friendly methods, but also supports a wide range of encryption methods, including RSA, AES and hashing. Overall, it can be ported onto a wide range of systems and supports C, C++, Go, Rust, Python, Java, Javascript and Swift. Along with this it supports limited capability devices such as the Arduino infrastructure. The GitHub repository is [here].
BN254
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.

Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- CL Signatures. CL. CL Signatures in Go using MIRACL.
- CL Signatures (advanced pairing). CL. CL Signatures in Go using MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages using MIRACL.
- PS Signatures. PS. Signatures using PS for short signatures using MIRACL.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures using MIRACL.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.

Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
Rust examples
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
NaCl

PyNaCl is a Python port of LibSodium. It integrates the latest cryptography methods, such as AES, XChaCha20, Blake2b and X25519.
Symmetric Key
- Symmetric key. Symmetric key (XChaCha20 and Poly1305). With symmetric key, Bob and Alice have the same key. NaCl uses the XChaCha20 method, and which supports stream encryption (and which does not require padding as a block cipher does, and is also faster than block cipher modes). ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16 byte nonce. XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24 byte nonce. It has a lower propability of nonce misuse than ChaCha20.
- Encryption with a password. Symmetric Key with KDF. In symmetric key, we generate a secret key. This key is typically a random value or generated from a password and a salt value. If we use a password, we typically use a KDF (Key Derivation Function), and which uses a password and a salt value, in order to create a key of a given size. In this case we will use Argon2i, and which is memory resilent.
Hybrid Encryption
- Box. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Hashing
- Hashing and KDF (Argon2 and scrypt). Hashing and KDF. This case we will use PyNaCl (Networking and Cryptography) library, and which is a Python binding to libsodium. We will hash a password using SHA-256 and SHA-512, and also create a KDF (Key Derivation Function) using scrypt and Argon2.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
Ed25519
-
Ed25519. Ed25519. Using Ed25519 for digital signatures.
-
Finding Points on Ed25519. X25519 (Points).
In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 (Key Exchange)
- X25519 + BLAKE2b key-exchange. X25519. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
Curve 25519
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
Node.js

Node.js uses the JavaScript programming langauge as its base, and allows for code to be run on a server, rather than in the browser (such as with pure JavaScript). To run a node.js program, we run "node myfile.js", and use NPM to install libraries.
Symmetric key
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
RSA and public key
- RSA Opt imal Asymmetric Encryption Padding (OAEP) using Node.js. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
ECC Keys
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.

Hashing
- Hashing with node.js (All). Hashing. Hashing with node.js.
- Hashing with node.js (Selection). Hashing. Hashing with node.js.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- ECDSA with node.js. ECDSA. ECDSA with node.js.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
Key exchange
- Diffie-Hellman with node.js (random prime). DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method and uses a randomly generated prime number (press the button to generate a new prime).
- Diffie-Hellman with node.js. DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method. Each time the prime number will be fixed for the DH group selected.
- ECDH with node.js. ECDH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Elliptic Curve Diffie Hellman (ECDH) key exchange method.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
Key derivation
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
CryptoJS
- CryptoJS (in node.js). CryptoJS (Node.js). Various crypto methods in the browser.
Bulletproofs
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
Blockchain
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
Proxy encryption
- Proxy Encryption - Encrypting With Public Key, And Decrypt with Private Key. Proxy01. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This page just creates a key pair for Alice, and uses it to encrypt with the public key , and decrypt with the private key.
- Proxy Encryption. Proxy02. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This will go through the full use case of proxy re-encryption.
Tokens
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
Random
- Fortuna with node.js. Fortuna. Fortuna random numbers with node.js.
Other
- FPE with node.js. FPR. FPE with node.js.
- Puny with node.js. Puny. Puny character format with node.js.
Accumulators and Witnesses
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
PGP
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Password Entropy
- Password Entropy with Node.js. Password Entropy. Password entropy measures the strength of a password, and is measured as the number of bits which could represent all of the possibilities. An entropy score of less than 25 identifies a poor password, and between 25 and 50 is a weak password. For 50 to 75 we have a reasonable password, and between 75 and 100 is a very good password. Over 100 is an excellent password. The strength of the password relates to the number of characters used, and also the number of characters in the password.
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
- Homomorphic Encryption with Node.js and BGV. Homomorphic Encryption with Node.js and BFG. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BGV method.
Oblivious Transfer (OT)

Oblivious Transfer allows Bob to select data from Alice, but for Alice not to know which value has been selected.
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
OpenSSH

OpenSSH supports the usage of the SSH protocol. This allows for a remote login. One tool which is uses is ssh-keygen, and which allow for the generation of RSA, DSA and elliptic-curve keys that. These can be used for user and host authentication, such as for GitHub login and Cloud instance login.
OpenSSH
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here].
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
Outline

OpenSSL

OpenSSL is a standard library that implements cryptography.
Symmetric key (Command line)
-
Symmetric Key Encryption (OpenSSL 1.x) [here]. In this case we will create cipher text from OpenSSL 1.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 1.x) [here].In this case we will decrypt cipher text from OpenSSL 1.x using a key derived from a password
-
Symmetric Key Encryption (OpenSSL 3.x) [here]. In this case we will create cipher text from OpenSSL 3.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 3.x) [here].In this case we will decrypt cipher text from OpenSSL 3.x using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password.
Hashing
-
Hashing [here] OpenSSL supports a wide range of hashing methods including BLAKE2b, Gost, MD4, MD5, RMD-160, SHA-1, SHA-3, SHA-256 and SHA-512.
Libre OpenSSL
-
Symmetric Key Encryption using Libre OpenSSL [here]. In this case we will create cipher text from Libre OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption using Libre OpenSSL [here]. In this case we will decrypt ciphertext from Libre OpenSSL using a key derived from a password.
-
Hashing [here] Libre OpenSSL supports a wide range of hashing methods including Gost, MD4, MD5, RMD-160, SHA-1, SHA-256 and SHA-512.
Diffie-Hellman parameter generation
-
DH Parameters with OpenSSL [here]. The Diffie-Hellman (DH) method is perhaps one of the greatest inventions in Cybersecurity, and was created by Whitfield Diffie and Marty Hellman. With the DH method, Bob creates a random value (\(b\)) and Alice also creates a random value (\(a\)). Next Bob computes \(B=g^b \pmod p\) and sends it to Alice. Alice computes \(A=g^a \pmod p\) and sends this to Bob. Bob raises the value of \(A\) to the power of \(b\) and takes \(\pmod p\), and Alice raises \(B\) to the power of \(a\) and takes \(\pmod p\). In the end, they will have the same shared value: \(g^{ab} \pmod p\). This can then be used to derive an encryption key that they can use for a secure tunnel. Overall, \(p\) is the large prime number, and also known as the shared modulus between Bob and Alice.
Key derivation function
-
PBKDF2 key derivation with OpenSSL [here] PBKDF2 (Password Key Derivation Function 2) is a key derivation method. Overall it is relatively slow in its operation and where we take a password, a salt value, hashing method, and a number of iterations, in order to produce a given size of encryption key.
-
HKDF key derivation with OpenSSL [here] HKDF (HMAC Key Derivation function) is used to derive an encryption key from a pass phrase. Initially HKDF creates a pseudorandom key (PRK) using a pass phrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), andalong with a salt value. Next the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys.
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Passwords
-
Password example [here]. This page uses the OpenSSL library hash password generator, which is used in UNIX systems for the hashing of passwords which are contained in /etc/shadow and /etc/passwd. For newer passwords, the "-1" options is used to created the hashed value.
-
Hashed passwords with OpenSSL [here].
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
Public key
-
Generating an ECC key pair with OpenSSL [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)).
-
Generating an RSA key pair with OpenSSL [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2).
-
Generating an RSA key pair with OpenSSL with encryption [here]. This page implements RSA key pair generation with an encrypted key pair. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). In this case we will encrypt the key pair with either 3DES, 128-bit AES, 192-bit AES or 256-bit AES. The same password must be used to encrypt and decrypt.
-
Generate prime with OpenSSL [here]. Prime numbers are important in public key encrytion, and are used with RSA and ECC. For RSA, we generate two prime numbers (\(p\) and \(q\)) and which are multiplied together to create a modulus (\(N\)). If these prime numbers have 512 bit values, the modulus will be a 1,024 bit value. This defines the basic secure of RSA. With elliptic curve we use smaller prime numbers, such as 256-bit values for the secp256k1 curve.
ASN1 parsing
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). We will parse using asn1parse, and reveal the parameters.
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)) [RSA key pair]. We will parse using asn1parse, and reveal the parameters.
- DSA Parameters with asn1parse. DSA parameters with OpenSSL with asn1parse. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA (Digital Signature Algorithm)
- DSA Parameters. DSA parameters with OpenSSL. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
MAC (Message Authentication Code)
- HMAC with OpenSSL. MACs with OpenSSL. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authenticate both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2) and SHA-3. In this case we will use OpenSSL to generate the HMAC value.
- MACs with OpenSSL. MACs with OpenSSL. In the following we will generate MACs for HMAC, GMAC, CMAC, Blake2bmac, Blake2smac, KMAC128 and KMAC256. Overall, we will use an encryption key defined as a hex value for GMAC and CMAC, and a pass phrase for the others. The message is "hello".
Signing
- Digital signing a plaintext message with OpenSSL. Signing with OpenSSL. With digital signing, we can take a message, and create a signature. This normally involves signing with a private key and digital certificate. The signed message can be an a MIME format, and which can be integrated into an email message. In this can we have a 512-bit RSA key pair that will sign a plain text message.
Encrypting emails
- Encrypting an email message in OpenSSL. Encrypting messages with OpenSSL. With public key encryption, we can take a message, and encrypt it with the recipiant's public key. In this can we have a 512-bit RSA public key to encrypt a message.
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Random number generation with OpenSSL
-
Random number generator [here]. Random numbers are important in generating encryption keys and salt values. In this case OpenSSL generates a random number (in a Base64 format) for a given number of bytes.
Outline (C#/Python)
-
Symmetric Key Encryption (C#) [here]. This page uses the OpenSSL library through a C#/.NET wrapper. The DLLs it interfaces to are libeay32.dll and ssleay32.dll. OpenSSL supports a wide range of encryption methods, including 128-bit AES, 192-bit AES, 256-bit AES and Blowfish (bf). Different modes of ECB, CBC, and OFB are implemented. The examples use a default IV of "1234".
-
AES in Python with OpenSSL output [here]
-
Producing OpenSSL AES Encrypted String from C# [here]
Digital Certificates
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
Paillier - Partial Homomorphic Encryption

The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Fundamentals
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier).
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Using RSA
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
Applications
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
Pallas Curve
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
Pairing-based Crypto
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
ElGamal and ECC
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a numerical input.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
Shamir Secret Shares
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Homomorphic Encryption
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Zero knowledge proofs
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
Verifiable Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Hash to scalar and point
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
CP-ABE
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Lattice cryptography

Latice cryptography is proposed as a post-quantum robust method for public key encryption, especially focused on digital signatures and key exchange mechanisms (KEMs).
Principles
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
NTRU
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- Lattice Encryption: NTRU Key Generation Python). NTRU. Outlines how NTRU operates for key generation.
Homomorphic
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Digital Signatures
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
Public-Key Encryption/Key Exchange
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
Light-weight cryptography

While AES and SHA work well together within computer systems, they struggle in an IoT/embedded world as they take up: too much processing power; too much physical space; and consume too much battery power. So NIST outlines a number of methods which can be used for light-weight cryptography, and which could be useful in IoT and RFID devices [1]. They define the device spectrum as:
- Conventional cryptography. Servers and Desktops. Tablets and smart phones.
- Light-weight cryptography. Embedded Systems. RFID and Sensor Networks.
With embedded systems, we commonly see 8-bit, 16-bit and 32-bit microcontrollers, and which would struggle to cope with real-time demands for conventional cryptography methods. And in the 40+ years since the first 4-bit processor, there is even a strong market for 4-bit processors. RFID and sensor network devices, especially, have limited numbers of gates available for security, and are often highly constrained with the power drain on the device.
So AES is typically a non-starter for many embedded devices. In light-weight cryptography, we often see smaller block size (typically 64 bits or 80 bits), smaller keys (often less than 90 bits) and less complex rounds (and where the S-boxes often just have 4-bits).
For light-weight cryptography the main constraints that we have are typically related to ener requirements, gate equivalents (GEs), and timing. With passive RFID devices, we do not have an associated battery for the power supply, and where the chip must power itself from energy coupled from the radio wave. An RFID device is thus likely to be severely constrained in the power drain associated with any cryptography functions, along with being constrained for the timing requirements and for the number of gates used. Even if an RFID device has an associated battery (active RFID), it may be difficult to recharge the battery, so the drain on power must often be minimised.
There is thus often a compromise between the cryptography method used and the overall security of the method. Thus often light-weight cryptography methods balance performance (throughput) against power drain and GE, and do not perform as well as main-stream cryptography standards (such as AES and SHA-256). Along with this the method must also have a low requirement for RAM (where the method requires the usage of running memory to perform its operation) and ROM (where the method is stored on the device). In order to assess the strengths of various methods we often define the area that the cryptography function will use on the device – and which is defined in \(µm^2\). The NIST finalists are defined in this [article]
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- GIFT AEAD. GIFT. GIFT is a light-weight block cipher. It is a (NIST Finalist)
- Elephant. Elephant. Elephant is a light-weight stream cipher. It is a (NIST Finalist).
- TinyJambu. TinyJambu. TinyJambu is a light-weight block cipher. It is a (NIST Finalist)
- Isap AEAD. Isap. Isap is a light-weight block cipher. It is a (NIST Finalist)
- PHOTON-Beetle AEAD. PHOTON-Beetle. PHOTON-Beetle is a light-weight block cipher. It is a (NIST Finalist)
- Romulus AEAD. Romulus. Romulus is a light-weight block cipher. It is a (NIST Finalist)
- Sparkle AEAD. Sparkle. Sparkle is a light-weight block cipher. It is a (NIST Finalist)
- CLEFIA. CLEFIA. CLEFIA is a light-weight block cipher.
- LED. LED. LED is a light-weight block cipher.
- Piccolo. Piccolo. Piccolo is an ultra light-weight block cipher.
- PRESENT. PRESENT. Present is a light-weight block cipher.
- Pyjamask. Pyjamask. Pyjamask is a light-weight block cipher.
- SIMON. SIMON. SIMON is a light-weight block cipher.
- SKINNY. SKINNY. SKINNEY is a light-weight block cipher.
- SPECK. SPECK. SPECK is a light-weight block cipher.
- XTEA. XTEA. XTEA is a light-weight block cipher.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encryption/Decryption. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.
Light-weight crypto (Other)
- Chaskey (MAC). Chaskey. Chaskey is a light-weight MAC function.
- Chaskey (MAC). Chaskey (Python). Chaskey is a light-weight MAC function.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (ASCON)
ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRFF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
Discrete Logs (Solving)

A discrete log problem is in the form of \(g^x \pmod p\) and where we know \(g\) and \(p\) and must solve for \(x\).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Message Authentication Code (MAC)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
HMAC
The following are the tips related to Key-based hashing:
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authentication both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2), Blake2b, SM3 and SHA-3. This page outlines the HMAC-MD5 methods using the Hazmat cryptography layer.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- HMAC (COSE). Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT with HMMAC. Go. In this case we create a CWT token, and sign with an HMAC signature.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- HMAC with Rust. HMAC. HMAC with Rust.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HMAC with OpenSSL. MACs with OpenSSL. HMAC in OpenSSL for a given input value, password and hashing method.
Cipher MACs
The following are the tips related to Key-based hashing:
- MACs with OpenSSL. MACs with OpenSSL. MAC methods implemented in OpenSSL, including CMAC and GMAC.
Key-based hashing
The following are the tips related to Key-based hashing:
- SipHash. Siphash. Siphash is a fast key-based hashing method.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Meow. Meow. Meow is one of the fastest hashing methods.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
Magic Numbers

This pages contains information related to magic numbers in file formats.
Network and File Forensics
- Magic numbers. Magic. This provides information on magic number for file forensics.
Graphics formats
- JPEG Analysis. JPEGs. This provides an analysis of JPEG files.
- GIF Analysis. GIFs. This provides an analysis of GIF files.
- TIF Analysis. TIFs. This provides an analysis of TIF files.
- PNG Analysis. PNGs. This provides an analysis of PNG files.
- BMP Analysis. BMPs. This provides an analysis of BMP files.
- PSD Analysis. PSDs. This provides an analysis of PSD files.
- WMF Analysis. WMF. This provides an analysis of WMF files.
- Adobe Illustrator Analysis. AI. This provides an analysis of AI files.
- Adobe In Design Analysis. INDD. This provides an analysis of INDD files.
- MIDI file. MIDI. This provides an analysis of MID files.
- ICO file. ICO. This provides an analysis of ICO files.
- PS file. PS. This provides an analysis of PS files.
- EPS file. EPS. This provides an analysis of EPS files.
- VSD file. VSD. This provides an analysis of Microsft Visio (VSD) files.
Video and audio formats
- MP3 Analysis. MP3s. This provides an analysis of MP3 files.
- AVI Analysis. AVIs. This provides an analysis of AVI files.
- Flash SWF Analysis. SWFs. This provides an analysis of Flash files.
- Flash FLV Analysis. FLVs. This provides an analysis of FLV files.
- MP4 Analysis. MP4. This provides an analysis of MP4 files.
- MOV Analysis. MOV. This provides an analysis of MOV files.
- WMV Analysis. WMV. This provides an analysis of WMV files.
- WMA Analysis. WMA. This provides an analysis of WMA files.
- JPEG 2000 Analysis. JPEG 2. This provides an analysis of JPEG 2000 files.
- WAV Analysis. WAV. This provides an analysis of WAV files.
Zips, Archives and Library files
- ZIP/Archive Analysis. ZIPs. This provides an analysis of ZIP/Achive files.
- GZ Analysis. GZ. This provides an analysis of GZip files.
- Tar Analysis. Tar. This provides an analysis of TAR files.
- MSI Analysis. MSI. This provides an analysis of MSI files.
- OBJ Analysis. OBJ. This provides an analysis of OBJ files.
- DLL Analysis. DLL. This provides an analysis of DLL files.
- CAB Analysis. CAB. This provides an analysis of CAB files.
- EXE Analysis. EXE. This provides an analysis of EXE files.
- RAR Analysis. RAR. This provides an analysis of RAR files.
- SYS Analysis. SYS. This provides an analysis of SYS files.
- HLP Analysis. HLP. This provides an analysis of HLP files.
- VMDK Analysis. VMDK. This provides an analysis of VMDK files (VMWare Virtual Disks).
- PST Analysis. PST. This provides an analysis of PST files (Outlook Email File).
- JAR Analysis. JAR. This provides an analysis of JAR files.
- SLN Analysis. SLN. This provides an analysis of Microsoft SLN files.
- Class Analysis. Class. This provides an analysis of Java Class files.
- Zlib. Zlib. This provides an analysis of Zlib files.
Documents
- PDF Analysis. PDFs. This provides an analysis of PDF files.
- DOC Analysis. DOCs. This provides an analysis of DOC files.
- RTF Analysis. RTFs. This provides an analysis of RTF files.
- XLS Analysis. XLSs. This provides an analysis of XLS files.
- PPT Analysis. PPTs. This provides an analysis of PPT files.
- MMP File. MMP. This provides an analysis of MMP files.
- DOCX Analysis. DOCX. This provides an analysis of DOCX files.
- XLSX Analysis. XLSX. This provides an analysis of XLSX files.
- PPTX Analysis. PPTX. This provides an analysis of PPTX files.
- MDB Analysis. MDB. This provides an analysis of MDB files.
- Outlook Message Analysis. MSG. This provides an analysis of MSG files.
Disk Image
- Raw disk format. RAW. This provides an analysis of the RAW disk format.
Tests
- File Forensics Test. File Test File Forensics Test.
- File Forensics Test (Fun). File Test (Fun) File Forensics Test.
Presentations
MIRACL Core Library

MIRACL Core is an open source library, and includes a wide range of public key encryption methods. It is especially focused on elliptic curve and pairing-friendly methods, but also supports a wide range of encryption methods, including RSA, AES and hashing. Overall, it can be ported onto a wide range of systems and supports C, C++, Go, Rust, Python, Java, Javascript and Swift. Along with this it supports limited capability devices such as the Arduino infrastructure. The GitHub repository is [here].
BN254
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.

Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- CL Signatures. CL. CL Signatures in Go using MIRACL.
- CL Signatures (advanced pairing). CL. CL Signatures in Go using MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages using MIRACL.
- PS Signatures. PS. Signatures using PS for short signatures using MIRACL.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures using MIRACL.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.

Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
Rust examples
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
NaCl

PyNaCl is a Python port of LibSodium. It integrates the latest cryptography methods, such as AES, XChaCha20, Blake2b and X25519.
Symmetric Key
- Symmetric key. Symmetric key (XChaCha20 and Poly1305). With symmetric key, Bob and Alice have the same key. NaCl uses the XChaCha20 method, and which supports stream encryption (and which does not require padding as a block cipher does, and is also faster than block cipher modes). ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16 byte nonce. XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24 byte nonce. It has a lower propability of nonce misuse than ChaCha20.
- Encryption with a password. Symmetric Key with KDF. In symmetric key, we generate a secret key. This key is typically a random value or generated from a password and a salt value. If we use a password, we typically use a KDF (Key Derivation Function), and which uses a password and a salt value, in order to create a key of a given size. In this case we will use Argon2i, and which is memory resilent.
Hybrid Encryption
- Box. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Hashing
- Hashing and KDF (Argon2 and scrypt). Hashing and KDF. This case we will use PyNaCl (Networking and Cryptography) library, and which is a Python binding to libsodium. We will hash a password using SHA-256 and SHA-512, and also create a KDF (Key Derivation Function) using scrypt and Argon2.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
Ed25519
-
Ed25519. Ed25519. Using Ed25519 for digital signatures.
-
Finding Points on Ed25519. X25519 (Points).
In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 (Key Exchange)
- X25519 + BLAKE2b key-exchange. X25519. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
Curve 25519
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
Node.js

Node.js uses the JavaScript programming langauge as its base, and allows for code to be run on a server, rather than in the browser (such as with pure JavaScript). To run a node.js program, we run "node myfile.js", and use NPM to install libraries.
Symmetric key
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
RSA and public key
- RSA Opt imal Asymmetric Encryption Padding (OAEP) using Node.js. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
ECC Keys
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.

Hashing
- Hashing with node.js (All). Hashing. Hashing with node.js.
- Hashing with node.js (Selection). Hashing. Hashing with node.js.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- ECDSA with node.js. ECDSA. ECDSA with node.js.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
Key exchange
- Diffie-Hellman with node.js (random prime). DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method and uses a randomly generated prime number (press the button to generate a new prime).
- Diffie-Hellman with node.js. DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method. Each time the prime number will be fixed for the DH group selected.
- ECDH with node.js. ECDH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Elliptic Curve Diffie Hellman (ECDH) key exchange method.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
Key derivation
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
CryptoJS
- CryptoJS (in node.js). CryptoJS (Node.js). Various crypto methods in the browser.
Bulletproofs
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
Blockchain
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
Proxy encryption
- Proxy Encryption - Encrypting With Public Key, And Decrypt with Private Key. Proxy01. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This page just creates a key pair for Alice, and uses it to encrypt with the public key , and decrypt with the private key.
- Proxy Encryption. Proxy02. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This will go through the full use case of proxy re-encryption.
Tokens
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
Random
- Fortuna with node.js. Fortuna. Fortuna random numbers with node.js.
Other
- FPE with node.js. FPR. FPE with node.js.
- Puny with node.js. Puny. Puny character format with node.js.
Accumulators and Witnesses
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
PGP
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Password Entropy
- Password Entropy with Node.js. Password Entropy. Password entropy measures the strength of a password, and is measured as the number of bits which could represent all of the possibilities. An entropy score of less than 25 identifies a poor password, and between 25 and 50 is a weak password. For 50 to 75 we have a reasonable password, and between 75 and 100 is a very good password. Over 100 is an excellent password. The strength of the password relates to the number of characters used, and also the number of characters in the password.
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
- Homomorphic Encryption with Node.js and BGV. Homomorphic Encryption with Node.js and BFG. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BGV method.
Oblivious Transfer (OT)

Oblivious Transfer allows Bob to select data from Alice, but for Alice not to know which value has been selected.
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
OpenSSH

OpenSSH supports the usage of the SSH protocol. This allows for a remote login. One tool which is uses is ssh-keygen, and which allow for the generation of RSA, DSA and elliptic-curve keys that. These can be used for user and host authentication, such as for GitHub login and Cloud instance login.
OpenSSH
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here].
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
Outline

OpenSSL

OpenSSL is a standard library that implements cryptography.
Symmetric key (Command line)
-
Symmetric Key Encryption (OpenSSL 1.x) [here]. In this case we will create cipher text from OpenSSL 1.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 1.x) [here].In this case we will decrypt cipher text from OpenSSL 1.x using a key derived from a password
-
Symmetric Key Encryption (OpenSSL 3.x) [here]. In this case we will create cipher text from OpenSSL 3.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 3.x) [here].In this case we will decrypt cipher text from OpenSSL 3.x using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password.
Hashing
-
Hashing [here] OpenSSL supports a wide range of hashing methods including BLAKE2b, Gost, MD4, MD5, RMD-160, SHA-1, SHA-3, SHA-256 and SHA-512.
Libre OpenSSL
-
Symmetric Key Encryption using Libre OpenSSL [here]. In this case we will create cipher text from Libre OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption using Libre OpenSSL [here]. In this case we will decrypt ciphertext from Libre OpenSSL using a key derived from a password.
-
Hashing [here] Libre OpenSSL supports a wide range of hashing methods including Gost, MD4, MD5, RMD-160, SHA-1, SHA-256 and SHA-512.
Diffie-Hellman parameter generation
-
DH Parameters with OpenSSL [here]. The Diffie-Hellman (DH) method is perhaps one of the greatest inventions in Cybersecurity, and was created by Whitfield Diffie and Marty Hellman. With the DH method, Bob creates a random value (\(b\)) and Alice also creates a random value (\(a\)). Next Bob computes \(B=g^b \pmod p\) and sends it to Alice. Alice computes \(A=g^a \pmod p\) and sends this to Bob. Bob raises the value of \(A\) to the power of \(b\) and takes \(\pmod p\), and Alice raises \(B\) to the power of \(a\) and takes \(\pmod p\). In the end, they will have the same shared value: \(g^{ab} \pmod p\). This can then be used to derive an encryption key that they can use for a secure tunnel. Overall, \(p\) is the large prime number, and also known as the shared modulus between Bob and Alice.
Key derivation function
-
PBKDF2 key derivation with OpenSSL [here] PBKDF2 (Password Key Derivation Function 2) is a key derivation method. Overall it is relatively slow in its operation and where we take a password, a salt value, hashing method, and a number of iterations, in order to produce a given size of encryption key.
-
HKDF key derivation with OpenSSL [here] HKDF (HMAC Key Derivation function) is used to derive an encryption key from a pass phrase. Initially HKDF creates a pseudorandom key (PRK) using a pass phrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), andalong with a salt value. Next the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys.
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Passwords
-
Password example [here]. This page uses the OpenSSL library hash password generator, which is used in UNIX systems for the hashing of passwords which are contained in /etc/shadow and /etc/passwd. For newer passwords, the "-1" options is used to created the hashed value.
-
Hashed passwords with OpenSSL [here].
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
Public key
-
Generating an ECC key pair with OpenSSL [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)).
-
Generating an RSA key pair with OpenSSL [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2).
-
Generating an RSA key pair with OpenSSL with encryption [here]. This page implements RSA key pair generation with an encrypted key pair. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). In this case we will encrypt the key pair with either 3DES, 128-bit AES, 192-bit AES or 256-bit AES. The same password must be used to encrypt and decrypt.
-
Generate prime with OpenSSL [here]. Prime numbers are important in public key encrytion, and are used with RSA and ECC. For RSA, we generate two prime numbers (\(p\) and \(q\)) and which are multiplied together to create a modulus (\(N\)). If these prime numbers have 512 bit values, the modulus will be a 1,024 bit value. This defines the basic secure of RSA. With elliptic curve we use smaller prime numbers, such as 256-bit values for the secp256k1 curve.
ASN1 parsing
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). We will parse using asn1parse, and reveal the parameters.
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)) [RSA key pair]. We will parse using asn1parse, and reveal the parameters.
- DSA Parameters with asn1parse. DSA parameters with OpenSSL with asn1parse. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA (Digital Signature Algorithm)
- DSA Parameters. DSA parameters with OpenSSL. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
MAC (Message Authentication Code)
- HMAC with OpenSSL. MACs with OpenSSL. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authenticate both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2) and SHA-3. In this case we will use OpenSSL to generate the HMAC value.
- MACs with OpenSSL. MACs with OpenSSL. In the following we will generate MACs for HMAC, GMAC, CMAC, Blake2bmac, Blake2smac, KMAC128 and KMAC256. Overall, we will use an encryption key defined as a hex value for GMAC and CMAC, and a pass phrase for the others. The message is "hello".
Signing
- Digital signing a plaintext message with OpenSSL. Signing with OpenSSL. With digital signing, we can take a message, and create a signature. This normally involves signing with a private key and digital certificate. The signed message can be an a MIME format, and which can be integrated into an email message. In this can we have a 512-bit RSA key pair that will sign a plain text message.
Encrypting emails
- Encrypting an email message in OpenSSL. Encrypting messages with OpenSSL. With public key encryption, we can take a message, and encrypt it with the recipiant's public key. In this can we have a 512-bit RSA public key to encrypt a message.
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Random number generation with OpenSSL
-
Random number generator [here]. Random numbers are important in generating encryption keys and salt values. In this case OpenSSL generates a random number (in a Base64 format) for a given number of bytes.
Outline (C#/Python)
-
Symmetric Key Encryption (C#) [here]. This page uses the OpenSSL library through a C#/.NET wrapper. The DLLs it interfaces to are libeay32.dll and ssleay32.dll. OpenSSL supports a wide range of encryption methods, including 128-bit AES, 192-bit AES, 256-bit AES and Blowfish (bf). Different modes of ECB, CBC, and OFB are implemented. The examples use a default IV of "1234".
-
AES in Python with OpenSSL output [here]
-
Producing OpenSSL AES Encrypted String from C# [here]
Digital Certificates
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
Paillier - Partial Homomorphic Encryption

The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Fundamentals
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier).
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Using RSA
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
Applications
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Pallas Curve. Pallas Curve. Some basic operations for the Pallas curve, such as scalar multiply and hashing to a curve/point..
Pairing-based Crypto
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
ElGamal and ECC
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a numerical input.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
Shamir Secret Shares
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Homomorphic Encryption
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Zero knowledge proofs
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
Verifiable Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Hash to scalar and point
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
CP-ABE
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Lattice cryptography

Latice cryptography is proposed as a post-quantum robust method for public key encryption, especially focused on digital signatures and key exchange mechanisms (KEMs).
Principles
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
NTRU
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- Lattice Encryption: NTRU Key Generation Python). NTRU. Outlines how NTRU operates for key generation.
Homomorphic
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Digital Signatures
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
Public-Key Encryption/Key Exchange
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
Light-weight cryptography

While AES and SHA work well together within computer systems, they struggle in an IoT/embedded world as they take up: too much processing power; too much physical space; and consume too much battery power. So NIST outlines a number of methods which can be used for light-weight cryptography, and which could be useful in IoT and RFID devices [1]. They define the device spectrum as:
- Conventional cryptography. Servers and Desktops. Tablets and smart phones.
- Light-weight cryptography. Embedded Systems. RFID and Sensor Networks.
With embedded systems, we commonly see 8-bit, 16-bit and 32-bit microcontrollers, and which would struggle to cope with real-time demands for conventional cryptography methods. And in the 40+ years since the first 4-bit processor, there is even a strong market for 4-bit processors. RFID and sensor network devices, especially, have limited numbers of gates available for security, and are often highly constrained with the power drain on the device.
So AES is typically a non-starter for many embedded devices. In light-weight cryptography, we often see smaller block size (typically 64 bits or 80 bits), smaller keys (often less than 90 bits) and less complex rounds (and where the S-boxes often just have 4-bits).
For light-weight cryptography the main constraints that we have are typically related to ener requirements, gate equivalents (GEs), and timing. With passive RFID devices, we do not have an associated battery for the power supply, and where the chip must power itself from energy coupled from the radio wave. An RFID device is thus likely to be severely constrained in the power drain associated with any cryptography functions, along with being constrained for the timing requirements and for the number of gates used. Even if an RFID device has an associated battery (active RFID), it may be difficult to recharge the battery, so the drain on power must often be minimised.
There is thus often a compromise between the cryptography method used and the overall security of the method. Thus often light-weight cryptography methods balance performance (throughput) against power drain and GE, and do not perform as well as main-stream cryptography standards (such as AES and SHA-256). Along with this the method must also have a low requirement for RAM (where the method requires the usage of running memory to perform its operation) and ROM (where the method is stored on the device). In order to assess the strengths of various methods we often define the area that the cryptography function will use on the device – and which is defined in \(µm^2\). The NIST finalists are defined in this [article]
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- GIFT AEAD. GIFT. GIFT is a light-weight block cipher. It is a (NIST Finalist)
- Elephant. Elephant. Elephant is a light-weight stream cipher. It is a (NIST Finalist).
- TinyJambu. TinyJambu. TinyJambu is a light-weight block cipher. It is a (NIST Finalist)
- Isap AEAD. Isap. Isap is a light-weight block cipher. It is a (NIST Finalist)
- PHOTON-Beetle AEAD. PHOTON-Beetle. PHOTON-Beetle is a light-weight block cipher. It is a (NIST Finalist)
- Romulus AEAD. Romulus. Romulus is a light-weight block cipher. It is a (NIST Finalist)
- Sparkle AEAD. Sparkle. Sparkle is a light-weight block cipher. It is a (NIST Finalist)
- CLEFIA. CLEFIA. CLEFIA is a light-weight block cipher.
- LED. LED. LED is a light-weight block cipher.
- Piccolo. Piccolo. Piccolo is an ultra light-weight block cipher.
- PRESENT. PRESENT. Present is a light-weight block cipher.
- Pyjamask. Pyjamask. Pyjamask is a light-weight block cipher.
- SIMON. SIMON. SIMON is a light-weight block cipher.
- SKINNY. SKINNY. SKINNEY is a light-weight block cipher.
- SPECK. SPECK. SPECK is a light-weight block cipher.
- XTEA. XTEA. XTEA is a light-weight block cipher.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encryption/Decryption. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.
Light-weight crypto (Other)
- Chaskey (MAC). Chaskey. Chaskey is a light-weight MAC function.
- Chaskey (MAC). Chaskey (Python). Chaskey is a light-weight MAC function.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (ASCON)
ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRFF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
Discrete Logs (Solving)

A discrete log problem is in the form of \(g^x \pmod p\) and where we know \(g\) and \(p\) and must solve for \(x\).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Message Authentication Code (MAC)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
HMAC
The following are the tips related to Key-based hashing:
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authentication both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2), Blake2b, SM3 and SHA-3. This page outlines the HMAC-MD5 methods using the Hazmat cryptography layer.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- HMAC (COSE). Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT with HMMAC. Go. In this case we create a CWT token, and sign with an HMAC signature.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- HMAC with Rust. HMAC. HMAC with Rust.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HMAC with OpenSSL. MACs with OpenSSL. HMAC in OpenSSL for a given input value, password and hashing method.
Cipher MACs
The following are the tips related to Key-based hashing:
- MACs with OpenSSL. MACs with OpenSSL. MAC methods implemented in OpenSSL, including CMAC and GMAC.
Key-based hashing
The following are the tips related to Key-based hashing:
- SipHash. Siphash. Siphash is a fast key-based hashing method.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Meow. Meow. Meow is one of the fastest hashing methods.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
Magic Numbers

This pages contains information related to magic numbers in file formats.
Network and File Forensics
- Magic numbers. Magic. This provides information on magic number for file forensics.
Graphics formats
- JPEG Analysis. JPEGs. This provides an analysis of JPEG files.
- GIF Analysis. GIFs. This provides an analysis of GIF files.
- TIF Analysis. TIFs. This provides an analysis of TIF files.
- PNG Analysis. PNGs. This provides an analysis of PNG files.
- BMP Analysis. BMPs. This provides an analysis of BMP files.
- PSD Analysis. PSDs. This provides an analysis of PSD files.
- WMF Analysis. WMF. This provides an analysis of WMF files.
- Adobe Illustrator Analysis. AI. This provides an analysis of AI files.
- Adobe In Design Analysis. INDD. This provides an analysis of INDD files.
- MIDI file. MIDI. This provides an analysis of MID files.
- ICO file. ICO. This provides an analysis of ICO files.
- PS file. PS. This provides an analysis of PS files.
- EPS file. EPS. This provides an analysis of EPS files.
- VSD file. VSD. This provides an analysis of Microsft Visio (VSD) files.
Video and audio formats
- MP3 Analysis. MP3s. This provides an analysis of MP3 files.
- AVI Analysis. AVIs. This provides an analysis of AVI files.
- Flash SWF Analysis. SWFs. This provides an analysis of Flash files.
- Flash FLV Analysis. FLVs. This provides an analysis of FLV files.
- MP4 Analysis. MP4. This provides an analysis of MP4 files.
- MOV Analysis. MOV. This provides an analysis of MOV files.
- WMV Analysis. WMV. This provides an analysis of WMV files.
- WMA Analysis. WMA. This provides an analysis of WMA files.
- JPEG 2000 Analysis. JPEG 2. This provides an analysis of JPEG 2000 files.
- WAV Analysis. WAV. This provides an analysis of WAV files.
Zips, Archives and Library files
- ZIP/Archive Analysis. ZIPs. This provides an analysis of ZIP/Achive files.
- GZ Analysis. GZ. This provides an analysis of GZip files.
- Tar Analysis. Tar. This provides an analysis of TAR files.
- MSI Analysis. MSI. This provides an analysis of MSI files.
- OBJ Analysis. OBJ. This provides an analysis of OBJ files.
- DLL Analysis. DLL. This provides an analysis of DLL files.
- CAB Analysis. CAB. This provides an analysis of CAB files.
- EXE Analysis. EXE. This provides an analysis of EXE files.
- RAR Analysis. RAR. This provides an analysis of RAR files.
- SYS Analysis. SYS. This provides an analysis of SYS files.
- HLP Analysis. HLP. This provides an analysis of HLP files.
- VMDK Analysis. VMDK. This provides an analysis of VMDK files (VMWare Virtual Disks).
- PST Analysis. PST. This provides an analysis of PST files (Outlook Email File).
- JAR Analysis. JAR. This provides an analysis of JAR files.
- SLN Analysis. SLN. This provides an analysis of Microsoft SLN files.
- Class Analysis. Class. This provides an analysis of Java Class files.
- Zlib. Zlib. This provides an analysis of Zlib files.
Documents
- PDF Analysis. PDFs. This provides an analysis of PDF files.
- DOC Analysis. DOCs. This provides an analysis of DOC files.
- RTF Analysis. RTFs. This provides an analysis of RTF files.
- XLS Analysis. XLSs. This provides an analysis of XLS files.
- PPT Analysis. PPTs. This provides an analysis of PPT files.
- MMP File. MMP. This provides an analysis of MMP files.
- DOCX Analysis. DOCX. This provides an analysis of DOCX files.
- XLSX Analysis. XLSX. This provides an analysis of XLSX files.
- PPTX Analysis. PPTX. This provides an analysis of PPTX files.
- MDB Analysis. MDB. This provides an analysis of MDB files.
- Outlook Message Analysis. MSG. This provides an analysis of MSG files.
Disk Image
- Raw disk format. RAW. This provides an analysis of the RAW disk format.
Tests
- File Forensics Test. File Test File Forensics Test.
- File Forensics Test (Fun). File Test (Fun) File Forensics Test.
Presentations
MIRACL Core Library

MIRACL Core is an open source library, and includes a wide range of public key encryption methods. It is especially focused on elliptic curve and pairing-friendly methods, but also supports a wide range of encryption methods, including RSA, AES and hashing. Overall, it can be ported onto a wide range of systems and supports C, C++, Go, Rust, Python, Java, Javascript and Swift. Along with this it supports limited capability devices such as the Arduino infrastructure. The GitHub repository is [here].
BN254
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.

Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- CL Signatures. CL. CL Signatures in Go using MIRACL.
- CL Signatures (advanced pairing). CL. CL Signatures in Go using MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages using MIRACL.
- PS Signatures. PS. Signatures using PS for short signatures using MIRACL.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures using MIRACL.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.

Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
Rust examples
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
NaCl

PyNaCl is a Python port of LibSodium. It integrates the latest cryptography methods, such as AES, XChaCha20, Blake2b and X25519.
Symmetric Key
- Symmetric key. Symmetric key (XChaCha20 and Poly1305). With symmetric key, Bob and Alice have the same key. NaCl uses the XChaCha20 method, and which supports stream encryption (and which does not require padding as a block cipher does, and is also faster than block cipher modes). ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16 byte nonce. XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24 byte nonce. It has a lower propability of nonce misuse than ChaCha20.
- Encryption with a password. Symmetric Key with KDF. In symmetric key, we generate a secret key. This key is typically a random value or generated from a password and a salt value. If we use a password, we typically use a KDF (Key Derivation Function), and which uses a password and a salt value, in order to create a key of a given size. In this case we will use Argon2i, and which is memory resilent.
Hybrid Encryption
- Box. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Hashing
- Hashing and KDF (Argon2 and scrypt). Hashing and KDF. This case we will use PyNaCl (Networking and Cryptography) library, and which is a Python binding to libsodium. We will hash a password using SHA-256 and SHA-512, and also create a KDF (Key Derivation Function) using scrypt and Argon2.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
Ed25519
-
Ed25519. Ed25519. Using Ed25519 for digital signatures.
-
Finding Points on Ed25519. X25519 (Points).
In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 (Key Exchange)
- X25519 + BLAKE2b key-exchange. X25519. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
Curve 25519
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
Node.js

Node.js uses the JavaScript programming langauge as its base, and allows for code to be run on a server, rather than in the browser (such as with pure JavaScript). To run a node.js program, we run "node myfile.js", and use NPM to install libraries.
Symmetric key
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
RSA and public key
- RSA Opt imal Asymmetric Encryption Padding (OAEP) using Node.js. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
ECC Keys
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.

Hashing
- Hashing with node.js (All). Hashing. Hashing with node.js.
- Hashing with node.js (Selection). Hashing. Hashing with node.js.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- ECDSA with node.js. ECDSA. ECDSA with node.js.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
Key exchange
- Diffie-Hellman with node.js (random prime). DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method and uses a randomly generated prime number (press the button to generate a new prime).
- Diffie-Hellman with node.js. DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method. Each time the prime number will be fixed for the DH group selected.
- ECDH with node.js. ECDH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Elliptic Curve Diffie Hellman (ECDH) key exchange method.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
Key derivation
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
CryptoJS
- CryptoJS (in node.js). CryptoJS (Node.js). Various crypto methods in the browser.
Bulletproofs
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
Blockchain
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
Proxy encryption
- Proxy Encryption - Encrypting With Public Key, And Decrypt with Private Key. Proxy01. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This page just creates a key pair for Alice, and uses it to encrypt with the public key , and decrypt with the private key.
- Proxy Encryption. Proxy02. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This will go through the full use case of proxy re-encryption.
Tokens
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
Random
- Fortuna with node.js. Fortuna. Fortuna random numbers with node.js.
Other
- FPE with node.js. FPR. FPE with node.js.
- Puny with node.js. Puny. Puny character format with node.js.
Accumulators and Witnesses
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
PGP
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Password Entropy
- Password Entropy with Node.js. Password Entropy. Password entropy measures the strength of a password, and is measured as the number of bits which could represent all of the possibilities. An entropy score of less than 25 identifies a poor password, and between 25 and 50 is a weak password. For 50 to 75 we have a reasonable password, and between 75 and 100 is a very good password. Over 100 is an excellent password. The strength of the password relates to the number of characters used, and also the number of characters in the password.
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
- Homomorphic Encryption with Node.js and BGV. Homomorphic Encryption with Node.js and BFG. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BGV method.
Oblivious Transfer (OT)

Oblivious Transfer allows Bob to select data from Alice, but for Alice not to know which value has been selected.
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
OpenSSH

OpenSSH supports the usage of the SSH protocol. This allows for a remote login. One tool which is uses is ssh-keygen, and which allow for the generation of RSA, DSA and elliptic-curve keys that. These can be used for user and host authentication, such as for GitHub login and Cloud instance login.
OpenSSH
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here].
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
Outline

OpenSSL

OpenSSL is a standard library that implements cryptography.
Symmetric key (Command line)
-
Symmetric Key Encryption (OpenSSL 1.x) [here]. In this case we will create cipher text from OpenSSL 1.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 1.x) [here].In this case we will decrypt cipher text from OpenSSL 1.x using a key derived from a password
-
Symmetric Key Encryption (OpenSSL 3.x) [here]. In this case we will create cipher text from OpenSSL 3.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 3.x) [here].In this case we will decrypt cipher text from OpenSSL 3.x using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password.
Hashing
-
Hashing [here] OpenSSL supports a wide range of hashing methods including BLAKE2b, Gost, MD4, MD5, RMD-160, SHA-1, SHA-3, SHA-256 and SHA-512.
Libre OpenSSL
-
Symmetric Key Encryption using Libre OpenSSL [here]. In this case we will create cipher text from Libre OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption using Libre OpenSSL [here]. In this case we will decrypt ciphertext from Libre OpenSSL using a key derived from a password.
-
Hashing [here] Libre OpenSSL supports a wide range of hashing methods including Gost, MD4, MD5, RMD-160, SHA-1, SHA-256 and SHA-512.
Diffie-Hellman parameter generation
-
DH Parameters with OpenSSL [here]. The Diffie-Hellman (DH) method is perhaps one of the greatest inventions in Cybersecurity, and was created by Whitfield Diffie and Marty Hellman. With the DH method, Bob creates a random value (\(b\)) and Alice also creates a random value (\(a\)). Next Bob computes \(B=g^b \pmod p\) and sends it to Alice. Alice computes \(A=g^a \pmod p\) and sends this to Bob. Bob raises the value of \(A\) to the power of \(b\) and takes \(\pmod p\), and Alice raises \(B\) to the power of \(a\) and takes \(\pmod p\). In the end, they will have the same shared value: \(g^{ab} \pmod p\). This can then be used to derive an encryption key that they can use for a secure tunnel. Overall, \(p\) is the large prime number, and also known as the shared modulus between Bob and Alice.
Key derivation function
-
PBKDF2 key derivation with OpenSSL [here] PBKDF2 (Password Key Derivation Function 2) is a key derivation method. Overall it is relatively slow in its operation and where we take a password, a salt value, hashing method, and a number of iterations, in order to produce a given size of encryption key.
-
HKDF key derivation with OpenSSL [here] HKDF (HMAC Key Derivation function) is used to derive an encryption key from a pass phrase. Initially HKDF creates a pseudorandom key (PRK) using a pass phrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), andalong with a salt value. Next the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys.
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Passwords
-
Password example [here]. This page uses the OpenSSL library hash password generator, which is used in UNIX systems for the hashing of passwords which are contained in /etc/shadow and /etc/passwd. For newer passwords, the "-1" options is used to created the hashed value.
-
Hashed passwords with OpenSSL [here].
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
Public key
-
Generating an ECC key pair with OpenSSL [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)).
-
Generating an RSA key pair with OpenSSL [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2).
-
Generating an RSA key pair with OpenSSL with encryption [here]. This page implements RSA key pair generation with an encrypted key pair. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). In this case we will encrypt the key pair with either 3DES, 128-bit AES, 192-bit AES or 256-bit AES. The same password must be used to encrypt and decrypt.
-
Generate prime with OpenSSL [here]. Prime numbers are important in public key encrytion, and are used with RSA and ECC. For RSA, we generate two prime numbers (\(p\) and \(q\)) and which are multiplied together to create a modulus (\(N\)). If these prime numbers have 512 bit values, the modulus will be a 1,024 bit value. This defines the basic secure of RSA. With elliptic curve we use smaller prime numbers, such as 256-bit values for the secp256k1 curve.
ASN1 parsing
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). We will parse using asn1parse, and reveal the parameters.
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)) [RSA key pair]. We will parse using asn1parse, and reveal the parameters.
- DSA Parameters with asn1parse. DSA parameters with OpenSSL with asn1parse. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA (Digital Signature Algorithm)
- DSA Parameters. DSA parameters with OpenSSL. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
MAC (Message Authentication Code)
- HMAC with OpenSSL. MACs with OpenSSL. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authenticate both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2) and SHA-3. In this case we will use OpenSSL to generate the HMAC value.
- MACs with OpenSSL. MACs with OpenSSL. In the following we will generate MACs for HMAC, GMAC, CMAC, Blake2bmac, Blake2smac, KMAC128 and KMAC256. Overall, we will use an encryption key defined as a hex value for GMAC and CMAC, and a pass phrase for the others. The message is "hello".
Signing
- Digital signing a plaintext message with OpenSSL. Signing with OpenSSL. With digital signing, we can take a message, and create a signature. This normally involves signing with a private key and digital certificate. The signed message can be an a MIME format, and which can be integrated into an email message. In this can we have a 512-bit RSA key pair that will sign a plain text message.
Encrypting emails
- Encrypting an email message in OpenSSL. Encrypting messages with OpenSSL. With public key encryption, we can take a message, and encrypt it with the recipiant's public key. In this can we have a 512-bit RSA public key to encrypt a message.
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Random number generation with OpenSSL
-
Random number generator [here]. Random numbers are important in generating encryption keys and salt values. In this case OpenSSL generates a random number (in a Base64 format) for a given number of bytes.
Outline (C#/Python)
-
Symmetric Key Encryption (C#) [here]. This page uses the OpenSSL library through a C#/.NET wrapper. The DLLs it interfaces to are libeay32.dll and ssleay32.dll. OpenSSL supports a wide range of encryption methods, including 128-bit AES, 192-bit AES, 256-bit AES and Blowfish (bf). Different modes of ECB, CBC, and OFB are implemented. The examples use a default IV of "1234".
-
AES in Python with OpenSSL output [here]
-
Producing OpenSSL AES Encrypted String from C# [here]
Digital Certificates
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
Paillier - Partial Homomorphic Encryption

The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Fundamentals
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier).
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Using RSA
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
Applications
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Pairing-based cryptography with Kryptology. Pairing. This implements pairing-based crypto to prove \(e(aU,bV)=e(bU,aV)\), \(e(aU,bV)=e(abU,V)\), and \(e(aU,bV)=e(U,V)^{ab}\).
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
ElGamal and ECC
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a numerical input.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
Shamir Secret Shares
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Homomorphic Encryption
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Zero knowledge proofs
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
Verifiable Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Hash to scalar and point
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
CP-ABE
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Lattice cryptography

Latice cryptography is proposed as a post-quantum robust method for public key encryption, especially focused on digital signatures and key exchange mechanisms (KEMs).
Principles
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
NTRU
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- Lattice Encryption: NTRU Key Generation Python). NTRU. Outlines how NTRU operates for key generation.
Homomorphic
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Digital Signatures
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
Public-Key Encryption/Key Exchange
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
Light-weight cryptography

While AES and SHA work well together within computer systems, they struggle in an IoT/embedded world as they take up: too much processing power; too much physical space; and consume too much battery power. So NIST outlines a number of methods which can be used for light-weight cryptography, and which could be useful in IoT and RFID devices [1]. They define the device spectrum as:
- Conventional cryptography. Servers and Desktops. Tablets and smart phones.
- Light-weight cryptography. Embedded Systems. RFID and Sensor Networks.
With embedded systems, we commonly see 8-bit, 16-bit and 32-bit microcontrollers, and which would struggle to cope with real-time demands for conventional cryptography methods. And in the 40+ years since the first 4-bit processor, there is even a strong market for 4-bit processors. RFID and sensor network devices, especially, have limited numbers of gates available for security, and are often highly constrained with the power drain on the device.
So AES is typically a non-starter for many embedded devices. In light-weight cryptography, we often see smaller block size (typically 64 bits or 80 bits), smaller keys (often less than 90 bits) and less complex rounds (and where the S-boxes often just have 4-bits).
For light-weight cryptography the main constraints that we have are typically related to ener requirements, gate equivalents (GEs), and timing. With passive RFID devices, we do not have an associated battery for the power supply, and where the chip must power itself from energy coupled from the radio wave. An RFID device is thus likely to be severely constrained in the power drain associated with any cryptography functions, along with being constrained for the timing requirements and for the number of gates used. Even if an RFID device has an associated battery (active RFID), it may be difficult to recharge the battery, so the drain on power must often be minimised.
There is thus often a compromise between the cryptography method used and the overall security of the method. Thus often light-weight cryptography methods balance performance (throughput) against power drain and GE, and do not perform as well as main-stream cryptography standards (such as AES and SHA-256). Along with this the method must also have a low requirement for RAM (where the method requires the usage of running memory to perform its operation) and ROM (where the method is stored on the device). In order to assess the strengths of various methods we often define the area that the cryptography function will use on the device – and which is defined in \(µm^2\). The NIST finalists are defined in this [article]
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- GIFT AEAD. GIFT. GIFT is a light-weight block cipher. It is a (NIST Finalist)
- Elephant. Elephant. Elephant is a light-weight stream cipher. It is a (NIST Finalist).
- TinyJambu. TinyJambu. TinyJambu is a light-weight block cipher. It is a (NIST Finalist)
- Isap AEAD. Isap. Isap is a light-weight block cipher. It is a (NIST Finalist)
- PHOTON-Beetle AEAD. PHOTON-Beetle. PHOTON-Beetle is a light-weight block cipher. It is a (NIST Finalist)
- Romulus AEAD. Romulus. Romulus is a light-weight block cipher. It is a (NIST Finalist)
- Sparkle AEAD. Sparkle. Sparkle is a light-weight block cipher. It is a (NIST Finalist)
- CLEFIA. CLEFIA. CLEFIA is a light-weight block cipher.
- LED. LED. LED is a light-weight block cipher.
- Piccolo. Piccolo. Piccolo is an ultra light-weight block cipher.
- PRESENT. PRESENT. Present is a light-weight block cipher.
- Pyjamask. Pyjamask. Pyjamask is a light-weight block cipher.
- SIMON. SIMON. SIMON is a light-weight block cipher.
- SKINNY. SKINNY. SKINNEY is a light-weight block cipher.
- SPECK. SPECK. SPECK is a light-weight block cipher.
- XTEA. XTEA. XTEA is a light-weight block cipher.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encryption/Decryption. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.
Light-weight crypto (Other)
- Chaskey (MAC). Chaskey. Chaskey is a light-weight MAC function.
- Chaskey (MAC). Chaskey (Python). Chaskey is a light-weight MAC function.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (ASCON)
ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRFF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
Discrete Logs (Solving)

A discrete log problem is in the form of \(g^x \pmod p\) and where we know \(g\) and \(p\) and must solve for \(x\).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Message Authentication Code (MAC)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
HMAC
The following are the tips related to Key-based hashing:
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authentication both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2), Blake2b, SM3 and SHA-3. This page outlines the HMAC-MD5 methods using the Hazmat cryptography layer.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- HMAC (COSE). Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT with HMMAC. Go. In this case we create a CWT token, and sign with an HMAC signature.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- HMAC with Rust. HMAC. HMAC with Rust.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HMAC with OpenSSL. MACs with OpenSSL. HMAC in OpenSSL for a given input value, password and hashing method.
Cipher MACs
The following are the tips related to Key-based hashing:
- MACs with OpenSSL. MACs with OpenSSL. MAC methods implemented in OpenSSL, including CMAC and GMAC.
Key-based hashing
The following are the tips related to Key-based hashing:
- SipHash. Siphash. Siphash is a fast key-based hashing method.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Meow. Meow. Meow is one of the fastest hashing methods.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
Magic Numbers

This pages contains information related to magic numbers in file formats.
Network and File Forensics
- Magic numbers. Magic. This provides information on magic number for file forensics.
Graphics formats
- JPEG Analysis. JPEGs. This provides an analysis of JPEG files.
- GIF Analysis. GIFs. This provides an analysis of GIF files.
- TIF Analysis. TIFs. This provides an analysis of TIF files.
- PNG Analysis. PNGs. This provides an analysis of PNG files.
- BMP Analysis. BMPs. This provides an analysis of BMP files.
- PSD Analysis. PSDs. This provides an analysis of PSD files.
- WMF Analysis. WMF. This provides an analysis of WMF files.
- Adobe Illustrator Analysis. AI. This provides an analysis of AI files.
- Adobe In Design Analysis. INDD. This provides an analysis of INDD files.
- MIDI file. MIDI. This provides an analysis of MID files.
- ICO file. ICO. This provides an analysis of ICO files.
- PS file. PS. This provides an analysis of PS files.
- EPS file. EPS. This provides an analysis of EPS files.
- VSD file. VSD. This provides an analysis of Microsft Visio (VSD) files.
Video and audio formats
- MP3 Analysis. MP3s. This provides an analysis of MP3 files.
- AVI Analysis. AVIs. This provides an analysis of AVI files.
- Flash SWF Analysis. SWFs. This provides an analysis of Flash files.
- Flash FLV Analysis. FLVs. This provides an analysis of FLV files.
- MP4 Analysis. MP4. This provides an analysis of MP4 files.
- MOV Analysis. MOV. This provides an analysis of MOV files.
- WMV Analysis. WMV. This provides an analysis of WMV files.
- WMA Analysis. WMA. This provides an analysis of WMA files.
- JPEG 2000 Analysis. JPEG 2. This provides an analysis of JPEG 2000 files.
- WAV Analysis. WAV. This provides an analysis of WAV files.
Zips, Archives and Library files
- ZIP/Archive Analysis. ZIPs. This provides an analysis of ZIP/Achive files.
- GZ Analysis. GZ. This provides an analysis of GZip files.
- Tar Analysis. Tar. This provides an analysis of TAR files.
- MSI Analysis. MSI. This provides an analysis of MSI files.
- OBJ Analysis. OBJ. This provides an analysis of OBJ files.
- DLL Analysis. DLL. This provides an analysis of DLL files.
- CAB Analysis. CAB. This provides an analysis of CAB files.
- EXE Analysis. EXE. This provides an analysis of EXE files.
- RAR Analysis. RAR. This provides an analysis of RAR files.
- SYS Analysis. SYS. This provides an analysis of SYS files.
- HLP Analysis. HLP. This provides an analysis of HLP files.
- VMDK Analysis. VMDK. This provides an analysis of VMDK files (VMWare Virtual Disks).
- PST Analysis. PST. This provides an analysis of PST files (Outlook Email File).
- JAR Analysis. JAR. This provides an analysis of JAR files.
- SLN Analysis. SLN. This provides an analysis of Microsoft SLN files.
- Class Analysis. Class. This provides an analysis of Java Class files.
- Zlib. Zlib. This provides an analysis of Zlib files.
Documents
- PDF Analysis. PDFs. This provides an analysis of PDF files.
- DOC Analysis. DOCs. This provides an analysis of DOC files.
- RTF Analysis. RTFs. This provides an analysis of RTF files.
- XLS Analysis. XLSs. This provides an analysis of XLS files.
- PPT Analysis. PPTs. This provides an analysis of PPT files.
- MMP File. MMP. This provides an analysis of MMP files.
- DOCX Analysis. DOCX. This provides an analysis of DOCX files.
- XLSX Analysis. XLSX. This provides an analysis of XLSX files.
- PPTX Analysis. PPTX. This provides an analysis of PPTX files.
- MDB Analysis. MDB. This provides an analysis of MDB files.
- Outlook Message Analysis. MSG. This provides an analysis of MSG files.
Disk Image
- Raw disk format. RAW. This provides an analysis of the RAW disk format.
Tests
- File Forensics Test. File Test File Forensics Test.
- File Forensics Test (Fun). File Test (Fun) File Forensics Test.
Presentations
MIRACL Core Library

MIRACL Core is an open source library, and includes a wide range of public key encryption methods. It is especially focused on elliptic curve and pairing-friendly methods, but also supports a wide range of encryption methods, including RSA, AES and hashing. Overall, it can be ported onto a wide range of systems and supports C, C++, Go, Rust, Python, Java, Javascript and Swift. Along with this it supports limited capability devices such as the Arduino infrastructure. The GitHub repository is [here].
BN254
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.

Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- CL Signatures. CL. CL Signatures in Go using MIRACL.
- CL Signatures (advanced pairing). CL. CL Signatures in Go using MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages using MIRACL.
- PS Signatures. PS. Signatures using PS for short signatures using MIRACL.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures using MIRACL.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.

Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
Rust examples
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
NaCl

PyNaCl is a Python port of LibSodium. It integrates the latest cryptography methods, such as AES, XChaCha20, Blake2b and X25519.
Symmetric Key
- Symmetric key. Symmetric key (XChaCha20 and Poly1305). With symmetric key, Bob and Alice have the same key. NaCl uses the XChaCha20 method, and which supports stream encryption (and which does not require padding as a block cipher does, and is also faster than block cipher modes). ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16 byte nonce. XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24 byte nonce. It has a lower propability of nonce misuse than ChaCha20.
- Encryption with a password. Symmetric Key with KDF. In symmetric key, we generate a secret key. This key is typically a random value or generated from a password and a salt value. If we use a password, we typically use a KDF (Key Derivation Function), and which uses a password and a salt value, in order to create a key of a given size. In this case we will use Argon2i, and which is memory resilent.
Hybrid Encryption
- Box. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Hashing
- Hashing and KDF (Argon2 and scrypt). Hashing and KDF. This case we will use PyNaCl (Networking and Cryptography) library, and which is a Python binding to libsodium. We will hash a password using SHA-256 and SHA-512, and also create a KDF (Key Derivation Function) using scrypt and Argon2.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
Ed25519
-
Ed25519. Ed25519. Using Ed25519 for digital signatures.
-
Finding Points on Ed25519. X25519 (Points).
In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 (Key Exchange)
- X25519 + BLAKE2b key-exchange. X25519. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
Curve 25519
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
Node.js

Node.js uses the JavaScript programming langauge as its base, and allows for code to be run on a server, rather than in the browser (such as with pure JavaScript). To run a node.js program, we run "node myfile.js", and use NPM to install libraries.
Symmetric key
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
RSA and public key
- RSA Opt imal Asymmetric Encryption Padding (OAEP) using Node.js. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
ECC Keys
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.

Hashing
- Hashing with node.js (All). Hashing. Hashing with node.js.
- Hashing with node.js (Selection). Hashing. Hashing with node.js.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- ECDSA with node.js. ECDSA. ECDSA with node.js.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
Key exchange
- Diffie-Hellman with node.js (random prime). DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method and uses a randomly generated prime number (press the button to generate a new prime).
- Diffie-Hellman with node.js. DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method. Each time the prime number will be fixed for the DH group selected.
- ECDH with node.js. ECDH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Elliptic Curve Diffie Hellman (ECDH) key exchange method.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
Key derivation
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
CryptoJS
- CryptoJS (in node.js). CryptoJS (Node.js). Various crypto methods in the browser.
Bulletproofs
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
Blockchain
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
Proxy encryption
- Proxy Encryption - Encrypting With Public Key, And Decrypt with Private Key. Proxy01. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This page just creates a key pair for Alice, and uses it to encrypt with the public key , and decrypt with the private key.
- Proxy Encryption. Proxy02. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This will go through the full use case of proxy re-encryption.
Tokens
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
Random
- Fortuna with node.js. Fortuna. Fortuna random numbers with node.js.
Other
- FPE with node.js. FPR. FPE with node.js.
- Puny with node.js. Puny. Puny character format with node.js.
Accumulators and Witnesses
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
PGP
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Password Entropy
- Password Entropy with Node.js. Password Entropy. Password entropy measures the strength of a password, and is measured as the number of bits which could represent all of the possibilities. An entropy score of less than 25 identifies a poor password, and between 25 and 50 is a weak password. For 50 to 75 we have a reasonable password, and between 75 and 100 is a very good password. Over 100 is an excellent password. The strength of the password relates to the number of characters used, and also the number of characters in the password.
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
- Homomorphic Encryption with Node.js and BGV. Homomorphic Encryption with Node.js and BFG. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BGV method.
Oblivious Transfer (OT)

Oblivious Transfer allows Bob to select data from Alice, but for Alice not to know which value has been selected.
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
OpenSSH

OpenSSH supports the usage of the SSH protocol. This allows for a remote login. One tool which is uses is ssh-keygen, and which allow for the generation of RSA, DSA and elliptic-curve keys that. These can be used for user and host authentication, such as for GitHub login and Cloud instance login.
OpenSSH
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here].
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
Outline

OpenSSL

OpenSSL is a standard library that implements cryptography.
Symmetric key (Command line)
-
Symmetric Key Encryption (OpenSSL 1.x) [here]. In this case we will create cipher text from OpenSSL 1.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 1.x) [here].In this case we will decrypt cipher text from OpenSSL 1.x using a key derived from a password
-
Symmetric Key Encryption (OpenSSL 3.x) [here]. In this case we will create cipher text from OpenSSL 3.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 3.x) [here].In this case we will decrypt cipher text from OpenSSL 3.x using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password.
Hashing
-
Hashing [here] OpenSSL supports a wide range of hashing methods including BLAKE2b, Gost, MD4, MD5, RMD-160, SHA-1, SHA-3, SHA-256 and SHA-512.
Libre OpenSSL
-
Symmetric Key Encryption using Libre OpenSSL [here]. In this case we will create cipher text from Libre OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption using Libre OpenSSL [here]. In this case we will decrypt ciphertext from Libre OpenSSL using a key derived from a password.
-
Hashing [here] Libre OpenSSL supports a wide range of hashing methods including Gost, MD4, MD5, RMD-160, SHA-1, SHA-256 and SHA-512.
Diffie-Hellman parameter generation
-
DH Parameters with OpenSSL [here]. The Diffie-Hellman (DH) method is perhaps one of the greatest inventions in Cybersecurity, and was created by Whitfield Diffie and Marty Hellman. With the DH method, Bob creates a random value (\(b\)) and Alice also creates a random value (\(a\)). Next Bob computes \(B=g^b \pmod p\) and sends it to Alice. Alice computes \(A=g^a \pmod p\) and sends this to Bob. Bob raises the value of \(A\) to the power of \(b\) and takes \(\pmod p\), and Alice raises \(B\) to the power of \(a\) and takes \(\pmod p\). In the end, they will have the same shared value: \(g^{ab} \pmod p\). This can then be used to derive an encryption key that they can use for a secure tunnel. Overall, \(p\) is the large prime number, and also known as the shared modulus between Bob and Alice.
Key derivation function
-
PBKDF2 key derivation with OpenSSL [here] PBKDF2 (Password Key Derivation Function 2) is a key derivation method. Overall it is relatively slow in its operation and where we take a password, a salt value, hashing method, and a number of iterations, in order to produce a given size of encryption key.
-
HKDF key derivation with OpenSSL [here] HKDF (HMAC Key Derivation function) is used to derive an encryption key from a pass phrase. Initially HKDF creates a pseudorandom key (PRK) using a pass phrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), andalong with a salt value. Next the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys.
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Passwords
-
Password example [here]. This page uses the OpenSSL library hash password generator, which is used in UNIX systems for the hashing of passwords which are contained in /etc/shadow and /etc/passwd. For newer passwords, the "-1" options is used to created the hashed value.
-
Hashed passwords with OpenSSL [here].
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
Public key
-
Generating an ECC key pair with OpenSSL [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)).
-
Generating an RSA key pair with OpenSSL [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2).
-
Generating an RSA key pair with OpenSSL with encryption [here]. This page implements RSA key pair generation with an encrypted key pair. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). In this case we will encrypt the key pair with either 3DES, 128-bit AES, 192-bit AES or 256-bit AES. The same password must be used to encrypt and decrypt.
-
Generate prime with OpenSSL [here]. Prime numbers are important in public key encrytion, and are used with RSA and ECC. For RSA, we generate two prime numbers (\(p\) and \(q\)) and which are multiplied together to create a modulus (\(N\)). If these prime numbers have 512 bit values, the modulus will be a 1,024 bit value. This defines the basic secure of RSA. With elliptic curve we use smaller prime numbers, such as 256-bit values for the secp256k1 curve.
ASN1 parsing
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). We will parse using asn1parse, and reveal the parameters.
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)) [RSA key pair]. We will parse using asn1parse, and reveal the parameters.
- DSA Parameters with asn1parse. DSA parameters with OpenSSL with asn1parse. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA (Digital Signature Algorithm)
- DSA Parameters. DSA parameters with OpenSSL. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
MAC (Message Authentication Code)
- HMAC with OpenSSL. MACs with OpenSSL. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authenticate both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2) and SHA-3. In this case we will use OpenSSL to generate the HMAC value.
- MACs with OpenSSL. MACs with OpenSSL. In the following we will generate MACs for HMAC, GMAC, CMAC, Blake2bmac, Blake2smac, KMAC128 and KMAC256. Overall, we will use an encryption key defined as a hex value for GMAC and CMAC, and a pass phrase for the others. The message is "hello".
Signing
- Digital signing a plaintext message with OpenSSL. Signing with OpenSSL. With digital signing, we can take a message, and create a signature. This normally involves signing with a private key and digital certificate. The signed message can be an a MIME format, and which can be integrated into an email message. In this can we have a 512-bit RSA key pair that will sign a plain text message.
Encrypting emails
- Encrypting an email message in OpenSSL. Encrypting messages with OpenSSL. With public key encryption, we can take a message, and encrypt it with the recipiant's public key. In this can we have a 512-bit RSA public key to encrypt a message.
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Random number generation with OpenSSL
-
Random number generator [here]. Random numbers are important in generating encryption keys and salt values. In this case OpenSSL generates a random number (in a Base64 format) for a given number of bytes.
Outline (C#/Python)
-
Symmetric Key Encryption (C#) [here]. This page uses the OpenSSL library through a C#/.NET wrapper. The DLLs it interfaces to are libeay32.dll and ssleay32.dll. OpenSSL supports a wide range of encryption methods, including 128-bit AES, 192-bit AES, 256-bit AES and Blowfish (bf). Different modes of ECB, CBC, and OFB are implemented. The examples use a default IV of "1234".
-
AES in Python with OpenSSL output [here]
-
Producing OpenSSL AES Encrypted String from C# [here]
Digital Certificates
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
Paillier - Partial Homomorphic Encryption

The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Fundamentals
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier).
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Using RSA
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
Applications
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- ElGamal with ECC. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a numerical input.
- ElGamal with ECC (with string). ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve. This uses a string input.
- ElGamal with ECC (with string) for a range of curves. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and using a range of elliptic curves (including secp256k1, P256 and Ed25519). This uses a string input.
- Authenticated ElGamal Encryption using Kryptology. Authenticated ElGamal. This implements a public key encryption method with authenicated ciphertext.
Shamir Secret Shares
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Homomorphic Encryption
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Zero knowledge proofs
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
Verifiable Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Hash to scalar and point
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
CP-ABE
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Lattice cryptography

Latice cryptography is proposed as a post-quantum robust method for public key encryption, especially focused on digital signatures and key exchange mechanisms (KEMs).
Principles
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
NTRU
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- Lattice Encryption: NTRU Key Generation Python). NTRU. Outlines how NTRU operates for key generation.
Homomorphic
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Digital Signatures
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
Public-Key Encryption/Key Exchange
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
Light-weight cryptography

While AES and SHA work well together within computer systems, they struggle in an IoT/embedded world as they take up: too much processing power; too much physical space; and consume too much battery power. So NIST outlines a number of methods which can be used for light-weight cryptography, and which could be useful in IoT and RFID devices [1]. They define the device spectrum as:
- Conventional cryptography. Servers and Desktops. Tablets and smart phones.
- Light-weight cryptography. Embedded Systems. RFID and Sensor Networks.
With embedded systems, we commonly see 8-bit, 16-bit and 32-bit microcontrollers, and which would struggle to cope with real-time demands for conventional cryptography methods. And in the 40+ years since the first 4-bit processor, there is even a strong market for 4-bit processors. RFID and sensor network devices, especially, have limited numbers of gates available for security, and are often highly constrained with the power drain on the device.
So AES is typically a non-starter for many embedded devices. In light-weight cryptography, we often see smaller block size (typically 64 bits or 80 bits), smaller keys (often less than 90 bits) and less complex rounds (and where the S-boxes often just have 4-bits).
For light-weight cryptography the main constraints that we have are typically related to ener requirements, gate equivalents (GEs), and timing. With passive RFID devices, we do not have an associated battery for the power supply, and where the chip must power itself from energy coupled from the radio wave. An RFID device is thus likely to be severely constrained in the power drain associated with any cryptography functions, along with being constrained for the timing requirements and for the number of gates used. Even if an RFID device has an associated battery (active RFID), it may be difficult to recharge the battery, so the drain on power must often be minimised.
There is thus often a compromise between the cryptography method used and the overall security of the method. Thus often light-weight cryptography methods balance performance (throughput) against power drain and GE, and do not perform as well as main-stream cryptography standards (such as AES and SHA-256). Along with this the method must also have a low requirement for RAM (where the method requires the usage of running memory to perform its operation) and ROM (where the method is stored on the device). In order to assess the strengths of various methods we often define the area that the cryptography function will use on the device – and which is defined in \(µm^2\). The NIST finalists are defined in this [article]
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- GIFT AEAD. GIFT. GIFT is a light-weight block cipher. It is a (NIST Finalist)
- Elephant. Elephant. Elephant is a light-weight stream cipher. It is a (NIST Finalist).
- TinyJambu. TinyJambu. TinyJambu is a light-weight block cipher. It is a (NIST Finalist)
- Isap AEAD. Isap. Isap is a light-weight block cipher. It is a (NIST Finalist)
- PHOTON-Beetle AEAD. PHOTON-Beetle. PHOTON-Beetle is a light-weight block cipher. It is a (NIST Finalist)
- Romulus AEAD. Romulus. Romulus is a light-weight block cipher. It is a (NIST Finalist)
- Sparkle AEAD. Sparkle. Sparkle is a light-weight block cipher. It is a (NIST Finalist)
- CLEFIA. CLEFIA. CLEFIA is a light-weight block cipher.
- LED. LED. LED is a light-weight block cipher.
- Piccolo. Piccolo. Piccolo is an ultra light-weight block cipher.
- PRESENT. PRESENT. Present is a light-weight block cipher.
- Pyjamask. Pyjamask. Pyjamask is a light-weight block cipher.
- SIMON. SIMON. SIMON is a light-weight block cipher.
- SKINNY. SKINNY. SKINNEY is a light-weight block cipher.
- SPECK. SPECK. SPECK is a light-weight block cipher.
- XTEA. XTEA. XTEA is a light-weight block cipher.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encryption/Decryption. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.
Light-weight crypto (Other)
- Chaskey (MAC). Chaskey. Chaskey is a light-weight MAC function.
- Chaskey (MAC). Chaskey (Python). Chaskey is a light-weight MAC function.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (ASCON)
ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRFF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
Discrete Logs (Solving)

A discrete log problem is in the form of \(g^x \pmod p\) and where we know \(g\) and \(p\) and must solve for \(x\).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Message Authentication Code (MAC)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
HMAC
The following are the tips related to Key-based hashing:
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authentication both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2), Blake2b, SM3 and SHA-3. This page outlines the HMAC-MD5 methods using the Hazmat cryptography layer.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- HMAC (COSE). Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT with HMMAC. Go. In this case we create a CWT token, and sign with an HMAC signature.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- HMAC with Rust. HMAC. HMAC with Rust.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HMAC with OpenSSL. MACs with OpenSSL. HMAC in OpenSSL for a given input value, password and hashing method.
Cipher MACs
The following are the tips related to Key-based hashing:
- MACs with OpenSSL. MACs with OpenSSL. MAC methods implemented in OpenSSL, including CMAC and GMAC.
Key-based hashing
The following are the tips related to Key-based hashing:
- SipHash. Siphash. Siphash is a fast key-based hashing method.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Meow. Meow. Meow is one of the fastest hashing methods.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
Magic Numbers

This pages contains information related to magic numbers in file formats.
Network and File Forensics
- Magic numbers. Magic. This provides information on magic number for file forensics.
Graphics formats
- JPEG Analysis. JPEGs. This provides an analysis of JPEG files.
- GIF Analysis. GIFs. This provides an analysis of GIF files.
- TIF Analysis. TIFs. This provides an analysis of TIF files.
- PNG Analysis. PNGs. This provides an analysis of PNG files.
- BMP Analysis. BMPs. This provides an analysis of BMP files.
- PSD Analysis. PSDs. This provides an analysis of PSD files.
- WMF Analysis. WMF. This provides an analysis of WMF files.
- Adobe Illustrator Analysis. AI. This provides an analysis of AI files.
- Adobe In Design Analysis. INDD. This provides an analysis of INDD files.
- MIDI file. MIDI. This provides an analysis of MID files.
- ICO file. ICO. This provides an analysis of ICO files.
- PS file. PS. This provides an analysis of PS files.
- EPS file. EPS. This provides an analysis of EPS files.
- VSD file. VSD. This provides an analysis of Microsft Visio (VSD) files.
Video and audio formats
- MP3 Analysis. MP3s. This provides an analysis of MP3 files.
- AVI Analysis. AVIs. This provides an analysis of AVI files.
- Flash SWF Analysis. SWFs. This provides an analysis of Flash files.
- Flash FLV Analysis. FLVs. This provides an analysis of FLV files.
- MP4 Analysis. MP4. This provides an analysis of MP4 files.
- MOV Analysis. MOV. This provides an analysis of MOV files.
- WMV Analysis. WMV. This provides an analysis of WMV files.
- WMA Analysis. WMA. This provides an analysis of WMA files.
- JPEG 2000 Analysis. JPEG 2. This provides an analysis of JPEG 2000 files.
- WAV Analysis. WAV. This provides an analysis of WAV files.
Zips, Archives and Library files
- ZIP/Archive Analysis. ZIPs. This provides an analysis of ZIP/Achive files.
- GZ Analysis. GZ. This provides an analysis of GZip files.
- Tar Analysis. Tar. This provides an analysis of TAR files.
- MSI Analysis. MSI. This provides an analysis of MSI files.
- OBJ Analysis. OBJ. This provides an analysis of OBJ files.
- DLL Analysis. DLL. This provides an analysis of DLL files.
- CAB Analysis. CAB. This provides an analysis of CAB files.
- EXE Analysis. EXE. This provides an analysis of EXE files.
- RAR Analysis. RAR. This provides an analysis of RAR files.
- SYS Analysis. SYS. This provides an analysis of SYS files.
- HLP Analysis. HLP. This provides an analysis of HLP files.
- VMDK Analysis. VMDK. This provides an analysis of VMDK files (VMWare Virtual Disks).
- PST Analysis. PST. This provides an analysis of PST files (Outlook Email File).
- JAR Analysis. JAR. This provides an analysis of JAR files.
- SLN Analysis. SLN. This provides an analysis of Microsoft SLN files.
- Class Analysis. Class. This provides an analysis of Java Class files.
- Zlib. Zlib. This provides an analysis of Zlib files.
Documents
- PDF Analysis. PDFs. This provides an analysis of PDF files.
- DOC Analysis. DOCs. This provides an analysis of DOC files.
- RTF Analysis. RTFs. This provides an analysis of RTF files.
- XLS Analysis. XLSs. This provides an analysis of XLS files.
- PPT Analysis. PPTs. This provides an analysis of PPT files.
- MMP File. MMP. This provides an analysis of MMP files.
- DOCX Analysis. DOCX. This provides an analysis of DOCX files.
- XLSX Analysis. XLSX. This provides an analysis of XLSX files.
- PPTX Analysis. PPTX. This provides an analysis of PPTX files.
- MDB Analysis. MDB. This provides an analysis of MDB files.
- Outlook Message Analysis. MSG. This provides an analysis of MSG files.
Disk Image
- Raw disk format. RAW. This provides an analysis of the RAW disk format.
Tests
- File Forensics Test. File Test File Forensics Test.
- File Forensics Test (Fun). File Test (Fun) File Forensics Test.
Presentations
MIRACL Core Library

MIRACL Core is an open source library, and includes a wide range of public key encryption methods. It is especially focused on elliptic curve and pairing-friendly methods, but also supports a wide range of encryption methods, including RSA, AES and hashing. Overall, it can be ported onto a wide range of systems and supports C, C++, Go, Rust, Python, Java, Javascript and Swift. Along with this it supports limited capability devices such as the Arduino infrastructure. The GitHub repository is [here].
BN254
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.

Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- CL Signatures. CL. CL Signatures in Go using MIRACL.
- CL Signatures (advanced pairing). CL. CL Signatures in Go using MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages using MIRACL.
- PS Signatures. PS. Signatures using PS for short signatures using MIRACL.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures using MIRACL.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.

Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
Rust examples
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
NaCl

PyNaCl is a Python port of LibSodium. It integrates the latest cryptography methods, such as AES, XChaCha20, Blake2b and X25519.
Symmetric Key
- Symmetric key. Symmetric key (XChaCha20 and Poly1305). With symmetric key, Bob and Alice have the same key. NaCl uses the XChaCha20 method, and which supports stream encryption (and which does not require padding as a block cipher does, and is also faster than block cipher modes). ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16 byte nonce. XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24 byte nonce. It has a lower propability of nonce misuse than ChaCha20.
- Encryption with a password. Symmetric Key with KDF. In symmetric key, we generate a secret key. This key is typically a random value or generated from a password and a salt value. If we use a password, we typically use a KDF (Key Derivation Function), and which uses a password and a salt value, in order to create a key of a given size. In this case we will use Argon2i, and which is memory resilent.
Hybrid Encryption
- Box. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Hashing
- Hashing and KDF (Argon2 and scrypt). Hashing and KDF. This case we will use PyNaCl (Networking and Cryptography) library, and which is a Python binding to libsodium. We will hash a password using SHA-256 and SHA-512, and also create a KDF (Key Derivation Function) using scrypt and Argon2.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
Ed25519
-
Ed25519. Ed25519. Using Ed25519 for digital signatures.
-
Finding Points on Ed25519. X25519 (Points).
In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 (Key Exchange)
- X25519 + BLAKE2b key-exchange. X25519. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
Curve 25519
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
Node.js

Node.js uses the JavaScript programming langauge as its base, and allows for code to be run on a server, rather than in the browser (such as with pure JavaScript). To run a node.js program, we run "node myfile.js", and use NPM to install libraries.
Symmetric key
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
RSA and public key
- RSA Opt imal Asymmetric Encryption Padding (OAEP) using Node.js. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
ECC Keys
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.

Hashing
- Hashing with node.js (All). Hashing. Hashing with node.js.
- Hashing with node.js (Selection). Hashing. Hashing with node.js.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- ECDSA with node.js. ECDSA. ECDSA with node.js.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
Key exchange
- Diffie-Hellman with node.js (random prime). DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method and uses a randomly generated prime number (press the button to generate a new prime).
- Diffie-Hellman with node.js. DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method. Each time the prime number will be fixed for the DH group selected.
- ECDH with node.js. ECDH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Elliptic Curve Diffie Hellman (ECDH) key exchange method.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
Key derivation
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
CryptoJS
- CryptoJS (in node.js). CryptoJS (Node.js). Various crypto methods in the browser.
Bulletproofs
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
Blockchain
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
Proxy encryption
- Proxy Encryption - Encrypting With Public Key, And Decrypt with Private Key. Proxy01. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This page just creates a key pair for Alice, and uses it to encrypt with the public key , and decrypt with the private key.
- Proxy Encryption. Proxy02. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This will go through the full use case of proxy re-encryption.
Tokens
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
Random
- Fortuna with node.js. Fortuna. Fortuna random numbers with node.js.
Other
- FPE with node.js. FPR. FPE with node.js.
- Puny with node.js. Puny. Puny character format with node.js.
Accumulators and Witnesses
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
PGP
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Password Entropy
- Password Entropy with Node.js. Password Entropy. Password entropy measures the strength of a password, and is measured as the number of bits which could represent all of the possibilities. An entropy score of less than 25 identifies a poor password, and between 25 and 50 is a weak password. For 50 to 75 we have a reasonable password, and between 75 and 100 is a very good password. Over 100 is an excellent password. The strength of the password relates to the number of characters used, and also the number of characters in the password.
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
- Homomorphic Encryption with Node.js and BGV. Homomorphic Encryption with Node.js and BFG. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BGV method.
Oblivious Transfer (OT)

Oblivious Transfer allows Bob to select data from Alice, but for Alice not to know which value has been selected.
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
OpenSSH

OpenSSH supports the usage of the SSH protocol. This allows for a remote login. One tool which is uses is ssh-keygen, and which allow for the generation of RSA, DSA and elliptic-curve keys that. These can be used for user and host authentication, such as for GitHub login and Cloud instance login.
OpenSSH
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here].
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
Outline

OpenSSL

OpenSSL is a standard library that implements cryptography.
Symmetric key (Command line)
-
Symmetric Key Encryption (OpenSSL 1.x) [here]. In this case we will create cipher text from OpenSSL 1.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 1.x) [here].In this case we will decrypt cipher text from OpenSSL 1.x using a key derived from a password
-
Symmetric Key Encryption (OpenSSL 3.x) [here]. In this case we will create cipher text from OpenSSL 3.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 3.x) [here].In this case we will decrypt cipher text from OpenSSL 3.x using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password.
Hashing
-
Hashing [here] OpenSSL supports a wide range of hashing methods including BLAKE2b, Gost, MD4, MD5, RMD-160, SHA-1, SHA-3, SHA-256 and SHA-512.
Libre OpenSSL
-
Symmetric Key Encryption using Libre OpenSSL [here]. In this case we will create cipher text from Libre OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption using Libre OpenSSL [here]. In this case we will decrypt ciphertext from Libre OpenSSL using a key derived from a password.
-
Hashing [here] Libre OpenSSL supports a wide range of hashing methods including Gost, MD4, MD5, RMD-160, SHA-1, SHA-256 and SHA-512.
Diffie-Hellman parameter generation
-
DH Parameters with OpenSSL [here]. The Diffie-Hellman (DH) method is perhaps one of the greatest inventions in Cybersecurity, and was created by Whitfield Diffie and Marty Hellman. With the DH method, Bob creates a random value (\(b\)) and Alice also creates a random value (\(a\)). Next Bob computes \(B=g^b \pmod p\) and sends it to Alice. Alice computes \(A=g^a \pmod p\) and sends this to Bob. Bob raises the value of \(A\) to the power of \(b\) and takes \(\pmod p\), and Alice raises \(B\) to the power of \(a\) and takes \(\pmod p\). In the end, they will have the same shared value: \(g^{ab} \pmod p\). This can then be used to derive an encryption key that they can use for a secure tunnel. Overall, \(p\) is the large prime number, and also known as the shared modulus between Bob and Alice.
Key derivation function
-
PBKDF2 key derivation with OpenSSL [here] PBKDF2 (Password Key Derivation Function 2) is a key derivation method. Overall it is relatively slow in its operation and where we take a password, a salt value, hashing method, and a number of iterations, in order to produce a given size of encryption key.
-
HKDF key derivation with OpenSSL [here] HKDF (HMAC Key Derivation function) is used to derive an encryption key from a pass phrase. Initially HKDF creates a pseudorandom key (PRK) using a pass phrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), andalong with a salt value. Next the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys.
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Passwords
-
Password example [here]. This page uses the OpenSSL library hash password generator, which is used in UNIX systems for the hashing of passwords which are contained in /etc/shadow and /etc/passwd. For newer passwords, the "-1" options is used to created the hashed value.
-
Hashed passwords with OpenSSL [here].
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
Public key
-
Generating an ECC key pair with OpenSSL [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)).
-
Generating an RSA key pair with OpenSSL [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2).
-
Generating an RSA key pair with OpenSSL with encryption [here]. This page implements RSA key pair generation with an encrypted key pair. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). In this case we will encrypt the key pair with either 3DES, 128-bit AES, 192-bit AES or 256-bit AES. The same password must be used to encrypt and decrypt.
-
Generate prime with OpenSSL [here]. Prime numbers are important in public key encrytion, and are used with RSA and ECC. For RSA, we generate two prime numbers (\(p\) and \(q\)) and which are multiplied together to create a modulus (\(N\)). If these prime numbers have 512 bit values, the modulus will be a 1,024 bit value. This defines the basic secure of RSA. With elliptic curve we use smaller prime numbers, such as 256-bit values for the secp256k1 curve.
ASN1 parsing
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). We will parse using asn1parse, and reveal the parameters.
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)) [RSA key pair]. We will parse using asn1parse, and reveal the parameters.
- DSA Parameters with asn1parse. DSA parameters with OpenSSL with asn1parse. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA (Digital Signature Algorithm)
- DSA Parameters. DSA parameters with OpenSSL. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
MAC (Message Authentication Code)
- HMAC with OpenSSL. MACs with OpenSSL. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authenticate both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2) and SHA-3. In this case we will use OpenSSL to generate the HMAC value.
- MACs with OpenSSL. MACs with OpenSSL. In the following we will generate MACs for HMAC, GMAC, CMAC, Blake2bmac, Blake2smac, KMAC128 and KMAC256. Overall, we will use an encryption key defined as a hex value for GMAC and CMAC, and a pass phrase for the others. The message is "hello".
Signing
- Digital signing a plaintext message with OpenSSL. Signing with OpenSSL. With digital signing, we can take a message, and create a signature. This normally involves signing with a private key and digital certificate. The signed message can be an a MIME format, and which can be integrated into an email message. In this can we have a 512-bit RSA key pair that will sign a plain text message.
Encrypting emails
- Encrypting an email message in OpenSSL. Encrypting messages with OpenSSL. With public key encryption, we can take a message, and encrypt it with the recipiant's public key. In this can we have a 512-bit RSA public key to encrypt a message.
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Random number generation with OpenSSL
-
Random number generator [here]. Random numbers are important in generating encryption keys and salt values. In this case OpenSSL generates a random number (in a Base64 format) for a given number of bytes.
Outline (C#/Python)
-
Symmetric Key Encryption (C#) [here]. This page uses the OpenSSL library through a C#/.NET wrapper. The DLLs it interfaces to are libeay32.dll and ssleay32.dll. OpenSSL supports a wide range of encryption methods, including 128-bit AES, 192-bit AES, 256-bit AES and Blowfish (bf). Different modes of ECB, CBC, and OFB are implemented. The examples use a default IV of "1234".
-
AES in Python with OpenSSL output [here]
-
Producing OpenSSL AES Encrypted String from C# [here]
Digital Certificates
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
Paillier - Partial Homomorphic Encryption

The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Fundamentals
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier).
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Using RSA
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
Applications
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Homomorphic Encryption
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Zero knowledge proofs
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
Verifiable Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Hash to scalar and point
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
CP-ABE
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Lattice cryptography

Latice cryptography is proposed as a post-quantum robust method for public key encryption, especially focused on digital signatures and key exchange mechanisms (KEMs).
Principles
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
NTRU
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- Lattice Encryption: NTRU Key Generation Python). NTRU. Outlines how NTRU operates for key generation.
Homomorphic
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Digital Signatures
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
Public-Key Encryption/Key Exchange
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
Light-weight cryptography

While AES and SHA work well together within computer systems, they struggle in an IoT/embedded world as they take up: too much processing power; too much physical space; and consume too much battery power. So NIST outlines a number of methods which can be used for light-weight cryptography, and which could be useful in IoT and RFID devices [1]. They define the device spectrum as:
- Conventional cryptography. Servers and Desktops. Tablets and smart phones.
- Light-weight cryptography. Embedded Systems. RFID and Sensor Networks.
With embedded systems, we commonly see 8-bit, 16-bit and 32-bit microcontrollers, and which would struggle to cope with real-time demands for conventional cryptography methods. And in the 40+ years since the first 4-bit processor, there is even a strong market for 4-bit processors. RFID and sensor network devices, especially, have limited numbers of gates available for security, and are often highly constrained with the power drain on the device.
So AES is typically a non-starter for many embedded devices. In light-weight cryptography, we often see smaller block size (typically 64 bits or 80 bits), smaller keys (often less than 90 bits) and less complex rounds (and where the S-boxes often just have 4-bits).
For light-weight cryptography the main constraints that we have are typically related to ener requirements, gate equivalents (GEs), and timing. With passive RFID devices, we do not have an associated battery for the power supply, and where the chip must power itself from energy coupled from the radio wave. An RFID device is thus likely to be severely constrained in the power drain associated with any cryptography functions, along with being constrained for the timing requirements and for the number of gates used. Even if an RFID device has an associated battery (active RFID), it may be difficult to recharge the battery, so the drain on power must often be minimised.
There is thus often a compromise between the cryptography method used and the overall security of the method. Thus often light-weight cryptography methods balance performance (throughput) against power drain and GE, and do not perform as well as main-stream cryptography standards (such as AES and SHA-256). Along with this the method must also have a low requirement for RAM (where the method requires the usage of running memory to perform its operation) and ROM (where the method is stored on the device). In order to assess the strengths of various methods we often define the area that the cryptography function will use on the device – and which is defined in \(µm^2\). The NIST finalists are defined in this [article]
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- GIFT AEAD. GIFT. GIFT is a light-weight block cipher. It is a (NIST Finalist)
- Elephant. Elephant. Elephant is a light-weight stream cipher. It is a (NIST Finalist).
- TinyJambu. TinyJambu. TinyJambu is a light-weight block cipher. It is a (NIST Finalist)
- Isap AEAD. Isap. Isap is a light-weight block cipher. It is a (NIST Finalist)
- PHOTON-Beetle AEAD. PHOTON-Beetle. PHOTON-Beetle is a light-weight block cipher. It is a (NIST Finalist)
- Romulus AEAD. Romulus. Romulus is a light-weight block cipher. It is a (NIST Finalist)
- Sparkle AEAD. Sparkle. Sparkle is a light-weight block cipher. It is a (NIST Finalist)
- CLEFIA. CLEFIA. CLEFIA is a light-weight block cipher.
- LED. LED. LED is a light-weight block cipher.
- Piccolo. Piccolo. Piccolo is an ultra light-weight block cipher.
- PRESENT. PRESENT. Present is a light-weight block cipher.
- Pyjamask. Pyjamask. Pyjamask is a light-weight block cipher.
- SIMON. SIMON. SIMON is a light-weight block cipher.
- SKINNY. SKINNY. SKINNEY is a light-weight block cipher.
- SPECK. SPECK. SPECK is a light-weight block cipher.
- XTEA. XTEA. XTEA is a light-weight block cipher.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encryption/Decryption. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.
Light-weight crypto (Other)
- Chaskey (MAC). Chaskey. Chaskey is a light-weight MAC function.
- Chaskey (MAC). Chaskey (Python). Chaskey is a light-weight MAC function.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (ASCON)
ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRFF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
Discrete Logs (Solving)

A discrete log problem is in the form of \(g^x \pmod p\) and where we know \(g\) and \(p\) and must solve for \(x\).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Message Authentication Code (MAC)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
HMAC
The following are the tips related to Key-based hashing:
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authentication both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2), Blake2b, SM3 and SHA-3. This page outlines the HMAC-MD5 methods using the Hazmat cryptography layer.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- HMAC (COSE). Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT with HMMAC. Go. In this case we create a CWT token, and sign with an HMAC signature.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- HMAC with Rust. HMAC. HMAC with Rust.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HMAC with OpenSSL. MACs with OpenSSL. HMAC in OpenSSL for a given input value, password and hashing method.
Cipher MACs
The following are the tips related to Key-based hashing:
- MACs with OpenSSL. MACs with OpenSSL. MAC methods implemented in OpenSSL, including CMAC and GMAC.
Key-based hashing
The following are the tips related to Key-based hashing:
- SipHash. Siphash. Siphash is a fast key-based hashing method.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Meow. Meow. Meow is one of the fastest hashing methods.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
Magic Numbers

This pages contains information related to magic numbers in file formats.
Network and File Forensics
- Magic numbers. Magic. This provides information on magic number for file forensics.
Graphics formats
- JPEG Analysis. JPEGs. This provides an analysis of JPEG files.
- GIF Analysis. GIFs. This provides an analysis of GIF files.
- TIF Analysis. TIFs. This provides an analysis of TIF files.
- PNG Analysis. PNGs. This provides an analysis of PNG files.
- BMP Analysis. BMPs. This provides an analysis of BMP files.
- PSD Analysis. PSDs. This provides an analysis of PSD files.
- WMF Analysis. WMF. This provides an analysis of WMF files.
- Adobe Illustrator Analysis. AI. This provides an analysis of AI files.
- Adobe In Design Analysis. INDD. This provides an analysis of INDD files.
- MIDI file. MIDI. This provides an analysis of MID files.
- ICO file. ICO. This provides an analysis of ICO files.
- PS file. PS. This provides an analysis of PS files.
- EPS file. EPS. This provides an analysis of EPS files.
- VSD file. VSD. This provides an analysis of Microsft Visio (VSD) files.
Video and audio formats
- MP3 Analysis. MP3s. This provides an analysis of MP3 files.
- AVI Analysis. AVIs. This provides an analysis of AVI files.
- Flash SWF Analysis. SWFs. This provides an analysis of Flash files.
- Flash FLV Analysis. FLVs. This provides an analysis of FLV files.
- MP4 Analysis. MP4. This provides an analysis of MP4 files.
- MOV Analysis. MOV. This provides an analysis of MOV files.
- WMV Analysis. WMV. This provides an analysis of WMV files.
- WMA Analysis. WMA. This provides an analysis of WMA files.
- JPEG 2000 Analysis. JPEG 2. This provides an analysis of JPEG 2000 files.
- WAV Analysis. WAV. This provides an analysis of WAV files.
Zips, Archives and Library files
- ZIP/Archive Analysis. ZIPs. This provides an analysis of ZIP/Achive files.
- GZ Analysis. GZ. This provides an analysis of GZip files.
- Tar Analysis. Tar. This provides an analysis of TAR files.
- MSI Analysis. MSI. This provides an analysis of MSI files.
- OBJ Analysis. OBJ. This provides an analysis of OBJ files.
- DLL Analysis. DLL. This provides an analysis of DLL files.
- CAB Analysis. CAB. This provides an analysis of CAB files.
- EXE Analysis. EXE. This provides an analysis of EXE files.
- RAR Analysis. RAR. This provides an analysis of RAR files.
- SYS Analysis. SYS. This provides an analysis of SYS files.
- HLP Analysis. HLP. This provides an analysis of HLP files.
- VMDK Analysis. VMDK. This provides an analysis of VMDK files (VMWare Virtual Disks).
- PST Analysis. PST. This provides an analysis of PST files (Outlook Email File).
- JAR Analysis. JAR. This provides an analysis of JAR files.
- SLN Analysis. SLN. This provides an analysis of Microsoft SLN files.
- Class Analysis. Class. This provides an analysis of Java Class files.
- Zlib. Zlib. This provides an analysis of Zlib files.
Documents
- PDF Analysis. PDFs. This provides an analysis of PDF files.
- DOC Analysis. DOCs. This provides an analysis of DOC files.
- RTF Analysis. RTFs. This provides an analysis of RTF files.
- XLS Analysis. XLSs. This provides an analysis of XLS files.
- PPT Analysis. PPTs. This provides an analysis of PPT files.
- MMP File. MMP. This provides an analysis of MMP files.
- DOCX Analysis. DOCX. This provides an analysis of DOCX files.
- XLSX Analysis. XLSX. This provides an analysis of XLSX files.
- PPTX Analysis. PPTX. This provides an analysis of PPTX files.
- MDB Analysis. MDB. This provides an analysis of MDB files.
- Outlook Message Analysis. MSG. This provides an analysis of MSG files.
Disk Image
- Raw disk format. RAW. This provides an analysis of the RAW disk format.
Tests
- File Forensics Test. File Test File Forensics Test.
- File Forensics Test (Fun). File Test (Fun) File Forensics Test.
Presentations
MIRACL Core Library

MIRACL Core is an open source library, and includes a wide range of public key encryption methods. It is especially focused on elliptic curve and pairing-friendly methods, but also supports a wide range of encryption methods, including RSA, AES and hashing. Overall, it can be ported onto a wide range of systems and supports C, C++, Go, Rust, Python, Java, Javascript and Swift. Along with this it supports limited capability devices such as the Arduino infrastructure. The GitHub repository is [here].
BN254
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.

Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- CL Signatures. CL. CL Signatures in Go using MIRACL.
- CL Signatures (advanced pairing). CL. CL Signatures in Go using MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages using MIRACL.
- PS Signatures. PS. Signatures using PS for short signatures using MIRACL.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures using MIRACL.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.

Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
Rust examples
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
NaCl

PyNaCl is a Python port of LibSodium. It integrates the latest cryptography methods, such as AES, XChaCha20, Blake2b and X25519.
Symmetric Key
- Symmetric key. Symmetric key (XChaCha20 and Poly1305). With symmetric key, Bob and Alice have the same key. NaCl uses the XChaCha20 method, and which supports stream encryption (and which does not require padding as a block cipher does, and is also faster than block cipher modes). ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16 byte nonce. XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24 byte nonce. It has a lower propability of nonce misuse than ChaCha20.
- Encryption with a password. Symmetric Key with KDF. In symmetric key, we generate a secret key. This key is typically a random value or generated from a password and a salt value. If we use a password, we typically use a KDF (Key Derivation Function), and which uses a password and a salt value, in order to create a key of a given size. In this case we will use Argon2i, and which is memory resilent.
Hybrid Encryption
- Box. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Hashing
- Hashing and KDF (Argon2 and scrypt). Hashing and KDF. This case we will use PyNaCl (Networking and Cryptography) library, and which is a Python binding to libsodium. We will hash a password using SHA-256 and SHA-512, and also create a KDF (Key Derivation Function) using scrypt and Argon2.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
Ed25519
-
Ed25519. Ed25519. Using Ed25519 for digital signatures.
-
Finding Points on Ed25519. X25519 (Points).
In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 (Key Exchange)
- X25519 + BLAKE2b key-exchange. X25519. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
Curve 25519
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
Node.js

Node.js uses the JavaScript programming langauge as its base, and allows for code to be run on a server, rather than in the browser (such as with pure JavaScript). To run a node.js program, we run "node myfile.js", and use NPM to install libraries.
Symmetric key
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
RSA and public key
- RSA Opt imal Asymmetric Encryption Padding (OAEP) using Node.js. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
ECC Keys
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.

Hashing
- Hashing with node.js (All). Hashing. Hashing with node.js.
- Hashing with node.js (Selection). Hashing. Hashing with node.js.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- ECDSA with node.js. ECDSA. ECDSA with node.js.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
Key exchange
- Diffie-Hellman with node.js (random prime). DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method and uses a randomly generated prime number (press the button to generate a new prime).
- Diffie-Hellman with node.js. DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method. Each time the prime number will be fixed for the DH group selected.
- ECDH with node.js. ECDH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Elliptic Curve Diffie Hellman (ECDH) key exchange method.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
Key derivation
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
CryptoJS
- CryptoJS (in node.js). CryptoJS (Node.js). Various crypto methods in the browser.
Bulletproofs
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
Blockchain
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
Proxy encryption
- Proxy Encryption - Encrypting With Public Key, And Decrypt with Private Key. Proxy01. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This page just creates a key pair for Alice, and uses it to encrypt with the public key , and decrypt with the private key.
- Proxy Encryption. Proxy02. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This will go through the full use case of proxy re-encryption.
Tokens
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
Random
- Fortuna with node.js. Fortuna. Fortuna random numbers with node.js.
Other
- FPE with node.js. FPR. FPE with node.js.
- Puny with node.js. Puny. Puny character format with node.js.
Accumulators and Witnesses
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
PGP
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Password Entropy
- Password Entropy with Node.js. Password Entropy. Password entropy measures the strength of a password, and is measured as the number of bits which could represent all of the possibilities. An entropy score of less than 25 identifies a poor password, and between 25 and 50 is a weak password. For 50 to 75 we have a reasonable password, and between 75 and 100 is a very good password. Over 100 is an excellent password. The strength of the password relates to the number of characters used, and also the number of characters in the password.
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
- Homomorphic Encryption with Node.js and BGV. Homomorphic Encryption with Node.js and BFG. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BGV method.
Oblivious Transfer (OT)

Oblivious Transfer allows Bob to select data from Alice, but for Alice not to know which value has been selected.
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
OpenSSH

OpenSSH supports the usage of the SSH protocol. This allows for a remote login. One tool which is uses is ssh-keygen, and which allow for the generation of RSA, DSA and elliptic-curve keys that. These can be used for user and host authentication, such as for GitHub login and Cloud instance login.
OpenSSH
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here].
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
Outline

OpenSSL

OpenSSL is a standard library that implements cryptography.
Symmetric key (Command line)
-
Symmetric Key Encryption (OpenSSL 1.x) [here]. In this case we will create cipher text from OpenSSL 1.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 1.x) [here].In this case we will decrypt cipher text from OpenSSL 1.x using a key derived from a password
-
Symmetric Key Encryption (OpenSSL 3.x) [here]. In this case we will create cipher text from OpenSSL 3.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 3.x) [here].In this case we will decrypt cipher text from OpenSSL 3.x using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password.
Hashing
-
Hashing [here] OpenSSL supports a wide range of hashing methods including BLAKE2b, Gost, MD4, MD5, RMD-160, SHA-1, SHA-3, SHA-256 and SHA-512.
Libre OpenSSL
-
Symmetric Key Encryption using Libre OpenSSL [here]. In this case we will create cipher text from Libre OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption using Libre OpenSSL [here]. In this case we will decrypt ciphertext from Libre OpenSSL using a key derived from a password.
-
Hashing [here] Libre OpenSSL supports a wide range of hashing methods including Gost, MD4, MD5, RMD-160, SHA-1, SHA-256 and SHA-512.
Diffie-Hellman parameter generation
-
DH Parameters with OpenSSL [here]. The Diffie-Hellman (DH) method is perhaps one of the greatest inventions in Cybersecurity, and was created by Whitfield Diffie and Marty Hellman. With the DH method, Bob creates a random value (\(b\)) and Alice also creates a random value (\(a\)). Next Bob computes \(B=g^b \pmod p\) and sends it to Alice. Alice computes \(A=g^a \pmod p\) and sends this to Bob. Bob raises the value of \(A\) to the power of \(b\) and takes \(\pmod p\), and Alice raises \(B\) to the power of \(a\) and takes \(\pmod p\). In the end, they will have the same shared value: \(g^{ab} \pmod p\). This can then be used to derive an encryption key that they can use for a secure tunnel. Overall, \(p\) is the large prime number, and also known as the shared modulus between Bob and Alice.
Key derivation function
-
PBKDF2 key derivation with OpenSSL [here] PBKDF2 (Password Key Derivation Function 2) is a key derivation method. Overall it is relatively slow in its operation and where we take a password, a salt value, hashing method, and a number of iterations, in order to produce a given size of encryption key.
-
HKDF key derivation with OpenSSL [here] HKDF (HMAC Key Derivation function) is used to derive an encryption key from a pass phrase. Initially HKDF creates a pseudorandom key (PRK) using a pass phrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), andalong with a salt value. Next the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys.
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Passwords
-
Password example [here]. This page uses the OpenSSL library hash password generator, which is used in UNIX systems for the hashing of passwords which are contained in /etc/shadow and /etc/passwd. For newer passwords, the "-1" options is used to created the hashed value.
-
Hashed passwords with OpenSSL [here].
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
Public key
-
Generating an ECC key pair with OpenSSL [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)).
-
Generating an RSA key pair with OpenSSL [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2).
-
Generating an RSA key pair with OpenSSL with encryption [here]. This page implements RSA key pair generation with an encrypted key pair. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). In this case we will encrypt the key pair with either 3DES, 128-bit AES, 192-bit AES or 256-bit AES. The same password must be used to encrypt and decrypt.
-
Generate prime with OpenSSL [here]. Prime numbers are important in public key encrytion, and are used with RSA and ECC. For RSA, we generate two prime numbers (\(p\) and \(q\)) and which are multiplied together to create a modulus (\(N\)). If these prime numbers have 512 bit values, the modulus will be a 1,024 bit value. This defines the basic secure of RSA. With elliptic curve we use smaller prime numbers, such as 256-bit values for the secp256k1 curve.
ASN1 parsing
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). We will parse using asn1parse, and reveal the parameters.
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)) [RSA key pair]. We will parse using asn1parse, and reveal the parameters.
- DSA Parameters with asn1parse. DSA parameters with OpenSSL with asn1parse. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA (Digital Signature Algorithm)
- DSA Parameters. DSA parameters with OpenSSL. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
MAC (Message Authentication Code)
- HMAC with OpenSSL. MACs with OpenSSL. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authenticate both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2) and SHA-3. In this case we will use OpenSSL to generate the HMAC value.
- MACs with OpenSSL. MACs with OpenSSL. In the following we will generate MACs for HMAC, GMAC, CMAC, Blake2bmac, Blake2smac, KMAC128 and KMAC256. Overall, we will use an encryption key defined as a hex value for GMAC and CMAC, and a pass phrase for the others. The message is "hello".
Signing
- Digital signing a plaintext message with OpenSSL. Signing with OpenSSL. With digital signing, we can take a message, and create a signature. This normally involves signing with a private key and digital certificate. The signed message can be an a MIME format, and which can be integrated into an email message. In this can we have a 512-bit RSA key pair that will sign a plain text message.
Encrypting emails
- Encrypting an email message in OpenSSL. Encrypting messages with OpenSSL. With public key encryption, we can take a message, and encrypt it with the recipiant's public key. In this can we have a 512-bit RSA public key to encrypt a message.
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Random number generation with OpenSSL
-
Random number generator [here]. Random numbers are important in generating encryption keys and salt values. In this case OpenSSL generates a random number (in a Base64 format) for a given number of bytes.
Outline (C#/Python)
-
Symmetric Key Encryption (C#) [here]. This page uses the OpenSSL library through a C#/.NET wrapper. The DLLs it interfaces to are libeay32.dll and ssleay32.dll. OpenSSL supports a wide range of encryption methods, including 128-bit AES, 192-bit AES, 256-bit AES and Blowfish (bf). Different modes of ECB, CBC, and OFB are implemented. The examples use a default IV of "1234".
-
AES in Python with OpenSSL output [here]
-
Producing OpenSSL AES Encrypted String from C# [here]
Digital Certificates
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
Paillier - Partial Homomorphic Encryption

The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Fundamentals
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier).
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Using RSA
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
Applications
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
- Homomorphic Encryption. Homomorphic. Homomorphic Encryption With Adding for Elgamal using Kryptology
Zero knowledge proofs
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
Verifiable Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Hash to scalar and point
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
CP-ABE
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Lattice cryptography

Latice cryptography is proposed as a post-quantum robust method for public key encryption, especially focused on digital signatures and key exchange mechanisms (KEMs).
Principles
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
NTRU
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- Lattice Encryption: NTRU Key Generation Python). NTRU. Outlines how NTRU operates for key generation.
Homomorphic
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Digital Signatures
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
Public-Key Encryption/Key Exchange
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
Light-weight cryptography

While AES and SHA work well together within computer systems, they struggle in an IoT/embedded world as they take up: too much processing power; too much physical space; and consume too much battery power. So NIST outlines a number of methods which can be used for light-weight cryptography, and which could be useful in IoT and RFID devices [1]. They define the device spectrum as:
- Conventional cryptography. Servers and Desktops. Tablets and smart phones.
- Light-weight cryptography. Embedded Systems. RFID and Sensor Networks.
With embedded systems, we commonly see 8-bit, 16-bit and 32-bit microcontrollers, and which would struggle to cope with real-time demands for conventional cryptography methods. And in the 40+ years since the first 4-bit processor, there is even a strong market for 4-bit processors. RFID and sensor network devices, especially, have limited numbers of gates available for security, and are often highly constrained with the power drain on the device.
So AES is typically a non-starter for many embedded devices. In light-weight cryptography, we often see smaller block size (typically 64 bits or 80 bits), smaller keys (often less than 90 bits) and less complex rounds (and where the S-boxes often just have 4-bits).
For light-weight cryptography the main constraints that we have are typically related to ener requirements, gate equivalents (GEs), and timing. With passive RFID devices, we do not have an associated battery for the power supply, and where the chip must power itself from energy coupled from the radio wave. An RFID device is thus likely to be severely constrained in the power drain associated with any cryptography functions, along with being constrained for the timing requirements and for the number of gates used. Even if an RFID device has an associated battery (active RFID), it may be difficult to recharge the battery, so the drain on power must often be minimised.
There is thus often a compromise between the cryptography method used and the overall security of the method. Thus often light-weight cryptography methods balance performance (throughput) against power drain and GE, and do not perform as well as main-stream cryptography standards (such as AES and SHA-256). Along with this the method must also have a low requirement for RAM (where the method requires the usage of running memory to perform its operation) and ROM (where the method is stored on the device). In order to assess the strengths of various methods we often define the area that the cryptography function will use on the device – and which is defined in \(µm^2\). The NIST finalists are defined in this [article]
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- GIFT AEAD. GIFT. GIFT is a light-weight block cipher. It is a (NIST Finalist)
- Elephant. Elephant. Elephant is a light-weight stream cipher. It is a (NIST Finalist).
- TinyJambu. TinyJambu. TinyJambu is a light-weight block cipher. It is a (NIST Finalist)
- Isap AEAD. Isap. Isap is a light-weight block cipher. It is a (NIST Finalist)
- PHOTON-Beetle AEAD. PHOTON-Beetle. PHOTON-Beetle is a light-weight block cipher. It is a (NIST Finalist)
- Romulus AEAD. Romulus. Romulus is a light-weight block cipher. It is a (NIST Finalist)
- Sparkle AEAD. Sparkle. Sparkle is a light-weight block cipher. It is a (NIST Finalist)
- CLEFIA. CLEFIA. CLEFIA is a light-weight block cipher.
- LED. LED. LED is a light-weight block cipher.
- Piccolo. Piccolo. Piccolo is an ultra light-weight block cipher.
- PRESENT. PRESENT. Present is a light-weight block cipher.
- Pyjamask. Pyjamask. Pyjamask is a light-weight block cipher.
- SIMON. SIMON. SIMON is a light-weight block cipher.
- SKINNY. SKINNY. SKINNEY is a light-weight block cipher.
- SPECK. SPECK. SPECK is a light-weight block cipher.
- XTEA. XTEA. XTEA is a light-weight block cipher.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encryption/Decryption. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.
Light-weight crypto (Other)
- Chaskey (MAC). Chaskey. Chaskey is a light-weight MAC function.
- Chaskey (MAC). Chaskey (Python). Chaskey is a light-weight MAC function.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (ASCON)
ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRFF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
Discrete Logs (Solving)

A discrete log problem is in the form of \(g^x \pmod p\) and where we know \(g\) and \(p\) and must solve for \(x\).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Message Authentication Code (MAC)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
HMAC
The following are the tips related to Key-based hashing:
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authentication both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2), Blake2b, SM3 and SHA-3. This page outlines the HMAC-MD5 methods using the Hazmat cryptography layer.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- HMAC (COSE). Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT with HMMAC. Go. In this case we create a CWT token, and sign with an HMAC signature.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- HMAC with Rust. HMAC. HMAC with Rust.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HMAC with OpenSSL. MACs with OpenSSL. HMAC in OpenSSL for a given input value, password and hashing method.
Cipher MACs
The following are the tips related to Key-based hashing:
- MACs with OpenSSL. MACs with OpenSSL. MAC methods implemented in OpenSSL, including CMAC and GMAC.
Key-based hashing
The following are the tips related to Key-based hashing:
- SipHash. Siphash. Siphash is a fast key-based hashing method.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Meow. Meow. Meow is one of the fastest hashing methods.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
Magic Numbers

This pages contains information related to magic numbers in file formats.
Network and File Forensics
- Magic numbers. Magic. This provides information on magic number for file forensics.
Graphics formats
- JPEG Analysis. JPEGs. This provides an analysis of JPEG files.
- GIF Analysis. GIFs. This provides an analysis of GIF files.
- TIF Analysis. TIFs. This provides an analysis of TIF files.
- PNG Analysis. PNGs. This provides an analysis of PNG files.
- BMP Analysis. BMPs. This provides an analysis of BMP files.
- PSD Analysis. PSDs. This provides an analysis of PSD files.
- WMF Analysis. WMF. This provides an analysis of WMF files.
- Adobe Illustrator Analysis. AI. This provides an analysis of AI files.
- Adobe In Design Analysis. INDD. This provides an analysis of INDD files.
- MIDI file. MIDI. This provides an analysis of MID files.
- ICO file. ICO. This provides an analysis of ICO files.
- PS file. PS. This provides an analysis of PS files.
- EPS file. EPS. This provides an analysis of EPS files.
- VSD file. VSD. This provides an analysis of Microsft Visio (VSD) files.
Video and audio formats
- MP3 Analysis. MP3s. This provides an analysis of MP3 files.
- AVI Analysis. AVIs. This provides an analysis of AVI files.
- Flash SWF Analysis. SWFs. This provides an analysis of Flash files.
- Flash FLV Analysis. FLVs. This provides an analysis of FLV files.
- MP4 Analysis. MP4. This provides an analysis of MP4 files.
- MOV Analysis. MOV. This provides an analysis of MOV files.
- WMV Analysis. WMV. This provides an analysis of WMV files.
- WMA Analysis. WMA. This provides an analysis of WMA files.
- JPEG 2000 Analysis. JPEG 2. This provides an analysis of JPEG 2000 files.
- WAV Analysis. WAV. This provides an analysis of WAV files.
Zips, Archives and Library files
- ZIP/Archive Analysis. ZIPs. This provides an analysis of ZIP/Achive files.
- GZ Analysis. GZ. This provides an analysis of GZip files.
- Tar Analysis. Tar. This provides an analysis of TAR files.
- MSI Analysis. MSI. This provides an analysis of MSI files.
- OBJ Analysis. OBJ. This provides an analysis of OBJ files.
- DLL Analysis. DLL. This provides an analysis of DLL files.
- CAB Analysis. CAB. This provides an analysis of CAB files.
- EXE Analysis. EXE. This provides an analysis of EXE files.
- RAR Analysis. RAR. This provides an analysis of RAR files.
- SYS Analysis. SYS. This provides an analysis of SYS files.
- HLP Analysis. HLP. This provides an analysis of HLP files.
- VMDK Analysis. VMDK. This provides an analysis of VMDK files (VMWare Virtual Disks).
- PST Analysis. PST. This provides an analysis of PST files (Outlook Email File).
- JAR Analysis. JAR. This provides an analysis of JAR files.
- SLN Analysis. SLN. This provides an analysis of Microsoft SLN files.
- Class Analysis. Class. This provides an analysis of Java Class files.
- Zlib. Zlib. This provides an analysis of Zlib files.
Documents
- PDF Analysis. PDFs. This provides an analysis of PDF files.
- DOC Analysis. DOCs. This provides an analysis of DOC files.
- RTF Analysis. RTFs. This provides an analysis of RTF files.
- XLS Analysis. XLSs. This provides an analysis of XLS files.
- PPT Analysis. PPTs. This provides an analysis of PPT files.
- MMP File. MMP. This provides an analysis of MMP files.
- DOCX Analysis. DOCX. This provides an analysis of DOCX files.
- XLSX Analysis. XLSX. This provides an analysis of XLSX files.
- PPTX Analysis. PPTX. This provides an analysis of PPTX files.
- MDB Analysis. MDB. This provides an analysis of MDB files.
- Outlook Message Analysis. MSG. This provides an analysis of MSG files.
Disk Image
- Raw disk format. RAW. This provides an analysis of the RAW disk format.
Tests
- File Forensics Test. File Test File Forensics Test.
- File Forensics Test (Fun). File Test (Fun) File Forensics Test.
Presentations
MIRACL Core Library

MIRACL Core is an open source library, and includes a wide range of public key encryption methods. It is especially focused on elliptic curve and pairing-friendly methods, but also supports a wide range of encryption methods, including RSA, AES and hashing. Overall, it can be ported onto a wide range of systems and supports C, C++, Go, Rust, Python, Java, Javascript and Swift. Along with this it supports limited capability devices such as the Arduino infrastructure. The GitHub repository is [here].
BN254
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.

Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- CL Signatures. CL. CL Signatures in Go using MIRACL.
- CL Signatures (advanced pairing). CL. CL Signatures in Go using MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages using MIRACL.
- PS Signatures. PS. Signatures using PS for short signatures using MIRACL.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures using MIRACL.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.

Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
Rust examples
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
NaCl

PyNaCl is a Python port of LibSodium. It integrates the latest cryptography methods, such as AES, XChaCha20, Blake2b and X25519.
Symmetric Key
- Symmetric key. Symmetric key (XChaCha20 and Poly1305). With symmetric key, Bob and Alice have the same key. NaCl uses the XChaCha20 method, and which supports stream encryption (and which does not require padding as a block cipher does, and is also faster than block cipher modes). ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16 byte nonce. XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24 byte nonce. It has a lower propability of nonce misuse than ChaCha20.
- Encryption with a password. Symmetric Key with KDF. In symmetric key, we generate a secret key. This key is typically a random value or generated from a password and a salt value. If we use a password, we typically use a KDF (Key Derivation Function), and which uses a password and a salt value, in order to create a key of a given size. In this case we will use Argon2i, and which is memory resilent.
Hybrid Encryption
- Box. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Hashing
- Hashing and KDF (Argon2 and scrypt). Hashing and KDF. This case we will use PyNaCl (Networking and Cryptography) library, and which is a Python binding to libsodium. We will hash a password using SHA-256 and SHA-512, and also create a KDF (Key Derivation Function) using scrypt and Argon2.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
Ed25519
-
Ed25519. Ed25519. Using Ed25519 for digital signatures.
-
Finding Points on Ed25519. X25519 (Points).
In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 (Key Exchange)
- X25519 + BLAKE2b key-exchange. X25519. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
Curve 25519
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
Node.js

Node.js uses the JavaScript programming langauge as its base, and allows for code to be run on a server, rather than in the browser (such as with pure JavaScript). To run a node.js program, we run "node myfile.js", and use NPM to install libraries.
Symmetric key
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
RSA and public key
- RSA Opt imal Asymmetric Encryption Padding (OAEP) using Node.js. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
ECC Keys
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.

Hashing
- Hashing with node.js (All). Hashing. Hashing with node.js.
- Hashing with node.js (Selection). Hashing. Hashing with node.js.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- ECDSA with node.js. ECDSA. ECDSA with node.js.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
Key exchange
- Diffie-Hellman with node.js (random prime). DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method and uses a randomly generated prime number (press the button to generate a new prime).
- Diffie-Hellman with node.js. DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method. Each time the prime number will be fixed for the DH group selected.
- ECDH with node.js. ECDH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Elliptic Curve Diffie Hellman (ECDH) key exchange method.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
Key derivation
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
CryptoJS
- CryptoJS (in node.js). CryptoJS (Node.js). Various crypto methods in the browser.
Bulletproofs
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
Blockchain
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
Proxy encryption
- Proxy Encryption - Encrypting With Public Key, And Decrypt with Private Key. Proxy01. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This page just creates a key pair for Alice, and uses it to encrypt with the public key , and decrypt with the private key.
- Proxy Encryption. Proxy02. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This will go through the full use case of proxy re-encryption.
Tokens
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
Random
- Fortuna with node.js. Fortuna. Fortuna random numbers with node.js.
Other
- FPE with node.js. FPR. FPE with node.js.
- Puny with node.js. Puny. Puny character format with node.js.
Accumulators and Witnesses
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
PGP
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Password Entropy
- Password Entropy with Node.js. Password Entropy. Password entropy measures the strength of a password, and is measured as the number of bits which could represent all of the possibilities. An entropy score of less than 25 identifies a poor password, and between 25 and 50 is a weak password. For 50 to 75 we have a reasonable password, and between 75 and 100 is a very good password. Over 100 is an excellent password. The strength of the password relates to the number of characters used, and also the number of characters in the password.
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
- Homomorphic Encryption with Node.js and BGV. Homomorphic Encryption with Node.js and BFG. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BGV method.
Oblivious Transfer (OT)

Oblivious Transfer allows Bob to select data from Alice, but for Alice not to know which value has been selected.
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
OpenSSH

OpenSSH supports the usage of the SSH protocol. This allows for a remote login. One tool which is uses is ssh-keygen, and which allow for the generation of RSA, DSA and elliptic-curve keys that. These can be used for user and host authentication, such as for GitHub login and Cloud instance login.
OpenSSH
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here].
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
Outline

OpenSSL

OpenSSL is a standard library that implements cryptography.
Symmetric key (Command line)
-
Symmetric Key Encryption (OpenSSL 1.x) [here]. In this case we will create cipher text from OpenSSL 1.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 1.x) [here].In this case we will decrypt cipher text from OpenSSL 1.x using a key derived from a password
-
Symmetric Key Encryption (OpenSSL 3.x) [here]. In this case we will create cipher text from OpenSSL 3.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 3.x) [here].In this case we will decrypt cipher text from OpenSSL 3.x using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password.
Hashing
-
Hashing [here] OpenSSL supports a wide range of hashing methods including BLAKE2b, Gost, MD4, MD5, RMD-160, SHA-1, SHA-3, SHA-256 and SHA-512.
Libre OpenSSL
-
Symmetric Key Encryption using Libre OpenSSL [here]. In this case we will create cipher text from Libre OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption using Libre OpenSSL [here]. In this case we will decrypt ciphertext from Libre OpenSSL using a key derived from a password.
-
Hashing [here] Libre OpenSSL supports a wide range of hashing methods including Gost, MD4, MD5, RMD-160, SHA-1, SHA-256 and SHA-512.
Diffie-Hellman parameter generation
-
DH Parameters with OpenSSL [here]. The Diffie-Hellman (DH) method is perhaps one of the greatest inventions in Cybersecurity, and was created by Whitfield Diffie and Marty Hellman. With the DH method, Bob creates a random value (\(b\)) and Alice also creates a random value (\(a\)). Next Bob computes \(B=g^b \pmod p\) and sends it to Alice. Alice computes \(A=g^a \pmod p\) and sends this to Bob. Bob raises the value of \(A\) to the power of \(b\) and takes \(\pmod p\), and Alice raises \(B\) to the power of \(a\) and takes \(\pmod p\). In the end, they will have the same shared value: \(g^{ab} \pmod p\). This can then be used to derive an encryption key that they can use for a secure tunnel. Overall, \(p\) is the large prime number, and also known as the shared modulus between Bob and Alice.
Key derivation function
-
PBKDF2 key derivation with OpenSSL [here] PBKDF2 (Password Key Derivation Function 2) is a key derivation method. Overall it is relatively slow in its operation and where we take a password, a salt value, hashing method, and a number of iterations, in order to produce a given size of encryption key.
-
HKDF key derivation with OpenSSL [here] HKDF (HMAC Key Derivation function) is used to derive an encryption key from a pass phrase. Initially HKDF creates a pseudorandom key (PRK) using a pass phrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), andalong with a salt value. Next the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys.
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Passwords
-
Password example [here]. This page uses the OpenSSL library hash password generator, which is used in UNIX systems for the hashing of passwords which are contained in /etc/shadow and /etc/passwd. For newer passwords, the "-1" options is used to created the hashed value.
-
Hashed passwords with OpenSSL [here].
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
Public key
-
Generating an ECC key pair with OpenSSL [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)).
-
Generating an RSA key pair with OpenSSL [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2).
-
Generating an RSA key pair with OpenSSL with encryption [here]. This page implements RSA key pair generation with an encrypted key pair. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). In this case we will encrypt the key pair with either 3DES, 128-bit AES, 192-bit AES or 256-bit AES. The same password must be used to encrypt and decrypt.
-
Generate prime with OpenSSL [here]. Prime numbers are important in public key encrytion, and are used with RSA and ECC. For RSA, we generate two prime numbers (\(p\) and \(q\)) and which are multiplied together to create a modulus (\(N\)). If these prime numbers have 512 bit values, the modulus will be a 1,024 bit value. This defines the basic secure of RSA. With elliptic curve we use smaller prime numbers, such as 256-bit values for the secp256k1 curve.
ASN1 parsing
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). We will parse using asn1parse, and reveal the parameters.
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)) [RSA key pair]. We will parse using asn1parse, and reveal the parameters.
- DSA Parameters with asn1parse. DSA parameters with OpenSSL with asn1parse. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA (Digital Signature Algorithm)
- DSA Parameters. DSA parameters with OpenSSL. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
MAC (Message Authentication Code)
- HMAC with OpenSSL. MACs with OpenSSL. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authenticate both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2) and SHA-3. In this case we will use OpenSSL to generate the HMAC value.
- MACs with OpenSSL. MACs with OpenSSL. In the following we will generate MACs for HMAC, GMAC, CMAC, Blake2bmac, Blake2smac, KMAC128 and KMAC256. Overall, we will use an encryption key defined as a hex value for GMAC and CMAC, and a pass phrase for the others. The message is "hello".
Signing
- Digital signing a plaintext message with OpenSSL. Signing with OpenSSL. With digital signing, we can take a message, and create a signature. This normally involves signing with a private key and digital certificate. The signed message can be an a MIME format, and which can be integrated into an email message. In this can we have a 512-bit RSA key pair that will sign a plain text message.
Encrypting emails
- Encrypting an email message in OpenSSL. Encrypting messages with OpenSSL. With public key encryption, we can take a message, and encrypt it with the recipiant's public key. In this can we have a 512-bit RSA public key to encrypt a message.
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Random number generation with OpenSSL
-
Random number generator [here]. Random numbers are important in generating encryption keys and salt values. In this case OpenSSL generates a random number (in a Base64 format) for a given number of bytes.
Outline (C#/Python)
-
Symmetric Key Encryption (C#) [here]. This page uses the OpenSSL library through a C#/.NET wrapper. The DLLs it interfaces to are libeay32.dll and ssleay32.dll. OpenSSL supports a wide range of encryption methods, including 128-bit AES, 192-bit AES, 256-bit AES and Blowfish (bf). Different modes of ECB, CBC, and OFB are implemented. The examples use a default IV of "1234".
-
AES in Python with OpenSSL output [here]
-
Producing OpenSSL AES Encrypted String from C# [here]
Digital Certificates
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
Paillier - Partial Homomorphic Encryption

The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Fundamentals
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier).
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Using RSA
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
Applications
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero knowledge proof. ZKPs. This implements a zero knowledge proof.
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- WPA3: SAE (Simultaneous Authentication of Equals) handshake - DragonFly. WPA3: Dragonfly. WPA3 overcomes the problems of the four-way handshake in WPA2. This overcomes offline dictionary attacks and provides Forward Secrecy (FS). WPA3 uses a SAE (Simultaneous Authentication of Equals) handshake, and which is commonly known as DragonFly. This method has a commit and confirm phase, and uses elliptic curve methods. Figure 1 illustrates these phases, and the corresponding curve operations. In the commit phase, Bob and Alice select two random numbers. Alice generates (\(r_a\),\(m_a\)) and Bob generates (\(r_b\),\(m_b\)). Bob computes (\(s_b = r_b + m_b\)) and then generates \(E_b = −m_b.G\), and sends these to Alice. Alice computes (\(s_a = r_a + m_a\)) and then generates \(E_a = −m_a.G\), and sends these to Bob.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
Verifiable Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Hash to scalar and point
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
CP-ABE
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Lattice cryptography

Latice cryptography is proposed as a post-quantum robust method for public key encryption, especially focused on digital signatures and key exchange mechanisms (KEMs).
Principles
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
NTRU
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- Lattice Encryption: NTRU Key Generation Python). NTRU. Outlines how NTRU operates for key generation.
Homomorphic
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Digital Signatures
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
Public-Key Encryption/Key Exchange
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
Light-weight cryptography

While AES and SHA work well together within computer systems, they struggle in an IoT/embedded world as they take up: too much processing power; too much physical space; and consume too much battery power. So NIST outlines a number of methods which can be used for light-weight cryptography, and which could be useful in IoT and RFID devices [1]. They define the device spectrum as:
- Conventional cryptography. Servers and Desktops. Tablets and smart phones.
- Light-weight cryptography. Embedded Systems. RFID and Sensor Networks.
With embedded systems, we commonly see 8-bit, 16-bit and 32-bit microcontrollers, and which would struggle to cope with real-time demands for conventional cryptography methods. And in the 40+ years since the first 4-bit processor, there is even a strong market for 4-bit processors. RFID and sensor network devices, especially, have limited numbers of gates available for security, and are often highly constrained with the power drain on the device.
So AES is typically a non-starter for many embedded devices. In light-weight cryptography, we often see smaller block size (typically 64 bits or 80 bits), smaller keys (often less than 90 bits) and less complex rounds (and where the S-boxes often just have 4-bits).
For light-weight cryptography the main constraints that we have are typically related to ener requirements, gate equivalents (GEs), and timing. With passive RFID devices, we do not have an associated battery for the power supply, and where the chip must power itself from energy coupled from the radio wave. An RFID device is thus likely to be severely constrained in the power drain associated with any cryptography functions, along with being constrained for the timing requirements and for the number of gates used. Even if an RFID device has an associated battery (active RFID), it may be difficult to recharge the battery, so the drain on power must often be minimised.
There is thus often a compromise between the cryptography method used and the overall security of the method. Thus often light-weight cryptography methods balance performance (throughput) against power drain and GE, and do not perform as well as main-stream cryptography standards (such as AES and SHA-256). Along with this the method must also have a low requirement for RAM (where the method requires the usage of running memory to perform its operation) and ROM (where the method is stored on the device). In order to assess the strengths of various methods we often define the area that the cryptography function will use on the device – and which is defined in \(µm^2\). The NIST finalists are defined in this [article]
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- GIFT AEAD. GIFT. GIFT is a light-weight block cipher. It is a (NIST Finalist)
- Elephant. Elephant. Elephant is a light-weight stream cipher. It is a (NIST Finalist).
- TinyJambu. TinyJambu. TinyJambu is a light-weight block cipher. It is a (NIST Finalist)
- Isap AEAD. Isap. Isap is a light-weight block cipher. It is a (NIST Finalist)
- PHOTON-Beetle AEAD. PHOTON-Beetle. PHOTON-Beetle is a light-weight block cipher. It is a (NIST Finalist)
- Romulus AEAD. Romulus. Romulus is a light-weight block cipher. It is a (NIST Finalist)
- Sparkle AEAD. Sparkle. Sparkle is a light-weight block cipher. It is a (NIST Finalist)
- CLEFIA. CLEFIA. CLEFIA is a light-weight block cipher.
- LED. LED. LED is a light-weight block cipher.
- Piccolo. Piccolo. Piccolo is an ultra light-weight block cipher.
- PRESENT. PRESENT. Present is a light-weight block cipher.
- Pyjamask. Pyjamask. Pyjamask is a light-weight block cipher.
- SIMON. SIMON. SIMON is a light-weight block cipher.
- SKINNY. SKINNY. SKINNEY is a light-weight block cipher.
- SPECK. SPECK. SPECK is a light-weight block cipher.
- XTEA. XTEA. XTEA is a light-weight block cipher.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encryption/Decryption. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.
Light-weight crypto (Other)
- Chaskey (MAC). Chaskey. Chaskey is a light-weight MAC function.
- Chaskey (MAC). Chaskey (Python). Chaskey is a light-weight MAC function.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (ASCON)
ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRFF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
Discrete Logs (Solving)

A discrete log problem is in the form of \(g^x \pmod p\) and where we know \(g\) and \(p\) and must solve for \(x\).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Message Authentication Code (MAC)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
HMAC
The following are the tips related to Key-based hashing:
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authentication both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2), Blake2b, SM3 and SHA-3. This page outlines the HMAC-MD5 methods using the Hazmat cryptography layer.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- HMAC (COSE). Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT with HMMAC. Go. In this case we create a CWT token, and sign with an HMAC signature.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- HMAC with Rust. HMAC. HMAC with Rust.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HMAC with OpenSSL. MACs with OpenSSL. HMAC in OpenSSL for a given input value, password and hashing method.
Cipher MACs
The following are the tips related to Key-based hashing:
- MACs with OpenSSL. MACs with OpenSSL. MAC methods implemented in OpenSSL, including CMAC and GMAC.
Key-based hashing
The following are the tips related to Key-based hashing:
- SipHash. Siphash. Siphash is a fast key-based hashing method.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Meow. Meow. Meow is one of the fastest hashing methods.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
Magic Numbers

This pages contains information related to magic numbers in file formats.
Network and File Forensics
- Magic numbers. Magic. This provides information on magic number for file forensics.
Graphics formats
- JPEG Analysis. JPEGs. This provides an analysis of JPEG files.
- GIF Analysis. GIFs. This provides an analysis of GIF files.
- TIF Analysis. TIFs. This provides an analysis of TIF files.
- PNG Analysis. PNGs. This provides an analysis of PNG files.
- BMP Analysis. BMPs. This provides an analysis of BMP files.
- PSD Analysis. PSDs. This provides an analysis of PSD files.
- WMF Analysis. WMF. This provides an analysis of WMF files.
- Adobe Illustrator Analysis. AI. This provides an analysis of AI files.
- Adobe In Design Analysis. INDD. This provides an analysis of INDD files.
- MIDI file. MIDI. This provides an analysis of MID files.
- ICO file. ICO. This provides an analysis of ICO files.
- PS file. PS. This provides an analysis of PS files.
- EPS file. EPS. This provides an analysis of EPS files.
- VSD file. VSD. This provides an analysis of Microsft Visio (VSD) files.
Video and audio formats
- MP3 Analysis. MP3s. This provides an analysis of MP3 files.
- AVI Analysis. AVIs. This provides an analysis of AVI files.
- Flash SWF Analysis. SWFs. This provides an analysis of Flash files.
- Flash FLV Analysis. FLVs. This provides an analysis of FLV files.
- MP4 Analysis. MP4. This provides an analysis of MP4 files.
- MOV Analysis. MOV. This provides an analysis of MOV files.
- WMV Analysis. WMV. This provides an analysis of WMV files.
- WMA Analysis. WMA. This provides an analysis of WMA files.
- JPEG 2000 Analysis. JPEG 2. This provides an analysis of JPEG 2000 files.
- WAV Analysis. WAV. This provides an analysis of WAV files.
Zips, Archives and Library files
- ZIP/Archive Analysis. ZIPs. This provides an analysis of ZIP/Achive files.
- GZ Analysis. GZ. This provides an analysis of GZip files.
- Tar Analysis. Tar. This provides an analysis of TAR files.
- MSI Analysis. MSI. This provides an analysis of MSI files.
- OBJ Analysis. OBJ. This provides an analysis of OBJ files.
- DLL Analysis. DLL. This provides an analysis of DLL files.
- CAB Analysis. CAB. This provides an analysis of CAB files.
- EXE Analysis. EXE. This provides an analysis of EXE files.
- RAR Analysis. RAR. This provides an analysis of RAR files.
- SYS Analysis. SYS. This provides an analysis of SYS files.
- HLP Analysis. HLP. This provides an analysis of HLP files.
- VMDK Analysis. VMDK. This provides an analysis of VMDK files (VMWare Virtual Disks).
- PST Analysis. PST. This provides an analysis of PST files (Outlook Email File).
- JAR Analysis. JAR. This provides an analysis of JAR files.
- SLN Analysis. SLN. This provides an analysis of Microsoft SLN files.
- Class Analysis. Class. This provides an analysis of Java Class files.
- Zlib. Zlib. This provides an analysis of Zlib files.
Documents
- PDF Analysis. PDFs. This provides an analysis of PDF files.
- DOC Analysis. DOCs. This provides an analysis of DOC files.
- RTF Analysis. RTFs. This provides an analysis of RTF files.
- XLS Analysis. XLSs. This provides an analysis of XLS files.
- PPT Analysis. PPTs. This provides an analysis of PPT files.
- MMP File. MMP. This provides an analysis of MMP files.
- DOCX Analysis. DOCX. This provides an analysis of DOCX files.
- XLSX Analysis. XLSX. This provides an analysis of XLSX files.
- PPTX Analysis. PPTX. This provides an analysis of PPTX files.
- MDB Analysis. MDB. This provides an analysis of MDB files.
- Outlook Message Analysis. MSG. This provides an analysis of MSG files.
Disk Image
- Raw disk format. RAW. This provides an analysis of the RAW disk format.
Tests
- File Forensics Test. File Test File Forensics Test.
- File Forensics Test (Fun). File Test (Fun) File Forensics Test.
Presentations
MIRACL Core Library

MIRACL Core is an open source library, and includes a wide range of public key encryption methods. It is especially focused on elliptic curve and pairing-friendly methods, but also supports a wide range of encryption methods, including RSA, AES and hashing. Overall, it can be ported onto a wide range of systems and supports C, C++, Go, Rust, Python, Java, Javascript and Swift. Along with this it supports limited capability devices such as the Arduino infrastructure. The GitHub repository is [here].
BN254
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.

Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- CL Signatures. CL. CL Signatures in Go using MIRACL.
- CL Signatures (advanced pairing). CL. CL Signatures in Go using MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages using MIRACL.
- PS Signatures. PS. Signatures using PS for short signatures using MIRACL.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures using MIRACL.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.

Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
Rust examples
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
NaCl

PyNaCl is a Python port of LibSodium. It integrates the latest cryptography methods, such as AES, XChaCha20, Blake2b and X25519.
Symmetric Key
- Symmetric key. Symmetric key (XChaCha20 and Poly1305). With symmetric key, Bob and Alice have the same key. NaCl uses the XChaCha20 method, and which supports stream encryption (and which does not require padding as a block cipher does, and is also faster than block cipher modes). ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16 byte nonce. XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24 byte nonce. It has a lower propability of nonce misuse than ChaCha20.
- Encryption with a password. Symmetric Key with KDF. In symmetric key, we generate a secret key. This key is typically a random value or generated from a password and a salt value. If we use a password, we typically use a KDF (Key Derivation Function), and which uses a password and a salt value, in order to create a key of a given size. In this case we will use Argon2i, and which is memory resilent.
Hybrid Encryption
- Box. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Hashing
- Hashing and KDF (Argon2 and scrypt). Hashing and KDF. This case we will use PyNaCl (Networking and Cryptography) library, and which is a Python binding to libsodium. We will hash a password using SHA-256 and SHA-512, and also create a KDF (Key Derivation Function) using scrypt and Argon2.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
Ed25519
-
Ed25519. Ed25519. Using Ed25519 for digital signatures.
-
Finding Points on Ed25519. X25519 (Points).
In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 (Key Exchange)
- X25519 + BLAKE2b key-exchange. X25519. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
Curve 25519
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
Node.js

Node.js uses the JavaScript programming langauge as its base, and allows for code to be run on a server, rather than in the browser (such as with pure JavaScript). To run a node.js program, we run "node myfile.js", and use NPM to install libraries.
Symmetric key
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
RSA and public key
- RSA Opt imal Asymmetric Encryption Padding (OAEP) using Node.js. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
ECC Keys
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.

Hashing
- Hashing with node.js (All). Hashing. Hashing with node.js.
- Hashing with node.js (Selection). Hashing. Hashing with node.js.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- ECDSA with node.js. ECDSA. ECDSA with node.js.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
Key exchange
- Diffie-Hellman with node.js (random prime). DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method and uses a randomly generated prime number (press the button to generate a new prime).
- Diffie-Hellman with node.js. DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method. Each time the prime number will be fixed for the DH group selected.
- ECDH with node.js. ECDH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Elliptic Curve Diffie Hellman (ECDH) key exchange method.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
Key derivation
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
CryptoJS
- CryptoJS (in node.js). CryptoJS (Node.js). Various crypto methods in the browser.
Bulletproofs
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
Blockchain
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
Proxy encryption
- Proxy Encryption - Encrypting With Public Key, And Decrypt with Private Key. Proxy01. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This page just creates a key pair for Alice, and uses it to encrypt with the public key , and decrypt with the private key.
- Proxy Encryption. Proxy02. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This will go through the full use case of proxy re-encryption.
Tokens
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
Random
- Fortuna with node.js. Fortuna. Fortuna random numbers with node.js.
Other
- FPE with node.js. FPR. FPE with node.js.
- Puny with node.js. Puny. Puny character format with node.js.
Accumulators and Witnesses
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
PGP
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Password Entropy
- Password Entropy with Node.js. Password Entropy. Password entropy measures the strength of a password, and is measured as the number of bits which could represent all of the possibilities. An entropy score of less than 25 identifies a poor password, and between 25 and 50 is a weak password. For 50 to 75 we have a reasonable password, and between 75 and 100 is a very good password. Over 100 is an excellent password. The strength of the password relates to the number of characters used, and also the number of characters in the password.
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
- Homomorphic Encryption with Node.js and BGV. Homomorphic Encryption with Node.js and BFG. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BGV method.
Oblivious Transfer (OT)

Oblivious Transfer allows Bob to select data from Alice, but for Alice not to know which value has been selected.
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
OpenSSH

OpenSSH supports the usage of the SSH protocol. This allows for a remote login. One tool which is uses is ssh-keygen, and which allow for the generation of RSA, DSA and elliptic-curve keys that. These can be used for user and host authentication, such as for GitHub login and Cloud instance login.
OpenSSH
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here].
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
Outline

OpenSSL

OpenSSL is a standard library that implements cryptography.
Symmetric key (Command line)
-
Symmetric Key Encryption (OpenSSL 1.x) [here]. In this case we will create cipher text from OpenSSL 1.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 1.x) [here].In this case we will decrypt cipher text from OpenSSL 1.x using a key derived from a password
-
Symmetric Key Encryption (OpenSSL 3.x) [here]. In this case we will create cipher text from OpenSSL 3.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 3.x) [here].In this case we will decrypt cipher text from OpenSSL 3.x using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password.
Hashing
-
Hashing [here] OpenSSL supports a wide range of hashing methods including BLAKE2b, Gost, MD4, MD5, RMD-160, SHA-1, SHA-3, SHA-256 and SHA-512.
Libre OpenSSL
-
Symmetric Key Encryption using Libre OpenSSL [here]. In this case we will create cipher text from Libre OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption using Libre OpenSSL [here]. In this case we will decrypt ciphertext from Libre OpenSSL using a key derived from a password.
-
Hashing [here] Libre OpenSSL supports a wide range of hashing methods including Gost, MD4, MD5, RMD-160, SHA-1, SHA-256 and SHA-512.
Diffie-Hellman parameter generation
-
DH Parameters with OpenSSL [here]. The Diffie-Hellman (DH) method is perhaps one of the greatest inventions in Cybersecurity, and was created by Whitfield Diffie and Marty Hellman. With the DH method, Bob creates a random value (\(b\)) and Alice also creates a random value (\(a\)). Next Bob computes \(B=g^b \pmod p\) and sends it to Alice. Alice computes \(A=g^a \pmod p\) and sends this to Bob. Bob raises the value of \(A\) to the power of \(b\) and takes \(\pmod p\), and Alice raises \(B\) to the power of \(a\) and takes \(\pmod p\). In the end, they will have the same shared value: \(g^{ab} \pmod p\). This can then be used to derive an encryption key that they can use for a secure tunnel. Overall, \(p\) is the large prime number, and also known as the shared modulus between Bob and Alice.
Key derivation function
-
PBKDF2 key derivation with OpenSSL [here] PBKDF2 (Password Key Derivation Function 2) is a key derivation method. Overall it is relatively slow in its operation and where we take a password, a salt value, hashing method, and a number of iterations, in order to produce a given size of encryption key.
-
HKDF key derivation with OpenSSL [here] HKDF (HMAC Key Derivation function) is used to derive an encryption key from a pass phrase. Initially HKDF creates a pseudorandom key (PRK) using a pass phrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), andalong with a salt value. Next the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys.
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Passwords
-
Password example [here]. This page uses the OpenSSL library hash password generator, which is used in UNIX systems for the hashing of passwords which are contained in /etc/shadow and /etc/passwd. For newer passwords, the "-1" options is used to created the hashed value.
-
Hashed passwords with OpenSSL [here].
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
Public key
-
Generating an ECC key pair with OpenSSL [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)).
-
Generating an RSA key pair with OpenSSL [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2).
-
Generating an RSA key pair with OpenSSL with encryption [here]. This page implements RSA key pair generation with an encrypted key pair. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). In this case we will encrypt the key pair with either 3DES, 128-bit AES, 192-bit AES or 256-bit AES. The same password must be used to encrypt and decrypt.
-
Generate prime with OpenSSL [here]. Prime numbers are important in public key encrytion, and are used with RSA and ECC. For RSA, we generate two prime numbers (\(p\) and \(q\)) and which are multiplied together to create a modulus (\(N\)). If these prime numbers have 512 bit values, the modulus will be a 1,024 bit value. This defines the basic secure of RSA. With elliptic curve we use smaller prime numbers, such as 256-bit values for the secp256k1 curve.
ASN1 parsing
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). We will parse using asn1parse, and reveal the parameters.
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)) [RSA key pair]. We will parse using asn1parse, and reveal the parameters.
- DSA Parameters with asn1parse. DSA parameters with OpenSSL with asn1parse. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA (Digital Signature Algorithm)
- DSA Parameters. DSA parameters with OpenSSL. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
MAC (Message Authentication Code)
- HMAC with OpenSSL. MACs with OpenSSL. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authenticate both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2) and SHA-3. In this case we will use OpenSSL to generate the HMAC value.
- MACs with OpenSSL. MACs with OpenSSL. In the following we will generate MACs for HMAC, GMAC, CMAC, Blake2bmac, Blake2smac, KMAC128 and KMAC256. Overall, we will use an encryption key defined as a hex value for GMAC and CMAC, and a pass phrase for the others. The message is "hello".
Signing
- Digital signing a plaintext message with OpenSSL. Signing with OpenSSL. With digital signing, we can take a message, and create a signature. This normally involves signing with a private key and digital certificate. The signed message can be an a MIME format, and which can be integrated into an email message. In this can we have a 512-bit RSA key pair that will sign a plain text message.
Encrypting emails
- Encrypting an email message in OpenSSL. Encrypting messages with OpenSSL. With public key encryption, we can take a message, and encrypt it with the recipiant's public key. In this can we have a 512-bit RSA public key to encrypt a message.
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Random number generation with OpenSSL
-
Random number generator [here]. Random numbers are important in generating encryption keys and salt values. In this case OpenSSL generates a random number (in a Base64 format) for a given number of bytes.
Outline (C#/Python)
-
Symmetric Key Encryption (C#) [here]. This page uses the OpenSSL library through a C#/.NET wrapper. The DLLs it interfaces to are libeay32.dll and ssleay32.dll. OpenSSL supports a wide range of encryption methods, including 128-bit AES, 192-bit AES, 256-bit AES and Blowfish (bf). Different modes of ECB, CBC, and OFB are implemented. The examples use a default IV of "1234".
-
AES in Python with OpenSSL output [here]
-
Producing OpenSSL AES Encrypted String from C# [here]
Digital Certificates
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
Paillier - Partial Homomorphic Encryption

The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Fundamentals
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier).
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Using RSA
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
Applications
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Hash to scalar and point
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
CP-ABE
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Lattice cryptography

Latice cryptography is proposed as a post-quantum robust method for public key encryption, especially focused on digital signatures and key exchange mechanisms (KEMs).
Principles
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
NTRU
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- Lattice Encryption: NTRU Key Generation Python). NTRU. Outlines how NTRU operates for key generation.
Homomorphic
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Digital Signatures
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
Public-Key Encryption/Key Exchange
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
Light-weight cryptography

While AES and SHA work well together within computer systems, they struggle in an IoT/embedded world as they take up: too much processing power; too much physical space; and consume too much battery power. So NIST outlines a number of methods which can be used for light-weight cryptography, and which could be useful in IoT and RFID devices [1]. They define the device spectrum as:
- Conventional cryptography. Servers and Desktops. Tablets and smart phones.
- Light-weight cryptography. Embedded Systems. RFID and Sensor Networks.
With embedded systems, we commonly see 8-bit, 16-bit and 32-bit microcontrollers, and which would struggle to cope with real-time demands for conventional cryptography methods. And in the 40+ years since the first 4-bit processor, there is even a strong market for 4-bit processors. RFID and sensor network devices, especially, have limited numbers of gates available for security, and are often highly constrained with the power drain on the device.
So AES is typically a non-starter for many embedded devices. In light-weight cryptography, we often see smaller block size (typically 64 bits or 80 bits), smaller keys (often less than 90 bits) and less complex rounds (and where the S-boxes often just have 4-bits).
For light-weight cryptography the main constraints that we have are typically related to ener requirements, gate equivalents (GEs), and timing. With passive RFID devices, we do not have an associated battery for the power supply, and where the chip must power itself from energy coupled from the radio wave. An RFID device is thus likely to be severely constrained in the power drain associated with any cryptography functions, along with being constrained for the timing requirements and for the number of gates used. Even if an RFID device has an associated battery (active RFID), it may be difficult to recharge the battery, so the drain on power must often be minimised.
There is thus often a compromise between the cryptography method used and the overall security of the method. Thus often light-weight cryptography methods balance performance (throughput) against power drain and GE, and do not perform as well as main-stream cryptography standards (such as AES and SHA-256). Along with this the method must also have a low requirement for RAM (where the method requires the usage of running memory to perform its operation) and ROM (where the method is stored on the device). In order to assess the strengths of various methods we often define the area that the cryptography function will use on the device – and which is defined in \(µm^2\). The NIST finalists are defined in this [article]
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- GIFT AEAD. GIFT. GIFT is a light-weight block cipher. It is a (NIST Finalist)
- Elephant. Elephant. Elephant is a light-weight stream cipher. It is a (NIST Finalist).
- TinyJambu. TinyJambu. TinyJambu is a light-weight block cipher. It is a (NIST Finalist)
- Isap AEAD. Isap. Isap is a light-weight block cipher. It is a (NIST Finalist)
- PHOTON-Beetle AEAD. PHOTON-Beetle. PHOTON-Beetle is a light-weight block cipher. It is a (NIST Finalist)
- Romulus AEAD. Romulus. Romulus is a light-weight block cipher. It is a (NIST Finalist)
- Sparkle AEAD. Sparkle. Sparkle is a light-weight block cipher. It is a (NIST Finalist)
- CLEFIA. CLEFIA. CLEFIA is a light-weight block cipher.
- LED. LED. LED is a light-weight block cipher.
- Piccolo. Piccolo. Piccolo is an ultra light-weight block cipher.
- PRESENT. PRESENT. Present is a light-weight block cipher.
- Pyjamask. Pyjamask. Pyjamask is a light-weight block cipher.
- SIMON. SIMON. SIMON is a light-weight block cipher.
- SKINNY. SKINNY. SKINNEY is a light-weight block cipher.
- SPECK. SPECK. SPECK is a light-weight block cipher.
- XTEA. XTEA. XTEA is a light-weight block cipher.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encryption/Decryption. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.
Light-weight crypto (Other)
- Chaskey (MAC). Chaskey. Chaskey is a light-weight MAC function.
- Chaskey (MAC). Chaskey (Python). Chaskey is a light-weight MAC function.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (ASCON)
ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRFF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
Discrete Logs (Solving)

A discrete log problem is in the form of \(g^x \pmod p\) and where we know \(g\) and \(p\) and must solve for \(x\).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Message Authentication Code (MAC)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
HMAC
The following are the tips related to Key-based hashing:
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authentication both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2), Blake2b, SM3 and SHA-3. This page outlines the HMAC-MD5 methods using the Hazmat cryptography layer.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- HMAC (COSE). Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT with HMMAC. Go. In this case we create a CWT token, and sign with an HMAC signature.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- HMAC with Rust. HMAC. HMAC with Rust.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HMAC with OpenSSL. MACs with OpenSSL. HMAC in OpenSSL for a given input value, password and hashing method.
Cipher MACs
The following are the tips related to Key-based hashing:
- MACs with OpenSSL. MACs with OpenSSL. MAC methods implemented in OpenSSL, including CMAC and GMAC.
Key-based hashing
The following are the tips related to Key-based hashing:
- SipHash. Siphash. Siphash is a fast key-based hashing method.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Meow. Meow. Meow is one of the fastest hashing methods.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
Magic Numbers

This pages contains information related to magic numbers in file formats.
Network and File Forensics
- Magic numbers. Magic. This provides information on magic number for file forensics.
Graphics formats
- JPEG Analysis. JPEGs. This provides an analysis of JPEG files.
- GIF Analysis. GIFs. This provides an analysis of GIF files.
- TIF Analysis. TIFs. This provides an analysis of TIF files.
- PNG Analysis. PNGs. This provides an analysis of PNG files.
- BMP Analysis. BMPs. This provides an analysis of BMP files.
- PSD Analysis. PSDs. This provides an analysis of PSD files.
- WMF Analysis. WMF. This provides an analysis of WMF files.
- Adobe Illustrator Analysis. AI. This provides an analysis of AI files.
- Adobe In Design Analysis. INDD. This provides an analysis of INDD files.
- MIDI file. MIDI. This provides an analysis of MID files.
- ICO file. ICO. This provides an analysis of ICO files.
- PS file. PS. This provides an analysis of PS files.
- EPS file. EPS. This provides an analysis of EPS files.
- VSD file. VSD. This provides an analysis of Microsft Visio (VSD) files.
Video and audio formats
- MP3 Analysis. MP3s. This provides an analysis of MP3 files.
- AVI Analysis. AVIs. This provides an analysis of AVI files.
- Flash SWF Analysis. SWFs. This provides an analysis of Flash files.
- Flash FLV Analysis. FLVs. This provides an analysis of FLV files.
- MP4 Analysis. MP4. This provides an analysis of MP4 files.
- MOV Analysis. MOV. This provides an analysis of MOV files.
- WMV Analysis. WMV. This provides an analysis of WMV files.
- WMA Analysis. WMA. This provides an analysis of WMA files.
- JPEG 2000 Analysis. JPEG 2. This provides an analysis of JPEG 2000 files.
- WAV Analysis. WAV. This provides an analysis of WAV files.
Zips, Archives and Library files
- ZIP/Archive Analysis. ZIPs. This provides an analysis of ZIP/Achive files.
- GZ Analysis. GZ. This provides an analysis of GZip files.
- Tar Analysis. Tar. This provides an analysis of TAR files.
- MSI Analysis. MSI. This provides an analysis of MSI files.
- OBJ Analysis. OBJ. This provides an analysis of OBJ files.
- DLL Analysis. DLL. This provides an analysis of DLL files.
- CAB Analysis. CAB. This provides an analysis of CAB files.
- EXE Analysis. EXE. This provides an analysis of EXE files.
- RAR Analysis. RAR. This provides an analysis of RAR files.
- SYS Analysis. SYS. This provides an analysis of SYS files.
- HLP Analysis. HLP. This provides an analysis of HLP files.
- VMDK Analysis. VMDK. This provides an analysis of VMDK files (VMWare Virtual Disks).
- PST Analysis. PST. This provides an analysis of PST files (Outlook Email File).
- JAR Analysis. JAR. This provides an analysis of JAR files.
- SLN Analysis. SLN. This provides an analysis of Microsoft SLN files.
- Class Analysis. Class. This provides an analysis of Java Class files.
- Zlib. Zlib. This provides an analysis of Zlib files.
Documents
- PDF Analysis. PDFs. This provides an analysis of PDF files.
- DOC Analysis. DOCs. This provides an analysis of DOC files.
- RTF Analysis. RTFs. This provides an analysis of RTF files.
- XLS Analysis. XLSs. This provides an analysis of XLS files.
- PPT Analysis. PPTs. This provides an analysis of PPT files.
- MMP File. MMP. This provides an analysis of MMP files.
- DOCX Analysis. DOCX. This provides an analysis of DOCX files.
- XLSX Analysis. XLSX. This provides an analysis of XLSX files.
- PPTX Analysis. PPTX. This provides an analysis of PPTX files.
- MDB Analysis. MDB. This provides an analysis of MDB files.
- Outlook Message Analysis. MSG. This provides an analysis of MSG files.
Disk Image
- Raw disk format. RAW. This provides an analysis of the RAW disk format.
Tests
- File Forensics Test. File Test File Forensics Test.
- File Forensics Test (Fun). File Test (Fun) File Forensics Test.
Presentations
MIRACL Core Library

MIRACL Core is an open source library, and includes a wide range of public key encryption methods. It is especially focused on elliptic curve and pairing-friendly methods, but also supports a wide range of encryption methods, including RSA, AES and hashing. Overall, it can be ported onto a wide range of systems and supports C, C++, Go, Rust, Python, Java, Javascript and Swift. Along with this it supports limited capability devices such as the Arduino infrastructure. The GitHub repository is [here].
BN254
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.

Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- CL Signatures. CL. CL Signatures in Go using MIRACL.
- CL Signatures (advanced pairing). CL. CL Signatures in Go using MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages using MIRACL.
- PS Signatures. PS. Signatures using PS for short signatures using MIRACL.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures using MIRACL.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.

Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
Rust examples
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
NaCl

PyNaCl is a Python port of LibSodium. It integrates the latest cryptography methods, such as AES, XChaCha20, Blake2b and X25519.
Symmetric Key
- Symmetric key. Symmetric key (XChaCha20 and Poly1305). With symmetric key, Bob and Alice have the same key. NaCl uses the XChaCha20 method, and which supports stream encryption (and which does not require padding as a block cipher does, and is also faster than block cipher modes). ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16 byte nonce. XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24 byte nonce. It has a lower propability of nonce misuse than ChaCha20.
- Encryption with a password. Symmetric Key with KDF. In symmetric key, we generate a secret key. This key is typically a random value or generated from a password and a salt value. If we use a password, we typically use a KDF (Key Derivation Function), and which uses a password and a salt value, in order to create a key of a given size. In this case we will use Argon2i, and which is memory resilent.
Hybrid Encryption
- Box. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Hashing
- Hashing and KDF (Argon2 and scrypt). Hashing and KDF. This case we will use PyNaCl (Networking and Cryptography) library, and which is a Python binding to libsodium. We will hash a password using SHA-256 and SHA-512, and also create a KDF (Key Derivation Function) using scrypt and Argon2.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
Ed25519
-
Ed25519. Ed25519. Using Ed25519 for digital signatures.
-
Finding Points on Ed25519. X25519 (Points).
In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 (Key Exchange)
- X25519 + BLAKE2b key-exchange. X25519. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
Curve 25519
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
Node.js

Node.js uses the JavaScript programming langauge as its base, and allows for code to be run on a server, rather than in the browser (such as with pure JavaScript). To run a node.js program, we run "node myfile.js", and use NPM to install libraries.
Symmetric key
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
RSA and public key
- RSA Opt imal Asymmetric Encryption Padding (OAEP) using Node.js. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
ECC Keys
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.

Hashing
- Hashing with node.js (All). Hashing. Hashing with node.js.
- Hashing with node.js (Selection). Hashing. Hashing with node.js.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- ECDSA with node.js. ECDSA. ECDSA with node.js.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
Key exchange
- Diffie-Hellman with node.js (random prime). DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method and uses a randomly generated prime number (press the button to generate a new prime).
- Diffie-Hellman with node.js. DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method. Each time the prime number will be fixed for the DH group selected.
- ECDH with node.js. ECDH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Elliptic Curve Diffie Hellman (ECDH) key exchange method.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
Key derivation
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
CryptoJS
- CryptoJS (in node.js). CryptoJS (Node.js). Various crypto methods in the browser.
Bulletproofs
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
Blockchain
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
Proxy encryption
- Proxy Encryption - Encrypting With Public Key, And Decrypt with Private Key. Proxy01. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This page just creates a key pair for Alice, and uses it to encrypt with the public key , and decrypt with the private key.
- Proxy Encryption. Proxy02. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This will go through the full use case of proxy re-encryption.
Tokens
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
Random
- Fortuna with node.js. Fortuna. Fortuna random numbers with node.js.
Other
- FPE with node.js. FPR. FPE with node.js.
- Puny with node.js. Puny. Puny character format with node.js.
Accumulators and Witnesses
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
PGP
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Password Entropy
- Password Entropy with Node.js. Password Entropy. Password entropy measures the strength of a password, and is measured as the number of bits which could represent all of the possibilities. An entropy score of less than 25 identifies a poor password, and between 25 and 50 is a weak password. For 50 to 75 we have a reasonable password, and between 75 and 100 is a very good password. Over 100 is an excellent password. The strength of the password relates to the number of characters used, and also the number of characters in the password.
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
- Homomorphic Encryption with Node.js and BGV. Homomorphic Encryption with Node.js and BFG. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BGV method.
Oblivious Transfer (OT)

Oblivious Transfer allows Bob to select data from Alice, but for Alice not to know which value has been selected.
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
OpenSSH

OpenSSH supports the usage of the SSH protocol. This allows for a remote login. One tool which is uses is ssh-keygen, and which allow for the generation of RSA, DSA and elliptic-curve keys that. These can be used for user and host authentication, such as for GitHub login and Cloud instance login.
OpenSSH
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here].
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
Outline

OpenSSL

OpenSSL is a standard library that implements cryptography.
Symmetric key (Command line)
-
Symmetric Key Encryption (OpenSSL 1.x) [here]. In this case we will create cipher text from OpenSSL 1.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 1.x) [here].In this case we will decrypt cipher text from OpenSSL 1.x using a key derived from a password
-
Symmetric Key Encryption (OpenSSL 3.x) [here]. In this case we will create cipher text from OpenSSL 3.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 3.x) [here].In this case we will decrypt cipher text from OpenSSL 3.x using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password.
Hashing
-
Hashing [here] OpenSSL supports a wide range of hashing methods including BLAKE2b, Gost, MD4, MD5, RMD-160, SHA-1, SHA-3, SHA-256 and SHA-512.
Libre OpenSSL
-
Symmetric Key Encryption using Libre OpenSSL [here]. In this case we will create cipher text from Libre OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption using Libre OpenSSL [here]. In this case we will decrypt ciphertext from Libre OpenSSL using a key derived from a password.
-
Hashing [here] Libre OpenSSL supports a wide range of hashing methods including Gost, MD4, MD5, RMD-160, SHA-1, SHA-256 and SHA-512.
Diffie-Hellman parameter generation
-
DH Parameters with OpenSSL [here]. The Diffie-Hellman (DH) method is perhaps one of the greatest inventions in Cybersecurity, and was created by Whitfield Diffie and Marty Hellman. With the DH method, Bob creates a random value (\(b\)) and Alice also creates a random value (\(a\)). Next Bob computes \(B=g^b \pmod p\) and sends it to Alice. Alice computes \(A=g^a \pmod p\) and sends this to Bob. Bob raises the value of \(A\) to the power of \(b\) and takes \(\pmod p\), and Alice raises \(B\) to the power of \(a\) and takes \(\pmod p\). In the end, they will have the same shared value: \(g^{ab} \pmod p\). This can then be used to derive an encryption key that they can use for a secure tunnel. Overall, \(p\) is the large prime number, and also known as the shared modulus between Bob and Alice.
Key derivation function
-
PBKDF2 key derivation with OpenSSL [here] PBKDF2 (Password Key Derivation Function 2) is a key derivation method. Overall it is relatively slow in its operation and where we take a password, a salt value, hashing method, and a number of iterations, in order to produce a given size of encryption key.
-
HKDF key derivation with OpenSSL [here] HKDF (HMAC Key Derivation function) is used to derive an encryption key from a pass phrase. Initially HKDF creates a pseudorandom key (PRK) using a pass phrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), andalong with a salt value. Next the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys.
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Passwords
-
Password example [here]. This page uses the OpenSSL library hash password generator, which is used in UNIX systems for the hashing of passwords which are contained in /etc/shadow and /etc/passwd. For newer passwords, the "-1" options is used to created the hashed value.
-
Hashed passwords with OpenSSL [here].
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
Public key
-
Generating an ECC key pair with OpenSSL [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)).
-
Generating an RSA key pair with OpenSSL [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2).
-
Generating an RSA key pair with OpenSSL with encryption [here]. This page implements RSA key pair generation with an encrypted key pair. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). In this case we will encrypt the key pair with either 3DES, 128-bit AES, 192-bit AES or 256-bit AES. The same password must be used to encrypt and decrypt.
-
Generate prime with OpenSSL [here]. Prime numbers are important in public key encrytion, and are used with RSA and ECC. For RSA, we generate two prime numbers (\(p\) and \(q\)) and which are multiplied together to create a modulus (\(N\)). If these prime numbers have 512 bit values, the modulus will be a 1,024 bit value. This defines the basic secure of RSA. With elliptic curve we use smaller prime numbers, such as 256-bit values for the secp256k1 curve.
ASN1 parsing
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). We will parse using asn1parse, and reveal the parameters.
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)) [RSA key pair]. We will parse using asn1parse, and reveal the parameters.
- DSA Parameters with asn1parse. DSA parameters with OpenSSL with asn1parse. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA (Digital Signature Algorithm)
- DSA Parameters. DSA parameters with OpenSSL. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
MAC (Message Authentication Code)
- HMAC with OpenSSL. MACs with OpenSSL. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authenticate both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2) and SHA-3. In this case we will use OpenSSL to generate the HMAC value.
- MACs with OpenSSL. MACs with OpenSSL. In the following we will generate MACs for HMAC, GMAC, CMAC, Blake2bmac, Blake2smac, KMAC128 and KMAC256. Overall, we will use an encryption key defined as a hex value for GMAC and CMAC, and a pass phrase for the others. The message is "hello".
Signing
- Digital signing a plaintext message with OpenSSL. Signing with OpenSSL. With digital signing, we can take a message, and create a signature. This normally involves signing with a private key and digital certificate. The signed message can be an a MIME format, and which can be integrated into an email message. In this can we have a 512-bit RSA key pair that will sign a plain text message.
Encrypting emails
- Encrypting an email message in OpenSSL. Encrypting messages with OpenSSL. With public key encryption, we can take a message, and encrypt it with the recipiant's public key. In this can we have a 512-bit RSA public key to encrypt a message.
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Random number generation with OpenSSL
-
Random number generator [here]. Random numbers are important in generating encryption keys and salt values. In this case OpenSSL generates a random number (in a Base64 format) for a given number of bytes.
Outline (C#/Python)
-
Symmetric Key Encryption (C#) [here]. This page uses the OpenSSL library through a C#/.NET wrapper. The DLLs it interfaces to are libeay32.dll and ssleay32.dll. OpenSSL supports a wide range of encryption methods, including 128-bit AES, 192-bit AES, 256-bit AES and Blowfish (bf). Different modes of ECB, CBC, and OFB are implemented. The examples use a default IV of "1234".
-
AES in Python with OpenSSL output [here]
-
Producing OpenSSL AES Encrypted String from C# [here]
Digital Certificates
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
Paillier - Partial Homomorphic Encryption

The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Fundamentals
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier).
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Using RSA
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
Applications
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Hashing to a scalar and also to a point using Kryptology. Hash to Curve. In ECC (Elliptic Curve Cryptography) we often have to hash our data to a scalar value or to a point on the curve. Once hashed, it is difficult to reverse the operation (unless we did a brute force search for it). In this case we hash a value into a scalar value, and also into a point using the Krytology Golang library.
CP-ABE
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Lattice cryptography

Latice cryptography is proposed as a post-quantum robust method for public key encryption, especially focused on digital signatures and key exchange mechanisms (KEMs).
Principles
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
NTRU
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- Lattice Encryption: NTRU Key Generation Python). NTRU. Outlines how NTRU operates for key generation.
Homomorphic
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Digital Signatures
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
Public-Key Encryption/Key Exchange
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
Light-weight cryptography

While AES and SHA work well together within computer systems, they struggle in an IoT/embedded world as they take up: too much processing power; too much physical space; and consume too much battery power. So NIST outlines a number of methods which can be used for light-weight cryptography, and which could be useful in IoT and RFID devices [1]. They define the device spectrum as:
- Conventional cryptography. Servers and Desktops. Tablets and smart phones.
- Light-weight cryptography. Embedded Systems. RFID and Sensor Networks.
With embedded systems, we commonly see 8-bit, 16-bit and 32-bit microcontrollers, and which would struggle to cope with real-time demands for conventional cryptography methods. And in the 40+ years since the first 4-bit processor, there is even a strong market for 4-bit processors. RFID and sensor network devices, especially, have limited numbers of gates available for security, and are often highly constrained with the power drain on the device.
So AES is typically a non-starter for many embedded devices. In light-weight cryptography, we often see smaller block size (typically 64 bits or 80 bits), smaller keys (often less than 90 bits) and less complex rounds (and where the S-boxes often just have 4-bits).
For light-weight cryptography the main constraints that we have are typically related to ener requirements, gate equivalents (GEs), and timing. With passive RFID devices, we do not have an associated battery for the power supply, and where the chip must power itself from energy coupled from the radio wave. An RFID device is thus likely to be severely constrained in the power drain associated with any cryptography functions, along with being constrained for the timing requirements and for the number of gates used. Even if an RFID device has an associated battery (active RFID), it may be difficult to recharge the battery, so the drain on power must often be minimised.
There is thus often a compromise between the cryptography method used and the overall security of the method. Thus often light-weight cryptography methods balance performance (throughput) against power drain and GE, and do not perform as well as main-stream cryptography standards (such as AES and SHA-256). Along with this the method must also have a low requirement for RAM (where the method requires the usage of running memory to perform its operation) and ROM (where the method is stored on the device). In order to assess the strengths of various methods we often define the area that the cryptography function will use on the device – and which is defined in \(µm^2\). The NIST finalists are defined in this [article]
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- GIFT AEAD. GIFT. GIFT is a light-weight block cipher. It is a (NIST Finalist)
- Elephant. Elephant. Elephant is a light-weight stream cipher. It is a (NIST Finalist).
- TinyJambu. TinyJambu. TinyJambu is a light-weight block cipher. It is a (NIST Finalist)
- Isap AEAD. Isap. Isap is a light-weight block cipher. It is a (NIST Finalist)
- PHOTON-Beetle AEAD. PHOTON-Beetle. PHOTON-Beetle is a light-weight block cipher. It is a (NIST Finalist)
- Romulus AEAD. Romulus. Romulus is a light-weight block cipher. It is a (NIST Finalist)
- Sparkle AEAD. Sparkle. Sparkle is a light-weight block cipher. It is a (NIST Finalist)
- CLEFIA. CLEFIA. CLEFIA is a light-weight block cipher.
- LED. LED. LED is a light-weight block cipher.
- Piccolo. Piccolo. Piccolo is an ultra light-weight block cipher.
- PRESENT. PRESENT. Present is a light-weight block cipher.
- Pyjamask. Pyjamask. Pyjamask is a light-weight block cipher.
- SIMON. SIMON. SIMON is a light-weight block cipher.
- SKINNY. SKINNY. SKINNEY is a light-weight block cipher.
- SPECK. SPECK. SPECK is a light-weight block cipher.
- XTEA. XTEA. XTEA is a light-weight block cipher.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encryption/Decryption. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
-
KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.
Light-weight crypto (Other)
- Chaskey (MAC). Chaskey. Chaskey is a light-weight MAC function.
- Chaskey (MAC). Chaskey (Python). Chaskey is a light-weight MAC function.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (ASCON)
ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRFF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
Discrete Logs (Solving)

A discrete log problem is in the form of \(g^x \pmod p\) and where we know \(g\) and \(p\) and must solve for \(x\).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Message Authentication Code (MAC)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
HMAC
The following are the tips related to Key-based hashing:
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authentication both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2), Blake2b, SM3 and SHA-3. This page outlines the HMAC-MD5 methods using the Hazmat cryptography layer.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
-
HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing
a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the
strength depends on the quality of the hashing function, and the resulting
number of code bits. Along with this the number of bits in the secret
key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- HMAC (COSE). Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT with HMMAC. Go. In this case we create a CWT token, and sign with an HMAC signature.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- HMAC with Rust. HMAC. HMAC with Rust.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HMAC with OpenSSL. MACs with OpenSSL. HMAC in OpenSSL for a given input value, password and hashing method.
Cipher MACs
The following are the tips related to Key-based hashing:
- MACs with OpenSSL. MACs with OpenSSL. MAC methods implemented in OpenSSL, including CMAC and GMAC.
Key-based hashing
The following are the tips related to Key-based hashing:
- SipHash. Siphash. Siphash is a fast key-based hashing method.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Meow. Meow. Meow is one of the fastest hashing methods.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
Magic Numbers

This pages contains information related to magic numbers in file formats.
Network and File Forensics
- Magic numbers. Magic. This provides information on magic number for file forensics.
Graphics formats
- JPEG Analysis. JPEGs. This provides an analysis of JPEG files.
- GIF Analysis. GIFs. This provides an analysis of GIF files.
- TIF Analysis. TIFs. This provides an analysis of TIF files.
- PNG Analysis. PNGs. This provides an analysis of PNG files.
- BMP Analysis. BMPs. This provides an analysis of BMP files.
- PSD Analysis. PSDs. This provides an analysis of PSD files.
- WMF Analysis. WMF. This provides an analysis of WMF files.
- Adobe Illustrator Analysis. AI. This provides an analysis of AI files.
- Adobe In Design Analysis. INDD. This provides an analysis of INDD files.
- MIDI file. MIDI. This provides an analysis of MID files.
- ICO file. ICO. This provides an analysis of ICO files.
- PS file. PS. This provides an analysis of PS files.
- EPS file. EPS. This provides an analysis of EPS files.
- VSD file. VSD. This provides an analysis of Microsft Visio (VSD) files.
Video and audio formats
- MP3 Analysis. MP3s. This provides an analysis of MP3 files.
- AVI Analysis. AVIs. This provides an analysis of AVI files.
- Flash SWF Analysis. SWFs. This provides an analysis of Flash files.
- Flash FLV Analysis. FLVs. This provides an analysis of FLV files.
- MP4 Analysis. MP4. This provides an analysis of MP4 files.
- MOV Analysis. MOV. This provides an analysis of MOV files.
- WMV Analysis. WMV. This provides an analysis of WMV files.
- WMA Analysis. WMA. This provides an analysis of WMA files.
- JPEG 2000 Analysis. JPEG 2. This provides an analysis of JPEG 2000 files.
- WAV Analysis. WAV. This provides an analysis of WAV files.
Zips, Archives and Library files
- ZIP/Archive Analysis. ZIPs. This provides an analysis of ZIP/Achive files.
- GZ Analysis. GZ. This provides an analysis of GZip files.
- Tar Analysis. Tar. This provides an analysis of TAR files.
- MSI Analysis. MSI. This provides an analysis of MSI files.
- OBJ Analysis. OBJ. This provides an analysis of OBJ files.
- DLL Analysis. DLL. This provides an analysis of DLL files.
- CAB Analysis. CAB. This provides an analysis of CAB files.
- EXE Analysis. EXE. This provides an analysis of EXE files.
- RAR Analysis. RAR. This provides an analysis of RAR files.
- SYS Analysis. SYS. This provides an analysis of SYS files.
- HLP Analysis. HLP. This provides an analysis of HLP files.
- VMDK Analysis. VMDK. This provides an analysis of VMDK files (VMWare Virtual Disks).
- PST Analysis. PST. This provides an analysis of PST files (Outlook Email File).
- JAR Analysis. JAR. This provides an analysis of JAR files.
- SLN Analysis. SLN. This provides an analysis of Microsoft SLN files.
- Class Analysis. Class. This provides an analysis of Java Class files.
- Zlib. Zlib. This provides an analysis of Zlib files.
Documents
- PDF Analysis. PDFs. This provides an analysis of PDF files.
- DOC Analysis. DOCs. This provides an analysis of DOC files.
- RTF Analysis. RTFs. This provides an analysis of RTF files.
- XLS Analysis. XLSs. This provides an analysis of XLS files.
- PPT Analysis. PPTs. This provides an analysis of PPT files.
- MMP File. MMP. This provides an analysis of MMP files.
- DOCX Analysis. DOCX. This provides an analysis of DOCX files.
- XLSX Analysis. XLSX. This provides an analysis of XLSX files.
- PPTX Analysis. PPTX. This provides an analysis of PPTX files.
- MDB Analysis. MDB. This provides an analysis of MDB files.
- Outlook Message Analysis. MSG. This provides an analysis of MSG files.
Disk Image
- Raw disk format. RAW. This provides an analysis of the RAW disk format.
Tests
- File Forensics Test. File Test File Forensics Test.
- File Forensics Test (Fun). File Test (Fun) File Forensics Test.
Presentations
MIRACL Core Library

MIRACL Core is an open source library, and includes a wide range of public key encryption methods. It is especially focused on elliptic curve and pairing-friendly methods, but also supports a wide range of encryption methods, including RSA, AES and hashing. Overall, it can be ported onto a wide range of systems and supports C, C++, Go, Rust, Python, Java, Javascript and Swift. Along with this it supports limited capability devices such as the Arduino infrastructure. The GitHub repository is [here].
BN254
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.

Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- CL Signatures. CL. CL Signatures in Go using MIRACL.
- CL Signatures (advanced pairing). CL. CL Signatures in Go using MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages using MIRACL.
- PS Signatures. PS. Signatures using PS for short signatures using MIRACL.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures using MIRACL.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.

Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
Rust examples
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
NaCl

PyNaCl is a Python port of LibSodium. It integrates the latest cryptography methods, such as AES, XChaCha20, Blake2b and X25519.
Symmetric Key
- Symmetric key. Symmetric key (XChaCha20 and Poly1305). With symmetric key, Bob and Alice have the same key. NaCl uses the XChaCha20 method, and which supports stream encryption (and which does not require padding as a block cipher does, and is also faster than block cipher modes). ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16 byte nonce. XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24 byte nonce. It has a lower propability of nonce misuse than ChaCha20.
- Encryption with a password. Symmetric Key with KDF. In symmetric key, we generate a secret key. This key is typically a random value or generated from a password and a salt value. If we use a password, we typically use a KDF (Key Derivation Function), and which uses a password and a salt value, in order to create a key of a given size. In this case we will use Argon2i, and which is memory resilent.
Hybrid Encryption
- Box. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Hashing
- Hashing and KDF (Argon2 and scrypt). Hashing and KDF. This case we will use PyNaCl (Networking and Cryptography) library, and which is a Python binding to libsodium. We will hash a password using SHA-256 and SHA-512, and also create a KDF (Key Derivation Function) using scrypt and Argon2.
-
Key hashing (SipHash). SipHash.
With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
Ed25519
-
Ed25519. Ed25519. Using Ed25519 for digital signatures.
-
Finding Points on Ed25519. X25519 (Points).
In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 (Key Exchange)
- X25519 + BLAKE2b key-exchange. X25519. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
Curve 25519
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
Node.js

Node.js uses the JavaScript programming langauge as its base, and allows for code to be run on a server, rather than in the browser (such as with pure JavaScript). To run a node.js program, we run "node myfile.js", and use NPM to install libraries.
Symmetric key
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
RSA and public key
- RSA Opt imal Asymmetric Encryption Padding (OAEP) using Node.js. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
ECC Keys
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.

Hashing
- Hashing with node.js (All). Hashing. Hashing with node.js.
- Hashing with node.js (Selection). Hashing. Hashing with node.js.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- ECDSA with node.js. ECDSA. ECDSA with node.js.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
Key exchange
- Diffie-Hellman with node.js (random prime). DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method and uses a randomly generated prime number (press the button to generate a new prime).
- Diffie-Hellman with node.js. DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method. Each time the prime number will be fixed for the DH group selected.
- ECDH with node.js. ECDH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Elliptic Curve Diffie Hellman (ECDH) key exchange method.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
Key derivation
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
CryptoJS
- CryptoJS (in node.js). CryptoJS (Node.js). Various crypto methods in the browser.
Bulletproofs
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
Blockchain
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
Proxy encryption
- Proxy Encryption - Encrypting With Public Key, And Decrypt with Private Key. Proxy01. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This page just creates a key pair for Alice, and uses it to encrypt with the public key , and decrypt with the private key.
- Proxy Encryption. Proxy02. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This will go through the full use case of proxy re-encryption.
Tokens
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
Random
- Fortuna with node.js. Fortuna. Fortuna random numbers with node.js.
Other
- FPE with node.js. FPR. FPE with node.js.
- Puny with node.js. Puny. Puny character format with node.js.
Accumulators and Witnesses
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
PGP
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Password Entropy
- Password Entropy with Node.js. Password Entropy. Password entropy measures the strength of a password, and is measured as the number of bits which could represent all of the possibilities. An entropy score of less than 25 identifies a poor password, and between 25 and 50 is a weak password. For 50 to 75 we have a reasonable password, and between 75 and 100 is a very good password. Over 100 is an excellent password. The strength of the password relates to the number of characters used, and also the number of characters in the password.
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
- Homomorphic Encryption with Node.js and BGV. Homomorphic Encryption with Node.js and BFG. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BGV method.
Oblivious Transfer (OT)

Oblivious Transfer allows Bob to select data from Alice, but for Alice not to know which value has been selected.
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
OpenSSH

OpenSSH supports the usage of the SSH protocol. This allows for a remote login. One tool which is uses is ssh-keygen, and which allow for the generation of RSA, DSA and elliptic-curve keys that. These can be used for user and host authentication, such as for GitHub login and Cloud instance login.
OpenSSH
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
-
Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [
here].
-
ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
-
DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
-
DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
Outline

OpenSSL

OpenSSL is a standard library that implements cryptography.
Symmetric key (Command line)
-
Symmetric Key Encryption (OpenSSL 1.x) [here]. In this case we will create cipher text from OpenSSL 1.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 1.x) [here].In this case we will decrypt cipher text from OpenSSL 1.x using a key derived from a password
-
Symmetric Key Encryption (OpenSSL 3.x) [here]. In this case we will create cipher text from OpenSSL 3.x using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption (OpenSSL 3.x) [here].In this case we will decrypt cipher text from OpenSSL 3.x using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password.
Hashing
-
Hashing [here] OpenSSL supports a wide range of hashing methods including BLAKE2b, Gost, MD4, MD5, RMD-160, SHA-1, SHA-3, SHA-256 and SHA-512.
Libre OpenSSL
-
Symmetric Key Encryption using Libre OpenSSL [here]. In this case we will create cipher text from Libre OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption using Libre OpenSSL [here]. In this case we will decrypt ciphertext from Libre OpenSSL using a key derived from a password.
-
Hashing [here] Libre OpenSSL supports a wide range of hashing methods including Gost, MD4, MD5, RMD-160, SHA-1, SHA-256 and SHA-512.
Diffie-Hellman parameter generation
-
DH Parameters with OpenSSL [here]. The Diffie-Hellman (DH) method is perhaps one of the greatest inventions in Cybersecurity, and was created by Whitfield Diffie and Marty Hellman. With the DH method, Bob creates a random value (\(b\)) and Alice also creates a random value (\(a\)). Next Bob computes \(B=g^b \pmod p\) and sends it to Alice. Alice computes \(A=g^a \pmod p\) and sends this to Bob. Bob raises the value of \(A\) to the power of \(b\) and takes \(\pmod p\), and Alice raises \(B\) to the power of \(a\) and takes \(\pmod p\). In the end, they will have the same shared value: \(g^{ab} \pmod p\). This can then be used to derive an encryption key that they can use for a secure tunnel. Overall, \(p\) is the large prime number, and also known as the shared modulus between Bob and Alice.
Key derivation function
-
PBKDF2 key derivation with OpenSSL [here] PBKDF2 (Password Key Derivation Function 2) is a key derivation method. Overall it is relatively slow in its operation and where we take a password, a salt value, hashing method, and a number of iterations, in order to produce a given size of encryption key.
-
HKDF key derivation with OpenSSL [here] HKDF (HMAC Key Derivation function) is used to derive an encryption key from a pass phrase. Initially HKDF creates a pseudorandom key (PRK) using a pass phrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), andalong with a salt value. Next the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys.
-
HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Passwords
-
Password example [here]. This page uses the OpenSSL library hash password generator, which is used in UNIX systems for the hashing of passwords which are contained in /etc/shadow and /etc/passwd. For newer passwords, the "-1" options is used to created the hashed value.
-
Hashed passwords with OpenSSL [here].
-
Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
Public key
-
Generating an ECC key pair with OpenSSL [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)).
-
Generating an RSA key pair with OpenSSL [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2).
-
Generating an RSA key pair with OpenSSL with encryption [here]. This page implements RSA key pair generation with an encrypted key pair. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). In this case we will encrypt the key pair with either 3DES, 128-bit AES, 192-bit AES or 256-bit AES. The same password must be used to encrypt and decrypt.
-
Generate prime with OpenSSL [here]. Prime numbers are important in public key encrytion, and are used with RSA and ECC. For RSA, we generate two prime numbers (\(p\) and \(q\)) and which are multiplied together to create a modulus (\(N\)). If these prime numbers have 512 bit values, the modulus will be a 1,024 bit value. This defines the basic secure of RSA. With elliptic curve we use smaller prime numbers, such as 256-bit values for the secp256k1 curve.
ASN1 parsing
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). We will parse using asn1parse, and reveal the parameters.
-
Generating an RSA key pair with OpenSSL with asn1parse [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)) [RSA key pair]. We will parse using asn1parse, and reveal the parameters.
- DSA Parameters with asn1parse. DSA parameters with OpenSSL with asn1parse. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA (Digital Signature Algorithm)
- DSA Parameters. DSA parameters with OpenSSL. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
MAC (Message Authentication Code)
- HMAC with OpenSSL. MACs with OpenSSL. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authenticate both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2) and SHA-3. In this case we will use OpenSSL to generate the HMAC value.
- MACs with OpenSSL. MACs with OpenSSL. In the following we will generate MACs for HMAC, GMAC, CMAC, Blake2bmac, Blake2smac, KMAC128 and KMAC256. Overall, we will use an encryption key defined as a hex value for GMAC and CMAC, and a pass phrase for the others. The message is "hello".
Signing
- Digital signing a plaintext message with OpenSSL. Signing with OpenSSL. With digital signing, we can take a message, and create a signature. This normally involves signing with a private key and digital certificate. The signed message can be an a MIME format, and which can be integrated into an email message. In this can we have a 512-bit RSA key pair that will sign a plain text message.
Encrypting emails
- Encrypting an email message in OpenSSL. Encrypting messages with OpenSSL. With public key encryption, we can take a message, and encrypt it with the recipiant's public key. In this can we have a 512-bit RSA public key to encrypt a message.
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Random number generation with OpenSSL
-
Random number generator [here]. Random numbers are important in generating encryption keys and salt values. In this case OpenSSL generates a random number (in a Base64 format) for a given number of bytes.
Outline (C#/Python)
-
Symmetric Key Encryption (C#) [here]. This page uses the OpenSSL library through a C#/.NET wrapper. The DLLs it interfaces to are libeay32.dll and ssleay32.dll. OpenSSL supports a wide range of encryption methods, including 128-bit AES, 192-bit AES, 256-bit AES and Blowfish (bf). Different modes of ECB, CBC, and OFB are implemented. The examples use a default IV of "1234".
-
AES in Python with OpenSSL output [here]
-
Producing OpenSSL AES Encrypted String from C# [here]
Digital Certificates
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
Paillier - Partial Homomorphic Encryption

The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Fundamentals
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier).
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Using RSA
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
Applications
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Lattice cryptography

Latice cryptography is proposed as a post-quantum robust method for public key encryption, especially focused on digital signatures and key exchange mechanisms (KEMs).
Principles
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
HEAAN
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers). HEAAN. HEAAN.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Scalar. HEAAN Scalar. HEAAN Scalar.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Subtract. HEAAN Sub. HEAAN Subtract.
- HEAAN (Homomorphic Encryption for Arithmetic of Approximate Numbers) - Homorphonic Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply. HEAAN Add, Subtract and Multiply.
NTRU
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- Lattice Encryption: NTRU Key Generation Python). NTRU. Outlines how NTRU operates for key generation.
Homomorphic
- Lattice Crypto: FV Homomorphic Encryption (Batch). Lattice. FV Homomorphic Encryption (Batch).
- Lattice Crypto: FV Homomorphic Encryption. Lattice. FV Homomorphic Encryption.
Ring LWE
- BGV - (Ring LWE). BGV. Outlines BGV.
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
Digital Signatures
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
Public-Key Encryption/Key Exchange
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
Light-weight cryptography

While AES and SHA work well together within computer systems, they struggle in an IoT/embedded world as they take up: too much processing power; too much physical space; and consume too much battery power. So NIST outlines a number of methods which can be used for light-weight cryptography, and which could be useful in IoT and RFID devices [1]. They define the device spectrum as:
- Conventional cryptography. Servers and Desktops. Tablets and smart phones.
- Light-weight cryptography. Embedded Systems. RFID and Sensor Networks.
With embedded systems, we commonly see 8-bit, 16-bit and 32-bit microcontrollers, and which would struggle to cope with real-time demands for conventional cryptography methods. And in the 40+ years since the first 4-bit processor, there is even a strong market for 4-bit processors. RFID and sensor network devices, especially, have limited numbers of gates available for security, and are often highly constrained with the power drain on the device.
So AES is typically a non-starter for many embedded devices. In light-weight cryptography, we often see smaller block size (typically 64 bits or 80 bits), smaller keys (often less than 90 bits) and less complex rounds (and where the S-boxes often just have 4-bits).
For light-weight cryptography the main constraints that we have are typically related to ener requirements, gate equivalents (GEs), and timing. With passive RFID devices, we do not have an associated battery for the power supply, and where the chip must power itself from energy coupled from the radio wave. An RFID device is thus likely to be severely constrained in the power drain associated with any cryptography functions, along with being constrained for the timing requirements and for the number of gates used. Even if an RFID device has an associated battery (active RFID), it may be difficult to recharge the battery, so the drain on power must often be minimised.
There is thus often a compromise between the cryptography method used and the overall security of the method. Thus often light-weight cryptography methods balance performance (throughput) against power drain and GE, and do not perform as well as main-stream cryptography standards (such as AES and SHA-256). Along with this the method must also have a low requirement for RAM (where the method requires the usage of running memory to perform its operation) and ROM (where the method is stored on the device). In order to assess the strengths of various methods we often define the area that the cryptography function will use on the device – and which is defined in \(µm^2\). The NIST finalists are defined in this [article]
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (Block)
- ASCON AEAD. ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
- GIFT AEAD. GIFT. GIFT is a light-weight block cipher. It is a (NIST Finalist)
- Elephant. Elephant. Elephant is a light-weight stream cipher. It is a (NIST Finalist).
- TinyJambu. TinyJambu. TinyJambu is a light-weight block cipher. It is a (NIST Finalist)
- Isap AEAD. Isap. Isap is a light-weight block cipher. It is a (NIST Finalist)
- PHOTON-Beetle AEAD. PHOTON-Beetle. PHOTON-Beetle is a light-weight block cipher. It is a (NIST Finalist)
- Romulus AEAD. Romulus. Romulus is a light-weight block cipher. It is a (NIST Finalist)
- Sparkle AEAD. Sparkle. Sparkle is a light-weight block cipher. It is a (NIST Finalist)
- CLEFIA. CLEFIA. CLEFIA is a light-weight block cipher.
- LED. LED. LED is a light-weight block cipher.
- Piccolo. Piccolo. Piccolo is an ultra light-weight block cipher.
- PRESENT. PRESENT. Present is a light-weight block cipher.
- Pyjamask. Pyjamask. Pyjamask is a light-weight block cipher.
- SIMON. SIMON. SIMON is a light-weight block cipher.
- SKINNY. SKINNY. SKINNEY is a light-weight block cipher.
- SPECK. SPECK. SPECK is a light-weight block cipher.
- XTEA. XTEA. XTEA is a light-weight block cipher.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encryption/Decryption. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Light-weight crypto (Hash)
- ACE. ACE. ACE is a light-weight hashing method.
- ASCON. ASCON. ASCON is a light-weight hashing method.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Xoodya in Golang Xoodya. In 2022, NIST defined the winner of the PQC (Post Quantum Cryptography) competition. These were Kyber for Key Exchange/Public Key Encryption, and Crystals for Digital Signatures. 2023 will bring the winner of the light-weight cryptography competition that has been running since 2018. Currently, there are 10 finalists: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. This page outlines the Xoodyak cipher.
- KangarooTwelve (Part of Xoodyak submission to NIST). KangarooTwelve. Implements KangarooTwelve (SHA-3 contender).
- KLEIN in Python. KLEIN. KLEIN is a light-weight hashing function. This example uses Python.
- KNOT. KNOT. KNOT is a light-weight hashing method.
- Lesamnta-LW. Lesamnta-LW. Lesamnta-LW is a light-weight hashing function.
- ORANGE. ORANGE. ORANGE is a light-weight hashing function.
- PHOTON. PHOTON. PHOTON is a light-weight hashing function.
- PHOTON-BEETLE. PHOTON-BEETLE. PHOTON is a light-weight hashing function.
- QUARK. QUARK. QUARK is a light-weight hashing function.
- SATURNIN. Saturnin. SATURNIN is a fast hashing method.
- Sparkle/Esch256. Sparkle. Esch256/Sparkle is a light-weight hashing method.
- Spooky. Spooky. Spooky is a fast hashing method.
- SPONGENT in C++ . SPONGENT. SPONGENT is a light-weight hashing function. This example uses C++.
- SPONGENT in Python. SPONGENT. SPONGENT is a light-weight hashing function. This example uses Python.
Light-weight crypto (Other)
- Chaskey (MAC). Chaskey. Chaskey is a light-weight MAC function.
- Chaskey (MAC). Chaskey (Python). Chaskey is a light-weight MAC function.
- ELLI. ELLI. ELLI is a light-weight asymmetric encryption method.
Light-weight cryptography (Benchark for NIST finalists)
- Finalist benchmark. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses performance requirements.
- Lightweight Encryption and Hashing Hardware and Energy Tests. Benchmark. Since 2016, researchers have been probing the submitted methods, and in 2022 NIST published the final 10: ASCON, Elephant, GIFT-COFB, Grain128-AEAD, ISAP, Photon-Beetle, Romulus, Sparkle, TinyJambu, and Xoodyak. A particular focus on the security of the methods, along with their performance on low-cost FPGAs/embedded processes and their robustness against side channel attacks. This test assesses the hardware requirements and energy efficiency.
Light-weight crypto (ASCON)
ASCON was designed by Christoph Dobraunig, Maria Eichlseder, Florian Mendel and Martin Schläffer from Graz University of Technology, Infineon Technologies, and Radboud University. It is both a light-weight hashing and encryption method. ASCON uses a single lightweight permutation with a Sponge-based modes of operation and a SPN (substitution–permutation network) permutation. Overall it has an easy method of implementing within hardware (2.6 gate equivalents) and software. A 5-bit S-box (as used in Keccak’s S-box core) is used to enable a light weight approach and it has no known side-channel attacks. It can also achieve high throughputs such as throughputs of between 4.9 and 7.3 Gbps. It stores its current state with 320 bits. Overall, ASCON won the NIST competition for a light-weight cryptography standard.
- ASCON AEAD (Python). ASCON AEAD (Python). The outlines the usage of AEAD for ASCON.
- ASCON Hashing and XOF (eXtendable-Output Functions). ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON.
- ASCON MAC and PRF (Pseudo-Random Function). ASCON MAC and PRFF (Python). This implements MAC and PDF for ASCON, and where we sign and verify a message with a secret key.
- ASCON AEAD (C code). ASCON. ASCON is a light-weight block cipher. It is a (NIST Finalist)
Discrete Logs (Solving)

A discrete log problem is in the form of \(g^x \pmod p\) and where we know \(g\) and \(p\) and must solve for \(x\).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Message Authentication Code (MAC)

Hashing methods take data and convert to a hash value. The most popular cryptographic hashing methods are: MD5, SHA-1, SHA-2 (SHA-256) and SHA-3. Blake 3 is also becoming popular as it is one of the fastest hashing methods around. SHA-3 is based on Keccak, and was standardized by NIST. There are also non-cryptographic hashes, and which do not have he same security levels as the cryptographic hashes, but are often much faster in their operation. Along with this there are slowing hashing methods, and which are used within password hash generation and in generating encryption keys from passwords. These include PBKDF2 and Bcrypt.
HMAC
The following are the tips related to Key-based hashing:
- Hazmat HMAC with MD5. Hazmat HMAC. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authentication both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2), Blake2b, SM3 and SHA-3. This page outlines the HMAC-MD5 methods using the Hazmat cryptography layer.
- Hazmat HMAC. Hazmat HMAC. HMAC methods using the Python cryptography primitives.
- HMAC. HMAC. HMAC is a message authentication code (MAC) and can be used to verify the integrity and authentication of a message. It involves hashing a message with a secret key. As with any MAC, it can be used with a standard hash function, such as MD5 or SHA-1, which results in methods such as HMAC-MD5 or HMAC-SHA-1. As with any hashing function, the strength depends on the quality of the hashing function, and the resulting number of code bits. Along with this the number of bits in the secret key is a factor.
- HMAC (Python). HMAC. HMAC is a message authentication code (MAC).
- HMAC (COSE). Go. In this case we will use a symmetric key to encrypt a message, and then decrypt it. Bob will take the message and the shared secret key, and create an HMAC message. Alice will then check the HMAC value based on the message received and the shared secret key.
- CWT with HMMAC. Go. In this case we create a CWT token, and sign with an HMAC signature.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- HMAC with Rust. HMAC. HMAC with Rust.
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- HMAC in Go. HMAC. Implementation of HMAC-SHA256 and HMAC-SHA512, and where we have a shared encryption key between Bob and Alice.
- HMAC with OpenSSL. MACs with OpenSSL. HMAC in OpenSSL for a given input value, password and hashing method.
Cipher MACs
The following are the tips related to Key-based hashing:
- MACs with OpenSSL. MACs with OpenSSL. MAC methods implemented in OpenSSL, including CMAC and GMAC.
Key-based hashing
The following are the tips related to Key-based hashing:
- SipHash. Siphash. Siphash is a fast key-based hashing method.
- Key hashing (SipHash). SipHash. With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
- Highway. Highway. Highway is one of the fastest hashing methods, and is key-based.
- Keyed hash with BLAKE2. Keyed hash. Keyed hashing with BLAKE2 is a faster method of creating a messge authentication code (MAC) than traditional HMAC methods (such as SHA-1 and SHA-256).
- Meow. Meow. Meow is one of the fastest hashing methods.
Message authentication codes (MACs)
- OMA Digest OMA. Open Mobile Alliance Device Management (OMA DM)
- MAC Triple-DES. MAC3DES. MACs can be used to authenticate a message, as a key is required to determine the hash value. With this the sender computes the hash with a secret key and sends to the receiver, where the receiver then calculates the hash of the message, and uses the secret key. If the hash received is the same as the computed one, the message has not been tampered with. The key size can be 8, 16 or 24 bytes. In this case, 24 bytes are used, and produces a hash of 8 bytes (64 bits), using the TripleDES encryption method.
Magic Numbers

This pages contains information related to magic numbers in file formats.
Network and File Forensics
- Magic numbers. Magic. This provides information on magic number for file forensics.
Graphics formats
- JPEG Analysis. JPEGs. This provides an analysis of JPEG files.
- GIF Analysis. GIFs. This provides an analysis of GIF files.
- TIF Analysis. TIFs. This provides an analysis of TIF files.
- PNG Analysis. PNGs. This provides an analysis of PNG files.
- BMP Analysis. BMPs. This provides an analysis of BMP files.
- PSD Analysis. PSDs. This provides an analysis of PSD files.
- WMF Analysis. WMF. This provides an analysis of WMF files.
- Adobe Illustrator Analysis. AI. This provides an analysis of AI files.
- Adobe In Design Analysis. INDD. This provides an analysis of INDD files.
- MIDI file. MIDI. This provides an analysis of MID files.
- ICO file. ICO. This provides an analysis of ICO files.
- PS file. PS. This provides an analysis of PS files.
- EPS file. EPS. This provides an analysis of EPS files.
- VSD file. VSD. This provides an analysis of Microsft Visio (VSD) files.
Video and audio formats
- MP3 Analysis. MP3s. This provides an analysis of MP3 files.
- AVI Analysis. AVIs. This provides an analysis of AVI files.
- Flash SWF Analysis. SWFs. This provides an analysis of Flash files.
- Flash FLV Analysis. FLVs. This provides an analysis of FLV files.
- MP4 Analysis. MP4. This provides an analysis of MP4 files.
- MOV Analysis. MOV. This provides an analysis of MOV files.
- WMV Analysis. WMV. This provides an analysis of WMV files.
- WMA Analysis. WMA. This provides an analysis of WMA files.
- JPEG 2000 Analysis. JPEG 2. This provides an analysis of JPEG 2000 files.
- WAV Analysis. WAV. This provides an analysis of WAV files.
Zips, Archives and Library files
- ZIP/Archive Analysis. ZIPs. This provides an analysis of ZIP/Achive files.
- GZ Analysis. GZ. This provides an analysis of GZip files.
- Tar Analysis. Tar. This provides an analysis of TAR files.
- MSI Analysis. MSI. This provides an analysis of MSI files.
- OBJ Analysis. OBJ. This provides an analysis of OBJ files.
- DLL Analysis. DLL. This provides an analysis of DLL files.
- CAB Analysis. CAB. This provides an analysis of CAB files.
- EXE Analysis. EXE. This provides an analysis of EXE files.
- RAR Analysis. RAR. This provides an analysis of RAR files.
- SYS Analysis. SYS. This provides an analysis of SYS files.
- HLP Analysis. HLP. This provides an analysis of HLP files.
- VMDK Analysis. VMDK. This provides an analysis of VMDK files (VMWare Virtual Disks).
- PST Analysis. PST. This provides an analysis of PST files (Outlook Email File).
- JAR Analysis. JAR. This provides an analysis of JAR files.
- SLN Analysis. SLN. This provides an analysis of Microsoft SLN files.
- Class Analysis. Class. This provides an analysis of Java Class files.
- Zlib. Zlib. This provides an analysis of Zlib files.
Documents
- PDF Analysis. PDFs. This provides an analysis of PDF files.
- DOC Analysis. DOCs. This provides an analysis of DOC files.
- RTF Analysis. RTFs. This provides an analysis of RTF files.
- XLS Analysis. XLSs. This provides an analysis of XLS files.
- PPT Analysis. PPTs. This provides an analysis of PPT files.
- MMP File. MMP. This provides an analysis of MMP files.
- DOCX Analysis. DOCX. This provides an analysis of DOCX files.
- XLSX Analysis. XLSX. This provides an analysis of XLSX files.
- PPTX Analysis. PPTX. This provides an analysis of PPTX files.
- MDB Analysis. MDB. This provides an analysis of MDB files.
- Outlook Message Analysis. MSG. This provides an analysis of MSG files.
Disk Image
- Raw disk format. RAW. This provides an analysis of the RAW disk format.
Tests
- File Forensics Test. File Test File Forensics Test.
- File Forensics Test (Fun). File Test (Fun) File Forensics Test.
Presentations
MIRACL Core Library

MIRACL Core is an open source library, and includes a wide range of public key encryption methods. It is especially focused on elliptic curve and pairing-friendly methods, but also supports a wide range of encryption methods, including RSA, AES and hashing. Overall, it can be ported onto a wide range of systems and supports C, C++, Go, Rust, Python, Java, Javascript and Swift. Along with this it supports limited capability devices such as the Arduino infrastructure. The GitHub repository is [here].
BN254
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Prove it!. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.

Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- CL Signatures. CL. CL Signatures in Go using MIRACL.
- CL Signatures (advanced pairing). CL. CL Signatures in Go using MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages using MIRACL.
- PS Signatures. PS. Signatures using PS for short signatures using MIRACL.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures using MIRACL.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.

Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
Rust examples
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
NaCl

PyNaCl is a Python port of LibSodium. It integrates the latest cryptography methods, such as AES, XChaCha20, Blake2b and X25519.
Symmetric Key
- Symmetric key. Symmetric key (XChaCha20 and Poly1305). With symmetric key, Bob and Alice have the same key. NaCl uses the XChaCha20 method, and which supports stream encryption (and which does not require padding as a block cipher does, and is also faster than block cipher modes). ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16 byte nonce. XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24 byte nonce. It has a lower propability of nonce misuse than ChaCha20.
- Encryption with a password. Symmetric Key with KDF. In symmetric key, we generate a secret key. This key is typically a random value or generated from a password and a salt value. If we use a password, we typically use a KDF (Key Derivation Function), and which uses a password and a salt value, in order to create a key of a given size. In this case we will use Argon2i, and which is memory resilent.
Hybrid Encryption
- Box. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Hashing
- Hashing and KDF (Argon2 and scrypt). Hashing and KDF. This case we will use PyNaCl (Networking and Cryptography) library, and which is a Python binding to libsodium. We will hash a password using SHA-256 and SHA-512, and also create a KDF (Key Derivation Function) using scrypt and Argon2.
- Key hashing (SipHash). SipHash. With SipHash we can apply a secret key to extend the range of hashes that are possible for a given input. In the following we will use a random key of 16 bytes (128 bits). Overall, for MACs, SipHash is more efficient than HMAC. We will also use BLAKE2b to create a MAC, and which uses a larger key.
Ed25519
- Ed25519. Ed25519. Using Ed25519 for digital signatures.
- Finding Points on Ed25519. X25519 (Points). In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 (Key Exchange)
- X25519 + BLAKE2b key-exchange. X25519. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
Curve 25519
- Curve 25519 in Python (with NaCl). Curve 25519 in Python (with NaCl). This page implements Curve 25519 in Python (with NaCl).
Node.js

Node.js uses the JavaScript programming langauge as its base, and allows for code to be run on a server, rather than in the browser (such as with pure JavaScript). To run a node.js program, we run "node myfile.js", and use NPM to install libraries.
Symmetric key
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
RSA and public key
- RSA Opt imal Asymmetric Encryption Padding (OAEP) using Node.js. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
ECC Keys
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.

Hashing
- Hashing with node.js (All). Hashing. Hashing with node.js.
- Hashing with node.js (Selection). Hashing. Hashing with node.js.
- HMAC (hash-based message authentication code) with Node.js. HMAC. HMAC with node.js.
- Keccak, SHAKE, cSHAKE and KMAC. cSHAKE. This implements Keccak, SHAKE, cSHAKE and KMAC in Node.js.
- MD6 (The Pumpkin Hash). MD6. Implements MD6 in node.js.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- ECDSA with node.js. ECDSA. ECDSA with node.js.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
Key exchange
- Diffie-Hellman with node.js (random prime). DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method and uses a randomly generated prime number (press the button to generate a new prime).
- Diffie-Hellman with node.js. DH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Diffie Hellman method. Each time the prime number will be fixed for the DH group selected.
- ECDH with node.js. ECDH. Node.js has an in-built crypto module and which can be used to run code using Javascript. This example implements the Elliptic Curve Diffie Hellman (ECDH) key exchange method.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
Key derivation
- HKDF with Node.js. HKDF. HMAC Key Derivation function (HKDF) is used to derive an encryption key from initial key material (IKM). With HKDF we use a given hashing method to the bases of the function, such as with SHA-512. With this, HKDF creates a pseudorandom key (PRK) using an IKM and a salt value in order to produce an HMAC hash function (such as HMAC-SHA256).
CryptoJS
- CryptoJS (in node.js). CryptoJS (Node.js). Various crypto methods in the browser.
Bulletproofs
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
Blockchain
- Ethereum with node.js. Ethereum. Ethereum with node.js.
- Merkle Tree with node.js. Merkle. Merkle Tree with node.js.
- Keys and Signatures in Ethereum (Node.js). Keys and Signatures in Ethereum. Public and private keys in Ethereum, and the ECDSA signature
Proxy encryption
- Proxy Encryption - Encrypting With Public Key, And Decrypt with Private Key. Proxy01. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This page just creates a key pair for Alice, and uses it to encrypt with the public key , and decrypt with the private key.
- Proxy Encryption. Proxy02. With proxy re-encryption, we can convert a key encrypted with Alice's private to into one that Bob can decrypt with his private key. In the first part, we will perform the basic operation of encrypting a message with Alice's public key, and then decrypting with her private key. This will go through the full use case of proxy re-encryption.
Tokens
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
Random
- Fortuna with node.js. Fortuna. Fortuna random numbers with node.js.
Other
- FPE with node.js. FPR. FPE with node.js.
- Puny with node.js. Puny. Puny character format with node.js.
Accumulators and Witnesses
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
PGP
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Password Entropy
- Password Entropy with Node.js. Password Entropy. Password entropy measures the strength of a password, and is measured as the number of bits which could represent all of the possibilities. An entropy score of less than 25 identifies a poor password, and between 25 and 50 is a weak password. For 50 to 75 we have a reasonable password, and between 75 and 100 is a very good password. Over 100 is an excellent password. The strength of the password relates to the number of characters used, and also the number of characters in the password.
Homomorphic Encryption
- Homomorphic Encryption with Node.js and BFV. Homomorphic Encryption with Node.js and BFV. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BFV method.
- Homomorphic Encryption with Node.js and BGV. Homomorphic Encryption with Node.js and BFG. The Microsoft SEAL library can support a range of homomorphic encryption methods, and which use Learning With Errors (LWE). In this case, we will implement with the BGV method.
Oblivious Transfer (OT)

Oblivious Transfer allows Bob to select data from Alice, but for Alice not to know which value has been selected.
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
OpenSSH

OpenSSH supports the usage of the SSH protocol. This allows for a remote login. One tool which is uses is ssh-keygen, and which allow for the generation of RSA, DSA and elliptic-curve keys that. These can be used for user and host authentication, such as for GitHub login and Cloud instance login.
OpenSSH
- RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used. .
- RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
- Ed25519 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed25519 Keys. Curve 25519 is one of the most widely used ECC methods. It uses a curve of \(y^2 = x^3 + 486662 x^2 + x\) [plot], and which is a Montgomery curve. The prime number used is \(2^{255}-19\). This page generates an Ed25519 key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
- Ed448 Keys (PEM, DER, Raw PKCS8 and OpenSSH). Ed448 Keys. X448 is based on Curve 448, and is used for key exchange with ECDH (Elliptic Curve Diffie Hellman). It supports a 224-bit security level, and where we use a 448-bit (56-byte) prime number of \(P = 2^{448} - 2^{224} - 1\). It has improved security over Curve 25519, and which has a 255-bit prime number (\(P = 2^{255} - 19\)). As with X25519, in X448 we use a Montgomery curve (\(v^2 = u^3 + A \times u^2 + u\)) with scalar multiplication. In X448, we use 56-byte string values, rather than 32-byte values for X25519. Overall, X448 uses a little-endian method to store an array of bytes, and has a value of \(A = 39,081\). The base point \(G\) is at (5, 355293926785 ... 42774147268105838985595290606362) and the paramaters based by on RFC 7748 [ here].
- ECC Keys (PEM, DER, Raw PKCS8 and OpenSSH). ECC Keys. With Elliptic Curve Cryptography (ECC) we can use a Weierstrass curve form of the form of \(y^2=x^3+ax+b \pmod p\). Bitcoin and Ethereum use secp256k1 and which has the form of \(y^2=x^3 + 7 \pmod p\). In most cases, though, we use the NIST defined curves. These are SECP256R1, SECP384R1, and SECP521R1, but an also use SECP224R1 and SECP192R1. SECP256R1 has 256-bit (x,y) points, and where the private key is a 256-bit scalar value (\(a\)) and which gives a public key point of \(a.G\). In this case, \(G\) is the base point of the curve. This page generates a range of ECC key pair, and displays the private and public key in various formats. The encoding formats are PEM, DER and Raw, and the formating is undertaken with OpenSSH, PublicSubjectInfo and Raw.
- DSA Keys (PEM, DER, Raw PKCS8 and OpenSSH). DSA Keys. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free. Initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
- DSA Keys (Y, g, p, q and x). DSA Keys. With DSA, initally, we created a private key of \(x\) and a prime number of \(p\) with a generator of \(g\). The public key is then \(Y=g^x \pmod p\), \(g\), \(p\), and the private key is \(x\).
Outline

OpenSSL

OpenSSL is a standard library that implements cryptography.
Symmetric key (Command line)
- Symmetric Key Encryption (OpenSSL 1.x) [here]. In this case we will create cipher text from OpenSSL 1.x using a key derived from a password, and a salt value (defined in hex).
- Symmetric Key Decryption (OpenSSL 1.x) [here].In this case we will decrypt cipher text from OpenSSL 1.x using a key derived from a password
- Symmetric Key Encryption (OpenSSL 3.x) [here]. In this case we will create cipher text from OpenSSL 3.x using a key derived from a password, and a salt value (defined in hex).
- Symmetric Key Decryption (OpenSSL 3.x) [here].In this case we will decrypt cipher text from OpenSSL 3.x using a key derived from a password
- Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
- Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password.
Hashing
- Hashing [here] OpenSSL supports a wide range of hashing methods including BLAKE2b, Gost, MD4, MD5, RMD-160, SHA-1, SHA-3, SHA-256 and SHA-512.
Libre OpenSSL
- Symmetric Key Encryption using Libre OpenSSL [here]. In this case we will create cipher text from Libre OpenSSL using a key derived from a password, and a salt value (defined in hex).
- Symmetric Key Decryption using Libre OpenSSL [here]. In this case we will decrypt ciphertext from Libre OpenSSL using a key derived from a password.
- Hashing [here] Libre OpenSSL supports a wide range of hashing methods including Gost, MD4, MD5, RMD-160, SHA-1, SHA-256 and SHA-512.
Diffie-Hellman parameter generation
- DH Parameters with OpenSSL [here]. The Diffie-Hellman (DH) method is perhaps one of the greatest inventions in Cybersecurity, and was created by Whitfield Diffie and Marty Hellman. With the DH method, Bob creates a random value (\(b\)) and Alice also creates a random value (\(a\)). Next Bob computes \(B=g^b \pmod p\) and sends it to Alice. Alice computes \(A=g^a \pmod p\) and sends this to Bob. Bob raises the value of \(A\) to the power of \(b\) and takes \(\pmod p\), and Alice raises \(B\) to the power of \(a\) and takes \(\pmod p\). In the end, they will have the same shared value: \(g^{ab} \pmod p\). This can then be used to derive an encryption key that they can use for a secure tunnel. Overall, \(p\) is the large prime number, and also known as the shared modulus between Bob and Alice.
Key derivation function
- PBKDF2 key derivation with OpenSSL [here] PBKDF2 (Password Key Derivation Function 2) is a key derivation method. Overall it is relatively slow in its operation and where we take a password, a salt value, hashing method, and a number of iterations, in order to produce a given size of encryption key.
- HKDF key derivation with OpenSSL [here] HKDF (HMAC Key Derivation function) is used to derive an encryption key from a pass phrase. Initially HKDF creates a pseudorandom key (PRK) using a pass phrase and a salt value (and any other random functions which are relavent), in order to produce an HMAC hash function (such as HMAC-SHA256), andalong with a salt value. Next the PRK output is used to produce a key of the required length. If we generate a 16-byte output (32 hex characters), we have a 128-bit key, and a 32-byte output (64 hex characters) will generate a 256-bit key. HKDF is used in TLS 1.3 for generating encryption keys.
- HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT key derivation with OpenSSL [here]. With ths we will generate an encryption key based on a key/password, a hashing method, a salt value and a key derviation method (HKDF, PBKDF2, SCRYPT, SSKDF, X963KDF and X942KDF-CONCAT).
Passwords
- Password example [here]. This page uses the OpenSSL library hash password generator, which is used in UNIX systems for the hashing of passwords which are contained in /etc/shadow and /etc/passwd. For newer passwords, the "-1" options is used to created the hashed value.
- Hashed passwords with OpenSSL [here].
- Hashed passwords with OpenSSL (crypt, MD5, APR1, SHA-256 and SHA-512) with salt [here]. In this case we will generate hashed passwords in different formats, and using a salt value. The methods are implemented with OpenSSL, and include crypt, APR1, SHA512 and SHA256.
Public key
- Generating an ECC key pair with OpenSSL [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)).
- Generating an RSA key pair with OpenSSL [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2).
- Generating an RSA key pair with OpenSSL with encryption [here]. This page implements RSA key pair generation with an encrypted key pair. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). In this case we will encrypt the key pair with either 3DES, 128-bit AES, 192-bit AES or 256-bit AES. The same password must be used to encrypt and decrypt.
- Generate prime with OpenSSL [here]. Prime numbers are important in public key encrytion, and are used with RSA and ECC. For RSA, we generate two prime numbers (\(p\) and \(q\)) and which are multiplied together to create a modulus (\(N\)). If these prime numbers have 512 bit values, the modulus will be a 1,024 bit value. This defines the basic secure of RSA. With elliptic curve we use smaller prime numbers, such as 256-bit values for the secp256k1 curve.
ASN1 parsing
- Generating an RSA key pair with OpenSSL with asn1parse [here]. This page implements RSA key pair generation. It uses either a 128-bit, 256-bit, 512-bit, 738-bit or a 1024-bit key, and where the public key is \((e,N)\) and the decryption key is \((d,N)\). The value of \(N\) is the modulus and is calculated by the product of two prime numbers \(N=pq\). The number of bits in \(N\) defines the key size for RSA. The \(e\) is normally selected as 65,537, and the \(d\) value selected to solve \(e \times d \pmod{(p-1)(q-1)}=1\), and where \(p\) and \(q\) are the selected prime numbers. The elements of the key are: N (Modulus), e (Exponent key), d (Decryption key), p (prime 1) and q (prime 2). We will parse using asn1parse, and reveal the parameters.
- Generating an RSA key pair with OpenSSL with asn1parse [here]. In the page, we generate an ECC key pair including with secp256k1 (as used in Bitcoin and Ethereum) and secp256r1 (NIST P-256). For a curve of \(y^2=x^3+a.x+b \pmod p\), we have the parameters include of \(p\), \(a\) and \(b\). We also have the generator point (\(G\)), and the order (\(n\)) [RSA key pair]. We will parse using asn1parse, and reveal the parameters.
- DSA Parameters with asn1parse. DSA parameters with OpenSSL with asn1parse. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
DSA (Digital Signature Algorithm)
- DSA Parameters. DSA parameters with OpenSSL. The Digital Signature Algorithm (DSA) is a standard defined in Federal Information Processing Standard (as FIPS 186) for digital signatures, and is based on discrete logarithms. It was outlined by NIST is 1991, and proposed within the Digital Signature Standard (DSS). This was then standardized with FIPS 186 in 1994, and FIPS 186-4 in 2013. Within FIPS 186-5, it is defined that DSA should not be used for the generation of signatures, but can be used for signature verification. Although DSA has a patent (Patent 5,231,668 by David W. Kravitz, who had previously worked for the NSA), NIST published the standard as a royality-free.
- DSA Signature. DSA signature with OpenSSL. This page contains the generation of a DSA signature, and which uses the private key to sign a message. This generates an output value of (\(r,s\)).
- DSA Verification. DSA verfication with OpenSSL. This page contains the generation of a DSA signature, and then the verification of the signature with OpenSSL.
MAC (Message Authentication Code)
- HMAC with OpenSSL. MACs with OpenSSL. HMAC (hash-based message authentication code) supports the usage of a key to hash data. This key is kept secret between Bob and Alice, and can be used to authenticate both the data and that the sender still knows the secret. Overall HMAC can be used with a range of different hashing methods, such as MD5, SHA-1, SHA-256 (SHA-2) and SHA-3. In this case we will use OpenSSL to generate the HMAC value.
- MACs with OpenSSL. MACs with OpenSSL. In the following we will generate MACs for HMAC, GMAC, CMAC, Blake2bmac, Blake2smac, KMAC128 and KMAC256. Overall, we will use an encryption key defined as a hex value for GMAC and CMAC, and a pass phrase for the others. The message is "hello".
Signing
- Digital signing a plaintext message with OpenSSL. Signing with OpenSSL. With digital signing, we can take a message, and create a signature. This normally involves signing with a private key and digital certificate. The signed message can be an a MIME format, and which can be integrated into an email message. In this can we have a 512-bit RSA key pair that will sign a plain text message.
Encrypting emails
- Encrypting an email message in OpenSSL. Encrypting messages with OpenSSL. With public key encryption, we can take a message, and encrypt it with the recipiant's public key. In this can we have a 512-bit RSA public key to encrypt a message.
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Random number generation with OpenSSL
- Random number generator [here]. Random numbers are important in generating encryption keys and salt values. In this case OpenSSL generates a random number (in a Base64 format) for a given number of bytes.
Outline (C#/Python)
- Symmetric Key Encryption (C#) [here]. This page uses the OpenSSL library through a C#/.NET wrapper. The DLLs it interfaces to are libeay32.dll and ssleay32.dll. OpenSSL supports a wide range of encryption methods, including 128-bit AES, 192-bit AES, 256-bit AES and Blowfish (bf). Different modes of ECB, CBC, and OFB are implemented. The examples use a default IV of "1234".
- AES in Python with OpenSSL output [here]
- Producing OpenSSL AES Encrypted String from C# [here]
Digital Certificates
- Reading digital certificates with OpenSSL. View. Using OpenSSL to view the details of digital certificates (from PEM format).
Paillier - Partial Homomorphic Encryption

The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [1]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Fundamentals
- Paillier Key Generation. Key Gen. Implements Paillier key generation for 1,024-bit, 1536-bit and 2048-bit key sizes. These will use 512-bit, 768-bit and 1,024-bit prime numbers for the generation of the keys.
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic Difference in Python (Pallier). Diff. This outlines Homomorphic Difference in Python (Pallier).
- Homomorphic encryption with Paillier. Paillier. Implements Paillier.
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Using RSA
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
Applications
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
Paillier with Kryptology
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Homomorphic Add and Scalar Multiply using Paillier. Paillier. This implements homomorphic adding and multiplying using Paillier.
- Homomorphic Subtraction using Paillier. Paillier. This implements homomorphic subtraction using Paillier.
- Add, subtract and scalar multiply with homomorphic encryption. Homomorphic. Homomorphic Encryption using Kryptology
Zero knowledge proofs
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus.
<
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
-
ECDSA for Multiple Curves and Different Hashing Methods with PowerShell
. ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
-
CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
-
FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
-
RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
-
RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used.
.
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
-
Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using Paillier and Kryptology
- HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology. ZKPs. HVZK (Honest Verifier Zero Knowledge) using RSA and Kryptology
Crypto Pairing

Crypto Pairing supports the mapping of two groups, and which has special properties that can be used for Identity Based Encryption (IBE), and zero-knowledge proofs (ZKPs). With crypto pairing we have some unique operations that can be used for things like IBE and Attribute-based Encryption (ABE). With pairing-based cryptography we have two cyclic groups (\(G_1\) and \(G_2\)), and which are of an order of a prime number (\(n\)). A pairing on \((G_1,G_2,G_T)\) defines the function \(\hat{e}:G_1 \times G_2 \rightarrow G_T\), and where \(g_1\) is a generator for \(G_1\) and \(g_2\) is a generator for \(G_2\). If we have the points of \(U_1\) and \(U_2\) on \(G_1\) and \(V_1\) and \(V_2\) on \(G_2\), we get the bilinear mapping of:
\(\hat{e}(U_1+U_2,V_1) =\hat{e}(U_1,V_1) \times \hat{e}(U_2,V_1)\)
\(\hat{e}(U_1,V_1+V_2) =\hat{e}(U_1,V_1) \times \hat{e}(U_1,V_2)\)
If \(U\) is a point on \(G_1\), and \(V\) is a point on \(G_2\), we get:
\(\hat{e}(aU,bV) = \hat{e}(U,V)^{ab}\)
If \(G_1\) and \(G_2\) are the same group, we get a symmetric grouping (\(G_1 = G_2 = G\)), and the following commutative property will apply:
\(\hat{e}(U^a,V^b) = \hat{e}(U^b,V^a) = \hat{e}(U,V)^{ab} = \hat{e}(V,U)^{ab}\)
Principles
- Simple pairing. Key pairing. This page outlines simple examples of pairing-based cryptography.
- Encrypted searching using crypto pairing using MIRACL. Enc. Using encrypted searching.
- Encrypted searching using crypto pairing using Kryptology. Enc. Using encrypted searching.
BN254
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(abU,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(U,V)^{ab}\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(U1+U2,V)=e(U1,V) \times e(U2,V)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing of \(e(aU,bV)=e(bU,aV)\).
- BN254 for pairing with MIRACL. Pairing. BN254 using Go for pairing for ID-based AKE.
- BN254 for tripartite key sharing with MIRACL. Tripartite. BN254 using Go lang for three-party key sharing.
- BN254 with key and signature aggregation with MIRACL. BN254. BN254 using Go lang, and merges the public keys and signatures.
- Key pairing over BN-curves. Key pairing over BN-curves. This page demonstrates key pairing over BN-curves.
Identity Based Encryption
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Enhanced Identity-based (authenticated) key agreement with two trust authorities using MIRACL. Enhanced IBE With Two TAs. Bob and Alice end up with the same shared secret.
- Encryption using IBE and MIRACL. Encryption with IBE. Bob sends Alice and encrypted message.
- IBE Signatures with MIRACL. IBE Sigs. IBE Signatures in Go.
- IBE using elliptic curves. IBE using elliptic curves. This page demonstrates IBE.
- Identity-based (authenticated) key agreement with MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Identity-based (authenticated) key agreement with secrets using MIRACL. IBE Secret Key. Bob and Alice end up with the same shared secret.
- Pairing-based cryptography Identity Based Encryption (IBE) with MIRACL. IBE. IBE Encryption.
Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
Attributed Based Encryption
- Attributed-based Encryption (ABE). ABE. Example of ABE.
- CP-Attributed-based Encryption (CP-ABE) using Golang. CP-ABE (Go). Example of CP-ABE using Go.
- CP-Attributed-based Encryption (CP-ABE). CP-ABE (Java). Example of CP-ABE using Java.
- CP-ABE (Cipher Policy - Attributed-Based Encryption) with Kryptology. CP-ABE. With CP-ABE (Cipher Policy - Attributed-Based Encryption) we can generate an encryption key based on a policy and a set of attributes.
Key exchange
- BNS-256 Crypto pairing (Triparty key exchange). BNS. Implementation of BNS-256 for triparty key exchange.
- Extended Triple Diffie Hellman (X3DH) with Go. X3DH. This generates pre-shared public keys for X3DH.
- Tripartite Diffie Hellman with Pairing. Tripartite. This page outlines Tripartite Diffie Hellman with pairing-based cryptography.
- Shared key over BN-curves. Shared key over BN-curves. This page demonstrates key generation over three parties with pairing over BN-curves.
Cracking
- The MOV attack. MOV. The MOV attack uses pairing-based cryptography to reduce the difficulty of elliptic curve cracking.
- MOV attack on elliptic curves with Kryptology. MOV. This implements the MOV attack with pairing-based crytography and using \(e(xG1,G2)=e(G1,G2)^x\).
Accumulators
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
ZKP and OT
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Zero Knowledge Proof using crypto pairing using Krytology (zk-SNARK). ZKP. Using crypto pairs for ZKP.
Crypto pairing (Rust)
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
CIRCL Pairing
- CIRCL Pairing with BLS12-381. Pairing. In this example, we will prove these mappings for a pairing for \(e(aU,bV)=e(abU,V)\) and \(e(aU,bV) = e(U,V)^{ab}\).
PAKE (password-authenticated key exchange)

PAKE (password-authenticated key exchange) is a protocol which supports the hiding of a password from the network communications. With this we can have a relatively weak shared password on either side, and then communicate to determine a strong shared key.
SPAKE2
The following are related:
- SPAKE2. Go. Outline of SPAKE2.
SPEKE
The following are related:
- SPEKE. Go. SPEKE (Simple Password Exponential Key Exchange) supports password-authenticated key agreement [1]. Bob and Alice share a secret password (\(\pi\)) and a shared prime number (\(p\)). This password is then hashed and used to determine a generator (\(g\)): \(g=H(\pi)^2 \pmod p\). The square function of the hash makes sure that \(g\) is a generator for the prime number \(p\). After this, we can use a standard Diffie-Hellman type exchange. For this, Alice generates a random number \(a\) and Bob generates a random number \(b\). Alice then sends \(g^a \pmod p\) and Bob sends \(g^b \pmod p\). Alice computes the shared key as \({(g^b \pmod p)}^a \pmod p\) and Bob computes the shared key as \({(g^a \pmod p)}^b \pmod p\). The resultant key is \(g^{ab} \pmod p\).
- SPEKE (Elliptic Curve). Go. Outline of SPEKE (Simple Password Exponential Key Exchange) using EC.
OPAQUE
The following are related areas::
- OPAQUE. Go. The OPAQUE protocol is a secure asymmetric password authenticated key exchange (aPAKE). This allows mutual authentication between a client and a server, and without using PKI. There is no secret salt values stored, which makes it free from pre-computation attacks.
J-PAKE
The following are related:
- J-PAKE. J-PAKE. J-PAKE (Password Authenticated Key Exchange by Juggling) was created by Hao and Ryan [2] and fully defined in RFC 8238 [3]. It is a Password Authentication Key Exchange method, and where Bob and Alice share the same secret password. They can then generate a shared secret key. It involves two stages: a one-time key establishment; and a key confirmation stage. Overall, it does not need access to the PKI infrastructure, and uses Non-Interactive Zero Knowledge (NI-ZKP) for proving secret values .
- J-PAKE (Elliptic Curve). J-PAKE (EC). This example generates a shared key based on a shared password and uses elliptic curve methods.
EKE
The following are related:
- Encrypted Key Exchange (EKE) - Discrete Logs. EKE (Discrete Logs). Encrypted Key Exchange (EKE) was created by Steven M. Bellovin and Michael Merritt [1] and uses a shared password to encrypt the Diffie-Hellman key exchange. In this method, an initial encryption key is generated from a shared password, and which is then used to generate a session key through an encrypted Diffie-Hellman handshaking process
- Encrypted Key Exchange (EKE) - Elliptic Curves. EKE (Elliptic Curve). This example generates a shared key based on a shared password, and which is used to encrypted the Diffie-Hellman method. It uses the sepc256k1.
Others
The following are related:
- Secure Remote Password (SRP) protocol . SRP. This outlines the Secure Remote Password protocol. It is an augmented PAKE.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly zero-knowledge proof method is used in WPA-3 for Simultaneous Authentication of Equals (SAE).
PGP, GPG and Box

This page outlines some applications of PGP (Pretty Good Privacy), GPG (GNU Privacy Guard) and Box.
GPG (Overview)
- GNU Privacy Guard (GPG). GNU Privacy Guard (GPG). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures.
Key Generation
- GNU Privacy Guard (GPG) with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. Also symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256. For hashing methods, we can use SHA1, RIPEMD160, SHA256, SHA384, SHA512, and SHA224. The compression methods supports are ZIP, ZLIB, and BZIP2.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
Key Viewing
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- PGP Encryption. PGP. This uses PGP encryption.
Signature Generation and Verification
- GNU Privacy Guard (GPG) Signatures with Python. GNU Privacy Guard (GPG) with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports the public key methods of RSA, ELG, DSA, ECDH, ECDSA, and EDDSA. In this case we will generate RSA, ECDSA and EdDSA signatures.
Encrypting with public key (RSA and ElGamal)
- GNU Privacy Guard (GPG) Encrypting with Public Key Encryption and Python. GNU Privacy Guard (GPG) Public Key Encryption with Python (RSA and ElGamal). The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. It supports the public key encrytion method of RSA and ElGamal. In this case we will encrypt with 1,024-, 2,048- and 3,072-bit public key modulus. <
Box Encryption
- Box with Go. Box. Box with Go.
- Box with Sodium: NaCl. Hybrid encryption. In this case we will use the Networking and Cryptography (NaCl) library, and which uses Curve25519 for the public key part, and 256-bit AES GCM for the symmetric key element.
Symmetric Key encryption with GPG
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
- PGP (Symmetric) with Go. PGP (Symmetric). This implements PGP Symmetric encryption.
PowerShell

This page outlines a few basic principles using using cryptography methods in PowerShell.
Symmetric Key
- Data Protection Application Programming Interface (DPAPI). DPAPI. Using DPAPI to protect a password.
- AES CBC, ECB, CFB, CTS and OFB Encryption with Powershell Encryption. AES CBC, ECB, CFB, CTS and OFB. Using AES AES CBC, ECB, CFB, CTS and OFB mode with Powershell.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
- Authenticated Encryption with Associated Data (AEAD) AES GCM Encryption with Encryption with PowerShell. AES GCM. Using AES GCM mode with Powershell.
Hashing
- MD5, SHA-1, SHA-256, and SHA-512 hashing. Hashing. MD5, SHA-1, SHA-256, and SHA-512 with hex/Base-64 outputs.
HMAC
- HMAC Hashing. HMAC. HMAC-MD5, HMAC-SHA1, HMAC-SHA256, HMAC-SHA384 and HMAC-SHA512 with hex/Base-64 outputs.
HKDF and PBKDF2
- HKDF (HMAC Key Derivation Function). HKDF. Creating HKDF using MD5, SHA-1, SHA-256, SHA-384 and SHA-512.
- Creating PBKDF2 using PowerShell. PBKDF2. Creating PBKDF2 using PowerShell. This requires a password, a salt value, the number of iterations, and the length of the output.
RSA
- RSA Key Pair. RSA Values. Creating RSA values, and where the public key is [e,N] and the decryption key is [d,N].
- RSA Signatures. RSA Signatures. With public-key encryption, we create a key pair: a public key and a private key. If Alice is sending data to Bob, she can add her digital signature, and which will prove that she is the sender and also verify that the data has not been changed. She does this by signing the data with her private key, and then Bob can prove the signature with Alice's public key. In this example, we will use RSA keys to sign a message, and then verify the correct signature, but verify that an incorrect signature will fail.
- Computing RSA cipher and decipher values in PowerShell. RSA cipher and decipher values. In this case we generate an RSA key pair. With this we have two prime numbers (\(p\) and \(q\)), and compute the modulus (\(N=pq\)). We then pick an encryption key value (\(e=0x010001\)) and then compute \(d=e^{-1} \pmod \phi\)), and where \(\phi=(p-1)(q-1)\). To encrypt a message (\(M\)), we create a cipher \(c=M^e \pmod N\), and then decrypt with \(M=c^d \pmod N\). In this case we will prove the computations with the generation of a message value and an RSA key pair.
- RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell. RSA Encryption and Decryption with PowerShell
- RSA Padding for Encryption and Decryption with PowerShell. RSA Padding for Encryption and Decryption with PowerShell. Optimal Asymmetric Encryption Padding (OAEP) allows for a message to be encrypted using RSA. It thus uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#v1.5 and RFC 2437 [here]. We use RSA-OAEP to pad the message, and then encrypt with \(C = {M_p}^e \pmod n\) and decrypt with \(M_p = C^d \pmod N\) and where \(M_p\) is the padded message. The padding is added before the encryption process, and then stripped off after decryption.
- Using dP, dQ and InvQ with RSA in PowerShell. Using dP, dQ and InvQ with RSA in PowerShell. If we use Using dP, dQ and InvQ with RSA in creates a simpler computation.
Random generator
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
ECC
- Generating an ECC key pair in PowerShell. Generating an ECC key pair in PowerShell. With ECC, we have a base point on the curve (\(G\) and then create a random value for the private key (\(D\)) and then generate the public key with \(P=D.G\).
- ECDSA for Multiple Curves and Different Hashing Methods with PowerShell . ECDSA for Multiple Curves and Different Hashing Methods with PowerShell. With ECDSA (Elliptic Curve Digital Signature) we use an elliptic curve to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private key. The public key can then be used to verify the signature. In this case we will use a range of curves, such as 192-bit, 256-bit, 384-bit and 521-bit curves, and create with a range of hashing methods (such as MD5, SHA-1 and SHA-256).
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Schnorr signatures
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
Zero Knowledge Proof
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
ElGamal encryption
- ElGamal encryption with Powershell. ElGamal encryption.
- ElGamal Homomorphic Cipher for Multiplication (PowerShell). ElGamal. This outlines ElGamal Homomorphic multiplication with PowerShell.
- ElGamal Homomorphic Cipher for Division (PowerShell). ElGamal. This outlines ElGamal Homomorphic division with PowerShell.
- ElGamal Homomorphic Cipher for Addition (PowerShell). ElGamal. This outlines ElGamal Homomorphic addition with PowerShell.
- ElGamal Homomorphic Cipher for Subtraction (PowerShell). ElGamal. This outlines ElGamal Homomorphic subtraction with PowerShell.
Inverse Mod
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
Primitive root
- Primitive root of a prime number p modulo p in PowerShell. Primitive root of a prime number p modulo p. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\).
Prime Number Test
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Object Identifier (OID)
- Object Identifier (OID) in PowerShell. OID. The object identifier (OID) tag is used to define the cryptography methods used. An example identifier for ECC encryption is “1.2.840.10045.2.1”, and where 1 is OSI, 2 is member body, 840 is US (ANSI), and 10045 is “ansi-X9–62”, and “2” is key type [1]. Other common algorithms are: “1.2.840.113549.1.1.1” (X509 RSA), “1.2.840.10040.4.1” (X509 Digital Signature Standard -DSS), and “1.2.840.10046.2.1” (Diffie-Hellman — DH).
QR Codes
- Wifi connect. Wifi QR. We can use PowerShell to create a QR connect for someone to connect to a Wifi network. In this case, we enter the SSDI and the password. Use your smart phone to test.
- Contact details. Contract QR. We can use PowerShell to create a QR code to generate contact details.
- Geolocation details. Geolocation QR. We can use PowerShell to create a QR code for geolocation.
- URI link. URI QR. We can use PowerShell to create a URI link.
- Text in a QR code. Text QR. We can use PowerShell to create text in a QR code.
A quick demo
A fun demonstration of the power of PowerShell is to compute \(10^{6400}-10^{6532}-1\):
Post quantum cryptography (PQC)

As if you didn’t know, quantum computers will put an end to our most popular public-key methods. And so NIST has been working on defining a standard for the best method to replace these, and yesterday they made their announcement on the final of the PQC (Post Quantum Cryptography) standardization process. For Public-Key Encryption and KEMs (Key Exchange) we have:
- Classic McEliece. This has been around for around 40 years, and has been shown to be fairly resistant to attack. It produces a fairly long encryption key, but produces a fairly small amount of ciphertext.
- CRYSTALS-KYBER (Lattice). Uses LWE (Learning with Errors) with lattice methods. A new lattice attack was discovered within the period of the assessment, but it is hoped that an updated version of KYBER can be produced for the final assessment. NIST have some worried about its side-channel robustness, and is a strong contender for KEM.
- NTRU (Lattice). This is a traditional structured lattice based approach, and has been around for longer than the other lattice methods — showing that it is perhaps more robust against attack and against intellitecual property claims.
- SABER (Lattice). This is based on modular learning with rounding, and uses lattice methods. SABER has excellent performance, and is possibly near production ready. NIST’s only recommendation is that updates should perhaps consider side-channel attacks.
and for digital signatures:
- CRYSTALS-DILITHIUM (Lattice). At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes.
- FALCON (Lattice). Falcon is one of the finalists for the NIST standard for PQC (Post Quantum Cryptography), along with NTRU (Nth degree‐truncated polynomial ring units) and CRYSTALS-DILITHIUM. It is derived from NTRU and is a lattice-based methods for quantum robust digital signing. Falcon is based on the Gentry, Peikert and Vaikuntanathan method for generating lattice-based signature schemes, along with a trapdoor sampler - Fast Fourier sampling.
- Rainbow (Oil and Vinegar). The multivariate polynomial problem is now being applied in quantum robust cryptography, where we create a trap door to allow us to quickly solve the n variables with m equations (which are multivariate polynomials). In the following example we sign a message with the private key and verify with the public key.
These are defined as the finalists, and a winner will be chosen from these, but because CRYSTALS-KYBER, NTRU, and SABER are lattice methods, NIST only wants one winner from a lattice technique. So it has drawn up a list for an alternative of: BIKE; FrodoKEM; HQC; NTRU Prime; and SIKE. And CRYSTALS-DILITHIUM and FALCON are lattice methods for digital signatures, so the alterative list has: GeMSS; Picnic; and SPHINCS+. NIST thus wants to guard against lattice methods being cracked in the future, and thus would like an alternative method as a back-up. A Windows binary for assessing the performance of the NIST finalists is here.
Quantum-robust Public Key (Principles)
- NIST Finalists (KEM) Speed Tests. KEM Speed. For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies). This page provides a performance speed test for these methods.
- NIST Finalists (Digital Signatures). Sig Speed. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP).
- NIST Finalists Information. PQC Information. For digital signatures, NIST have defined the finalists of CRYSTALS Dilithium (Lattice), Falcon (Lattice), and Rainbow (Multivariate Quadractic). The alterative finalists are: SPHINCS+ (Hash-based stateless), and Picnic (Hash-based ZKP). For KEM, NIST have defined the finalists of CRYSTALS Kyber (Lattice), Saber (Lattice), McEliece (Code-based) and NTRU (Lattice), and with alternative finalists of BIKE (code-based), HQC (code-based), FrodoKEM (Lattice), and SIKE (isogenies).
Quantum-robust Public Key (Principles)
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Homomorphic Encryption with Learning With Errors (LWE). LWE. Outlines homomorphic encryption with Learning With Errors (LWE).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
- Lattice plot. Lattice (Plot). Outlines how lattices are created.
- Lattice nearest point. Lattice (Nearest). Outlines how lattices finds nearest point.
- Lattice Encryption. Lattice. This outlines Lattice encryption.
- LWE (Very simple). LWE. Outlines Learning With Errors.
- LWE and Ring LWE. LWE. Outlines Learning With Errors and RLWE.
- Unbalanced Oil and Vinegar (UOV). UOV. Outlines Unbalanced Oil and Vinegar (UOV) cryptosystem.
- Multivariate cyptography. MQ. Outlines a simple example of multivariate cyptography. We define this as a quadratic polynomial as a polynomial of degree 2 (the largest power is 2) - also known as Multivariate Quadratic (MQ). We use \(n\) quadratic polynomials with \(n\) variables.
- Oil and Vinegar example. Oil and Vinegar. Simple example of Oil and Vinegar
Isogenies
- Isogenies in Go. Isogeny. Application of isogenies.
- Real-life Example of an isogeny in Go. Real-life Isogeny. Application of isogenies.
NIST Finalists (Public-Key Encryption/Key Exchange)
- Simple Kyber Example. Simple Kyber. NIST has defined that Kyber will be developed as a standard for PQC (Post Quantum Cryptography) key exchange and public key encryption. In this case, we will implement a very simple Kyber example. The main methods are Kyber512 (128-bit AES security level equivalent), Kyber768 (192-bit AES security level equivalent) and Kyber1024 (256-bit AES security level equivalent.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using C.
- McEliece key exchange mechanism (KEM) in Node.js. mce. Outlines McEliece key exchange using Node.js.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
- Frodo. Frodo. Frodo KEM is based on the learning with errors (LWE) problem, and has a number of levels: FrodoKEM-640 (Level 1, equivalent in security to AES-128), FrodoKEM-976 (Level 3, equivalent in security to AES-192), and FrodoKEM-1344 (Level 5, equivalent in security to AES-256). There are two main variants of these for FrodoKEM-X-AES and FrodoKEM-X-SHAKE. The -AES version has hardware acceleration for AES, and can run faster on processors that support hardware acceleration for AES, while the -SHAKE version is faster on systems that do not support this. For FrodoKEM-640-SHAKE, we can see that the size of Alice's public key is 9,616 bytes long, and her private key is 19,888 bytes long. The ciphertext passed is 9,270 bytes long.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature with Golang. SPHINCS+ with Golang. Implementation of SPHINCS+ in Golang, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
Quantum-robust Public Key (Public-Key Encryption/Key Exchange)
- BGV - (Ring LWE). BGV. Outlines BGV.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- Goldreich–Goldwasser–Halevi (GGH). GGH. Outlines GGH.
- McEliece cryptosystem (Java). mce. Outlines McEliece cryptosystem.
- McEliece key generation. mce. Outlines simple McEliece key generation cryptosystem with a (7,4) Hamming code.
- McEliece key exchange mechanism (KEM). mce. Outlines McEliece key exchange using Node.js.
- Lattice Encryption: NTRU (Python). NTRU. Outlines how NTRU operates for key generation.
- Lattice Encryption (NTRU). Lattice. This outlines Lattice encryption.
- NTRU Key Encapsulation Method. NTRU. NIST finalist NTRU for KEM.
- CRYSTALS-KYBER (Lattice + LWE) - Key Encapsulation Mechanism (KEM). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and where Bob passes a symmetric key to Alice, and using her public key.
- CRYSTALS-KYBER (Lattice + LWE) - Key EXchange Mechanism (KEX). Kyber-CRYSTALS. Implementation of Kyber-CRYSTALS in C, and which uses Lattice and Learning With Errors (LWE) and defined a method where Bob and Alice generate the same key.
- SABER (Lattice + LWR) - Key EXchange Mechanism (KEX). SABER. Implementation of SABER, and which uses Lattice and Learning With Rounding (LWR) and defined a method where Bob and Alice generate the same key.
- NewHope for Key Exchange. NewHope. Outlines NewHope for shared key generation.
- Multibit Encryption with Learning With Errors (LWE). LWE. Outlines multibit Encryption encryption with Learning With Errors (LWE).
- Ring Learning With Errors for Key Exchange (RLWE-KEX). LWE. Outlines RLWE-KEX.
- Supersingular Isogeny Diffie-Hellman for Key Generation. SIDH. Outlines SIDH.
- SIDH Go. SIDH. Post-quantum key exchange.
- SIKE for KEM. SIKE. Post-quantum key exchange with key encapulation for SIKE (Supersingular Isogeny Key Encapsulation).
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Quantum-robust Public Key (signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Falcon. Falcon. Creating a digital signature with Falcon.
- CRYSTALS Dilithium using CIRCL with Golang. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Hybrid Signature (X25519 and Dilithium)
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium2-X25519. At present, CRYSTALS (Cryptographic Suite for Algebraic Lattices) supports two quantum robust mechanisms: Kyber for key-encapsulation mechanism (KEM) and key exchange; and Dilithium for a digital signature algorithm. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 2 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation. To support both Ed25519 and Dilithium, we can implement a hybrid signature scheme, and where the signature contains both the Ed25519 and Dilithium keys and signatures.
- Dilithium2-X25519 (Lattice) - Hybrid Digital Signature. Dilithium3-X25519. This supports a hybrid signature method with X25519 and Dilithium3.
Quantum-robust Public Key (Hash-based signature)
With hash based methods we can create multiple key-pairs and then use the only once. We must thus keep a track of the private keys which have been used to create a signature.
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- Haraka v2 - Short-input hashing. Haraka v2. Outlines Haraka v2 hashing method, and which is used within speeds-up of Hashing-based signature methods.
Post Quantum Key with CIRCL using Golang
- SIDH using Cloudflare. SIDH. Post-quantum key exchange.
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
- CSIDH Go. CSIDH. Post-quantum key exchange.
- Kyber Key Exchange. Kyber. In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange.
- SIKE Key Exchange. SIKE. Supersingular Isogeny Key Encapsulation (SIKE) is a post-quantum cryptography key encapsulation method for key exchange, and is based on Supersingular Isogeny Diffie-Hellman (SIDH). In this case we will implement Kyber512, Kyber738 and Kyber1024, in order to create a quantum-robust key exchange. In this case we will implement SIKEp434, SIKEp503 and SIKEp751.
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Prime numbers

This outlines the usage of prime numbers. We use random numbers in many places in cryptography. This includes generating random values for encryption keys and also in creating nonce values which are used for salt values. A salt value is often used to randomize a cipher or a hash value.
Safe Prime numbers
- Safe prime numbers. Safe prime. A prime number (p) is safe if \(\frac{p-1}{2}\) is also a prime number .
- Generating a safe prime number with n bits using Golang. Safe prime. In cryptography, we often search for safe primes. A safe prime (p) - or also known as a Sophie Germain prime - is safe when \(2p+1\) is also prime. Sophie Germain was a French mathematician and who used safe primes to investigate Fermat's Last Theorem. Overall safe primes are used in cryptography, as they are robust against attacks within discrete log methods (such as for the Diffie Hellman methods). .
Prime numbers (Principles)
- Jacobi symbol. Jacobi symbol. Calculate Jacobi symbol.
- Quadratic residues using the Jacobi and Legendre symbol. Quadratic residues. Determine the range of values for \(y\) given \(y=x^2 \pmod n\).
- Jumping champion. Jumping champion. The jumping champion is the most popular difference for a sequence of prime numbers.
- Truncatable prime. Truncatable prime. A left-truncatable prime (or Russian Doll prime) is defined as a prime number, that when we take away the leading left digit successively, it still reveals a prime number.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Golang. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
Prime numbers (Finding)
- Find primes. Find Prime Numbers. Many public key algorithms depend on primary number, which are difficullt to factorize when multiplied together. This program creates the ones from 1 to 1,000,000.
- Prime numbers. Prime. Prime numbers are used extensively in encryption, such as in the Diffie-Hellman method.
- Finding primes (Wilson's theorem). Primes. We can find prime numbers with Wilson's theorem.
- Finding primes (with a RegEx). Find with RegEx. We can find prime numbers using a Regular Expression.
Prime numbers (Generating)
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
- Prime Number sieve. Sieve. Implementation of the fast method to generate a range of prime numbers.
- Generate prime numbers from strings. String to prime. Match a prime number to a string.
- Random Prime Numbers in PowerShell. Random Prime Number. The Miller-Rabin Test for primes is one of the most popular methods for testing for prime numbers used in RSA. In this case we will generate a random prime number for a given number of bits. Initially we will generate a random number, and then test it for primality. If it is not, we will keep incrementing it by two until we find a prime number.
Prime numbers (Testing)
- Test if prime? testprime. This s for whether a number is prime.
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. This outlines Miller-Rabin Test
- Miller-Rabin Test for prime. M-R. In this case, we will calculate the value of (n-1) and then determine \(2^s d\) for \(s\) and \(d\).
- Miller-Rabin Test for Prime Numbers in PowerShell. Miller-Rabin Test. Miller-Rabin Test for Primes is one of the most popular methods for testing for prime numbers used in RSA. Given an odd number (\(n\)), we will have an odd number of (\(n-1\)), of which we can calculate the power of 2 with a value of \(s\) so that \(n-1 = 2^s d\). For example, if \(n\) is 25, \((n-1)\) will be 24, and which is \(2 \times 2 \times 2 \times 3\) and which is \(2^3 \times 3\). We then select a random value of \(a\) and which is between 1 and \((n-1)\).
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Strong prime (Gordon method). Strong prime. This generates a strong prime using the Gordon method.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Solovay-Strassen Primeabilty Test. Solovay-Strassen Primeabilty Test. The Solovay-Strassen test for probable prime numbers.
Prime numbers (Factorizing)
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Difference of squares . Diffsq. This factorizes using the difference of squares method.
- Factors of integers. Factors. Determine factors of an integer.
- Pollard's ρ method (Factoring integers). Pollard. The Pollard ρ method factorises integers.
- Elliptic Curve method (Factoring integers). Elliptic. The Elliptic Curve method factorises integers.
- Simplify \(a^p \pmod N\). Go. Simplify the \(a^p \pmod N\) operation.
- Smooth numbers. Go. Outline of smooth numbers.
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) using libnum. Go. Outline of quadratic residue (mod p) using libnum.
- Quadratic residue (mod N) and where \(N=pq\). Go. Outline of quadratic residue (mod N) with N made-up of two prime numbers.
- Dixon. Go. Dixon Method.
- Lenstra elliptic-curve factorization. Go. ECM.
- Lenstra elliptic-curve factorization using a range of curves. Go. ECM.
Prime numbers (Estimating number)
The following are the tips related to prime numbers, which are a key principle in public-key encryption:
- Prime Number estimation. Primes. Estimation of the number of prime numbers.
- Prime Number estimation for bit size. Primes. Estimation of the number of prime numbers for a given prime number bit size.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Crypto Principles

This page outlines some crypto principles, including oulining the usage of Big Integers, combinations and permutations, and converting ciphertext into plain English.
A few basic principles
- Large numbers. Large. With encryption we normally deal with large numbers. This example shows how we can display these.
- Big Integer operations with Golang. Big Int. With Big Integers we can perform arithmetic operations on large numbers.
- Combinations and Permutations. Calc. This provides an outline of combinations and permutations
- Caesar codes. Caesar. This outlines of the possible Caesar code shifts
- Convert keys to plain English. English. Convert to plain English.
- Convert ciphertext to plain English. English. Convert ciphertext to plain English.
- DNA storage. DNA. DNA storage
- Reed Solomon. Reed. This outlines Reed Solomon coding.
- Merkle Tree. Merkle. This outlines a Merkle Tree.
- Formal proof (Power of 2) . Proof. This outlines a formal proof using Z3.
- Solver for Suduko. Suduko. This is a solver for Suduko using Z3.
- Carmichael number. Carmichael. This generates Carmichael's numbers.
- Blum integers. Blum integers. This outlines Blum integers.
- Hex to integer. Hex to int. Converts a hex number to an integer for big-endian and little-endian formats.
- Euclidean Distance. Euclidean. This determines the Euclidean distance between three vectors, and uses polynomial operations.
- Mordell Curve. Mordell Curve. In the elliptic cryptography field we use finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve.
- Mordell Curve with finite field. Mordell Curve. In the elliptic cryptography field we use a finite field and use a form of: \(y^2 = x^3 + a.x + b \pmod p\). The Mordell curve does not constrain the computation into a finite field and has the form of: \(y^2 = x^3 + n\). It was analysed by Louis Mordell and who showed that there are only a finite number of integer solutions to this. In this case, we will determine the integer solutions to a Mordell curve, but using a finite field - and using a prime number (\(p\)) of the form of \(y^2=x^3+n \pmod p\).
Brute Force Calculation
- Brute Force (with increasing keys). Brute Force. This is an outline for brute force calculations.
- Brute Force (with parallel processing). Brute Force. This is an outline for brute force calculations with multiple processors.
- Brute Force (with increasing computing power). Brute Force (over the years). This is an outline for brute force calculations for increasing computing power.
Galois fields (polynomial operations)
- Addition and Multiplication in Galois Fields GF(\(2^m\)). Galois Fields GF(2^m). Implements Galois Fields GF(\(2^m\)) with Python.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
- Binary multiplication (modulo 2) - GF(2). Bin. This outlines the calculation of binary multiplication (modulo 2).
- Binary division (modulo 2) - GF(2). Bin. This outlines the calculation of binary divide (modulo 2).
- Finding polynomial factors for GF(2). Factors. This outlines the search for polynomial factors for GF(2).
- Polynomial operations (mod p). Poly. Polynomial operations (mod p).
- Inverse of a modulo polynomial. Inv Poly. Outlines how we determine modulo inverse of a polynomial.
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 ) \). \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- \(R=\mathbb{Z}[X]/ ( X^{n}+1 )\) - Additional of polynomials. \((X^N+1)\). Outlines dividing by (\(X^{n}+1\)).
- Lattice Encryption: Mod P polynomial operations. Poly. Outlines Mod P polynomial operations.
- Lattice Encryption: Inverse polynomial (mod p). Inv Poly. Inverse polynomial (mod p).
Solving discrete logs
- Baby-step, Giant-Step Solving of Discrete Logs. BSGS. This solves for x when we have \(h=g^x \pmod p\).
- Pollard's rho algorithm for logarithms. RHO. This solves for x when we have \(h=g^x \pmod p\).
- Pohlig-Hellman's algorithm for logarithms. Pohlig. This solves for x when we have \(h=g^x \pmod p\).
- Order of a prime and factorization into small primes. order. This calculates the order of a prime and factorizes into small primes.
- Picking a safe value of g for \(g^x \pmod p\). Picking safe g. In this case we make sure that \(g^x \pmod p\) gives us a unique output for \(x\) values from 0 to \(p-1\). We define the field of \(G\) as all the possible values.
Proof-of-work
- Time-locked encryption (hashing). Time-locked encryption. This creates a key with a given amount of work related to consecutive hashing.
- Time-locked encryption (squaring). Time-locked encryption. This creates a key with a given amount of work related to squaring.
- Time-locked encryption (cracking). Time-locked encryption. This creates a time-based challenge, without knowing the number of iterations of a hashed key.
- Verifier Delay Function (VDF). Verifier Delay Function (VDF). This creates a Verifier Delay Function (VDF).
Integer arithmatic
- Radix. Radix. Determine the value for a given radix.
Public Key Principles

This page outlines some crypto principles related to public key encryption. This includes computing the GCD (Greatest Common Divisor), Quadratic residues (mod p), and Exponentiation.
Principles
- GCD. GCD. GCD is the greatest common divisor.
- Exended GCD. Extended GCD. GCD is the greatest common divisor. This problem solves \(ax + by = v\) for \(a\) and \(b\), and where \(v=gcd(x,y)\)
- Quadratic residue (mod p). Go. Outline of quadratic residue (mod p).
- Quadratic residue (mod p) - first principles. Go. Outline of quadratic residue (mod p) with core Python code.
- Lehmann's Primality Test. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Lehmann's Primality Test on large primes. Lehmann's Primality Test. This outlines Lehmann's Primality Test.
- Blum integers. Blum integers. This outlines Blum integers.
- kth root of N (mod p) - with search. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \).
- kth root of N (mod p) - - Using Extended Euclidean method. kth root of n (mod p). This outlines the solution for \( \sqrt[n]{x} \pmod p \) and using - Using Extended Euclidean method.
- Creating a safe generator (\(g\)): Primitive root of a prime number p modulo p in Python. Safe generator. If we have \(g^x \pmod p\) and where \(p\) is a prime number, can we find a value of \(g\) that makes sure that we get a unique output from 1 to \(p-1\), for every value of \(x\) from 0 to \(p-2\). This is known as the primitive root under modulo \(p\). In this case, we will discover the first 10 safe generators for a given prime number.
Exponentiation
The following are the tips related to encryption:
- Exponentiation cipher. Exp. This outlines Exponentiation cipher which provides the basis of several encryption methods, such as RSA and Pohlig-Hellman.
- Brickell, Gordon, McCurley and Wilson method for Fast Exponentiation With Pre-computed values. BGMW. This outlines a fast exponentiation methods with pre-computed values.
Finite fields
The following are the tips related to encryption:
- Rings and finite field. Rings. This outlines some basic rules of rings and finite fields.
- Inverse of n mod m. Inv. This outlines the inverse of n mod m (used in RSA and Knapsack).
- Inverse of n mod m (Euclidean method - Python). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m (Euclidean method). Inv. This outlines the inverse of n mod m (Euclidean method)
- Inverse of n mod m with Go. Inv. This outlines the inverse of n mod m
- Inverse of \(x \pmod p\) in PowerShell. Inverse mod. In cryptography, we often need \(x^{−1}\), and which is a multiplicative inverse of \(x \pmod p\), i.e. \( x/x^{−1} = 1 \pmod p\). It is used in the calculation of the decryption key in RSA, and in other cryptography methods. With RSA, we get \((e \times d \pmod {\varphi} =1\) = 1, where we have \(e\) and \(\varphi\), and must calculate \(d\) using the multiplicative inverse of \(e \pmod {\varphi}\).
- Multiplicative group for \(Z_n\) [ \(Z^*_n \)]. Z_n. This outlines Multiplicative group for \(Z_n\) [ \(Z^*_n \)]
- Multiplicative group of \(\mathbb{Z}_n\) (\(\mathbb{Z}^*_{n}\)) in Python. Z_n. The multiplicative group of integers modulo \(n\) is represented by \(\mathbb{Z}^*_n\), and represents the numbers which do not share a factor with \(n\). If \(n\) is a prime number, the values will range from 1 to \(n-1\). If \(n=6\), we have two factors of 2 and 3, and where \(\mathbb{Z}^*_{6}\) will thus be {\(1, 5\)}, and the other values share 2 or 3 as a factor.
- Finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\). Finite. This page outlines finite fields for modulo of prime numbers - GF\((p\)) - Galois field of \(p\) or with \(\mathbb{F}_p\)
Montgomery Reduction
The following are the tips related to encryption:
- Calculating \(a^b\) with Square and Multiply method. SQM. Calculates \(a^b\).
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction.
Euler's and Fermat's theorem
The following are the tips related to encryption:
- Fermat's Little Theorem. Fermat. This outlines Fermat's Little Theorem
- Euler's Theorem (one value). Euler. This outlines Euler's Theorem
- Euler's Theorem (two primes). Euler. This outlines Euler's Theorem
- Euler's Theorem (operations). Euler. This shows the operations of \(g^x \pmod n \equiv g^{x \pmod {(p'q')}} \pmod n\) and where \(n=pq\), \(p=2p'+1\) and \(q=2q'+1\).
Chinese Remainder Theory (CRT)
The following are the tips related to encryption:
- Chinese Remainder Theory. CRT. This outlines Chinese Remainder Theory.
- Chinese Remainder Theory (Alt code). CRT. This outlines Chinese Remainder Theory (Alt).
- Chinese Remainder Theory (Garner method). Garner (CRT). This outlines Chinese Remainder Theory using a core algorithm (Garner Method).
Knapsack
The following are the tips related to encryption:
- Knapsack Encryption (Example). Knapsack. This outlines Knapsack public encryption
- Knapsack Encryption (Theory). Knapsack. This outlines Knapsack public encryption
- Naccache–Stern cryptosystem. Naccache–Stern cryptosystem. This outlines the Naccache–Stern public key cryptosystem and which uses a Knapsack method.
Paillier
The following are the tips related to encryption:
- Paillier crypto system (JavaScript). Paillier. Outlines Paillier crypto system using JavaScript.
- Simple Paillier example (Python). Paillier. Outlines a simple Paillier crypto system using Python.
- Homomorphic encryption (add and subtract) and RSA protection. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key.
- Homomorphic encryption (add and subtract) and RSA protection - with Montgomery reduction. Paillier + RSA. In this case we will use add and subtract using homomorphic methods, but will protect these values using an RSA public key. In this case we will use the Montgomery reduction method for the multiplications.
IBE
The following are the tips related to encryption:
- Identity Based Encryption (IBE). IBE. Outlines Identity Based Encryption.
PGP
The following are the tips related to encryption:
- PGP Encryption (Key Generation - Elliptic Curve) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- PGP Encryption. PGP. This uses PGP encryption.
Public-key encryption (Others)
The following are the tips related to encryption:
- Congruential Public Key. Congruential. A public key method.
- Cramer-Shoup. Cramer-Shoup. Outlines Cramer-Shoup public key encryption.
- DSA (with C#). DSA Encryption. This uses DSA key and fingerprint generation.
- Goldwasser–Blum method: probablitistic encryption. Goldwasser–Blum. The uses the Goldwasser–Blum and which is a probabilistic encryption met
- Goldwasser–Micali method: probablitistic encryption. Goldwasser–Micali. The uses the Goldwasser–Micali and which is a probabilistic encryption met
- Okamoto–Uchiyama. OU. This performs the Okamoto–Uchiyama public key method.
- Rabin. Rabin. This performs the Rabin public key method.
- Schmidt-Samoa. SS. This performs the Schmidt-Samoa public key method.
- Massey–Omura Cryptosystem. Massey–Omura. The Massey–Omura Cryptosystem can be used for commutative encryption.
- Massey–Omura Cryptosystem Commutative Example. Massey–Omura (Commutative). The Massey–Omura Cryptosystem can be used for commutative encryption. This example shows how we can apply the keys in order order.
- EMO-1 (Enhanced Massey-Omura) Private Key System. EMO-1. The Massey–Omura Cryptosystem can be used for commutative encryption. The EMO-1 system uses two prime numbers to overcome the weakness of the Massey–Omura, and where we can discover the other key if we know one of the keys.
S/MIME (Encrypted email)
- S/MIME. S/MIME. S/MIME (Secure/Multipurpose Internet Mail Extensions) supports the encryption and signing of email messages, while keeping compatibility with existing MIME formats. A specified digital certificate is required to read the encrypted email. RFC 822 defines the usage of an electronic message format for header fields, and S/MIME 4.0 is defined in RFC 8551.
- Generate X.509 certificate. X.509. This generates an X.509 certificate and shows the details.
Mersenne primes
- Mersenne primes. Mersenne primes. This outlines a range of Mersenne numbers.
- Lucas-Lehmer Test. Lucas-Lehmer Test. Lucas-Lehmer Test for Primality for Mersenne numbers.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
Random number

This page implements a nunmber of random number methods.
Random Number generators
- Blum Blum Shub. Blum Blum Shub. This outlines the usage of the Blum Blum Shub random number generator.
- Dual EC. Dual EC. This outlines the Dual EC method and the discovery of a trap door.
- Gimli. Gimli. This provides a 384-bit permutation that provides high levels of security and performance levels.
- Lagged Fibonacci Generator. Calc. This provides a Lagged Fibonacci Generator.
- Linear Congruential Random Number Generator. Calc. This provides a random number generator.
- Mersenne Twister. Calc. This provides a Mersenne Twister.
- Random number (512-bit). Random. This provides a 512-bit random number which is used in 1024-bit encryption.
- Random number. Random. This provides a 192-bit random number.
- Xoroshiro128+. Calc. This provides a random number generator using Xoroshiro128+ and solves for two random seeds to generate a given string in the random number.
- Xoroshiro128+ Solver. Calc. This provides a random number generator using Xoroshiro128+.
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
- Generating a random number in PowerShell. Generating a random number in PowerShell. This page generates a random number in PowerShell and displays as a hex, Base64 and integer value.
Randomization
- Monte Carlo Test for randomness. Monte. This outlines the Monte Carlo Test for randomness.
- File Entropy. Entropy. This outlines the calculation of Shannon's entropy.
- Key Entropy. Entropy. Determines key entropy.
Random Prime numbers
- Get prime numbers of n bits long. Get Prime (n bits). In this case we determine a random prime with n bits.
- Get prime numbers of n bits long (using libnum). Get Prime (n bits). In this case we determine a random prime with n bits (using libnum).
- Random Prime Number generator. Primes. Generates two prime numbers of various bit sizes, and creates the product of these.
Key generation
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
RSA

With RSA, we have the magic of public key encryption, and where Bob can generate a key pair: a public key and a private key, and then send Alice his public key. If she wants to encrypt something for him, she encrypts it with his public key, and then the only key which can decrypt it is his private key. A truly wonderful concept, and it was Rivest, Shamir and Adleman who made it come alive with the RSA method. In RSA, we start by generating two prime numbers (\(p,q\)) and then calculate the modulus (\(N\)) of \(N=pq\). It is this modulus (\(N\)) that provides the core of the security of RSA, and it must be difficult to determine the prime numbers for a given modulus value. Our prime numbers must thus be of a size that makes it difficult to factorize, and they must be randomly generated.
RSA Simple
- RSA in 12 lines of Python. RSA in 12 lines. This is a simple key generation, encryption and decryption program in 12 lines of Python code.
- Simple RSA Encrypting and Signing in Python. Simple RSA . This is a simple key generation, encryption, decryption and signing program in Python code.
CTF Generators and Solvers
- CTF Generator: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli.
- CTF Solver: Cracking RSA with Chinese Remainder Theory - Håstad’s Broadcast Attack. CRT. In this example, an RSA cipher has used the same message and with three different moduli, and produce a solution.
- CTF: RSA Challenge Generator. RSA. This provides values for \(e\) and \(N\), and gives the cipher, and you must crack it by finding \(d\).
- CTF Generator: Low exponent in RSA (for public exponent). Low public exponent in RSA. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\). But, if \(M^e \le N\), then the message can be determined from \(M=\sqrt[e]{C}\). In this case, we will use a value of \(M^e\) that is less than \(N\), and thus make it easy (with just one line of Python) to crack the RSA cipher.
- CTF Generator: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack). In RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). We then compute the cipher as \(C=M^e \pmod {N}\) and where we decrypt with \(M=C^d \pmod N\). With this we have a public exponent of \(e\), and a private exponent of \(d\). The value of \(d\) is computed from \(e^{-1} \pmod {\phi}\), and where \(\phi=(p-1)(q-1)\). While these days, we normally use \(e=65537\), we could select a range of values of \(e\). If we select a fairly large value, then the value of \(d\) could be discovered. In this case we will use the Wiener attack [1] to discover \(p\), \(q\) and \(d\).
- CTF Solver: Low exponent in RSA (Wiener attack). Low exponent in RSA (Wiener attack).
- CTF Generator: Fermat’s attack. CTF Generator: Fermat’s attack. Normally, in RSA, we select two prime numbers of equal length (\(p\) and \(q\)), and then multiply these to give a modulus (\(N=p.q\)). If these numbers have a small difference between them, we can use the Fermat's attack to factorize the modulus. With this, we discover \(p\) and \(q\), and where it is then easy to crack RSA.
- CTF Generator: RSA with a different public exponent and the same modulus (N). CTF Generator: RSA with a different public exponent and the same modulus (N). This provides a CTF Generator for RSA with a different public exponent and the same modulus (N).
- CTF Solver: RSA with a different public exponent and the same modulus (N). CTF Solver: RSA with a different public exponent and the same modulus (N). This provides a CTF Solver for RSA with a different public exponent and the same modulus (N).
- CTF Generator: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In this case, we will use a low value of \(p\) to create the modulus, and where an intruder could search low prime numbers to find \(p\) and easily compute \(q\). Once these are discovered, it is then easy to crack the message.
- CTF Solver: RSA with a low factor in the modulus. CTF Solver: RSA with a low factor in the modulus. If the RSA modulus has a low prime factor, it is easy to crack the cipher. In this case, we will enter the cipher value and the modulus, and discover the low factor value (\(p\)), and then derive the other prime number (\(q\)). With this, we can compute \(\varphi=(p-1) \times (q-1)\), and thus discover \(d=e^{-1} \pmod \varphi\). Once discovered, we recover the message with \(M=c^d \pmod N\).
- CTF Generator: Cracking RSA with known partial bits. Cracking RSA with known partial bits. With RSA, it is possible to factorize the modulus if a few bits of one of the factors of a private key are revealed. Coppersmith outlined that \(n\)/4 of the most significant bits or the least significant bits were enough -and where \(n\) is the number of bits of one of the factors.
- CTF Generator: RSA Fault. RSA Fault in signature. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message. In this case we will introduce a fault into the generation of the signature elements, and then be able to recover \(p\) and \(q\).
Principles
- RSA. Simple RSA Calculation. This is a simple tutorial for RSA key generation.
- RSA. RSA Encryption. This uses RSA key generation and encryption.
- RSA encryption/decryption. RSA Encryption/Decryption (Python). This uses RSA encryption/decryption with Python.
- RSA Decrypt. RSA. This outlines RSA decryption.
- RSA in Python with varying prime number sizes. RSA with prime lengths. This generates keys for differing lengths of prime numbers.
- Ephemeral Diffie-Hellman with RSA (DHE-RSA). DHE. This outlines DHE.
- RSA. RSA. RSA using JavaScript
- RSA Principles in Golang. RSA Principles. The basics of RSA.
- RSA with Golang. RSA. RSA encryption with Go.
- RSA with Go (OAEP padding). RSA OSEP. RSA encryption with Go using OAEP.
- RSA with Go (PKCS1v15 padding). RSA PKCS1v15. RSA encryption with Go using PKCS1v15.
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature with PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA with Rust. RSA. RSA with Rust.
- Hazmat with RSA. Hazmat with RSA. RSA encryption using Python and with Hazmat.
- RSA using COSE and CBOR. Go.
- Key pair using Node.js. RSA. This generates key pairs for RSA, DSA, EC, ED25519, Ed448, X25519 and X448.
Using dQ, dP and InvQ
We can simplify RSA decryption using dP, dQ, qInv, and use CRT and Euler's Theorem:
- RSA: dQ, dP and InvQ. Go.
- RSA Key Generation in Golang: dQ, dP and InvQ. Go.
- RSA Decryption using dP, dQ, qInv: CRT and Euler's Theorem. Go. With RSA, we create two random prime numbers (\(p\) and \(q\)), and determine the modulus (\(N=pq\)). We encrypt a message with \(C=M^e \pmod{N}\) and decrypt with \(M=C^d \pmod{N}\), and where \((e,N)\) is the encryption key and \((d,N)\) is the decryption key. In order to perform the decrypt, we can apply CRT (Chinese Remainder Theory) to solve \(M=C^e \pmod{N}\). For this we need \( dP = e^{-1} \pmod {p-1}\), \( dQ = e^{-1} \pmod {q-1}\) and \(qInv= q^{-1} \pmod p\). Typically the private key is stored with \(p\), \(q\), \(dP\), \(dQ\), and \(qInv\), in order that we can use CRT and Euler's Theorem to decrypt a ciphered message.
- CBOR RSA: dQ, dP and InvQ. Go.
- RSA Keys (d, p, q, dQ, qP, invQ, e, N). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. With RSA, intially we start with two random prime numbers (\(p\) and \(q\) and then generate the modulus \(N=p.q\). From this we select the public exponent (\(e\) and then derivate the private exponent (\(d\)). For a message (\(M\) we create a cipher of \(C=M^e \pmod N\) and can then decipher with \(M=C^d \pmod N\). Overall, we have a private key which has the values of \(d, p, q, dQ, qP, invQ\), and a public key with (\(N, e\)).
RSA Key Pairs
- RSA key generation with Hazmat. RSA Key Gen. RSA key generation using Python and with Hazmat.
- PGP Encryption (Key Generation - RSA) with Node.js. PGP Keys. This uses PGP encryption with Node.js.
- RSA Keys (PEM, DER, PKCS1, PKCS8 and OpenSSH). RSA Keys. With RSA, we generate a private key and a public key. The public key can be used to encrypt data, and the private key to decrypt it. We can also sign data with the private key, and prove the signature with the public key. With our RSA key, there are a number of formats that can be used for the keys. For the private key, we can have a DER or a PEM encoding. With DER, we have binary encoding, and with PEM we have a Base64 encoding. With the private key format, we normally have a PKCS8 or OpenSSH format. For the public key format, we typically use either PKCS1 or OpenSSH format. PKCS1 (RFC 8017 [here]) is used for RSA public keys, and PKCS8 (RFC 5208 [here]) for RSA private keys. The OpenSSH format is used when OpenSSH is used. .
Padding
- RSA Optimal asymmetric encryption padding (RSA-OAEP). RSA OAEP. This uses RSA encryption and integrates a padding scheme. It was defined by Bellare and Rogaway, and has been standardized in PKCS#1 v2 and RFC 2437.
- RSA with PKCS1 OAEP padding. RSA. RSA with PKCS1 OAEP padding for 728-bit, 1,024-bit and 2,048-bit modulus.
- RSA Padding: PCKS#1v1.5. RSA PCKS#1v1.5. In RSA, we require to pad input data to the size of the modulus (\(N\)), and can use PCKS#1v1.5. This pads the input data with 0x00 and 0x02, followed by random data, and then by 0x00, and then by the bytes of the input message.
Signing
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Hazmat RSA signing. RSA signing with Hazmat. RSA signing using Python and with Hazmat.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- ECDHE with RSA. Go. This creates an ECDH key exchange, and uses RSA signatures to authenticate the passed values.
Blinded RSA Signatures
- Blinded Signatures with RSA. Blind signature with RSA. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote).
- RSA Blind Signature using Go (Cloudflare). RSA Blind Signature. A blind signature allows Bob to hide the content of a message before it is signed by a trusted entity (the signer). This is typically used when the creator of a message is different to the entity which signs it. For example, Bob may blind the message (such as his vote), and then for Trent to sign it as being valid, but where Trent will not know the contents of the message (or his vote). In this case we will use the CIRCL library from Cloudflare to implement a blind RSA signature for RSA-2048, RSA-3072 and RSA-4096.
RSA (Keys)
- Public Key (ASCII format). RSA Public Key. Often we have to convert the public key to an ASCII format.
- RSA (range of keys). RSA Encryption. This uses RSA key generation and encryption using a range of key sizes from 512-bits up to 16,384 bit.
- RSA (key pair generation). RSA Keypair. This uses generates an RSA keypair.
- RSA key formats (PEM, DER and OpenSSH). RSA key formats (PEM, DER and OpenSSH). RSA key formats using Python and with Hazmat.
- RSA and ECC keys. RSA and ECC keys. This page will generate either RSA and ECC key pairs, and which will display the main formats for these keys: PEM, Hex string and ANS1 format.
Montgomery Method
- Montgomery reduction algorithm. Montgomery. This performs multipication using Montgomery reduction algorithm.
- Multiply and Square algorithm. MSM. This performs exponent calculation.
- Calculating \(a^b \pmod N\) and \(a \times b \pmod N\) with using Montgomery Reduction in Python. Mont. Calculates \(a^b \pmod N\) and \(a \times b \pmod N\) using Montgomery reduction in Python.
RSA (Commutative)
- RSA with Commutative Keys. Comm. Commutative encryption allows Bob and Alice to encrypt in any order, and then they can decrypt in any order.
- Commutative Keys (with SRA - Shamir, Rivest and Aldeman). Comm. Commutative encryption examples.
- Real-life Commutative Keys with RSA. Comm. Uses an example with varing sizes of prime numbers.
Partial homomorphic
- RSA -partially homomorphic cryptosystem: Multiply. RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide. RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- RSA -partially homomorphic cryptosystem: Multiply (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for multiplication.
- RSA -partially homomorphic cryptosystem: Divide (real values). RSA. This outlines RSA as a partially homomorphic cryptosystem for integer divide (and using the extended euclidean method for the divide).
- Multiplying with RSA. Multiply. This outlines the multiplication of ciphers with RSA.
- (Un)Linkbable IDs with homomorphic encryption. CL-15. This outlines (un)linkage IDs using homomorphic encryption and RSA.
RSA Crack
- RSA with Weak Prime Numbers (RSALib). copper. Weak generation of prime numbers within RSA (using RSALib).
- RSA Crack in 12 lines of Python. RSA Crack in 12 lines. This is a simple RSA crack, in 12 lines of Python code.
- RSA Crack with weak keys. RSA Crack: e shares with PHI. This is a simple RSA crack when \(e\) shares a factor with PHI.
- Cracking RSA with Chinese Remainder Theory (with different primes). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem with varying prime numbers and an ASCII string.
- RSA - Bleichenbacher's attack. RSA. This outlines the RSA Bleichenbacher's attack.
- RSA - Bleichenbacher's attack for a range of modulus values. RSA. This outlines the RSA Bleichenbacher's attack for a range of modulus size.
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA - chosen cipher attack. RSA. This outlines of the cracking of RSA with a chosen cipher attack.
- RSA Crack (same message, different e). RSA. This outlines the usage of modified e value and the same message and N value.
- RSA Crack 2 (CRT). RSA. This outlines of the cracking of RSA with Chinese Remainder Theorem.
- RSA Crack 2. RSA. This outlines of the cracking of RSA when \(M^e\) is less than N.
- RSA Crack. RSA. This outlines the factorisation of the N value in the RSA method.
- RSA - Cracking the private key. Go.
- RSA - Fault Attacks . Go. In this case there is a fault in creating the RSA signature, and where the decryption key can be cracked from this.
Paranoid Crypto
These challenges are based on the Paranoid Cryptography library [3]:
- RSA Weakness: Fermat's Attack. Fermat's attack. Pierre de Fermat defined a factorization method which could factor prime number factors, if these prime numbers were close to each other. In RSA, we use a modulus (\(N\)) and which is the multiplication of two prime numbers (\(p\) and \(q\)). If these prime numbers are close to each other, then \(N\) can be factorized, and the RSA methods can be easily broken. In 2019, it was discovered that the Rambus cryptographic module was selecting a prime number, and then another which was close. These led to vulnerabilities in a number of printers which used Rambus module. In this case, we will use Fermat's method to factorize a modulus, and where the prime numbers are within \(2^{100}\) of each other. We will also try two random prime numbers, and see if we can factorize.
- RSA Weakness: ROCA (Return of the Coppersmith Attack). ROCA. With the ROCA (Return of the Coppersmith Attack) vulnerability an RSA private key can be recovered from the knowledge of the public key. It has the CVE identifier of CVE-2017-15361. The vulnerability is related to the Infineon RSA library on the Infineon Trusted Platform Module (TPM) firmware. It affected BitLocker with TPM 1.2 and YubiKey 4. In this case, we compute two prime numbers from \(Prime=k \times M + (65537^a \pmod M)\), and where \(k\) and \(a\) are generated randomly. These are then multiplied to produce an RSA modulus (\(N=p.q\)), and will then determine if the modulus is weak.
- RSA Weakness: RSA attack with continued fractions (Wieners attack). Wieners attack. In 1990, Michael Wiener defined a crack on RSA which involved a short decryption exponent and which used continued fractions [1]. For this, we can create a continued fraction for an RSA modulus and use a power of two. In 2013, Bernstein et al factored a number of RSA keys from a database of over two million keys used in the Tawainese Citizen Identity database. The research team found that many of the prime numbers found had a repetitive pattern [2].
- RSA Weakness: Powersmooth and Pollard's p − 1 algorithm. Pollard's p − 1 algorithm. RSA is used in many areas of cybersecurity, and is often key in proving the identity of a person or a remote Web site. But, the strength of RSA depends on the prime numbers (\(p\) and \(q\)) selected to provide the modulus (\(n=p.q\)). If there are weaknesses in the selection of \(p\) and \(q\), it may be possible to factorize the modulus and thus discover the private key. One method that can be used to discover whether we have weak prime numbers is the Pollard p-1 method. John Pollard, in 1974, defined a method of factorization which factorized values into their prime number roots. It finds these factors when the value of \(p-1\) is powersmooth. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value - apart from prime numbers - can be reduced to the multiplication of prime numbers. For example 102 is equal to \(2 \times 3 \times 17\). A value of 56 is \(2 \times 2 \times 2 \times 7\), and is thus 7-smooth, but not 3-smooth nor 5-smooth. With powersmooth, we say we are B-powersmooth, if all the prime number powers up to \(v\) are \(B \gt p^v\). For example, with 56, we have \(2^3 \times 7\), and thus it is 8-powersmooth (\(2^3\)).
Random
- RSA pseudorandom bit generator. RSA Rand. This method uses the RSA technique to generate a random bit stream.
Zero-knowledge
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
Secret shares
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.

Public Key (RSA) with Rust
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
RSA and Sage
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
Rust and Cryptography

The following outlines some Rust examples. Unlike Python, Java and Node.js, Rust compiles to a binary code and does not need a run time environment like .NET/C# and Java. For this, it has a “borrow checking” method and where a developer does not have to release used-up memory — the compiler does it. It thus avoids the C programming nightmare of memory overruns and underruns (and is memory safe) — no memory leakage. Along with this, it supports concurrent operations. Overall, Rust runs as fast as C, and faster in many applications. At the core of this, is the ability for the Rust compiler to code directly to native machine code, and thus optimize the operations. This leads to not having to worry about garbage collection, as we do with many other programming languages.

Symmetric Key (Stream)
Interested in learning more about symmetric key cryptography? Try [here].
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AES OFB in Rust. AES OFB. This involves coding for OFB in Rust.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
- ASCON AEAD (Rust). ASCON AEAD (Rust). The outlines the usage of AEAD for ASCON using Rust.
- ASCON with Rust. ASCON. This is an implementation of the ASCON hash using Rust.
- ASCON Hashing and XOF (eXtendable-Output Functions) with Rust. ASCON Hashing/XOF (Python). This implements a hashing and XOF for ASCON with Rust.
Symmetric Key (Block)
Interested in learning more about symmetric key cryptography? Try [here].
- Generate a random key with Rust. Key generation. This involves generating a 128-bit and a 256-bit random key in Rust.
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

FFX
- FFX. FFX. This is an implementation of FFX.
Public Key (RSA)
Interested in learning more about RSA? Try [here].
- Bare Bones with Rust. Bare Bones RSA. This is an implementation of RSA in Rust using bare bones code.
- RSA using BigInt's with Rust. RSA and BigInt's. RSA with Rust using Big Integers.
- RSA with Rust. RSA. RSA with Rust.
Public Key (Elliptic Curve)
Interested in learning more about elliptic curve cryptography? Try [here].
- Ed25519 signatures using the Ring crate. Ed25519. We can use Curve 25519 to sign messages with a private key, and then use the associated public key to verify the signature. In this case we will implement Ed25519 with Rust. With Ed25519 we use a private key to sign data, and then the public key can prove it.
- Ed25519 signatures using the Ed25519-Dalek crate. Ed25519. Ed25519 signatures with Rust and the Ed25519-Dalek library.
- ECDSA signatures using secp256k1. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using secp256k1 with Rust.
- ECDSA signatures using P256. ECDSA. ECDSA signatures can be used with curves such as sepc256k1 and P256. This code implements an ECDSA signature using P256 with Rust.
- Transform encryption with Rust. Transform. Transform encryption with Rust.
- Schnorr signatures with Rust. Schnorr. Schnorr signatures allow for a signature to be aggregated across multiple signers.
- Finding a point on Curve 25519 with Rust. Find point. Finding a point on Curve 25519 with Rust.
- Inverse function with Ed25519 using Rust. Find. Inverse of a scalar value with Ed25519 using Rust.
Key Exchange
Interested in learning more about key exchange? Try [here].
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
- Key exchange with P256. ECDH (P256). Key exchange with ECDH using P256 with Rust.
- Key exchange with secp256k1. ECDH (secp256k1). Key exchange with ECDH using secp256k1 with Rust.
Password-hashing functions
Interested in learning more about hashing? Try [here].
- HKDF HMAC-SHA256. HMAC-SHA256. HMAC-SHA256 with Rust.
- HKDF HMAC-SHA512. HMAC-SHA512. HMAC-SHA512 with Rust.
- Argon2. Argon 2. Argon 2 with Rust.
- PBKDF2. PBKDF2. PBKDF2 with Rust.
- BCrypt. BCrypt. BCrypt with Rust.
- Pwhash. Pwhash. Pwhash with Rust, including bcrypt, md5_crypt, sha1_crypt, sha256_crypt, sha512_crypt, bsdi_crypt, and unix_crypt.
Hashing and MAC
Interested in learning more about hashing? Try [here].
- Hashing with Rust. Hashing. Hashes with Rust.
- GHash. GHash. Using GHash in Rust.
- HMAC with Rust. HMAC. HMAC with Rust.
- Blake 3 in Rust. Hashing. Blake 3 hashing using Rust.
Zero-knowledge proofs
Interested in learning more about zero knowledge proofs? Try [here].
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
Crypto pairings
Interested in learning more about pairing-based cryptography? Try [here].
- 3-way secret share in Rust. 3-way share. 3-way handshake.
- Tripartite key sharing using Pairing in Rust. 3-way share. 3-way handshake using cryptography pairing.
- Crypto pairing with MIRACL in Rust. Pairing using MIRACL. Implementation of cryptography pairing using the MIRACL library.
- Encrypted search using crypto pairing with MIRACL in Rust. Encrypted search using MIRACL. Implementation of cryptography pairing using the MIRACL library for encrypted searching.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- Cracking Elliptic curves with the MOV Attack using Rust. MOV Attack. Using crypto pairs for elliptic curve cracking.
- Enhanced Identity-based (authenticated) key agreement with secrets using MIRACL. Enhanced IBE Secret Key. Bob and Alice end up with the same shared secret.
- Signcryption with MIRACL using Rust. Signcryption. Signcryption with MIRACL using Rust.
Principles
- Smooth numbers. Smooth numbers. Smooth numbers are used in cryptography to provide fast factorization methods. A smooth number is defined as a number whose factors are smaller than a given value. For a 5-smooth number, the factors must be equal to five or less. Every value, apart from prime numbers can be reduced to the multiplication of prime numbers.
- Password gen in Rust. Passwords. Using genpass in Rust.
- Integer Factorization in Rust. Integer factorization. All non-prime numbers can be represented as a multiplication of prime numbers.
- Galious Fields in GF(\(2^8\)) in Rust. Galious Fields. Implements GF(\(2^8\)) using an irreducible polynomial of \(x^8 + x^4 + x^3 + x + 1\) - as used with AES.
- Polynomials in Rust. Polynomials. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(p^n\))). For example GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomals (where the co-efficients of the polynomial factors either are either zero or one values. For example, a value of 10110 can be represented as \(x^4+x^2+x\). In this case we will add and multiply two polynomials.
Secret shares
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Ciphers
- Rail cipher in Rust. Rail. Rail cipher with Rust.
- Scytale with Rust. Scytale. Scytale cipher with Rust.
- Vigenère cipher with Rust. Vigenère. Vigenère cipher with Rust.
Post Quantum Key Exchange in Rust
- Supersingular Isogeny Diffie-Hellman (SIDH) with Rust. SIDH. This is an implementation of SIDH in Rust.
- McEliece Key Exchange in Rust. McEliece. McEliece is a post-quantum key exchange mechanism, and a finalist for the NIST PQC competition. This page uses various methods including mceliece348864, mceliece460896, mceliece6688128, mceliece6960119 and mceliece8192128. In McEliece methods, we have three main parameters: \(m\), \(n\) and \(t\). With mceliece348864, we have a Level 1 security level with a public key size of 261,120 bytes, a private key size of 6,492 bytes, and a cipher text size of 128 bytes.
Sage

Sage provides a level of abstraction of maths that sits on top of Python.
Elliptic Curve
Here are some examples:
- Sage and Elliptic Curves (NIST P-256 and secp256k1). Go. Our world of trust on the Internet is built on a foundation of elliptic curves. Two of the most important of these are NIST P-256 and secp256k1 (as used in Bitcoin, Ethereum and Tor. In this case, we will implement P-256 and secp256k1 using Sage.
- Sage and Elliptic Curve Point Operations (NIST P256). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the NIST defined P256 curve (as typically used in TLS).
- Sage and Elliptic Curve Point Operations (sepc256k1). Go. Elliptic curves have a base point (\(G\)) and then we perform either point additions, point doubling or point scaling operations. These are simple operations, and allow us to use fast computation of elliptic curve points. In this case we will use \(G+G\), \(2.G\) and double G operations, along with generating a random private key (\(n\)) and then computing the associated public key of \(n.G\). In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
ECDSA
Here are some examples:
- Sage and ECDSA (P256). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1). Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve.
Homomorphic Encryption
Here are some examples:
- Sage and Paillier. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
Public Key (RSA and ElGamal)
Here are some examples:
- Sage and RSA. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\).
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\).
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\).
Key Exchange
Here are some examples:
- Sage and Diffie-Hellman. Go. With the Diffie-Hellman method, Bob and Alice agree on a base generator (\g\)) and a large random prime number (\(n\)). Bob then generators a random value (\(b\)) which is between 0 and \(n-1\), and Alice does the same (\(a\)). Bob computes \(B=g^b \pmod n\) and Alice computes \(A=g^a \pmod n\). They exchange these values, and Bob generates the shared secret as \(K_b=A^b \pmod n\) and Alice generates with \(K_a=B^a \pmod n\).
Galois fields
Here are some examples:
- Galois fields. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value).
- Galois fields and modulus. Go. A finite field or Galois field (GF) has a finite number of elements, and has an order which is equal to a prime number (GF(p)) or to the power of a prime number (GF(\(2^p\))). For example, GF(\(2^n\)) has \(2^n\) elements, and its elements are known as binary polynomials (where the coefficients of the polynomial factors either are either zero or one value. In order to reduce a polynomial to a given size, we use a modulus polynomial, and which divides the output value. For GF(128), we can use a modulus of \(x^7 + x + 1\).
Examples with parameters
Here are some examples where we pass values into the Sage script:
- Sage and Elliptic Curves (secp256k1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and Elliptic Curves (NIST P256/secp256r1). Go. This will compute \(n.G\) for a given value of \(n\) and using the base point on the curve (\(G\)).
- Sage and ECDSA (P256) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the NIST defined P256 curve.
- Sage and ECDSA (secp256k1) with parameters. Go. ECDSA [1] is used in Bitcoin and Ethereum, and creates a signature (\(r,s\)) for a message (\(m\)). This involves creating a key pair. The private key is \(d\) and the public key is \(Q=d.G\), and where \(G\) is the base point on the curve. The private key is used to sign the message, and the public key will prove that the private key signed it. In this case we will use the secp256k1 curve (as used in Bitcoin and Ethereum).
- Sage and Paillier with parameters. Go. The Paillier cryptosystem is a partial homomorphic encryption (PHE) method, and here two encrypted values can be added together, and the decryption of the result gives the addition [2]. If we take two values: \(m_1\) and \(m_2\), we get two encrypted values of Enc(\(m_1\)) and Enc(\(m_2\)). We can then multiply the two cipher values to get Enc(\(m_1+m_2\)). We can then decrypt to get \(m_1+m_2\). Along with this we can also subtract to Enc(\(m_1-m_2\)). This is achieved by taking the inverse modulus of Enc(\(m_2\)) and multiplying it with Enc(\(m_1\)). Finally we can perform a scalar multiply to get Enc(\(m_1 \cdot m_2\)) and which is generated from Enc\((m_1)^{m_2}\).
- Sage and RSA with parameters. Go. With RSA, we create a public key (\(e,N\)) and a private key (\(d,N\)), and where the modulus (\(N\)) is generated from two random prime numbers (\(p\) and \(q\)). We encrypt a message (\(M\)) with \(C=M^e \pmod N\), and recover the message with \(m=C^d \pmod N\). In this case, we will use 256-bit prime numbers to produce a 512-bit public modulus.
- Sage and ElGamal. Go. With ElGamal encryption, Bob selects his public key by selecting a \(g\) value and a prime number (\(p\)) and then selecting a private key (\(x\)). He then computes \(Y\) which is: \(Y=g^x \pmod p\). His public key is \((Y, g, p)\) and he will send this to Alice. Alice then creates a message (\(M\)) and selects a random value (\(k\)). She then computes \(a\) and \(b\) so that \(a=g^k \pmod p\) and \(b=y^k M \pmod p\). Bob then receives these (\(a\) and \(b\)), and then uses his private key (\(x\)) to decrypt the values and discover the message: \(M=\frac{b}{a^x} \pmod p\). In this case, we will use a 128-bit prime number.
- Sage and Picking a Generator Value. Go. In a discrete log method, we use a generator (\(g\)), a prime number (\(p\) and a value \(x\), and determine \(Y=g^x \pmod p\). The generator value must be a primitive root of \(p\). In this case, we
Installing Sage
Sage is open source, and can be installed [here]:

References
[1] Johnson, D., Menezes, A., & Vanstone, S. (2001). The elliptic curve digital signature algorithm (ECDSA). International journal of information security, 1(1), 36–63 [here].
[2] Paillier, P. (1999, May). Public-key cryptosystems based on composite degree residuosity classes. In International conference on the theory and applications of cryptographic techniques (pp. 223-238). Springer, Berlin, Heidelberg [here].
secp256k1 Curve

If it wasn’t for Satoshi Nakamoto, you probably would never have heard of the secp256k1 Elliptic Curve Cryptography (ECC) method. But, Satoshi used it to take a private key and then produce a public key. At its core was the usage of the ECDSA (Elliptic Curve Digital Signature Algorithm), where it was possible to verify a transaction from the public Bitcoin identifier. It thus did not use PKI (Public Key Infrastructure) and it had all it needed to integrate trust into transactions. This is a Weierstrass form of elliptic curve, and uses:
\(y^2=x^3+7 \pmod p\)
It has a base point of g=(0x79be667ef9dcb … 959f2815b16f81798, 0x483ada77 … 8ffb10d4b8) and a prime number of \(2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1\). The order of the curve is \(n\)=0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141. Overall we have a private key of \(a\) and then produce a public key of \(aG\). We do this though point addition. For secp256k1, we have a 256-bit private key value, and a 512-bit public key value (and which is a point on the elliptic curve).
ECDH with secp256k1
- Elliptic Curve Diffie-Hellman (ECDH) with secp256k1 . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key.
- Elliptic Curve Diffie-Hellman (ECDH) with different curves . ECDH. Elliptic Curve Diffie Hellman is used to create a shared key using different curves, including secp256k1, p192 and p224.
- secp256k1 ECDH with Python. secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- Authenticated secp256k1 ECDH with Python. Authenticated secp256k1 ECDH. Elliptic Curve Diffie Hellman using secp256k1 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
- MTI/A0 - Elliptic Curve (secp256k1). MTI/A0 (EC). This outlines MTI/A0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((ab+xy)G\). MTI (Matsumoto, Takashima, Imai).
- MTI/B0 - Elliptic Curve (secp256k1). MTI/B0 (EC). This outlines MTI/B0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \((x+y)G\).
- MTI/C0 - Elliptic Curve (secp256k1). MTI/C0 (EC). This outlines MTI/C0, and which is a two-pass Diffie-Hellman key exchange method. It uses a one-time registration of keys, and then session key generation. We use elliptic curve methods, and the resultant key is \(xyG \)/
Point multiplication
- Real ECC curves for (1G, 2G and nG). Elliptic Curve real. Curve 25519, secp256k, and so on.
- Inverse of private key for secp256k1 with Python. Inverse of private key secp256k1 . In this example Alice sends \(aG\) and Bob sends back \(abG\). Alice then calculates \(a^{-1} \pmod n\) and can then determine \(a^{-1} a b G = bG\). The secp256k1 curve is in the Weierstrass curve form (\(y^2=x^3+ax+b\)).
Key generation
- Elliptic Curve (OpenSSL Key Generator). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC key, including secp128r1.
- Elliptic Curve (Keys). Elliptic Curve (Keys). Elliptic Curv is a public key method. This page outline the generation of ECC keys in Bitcoin.
- Elliptic Curve (Key pair). Elliptic Curve (Key pair). Elliptic Curv is a public key method. This page generates various ECC key sizes.
- 02, 03 or 04? So What Are Compressed and Uncompressed Public Keys?. Compressed and Uncompressed Public Keys. Compressing and uncompressing the public key in secp256k1.
ECDSA
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
Points on secp256k1
- Elliptic Curve points for common curves in an x-range. Elliptic Curve points. This examples uses Curve 25519, secp256k1, P256 and P512 to show the range of points for a given x-co-ordinate range.
- First 20 Elliptic Curve points in Finite Field for common curves. Elliptic Curve points. Locating the first 20 points in an elliptic curve in a finite field for curves including Curve25519 (Tor), secp256k1 (Bitcoin) and NIST P-256.
- First 20 Elliptic Curve points in Finite Field. Elliptic Curve points (plot). Locating the first 100 points in an elliptic curve in a finite field and using a simple Python program.
- Elliptic Curve Operations Within a Solidity Contract. Go.
Montgomery Ladder with secp256k1
- Montgomery Ladder in calculating \(kG\) in a fixed time.. Ladder. Calculates \(kG\) for secp256k1.
Charting
- Draw \(y^2=x^3+7 \pmod p\) Try.
Barebones secp256k1
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
-
Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
-
HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
-
Rabbit Encrypt
ion/Decryption
. Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- secp256k1 in Python. Barebones secp256k1. This page implements secp256k1 in pure Python.
Factoring based signatures
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
Verifiable Encryption
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
- ElGamal with ECC using secp256k1. ElGamal and ECC. This implements a public key encryption method using ECC and ElGamal methods and using the Kryptology library and the secp256k1 curve.
Secret Shares

The following outlines some secret share examples.
Shamir secret share
The following are the tips related to associated material:
- Shamir Secret Shares with Go. SSS. Creating Secret Shares.
- Shamir's Secret Sharing (creator). Shamir.
- Shamir's Secret Sharing (decrypt). Shamir.
- Shamir's Secret Sharing (Python). Secret shares.
- Shamir's Secret Sharing example (Python Numpy). Secret shares.
- Proactive Secret Sharing example (Python Numpy). Secret shares.
- Secret shares in Rust. Secret shares. Secret shares in Rust.
Shamir secret share theory
The following are the tips related to associated material:
- Shamir Secret Share with Lagrange interpretation constant. Lagrange interpretation constant. This computes a simple example of rebuilding Lagrange interpretation constants.
- Disenroll Parties with Shamir Secret Share and Lagrange interpretation constants. Disenroll Parties with Shamir Secret Share. This refreshes shares, and disenrolls one or more nodes from the secret share.
Chinese Remainder Theory and Blakley
The following are the tips related to associated material:
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Asmuth-Bloom threshold secret share scheme.
- Secret Shares With Chinese Remainder Theory (CRT). Secret shares (CRT). This example uses the Mignotte threshold secret sharing scheme.
- Secret Shares With Blakley method). Secret shares (Blakley). This example uses the Blakley threshold secret sharing scheme.
RSA and ECC
The following are the tips related to associated material:
- RSA Secret Shares with Python. RSA. Creating Secret Shares in RSA.
- ECC threshold encryption. ECC.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
BLS
The following are the tips related to associated material:
- (t,n)-threshold Boneh-Lynn-Shacham (BLS) signature scheme. TBLS. Create n shares and where we need to get t back to verify the signature.
Post quantum
- SIKE Secret Shares with Go. SIKE. Post-quantum key exchange with key encapulation.
Methods using Krytology
- Implementing SSS. SSS. With this we have a threshold of \(t\) from \(n\) shares.
- Implementing SSS (Theory). Shamir Secret Share Theory. With this we have a threshold of \(t\) from \(n\) shares and outline the core theory.
- Dealing SSS. Dealing out SSS. With this we have a threshold of \(t\) from \(n\) shares and will regenerate a random secret
- Pedersen Verifiable Secret Sharing Scheme using Kryptology. Pedersen VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Feldman Verifiable Secret Sharing Scheme using Kryptology. Feldman VSS. With this we have a threshold of \(t\) from \(n\) shares.
- Distributed key generation (DKG) using the FROST method in Kryptology. FROST DKG. Implementation of the FROST method.
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. e GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
Asynchronous Verifiable Secret Sharing
- Implementing AVSS. AVSS. With this we have a threshold of \(t\) from \(n\) shares and using AVSS as defined by Cachin et al.
Digital Signatures

This page contains signature related pages. A digital signature is normally created by encrypting something with a private key, and then proving the signature with the public key.
ECDSA
The following are the tips related to ECDSA:
- Deterministic ECDSA Signatures - k random and RFC6979. ECDSA methods. Using the RFC6979 mode to improve security and produce deterministic signatures.
- ECDSA Signing in 12 lines of Python. ECDSA Signing in 12 lines. This is an example of ECDSA signing, in 12 lines of Python code.
- Elliptic Curve Digital Signature Algorithm (ECDSA). ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data.
- Elliptic Curve Digital Signature Algorithm (ECDSA) with core operations. ECDSA. Elliptic Curve Digital Signature Algorithm (ECDSA) is used to sign data with core operations.
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Ed25519 with Go. ECC. This creates a signature for a message given a private and a public key.
- Secret shares with ECDSA. ECDSA Secret shares. Secret shares in ECDSA.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- ECDSA Creation. ECDSA Creation. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\).
- ECDSA Verification. ECDSA Verification. Elliptic Curve Digital Signature Algorithm (ECDSA) is used within Bitcoin and Ethereum. In this case we will use the \((x,y)\) point of Bob's public key, the \((R,S)\) value of the signature and the message (\(m\) and will check that the signature is valid.
- Recovering The Public Key From ECDSA. ECDSA Verification. With ECDSA we create a signature with a private key, and then prove with a public key. A special feature of ECDSA is that we can recover the public key from the signature. Overall we have a signature value of \((r,s,v)\) and can use these values to recover the public key. In this case we will create a random private key, and then derive the public key.
- Elliptic Curve Digital Signatures with Node.js (ECDSA). Signatures. With a digital signature, Bob signs a message with his private key, and then Alice verifies it with his public key. In this case we will use a range of elliptic curve methods and hashing methods in order to sign a message, and then verify it. One example is the secp256k1 curve and which is used in Bitcoin and Ethereum.
- RSA and ECDSA signatures in JavaScript. RSA and ECDSA signatures. This page will generate either RSA and ECC key pairs, and then use these to sign for a message. We will use SHA-1 and SHA-256 for the signatures, and which are implemented in RSA or ECDSA. The main signatures implemented are SHA-1 with RSA, SHA-256 with RSA, SHA-1 with ECDSA, and SHA-256 with ECDSA. Overall, a private key is used to sign for a message, and the public key will be used to verify the signature.
ECDSA Crack
The following are the tips related to ECDSA:
- Crack ECDSA from leak of nonce (NIST256p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST256p.
- Crack ECDSA from leak of nonce (SECP256k1). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for SECP256k1.
- Crack ECDSA from leak of nonce (NIST521p). ECDSA with nonce. This outlines ECDSA how the private key can be recovered with a leak of the nonce value for NIST521p.
- Crack ECDSA with weak nonces. ECDSA with weak nonces. This outlines ECDSA how the private key can be recovered with weak nonce values.
- Crack ECDSA with weak nonces (sepc256k1). ECDSA: Revealing the private key from same nonce. This outlines ECDSA how the private key can be recovered with weak nonce values.
- ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). ECDSA: Revealing the private key, from two keys and shared nonces (SECP256k1). This outlines ECDSA how we can reveal two private keys from four signed messages.
EdDSA
The following are the tips related to EdDSA:
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- EdDSA with node.js. EdDSA. EdDSA with node.js.
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Edwards-curve Digital Signature Algorithm (EdDSA) with core operations. EdDSA. Edwards-curve Digital Signature Algorithm (EdDSA) is used to sign data with core operations.
- Ed448 with Go. Ed448. Ed448 with Go.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA) using RFC 8032. EdDSA using RFC 8032. This page implements EdDSA using the code from RFC 8032.
- Ed25519 - Edwards-curve Digital Signature Algorithm (EdDSA). EdDSA. This page implements EdDSA.
- Testing Ed25519 . EdDSA. This page tests EdDSA with standard test vectors.
- Testing Ed448 and Ed25519 for EdDSA signatures. EdDSA: Ed448 and Ed25519. This page tests EdDSA with standard test vectors.
- Signing digital credentials with EdDSA. W3C signing. Digital signing of academic claims using an Ed25519 key pair.
- EdDSA and Ed25519 with Golang. EdDSA/Ed25519. Signing with Ed25519 using Golang.
- Ed25519 signatures with raw key values and Hazmat. Ed25519 signatures with raw key values. With Ed25519 we use a private key to sign data, and then the public key can prove it. We use Curve 25519 for the generation of the public key and for the signing process. Curve 25519 uses a Montgomery curve of the form of \(y^2 = x^3+a x^2+x \pmod p\). If we have a point \(P\), we then find a point \(nP\) - where \(n\) is the number of times we add \(P\)). Curve 25519 takes the form of \(y^2 = x^3+486662 x^2+x \pmod p\) and a base point at \(x=9\). This gives a base point (\(G\)), and where we find the point \(nG\) for a given \(n\) value, and where \(n\) is the private key value, and \(nG\) is the public key point. Normally in Curve 25519 we only focus on the x-point, and do not need the \((x,y)\) value.
RSA signatures
- RSA Signatures in Golang (PKCS1v15 padding). RSA signature with PKCS1v15. RSA signature with Go using PKCS1v15.
- RSA Signatures in Golang (PSS). RSA signature PSS. RSA signature with Go using PSS (Probabilistic signature scheme).
- RSA - blinding attack. RSA. This outlines the RSA blinding attack, which tricks a user to sign a message.
- RSA Signing in 12 lines of Python. RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- RSA Signing in 12 lines of Python (signed hash). RSA Sign in 12 lines. This is an example of RSA signing, in 12 lines of Python code.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- RSA Signatures using dP, dQ and qInv. Go. In this case we will compute the RSA signature of a message using \(S=M^e \pmod N\) and also with \(dP\), \(dQ\) and \(qInv\), and see which is the fastest.
- RSA signatures with Hazmat. RSA signatures wih Hazmat. This outlines the creation of RSA signatures with Hazmat.
DSA (Digital Signature Algorithm)
- DSA in PowerShell. DSA Signatures in PowerShell. With DSA (Digital Signature Algorithm) we use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes (512-bit, 1,024 bits and 2,048 bits), and a range of hashing methods (such as MD5, SHA-1 and SHA-256).
Threshold methods
The following are some examples of threshold signing:
- 2-of-2 threshold ECDSA signing algorithm of DKLS using Kryptology. 2-of-2 threshold ECDSA. The DKLS [Doerner, Kondi, Lee, and Shelat) method implements an ECDSA signing algorithm using threshold protocols. In this case, Bob and Alice will communicate using a DKG method, and then Bob will be able to create a valid signature. The secret key will be split into two shares, and Bob and Alice will use these shares to generate the digital signature and a public key. The signature generated will be defined as (\(R.S\)) and checked for its validity against the generated public key.
- 2-of-2 threshold ECDSA signing algorithm using GG20 with Kryptology. 2-of-2 threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. nce Bob and Alice have communicated, Bob will hold a signature for the message. We will then check this signature for its validity. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- t-of-n threshold ECDSA signing algorithm using GG20 with Kryptology. t-of-n threshold ECDSA. The GG20 (Gennaro, R., & Goldfeder, S. (2020)) method implements an ECDSA signing algorithm using threshold protocols. We will thus split a private key up into two secret shares and then will be able to sign with the shares of the key.
- Threshold EdDSA and Ed25519 with Golang. Threshold EdDSA/Ed25519. Signing with threshold Ed25519 using Golang.
X448
The following are the tips related to X448:
- X448 with Go. X448. X448 with Go.
Schnorr, BN and Bellare-Neven (BN)
The following are the tips related to Schnorr:
- Schnorr signature. Schnorr. This is an implementation in node.js.
- Schnorr signature with multiple public keys. Schnorr. This is an implementation in node.js for multiple public keys.
- Schnorr multi-signatures. Go.
- Schnorr with Go. Schnorr. Schnorr signatures with Go.
- Schnorr signature aggregation in Python with secp256k1. Schnorr. Schnorr aggregation of signatures with Python.
- Schnorr signature aggregation in Python with NIST P-256. Schnorr. Schnorr aggregation of signatures with Python.
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
- Schnorr Signature Method with Discrete Logs using PowerShell. Schnorr Signature Method with Discrete Logs using PowerShell. With Schnorr signatures can use discrete logarithms to produce a digital signature. Overall, we take a hash of a message, and then create a signature using a private (secret) key and a random nonce value (\(k\)). The public key and a hash of the message is then be used to verify the signature. In this case, we will create the signature using a range of key sizes, and a range of hashing methods (such as MD5, SHA-1 and SHA-256)
MuSig and Bellare-Neven (BN) Multi-signature
The following are the tips related to MuSig and BN:
- MuSig signature aggregation in Python with NIST P-256. MuSig. MuSig aggregation of signatures with Python.
- Bellare-Neven (BN) multi-signature aggregation in Python with NIST P-256. Bellare-Neven. BN aggregation of signatures with Python.
Redacted signatures
The following are the tips related to redacted signatures:
- Redacted signatures with Go. redacted signatures. Outlines how we can redact parts of a message for signing in Go.
- Redacted signatures with Go (Johnson-Merkle). Redacted signatures (Johnson-Merkle). Outlines how we can redact parts of a message for signing in Go using the Johnson-Merkle method.
Blockchain
The following are the tips related to ECC:
- Bitcoin signing. Bitcoin signing.
- Creating Ethereum signing with Python. Go.
Crypto Pair Signatures
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
- Camenisch-Lysyanskaya Signatures. CL. Example of Camenisch-Lysyanskaya Signatures.
- CL Signatures (advanced pairing). CL. CL Signatures in Go.
- CL Signatures. CL. CL Signatures in Go.
- BBS Signatures. BBS. Group signatures using BBS for short signatures.
- Signcryption with MIRACL. Signcryption. Signcryption with MIRACL.
- Group PS Signatures. Group PS. Group signatures using PS for the signing of multiple messages.
- PS Signatures. PS. Signatures using PS for short signatures.
- Randomized PS Signatures. PS. Signatures using PS for randomized short signatures.
ElGamal
- ElGamal Signing in 12 lines of Python. ElGamal Sign in 12 lines. This is an example of ElGamal signing, in 12 lines of Python code.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
Ring, group and blinded
- Collective signing (CoSi) algorithm. CoSi. This involves collective signing and witnessing.
- Linkable Ring signatures. Ring. This involves creating a linkage ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Ring signatures. Ring. This involves creating a ring signature, and where the signer gathers a number of public keys, and then adds their own private key, but no-one can tell who has signed the message.
- Undeniable signature. Undeniable. This implements the Chaum-van Antwepen method.
- Blinded signature. Blinded. This implements the Chaum method for blinded signatures, and where Bob can sign with his private key, without actually y seeing the message that he is signing.
- Fail-stop signature. Fail-stop. This implements the van Heijst-Pedersen method for fail-stop signatures, and can be used by Alice to prove the a valid signature from her, is actually a forgery.
- Borromean ring signature. Borromean. This page implements the Borromean ring signature.
Hash-based signature
- BLISS - Post-quantum signing. BLISS. BLISS method.
- HORS - Hash to Obtain Random Subset Signatures. HORS Signature. Outlines Hash to Obtain Random Subset (HORS) signatures.
- Lamport Signatures. Lamport. Outlines Lamport signatures.
- Merkle Signatures. Merkle Signature. Outlines Merkle signatures.
- SPHINCS. SPHINCS. Outlines SPHINCS.
- SPHINCS+ Tree. SPHINCS Tree. Outlines a SPHINCS tree.
- Winternitz Signatures. Winternitz. Outlines Winternitz signatures.
- BiBa (Go). BiBa. An overview of BiBa One Time Signature.
- BiBa (Python). BiBa. An overview of BiBa One Time Signature.
- Generalised Merkle Signature Scheme. GMSS. Outlines Generalised Merkle Signature Scheme.
- eXtended Merkle Signature Scheme (XMSS) with Go. Merkle Signature. Outlines eXtended Merkle Signature Scheme (XMSS) with Go.
NIST Finalists (Digital Signatures)
- CRYSTALS-Dilithium (Lattice) - Digital Signature. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice defined as a method where Alice can sign a message.
- CRYSTALS-Dilithium (Lattice) - Digital Signature - speed test. CRYSTALS Dilithium. Implementation of CRYSTALS Dilithium in C, and which uses Lattice and defined as a method where Alice can sign a message. This page proves a benchmark test.
- RAINBOW - Digital Signature - speed test. RAINBOW. Implementation of RAINBOW in C, and which uses the Oil-and-Vinegar method and defined as a method where Alice can sign a message.
- FALCON - Digital Signature. FALCON. Implementation of FALCON in C, and which uses Lattice and defined as a method where Alice can sign a message.
- SPHINCS+ - Digital Signature. SPHINCS+. Implementation of SPHINCS+ in C, and which uses a stateless hash-based signature method and defined as a method where Alice can sign a message.
- Picnic - Digital Signature. Picnic. Implementation of Picnic in C, and which uses Zero-knowledge proofs (ZKPs) as a signature method and defined as a method where Alice can sign a message.
- LowMC (Rounds). LowMC (Rounds). Determine number of rounds for LowMC and which is used in Picnic.
- LowMC. LowMC. Implementation of LowMC and which is used in Picnic.
- GeMSS. GeMSS. Implementation of GeMSS (Great Multivariate Short Signature) and which has short signatures and private keys, but a large public key.
BLS
- Boneh–Lynn–Shacham (BLS) signature. BLS. Example of BLS signature.
Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption).
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
Others
- Feige-Fiat-Shamir. Feirge. This implements the Feige-Fiat-Shamir method.
- Recovering a message from a signature. Recover. This message uses the ElGamal method to recover a message from a signature.
- ESIGN. ESIGN. The ESIGN (Efficient digital SIGNature) method involves the generation of two random prime numbers (\(p\) and \(q\)), and generates a value of \(n=p^2 q\). It was created by Fujioka et al [1], and is defined as a fast method of creating signatures, and where the difficulty relates to the factorization of integers.
- Offline/Online signature. Offline. This page uses an offline/online signature scheme, based on the paper: "An online/offline signature scheme based on the strong rsa assumption".
- Goldwasser, Micali and Rivest (GMR) one-time signature sheme. GMR. The GMR (Goldwasser, Micali and Rivest) one-time signature scheme uses a claw-free permutation. It is one-time only method can once Alice release her public key, she must show the private key, and which will show the mapping between the two. With a claw-free pair, we have a claw whhere \(g_0(x)=g_1(y)=z\), and where \(g_0\) and \(g_1\) are functions of \(x\) and \(y\), respectively.
Digital Certificate Format
- Distinguished Encoding Rules (DER) format. View. This defines the usage of DER.
- ASN.1: DER and PEM formats. View. This reads in either DER or PEM format, an then parses for ASN.1 information.
- ASN.1: DER for Digital Signatures - Reading (r,s). View. This page interprets ASN.1 DER format within Digital Signatures and thus discovers (r,s).
Digital Signaures with CIRCL
- Ed25519 and Ed448. Ed25519/Ed448. With digital signatures we take a hash of a message and sign it with a private key, and then use a public key to verify it. Two popular signatures use EdDSA and are Ed25519 and Ed488. Overall Ed25519 gives 128-bit security, while Ed448 gives 256-bit security. We can merge these with the Dilithium post quantum cryptography method. In this case we will use Ed25519, Ed488, Ed25519-Dilithium2 and Ed448-Dilithium3.
Post Quantum Digital Signaures with CIRCL
- CRYSTALS Dilithium. Dilithium. CRYSTALS Dilithium uses lattice-based Fiat-Shamir schemes, and produces one of the smallest signatures of all the post-quantum methods, and with relatively small public and private key sizes. The three main implementations for the parameters used are: Dilithium 2, Dilithium 3 and Dilithium 5. Overall, Dilithium 3 is equivalent to a 128-bit signature, and is perhaps the starting point for an implementation This page implements Dilithium 2, Dilithium 3 and Dilithium 5 using the Cloudflare CIRCL library.
Vaccine Passport
- Vaccine Passport (COVID-19) - Green Pass . Vaccine Passport. Implementation of Green Pass.
Stream Ciphers

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. Unfortunately block ciphers can be slow, as they require the processing of a block of data. In a stream cipher, we basically create a key stream which is then EX-ORed with the plaintext stream. To decrypt, we basically just do the same, and EX-OR the cipher stream with the key stream. With a block cipher we need padding, and there is no padding required for a stream cipher. Overall, stream ciphers are generally faster in their operation, and often require less processing.
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- HC256. HC256. HC-256 is a stream cipher that was created in 2004 by Hongjun Wu. It has a 256-bit key and a 256-bit nonce value. It focuses on bulk encryption in software at high speeds and also provides strong security levels. It has a performance level of around 1.93 bits/cycle.
GCM
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Light-weight crypto (Stream)
- Grain-128 AEAD. Grain-128. Grain-128 AEAD is a light-weight stream cipher. It is a (NIST Finalist).
- Enocoro. Enocoro. Enocoro is a light-weight stream cipher.
- Grain. Grain. Grain is a light-weight stream cipher.
- Mickey. Mickey. Mickey is a light-weight stream cipher.
- Rabbit Keystream Test. Rabbit keystream. Rabbit is a light-weight stream cipher.
- Rabbit Encrypt ion/Decryption . Rabbit encryption. Rabbit is a light-weight stream cipher.
- RC4 key generation. RC4. This illustrates how we generate the key.
- Trivium. Trivium. Trivium is a light-weight stream cipher.
Symmetric Key

With symmetric key, we use the same key to encrypt and to decrypt. The most popular symmetric key methods are AES and ChaCha20. In its pursest form, AES is a block cipher, with 128-bit block sizes. ChaCha20 is a stream cipher. With a block cipher we need padding, and there is no padding required for a stream cipher. The main modes that we get with symmetric key are ECB (Electronic Code Book), CBC (Cipher Block Chain), CTR (Counter) and GCM (Galois Counter Mode), and with either a 128-bit or a 256-bit encryption key. With symmetric key we can also use AEAD (Authenticated Encryption with Associated Data), and which allows additional data to be added into the cipher, and which can then be used to authenticate it. This additional data might relate to a session number.
Principles
- Block size. Block. A block cipher uses a block size of a given number of bits. DES has a 64-bit block size, and AES has a 128-bit block size.
- Padding in Go. Padding. Block ciphers have a defined block size, such as a 64-bit block size in DES, and a 128-bit block size for AES. As the data will not fill all the blocks, we need to pad before encryption, and then unpad after decryption.
- Padding (AES). Padding. This outlines how data is padded for AES.
- Padding (DES). Padding. This outlines how data is padded for DES.
- Padding (3DES) with Hazma. Padding. This outlines how data is padded for DES2.
- Padding (DES) with CBC. Padding. This outlines how data is padded for DES for CBC.
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
- Range of methods. OpenSSL. This includes the encryption of a wide range of methods.
- Hazmat Symmetric Key. Symmetric key. This includes the encryption of a wide range of methods implemented with Hazmat.
- Symmetric Key Details. Details. Details of symmetic key methods, including key size and IV.
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
-
Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
-
Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
-
Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
-
Producing OpenSSL AES Encrypted String from C# [here]
-
AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
-
Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
-
Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
-
Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
AES
- AES (Python) with OpenSSL format. AES. This implements AES using Python for CBC and with an OpenSSL output.
- AES (Python). AES. This implements AES using Python for a number of AES modes.
- AES GCM Mode (Python). AES GCM (Python). This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Python) with PBKDF2. AES GCM (Python) with PBKDF2. This implements AES using Python for GCM mode. GCM mode does not require padding and is a stream cipher. It also has integrated authentication.
- AES GCM Mode (Golang). AES GCM (Golang). This implements AES using Golang for GCM mode.
- AES. AES. AES (or Rijndael) is a new block cipher, and is the new replacement for DES, and uses 128-bit blocks with 128, 192 and 256-bit encryption keys. It was selected by NIST in 2001 (after a five-year standardisation process). The name Rijndael comes from its Belgium creators: Joan Daemen and Vincent Rijmen.
- C# AES and OpenSSL. Csharp for OpenSSL. This produces the same AES CBC output for C# as for OpenSSL.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- AES GCM, OFB and CBC (Golang). AES GCM, OFB and CBC (Golang). This implements AES using Golang for AES GCM, OFB and CBC .
- Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Hazmat Symmetric key modes: GCM, ChaCha20, CBC, CFB8, CFB, OFB, GCM, CTR, and XTS. Basically, we have give basic classications of modes: Mode With Initialization Vector: (ChaCha20, CBC, CFB8, CFB, and OFB); Mode With Initialization Vector and Tag (GCM); Mode With Nonce (CTR); Mode With Tweak (XTS); and Mode (ECB). CTR (Counter) mode uses a nonce, while ChaCha, GCM, CBC, CFB8, CFB, and OFB use an IV. The IV and Nonce values are 16 bytes long (128 bits) for AES. With XTS, we use a "tweak", and where we take an encryption key, and encrypt the sector number, and use this to X-OR the data within the sector. Overall, GCM and ChaCha20 are stream ciphers, where the others are block ciphers. The block ciphers thus require the padding of the data, so that all of the blocks are filled.
Symmetric key
- Symmetric Key Encryption [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex).
- Symmetric Key Decryption [here].In this case we will decrypt cipher text from OpenSSL using a key derived from a password
- Symmetric Key Encryption with PBKDF2 key derivation [here]. In this case we will create cipher text from OpenSSL using a key derived from a password, and a salt value (defined in hex). In this case we will use the PBKDF2 key derivation method.
- Symmetric Key Decryption with PBKDF2 key derivation [here]. In this case we will decrypt cipher text from OpenSSL using a key derived from a password
- Producing OpenSSL AES Encrypted String from C# [here]
- AES in Python with OpenSSL output [here]
DES, 3DES and Feistel ciphers
The following are the tips related to DES, 3DES and Feistel ciphers:
- 3DES (with clear text keys). 3DES. This example generates the 3DES key clear text keys.
- 3DES. 3DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key (of which only 56 bits are actively used in the encryption process). Unfortunately, DES has been around for a long time, and the 56-bit version is now easily crackable (in less than a day, on fairly modest equipment). An enhancement, and one which is still fairly compatible with DES, is the 3-DES algorithm. It has three phases and splits the key into two. Overall the key size is typically 112 bits (2x54 bits - with a combination of the three keys - of which two of the keys are typically the same). The algorithm is EncryptK3( DecryptK2( EncryptK1(message), where K1 and K3 are typically the same (to keep compatibility).
- DES (Python). DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key. This example shows some Python code.
- DES. DES. DES encryption algorithm is block cipher and uses a 64-bit block and a 64-bit encryption key.
- Feistel Ciphers. Feistel Ciphers. This provides an implementation of a Feistel Cipher.
- DES CBC or ECB Encryption with Powershell Encryption. DES (CBC/ECB). Using DES encryption with Powershell.
- 3DES CBC or ECB Encryption with Powershell Encryption. 3DES (CBC/ECB). Using 3DES encryption with Powershell.
RC2
The following are the tips related to RC2 encryption:
- RC2. RC2. RC2 ("Rivest Cipher") is a block cipher and is seen as a replacement for DES. It was created by Ron Rivest in 1987, and is a 64-bit block code and can have a key size from 40 bits to 128-bits (in increments of 8 bits). The 40-bit key version is seen as weak, as the encryption key is so small, but is favoured by governments for export purposes, as it can be easily cracked. In this case, the key is created from a Key and an IV (Initialisation Vector). The key has 12 characters (96 bits), and the IV has 8 characters (64 bits), which go to make the overall key.
- RC5. RC5. RC5 is a block cipher with variable key size, block size and rounds.
- RC6. RC6. RC6 is a block cipher with variable key size, block size and rounds.
- RC2 CBC or ECB Encryption with Powershell Encryption. RC2 (CBC/ECB). Using RC2 encryption with Powershell.
Block encryption methods
The following are the tips related to block encryption methods:
- Commutative encryption with Go. Comm. With commutative encryption we can encrypt and decrypt in any order.
- Pohlig-Hellman. Pohlig. This uses the Pohlig-Hellman algorithm.
- Red Pike. Red Pike. This provides an implementation of Red Pike.
- Serpent in Go. Serpent. Serpent symmetric key encryption method.
- Skipjack. Skip jack. Skipjack is a block cipher, using private-key encryption algorithm, and designed by NSA.
- GNU Privacy Guard (GPG) using Symmetric Key with Python. GNU Privacy Guard (GPG) using Symmetric Key with Python. The GNU Privacy Guard (GPG) is a program that is based on OpenPGP and can generation a keys pairs, encrypt and decrypt data, and digitally sign files and verify digital signatures. This page uses Version 2.4.0. It supports symmetric key ciphers of IDEA, 3DES, CAST5, BLOWFISH, AES, AES192, AES256, TWOFISH, CAMELLIA128, CAMELLIA192, and CAMELLIA256.
CAST
- Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat CAST5 Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. CAST5 (or CAST-128) was created by Carlisle Adams and Stafford Tavares in 1996. It defines a symmetric key method that has a 64-bit block size, and key sizes from 40 bits up to 128 bits (in jumps of 8 bits). Typically any key less than 80 bits would be seen as being insecure. It uses a 12- or 16-round Feistel cipher. The 16-round version is used for keys for 80 bits and above. It has been standardized in RFC2612.
Camellia
- Camellia. Camellia. Camillia is a block cipher created by Mitsubishi and NTT.
- Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Camellia Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Like AES, Camellia has a block size of 128 bits (16 bytes), and can use 128-, 192-, and 256-bit encryption keys. It was created by Mitsubishi and NTT and has been approved by the ISO/IEC. Camellia is also efficient for both hardware and software implementations, and is part of the TLS stack. Camellia is a Feisitel cipher and uses 18 rounds for 128-bit keys or 24 rounds for 192/256-bit keys. It also uses four 8x8 S-boxes. These s-boxes have a similar structure to the ones used by AES. This means that its performance can be enhanced by using the x86 AES-NI instruction set.
Blowfish
- Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB . Hazmat Blowfish Symmetric key modes: CBC, CFB8, CFB, OFB, and ECB. Bruce Schneier is a legend in Cybersecurity ... possibly one of the most influential people in the industry. He mainly writes books and lectures these days, but at one time he created symmetric key encryption methods. The most famous of these is the Blowfish method. Like DES and 3DES, it uses a 64-bit block size (8 bytes), but unlike DES, it is unpatented [1]. Overall it uses 16 Feistel-like iterations, and where the data input from the 64-bit block is split into two 32-bit words. An important strength of the method is that it can support key sizes up to 448 bits (56 bytes).
- Twofish. Twofish. Bruce Schneier created Twofish with a general-purpose private key block cipher encryption algorithm.
- All-or-nothing. AONT. The All-or-nothing created messages, of which all the messages are required to rebuild the original message.
- Blowfish (with CBC). Blowfishcbc. With CBC we split the message into blocks and encrypt each block. The input from the first stage is the IV (Initialisation Vector), and the input to the following stages is the output from the previous stage. In this example we will use Blowfish to encrypt, using CBC.
- Blowfish. Blowfish. Bruce Schneier created Blowfish with a general-purpose private key block cipher encryption algorithm.
SM4 Block cipher
- Hazmat SM4 Symmetric key . Hazmat SM4 Symmetric key. And, so, NIST has defined AES as the standard for symmetric key encryption. But, NIST were pin-pointed in possibly pushing a cipher with an NSA backdoor. For companies in China, the ShāngMì (SM) series of ciphers provides one alternative for TLS 1.3 integration and Wireless authentication. SM2 defines authentication, SM3 define a hashing function and SM4 for encryption. SM4 was developed by Lü Shuwang in 2007, and became a national standard (GB/T 32907–2016) in 2016. It has also been defined in RFC 8998. With the SM4 block cipher we have a block size of 128-bits, and with a 128-bit encryption key. Each block of data has 32 rounds of processing. Overall, we can add a salt value of 128 bits in an IV (Initialisation Vector).
Stream ciphers
- Affine. Affine. Affine is a stream cipher which uses an equation to encrypt.
- ARIA. ARIA. ARIA is a stream cipher and has a similar operation to AES but has two S-boxes.
- ChaCha20. ChaCha20. ChaCha is a stream cipher and is three-times faster than AES.
- ChaCha20 and Poly1305. ChaCha. ChaCha20 and Poly1305.
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- ChaCha20. ChaCha20. This involves creating the ChaCha20 key stream cipher.
- NaCl - Symmetric Key (XChaCha20 and Poly1805). XChaCha20. This involves creating the XChaCha20 key stream cipher using NaCl.
RC4 (Stream)
- RC4. RC4. RC4 is a stream cipher used in WEP (in wireless encryption).
- RC4 (repeating IV). RC4. This illustrates how we can EX-OR two values with the same IV value.
- RC4 key generation. RC4. This illustrates how we generate the key.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Salsa20. Salsa20. Salsa20 is a stream cipher and is three-times faster than AES.
- Hazmat RC4 Symmetric key . Hazmat RC4 Symmetric key . RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream. As we are using a stream cipher, there is no need for padding, and where the ciphertext stream size will be the same as the plaintext length.
Secret-key encryption methods (Hybrid)
The following are the tips related to encryption:
- IES (Integrated Encryption Scheme) - Discrete Logs. IES. This example generates a symmetric key using public key encryption. This method uses discrete logarithms.
- IES (Integrated Encryption Scheme)- Elliptic Curve. IES. This example generates a symmetric key using public key encryption. This method uses elliptic curves.
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Golang) AES GCM. Google Tink (Hybrid Encryption). This outlines AES GCM using Golang with Google Tink
- Elliptic Curve Integrated Encryption Scheme (ECIES with AES Encryption). Elliptic Curve (Encryption). Elliptic Curv is a public key method. This page outlines how we can use it to encrypt with AES.
- ECIES. ECIES. Create encryption with elliptic curve to generate a key pair and AES to encrypt.
- NHSX Contract Tracing with ECIES. NHSX. Create encryption with elliptic curve to generate a key pair and AES to encrypt
- Box using NaCl. Box. Using a Box method authenicated encryption using public key.
Encryption cracking (AES)
- AES Crack (Brute force). AES. This outlines of the cracking of AES with common passwords.
- AES Crack (Copy-and-paste). AES. This outlines of the cracking of AES with copy-and-paste attacks.
- AES Crack (Non-random numbers). AES. This outlines of the cracking of AES with non-random numbers.
- Differential Cryptanalysis (AES CBC). Cryptanalysis (AES CBC). This provides an implementation of differential cryptanalysis for the AES cipher within CBC mode.
- Differential Cryptanalysis (AES CFB). Cryptanalysis (AES CFB). This provides an implementation of differential cryptanalysis for the AES cipher within CFB mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES CTR). Cryptanalysis (AES CTR). This provides an implementation of differential cryptanalysis for the AES cipher within CTR mode (converts to a stream cipher, so no need for padding).
- Differential Cryptanalysis (AES ECB). Cryptanalysis (AES ECB). This provides an implementation of differential cryptanalysis for the AES cipher within ECB mode.
- Hazmat Symmetric Key - Bit-flipping Ciphertext. Symmetric key bitflipping. Some AES modes are vulnerable to bit flipping attacks. In this case, we will use AES CTR mode, and flip the bits of the 9th character in the ciphertext.
Mobile networks (crypto)
- A5/1. A5. This uses the A5/1 algorithm.
- A5/3 (Kasumi). Kasumi. This uses the A5/3 (Kasumi) algorithm.
- Snow. Snow. This uses the Snow stream cipher algorithm.
- Zuc. Zuc. This uses the Zuc stream cipher algorithm.
Disk encryption
The following are examples of disk encryption:
- XTS. XTS. This outlines XTS (XEX-based tweaked-codebook mode with ciphertext stealing).

Symmetric Key (Block) in Rust
- AES CBC. AES CBC. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CBC (Cipher Block Chaining) mode, and which uses a salt value define by the IV (Initialisation Vector) value.
- AES ECB. AES ECB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the ECB (Electronic Codebook) mode. Within ECB, we do not use a salt value, so that the IV (Initialisation Vector) value is ignored when we pass it. In this case we will use Rust to implement 128-bit AES with ECB mode.
- AES CFB. AES CFB. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the CFB (Cipher Feedback) mode. Within CFB, we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with CFB mode.
- AES IGE. AES IGE. Symmetric key encryption uses the same key to encrypt and decrypt. It is mainly a block cipher with a block size of 128 bits. In this case we will use the IGE (Infinite Garble Extension) mode. Within IGE [1], we use a salt value, so that the IV (Initialisation Vector) value is used in the encryption process. In this case we will use Rust to implement 128-bit AES with IGE mode. It has the advantage of propagating errors infinitely forward, so if the ciphertect is modified by just single bit will propagate errors for the rest of the ciphertext. This will show the ciphertext as being corrupted.

Symmetric Key (Stream) in Rust
- ChaCha20. ChaCha20. Chacha20 is a stream cipher which uses a 128-bit or 256-bit key and a 96-bit nonce.
- XChaCha20. XChaCha20. ChaCha20 was created by Daniel J. Bernstein, and has an eight byte or 16-byte nonce (96 bits). XChaCha20 (eXtended-nonce ChaCha) is an update to ChaCha20, and uses a 24-byte nonce (192 bits). It has a lower propability of nonce misuse than ChaCha20.
- ChaCha20/Poly1305. ChaCha20/Poly1305. The cipher text is made up of the cipher message (and which is the same length of the plaintext message) is the same number of bytes as the message (five bytes), and that the cipher text has an extra 16 bytes (used for AEAD - Authenticated Encryption with Associated Data). The MAC bytes uses Poly1305 and provides an integrity check for the cipher. An example of a tag is "e956cf49a523b46f7e9fbfe3fee398bd". We generate this when encrypting, and then use it with the authenication data to prove the decryption process.
- AES GCM. AES GCM. GCM (Galois Counter Mode) is an encryption method with authentication for symmetric key encryption. It is fast and allows for parallel processing. For this, we can use the wonderful AES GCM (Galois Counter Mode). And, another great advantage is that it has the option of adding additional data that is not encrypted but can be used to authenticate the cipher. For this, we might allow the additional data to be bound to a specific session ID or with a given time. When we read the cipher, we can check it against the additional data. This option is named AEAD (Authenticated Encryption with Additional Data).
- RC4. RC4. RC4 is a stream cipher that was created by Ron Rivest, and created in 1987. It is generally a fast cipher, and where we create a key stream based on a password. RC4 was used in WEP (Wired Equivalent Privacy), and where a small IV value caused serious security problems. The key length can vary from one to 256 bytes, and is used to create an initial 256-byte state vector (S). The output is basically X-OR'ed one bit at a time with the keystream, and the plaintext is recovered by X-OR'ing the cipherstream with the keystream.
- AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3 with Hazmat. AEAD: SIV, CCM, GCM, ChaCha20 and SOCB3. With enhanced encryption methods, we can both authenticate the cipher and prove its integrity. This is known as Authenticated Encryption with Associated Data (AEAD). For this we provide additional data to authenticate the encryption process, and where we can identify where the ciphertext has been modified, and for it not to be decrypted. In this case, we will investigate the main methods used to create AEAD: SIV (Synthetic Initialization Vector), CCM (counter with cipher block chaining message authentication code; counter with CBC-MAC), GCM (Galois/Counter Mode), ChaCha20 and SOCB3.

Symmetric key in Node.js
- ChaCha20 in node.js. ChaCha20. Implements ChaCha20 in node.js.
- RC4 in node.js. RC4. Implements RC4 in node.js.
- Symmetric encryption with node.js. Crypto. AES with node.js.
- Symmetric encryption (AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on) with node.js (all methods). Crypto. AES, ARIA, Blowfish, Camellia, ChaCha20, Cast, DES, and so on, with node.js.
- Symmetric Key Decryption Methods with PBKDF2 key derivation. Crypto. Symmetric Key Decryption Methods with PBKDF2 key derivation.
Google Tink
Google has released Tink and which is a multi-language, cross-platform cryptographic library. With OpenSSL we have complex bindings and which were often focused on specific systems, such as for DLLs in Windows systems. Tink is open-source and focuses on creating simple APIs and which should make the infrastructure more portable
Google Tink (Java)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (MAC). Google Tink (MAC). this outlines the integration of MACs into Google Tink
- Google Tink (Digital Signature). Google Tink (Digital Signature). This outlines the integration of digital signatures into Google Tink
- Google Tink (Hybrid Encryption). Google Tink (Hybrid Encryption). This outlines the integration of hybrid encryption into Google Tink
- Google Tink (Envelope Encryption). Google Tink (Envelope Encryption). This outlines the integration of envelope encryption into Google Tink
- Google Tink (HKDF). Google Tink (HKDF). This outlines the integration of HKDF into Google Tink
- Google Tink (AAD). Google Tink (AES-SIV). This outlines the integration of Deterministic Authenticated Encryption into Google Tink
- Google Tink (DTink AES with fixed hex key). Google Tink (Tink AES with fixed hex key). Deterministic Aead provides authenticity without the need for a a nonce or IV. The SIV (Synthetic Initialization Vector) mode calculates an IV based on the entire input. A single bit of change in the plaintext results in ciphertext that cannot be differentiated from other ciphertext. SIV is defined in RFC 5297.
Google Tink (Golang)
- Google Tink (Symmetric key - AEAD). Google Tink (AEAD). In this case we will use Tink with symmetric key encryption for the keys of 128-bit AES CTR with HMAC/SHA256, 128-bit GCM, 256-bit CTE HMAC/SHA256, 256-bit AES GCM, Chacha20, and XChaCha20.
- Google Tink (Golang) AES GCM. Google Tink (AES Encryption). This outlines AES GCM using Golang with Google Tink
- Google Tink with Go with fixed IV and Password Salt (AES GCM). Google Tink AES Encryption. This outlines AES GCM using Golang with Google Tink and uses a fixed IV and fixed salt for the password.
- Google Tink (Golang) MAC. Google Tink (MAC). This outlines MAC using Golang with Google Tink
- Google Tink (Golang) ECDSA. Google Tink (ECDSA Signature). This outlines ECDSA using Golang with Google Tink
- Google Tink (Golang) Ed25519 Signature. Google Tink (Ed25519 Signature). This outlines Ed25519 using Golang with Google Tink
- Google Tink (Golang) ECIES. Google Tink (Ed25519 Signature). This page uses ECIES (Hybrid Encryption) and where Alice sends Bob her public key, and Bob encrypts data for him. She then uses her private key to decrypt.
JWT tokens
- Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
- Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
Tokens

The following outlines some token based examples.
Fernet
- Fernet. Fernet. This outlines Fernet encryption
- Fernet with PBKDF2 key generation. Fernet (PBKDF2). This outlines Fernet encryption with PBKDF2 key generation
- Fernet with key rotation. Fernet (Key rotation). This outlines Fernet encryption with key rotation.
- Fernet (Auto key). Fernet. This outlines Fernet encryption
- Fernet (Decoding token). Fernet Decode. This outlines Fernet decoding of the token
- Fernet tokens with Hazmat. Fernet with Hazmat. This outlines Fernet encryption
JWT, JSON Web and HOTP/TOTP tokens
- JWT Tokens. JWT Tokens. JWT Tokens with node.js.
- JSON Web Signatures and JSON Web Tokens. Web Tokens. JSON Web Tokens with node.js.
- JWT with HMAC signatures in JavaScript. JWT with HMAC signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the HMAC method we just have to define a password to sign and verify the token.
- JWT with RSA/ECDSA signatures in JavaScript. JWT with RSA/ECDSA signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). With the ECDSA/RSA method we just have to define a private key sign the token and the public key to verify it.
- JWT with RSA-PSS signatures in JavaScript. JWT with RSA-PSS signatures. One of the most widely used methods in creating trusted tokens is JSON Web Tokens (JWT). For this we have three fields: header; payload; and signature. Overall the signature is used to sign for the data, and can either be with an HMAC method (with a shared secret) or with public key encryption (such as with RSA and ECDSA). Overall the RSA-PSS method is more secure in creating signatures.
- Google Tink (Golang) JWT (ECC Signing). Google Tink (Golang) JWT (ECC Signing). This page uses signs a JWT token with Elliptic Curve methods.
- Google Tink (Golang) JWT (HMAC Signing). Google Tink (Golang) JWT (HMAC Signing). This page uses signs a JWT token with HMAC methods.
One time passwords
- HOTP with Hazmat. HOTP with Hazmat. Generate a sequence of HOTP using Hazmat.
- HOTP with URI provisioning using Hazmat. HOTP with URI provisioning using Hazmat. Generate URI provisioning using Hazmat.
- TOTP with Hazmat. TOTP with Hazmat. Generate a sequence of TOTP using Hazmat.
ERC20 and ERC721 tokens
- ERC20 Tokens. Go.
- Creating ERC20 tokens on the Ethereum Test Network. Go.
- A Practical Guide in Creating an NFT (ERC-721). Go.
Tunnelling (SSL, TLS and IPSec)
This provides an outline of tunnelling, including for SSL/TLS and IPSec. For TLS 1.3, we have some information here.
SSL/TLS Connection
- SSL. SSL. This outlines the debug information returned from an SSL/TLS connection.
Network Traces
The following are some sample PCAP files (you will need to install Wireshark to view them):
- IPSec (PCAP file): here
- SSL (PCAP file): here
- Client Server Connection on Port 443 (See lab, Section E.1): here
- HTTPs (PCAP file): here
- ECDHE (PCAP file): here
- SFTP (PCAP file): here
- TOR (PCAP file): here
- Heartbleed (PCAP file): here
Outline content
- Presentation (PDF): here
- Presentation (Video): here
- Heartbleed Demo (Video): here
- Lab (PDF): here
- Lab (Video): here
TLS
- TLS protocols with OpenSSL. TLS protocols with OpenSSL. Initially, Bob and Alice determine the symmetric key that the data will be encrypted with. This is defined by the key exchange method (kex). The key that is then exchanged is then encrypted with a defined symmetric key (enc). The authentication of Alice to Bob is achieved from an authentication method (au) and each of the encrypted packets is then authenticated with a hashing method (mac).
Message Layer Security
- Message Layer Security (MLS). MLS. Messaging Layer Security (MLS) was initially proposed in 2016 and integrates end-to-end encrypting of messages. It has been defined by the IETF MLS working group, and integrates message confidentiality, message integrity and authentication, membership authentication, asynchronicity, forward secrecy, post-compromise security, and scalability. A final draft from the IETF for MLS was published on 29 Mar 2023 [here]. In this case, we will use PBKDF2 to generate an encryption key.
- Messaging Layer Security (MLS) with Signing in Go. MLS with signatures. Messaging Layer Security (MLS) integrates digital signing methods of ECDSA and Ed25519.
Articles
- The New Way To Create A Secure Tunnel ... The WireGuard Protocolhere
- Bufferbloat, The Blind Men and the Elephant (Coverage of the QUIC protocol)here
Presentation
Key Wrapping

The protection of encryption keys is important, and where they often have to be protected. This is especially important for symmetric keys and the private key of a public key pair. One standard for this is RFC 5649 [here], and which supports Advanced Encryption Standard (AES) Key Wrap algorithm [AES-KW1, AES-KW2]. We then use an AES key-encryption key (KEK) with a length of 128, 192, or 256 bits, and where we will get 64-bit blocks as an output. We can then encrypt data with a key (\(K_1\)) and which will then be wrapped to give WRAP(\(K_1\)). To decrypt, we then need the KEK to recover \(K_1\). The unwrapping process also checks the integrity of the key. One method is to perhaps use a production environment, and where the keys are stored and wrapped within a Cloud-based system. The KEK will then be protected from access, and used to produce the actual encryption key [article].
Key Wrap
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
-
Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme.
Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr
NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Key Wrap. Key Wrap. This wraps an encryption for so that it can be protected, and also checked for integrity.
- Key Wrap using a password. Key Wrap with a password. We can create a master key from a pasword, and then use this to protect an existing data encryption key. The master key will be derived from PBKDF2, as we would use with TrueCrypt.
- Key Wrap with Hamat (Symmetric key). Key Wrap with Hazmat (Symmetric). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (RSA). Key Wrap with Hazmat (RSA). Generate an encrypted key using Hazmat.
- Key Wrap with Hamat (EC). Key Wrap with Hazmat (EC). Generate an encrypted key using Hazmat.
X25519, X448 and FourQ

Elliptic Curve Diffie Hellman (ECDH) is used to create a shared key. In this we use the elliptic curve defined as Curve 25519 to generate points on the curve. Bob will generate a public key (\(B\)) and private key (\(b\)), as will Alice (\(A\) and \(a\)). They then exchange their public keys, and the shared key will then be \(a \times b \times G\), and where \(G\) is the generator point on the elliptic curve.

Elliptic Curve (ECDH) X25519 and X448 - Python
The following are the tips related to ECC:
- X25519 with Hazmat. X25519 with Hazmat. Generate a shared key with X25519 and using the Hazmat primitives.
- X448 with Hazmat. X448 with Hazmat. Generate a shared key with X448 and using the Hazmat primitives.
- X25519 ECDH with Python. X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- X448 ECDH with Python. X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\)).
- Authenticated X25519 ECDH with Python. Authenticated X25519 ECDH. Elliptic Curve Diffie Hellman using Curve 25519 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 25519 is in the Montgomery curve form (\(y^2 = x^3 + Ax^2 + x\))
- Authenticated X448 ECDH with Python. Authenticated X448 ECDH. Elliptic Curve Diffie Hellman using Curve 448 with Python, and where we use a long-term key for Bob and Alice to create a shared session keys. Curve 448 is in the Edwards curve form (\(x^2 + y^2 = 1 + dx^2y^2\))
Elliptic Curve (ECDH) - Golang
The following are the tips related to ECC:
- ECDH with Curve 25519 using Go. ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve 25519 using Go (Cloudflare). ECC. Curve 25519 is one of the most widely used elliptic curve methods, including with Tor, WhatsApp and Signal. This page uses the curve to implement ECDH.
- ECDH with Curve X448 using Go (Cloudflare). X448. Curve X448 has improved security over Curve 25519. This page uses the curve to implement ECDH.
- ECDH with FourQ using Go (Cloudflare). FourQ. FourQ is a curve developed by Microsoft Research, and has been evaluated as running at least three times faster than Curve 25519. It offers 128-bit security. This page uses the curve to implement ECDH.
Elliptic Curve (ECDH) - Rust
The following are the tips related to ECC:
- Curve 25519 and ECDH in Rust. Curve 25519. With this we have a base point (\(G)\)) and then take a secret key (\(n\)) and produce a public key of \(nG\). For key exchange for ECDH, Alice generates a secret of \(a\) and produces a public key of \(A=aG\). Bob generates a secret of \(b\) and produces a public key of \(B=bG\). The shared key is then \(shared_{alice}=aB\) and which is the same as \(shared_{bob}=bA\). In the following we use Rust to determine the public key values and the shared key.
Nacl
- X25519 + BLAKE2b key-exchange. Hybrid. In this case we will use X25519 and BLAKE2b to create a key-exchange method. For the keys of (alice_sk, alice_pk) and (bob_sk, bob_pk), we generate keys of: bob_rx, bob_tx = Blake512((bob_sk . alice_pk) || bob_pk || alice_pk) and alice_tx, alice_rx = Blake512(alice_sk . bob_pk) || bob_pk || alice_pk).
- Points on X25519. Hybrid. In elliptic curve we have a base point (\(G\)), and then take a scalar value of \(n\) to produce \(n.G\). Normally \(n\) is the private key value, and \(n.G\) is the public key point. In Ed25519 we only need one of the co-ordinate point values. In this case we will determine the y-axis point for the Ed25519 curve, and then compute the x-axis point. The generalised form of a twisted Edwards curve is \(x^2 = (y^2 - 1) / (d y^2 + 1) \pmod p \) and where \(p=2^{255}-19\).
X25519 and X448 with PQC
- Kyber, SIKE and Hybrid Key Exchange. Hybrid. Two popular PQC key exchange methods are SIKE and Kyber. In order to improve the performance of PQC key exchange, we can create a hybrid model and use X25519 and X488. In this case we will use Kyber512-X25519, Kyber768-X448 and Kyber1024-X448, and which uses X25519 and X448 key exchange methods. The key size for this change a little, and where Kyber512 produces an 800 byte public key, and with 832 bytes for Kyber512-X25519.
Zero knowledge proofs

A zero-knowledge proof allows for a proof of something without revealing the source data.
Zero-knowledge proof (Fiat Shamir)
- Fiat Shamir and ECC (Interactive ZKP). Fiat. Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interative ZKP). Fiat. Non-Interative Zero-knowledge proof with Fiat-Shamir.
- Fiat Shamir and ECC (Non-Interactive ZKP) - sepc256k1. Fiat Shamir (sepc256k1). Non-Interative Zero-knowledge proof with Fiat-Shamir using the sepc256k1 curve.
- Fiat Shamir and discrete logs (Non-Interactive ZKP). Fiat Shamir. Non-Interative Zero-knowledge proof with Fiat-Shamir using discrete logs.
- Zero-knowledge proof (discrete logs). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (Feige-Fiat-Shamir). ZKP. Outlines zero-knowledge proof using the Feige-Fiat-Shamir method.
- Zero-knowledge proof (Fiat-Shamir) with password. ZKP. Outlines zero-knowledge proof with a password hash and an inverse power.
- Zero-knowledge proof (Fiat-Shamir). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (non-interactive random oracle access). ZKP. Non-interactive random oracle access for the Fiat-Shamir heuristic.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using secp256k1.
- Factoring based Signature with Fiat Shamir (Elliptic Curve). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium using different elliptic curves.
- Factoring based Signature with Fiat Shamir (Discrete Logs). Factoring based. Implementation of factoring based signatures as used in CRYSTALS-Dilithium.
- Weak Fiat-Shamir in ZKPs (adaptive attack) - using discrete log. Weak Fiat-Shamir in ZKP. Many blockchain based systems have rushed to use the Fiat-Shamir transformation as a public-coin verifier. Within this, Alice will generate a random oracle, and then take a hash of the secret value and its public value, and create a zero knowledge proof of the knowledge of x. But, a new paper [1] shows that there are weak implementations of these, and identifies an adaptive attack.
Zero-knowledge proof (Chaum-Pedersen)
- NIZK proofs of discrete - log equality (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with Python for Chaum-Pedersen proof.
- NIZK proofs of discrete - log equality with Golang and Kryptology (Chaum-Pedersen proof). Log equality. Outlines zero-knowledge proof of log equality to prove that two public key values share the same private key with with Golang and Kryptology (Chaum-Pedersen proof).
- Proving your password with NIZK proofs of discrete-log equality (Chaum-Pedersen proof). Log equality (password). Outlines zero-knowledge proof of log equality to prove Peggy's password (Chaum-Pedersen proof).
- NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. NIZK (Non-interactive Zero Knowledge) proofs of discrete - log equality with PowerShell. Let's say we have two generator values (\(g\) and \(h\)), and a secret value (\(x\)). If we have \(Y=g^x \pmod p\) and \(Z=h^x \pmod p\), can we prove that \(Y\) and \(Z\) use the same exponential value (\(x\))? For this, we then use \(g,Y,h,Z\) within a Chaum-Pedersen proof [1] to provide a zero-knowledge proof that \(log_G(Y) == log_M(Z)\). This is defined as DLEQ(Z/M == Y/G) - discrete log equality. With this we can prove that the same private key has been used for \(g^x \pmod p\) and \(h^x \pmod p)\), and use a random oracle (\(k\)) for each proof.
- Zero-knowledge proofs of Discrete-Logarithm Equivalence (DLEQ). using CIRCL. Discrete Log Equivalence (DLEQ) using CIRCL. A non-interactive zero-knowledge proof (NI-ZKP) for discrete logarithm equivalence (DLEQ) creates VOPRF (Verifiable Oblivious Pseudorandom Function)and POPRF (partially-oblivious PRF). It shows that two group elements have the same discrete logarithm. We can use Non-interactive zero-knowledge (NIZK) proofs, and where Peggy (the 'Prover') just has to prove that she still knows her secret. For this Victor (the 'Verifier') can send Peggy a challenge, and where Peggy can prove that she can provide a solution for it. Peggy creates a secret value (\(x\)) and then we creates two values \(xG\) and \(xH\), and can check that \(log_{G}(xG) == log_{H}(xH)\). Peggy first creates her secret (\(x\)), and then calculates \(xG\) and \(xH\), and where \(G\) and \(H\) are two random points on an elliptic curve. The secret in this case is \(x\).
Zero-knowledge proof (Schnorr)
- Zero-knowledge proof (Schnorr). Schnorr. Outlines zero-knowledge proof with Schnorr identification scheme. Schnorr ZKP with Elliptic Curves. Schnorr ZKP with elliptic curves. With the Schnorr non-interactive zero-knowledge (NIZK) proof, we can prove knowledge of a discrete logarithm without leaking its value. For example, we can prove that we know \(g^r \pmod p\) without revealing \(r\). In this page we convert the Schnorr NIZK proof into an elliptic curve method.
Zero-knowledge proof (zkSnark)
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
- zkSnarks, Smart Contracts and Ethereum. Go.
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
Accumulators and Witnesses
- Accumulators. Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof.
- Witness and ZKP. Witness. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. We will then create a witness proof to show that a given data element is added within the accumulator.
- RSA Accumulators. RSA Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate RSA-based proofs of knowledge.
- ECC Accumulators with Golang. ECC Accumulator. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge.
- ECC Accumulators with Node.js. ECC Accumulator with JavaScript. An accumulator can be used for zero-knowledge proof of knowledge. In this case we will use the BLS curve and create an accumulator and data a proof onto it, and then remove the proof. In this case we will generate ECC-based proofs of knowledge using JavaScript.
Range proof
- Zero-knowledge Proof: Proving age with hash chains. Age. Proving someone's age, without revealing their age.
- Zero-knowledge proof (Damgard-Fujisaki method) for square. DF (Square). Peggy proves to Victor she knows the sqaure of the secret.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value. DF (positive Value). Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for positive value with ECC. DF (positive Value) with ECC. Peggy proves to Victor she has a positive value.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof. DF (range proof). Peggy proves to Victor she has a value in a given range.
- Zero-knowledge proof (Damgard-Fujisaki method) for range proof with ECC. DF (range proof). Peggy proves to Victor she has a value in a given range with ECC.
DLEQ: Discrete Log Equality (EQ)
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Golang. DLEQ. Create a non-interactive ZKP for discrete logs with Golang.
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python. DLEQ. Create a non-interactive ZKP for discrete logs with Python (and created for smart contract).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and with a range of curves. DLEQ. Create a non-interactive ZKP for discrete logs with Python and for a range of curves (and using SHA-256).
- DLEQ: Non-interactive zero-knowledge (NIZK) proofs for the equality (EQ) of discrete logarithms (DL) with Python and discrete logs. DLEQ. Create a non-interactive ZKP for discrete logs with Python with discrete logs.
- ZKPs with Decisional Diffie–Hellman (DDH) assumption (Chaum-Pedersen) . DLEQ. Chaum-Pedersen Zero Knowledge Proof using discrete logs.
- DLEQ: Non-interactive zero-knowledge (NIZK) using BN128 curve and Keccak. DLEQ. This page provides a Non-interactive zero-knowledge (NIZK) proof for the equality (EQ) of discrete logarithms (DL). For this, Peggy (the 'Prover') is able to prove that she still knows her secret (such as being the holder of a private key), without giving away its value. Peggy creates a secret value (\(x\)) and then registers two values of \(xG\) and \(xH\), and where \(G\) and \(H\) are two points on the BN128 curve. Victor can check that \(log_{G}(xG) == log_{H}(xH)\). For each proof, Peggy produces her own challenge (\(c\)) and a response (\(r\)) - these provide the proof of knowledge. Victor (the 'Verifier') can then prove this against the two public key values that she has already sent to Victor. In this case, we will use the BN128 curve, and use the Keccak256 hash for the challenge. The use of the BN128 curve and Keccak are well matched to an implementation within an Ethereum smart contract [1].
Zero-knowledge proof
- A Fair and Open Election. Election. Outline of a Fair and Open Election process.
- Chaum-Pedersen ZKP. Chaum. Chaum-Pedersen Zero Knowledge method.
- Diffie-Hellman with Zero-knowledge proof. Diffie. Example of ZKP with Diffie-Hellman key exchange.
- Dragonfly (used in WPA-3). Dragonfly. The Dragonfly protocol is used in WPA-3.
- Dragonfly (used in WPA-3). Dragonfly (ECC). The Dragonfly protocol is used in WPA-3 with ECC.
- Pedersen Commitment. Pedersen. The Pedersen Commitment.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Privacy-preserving Contact Tracing (COVID-19). COVID19. Using cryptography to preserve privacy in contact tracking with Bluetooth Advertisements.
- Privacy-preserving Contact Tracing (COVID-19) - Epione Protocol . Epione Protocol. Matching the number of contacts withe the Epione Protocol.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
- RAPPOR. RAPPOR. Outlines RAPPOR (Randomized Aggregatable Privacy-Preserving. Ordinal Response) which allows for privacy in gathered data.
- Voting with Paillier crypto system. ZKP. Outlines voting with Paillier crypto system.
- Zero-knowledge proof (GQ). GQ. Outlines zero-knowledge proof with Guillou-Quisquater (GQ) identification scheme.
- Zero-knowledge proof (Graphs). ZKP. Outlines zero-knowledge proof using graphing methods.
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- Schnorr proof for ZKP with Kryptology and Golang. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Schnorr proof for ZKP with Kryptology and Golang using proof of four strings. Schnorr proof for ZKP. This implements a range proof using a Schnorr proof
- Factorization Zero Knowledge Proof. Factorization proof. In RSA, we take two prime numbers (\(p\) and \(q\)) and then create a modulus (\(N\)). For this, can we create a proof that we know the values of \(p\) and \(q\), without revealing them?
- Paillier Square Free Proof and Kryptology. PSF. In Paillier we pick two large prime numbers (\(p\) and \(q\))). We then calculate a modulus (\(N=pq\)) and \(\phi(N)=(p-1)(q-1)\). We then make sure that \(gcd(pq,\phi(N))=1\). Overall Pallier can be used to create partial homomorphic encryption. In this case we will use a HVZK (Honest Verifier Zero Knowledge) method for Peggy to prove the Victor that she has generated a modulus which is secure (that is, it is square free).
Proof of Knowledge
- Proof of Knowledge. Knowledge. This involves proving predicates.
- Proof of Knowledge (Logical). Knowledge. This involves proving predicates.
- Zero-knowledge proof (Proof of Exponentiation using the Wesolowski’s Method) for range proof. Exponentiation. Peggy proves to Victor still knows \(x\) by proving proof of an exponentiation operation.
Millionaire Problem
- Millionaire's Problem . Mill. Yao's Millionaire Problem.
- Millionaire's Problem with real-life RSA . Mill2. Yao's Millionaire Problem within prime numbers of a given length for RSA.
- Socialist Millionaire Problem (SMP). SMP. We use zero-knowledge proof to show the Bob and Alice have the same value.
- Socialist Millionaire Problem (SMP) with ECC. SMP. We use zero-knowledge proof to show the Bob and Alice have the same value with ECC (secp256k1).
Oblivious transfer
- Oblivious transfer. OT. Oblivious transfer.
- EC-VOPRF (Elliptic Curve Verifiable Oblivious Pseudo-Random Function). EC-VOPRF. EC-VOPRF.
- Oblivious Transfer (OT) using crypto pairing using MIRACL. OT. Using OT.
- Privacy pass protocol using VOPRF (Verifiable Oblivious Pseudo-Random Function). Privacy pass. The Privacy pass protocol was developed by Cloudflare and is a realization of 'Verifiable, Oblivious Pseudorandom Function' (VOPRF).
- Oblivious Transfer. Oblivious Transfer 1-to-N. With this Alice will generate a range of encrytion keys, and where Bob will only be able to generate one of them.
Bulletproofs
- Bulletproofs and Rangeproofs (Go). Bulletproof. Golang implementation of Bulletproofs.
- Bulletproofs and Rangeproofs (Node.js). Bulletproof. Node.js implementation of Bulletproofs.
- Bulletproof in Rust. Bulletproof. Bulletproofs with Rust.
- Bulletproofs with Kryptology. Bulletproofs. This implements a range proof.
Secure Function Evaluation/MPC
- Scrambled circuits. Scrambled. Scrambled circuits - SFE.
- Fair coin flip. ZKP. Outlines how a fair coin flip can be created, without a trusted verifier.
- SFE. SFE. SFE can be used to verify a value, without releasing the original data. For example, if we have a voting competition with Bob, Alice, and Carol. Bob, Alice and Carol vote, and they want to keep their votes secret, but they need to calculate the overall total. Typically an independent person would tally up the votes, but what if they do not trust anyone. This is where SFE comes in, where they can calculate the total with knowing the votes from the others.
- MPC with Shamir Share. MPC. We can setup an infrastructure with \(n\) nodes and compute a result where at least \(t\) are honest nodes.
Verified Encryption
- Camenisch-Shoup Verifiable encryption using Kryptology. Camenisch-Shoup. Jan Camenisch and Victor Shoup reated a discrete logarithm method which implements verifiable encryption. With this, Bob can prove to Alice that he has used a given encryption key with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will encrypt an integer value, and then create a valid proof of the encryption key used, and then generate another encryption key which will fail the proof.
- ElGamal Verifiable encryption using Kryptology. ElGamal. With verifiable encryption, Bob can prove to Alice that he has used a given encryption key of a ciphertext with a NIZK (Non-interactive Zero Knowledge Proof). In this case we will use ElGamal encryption and generate a proof of the public key which has been used for the encryption. If Bob uses Trent's public key to encrypt some ciphertext for Alice, then Bob can produce a proof that it has been encrypted with Trent's public key. Alice will then be able to check this against Trent's public key. In this case, we will use the secp256k1 elliptic curve, and use AEAD encryption to perform the actual encryption on the message.
Verifiable Random Function
- Verifiable Random Function. Verifiable Random Function. A Verifiable Random Function (VRF) allows the owner of a private key the ability to create a hashed value of data, while anyone with the associated public key can prove the validity of the hash. Thus the onwer of the private key can produce \(H(x\) from \(H(x)=f_{priv}(x)\), while someone with the public key can prove that \(H(x)\) is the hash of \(x\). This is similar to the approach of keyed cryptography hashes, but uses public key encryption for the key operation.
Proof of shuffle
- Proof of shuffle. Proof of shuffle. A This provides a proof that values have been properly shuffled.
zkSnarks

With a zkSnark — a non-interactive adaptive argument of knowledge — we provide a short proof from a Prover to one or more verifiers that we have specific knowledge of some private data and of a function (f). The proof is fast to prove. So, let me take you through the steps taken to create a zero-knowledge proof with zkSnarks.
zkSnark Examples
- Creating zkSnarks circuits and verifiying zkSnarks. ZKP. Outlines creating circuits
- zkSnarks: Proving you know the answer of \(x^2+x+5=11\). ZKP. Proving you know the answer of \(x^2+x+5=11\) using zkSnarks
- zkSNARKs in Go (gsnark). zkSNARKs. Implementation of zkSNARKs in Go with gsnark.
zkSnark Smart Contracts
- zkSnarks, Smart Contracts and Ethereum. Go.
skSnark with MIRACL
- Zero Knowledge Proof using crypto pairing using MIRACL (zk-SNARK). ZKP. Using crypto pairs for ZKP.
zkSnark Theory
- Zero-knowledge proof (zkSnark - Blind evaluation problem). ZKP. Outlines zero-knowledge proof.
- Zero-knowledge proof (zkSnark - Hidden Homomorphic). ZKP. Outlines zero-knowledge proof.
- zkSNARKs in Go. zkSNARKs. Implementation of zkSNARKs.
- QAP in zkSNARKs using Go. QAP. Implementation of zkSNARKs QAP.
- R1CS (Rank 1 Constraint System) in Go. R1CS. Implementation of the method used with zk-SNARKs for zero-knowledge proofs.
 [
[
 [
[ [
[ [
[ [
[ [
[ [
[ [
[ [
[ [
[ [
[ [
[ [
[ [
[ [
[ [
[ [
[ [
[ [
[ [
[ [
[ [
[ [
[ [
[ [
[